SCATTERING OF ELECTROMAGNETIC WAVE BY OFFSET
SPHERICAL PARTICLES
Felix O. Ngobigha and David H. O. Bebbington
School of Computer Science and Electronic Engineering, University of Essex,
Wivenhoe Park, Colchester CO4 3SQ, United Kingdom
Keywords: Offset spherical particle, T-matrix method, electromagnetic waves scattering.
Abstract: The Lorentz–Mie theory is applicable to calculating scattering characteristics of spherical shaped particles.
It is often applied to slightly non-spherical particles where its range of validity is uncertain. This paper
defines the range of validity of the T-matrix technique of Barber and Hill as applied to homogeneous
spherical and non-spherical particles. Scattering calculations are made for a set of non-absorbing
homogeneous spherical particles with the origin of the particle offset over a certain range. The numerical
results show that even for small offset value with the same input parameters, the phase function, extinction
and scattering cross sections differ quite significantly compared to the generalized Lorentz–Mie technique
known to give accurate scattering characteristics for spherical particle.
1 INTRODUCTION
The scattering of electromagnetic waves by
spherical object is a problem that has received
increased attention in past and recent years.
Knowledge of the scattered field is required in many
areas of science and engineering applications. The
idea was first developed by Gustav Mie in 1908 in
order to understand the colours that resulted from
light scattering of gold particles suspended in water.
Applications of Mie solution has been extended
from one end of the electromagnetic spectrum to the
other, from Ultraviolent solar radiation
backscattered by stratospheric aerosols to satellites,
through visible and Infrared radiation scattered by
clouds and aerosols, to microwaves and radar
scattered from large hydrometeors. An excellent
introduction to the theory is reported in (Kerker
1969; van de Hulst 1981; Mishchenko, Travis et al.
2002; Bohren and Huffman 2008). Although, the
Mie-theory it is exact, but with the emergence of
computing it has become practical to calculate
various scattering characteristics (Wiscombe 1980).
The Mie-theory has limitation of being restricted to
spherical particles. However, it has served as a
reference for validation of other techniques for
evaluating scattering properties from scatterers, and
implementation of this theory with slightly non-
spherical particles has yielded similar results.
This paper deals with the range of validity of T-
matrix method reported in (Barber and Hill 1990) as
applied to a lossless dielectric spherical particle with
the origin moved of centre over a certain range. Our
aim is show the uncertainty with reference to
particle shape when calculating scattering cross
sections in which the origin is displaced from the
centre of the spherical object as previously reported
(Waterman 1965; Barber and Yeh 1975; Barber and
Hill 1990) by adopting and implementing the code
in (Barber and Hill 1990) and not the theoretical
analysis as numerous papers have already addressed
this aspect. Nevertheless, the results in the cited
references differ with ours. Clearly, the final results
given in this paper are not new. Rather, our
contribution is based on offset range validity at
various frequency bands with the goal of providing a
consistent result regardless of the mathematics that
led to their derivation.
135
O. Ngobigha F. and H. O. Bebbington D.
SCATTERING OF ELECTROMAGNETIC WAVE BY OFFSET SPHERICAL PARTICLES.
DOI: 10.5220/0004786301350139
In Proceedings of the Second International Conference on Telecommunications and Remote Sensing (ICTRS 2013), pages 135-139
ISBN: 978-989-8565-57-0
Copyright
c
 2013 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
The approach adopted in this paper was originally
introduced by P C Waterman (Waterman 1965) as a
technique for computing electromagnetic scattering
by a smooth, perfectly conducting, homogeneous,
arbitrarily shaped particle illuminated by an incident
plane electromagnetic wave. This technique is also
known as null field method (Zheng 1988) or
extended boundary condition method (EBCM)
(Barber and Wang 1978), and is developed further
by (Barber and Yeh 1975), (Mishchenko and Travis
1994; Mishchenko, Travis et al. 1996; Mishchenko
and Travis 1998; Mishchenko, Hovenier et al. 1999).
The technique has also gained wide acceptance in
the field of electromagnetic waves scattering due to
its capability to calculate the scattering properties of
arbitrarily shaped scatterers. The approach of the T-
matrix formulation utilizes vector spherical
harmonic function expansions of the incident and
scattered fields in conjunction with boundary
conditions at the surface of the scattering particles to
obtain a system of linear equations relating the
unknown expansion coefficients of the scattered
field to the known coefficients of the incident field.
The most attractive feature of T-matrix technique
starts as Lorenz-Mie theory when the scattering
particle is homogeneous or layered sphere composed
of isotropic materials.
Given a specific scattering object, first step is to
select an internal origin on the scattering particle and
surround the object with imaginary sphere of radius
large enough to circumscribe the scatterer
(Barber and Hill 1990; Mishchenko, Travis et al.
2002), and numerically perform the surface
integrations over the scatterer which are required to
fill the coefficient matrix. The next step is to carry
out matrix operation to obtain the scattered field
coefficients
and . The final step then is to
substitute the scattered field coefficients into (1) to
yeild the scttered field and other desire
characteristics.
()
() ()
0
1
s
Ekr
E D f M kr g N kr
λλ
ννν νν
ν
∞
=
=
⎡⎤
×+
⎣⎦
∑
(1)
where M and N are the vector spherical harmonic
functions and the superscript 3 on
and
indicates that these functions are of the type suitable
for radiation or outgoing fields (Hankel function),
represents the spherical harmonic triple index
(even or odd), m, n. The argument of the vector
spherical wave functions
, where
denotes wave number in the surrounding medium,
is the incident wavelength, and is the position
vector which defines a point in three-dimensional
space. The
is the amplitude of the incident
electric field, and
denotes normalization
constant.
The important formulas for Mie scattering are
well defined (Kerker 1969). The quantities required
at this level are summarized. The amplitude matrix
for spherical object is a diagonal matrix; due to
symmetry it takes the form:
0
0
s
i
ikr
hh
s
s
i
vv
S
E
E
e
E
S
E
E
r
⊥⊥
⎛⎞ ⎛⎞
⎛⎞
==
⎜⎟ ⎜⎟
⎜⎟
⎜⎟ ⎜⎟
⎝⎠
⎝⎠ ⎝⎠
&&
(2)
where
(
)
()
() ()
1
21
cos cos
1
vv
n
nn nn
n
S
ab
nn
π
θτ θ
∞
=
Θ=
+
⎡
⎤
=+
⎣
⎦
+
∑
(3)
(
)
()
() ()
1
21
cos cos
1
hh
n
nn nn
n
S
ba
nn
π
θτ θ
∞
=
Θ=
+
⎡
⎤
=+
⎣
⎦
+
∑
(4)
which are respectively, scattered electric field and
complex scattering amplitude for the two orthogonal
directions of incident polarization.
and
are the scattered intensities, and are
the angular function,
and are Mie expansion
coefficients in terms of the vector spherical
harmonic, depend on the size parameter and on the
complex refractive index. They are also expressed in
terms of spherical Bessel functions.
3 SIMULATION RESULTS
An incident plane polarized wave propagating in the
direction is assumed, with the origin of the
scatterer coincides with the spherical coordinate
system for the calculation of differential scattering
Second International Conference on Telecommunications and Remote Sensing
136

cross section of spherical, and slightly non-spherical
particles. Some of the input parameters such as size
parameter
and refractive index
(
)
are chosen to compare results (van de Hulst 1981).
For a sphere,
is the radius of the scattering object
but for non-spherical particles (oblate or prolate
spheroid), the choice of
gives users the option of
defining
as the radius of a sphere of either equal
volume, or equal surface area to that of the
scattering object while for offset spherical particle, it
is the distance from the origin of the spherical
coordinate system to the surface of offset spherical
scatterer calculated by applying Pythagoras or
Cosine rule.
Numerical illustrations confirm that the results
for spherical bodies are identical at different
frequencies compared to those obtained by the Mie
theory. The check was extended to slightly non-
spherical particles (oblate and prolate spheroids); a
similar agreement is generally observed for both
particles. The vertical and horizontal polarizations
are denoted
and respectively.
0 20 40 60 80 100 120 140 160 180
10
-4
10
-3
10
-2
10
-1
scatterin
g
An
g
le, de
g
rees
Differential Scattering cross section
VV(Mie)
HH(Mie)
VV(T-matrix)
HH(T-matrix)
Figure 1: Comparison of Mie-theory and T-Matrix method
for differential scattering cross sections of non-absorbing
spherical and offset spherical particles at 220 GHz.
0 20 40 60 80 100 120 140 160 180
10
-3
10
-2
10
-1
scatterin
g
An
g
le
,
de
g
rees
Differential Scattering cross section
VV(Mie)
HH(Mie)
VV(T-matrix)
HH(T-matrix)
Figure 2: Comparison of Mie-theory and T-Matrix method
for differential scattering cross sections of non-absorbing
oblate spheroid at 94 GHz.
0 20 40 60 80 100 120 140 160 180
10
-3
10
-2
10
-1
scatterin
g
An
g
le, de
g
rees
Differential Scattering cross section
VV(Mie)
HH(Mie)
VV(T-matrix)
HH(T-matrix)
Figure 3: Comparison of Mie-theory and T-Matrix method
for differential scattering cross sections of non-absorbing
prolate spheroid at 94 GHz.
0 20 40 60 80 100 120 140 160 180
10
-3
10
-2
10
-1
scattering Angle, degrees
Differential Scattering cross section
offset VV=0.0
offset VV=0.006
offset VV=0.013
offset VV=0.025
offset VV=0.051
Figure 4: Comparison of Mie-theory and T-Matrix method
for non-absorbing spherical and offset spherical particles
at 94 GHz.
Scattering of Electromagnetic Wave by Offset Spherical Particles
137

0 20 40 60 80 100 120 140 160 180
10
-1.7
10
-1.6
10
-1.5
scattering Angle, degrees
Differential Scattering cross section
offset HH=0.0
offset HH=0.006
offset HH=0.013
offset HH=0.025
offset HH=0.051
Figure 5: Comparison of Mie-theory and T-Matrix method
non-absorbing spherical and offset spherical particles at 94
GHz.
0 20 40 60 80 100 120 140 160 180
10
-2
10
-1
10
0
10
1
scattering Angle, degrees
Differential Scattering cross section
offset VV=0.0
offset VV=0.102
offset VV=0.204
offset VV=0.408
offset VV=0.816
Figure 6: Comparison of Mie-theory and T-Matrix method
for non-absorbing spherical and offset spherical particles
at 5.8 GHz.
0 20 40 60 80 100 120 140 160 180
10
0
scattering Angle, degrees
Differential Scattering cross section
offset HH=0.0
offset HH=0.102
offset HH=0.204
offset HH=0.408
offset HH=0.816
Figure 6: Comparison of Mie-theory and T-Matrix method
for non-absorbing spherical and offset spherical particles
at 5.8 GHz.
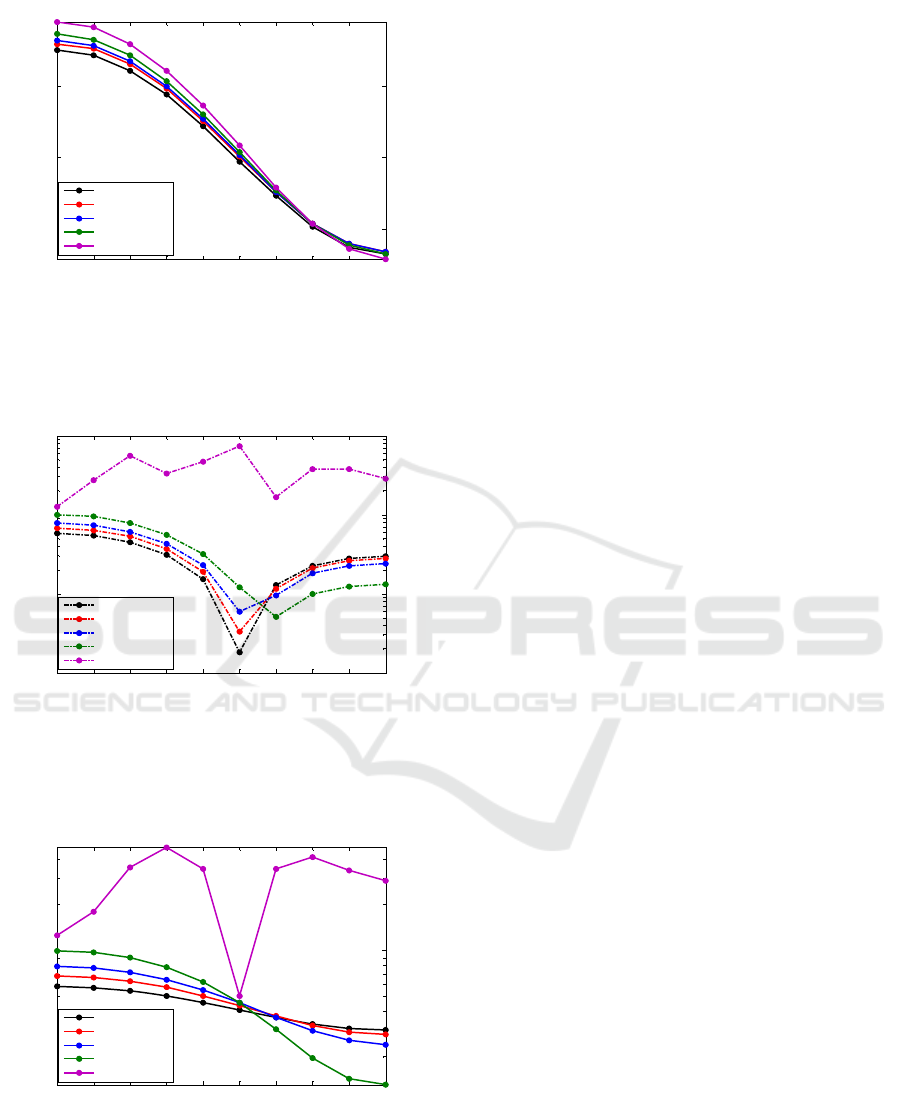
It is evident from Figure 1 that our results for
both approach show good agreement with (Barber
and Yeh 1975; Barber and Hill 1990) and
(Waterman 1965) regardsless of the scatterer (i.e.
spherical or offset spherical particles) at 220 GHz.
This is also observed in Figure 2 and 3 comparing
Mie-theory and T-Matrix method for differential
scattering cross sections of non-absorbing spheroid
at 94 GHz.
Evaluation of results from Mie-theory and T-
Matrix method for non-absorbing spherical and with
the spherical particle origin moved over a range at
94 GHz for vertical polarization still show
reasonable agreement, but with horizontal
polarization in Figure 5, it is obvious that the
differential scattering cross-sections increases as the
offset range increases, this effect is least noticed
with increase in scattering angle. This shows that at
higher operating frequencies the effect is
insignificant; however, Figure 6 and 7 results show
that even for small offset value with the same input
parameters, the phase function, extinction and
scattering cross sections differ quite significantly at
5.8 GHz compared to the generalized Lorentz–Mie
technique.
4 CONCLUSIONS
We have demonstrated in our results that the effect
of offset values relative to the frequency bands and
how the scattering calculation in terms of geometric
properties of the particles; (shapes and size
parameter) for spherical and slightly non-spherical
particles adopting Mie theory and T-matrix
techniques are similar with previous works at higher
frequency bands. Furthermore, the same trends of
results are observed in terms of vertical polarization
for non-absorbing offset spherical scatterer at 94
GHz. On the other hand, scattering characteristics
for horizontal polarization at 94 GHz, and at lower
frequency bands (i.e. 5.8 GHz) differs quite
significantly with the same input parameters. Hence,
scattering calculation from non-absorbing
homogeneous spherical particles with the origin of
the particle moved over a certain range should be
used with caution depending on the wave frequency.
This is particularly important due to previous
concept that the same scattered cross section is
obtained with the origin of the spherical scatterer at
the centre. Obviously, the difference in our results
with the former at lower frequency (i.e. 5.8 GHz)
would lead to erroneous values being generated as
the offset value increases and tends toward the
Second International Conference on Telecommunications and Remote Sensing
138

radius of scattering object, and inaccurate prediction
of hydrometeor shapes are likely if the previous
concept is applied in radar and remote sensing
applications.
ACKNOWLEDGEMENT
This work was supported by Petroleum Technology
Development Fund (PTDF) under scholarship
number PTDF/E/OSS/PHD/NF/355/11.
REFERENCES
Barber, P. and C. Yeh (1975). "Scattering of
electromagnetic waves by arbitrarily shaped dielectric
bodies." Applied optics 14(12): 2864-2872.
Barber, P. W. and S. C. Hill (1990). Light scattering by
particles: computational methods, World Scientific
Publishing Company Incorporated.
Barber, P. W. and D. S. Wang (1978). "Rayleigh-Gans-
Debye applicability to scattering by nonspherical
particles." Applied optics 17(5): 797-803.
Bohren, C. F. and D. R. Huffman (2008). Absorption and
scattering of light by small particles, Wiley-Vch.
Kerker, M. (1969). "The scattering of light, and other
electromagnetic radiation."
Mishchenko, M. I., J. W. Hovenier, et al. (1999). Light
scattering by nonspherical particles: theory,
measurements, and applications, Academic Press.
Mishchenko, M. I. and L. D. Travis (1994). "T-matrix
computations of light scattering by large spheroidal
particles." Optics communications 109(1): 16-21.
Mishchenko, M. I. and L. D. Travis (1998). "Capabilities
and limitations of a current FORTRAN
implementation of the< i> T</i>-matrix method for
randomly oriented, rotationally symmetric scatterers."
Journal of Quantitative Spectroscopy and Radiative
Transfer 60(3): 309-324.
Mishchenko, M. I., L. D. Travis, et al. (2002). Scattering,
absorption, and emission of light by small particles,
Cambridge university press.
Mishchenko, M. I., L. D. Travis, et al. (1996). "< i>
T</i>-matrix computations of light scattering by
nonspherical particles: A review." Journal of
Quantitative Spectroscopy and Radiative Transfer
55(5): 535-575.
van de Hulst, H. C. (1981). Light scattering by small
particles, Dover publications.
Waterman, P. (1965). "Matrix formulation of
electromagnetic scattering." Proceedings of the IEEE
53(8): 805-812.
Wiscombe, W. J. (1980). "Improved Mie scattering
algorithms." Applied optics 19(9): 1505-1509.
Zheng, W. (1988). "The null field approach to
electromagnetic scattering from composite objects:
The case with three or more constituents." Antennas
and Propagation, IEEE Transactions on 36(10): 1396-
1400.
Scattering of Electromagnetic Wave by Offset Spherical Particles
139