
Polygonal Approximation of an Object Contour by Detecting Edge
Dominant Corners using Iterative Corner Suppression
Rabih Al Nachar
1
, Elie Inaty
1
, Patrick J. Bonnin
2
and Yasser Alayli
2
1
Department of Computer Engineering, University of Balamand, PO Box 100, Elkoura, Lebanon
2
Laboratoire d'Ingénierie des Systèmes de Versailles-LISV, 10-12 Av de l'Europe, 78140 Vélizy, France
Keywords: Straight Edges, Corners, Polygonal Approximation, Contour.
Abstract: A new algorithm to detect straight edge parts which form the contour of an object presented in an image is
discussed in this paper. This algorithm is very robust and can detect true straight edges even when their pix-
el's locations are not straight due to natural noise at the object borders. These straight edges are than used to
report and classify contour's corners according to their angle and their adjacent segments lengths. A new
technique for polygonal approximation is also presented to find the best set among these corners to con-
struct the polygon vertices that best describe the approximating contour. It starts by eliminating the corners,
one after the other using Iterative Corner Suppression (ICS) process. This in turn enables us to obtain the
smallest possible error in the approximation. Experimental results demonstrate the efficiency of this tech-
nique in comparison with recently proposed algorithms.
1 INTRODUCTION
The problem of straight edge detection can be de-
fined as follows: Given a binary image of edges ex-
tracted from a real image using an existing edge de-
tector based on Sobel, Prewitt, Kirsh or Canny algo-
rithms (Prewitt 1979, Sobel 1978, Kirsh 1971 and
Deriche 1987), find the parts of an edge that can be
classified as straight edges or segments of length
greater than a given threshold. The importance of
developing an algorithm that can detect these
straight edges remains a very important task in com-
puter vision and pattern recognition (Loncaric 1998).
In addition, straight edges are encountered a lot in
human made internal and external urban environ-
ments and objects. For example, Herman in (Herman,
Kanade and Kuroe 1984) presents an application for
an aerial robot to form and update of a 3D map of a
sequence of aerial scenes. The dedicated objects to
be detected in these images are the buildings. So he
identified them by their straight edges and their in-
tersection at the corners. Other applications are in-
door applications where a robot tries to build a map
of its environment and localize itself in it which is
called the SLAM problem. The target objects, used
for this purpose, are identified by their straight edges
like doors and walls intersection. In other applica-
tion, a combination of straight edges is used
(Bouchafa and Zavidovique 2006) to form specific
shapes like V-shape, W-shape and Z-shape. Each
shape is invariant under a specific image transfor-
mation. For this reason, it is used for image registra-
tion.
The most important objective of extracting
straight edges is their role in identifying corners that
are used as interest points in a lot of algorithms in
image processing. A corner (Nachar, Inaty, Bonnin
and Alayli 2012) can be defined as intersection of
non collinear straight edges with appropriate length.
From here, correct detection of straight edges will
lead to efficient corners detection.
After extracting the image corners based on
straight edges of a shape, we have developed a new
technique for "polygonal approximation" that con-
sists of selecting a number of well chosen corners to
construct the polygon that best approximates the
contour of that shape. Polygonal approximation is
widely used in object recognition (Ayache and
Faugeras 1986) because it smoothes the contour of
the objects in the images without loss of critical in-
formation. Related works to this algorithm are cited
in the next section.
The rest of the paper is organized as follows:
Section 2 presents some related works on polygonal
approximation. Section 3 describes the edge extrac-
tion and the chain code of every edge point. Section
247
Al Nachar R., Inaty E., J. Bonnin P. and Alayli Y..
Polygonal Approximation of an Object Contour by Detecting Edge Dominant Corners using Iterative Corner Suppression.
DOI: 10.5220/0004650602470256
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 247-256
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

4 explains our proposed algorithm using polygonal
approximation. Experimental results are revealed in
Section 5. The conclusion is shown in Section 6.
2 RELATED WORKS
A large number of methods were proposed so far
(Dunham 1986). Pavlidis in (Pavlidis 1982) presents
an algorithm, known as split and merge technique. It
divides an edge into a set of segments that has each
one a maximal distance to the edge less than a given
threshold d as shown in Figure 1.
Figure 1: Polygonal Approximation.
The parameter used in this technique is the maximal
distance d
max
between the segment and the edge as
described in Figure 2. If d
max
is greater than the
threshold d, the segment [AB] is divided into two
segments; [AM] and [MB] where M is the edge
point corresponding to d
max
.
Figure 2: Segment division according to maximal distance.
Wall and Danielsson in (Wall and Danielsson 1984)
presented another algorithm that tries to find the
segment [AB] shown in Figure 2 by moving its end-
point B starting from the edge point A along the
edge until a certain criterion is no longer verified.
The criterion used here is the maximal area per unit
of length of the deviation between the edge and the
corresponding approximated segment that should be
less than a given threshold. Another technique for
obtaining a polygonal approximation of an object's
contour based on an updated Hough Transform is
presented in (Gupta, Chaudhury and Parthasarathy
1992). On the other hand, the method in (Mikheev ,
Vincent and Faber 2001) is dedicated for the pol-
yline representation of a scanned text or graphic
objects. Kolesnikov in (Kolesnikov 2008, 2009,
2011) focused on the approximation of a polygonal
edge or curve P of N vertices by another polygonal
edge Q with a minimal number of segments or verti-
ces M (M<N) while conserving a given criterion so
that the resulting error does not exceed a given
threshold. The error is the sum of the square distanc-
es of the N vertices of curve P relative to the curve
Q. Pinheiro in (Pinheiro 2010) searched for edge
points, called curvature extremes, that correspond to
a change in the direction of the curve (edge) using a
curvature function which form the polygon vertices.
These extremes are selected at different scale level
of the smoothed image. When the scale level in-
creases, the edge details become smoother so the
number of extremes will be reduced. Parverz and
Mahmoud in (Parvez and Mahmoud 2010) searched
for cut-points on the contour of the studied shape.
These points correspond to a deviation in the con-
tour direction. Then the algorithm tries to minimize
the number of detected cut-points until a terminating
condition is satisfied. The final approximated poly-
gon will have these cut points as extremes.
In (Carmona-Poyato, Madrid-Cuevas , Medi-
naCarnicer and Munoz-Salinas 2010), the authors
presented a technique based on detecting dominant
points on the contour and then iteratively suppress-
ing the redundant ones in order to obtain the best
approximated polygon with the minimal number of
segments. The algorithm of Masood in (Masood
2008) also detects first dominant points called break
points then starts to eliminate the ones with minimal
error value based on global measure. The optimal
result is not guaranteed even with the usage of an
optimization procedure. Finally, Marji and Siy in
(Marji and Siy 2004) presented a very similar tech-
nique to the one used in (Masood 2008) but it differs
by the measure of error of each dominant point.
Here, a dominant point is characterized especially by
its strength that means its non collinearity with re-
spect to its direct neighbors.
We have proposed in this paper an approach in-
spired by that presented in (Marji and Siy 2004 and
Masood 2008). We have searched for dominant cor-
ners that best approximate a given shape by a poly-
gon having these corners as vertices. The differences
between our work and their works are in the nature
and stability of the selected points and in the method
used to select these points among others. On the
other hand, the error measure used to eliminate or to
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
248

keep a corner is based on the Integral Square Error
between an edge part and the straight segment ap-
proximating it. So, it is similar to the criterion used
by Wall and Danielson (Wall and Danielsson 1984)
that relies on the area of the region included between
the edge part and its approximated segment rather
than only relying on the maximal distance like in the
method of Pavlidis (Pavlidis 1982).
3 EDGE EXTRACTION AND
CHAIN CODE
3.1 Edge Points Extraction
Given an original image, the extraction of edge
points is performed in several steps:
Gradient computation: in norm (magnitude of the
edge) and direction (normal to the edge direction).
Threshold on gradient norm, to extract initial edge
points.
Thinning edge points to thin thick edges to one
pixel width.
Prolongation of edge points to close open edges.
Linking edge points to obtain edges (lists of
hooked edge points) from edge points.
Three possibilities to obtain gradient computation, in
norm and direction, which are:
1) Either Prewitt (Prewitt 1979) or Sobel Algorithm
(Sobel 1978), which consist in two steps :
Compute the gradient projections on X and Y ax-
is, using two masks : Gx and Gy,
then compute the norm and the direction using a
rectangular to polar transform,
2) Kirsh algorithm (Kirsch 1971), which obtains
directly the gradient in norm and direction, by
choosing the best approximation among the four
projections: horizontal, vertical, and two oblics
using four masks: Gx, Gy and G+45 and G-45.
3) Canny edge detector (Canny 1986 and Deriche
1987) using the first derivative of a Gaussian
function. The zero-crossing points are the edge
points.
3.2 Edge Chain Codes
Linking an edge pixel C consists of identifying the
direction of transfer from it to one of its eight neigh-
bors, who has the greatest gradient norm. This direc-
tion is one of the eight Freeman directions coded in
Figure 3.
Figure 3: Freeman Codes.
As a result, a linked edge can be viewed as a chain
of Freeman codes of length equal to the number of
linked edge pixels (edge length) minus one. As an
example, Figure 4 shows a particular edge of nine
pixels with its chain codes.
Figure 4: An edge with its chain codes.
4 POLYGONAL APPROXIMA-
TION
The main goal of this paper is to introduce an opera-
tor that is able to extract a polygon that best approx-
imate an object's contour. The operator's algorithm is
composed of three functions that work sequentially
as shown in Figure 5.
Figure 5: Algorithm's Block Diagram.
4.1 Straight Edge and Corner
Detectors
Our objective is to detect edge parts that can be con-
sidered straight using only their chain codes. Then,
the intersection edge points of every two non collin-
ear edge parts are detected as corners. To do that, we
must introduce the chain codes of straight edges.
4.1.1 Perfect Straight Edges
A perfect straight edge is an edge whose chain code
is composed of one code or two codes at maximum.
There are eight different straight edges correspond-
ing to a unique code among the eight Freeman codes.
For example, a perfect horizontal straight edge has a
chain code of only 0 or 4 and a perfect straight edge
PolygonalApproximationofanObjectContourbyDetectingEdgeDominantCornersusingIterativeCornerSuppression
249

along the first diagonal has a chain code of 1 or 5 as
shown in Figure 6.
In addition to these eight cases, a perfect straight
edge has a chain code composed of two codes: one
primary and the other secondary with a difference
equal to one between them. The classification of
these two codes is done according to their frequency
of occurrence in the edge's chain code. This is illus-
trated in Figure 7.
Figure 6: Straight Edges with unique code.
In Figure 7, five edges are considered starting
from one origin O. Edges1 and edge5 are those that
have a unique code 0 and 1 respectively, and their
slope are 0
o
and 45
o
. Edge3 is the one that have dou-
ble codes 0 and 1 of the same frequency of occur-
rence so its slope is 22.5
o
and it is the bisector of the
angle formed by edge1 and edge5. Edge2 is near to
edge1 and has also double codes 0 and 1 but with
different frequency of occurrence. Code 0 is primary
and code 1 is secondary. Same result can be seen in
edge4 that has code 1 as a primary and code 0 as
secondary.
Figure 7: Straight edges with double Freeman codes.
As a conclusion, we can say that the perfect straight
edges that have double codes are of two kinds. The
first kind of edges has double codes of same fre-
quency (edge3). It is equidistant between two
straight edges of unique code (edge1 and edge5).
The second kind of edges also has double codes but
of different frequency (edges2 and4) and it is also
between two straight edges of unique code corre-
sponding to the primary or secondary code. Here,
the nearest one's code forms the primary code. In
Figure 7, Edge1 is the nearest to Edge2, so the pri-
mary code for Edge2 is 0.
4.1.2 Algorithm Explanation and Real
Straight Edges
In real images, the chain code of a straight edge that
should be composed of one or two successive codes
has usually more than two codes. Our goal is to
identify which of them are the primary and second-
ary codes and reject the remaining codes. This prob-
lem is due to natural noise at the object borders.
Real straight edges are shown in Figure 8 (a)
where some perturbations, circled in the image of
edges Figure 8 (b), are encountered along these edg-
es. The challenge is to build an intelligent algorithm
that can identify these perturbations and detect real
straight edges that meet at corner points as shown
with their angles in Figure 8 (c).
Our algorithm can be initiated at any edge point
E. The purpose is to test the existence of a real
straight edge with successive noisy pixels less than
m and of a length greater than a threshold d. The
idea behind the algorithm is to start testing an image
edge starting from its head to its tail. Consider the
first encountered edge direction as primary direction
and the next encountered edge direction as second-
ary edge direction. While moving the current pixel
to the tail, increment the frequency of primary or
secondary directions when the current pixel's direc-
tion corresponds to primary or secondary directions,
respectively. Or increment the frequency of noisy
pixels, if the current pixel's direction differs from
them. If the number of noisy pixels exceeds a given
threshold m, the edge test stops at the current pixel.
Now, if the edge length is greater than another
threshold d, the edge traversed so far is considered
as a straight edge.
Let us define the variables used in the algorithm:
- pdir: edge primary direction.
- pdirfreq: frequency of pdir.
- sdir: edge secondary direction.
- sdirfreq: frequency of sdir.
- cdir: current pixel direction.
- InfectedCount: number of noisy pixels en coun-
tered so far.
- el: edge length.
- SecondaryFound: a flag that is set when a second
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
250

ary direction is found.
- diff: absolute difference between cdir and pdir
(a)
(b)
(c)
Figure 8: (a) Real image, (b) image of edges, (c) detected
corners.
The algorithm details can be listed as follows:
Record the first edge direction at E (Freeman
code) as pdir and initialize pdirfreq = 1. Initial-
ize InfectedCount = 0, el=1 and Second-
aryFound = false and proceed to the next linked
pixel.
Iterate until the current pixel C reaches the tail
of the edge.
Calculate diff .
If (Not SecondaryFound):
if (diff==1), record cdir as sdir, initialize
sdirfreq = 1 and put SecondaryFound = true.
else if (cdir==pdir) than increment pdirfreq.
else increment InfectedCount.
Else
If(diff>=2)or((diff==1)and(cdir!=sdir
))current pixel is a noisy pixel than in-
crement InfectedCount.
o if (InfectedCount>m): meaning
that we are reached the maximum
allowable noisy pixels: stopping
criterion=>Ends of straight edge
test:
if(el>=d) than the current edge
is a real straight edge.
else if (cdir==pdir) than increment
pdirfreq and set InfectedCount=0.
else if (cdir ==sdir) than increment
sdirfreq.
update pdir and sdir: pdir is the direc-
tion that has the maximum frequency
between (pdir, pdirfreq) and (sdir,
sdirfreq).
el++.
A noisy pixel is an edge pixel, located on a real
straight edge, whose edge direction is different than
those of the corresponding perfect edge. From here,
the variable diff is introduced. Next, the search is for
the edge direction, if exists, that differs by one from
the primary direction pdir knowing that a perfect
straight edge can have a chain code composed at
maximum of two codes with difference equal to one.
The variable InfectedCount is incremented each time
a noisy pixel in encountered and it is cleared only if
the current edge pixel direction cdir is equal to pdir.
On the other hand, if cdir is equal to sdir, the varia-
ble InfectedCount should not be cleared. In Figure 9
(a), consider the example of a straight edge whose
pixels are in black. It is linked with pdir = 1 and sdir
= 2. At point A, the cdir is 3 so InfectedCount is
incremented. Next at point B, the cdir is 2 and it is
clear that the remaining edge in gray forms a differ-
ent straight edge. If we reset InfectedCount at B
when cdir = sdir = 2, the algorithm will not stop and
will consider both edges, in black and in gray, as one
straight edge which is incorrect. A final point should
be discussed which is the need to update pdir and
sdir. The logical reason for this case is that a straight
edge primary direction is not necessary the first en-
countered cdir as shown on the straight edge in Fig-
ure 9 (b). Initially pdir = 4 and sdir = 5. But after
traversing the remaining edge pixels, it is clear that
pdir should be 5 and sdir should be 4.
PolygonalApproximationofanObjectContourbyDetectingEdgeDominantCornersusingIterativeCornerSuppression
251

Figure 9: Two straight edges.
Finally, after the detection of straight edges the cor-
ner detection process starts by considering the inter-
section points of every two non collinear straight
edges as corners.
4.2 Polygonal Approximation using
Iterative Corner Suppression
In this section, we develop a novel technique based
on corner points called Iterative Corner Suppression
(ICS). Here, the corners, reported by the corner
detector, are characterized by the lengths of its two
sides (straight edges) and by its angle between its
two sides. The corners for the chromosome shape in
Figure 10 are shown in the linked edge image in
Figure 10 (b) with their angle directions.
(a)
(b)
Figure 10: Detected corners for a chromosome shape: (a)
Chromosome shape, (b) Linked edge image.
The global algorithm starts with the straight edge
detector, detects the straight edges of every contour
in the image, and reports the intersection of every
two non collinear straight lines as corners. Then, the
polygonal approximation algorithm examines every
contour, selects from its corners the dominant ones
that form a polygon that best fit it.
Thus, the goal of our polygonal approximation
algorithm is to find the optimal polygon, approxi-
mating the contour of a given shape, given a re-
quired compression ratio CR:
⁄
(1)
where n is the number of shape's edge points and nc
is the number of selected corners called dominant
corners that form the polygon vertices. At a given
CR, the objective function is to minimize the global
integral square error (ISE) which is the sum of
squared distance of each contour's edge point to the
nearest approximated polygon segment. The ISE of
a polygon's segment corresponds to the area of the
region bounded between it and the corresponding
edge part. For a particular shape as in Figure 11,
since n is constant CR becomes a function of nc only.
Therfore, the problem is limited to obtain the mini-
mal possible ISE for a given number of dominant
corners nc. In general, the entry of the algorithm is
the parameter CR, nc will be calculated automatical-
ly for every contour.
Figure 11: Polygonal Approximation at various nc.
Figure 11 shows the approximated polygon of the
chromosome shape used in Figure 10 at various nc.
The global ISE decreases while nc increases.
Two parameters are used in the algorithm and
should be understood at the beginning. The first one
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
252

is the local ISE which is the ISE corresponding to a
given polygon's segment. The second one is the local
ISE variation "LISEV" due to the removal of a cor-
ner from the list of polygon's vertices. In Figure 12,
at iteration i+1, the LISEV due to the removal of
corner Cor3 has the same meaning as LISEV due to
the introduction of segment [Cor2Cor4]. The algo-
rithm can be summarized as follows:
For a given contour of n edge points and m cor-
ners, select all the detected corners as polygon's
vertices following the linking order.
The number of dominant corners nc = m.
Iterate until the current CR = n/nc becomes
greater than or equal to a specified threshold.
For each current corner "Corc" from the list
of selected corners:
Find the previous and next selected corners
"Corp" and "Corn".
Calculate the LISEV due to its removal:
LISEV
c
= new segment LISE – old segments
LISEs (see illustration in Figure 12).
If any of the previously removed corner lo-
cated between "Corp" and "Corn" has a
greater LISE variation (LISEV
r
) than rese-
lect this corner, remove the current corner
"Corc" from the list of vertices and set the
final LISEV as LISEV
r
.
Remove the corner that corresponds to the
minimal LISEV from the list of selected corner.
Decrement nc by 1.
Calculate the global ISE for the entire polygon
which is the sum of LISEs of introduced seg-
ments.
Figure 12: Corner Suppression.
Starting by considering all the corners as
polygon's vertices, the idea behind the ICS algorithm
is to decrease the number of vertices iteratively of
the approximated polygon. Here, the suppressed
corner (vertex) is the one that its suppression will
cause the minimal increase to the current global ISE
and this will ensure the selection of the optimal pol-
ygon at every iteration (at every value of nc). Con-
sider the case presented in Figure 12. We have four
selected corners at iteration i so there are three
polygon's segments with their corresponding LISE
represented by the areas A, B and C. The idea is to
calculate the LISEV caused by the removal of one of
the two corners Cor2 or Cor3, for example, at itera-
tion i+1. D is the area that represents the LISE of
Cor3 and E is the one that represents the ISE of Cor2.
The removal of Cor3 will add a new polygon's seg-
ment [Cor2Cor4] and eliminate two others
[Cor2Cor3] and [Cor3Cor4]. Therefore, we can
write
LISEV
DBC
(2)
Same procedure will apply for calculating the
LISEV caused by the removal of Cor2 with:
LISEV
E
AB
(3)
If LISEV
3
is smaller than LISEV
2
than Cor2 will be
removed otherwise Cor3 will be removed.
Figure 13: Corner Reselection.
While the corners are suppressed one after the other,
the LISEV of a corner that depends on the current
corner "Corc" and the directly selected neighboring
corners (previous one "Corp" and next one "Corn"),
may change since "Corp" or "Corn" may also
change. So we should always update and then check
the LISEV of even the suppressed corners to ensure
the optimality of the suppression at each iteration.
This can be illustrated using the list of corners
shown in Figure 13 where all the five corners are
selected initially. This is a tested case by the algo-
rithm where C4 (Figure 13 (a)), C5 (Figure 13 (b))
then C3 (Figure 13 (c)) are suppressed iteratively
PolygonalApproximationofanObjectContourbyDetectingEdgeDominantCornersusingIterativeCornerSuppression
253
first and the remaining polygon has only C1, C2 and
C6 as vertices. Now if we calculate the LISEV of
removing C2 and that of removing C3, C4 and C5
taking C1 as "Corp" and C6 as "Corn", we find that
the LISEV of removing C3 is the greatest one. So
we should suppress C2 and reselect C3 (Figure 13
(d)). Then, the LISEV resulting from adding [C1C6]
is that of removing C3 and it will be compared with
the LISEV of removing the remaining selected cor-
ners existing on the whole contour to deselect the
corner with the minimal one.
5 EXPERIMENTAL RESULTS
Our proposed algorithm is tested on three different
shapes shown in Figure 14: (a) Chromosome, (b)
Leaf and (c) semicircles (The and Chin 1989). The
results obtained are compared to those presented in
various papers (Parvez and Mahmoud 2010, Carmo-
na-Poyato, Madrid-Cuevas, MedinaCarnicer and
Munoz-Salinas 2010, Marji and Siy 2004 and
Masood 2008).
Other than the ISE, a new parameter is intro-
duced for the comparison: the weighted sum of
square error WE given by
(4)
Since our algorithm requires a colored or grey image
as an input not only a digital image or edge image
while the others are tested directly on a digital image,
we need a unique platform for comparison. From
here, we have selected manually on the edge image
derived by our algorithm the vertices of the polygon
reported by each method in (Parvez and Mahmoud
2010, Carmona-Poyato, Madrid-Cuevas, Medi-
naCarnicer and Munoz-Salinas 2010, Marji and Siy
2004 and Masood 2008), then calculate the corre-
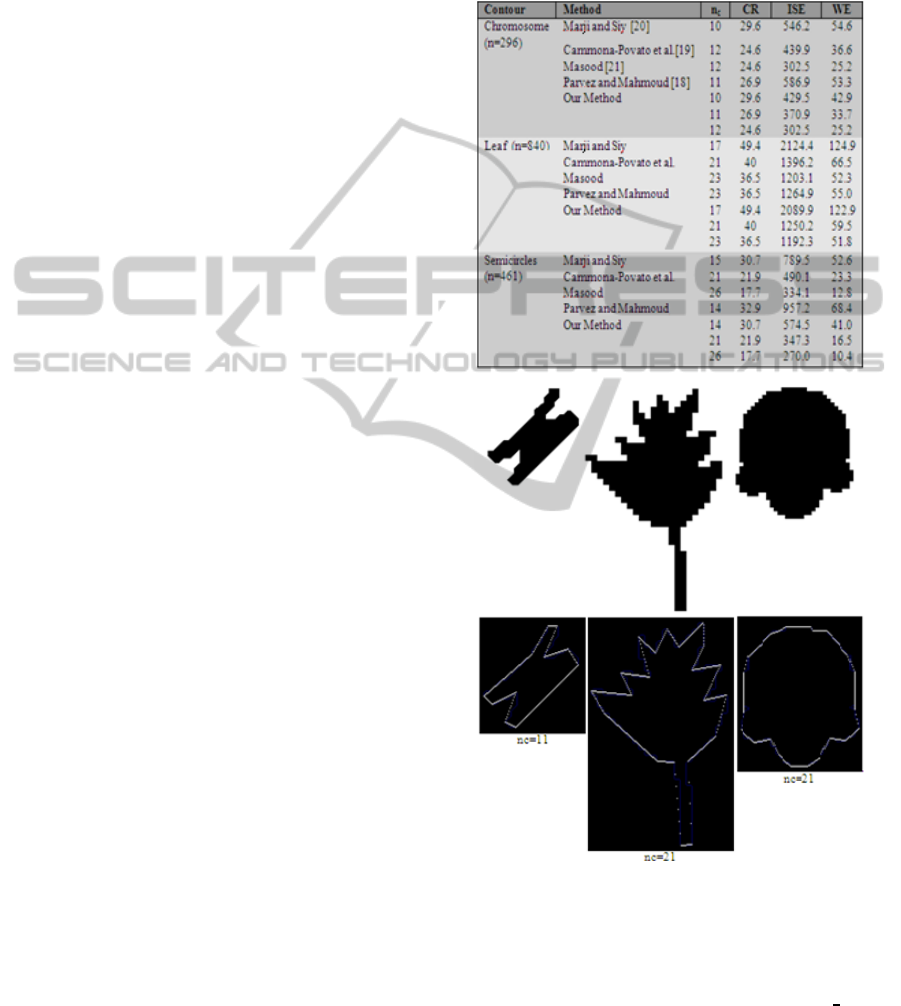
sponding ISE and show the results in Table 1.
From Table 1, it can be seen clearly that our algo-
rithm has better ISE and WE compared to others.
This is due to three main reasons. The first one is the
excellent location of the corners due to the efficient
straight edge detector. So, the optimal polygon is the
one whose vertices are selected among these corners.
The second one is the efficient technique to select
the best corners as polygon vertices that will lead to
the minimal error (ISE) at a specific nc. The third
one is the update of the LISE, at each iteration, even
for previously suppressed corners. This feedback
will ensure that, when eliminating a corner or select-
ing a new segment, the maximal LISE is set for this
segment. This fact will show the real LISEV caused
by selecting this segment and as a result will ensure
the selection of the segment with the real minimal
LISEV.
Table 1: Comparative Results for the Chromosome, Leaf
and semicircle shapes.
(a) (b) (c)
Figure 14: Tested Shapes and their polygonal approxima-
tions at a particular nc.
For a real image that contains more than one shape
or contour, nc cannot be fixed and considered as an
input for the algorithm since existing contours may-
be best approximated by polygons of different num-
ber of vertices. In other words, nc cannot be fixed
for all contours. Here, CR or WE plays the big role
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
254

and must be used both or at least one of them as in-
puts. By specifying a threshold for the WE parameter
used as an input, the role of a polygonal approxima-
tion algorithm becomes to find the greatest nc per
contour that corresponds to the greatest WE less than
the specified threshold. Here the CR is an output. On
the other hand, by specifying a threshold for CR
used as an input, the goal still to find the greatest nc
per contour, that corresponds to the minimal CR
greater than the threshold. In this case, WE is an
output. So the choice of selecting which parameter
or maybe both depends on the specific application.
Finally, Figure 14 shows the polygons approxi-
mating the tested shapes at a given nc. It can be seen
clearly that the results are very precise.
Finally, we suggest an application based on DCs
which is shape recognition of 2D objects dedicated
for a robot embedded with a vision system where
our polygonal approximation's algorithm is imple-
mented. The goal is to present first a 2D shape to the
robot and then it tries automatically to locate it in a
simple scene.
To simulate this experiment, we present two im-
ages to the algorithm; the first one is a training im-
age, shown in Figure 15, containing only the desired
shape and the second one is a test image containing
a scene of multiple shapes as shown in Figure 16 (a).
For the training image, the algorithm detects the
DCs located on the shape's contour. For the test one,
it detects and groups the DCs per contour represent-
ing each shape. After that the matching procedure
starts by comparing every test group of DCs with the
trained DCs using the DC angle and ratio of the
lengths of their sides as matching parameters.
Figure 15: Training image.
This matching criterion remains feasible when the
image transformation that relates the two images is a
translation-rotation, similarity or conditioned affinity.
In general, an affine transformation preserves ratio
but does not preserve angles (Hartley and Zisserman,
2003) so the matching criterion does not hold for
this type of transformation only if the camera plane
and the shape plane are parallel (Hartley and Zis-
serman 2003); in this case, the angles are nearly pre-
served. This is the conditioned affinity.
The result of matching is shown in Figure 16 (b)
where the DCs are shown only on the matched
shape's contour which is the star shape.
(a)
(b)
Figure 16: (a) Test image. (b) Corresponding Image of
contours with DCs shown on matched contour.
6 CONCLUSIONS
In this paper, a new polygonal approximation tech-
nique is proposed. It is composed of two procedures.
The first is called "Straight Edges Detector" which
examines all the contours existing in the input image
and detects the edge parts that can be considered as
straight edges. These straight edges are straight lines
that exist frequently at the borders of various objects
in real scenes especially human made environments
like buildings, cars, doors… The importance of de-
tecting these straight edges remains in their role of
detecting edge corner points. The intersection of two
non collinear straight edges of appropriate length
(greater than a threshold) is reported as a corner.
The second part of our work is a polygonal ap-
proximation algorithm that takes the detected cor-
ners as an entry. By fixing an entry parameter like
PolygonalApproximationofanObjectContourbyDetectingEdgeDominantCornersusingIterativeCornerSuppression
255

Compression ratio CR or weighted sum error WE,
the algorithm starts, per contour, by removing itera-
tively the corners that introduce the minimal possi-
ble ISEV to the global ISE measure until reaching
the stopping criterion. At the end, the remained cor-
ners form the vertices of the polygon that can best
approximate the current contour.
The experimental results have shown good re-
sults in comparison with other existing methods. In
our opinion, this is due to the efficient straight edge
detector that explores all the contour corners effi-
ciently and then to the iterative polygonal approxi-
mation algorithm that removes, at each iteration, the
corner with the smallest LISEV and at the same time
updates and reexamines the LISEV of already re-
moved corners. This way, we can ensure that the
remained corners form the polygon that best fit their
contour.
Finally, as a future work, we suggest an image
registration application that can benefit from detect-
ed straight edges and corners. These image features
can be combined together in a certain number to
form specific shapes or primitives that can have in-
variant measures versus different image transfor-
mation.
REFERENCES
Loncaric, S., 1998. A survey of shape analysis techniques,
Pattern Recognition, vol.31.
Herman M., Kanade T. and Kuroe S., 1984. Incremental
Acquisition of a Three-Dimensional Scene Model from
Images, IEEE Transactions on Pattern Analysis and
Machine Intelligence, Vol. Pami-6, No. 3.
Bouchafa S. and Zavidovique B., 2006. Efficient cumula-
tive matching for image registration. Image and Vi-
sion computing, Vol. 24.
Ayache N. and Faugeras O., 1986. A new approach for the
recognition and positioning of two dimensional ob-
jects, IEEE Transaction on Pattern Analysis and Ma-
chine Intelligence, vol.8.
Nachar R., Inaty E., Bonnin P. and Alayli Y., 2012. A
Robust Edge Based Corner Detector, Submitted for
possible publication in Autonomous Robots Springer,
September 2013, under review.
Dunham J.,1986. Optimum Uniform Piecewise Linear
Approximation of Planar Curves, IEEE Trans on Pat-
tern Analysis and Machine Intelligence vol PAMI 8
n°1, pp 67-75.
Pavlidis T., 1982. Algorithms for Graphics and Image
Processing, Springer Verlag.
Wall K. and Danielsson P., 1984. A fast sequential method
for polygonal approximation of digitized curves,
Computer Vision Graphics and Image Processing, vol
28, pp 220-227.
Gupta A., Chaudhury S. and Parthasarathy G., 1992. A
Hough Transform Based Approach to Polyline Ap-
proximation of Object Boundaries, Proceedings. 11th
IAPR International Conference on Pattern Recognition.
Vol.III. Conference C: Image, Speech and Signal
Analysis.
Mikheev A., Vincent L. and Faber V., 2001. High-Quality
Polygonal Contour Approximation Based on Relaxa-
tion, Pr ceedings Sixth International Conference on
Document Analysis and Recognition.
Prewitt J., 1979. Object enhacement and extraction, Pic-
ture processing & psychopictorics, BS Lip-
kin&A.Rosenfelded, Academic Press, New York USA.
Sobel, 1978. Neighbourhood coding of binary images for
fast contour following and general binary array pro-
cessing, Computer Graphics & Image Processing USA,
vol 8 pp 127-135.
Kirsch R., 1971. Computer determination of the constitu-
ent structure of biological images, Computers and Bi-
omedical Research 4.
Kolesnikov A., 2008. Fast Algorithm for ISE-Bounded
Polygonal Approximation, 15th IEEE International
Conference on Image Processing.
Kolesnikov A., 2009. Minimum Description Length Ap-
proximation of Digital Curves, 16th IEEE Internation-
al Conference on Image Processing.
Kolesnikov A., 2011. Nonparametric Polygonal and Mul-
timodel Approximation of Digital Curves with Rate-
Distortion Curve Modeling, 18th IEEE International
Conference on Image Processing.
Pinheiro A., 2010. Piecewise Approximation of Contours
Through Scale-Space Selection of Dominant Points
,
IEEE Transaction on Image Processing, Vol. 19, No. 6.
Parvez M. T. and Mahmoud S. A., 2010. Polygonal Ap-
proximation Of Planar Curves Using Triangular Sup-
pression, 10th International Conference on Infor-
mation Science, Signal Processing and their Applica-
tions.
Carmona-Poyato A., Madrid-Cuevas F.I., MedinaCarnicer
R. and Munoz-Salinas R., 2010. Polygonal approxi-
mation of digital planar curves through break point
suppression, Pattern Recognition, 43( 1), pp. 14-25.
Marji M. and Siy P., 2004. Polygonal representation of
digital planar curves through dominant point detec-
tion – a nonparametric algorithm, Pattern Recognition
37, pp. 2113- 2130.
Masood A., 2008. Optimized polygonal approximation by
dominant point deletion, Pattern Recognition 4 1, pp.
227- 239.
The C. H. and Chin R.T., 1989. On the detection of domi-
nant points on digital curves, IEEE Transactions of
Pattern Analysis and Machine Intelligence 11, pp.
859-872.
Canny J., 1986. A computational approach to edge detec-
tion, IEEE Transactions of Pattern Analysis and Ma-
chine Intelligence., vol. PAMI-8, pp. 679–698.
Deriche R., 1987. Optimal Edge detection using recursive
filtering, Int journal on Computer Vision.
Hartley R. and Zisserman A., 2003. Multiple View Geome-
try in Computer Vision, Cambridge university press,
2
nd
Edition.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
256
