Generalized Pythagoras Trees for Visualizing Hierarchies

Fabian Beck

, Michael Burch

, Tanja Munz

Lorenzo Di Silvestro

and Daniel Weiskopf

VISUS, University of Stuttgart, Stuttgart, Germany

Dipartimento di Matematica e Informatica, Universit

a di Catania, Catania, Italy

Keywords:

Hierarchy Visualization.

Abstract:

Pythagoras Trees are fractals that can be used to depict binary hierarchies. But this binary encoding is an

obstacle for visualizing hierarchical data such as ﬁle systems or phylogenetic trees, which branch into n sub-

hierarchies. Although any hierarchy can be modeled as a binary one by subsequently dividing n-ary branches

into a sequence of n − 1 binary branches, we follow a different strategy. In our approach extending Pythago-

ras Trees to arbitrarily branching trees, we only need a single visual element for an n-ary branch instead of

spreading the binary branches along a strand. Each vertex in the hierarchy is visualized as a rectangle sized

according to a metric. We analyze several visual parameters such as length, width, order, and color of the

nodes against the use of different metrics. The usefulness of our technique is illustrated by two case studies

visualizing directory structures and a large phylogenetic tree. We compare our approach with existing tree

diagrams and discuss questions of geometry, perception, readability, and aesthetics.

1 INTRODUCTION

Hierarchical data (i.e., trees) occurs in many applica-

tion domains, for instance, as results of a hierarchical

clustering algorithm, as ﬁles organized in directory

structures, or as species classiﬁed in a phylogenetic

tree. Providing an overview of possibly large and

deeply nested tree structures is one of the challenges

in information visualization. An appropriate visual-

ization technique should produce compact, readable,

and comprehensive diagrams, which ideally also look

aesthetically appealing and natural to the human eye.

A prominent visualization method are node-link

diagrams, which are often simply denoted as tree di-

agrams; layout and aesthetic criteria have been dis-

cussed (Reingold and Tilford, 1981; Wetherell and

Shannon, 1979). Although node-link diagrams are

intuitive and easy to draw, visual scalability and la-

beling often is an issue. An alternative, in particular

easing the labeling problem, are indented trees (Burch

et al., 2010) depicting the hierarchical structure by in-

dentation. Further, layered icicle plots (Kruskal and

Landwehr, 1983) stack boxes on top of each other for

encoding a hierarchy, but waste space by assigning

large areas to inner nodes on higher levels of the hier-

archy. The Treemap approach (Shneiderman, 1992),

which is applying the concept of nested boxes, pro-

duces space-efﬁcient diagrams but complicates inter-

preting the hierarchical structure.

In this paper, we introduce Generalized Pythago-

ras Trees as an alternative to the above hierarchy visu-

alization techniques. It is based on Pythagoras Trees

(Bosman, 1957), a fractal technique showing a binary

hierarchy as branching squares (Figure 1, a); the frac-

tal approach is named after Pythagoras because every

branch creates a right triangle and the Pythagorean

theorem is applicable to the areas of the squares. We

extend this approach to n-arily branching structures

and use it for depicting information hierarchies (Fig-

ure 1, b). Instead of triangles, each recursive render-

ing step produces a convex polygonal shape where the

corners are placed on a semi circle. The size of the

created rectangles can be modiﬁed for encoding nu-

meric information such as the number of leaf nodes

of the respective subhierarchy (Figure 1, c).

We implemented the approach as an interactive

tool and demonstrate its usefulness by applying it to

large and deeply structured abstract hierarchy data

from two application domains: a ﬁle system orga-

nized in directories and the NCBI taxonomy, a phy-

logentic tree that structures the living organisms on

earth in a tree consisting of more than 300,000 ver-

tices. Furthermore, a comparison to existing hier-

archy visualization approaches provides ﬁrst insights

Beck F., Burch M., Munz T., Di Silvestro L. and Weiskopf D..

Generalized Pythagoras Trees for Visualizing Hierarchies.

DOI: 10.5220/0004654500170028

In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 17-28

ISBN: 978-989-758-005-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c)

Figure 1: Extending Pythagoras Trees for encoding information hierarchies: (a) traditional fractal approach; (b) Generalized

Pythagoras Tree applied to an n-ary information hierarchy; (c) additionally visualizing the number of leaves by the size of the

inner nodes.

into the unique characteristic of Generalized Pythago-

ras Trees: a higher visual variety leads to more dis-

tinguishable visualizations, the fractal origin of the

method supports identifying self-similar structures,

and the speciﬁc layout seems to be particularly suit-

able for visualizing deep hierarchies. Finally, the

created images are visually appealing as they show

analogies to natural tree and branching structures.

2 RELATED WORK

The visualization of hierarchical data is a central in-

formation visualization problem that has been stud-

ied for many years. Typical respresentations in-

clude node-link, stacking, nesting, indentation, or

fractal concepts as surveyed by J

urgensmann and

Schulz (2010); Schulz (2011). Many variants of the

general concepts exist, for instance, radial (Battista

et al., 1999; Eades, 1992) and bubble layouts (Grivet

et al., 2004; Lin and Yen, 2007) of node-link dia-

grams, circular approaches for stacking techniques

(Andrews and Heidegger, 1998; Stasko and Zhang,

2000; Yang et al., 2003), or nested visualizations

based on Voronoi diagrams (Balzer et al., 2005; Nocaj

and Brandes, 2012).

Although many tree visualizations were proposed

in the past, none provides a generally applicable solu-

tion and solves all related issues. For example, node-

link diagrams clearly show the hierarchical structure

by using explicit links in a crossing-free layout. How-

ever, by showing the node-link diagram in the tradi-

tional fashion with the root vertex on top and leaves

at the bottom, much screen space stays unused at the

top while leaves densely agglomerate at the bottom.

Transforming the layout into a radial one distributes

the nodes more evenly, but makes comparisons of

subtrees more difﬁcult. Node-link layouts of hierar-

chies have been studied in greater detail, for instance,

Burch et al. (2011) investigated visual task solution

strategies whereas McGufﬁn and Robert (2009) ana-

lyzed space-efﬁciency.

Indented representations of hierarchies are well-

known from explorable lists of ﬁles in ﬁle browsers.

Recently, Burch et al. (2010) investigated a variant

as a technique for representing large hierarchies as

an overview representation. Such a diagram scales

to very large and deep hierarchies and still shows

the hierarchical organization but not as clear as in

node-link diagrams. Layered icicle plots (Kruskal

and Landwehr, 1983), in contrast, use the concept of

stacking: the root vertex is placed on top and, analo-

gous to node-link diagrams, consumes much horizon-

tal space that is as large as all child nodes together.

Treemaps (Shneiderman, 1992), a space-ﬁlling

approach, are a prominent representative of nesting

techniques for encoding hierarchies. While proper-

ties of leaf nodes can be easily observed, a limitation

becomes apparent when one tries to explore the hi-

erarchical structure because it is difﬁcult to retrieve

the exact hierarchical information from deeply nested

boxes: representatives of inner vertices are (nearly)

completely covered by descendants. Treemaps have

been extended to other layout techniques such as

Voronoi diagrams (Balzer et al., 2005; Nocaj and

Brandes, 2012) producing aesthetic diagrams that,

however, suffer from high runtime complexity.

Also, 3D approaches have been investigated, for

instance, in Cone Trees (Carri

ere and Kazman, 1995),

each hierarchy vertex is visually encoded as a cone

with the apex placed on the circle circumference of

the parent. Occlusion problems occur that are solved

by interactive features such as rotation. Botanical

Trees (Kleiberg et al., 2001), a further 3D approach,

imitate the aesthetics of natural trees but are restricted

to binary hierarchies, that is, n-ary hierarchies are

modeled as binary trees by the strand model of Holton

(1994); it becomes harder to detect the parent of a

node.

The term fractal was coined by Mandelbrot (1982)

and the class of those approaches has also been used

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

for hierarchy visualization due to their self-similarity

property (Koike, 1995; Koike and Yoshihara, 1993).

With OneZoom (Rosindell and Harmon, 2012), the

authors propose a fractal-based technique for visu-

alizing phylogenetic trees; however, n-ary branches

need to be visually translated into binary splits. De-

vroye and Kruszewski (1995) visualize random bi-

nary hierarchies with a fractal approach as botan-

ical trees; no additional metric value for the ver-

tices is taken into account; instead, they investigate

the Horton-Strahler number for computing the branch

thicknesses.

The goal of our work is to extend a fractal ap-

proach, which is closer to natural tree structures, to-

wards information visualization. This goal promises

embedding the idea of self-similarity and aesthet-

ics of fractals into hierarchy visualization. Central

prerequisite—and in this, our approach differs from

existing fractal approaches—is that n-ary branches

should be possible. With respect to information vi-

sualization, the approach targets at combining ad-

vantages of several existing techniques: a readable

and scalable representation, an efﬁcient use of screen

space, and the ﬂexibility for encoding additional in-

formation. A downside of the approach, however, is

that overlap may occur similar as in 3D techniques

(though it is a 2D representation)—only varying the

parameters of the visualization or using interaction al-

leviates this issue.

3 VISUALIZATION TECHNIQUE

Our general hierarchy visualization approach extends

the idea of Pythagoras Trees. Instead of basing the

branching of subtrees on right triangles, we exploit

convex polygons with edges on the circumference of

a semi circle.

3.1 Data Model

We model a hierarchy as a directed graph H = (V, E)

where V = {v

, . . . , v

} denotes the ﬁnite set of k

vertices and E ⊂ V × V the ﬁnite set of edges, i.e.,

parent–child relationships. One vertex is the desig-

nated root vertex and is the only vertex without an

incoming edge; all other vertices have an in-degree of

one. We allow arbitrary hierarchies, that is, the out-

degree of the vertices is not restricted. A maximum

branching factor n ∈ N of H can be computed as the

maximum out-degree of all v ∈ V . For an arbitrary

vertex v ∈ V , H

denotes the subhierarchy having v as

root vertex; | H

| is the number of vertices included

in the H

(including v). The depth of a vertex v

(a) (b)

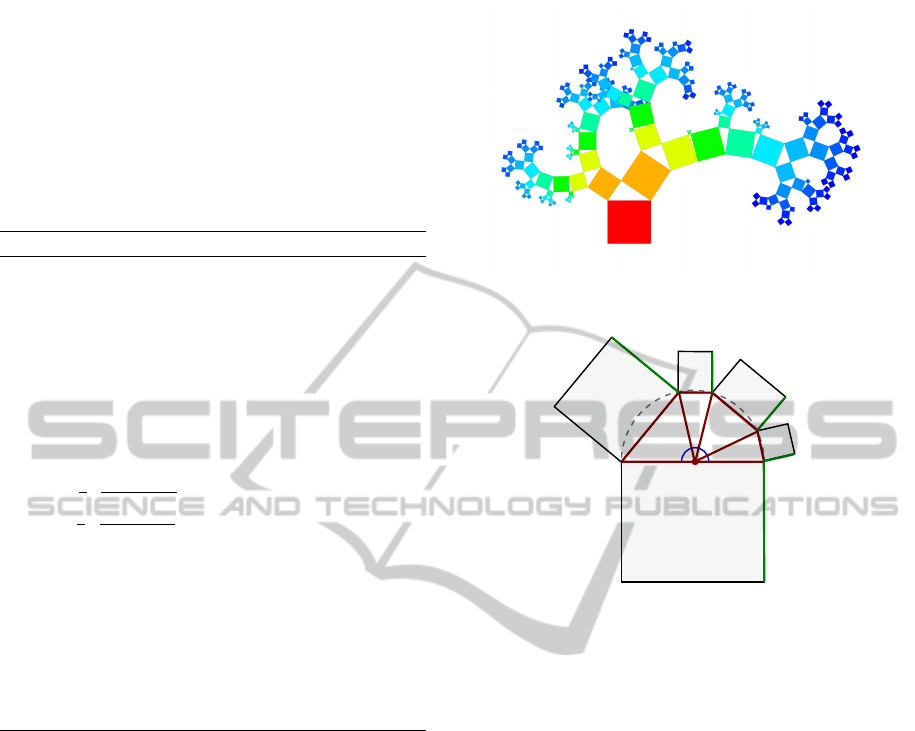
Figure 2: Illustration of the traditional Pythagoras Tree ap-

proach: (a) a single binary branch; (b) recursively applied

branching step.

is the number of vertices on the path through the

hierarchy from v to v

. We allow positive weights to

be attached to each vertex of the hierarchy v ∈ V rep-

resenting metric values such as sizes. We model them

as a function w : V → R. The weight w(v) ∈ R

of an

inner vertex v does not necessarily need to be the sum

of its children, but can be.

3.2 Traditional Pythagoras Tree

The Pythagoras Tree is a fractal approach describing

a recursive procedure of drawing squares. In that, it

was initially not intended to encode information, but

its tree structure easily allows representing binary hi-

erarchies: each square represents a vertex of the hier-

archy; the recursive generation follows the structure

of the hierarchy and ends at the leaves.

Drawing a fractal Pythagoras Tree starts with

drawing a square of side length c. Then, two smaller

squares are attached at one side of the square—

usually, at the top—according to the procedure illus-

trated in Figure 2 (a): Then, a right triangle with an-

gles α and β where α + β =

is drawn using the

side of the square as hypotenuse, which also becomes

a diameter of the circumcircle of the triangle. The

two legs of the triangle are completed to squares hav-

ing side lengths a and b. In the right triangle, the

Pythagorean theorem a

= c

holds, i.e., the sum

of the areas of the squares over the legs is equal to

the area of the square over the hypotenuse. Applying

this procedure recursively to the new squares as de-

picted for the next step in Figure 2 (b) creates a frac-

tal Pythagoras Tree (the recursion is only stopped for

practical reasons at some depth). The angles α and β

can be set to a constant value or be varied according to

some procedural pattern. Figure 1 (a) provides an ex-

ample of a fractal Pythagoras Tree where α = β =

Transforming the fractal approach into an infor-

mation visualization technique, the squares are inter-

preted as representatives of vertices of the hierarchy,

GeneralizedPythagorasTreesforVisualizingHierarchies

called nodes. As a consequence, the fractal encodes

a complete binary hierarchy, the recursion depth be-

ing the depth of the hierarchy. If the generated image

should represent a binary hierarchy that is not com-

pletely ﬁlled to a certain depth, the recursion has to

stop earlier for the respective subtrees. If the hier-

archy is weighted as speciﬁed in the data model, the

weights can be visually encoded by adjusting the sizes

of the squares, i.e., the corresponding angles α and β.

Algorithm 1: Pythagoras Tree.

PythagorasTree(H

, S):

// H

: binary hierarchy

// S: representative square S = (c, ∆s, θ)

// c = (x

, y

): center

// ∆s: length of a side

// θ: slope angle

drawSquare(S); // draw square for current root vertex

if | H

|> 1 then

// v

and v

: children of H

α :=

w(v

)

w(v

)+w(v

)

;

β :=

w(v

)

w(v

)+w(v

)

;

∆s

:= ∆s · sin β;

∆s

:= ∆s · sin α;

:= ComputeCenterLe f t(c, ∆s, ∆s

, );

:= ComputeCenterRight(c, ∆s, ∆s

);

:= (c

, ∆s

, θ + α);

:= (c

, ∆s

, θ − β);

PythagorasTree(H

, S

); // draw subhierarchy H

PythagorasTree(H

, S

); // draw subhierarchy H

end if

Algorithm 1 describes in greater detail how an ar-

bitrary binary hierarchy (i.e., a hierarchy where each

vertex either has an out-degree of 2 or 0) can be recur-

sively transformed into a Pythagoras Tree visualiza-

tion. It is initiated by calling PythagorasTree(H

, S):

where H

= (V, E) is a binary hierarchy and S =

(c, ∆s, θ) is the initial square with center c, length of

the sides ∆s, and slope angle θ. The recursive pro-

cedure ﬁrst draws square S and proceeds if the cur-

rent hierarchy still contains more than a single node.

Then, encoding the node weights in the size of the

squares, the angles α and β are computed according

to the normalized weight of the node opposed to the

angle. The angles form the basis for further com-

puting the parameters of the two new rectangles S

and S

. The drawing procedure is ﬁnally continued

by recursively calling PythagorasTree(H

, S

) and

PythagorasTree(H

, S

) for the two children v

and

of the current root vertex.

When, for instance, using the number of leaf ver-

tices as the weight of each vertex, the algorithm pro-

duces visualizations such as Figure 3 that encodes a

Figure 3: Random binary hierarchy visualized as a

Pythagoras Tree that encodes the number of leaves in the

size of the nodes.

Δx

Δy

Δx

Δy

Δx

Δy

Δx

Δy

Δx

Figure 4: Polygonal split of Generalized Pythagoras Trees

creating an n-ary branch.

random binary hierarchy. Like the fractal approach,

the visualization algorithm still produces overlap of

subtrees that, however, becomes rarer through sparser

hierarchies.

3.3 Generalized Pythagoras Tree

The Generalized Pythagoras Tree, as introduced in the

following, can be used for visualizing arbitrary hier-

archies, that are hierarchies allowing n-ary branches.

Right triangles are replaced by convex polygons shar-

ing the same circumcircle; the former hypotenuse of

the triangle becomes the longest side of the triangle.

For increasing the visual ﬂexibility of the approach,

squares are exchanged for general rectangles.

Figure 4 illustrates an n-ary branch, showing the

polygon and its circumcircle. The polygon is split

into a fan of isosceles triangles using the center of

the circumcircle as splitting point. While the number

of rectangles is speciﬁed by the degree of the repre-

sented branch, the angles and lengths can be modiﬁed

to encode further information. In particular, we have

two degrees of freedom:

• Width function w

: V → R

of rectangles: Sim-

ilar to binary hierarchies, the width ∆x

of a rect-

angle R

can be changed, here, by modifying the

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

corresponding angle α

accordingly. The angle α

should reﬂect weight w

) of a vertex v

in rela-

tion to the weight of its siblings:

:= π ·

)

∑

j=1

)

The width of the rectangle is ∆x

:= ∆x · sin

where ∆x is the width of the parent node.

• Length stretch function w

of rectangles: Anal-

ogously, the length ∆y

of the rectangle R

can be

varied. This length, in contrast to the width ∆x

does not underly any restrictions such as the size

of a cirumcircle. Nevertheless, we formulate the

length dependent on the length of the parent ∆y

and the relative width sin

in order to consider

the visual context (otherwise, it would be difﬁ-

cult to deﬁne appropriate metrics not producing

degenerated visualizations): the length of the rect-

angle is ∆y

:= w

) · ∆y · sin

Algorithm 2: Generalized Pythagoras Tree.

GeneralizedPythagorasTree(H

, R):

// H

: hierarchy branching into n ∈ N

subhierarchies

, . .. , H

// R: representative rectangle R = (c, ∆x, ∆y, θ)

// c = (x

, y

): center

// ∆x, ∆y: width and length

// θ: slope angle

drawRectangle(R); // draw rectangle for parent vertex

for all H

:= π ·

)

∑

j=1

)

;

∆x

:= ∆x · sin

;

∆y

:= w

) · ∆y · sin

;

:=ComputeCenter(c, ∆x, ∆y, (α

, . .. , α

i−1

), ∆x

, ∆y

);

:=ComputeSlope(θ, (α

, . .. , α

));

:= (c

, ∆x

, ∆y

, θ

);

GeneralizedPythagorasTree(H

, R

);

end for

Algorithm 2 extends Algorithm1 and describes the

generation of Generalized Pythagoras Tree visualiza-

tions. Again, it is a recursive procedure and is initial-

ized by calling GeneralizedPythagorasTree(H

, R)

where H

= (V, E) is an arbitrary hierarchy and R =

(c, ∆x, ∆y, θ) represents the initial rectangle that, in

contrast to the previous case, has a width ∆x and

a length ∆y. For an n-ary branching hierarchy H

with root vertex v, the algorithm ﬁrst draws the re-

spective rectangle before all children v

, . . . , v

are

handled: for each child v

, the computation of an-

gle α

forms the basis for deriving the width ∆x

and length ∆y

of the respective rectangle R

as de-

scribed above. Furthermore, the center and slope

Figure 5: Generalized Pythagoras Trees showing n-ary hi-

erarchy using a constant width and length stretch function.

of the new rectangle need to be retrieved. Finally,

GeneralizedPythagorasTree(H

, R

) can be recur-

sively applied to subhierarchy H

having rectangle R

as root node.

Figure 5 shows a sample visualization created

with the algorithm. For this initial image width func-

tion w

is set to a constant value and the length stretch

function w

is deﬁned as 1. As a consequence, the

nodes are squares again, equally sized for each branch

but n-arily branching. An example with a similar

conﬁguration can be found in Figure 1 (a); the same

dataset is shown in Figure 1 (b) applying the num-

ber of leaf nodes as the width function w

. Further

conﬁgurations are discussed more systematically be-

low. The discussion also includes the usage of color,

which, in all ﬁgures referenced so far, visualizes the

depth of the nodes. Furthermore, the order of rectan-

gles can be modiﬁed and has an impact on the lay-

out; in the generalized approach, we have a higher

degree of freedom (n! possibilities) than in the stan-

dard Pythagoras Trees where only a ﬂipping between

two angles can be applied.

3.4 Excursus: Fractal Dimension

The fractal dimension is typically used as a complex-

ity measure for fractals. Looking back to the origin of

the Generalized Pythagoras Tree visualization and in-

terpreting it as a fractal approach, the extended fractal

approach can be characterized by this dimension. To

this end, however, not an information hierarchy can

be encoded, but the approach needs to be applied for

inﬁnite n-arily branching structures; for simpliﬁcation

we do not consider scaling of rectangles. The follow-

ing analysis shows that the fractal dimension, which

is 2 for traditional Pythagoras Tree fractals, asymptot-

ically decreases to 1 for a branching factor approach-

ing inﬁnity.

Any fractal can be characterized by its fractal di-

mension D ∈ R that is deﬁned as a relation between

GeneralizedPythagorasTreesforVisualizingHierarchies

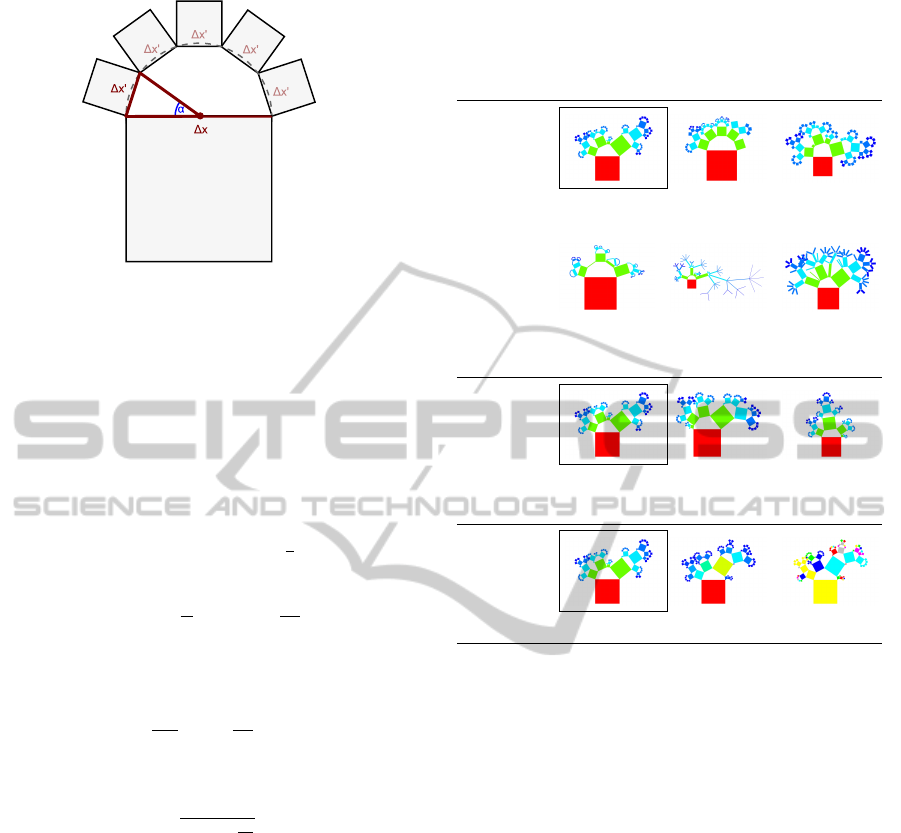
Figure 6: Illustrating the fractal dimension of an n-ary

branching hierarchy by showing the splitting into equally

sized angles.

the branching factor n and the scaling factor r given

by D = −log

n. In our scenario, we have to ﬁrst com-

pute the scaling factor r depending on the branching

factor n. Figure 6 illustrates the following formulas

and shows an n-ary branch.

First of all, the n-ary branch creates a convex poly-

gon, which is split into isosceles triangles as described

before. Since all rectangles have the same width, the

angle at the tip of the triangle is α =

. The width of

the rectangle then is

∆x

= ∆x · sin

Relating the size of the square to the original square,

the scaling factor can be derived as follows:

r =

∆x

= sin

The fractal dimension ﬁnally is

= −

log n

log sin

This result conﬁrms D

= 2 (traditional binary

branches) and shows that the fractal dimension is ap-

proaching 1 for increasing n, i.e.,

lim

n→∞

= 1 .

3.5 Visual Parameters

The visualization approach has been described pre-

cisely but still has some degrees of freedom that shall

be explored in the following. For example, the size of

the rectangles can be varied, the order of the subhier-

archies in a branch is not restricted, or the coloring of

the nodes is open for variation. These parameters help

optimizing the layout and support the visualization by

extra information in form of weights assigned to each

node. For illustrating the effect, Table 1 shows the

Table 1: Exploring different parameter settings such as size,

order, and color of rectangles for a sample dataset; framed

images represent the default setting and are equivalent; the

number of leaf nodes is applied as weight.

size

(squares) (S1) sides: weight (S2) sides: equal

size

(S3) sides:

weight; enlarged

circle

size

(rectangles) (S4) width: equal

size; length:

weight

(S5) width: equal

size; area: weight

(S6) width:

weight; area:

weight

order

(O1) external (O2) ascending

weight

(O3) maximum

weight in the

center

color

(C1) depth (C2) weight (C3) category

same random hierarchy (75 nodes; maximum depth

of 5) in different parameter settings. As a weight,

the number of leaf nodes is applied; but the metric is

interchangeable, for instance, by the number of sub-

nodes, the depth of the subtree, or a domain-speciﬁc

weight. One setting (Table 1, S1 = O1 = C1), which

seemed to work most universally in our experience, is

selected as default and applied in all following ﬁgures

of the paper if not indicated otherwise.

3.5.1 Size

Already for the traditional Pythagoras Tree approach,

rectangles can be split in uniform size or non-uniform

size. For the generalized approach, we deﬁne a width

function as well as a length function (Section 3.3).

When employing the same metric for both, all nodes

are represented as squares. Table 1 (S1) uses the num-

ber of leaf nodes as the common metric, which seems

to be a good default selection because more space is

assigned to larger subtrees. In contrast, when all sub-

nodes are assigned the same size (i.e. a constant func-

tion is employed), small subtrees become overrepre-

sented as depicted in Table 1 (S2). A variant of the

approach, which is shown in Table 1 (S3), extends the

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

approach from using semi circles to larger sectors of

a circle.

Inserting different functions for width and length

further increases the ﬂexibility—nodes are no longer

squares, but differently shaped rectangles. For in-

stance, Table 1 (S4) encodes the number of leaf nodes

in the height and applies a constant value to the width.

When deﬁning the length function relative to the (con-

stant) width so that the area of the rectangle is propor-

tional to the number of leaves, those leaf nodes are

emphasized as depicted in Table 1 (S5). A similar

variant shown in Table 1 (S6) has a constant length

and chooses the width accordingly for encoding the

number of leaf nodes in the area.

3.5.2 Order

The subnodes of an inner node of a hierarchy are vi-

sualized as an ordered list. While, for some applica-

tions, there exist a speciﬁc, externally deﬁned order,

many other scenarios do not dictate a speciﬁc order.

In case of the latter, the subnodes can be sorted ac-

cording to a metric, which again is the number of leaf

nodes in this example. The sorting criterion mainly

inﬂuences the direction in which the diagram is grow-

ing but also inﬂuences overlapping effects. Often the

external order, at least in case it is random or inde-

pendent of size, creates quite balanced views as de-

picted in Table 1 (O1). When, for instance, applying

an ascending order, the image like the one shown in

Table 1 (O2) grows to the right. More symmetric visu-

alizations such as in Table 1 (O3) are generated when

placing the vertices with the larger size in the center.

3.5.3 Color

The areas of the rectangular nodes can be ﬁlled with

color for encoding some extra information. Selecting

the color on a color scale according to the depth of

the node in the hierarchy helps comparing the depth

of subtrees: for instance, in Table 1 (C1) this encod-

ing reveals that the leftmost main subtree, though be-

ing shorter, is as deep as the rightmost one. Alterna-

tively, the weight of a node can be encoded in color

like shown in Table 1 (C2), which, however, is more

suitable if the size of the node not already encodes

the weight. If categories of vertices are available, also

these categories can be color-coded by discrete colors

as depicted in Table 1 (C3).

3.6 Analogy to Node-Link Diagrams

Though being derived from a fractal approach, Gen-

eralized Pythagoras Trees can be adapted—without

changing the position of nodes—to become variants

(a) (b) (c)

Figure 7: Relationship between Generalized Pythagoras

Trees and node-link diagrams: (a) Generalized Pythagoras

Tree; (b) Generalized Pythagoras Tree and analogous node-

link diagram; (c) analogous node-link diagram.

of node-link diagrams. An analogous diagram can

be created as illustrated in Figure 7 by connecting

the circle centers of the semi circles of branches by

lines. The circle centers become the nodes, the lines

become the links of the resulting node-link diagram.

Like the subtrees of a Generalized Pythagoras Tree

might overlap, the analogous node-link drawing is not

guaranteed to be free of edge crossings. We prefer the

Pythagoras variant over the analogous node-link vari-

ant because it uses the available screen space more

efﬁciently (which is important, for instance, for color

coding) and shows the width of a node explicitly.

4 CASE STUDIES

To illustrate the usefulness of our Generalized

Pythagoras Tree visualization, we applied it to two

datasets from different application domains—ﬁle sys-

tems with ﬁle sizes as well as the NCBI taxonomy that

classiﬁes species. In these case studies we demon-

strate different parameter settings and also show how

interactive features can be applied for exploration.

4.1 File System Hierarchy

While the approach can be applied to any directory

structure, we decided to demonstrate this use case

by reading in the ﬁle structure of an early version of

this particular paper. Since we use L

X for writing,

the paper directory contains multiple text ﬁles includ-

ing temporary ﬁles as well as a list of images. Also

included are supplementary documents and a script

used for creating exemplary random information hier-

archies. All in all, the directory structure contains 139

vertices (7 directories and 132 ﬁles) having a maxi-

mum depth of 4 and a maximum branching factor of

38 (ﬁgures directory). Figure 8 shows two visualiza-

tions of this directory structure employing different

parameter settings.

In Figure 8 (a), we applied the default settings siz-

ing the vertices in relation to the number of leaf nodes

and using color for encoding depth. The image shows

that, among the main directories, the ﬁgures directory

GeneralizedPythagorasTreesforVisualizingHierarchies

(a) (b)

Figure 8: Directory hierarchy of this paper on the ﬁle sys-

tem: (a) size based on the number of leaf nodes with color-

coded depth information; (b) size encoding the ﬁle and di-

rectory sizes with color-coded ﬁle types.

contains by far the most leaf nodes (94) and itself is

split into three further directories, which include the

images needed for the three more complex ﬁgures and

tables of this paper: canis (Figure 9), parameters (Ta-

ble 1), and samples (Table 2). Additionally, ﬁgures

also directly includes a number of images, which are

needed for the other ﬁgures. The only other directory

containing a reasonable number of ﬁles is the hierar-

chy generator folder; besides the generator script it

contains a number of generated sample datasets.

Customizing the parameters of the visualization

for the use case of investigating ﬁle systems, we as-

signed the ﬁle size to the size of the vertices (directory

sizes are the sum of the contained ﬁle sizes). More-

over, the ﬁle type is encoded in the color of the vertex

(category coding) a legend providing the color–type

assignments; directories are encoded in the color of

the dominating ﬁle type of the contained ﬁles. The re-

sulting visualization as depicted in Figure 8 (b) shows

that the ﬁgures directory is also one of the largest

main directories, but there exist other ﬁles and direc-

tories that also consume reasonable space such as the

additional material directory. Comparing the size of

the main PDF document to the images directory, it can

be observed that not all image ﬁles contained in the di-

rectory are integrated into the paper because the paper

is smaller than the images directory. The color-coded

ﬁle types reveal that the most frequently occurring

type are PNG ﬁles, not only in the images directory

but also in general. The hierarchy generator direc-

tory mostly includes TRE ﬁles (Newick format), but

is dominated with respect to size by two TXT ﬁles (an

alternative hierarchy format not as space-efﬁcient).

4.2 Phylogenetic Tree

Moreover, our approach is tested on a hierarchical

dataset commonly used by the biology and bioinfor-

matics communities. The taxonomy here used has

been developed by NCBI and contains the names

of all organisms that are represented in its genetic

database (Benson et al., 2010). The speciﬁc dataset

encoding the taxonomy contains 324,276 vertices

(60,585 classes and 263,691 species) and has a max-

imum depth of 42. The Generalized Pythagoras Tree

visualization applied to this dataset (Figure 9 I) cre-

ates a readable overview visualization of the very

complex and large hierarchical structure. The vertices

of the tree have different sizes according to the num-

ber of leaves of their subtrees. Each inner vertex rep-

resents a class of species and it is easy to point out

the class that contains more species. The root node

is an artiﬁcial class of the taxonomy that contains ev-

ery species for which a DNA sequence or a protein is

stored in the NCBI digital archive.

At the ﬁrst level of the tree (see Figure 9 I), a big

node represents cellular organisms and further nodes

the Viruses, Viroids, unclassiﬁed species, and others

(this information can be retrieved by using the ge-

ometric zoom). Selecting nodes and retrieving ad-

ditional information facilitate the exploration of the

tree. For instance, the biggest node at level 2 is the

Eukaryota class, which includes all organisms whose

cells contain a membrane-separated nucleus in which

DNA is aggregated in chromosomes; it still contains

177,258 of the 263,691 species.

Besides gaining an overview of the main branches

of the taxonomy, the visualization tool allows for an-

alyzing subsets of the hierarchy down to the level of

individual species by applying semantic zooming. As

a concrete example, we demonstrate the exploration

process in the right part of Figure 9; in each step we

selected the subtree of the highlighted node (red cir-

cle): Figure 9 II shows the Amniota class, which be-

longs to the tetrapoda vertebrata taxis (four-limbed

animals with backbones or spinal columns). In the

next steps (Figure 9 III-V), we followed interesting

branches until we reach the Carnivora class in Fig-

ure 9 V, which denotes meat-eating organisms; the

subtree contains 301 species. From here, it is simple

to proceed the exploration towards a well-known an-

imal, such as the common dog, deﬁned as Canis Fa-

miliaris, by zooming in the subtrees of Caniformia,

literally “dog shaped” (Figure 9 VI), then through

Canidae, the family of dogs (Figure 9 VII) with 45

species, and ﬁnally Canis Familiaris.

5 DISCUSSION

The introduced technique for representing hierar-

chical structures is discussed by taking existing

other hierarchy visualization approaches into account.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

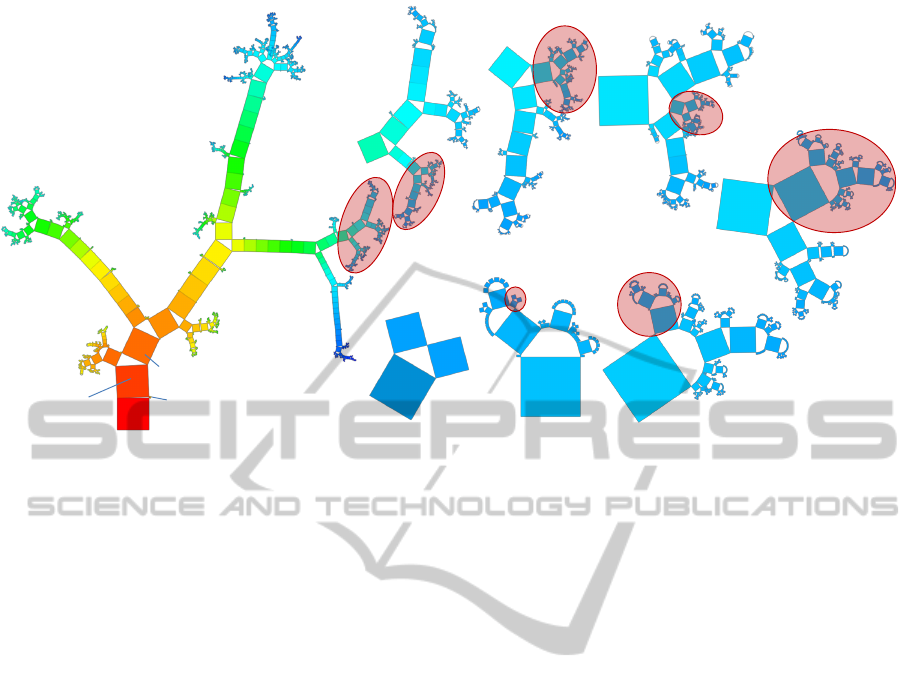
II. Amniota

III. Eutheria

IV. Laurasiatheria

V. Carnivora

VI. Caniformia

VII. Canidae VIII. Canis Familiaris

I. NCBI Taxonomy

Eukaryota

cellular

organisms

others

Figure 9: NCBI taxonomy hierarchically classifying species; rectangles sizes indicate the number of species in a subtree,

color encodes the depth; an example for exploring the taxonomy by semantic zooming is provided.

We applied different standard hierarchy visualization

techniques to a number of randomly generated artiﬁ-

cial datasets. The results are listed in Table 2. Each

column represents a different data set with some char-

acteristic feature: a binary hierarchy with a branch-

ing factor of 2, a deep hierarchy with many levels, a

ﬂat hierarchy with a high maximum branching factor,

a degenerated hierarchy that grows linearly in depth

with the number of nodes, a symmetric hierarchy hav-

ing two identical subtrees, and a self-similar hierarchy

following the same pattern at each level. The rows

show standard visualization techniques in comparison

to Generalized Pythagoras Trees. Though the graph-

ics can only act as previews in a printed version of the

paper, they are included in high resolution and are ex-

plorable in a digital version. The following analysis

considers multiple levels of abstraction from geome-

try and perception to readability and aesthetics.

5.1 Geometry and Perception

Hierarchy visualizations aim at showing containment

relationships between nodes and their descendants.

Considering Gestalt theory (Wertheimer, 1923), dif-

ferent approaches exist for visually encoding rela-

tionships: for instance, node-link diagrams use con-

nectedness to express containment, while Treemaps

are based on common region for showing that several

nodes belong to the same parent. In contrast, Gen-

eralized Pythagoras Trees do neither directly draw a

line between the nodes nor nest one node into the

other, but they draw rectangles of decreasing size onto

an imaginary curve. The human reader automatically

connects the rectangles on the curve, which is denoted

as the law of continuation. In all hierarchy visual-

ization approaches shown in Table 2, proximity also

plays a certain role (i.e., related nodes are placed next

to each other) but should not be overinterpreted (i.e.,

nodes placed next to each other are not necessarily

related).

In node-link diagrams, indented tree diagrams, or

icicle plots, each level in the hierarchy creates an-

other layer in the visualization. As a consequence,

the amount of (vertical) space available for a layer is

reduced when adding further levels. In Generalized

Pythagoras Trees, however, there are no global lay-

ers for levels of nodes: adding a level only produces

a kind of local layer that is arranged on a semi cir-

cle. With respect to this characteristic, Generalized

Pythagoras Trees are similar to Treemaps, which nei-

ther have global layers but split the area of a node for

introducing the next level.

Like in icicle plots and Treemaps, larger areas are

used to encode the nodes in Generalized Pythagoras

Trees. This makes it easier to use color for encod-

ing some metrics (such as the hierarchy level) in the

nodes because colors are easier to perceive for larger

areas (Ware, 2004) (Color for Labeling). In contrast

to Treemaps (and complete icicle plots), Generalized

Pythogoras Trees do not create space-ﬁlling images.

Areas, however, might overlap, which is discussed in

detail below.

Comparing the images shown in Table 2 with re-

spect to uniqueness, Generalized Pythagoras Trees

GeneralizedPythagorasTreesforVisualizingHierarchies

Table 2: Comparison of hierarchy visualization approaches for representatives of a selected set of hierarchy classes.

binary hierarchy deep hierarchy ﬂat hierarchy degenerated

hierarchy

symmetric

hierarchy

self-similar

hierarchy

node degree of 2 high number of

hierarchy levels (25)

high maximum node

degree (20)

linearly growing depth two equivalent

subtrees

self similar tree

structure

node-link

indented tree

icicle plot

Treemap

Generalized

Pythagoras Tree

show a high visual variety: not only the subtrees vary

in size, they are also rotated. Only the splitting ap-

proach in Treemaps creates similarly varying images,

however, just with respect to texture but not shape.

A positive effect of a high visual variety is that the

different datasets can be distinguished more easily—

the visualization acts as a ﬁngerprint. Together with

the fractal roots of the approach, the uniqueness helps

detect self-similar structures: Table 2 (last column)

shows a tree having a self-similar structure, which is

generated according to the same recursive, determin-

istic procedure for every node; the self-similar prop-

erty of the hierarchy is best detectable in the Gener-

alized Pythagoras Trees because every part of the tree

is just a rotated version of the complete tree.

5.2 Readability and Scalability

A hierarchy visualization is readable if the users are

able to efﬁciently retrieve the original hierarchical

data from it and easily observe higher-level charac-

teristics. However, readability is also related to vi-

sual scalability, which means preserving readability

for larger datasets. While, for smaller datasets, the

exact information is usually recognizable in any hi-

erarchy visualization, the depicted information often

becomes too detailed when increasing the scale of the

dataset. The visualization approach, hence, needs to

use the available screen space efﬁciently and has to

focus on the most important information.

Generalized Pythagoras Trees clearly emphasize

the higher-level nodes of the tree (i.e., the root node

and its immediate descendants): most of the area that

is ﬁlled by the visualization is consumed by these

higher-level nodes, which can be easily perceived be-

cause surrounded by whitespace. Lower-level nodes

and leaf nodes, however, become very small and are

not visible. But the visualization allows for sizing

the nodes according to their importance by using the

number of leaf nodes as a metric as done in Table 2.

Node-link diagrams, indented trees, and icicle plots

are similar in their focus on the higher-level nodes;

as well, lower-level nodes become difﬁcult to discern

because of lack of horizontal space. Since the ver-

tical space assigned to each level does not become

smaller in these visualizations, it is easier to retrieve

the maximum depth of a subtree. Treemaps focus on

leaf nodes and show largely different characteristics.

The ability of a visualization technique to display

also large datasets in a readable way considerably

widens its area of application. As shown in the case

study, Generalized Pythagoras Trees can be used for

browsing large hierarchies such as the NCBI taxon-

omy. While it is possible to interactively explore large

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

hierarchies in a similar way with the other paradigms

listed in Table 2, Generalized Pythagoras Trees show

some characteristic scalability advantages: for specif-

ically deep hierarchies such as the one in the sec-

ond column of Table 2, it adaptively expands into

the direction of the deepest subtree, here in spiral

shape. Comparing it to the other approaches, deep

subtrees are still readable in surprising detail. In con-

trast for ﬂat hierarchies, which have a speciﬁcally

high branching factor, Generalized Pythagoras Trees

do not seem to be as suitable: the size of the nodes

decreases too fast which constrains readability.

For a degenerated hierarchy (Table 2, fourth col-

umn), which grows linearly in depth with the number

of nodes, Generalized Pythagoras Trees create an id-

iosyncratic but readable visualization, similar as it is

the case for the other visualization approaches. Also

a symmetry in a hierarchy such as two identical sub-

trees (Table 2, ﬁfth column) can be detected: the iden-

tical tree creates the same image, which is rotated in

contrast to the other approaches, where it is moved

but not rotated.

A problem limiting the readability of Generalized

Pythagoras Trees is that, depending on the visualized

hierarchy, subtrees might overlap. The other visual-

ization approaches do not share this problem; only

Treemaps also employ a form of overplotting: inner

nodes are overplotted by its direct descendants. While

Treemaps use overplotting systematically, overlap

only occurs occasionally in Generalized Pythagoras

Trees and is unwanted. A simple way to circumvent

the problem using the interactive tool is selecting the

subset of the tree that is overdrawn by another. Also,

reordering the nodes or adapting the parameters of the

algorithm could alleviate the problem.

5.3 Aesthetics

Fractals often show similarities to natural structures

such as trees, leaves, ferns, clouds, coastlines, or

mountains (Peitgen and Saupe, 1988). Among the

images shown in Table 2, the Generalized Pythagoras

Trees clearly show the highest similarity to natural

tree and branching structures. Since, according to

the biophilia hypothesis, humans are drawn towards

every form of life (Wilson, 1984), this similarity

suggests that Generalized Pythagoras Trees might

be considered as being speciﬁcally aesthetic. Also

the property of self-similarity that is partly preserved

when generalizing Pythagoras Trees supports aesthet-

ics: “fractal images are usually complex, however, the

propriety of self-similarity makes these images easier

to process, which gives an explanation to why we

usually ﬁnd fractal images beautiful.” (Machado and

Cardoso, 1998)

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we introduced an extension of Pythago-

ras Tree fractals with the goal of using these for vi-

sualizing information hierarchies. Instead of depict-

ing only binary trees, we generalize the approach

to arbitrarily branching hierarchy structures. An al-

gorithm for generating these Generalized Pythagoras

Trees was introduced and the fractal characteristics of

the new approach were reported. A set of parame-

ters allows for customizing the approach and creating

a variety of visualizations. In particular, metrics can

be visualized for the nodes. The approach was imple-

mented in an interactive tool. A case study demon-

strates the utility of the approach for analyzing large

hierarchy datasets. The theoretical comparison of

Generalized Pythagoras Trees to other hierarchy visu-

alization paradigms, on the one hand, suggested that

the novel approach is capable of visualizing various

features of hierarchies in a readable way comparably

to previous approaches and, on the other hand, might

reveal unique characteristics of the approach such as

an increased distinguishability of the generated im-

ages and detectabiltiy of self-similar structures. Fur-

ther, the approach may have advantages for visualiz-

ing deep hierarchies and provides natural aesthetics.

An open research questions is how the overplot-

ting problem of the approach can be solved efﬁciently

and how the assumed advantages can be leveraged in

practical application. Moreover, formal user studies

have to be conducted to further explore the character-

istics of the approach.

ACKNOWLEDGMENTS

We would like to thank Kay Nieselt, University of

ubingen, for providing the NCBI taxonomy dataset.

REFERENCES

Andrews, K. and Heidegger, H. (1998). Information slices:

Visualising and exploring large hierarchies using cas-

cading, semicircular disks. In Proceedings of IEEE

Symposium on Information Visualization, pages 9–11.

Balzer, M., Deussen, O., and Lewerentz, C. (2005). Voronoi

treemaps for the visualization of software metrics.

GeneralizedPythagorasTreesforVisualizingHierarchies

In Proceedings of Software Visualization, pages 165–

172.

Battista, G. D., Eades, P., Tamassia, R., and Tollis, I. G.

(1999). Graph Drawing: Algorithms for the Visual-

ization of Graphs. Prentice-Hall.

Benson, D. A., Karsch-Mizrachi, I., Lipman, D. J., Ostell,

J., and Sayers, E. W. (2010). Genbank. Nucleic Acids

Research, 38(suppl 1):D46–D51.

Bosman, A. E. (1957). Het wondere onderzoekingsveld der

vlakke meetkunde. Breda, N.V. Uitgeversmaatschappij

Parcival.

Burch, M., Konevtsova, N., Heinrich, J., H

oferlin, M., and

Weiskopf, D. (2011). Evaluation of traditional, or-

thogonal, and radial tree diagrams by an eye tracking

study. IEEE Transactions on Visualization and Com-

puter Graphics, 17(12):2440–2448.

Burch, M., Raschke, M., and Weiskopf, D. (2010). Indented

Pixel Tree Plots. In Proceedings of International Sym-

posium on Visual Computing, pages 338–349.

Carri

ere, S. J. and Kazman, R. (1995). Research report: In-

teracting with huge hierarchies: beyond cone trees. In

Proceedings of Information Visualization, pages 74–

81.

Devroye, L. and Kruszewski, P. (1995). The botanical

beauty of random binary trees. In Proceedings of

Graph Drawing, pages 166–177.

Eades, P. (1992). Drawing free trees. Bulletin of the Institute

for Combinatorics and its Applications, 5:10–36.

Grivet, S., Auber, D., Domenger, J., and Melanc¸on, G.

(2004). Bubble tree drawing algorithm. In Proceed-

ings of International Conference on Computer Vision

and Graphics, pages 633–641.

Holton, M. (1994). Strands, gravity, and botanical tree

imaginery. Computer Graphics Forum, 13(1):57–67.

urgensmann, S. and Schulz, H.-J. (2010). A visual survey

of tree visualization. IEEE Visweek 2010 Posters.

Kleiberg, E., van de Wetering, H., and van Wijk, J. J.

(2001). Botanical visualization of huge hierarchies. In

Proceedings of Information Visualization, pages 87–

94.

Koike, H. (1995). Generalized fractal views: A

fractal-based method for controlling information dis-

play. ACM Transactions on Information Systems,

13(3):305–324.

Koike, H. and Yoshihara, H. (1993). Fractal approaches for

visualizing huge hierarchies. In Proceedings of Visual

Languages, pages 55–60.

Kruskal, J. and Landwehr, J. (1983). Icicle plots: Better dis-

plays for hierarchical clustering. The American Statis-

tician, 37(2):162–168.

Lin, C. C. and Yen, H. C. (2007). On balloon drawings

of rooted trees. Graph Algorithms and Applications,

11(2):431–452.

Machado, P. and Cardoso, A. (1998). Computing aesthetics.

In Advances in Artiﬁcial Intelligence, volume 1515 of

Lecture Notes in Computer Science, pages 219–228.

Springer Berlin Heidelberg.

Mandelbrot, B. (1982). The Fractal Geometry of Nature.

W.H. Freeman and Company. New York.

McGufﬁn, M. and Robert, J. (2009). Quantifying the space-

efﬁciency of 2D graphical representations of trees. In-

formation Visualization, 9(2):115–140.

Nocaj, A. and Brandes, U. (2012). Computing

Voronoi Treemaps: Faster, simpler, and resolution-

independent. Computer Graphics Forum, 31(3):855–

864.

Peitgen, H.-O. and Saupe, D., editors (1988). Science of

Fractal Images. Springer-Verlag.

Reingold, E. and Tilford, J. (1981). Tidier drawings of trees.

IEEE Transactions on Software Engineering, 7:223–

228.

Rosindell, J. and Harmon, L. (2012). OneZoom: A fractal

explorer for the tree of life. PLOS Biology, 10(10).

Schulz, H.-J. (2011). Treevis.net: A tree visualization ref-

erence. IEEE Computer Graphics and Applications,

31(6):11–15.

Shneiderman, B. (1992). Tree visualization with tree-maps:

2-D space-ﬁlling approach. ACM Transactions on

Graphics, 11(1):92–99.

Stasko, J. T. and Zhang, E. (2000). Focus+context display

and navigation techniques for enhancing radial, space-

ﬁlling hierarchy visualizations. In Proceedings of the

IEEE Symposium on Information Visualization, pages

57–65.

Ware, C. (2004). Information Visualization, Second Edi-

tion: Perception for Design (Interactive Technolo-

gies). Morgan Kaufmann, 2nd edition.

Wertheimer, M. (1923). Untersuchungen zur Lehre von der

Gestalt. II. Psychological Research, 4(1):301–350.

Wetherell, C. and Shannon, A. (1979). Tidy drawings of

trees. IEEE Transactions on Software Engineering,

5(5):514–520.

Wilson, E. O. (1984). Biophilia. Harvard University Press.

Yang, J., Ward, M. O., Rundensteiner, E. A., and Patro, A.

(2003). InterRing: A visual interface for navigating

and manipulating hierarchies. Information Visualiza-

tion, 2(1):16–30.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications