High Performance Particle Tracking Velocimetry for Fluidized Beds

Jouni Elfvengren, Jari Kolehmainen and Pentti Saarenrinne

Department of Engineering Design, Tampere University of Technology, Korkeakoulunkatu 6, Tampere, Finland

Keywords:

Particle Tracking Velocimetry, Fluidized Bed, Particle Sizing, GPU Computing.

Abstract:

Fluidized beds are used in wide variety of industrial applications. These applications range from energy

production to chemical industry. Particle tracking velocimetry (PTV) is an efﬁcient way to study small scale

behavior inside ﬂuidized beds. An accurate PTV algorithm has to be able to perform also in relatively dense

suspensions where particles may overlap and form clusters. PTV algorithms typically proceed from locating

the particles to tracking their motion. Typically the particle locating has been based on either proﬁle matching

or image intensity thresholding. This study proposes a combined method that tries to take advantage of the

both methods to overcome difﬁculties associated with dense suspensions. The method was tested in a synthetic

case and in an experimental ﬂuidized bed case. The synthetic tests showed a slight increase in error when the

number of particles increased, but the error level remained acceptable. Results obtained from the ﬂuidized

bed were visually inspected. Visual inspection showed that most of the particles were tracked correctly, which

suggests that the proposed method performs well also in practice.

1 INTRODUCTION

In a ﬂuidized bed, the upward air ﬂow from the grate

(located at the bottom of the bed) causes sand and

other solid particles to behave in a more ﬂuid-like

manner. Fluidized beds are used in many industrial

applications, such as fuel boilers and other multiphase

chemical reactors. Due to the complexity of the ﬂow

inside a ﬂuidized bed, most of the research in this ﬁeld

is more or less dependent on experimental informa-

tion.

Particle Tracking Velocimetry (PTV), as the name

suggests, is a measurement method where individual

particles are tracked. The particles may be already

present in the ﬂow, for instance in a ﬂuidized bed,

or they are inserted into the ﬂow as tracer particles.

The examined ﬂow must be illuminated by a powerful

light source (typically a laser) to obtain high enough

frame rate to capture quickly moving particles within

the short exposure time of a high-speed camera. Dis-

placement vectors are obtained by tracking the move-

ment of particles between sequential frames. Since

the frame rate is known, the velocity can be obtained

from the displacement.

PTV has been used in a wide variety of applica-

tions ranging from laser machining (Viitanen et al.,

2012) to biomedical research (Smal et al., 2007). In

the ﬂuidized bed research, PTV is effective analysis

method for low volume fraction ﬂows, where the solid

suspension is not too dense. This type of ﬂow condi-

tion typically exists in the upper parts of the ﬂuidized

bed. One of the main advantages of PTV is that it can

be used to describe the very small scale behavior, such

as the solid phase turbulence associated to so called

granular temperature (Dijkhuizen et al., 2006).

PTV is typically based on either proﬁle matching

based on cross correlations, see for instance (Marxen

et al., 2000), or thresholding image greyscale values,

as done by (Feng et al., 2007). While the thresholding

approach is effective when there are only few particles

present, and their proﬁle is simple, it fails in dense

suspensions. On the other hand, the proﬁle matching

yields in poor accuracy for particle center points if no

interpolation or distribution ﬁtting is applied. Reli-

able sub-pixel accuracy is a crucial property in high

frame rate applications, where the consecutive dis-

placements are small.

In this study, the solid phase of the ﬂuidized bed

consisted of small spherical glass particles. The trans-

parent glass particles tend to generate non-Gaussian

proﬁles to image plane when light is supplied from

behind the particles relative to camera. The parti-

cles can be observed from the images as dark rings

which have bright centers. Although the proﬁle is

non-Gaussian in general, the proﬁle of a dark ring can

be approximated as Gaussian. The described shadow

441

Elfvengren J., Kolehmainen J. and Saarenrinne P..

High Performance Particle Tracking Velocimetry for Fluidized Beds.

DOI: 10.5220/0004659404410449

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 441-449

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

proﬁle of a particle is relatively easy to detect, and the

bright center points increase the performance of PTV

in dense suspensions.

In this work, a combined approach based on both

thresholding and proﬁle matching is proposed. The

goal is to formulate a credible PTV algorithm that

would have excellent sub-pixel accuracy, while be-

ing able to perform also in dense suspensions, where

some particles are inevitably overlapped. The latter

property is crucial in ﬂuidized bed research, since the

particles tend to form clusters, where they are very

close to each other. The performance of the pro-

posed method is improved by parallel computing on a

Graphics Processing Unit (GPU).

2 EXPERIMENTAL SETUP

The experimental setup of this study consists of a

nearly 2-dimensional ﬂuidized bed, a diode laser and

a high-speed camera. A schematic illustration of the

experimental setup is shown in Figure 1. The ﬂu-

idized bed is 6mm thick, and 100mm wide. It was

operated with inlet pressure of 0.8bar. The high speed

camera was placed in front of the bed. The bed was il-

luminated from behind by Cavitar HF diode laser with

wavelength of 810nm. The laser beam was expanded

with Cavitar micro optics. An optical bandbass ﬁlter

was also used to reduce random noise. The bandpass

ﬁlter was designed for the mean value of 810nm with

the bandwidth of ±10nm. Pressurized air was sup-

plied to an expansion zone beneath the bed and blown

to the ﬂuidized bed via four grate nozzles. Before en-

tering the grate, air ﬂow passes a humidiﬁer, which

was used to decrease static electricity. Static electric-

ity can cause unwanted clustering and particle stick-

ing to the walls of the ﬂuidized bed.

Particles tracked from digital images are typically

small tracer particles designed to follow closely the

motions of the examined ﬂow. These tracer particles

range from < 1 to 30µm in diameter in gas ﬂows ac-

cording to (Melling, 1997). However, in the exper-

imental case presented in this paper, the interest is

aimed at tracking the motion of substantially larger

spherical glass particles with the nominal diameter of

200µm. Most of these particles are clearly visible,

but some may be a bit out of focus, even though max-

imum possible depth of ﬁeld (DOF) is achieved by

minimizing the size of the camera aperture while en-

suring sufﬁcient exposure. Problems in detecting sin-

gle particles arise when multiple particles are packed

in clusters. Particles in a cluster can be only momen-

tarily joined together while moving in different direc-

tions at different velocities. They can also be bonded

together by surface forces and move as a group, which

is less usual based on the experimental data.

In general, an adequately high frame rate should

be chosen when recording very fast particle mo-

tions. The frame rate of the camera was thus set to

1500fps, and the focal ratio to f /12. These settings

kept the displacements of particles between consecu-

tive frames relatively small, while allowing sufﬁcient

DOF as explained in the previous section. It should

be noted that when a coherent laser, such as Nd-YAG

laser, is used, setting the focal ratio too high can cause

unwanted total reﬂections from the diffuser. However,

the laser used in this study was not of the coherent

type, and the mentioned problem does not occur.

Optical ﬁbre

Fluidized bed

Diffuser

Bandpass ﬁlter

Camera

Figure 1: Schematic picture of the measurement setup.

3 PTV ALGORITHM

3.1 Proﬁle Matching Algorithm

When particle suspension is illuminated from behind,

there is usually a bright spot in the middle of the parti-

cle. The mid area between the boundary and the cen-

ter of the particle has typically the smallest intensity.

The detailed proﬁle could be computed from the Mie

scattering theory (Bohren and Huffman, 1983). How-

ever, camera causes Gaussian blur to the proﬁle an-

ticipated by the Mie theory. In addition, the sensor

voltage of the camera cell and light intensity might

not be linear. Therefore, in this study a more direct

approach is taken.

A particle image is thought to consist of a torus of

dark points with a diameter of d. Camera then sees a

shadow of each of these points. If the lowest intensity

of the particle is denoted by b, and the bright back-

ground intensity by w then the particle proﬁle at point

x can be given by superposition

J(x) = w(1 − φ(x)) + bφ(x), (1)

where φ(x) is a proﬁle function.

The proﬁle function for the above mentioned torus

with Gaussian blur is given by

φ(x) =

kyk=d

N(x|y,Σ)dy, (2)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

442

where N(·|y,Σ) denotes the density function of a 2D

normal distribution with mean value y, and covariance

matrix Σ. In this study, the covariance matrix had a

diagonal structure.

The algorithm proceeds by looping over all the

points in an image. From each point y a neighbor-

hood of that point I

(x), also referred as the mask,

is compared to the proﬁle computed by Equation (1).

The background intensity of the Equation (1) is cho-

sen prior any computations. The lower intensity value

b is estimated as the average color on a circle of ra-

dius d around the point y. The likelihood of point y

being the center of a particle is estimated as

f (y) =

kJ(x) − I

(x)k

N(x|0,Σ

)dx, (3)

where Σ

is covariance matrix of the mask. The co-

variance matrix is used to increase the value of inte-

rior points over the boundary points, and is a common

approach when computing image correlations.

The mask was chosen as a square, with size of

12 × 12 pixels. A circular or ellipsoidal mask could

also be interesting, but a square mask was used due to

its simplicity. In Figure 2 an example particle and a

suitable mask for proﬁle matching has been plotted.

Figure 2: Example particle (left) and suitable proﬁle match-

ing mask (right).

Since the f values computed by Equation (3) are

independent on other f values, they can be com-

puted quite efﬁciently by a Graphics Processing Unit

(GPU). In the study, it was found out that most of the

time was spend in transferring the image to the GPU

memory from the Random Access Memory (RAM).

The bright particle centers were recognized from

the f values by searching local minimums. Since

the background is not completely homogenous due

to auto interference of the laser, there is typically a

large number of local minimums in the background.

However, the local minimums appearing in the back-

ground are typically larger by a magnitude than the

actual particles, and therefore are relatively ease to

distinguish from the actual particles.

The downside of the above described method is

that it is very sensitive to diameter value d. This

can cause multiple recognitions inside a single par-

ticle and some systematic errors, where the algorithm

places the center of particle systematically too near

the boundary of the particle. To remedy this problem

a clustering method can be used to connect too-near

recognitions.

3.2 Thresholding Method

In order to identify particles from a greyscale image,

it must be ﬁrst decided whether a pixel of the image

contains information about a particle or not. In this

process, a binary image with ones representing the in-

formative particle regions and zeros representing the

non-informative background region is generated.

The most common binarization method is proba-

bly the single threshold binarization. In this method,

a single threshold value is selected and the binary im-

age is computed based on whether a pixel is above

or below the selected threshold value. Although

this method is simple and fast to execute, it requires

clearly separable particle greyscale values from the

background greyscale values. Even though the signal

to noise ratio (SNR) in the images would be sufﬁcient,

this method lacks the ability to take account the non-

uniform illumination conditions typically present in

experimental setups.

In this paper, a correction of inhomogeneous illu-

mination is combined with the single threshold bina-

rization, leading to an efﬁcient and reliable binariza-

tion method.

3.2.1 Correction of Inhomogeneous Illumination

In experimental setups, the inhomogeneous illumi-

nation conditions can be caused by several factors.

For example, the amount of illumination decreases to-

wards the light direction due to absorption and scat-

tering from the measured particles and the ﬂuid, when

a laser light sheet is passed from one side to the cam-

era’s ﬁeld of view. Also possible reﬂections from the

solid structures cause problems when using the sin-

gle threshold method. In the experimental setup pre-

sented in this paper, the uneven background illumi-

nation proﬁle is caused by the diverging optics of the

back laser. The unevenness can be observed from the

decreasing greyscale values towards image edges.

The inhomogeneous illumination conditions can

be easily corrected if it is possible to obtain images

where the illumination conditions are otherwise sim-

ilar to the experimental setup but no particles are

present (J

ahne, 2004). These images are usually

called as reference or background images. In order to

reduce the effect of random noise in the background

images, it is recommeded to compute pixelwise av-

erages across a reasonable set of background images.

HighPerformanceParticleTrackingVelocimetryforFluidizedBeds

443

The inhomogeneous illumination is corrected by di-

viding every pixel of the image G by the correspond-

ing pixel of the average background image R

= c

, (4)

where scalar c is used to scale the grey values of the

corrected image. The scaling factor c was selected

as 100 in this work. Values of the corrected image C

can be thus considered as percentage of the image G

greyscale value to the background image R greyscale

value. Notice that the corrected image C is stored as

double precicion data type instead of the original im-

age’s 8-bit unsigned integers. An example of a ran-

dom particle image corrected by the average back-

ground image is given in Figure 3.

Figure 3: Particle image, average background image and

illumination corrected particle image.

3.2.2 Single threshold Binarization

After the correction of inhomogeneous illumination,

it is possible to use the single threshold binarization

method with outstanding results compared to the non-

corrected images. The single threshold binarization

for corrected images is deﬁned as logical operation



1, if C

≤ C

0, if C

> C

(5)

where C

is the optimum threshold value.

While the correction of inhomogeneous illumina-

tion enables the usage of the single threshold binariza-

tion, it still leaves us the problem of selecting an opti-

mal threshold value. Basically the thresholded pixels

should contain as much information about the parti-

cle as possible, but false particles stepping out of the

background should not occur. On the one hand, when

decreasing the threshold value (in the case of dark

particles), some boundary pixels are left outside the

thresholded region. In this case some information of

the particle has been lost and the shape of the thresh-

olded boundary starts to have an effect on the particle

center point computation, leading to increased pixel

locking effect as shown by (Feng et al., 2007). On the

other hand, when increasing the threshold value (in

the case of dark particles) beyond the optimum value,

false particles start to arise from the background. The

size of the false particles range from 1 pixel to several

pixels, and the size increases as the threshold value

increases.

It is possible to search the optimum threshold

value by comparing the total amount of found par-

ticles at different threshold values from an extensive

sample of corrected particle images. If the minimum

size of the measured particles is clearly larger than the

size of the small false particles, containing only some

pixels, it is practical to remove all particles below a

selected minimum size in pixels (see Section 3.3.3).

It should be noted that also some incomplete parti-

cles located at the image edges are thus considered as

small particles. In the case of dark particles, the max-

imum threshold value, with which the total amount

of found particles remains at fairly constant level, is

selected as an optimum threshold. As pointed out by

(Feng et al., 2007), it should be also checked from a

sub pixel map that the pixel locking effect does not

occur at the selected threshold value.

The optimum threshold is determined experimen-

tally using every twentieth frame of the recorded data.

As can be seen from Figure 4, the amount of all

found particles begins to rise notably after the thresh-

old value 72, which is thus selected as the optimum

value. Interestingly, the amount of selected particles

remains very stable even when the total amount of

found particles starts a rapid rise. This is because the

small particles below a selected minimum size are re-

moved from the total amount of found particles lead-

ing to the number of selected particles. The observed

stability in the amount of selected particles is a highly

desirable feature of the algorithm.

50 60 70 80

8800

9000

9200

9400

threshold value

number of particles

← C

= 72

all particles

selected particles

Figure 4: Amount of all particles and selected particles as

function of threshold value.

A sub pixel map of particle locations in the opti-

mum threshold selection is presented in Figure 5. The

sample size of the corrected particle images was the

same as in the optimum threshold determination. No

visible pixel locking pattern (Feng et al., 2007) can be

observed, so the selected optimum threshold value is

adequate. In general, when the particle average size is

quite large (as in the experimental case), pixel locking

occurs in a smaller degree than in the case of particles

containing only some pixels.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

444

0 0.5 1

0.5

Figure 5: Subpixel image for particle center point locations

at optimum threshold value.

3.3 Particle Indexing

In this work, the thresholding method is combined

with the proﬁle matching method. The particle index-

ing is thus performed in two steps. In the ﬁrst step,

thresholded particle regions in the binary image are

indexed by tracking their outer boundaries. In the sec-

ond step, particle clusters are separated based on the

center points recognized by the proﬁle matching al-

gorithm. Each pixel of a particle cluster is re-indexed

using the criteria of closest distance to a center point.

After these steps, every pixel of every thresholded

particle region is given an index that determines the

particle in which it belongs to.

A major advantage in combining the proﬁle

matching method with the thresholding method is the

sub pixel accuracy obtained by the calculation of the

particle center points from thresholded and indexed

pixels as explained in Section 3.4. Additionally, the

separation of particles from particle clusters increases

signiﬁcantly the reliability of the identiﬁed particles

in comparison to plain thresholding method.

3.3.1 Thresholded Particle Region Indexing

The thresholded particle regions are indexed by track-

ing their outer boundaries using the Freeman chain

code of eight directions, explained by (J

ahne, 2004).

In this algorithm, the binary image is scanned line by

line and when a binary value one (that is not yet in-

dexed) is found, the outer boundary binary ones are

tracked in clockwise direction using 8 possible neigh-

bor directions. In this work, all pixels inside the ob-

tained closed boundary are indexed by a number that

deﬁnes the particle. Even though there may be some

binary zero pixels inside the closed boundary (typi-

cally the bright spot in the middle of the particle), the

corresponding pixels of the corrected image C proba-

bly contain in some extent useful information and can

be thus considered as a part of the particle region.

3.3.2 Particle Cluster Separation

It is possible that an indexed particle region contains

multiple particles. The recognized particle center

points calculated with the proﬁle matching algorithm

are used here to separate single particles from particle

clusters. If the indexed particle region contains more

than one center point, the pixels inside are separated

into re-indexed regions based on their closest distance

to a center point. When particles are not too over-

lapped and the center points are correctly recognized,

this method usually leads to well-separated particles.

The presented particle separation process com-

bines the advantages of the thresholding method and

the proﬁle matching method. The thresholded particle

regions are considered to contain reliable information

of the particles being measured. By checking that a

center point recognized by the proﬁle matching algo-

rithm is inside a thresholded region, it is ensured that

no false particle center point matches arising from the

background, are considered as actual particles. If the

proﬁle matching algorithm has failed to recognize a

center point inside an indexed particle region, it is as-

sumed that the thresholded region is correct and con-

tains a single particle.

When particles are partially overlapped, some pix-

els evidently belong to both particles, but are straight-

forwardly divided to different particles using the pre-

sented separation method. This clearly leads to some

error in the calculation of the particle center point in

Section 3.4. In cases where particles are so over-

lapped that only one or no center point at all is rec-

ognized by the proﬁle matching method, some error

also occurs in the calculation of the center point of the

overlapped particle cluster. The magnitude of these

errors can be examined by testing the method using

synthetic particle data.

3.3.3 Removing Small Particles

Even with the optimal threshold value some small

false particles can still occasionally arise from the

background. To ensure that no false particles are con-

sidered as real particles, all particles below a selected

minimum size in pixels are removed. Evidently, the

particle minimum size should be notably smaller than

the minimum size of the measured particles. The par-

ticle minimum size should be selected with care, be-

cause also some incomplete particles are inevitably

removed from the image edges. In this paper, approx-

imately 20% of the average size of the measured par-

ticles is used as the particle minimum size.

HighPerformanceParticleTrackingVelocimetryforFluidizedBeds

445

3.4 Particle Center Point Computation

The center point position of a particle is determined

by the greyscale value weighted position of pixels

X =

∑

−C

base

)

∑

−C

base

)

, (6)

where i represents the pixels belonging to an indexed

particle, X

is the pixel center point location vector,

is the corrected greyscale value of a pixel of the

particle i and C

base

is the base line value.

It has been shown by (Feng et al., 2007) that se-

lecting C

base

= C

minimizes the total error in the sub

pixel accuracy caused by the pixel locking effect as-

sociated with the pedestal part of the intensity that re-

mains below the threshold value. Also in this work,

the base line value equal to the optimum threshold

value is selected.

3.5 Particle Tracking

Several particle tracking algorithms have been devel-

oped for tracking the motion of single particles from

digital images. Although promising results have been

obtained using many of these methods, the authors de-

cided to demonstrate the performance of a relaxation

based tracking method. In this work, the original re-

laxation method (ORX), summarized by (Ohmi and

Li, 2000) and originally developed by (Barnard and

Thompson, 1980), is selected for tracking the parti-

cles. The implementation of the original relaxation

method used in this work follows closely to the one

presented by (Ohmi and Li, 2000). The new relax-

ation method introduced by (Ohmi and Li, 2000) was

recently further improved by (Jia et al., 2013). For the

sake of simplicity, the additional relaxation parame-

ters and other improvements to the original relaxation

method, discussed by (Ohmi and Li, 2000) and (Jia

et al., 2013) among other authors, are not studied in

this work. The original relaxation algorithm is eas-

ily expandable to include the latest improvements on

demand.

The relaxation methods calculate particle match-

ing probabilities iteratively until the probabilities

have converged to nearly constant levels. During

these iterations, the probability of a correct matching

particle is increased close to one. A major advantage

of the relaxation methods is the no-match probabil-

ity formulated in the relaxation algorithm, which re-

duces clearly the amount of false matching particles

compared to other particle tracking methods. A useful

feature is also the ability to deﬁne the search radiuses

, R

and R

(Ohmi and Li, 2000) to suitable values

depending on the examined case in order to achieve

high quality tracking results. In general, the relax-

ation methods work well in complicated ﬂows and

dense particle regions in comparison to other meth-

ods (Jia et al., 2013), which suggest that these meth-

ods are applicable to the turbulent two-phase ﬂow of

the ﬂuidized bed examined in this article.

4 SYNTHETIC IMAGES

In this work, an artiﬁcial particle grayscale distribu-

tion is used to generate synthetic particles that re-

semble the particle proﬁle observed in the actual im-

ages. The artiﬁcial greyscale distribution is deﬁned as

a twin normal distribution expanded into two dimen-

sions by the equation

z(x,y) ∝ N(r(x,y))|µ,σ) + N(r(x,y))| − µ, σ), (7)

where

r(x, y) =

(x − x

)

+ (y − y

)

(8)

is the radius from the center point of the distribution

) to any speciﬁc point (x,y). The normal dis-

tribution N parameters were selected as µ = 2.6 and

σ = 1.7 and the distribution values z(x, y) were mul-

tiplied by an appropriate scaling constant c

to make

the greyscale values computed from the given distri-

bution similar to measured greyscale intensity proﬁle.

Accurate values in every pixel of the synthetic image

were obtained by numerically evaluating the double

integral

p,mn

= c

m+0.5

m−0.5

n+0.5

n−0.5

z(x,y)dxdy (9)

using a 9-point Gauss quadrature rule. The result-

ing center line proﬁle of a synthetic particle G

with

center point placed at origin (X

) = (0,0) is pre-

sented in Figure 6. Notice the slight difference be-

tween the values integrated over every center line

pixel presented with bars and the values of the dis-

tribution function multiplied with c

and marked with

plus signs.

The synthetic particle images are generated by

randomly spreading a selected amount of the distri-

bution center points (x

) into an image area of

1024 × 1024 pixels. Particles are then integrated one

by one from the distribution values using Equation

(9). When combining overlapped particles to a sin-

gle synthetic image, the maximum greyscale value in

the corresponding pixels is selected. In reality, the

scattering light does not behave this way, but this is

a reasonable simpliﬁcation since the actual scattering

proﬁle is not modeled.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

446

−8 −4 0 4 8

position (pixels)

grayscale value

Figure 6: Cross-sectional greyscale proﬁle of synthetic par-

ticle.

The standard deviation of the background

greyscale values is estimated based on an image,

where no particles are present, corrected by Equation

(1). The mean of the normal distribution in the syn-

thetic background images is selected as µ = 100 and

the standard deviation is approximated as σ = 1.5. As

a result, a synthetic particle image including the back-

ground random noise is generated by subtracting the

synthetic particle image from the background image.

5 RESULTS

5.1 Generic Test

The errors encountered in particle center point calcu-

lation can be divided into two different groups. This

is achieved by computing the nearest computed center

point for every synthetic center point. If the amount

of synthetic center points connected to a single com-

puted center point is more than one, the synthetic

center point is considered to belong to multi-match

group. Otherwise it belongs to single-match group.

Obviously the sum of synthetic single-match particles

and synthetic multi-match particles equals the total

number of synthetic particles in a single frame.

The overall error in the synthetic test is computed

for each frame as the average of all distances between

a synthetic center point location and the closest com-

puted center point location. The average overall error

increases at nearly linear rate from 0.13 pixels (250

particles) to 0.42 pixels (1000 particles) as Figure 7

indicates. In Figures 7 and 8 there are 250, 500, 750

and 1000 synthetic particles in the frames 1-100, 101-

200, 201-300 and 301-400, respectively. The aver-

age value for every set of 100 frames is plotted as a

straight line to these ﬁgures.

In Figure 8 the effect of multi-match particles to

the overall error is compared. The increase of the

overall error is mostly caused by the synthetic center

points that are connected to multiple computed cen-

0 100 200 300 400

frame

error (pixels)

↓ multi−match

0 100 200 300 400

0.1

0.2

0.3

0.4

0.5

frame

error (pixels)

overall ↓

↓ single−match

Figure 7: Multi-match, single-match and overall error in

synthetic test.

ter points. The average effect of multi-match parti-

cles to the overall error increases as the total amount

of particles increases. Although the average error of

multi-match particles remains at almost constant level

around 2.45 pixels as Figure 7 indicates, the effect to

total error increases due to the increasing ratio of mul-

tiple matching particles presented in Figure 8.

0 100 200 300 400

frame

ratio to all particles (%)

multi−match ↓

0 100 200 300 400

100

frame

effect to overall error (%)

↓ multi−match

Figure 8: Ratio of multi-match particles to all synthetic par-

ticles. Effect of multi-match particles to overall error in syn-

thetic test.

The average error of single-match particles in-

creases as the amount of particles increases as can

be seen from Figure 7. Although the ratio of single-

match particles to all synthetic particles decreases

as Figure 8 conversely indicates, the average error

of single-match particles increases from 0.05 to 0.11

pixels. This is probably caused by the increased prob-

ability of neighboring particles, which inevitably re-

duces the sub-pixel accuracy as the thresholded pixels

of particle clusters are divided to separate particles.

5.2 Experimental Test

Figure 9 shows the selected amount of particles af-

ter thresholding, particle cluster separation and re-

moval of small particles. The selected amount of par-

ticles shows a high ﬂuctuation because also the actual

amount of particles varies with a large amplitude in

the measurement area of the highly turbulent upper

part of the ﬂuidized bed. However, the amount of se-

lected particles in sequential frames shows only mod-

erate ﬂuctuations, which means that the amount of

HighPerformanceParticleTrackingVelocimetryforFluidizedBeds

447

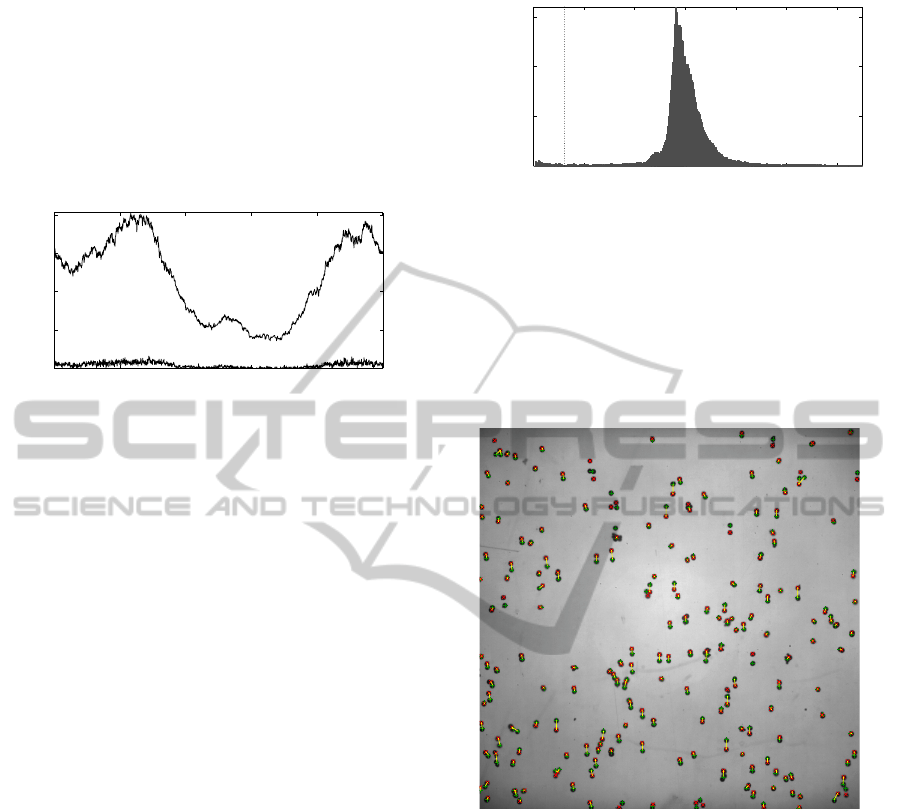
computed particles in sequential frames is quite con-

tinuous, as it should. No unexpected outliers are ob-

served, which proves the robustness of the algorithm.

The amount of separated particles from the thresh-

olded particle regions is also presented in Figure 9. As

expected, the amount of separated particles increases

notably when the total amount of particles increases

and more particles become close to each other.

300 600 900 1200 1500

100

150

200

frame

number of particles

↓ selected

↓ separated

Figure 9: Selected amount of particles and separated

amount of particles from particle clusters.

The sub-pixel image for all computed center

points in every frame of the experimental test shows

no signs of pixel locking. This implies that the

computed center points matching a single particle

are within excellent sub-pixel accuracy (Feng et al.,

2007). As the synthetic test demonstrates, the ac-

curacy drops to pixel scale in cases where multiple

actual particles computed as one particle. However,

the degreased accuracy in the case of particle clusters

is at some degree diminished at the particle tracking

stage when suitable matching particles are not found

between sequential frames.

The particle size distribution is plotted as a his-

togram in Figure 10. The distribution contains a sin-

gle peak at the particle size of 141 pixels and has a

mean value of approximately 150 pixels. The num-

ber of particles is thus slightly more concentrated on

the right-hand side from the peak value. The reason

for this is probably that the algorithm is not able to

separate all particle clusters to single particles. If the

particles are somewhat normally distributed around

the nominal value, the measured particle size distribu-

tion should also resemble this distribution. The non-

separated particle clusters evidently shift the balance

towards larger size particles.

In Figure 11 a vector ﬁeld computed from frames

319-320 is presented. The particle tracking is com-

puted by the original relaxation method (Ohmi and

Li, 2000). Parameters used in the experimental test

are R

= 28 for sequential radius (sequential frames),

= 90 for neighbor radius (ﬁrst frame) and R

= 20

for parallel motion radius (sequential frames). The

selected value for parallel motion radius allows some

clearly erroneous displacement vectors. On the other

0 50 100 150 200 250 300

2000

4000

6000

particle size (pixels)

number of particles

← min size

Figure 10: Particle size histogram in experimental test. Par-

ticles below minimum size are removed.

hand, decreasing this value will cancel out many

good matching particles in sequential frames. In gen-

eral, when applied to highly turbulent ﬂow where the

motion of single particles is chaotic, this parameter

should have clearly higher value than in ﬂows where

the particle random motion is considerably smaller.

Figure 11: Sample vector ﬁeld. Green equals initial and red

ﬁnal computed center point locations.

The sequential radius of the particle tracking al-

gorithm is selected based on the observed particle

motion between two sequential frames. It should be

pointed out, that displacements exceeding this value

are not considered as possible matching particles. The

selection of the neighbor radius R

proves out to be

quite tricky, because the particle density varies highly

in different locations of a single frame and in different

frames of the experimental test. This problem is rarer

in tracer particle experiments, where the density of the

seeding particles remains typically at constant level.

As a solution to this problem, the authors propose in-

creasing the radius R

, until an adequate number of

neighbor particles are inside the perimeter. However,

in the experimental test of this work, the neighbor ra-

dius is simply set to a high enough value to include

some neighbor particles also in dilute regions.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

448

6 CONCLUSIONS

The proposed method was tested in a synthetic test

case with computer generated random data, and with

a cold model ﬂuidized bed. The synthetic test case

allowed one to inspect the behavior of the PTV al-

gorithm with varying number of particles. From the

synthetic test cases one can conclude that there are

two major sources of error, namely error caused by

ﬁnite sub pixel accuracy, and error caused by inabil-

ity to detect the particle. Both errors increased when

the number of particles was increased. However, the

latter error type became quickly dominant.

In statistical studies, usually the number of detec-

tions is not of main concern, but rather the credibil-

ity of the detections. As shown in the synthetic test

case results, sub pixel accuracy showed only slight

increase with the increase of particles. On the other

hand, most PTV based studies in ﬂuidized beds are of

the statistical type. Thus the proposed method is well

suited for the ﬂuidized bed research, or other simi-

lar problems, where particles exist in relatively dense

suspensions.

The proposed method was also tested in a cold-

model of a ﬂuidized bed. Since the real displacements

are not known the data was only visually inspected.

Visual inspections showed that the method most of the

time able to detect particles, but failed occasionally to

detect all of the particles from clusters. On the other

hand, number of false positives (particle detections on

the background) was very small, which is especially

important in statistical studies.

Structure of the algorithm is easy to parallelize,

as particles interact with each other in very limited

way on the detection phase. The particle tracking al-

gorithm uses information of the neighboring particles,

which is difﬁcult to parallelize, but is computationally

much less expensive than the detection phase. Proﬁle

matching algorithm used in this study does assume

that the particle proﬁles are independent of the neigh-

boring particles. While this assumption is the key for

computational efﬁciency, it limits the maximum par-

ticle density. Future developments in this ﬁeld are

likely to include interacting particles models, for fur-

ther improvements in accessible particle density.

ACKNOWLEDGEMENTS

This work has been done as a part of Online FB-CFD

project funded by TEKES. The authors would like to

thank S. Kallio and J. Peltola for helpful discussions

regarding the topic. In addition, authors would like

to thank Cavitar Ltd. for supplying lasers and optics.

As a source of useful information about multiphase

ﬂows, the authors also wish to thank COST FP-1005

project for cooperation.

REFERENCES

Barnard, S. and Thompson, W. (1980). Disparity analysis

of images. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 2:333–340.

Bohren, C. and Huffman, D. (1983). Absorption and Scat-

tering of Light by Small Particles. John Wiley and

Sons, New York, 1st edition.

Dijkhuizen, W., Bokkers, G. A., Deen, N. G., van Sint An-

naland, M., and Kuipers, J. A. M. (2006). Extension of

piv for measuring granular temperature ﬁeld in dense

ﬂuidized beds. American Insitute of Chemical Engi-

neering, 53:108–118.

Feng, Y., Goree, J., and Liu, B. (2007). Accurate particle

position measurement from images. Review of Scien-

tiﬁc Instruments, 78.

ahne, B. (2004). Practical Handbook on Image Processing

for Scientiﬁc and Technical Applications. CRC Press,

Boca Raton, 2nd edition.

Jia, P., Wang, Y., and Zhang, Y. (2013). Improvement in

the independence of relaxation method-based particle

tracking velocimetry. Measurement Science and Tech-

nology, 24:055301 (13pp).

Marxen, M., Sullivan, P. E., Loewen, M. R., and Jahne, B.

(2000). Comparison of gaussian particle center es-

imators and the achievable measurement density for

particle tracking velocimetry. Experiments in Fluids,

29:145–153.

Melling, A. (1997). Tracer particles and seeding for par-

ticle image velocimetry. Measurement Science and

Technology, 8:1406–1416.

Ohmi, K. and Li, H. (2000). Particle-tracking velocimetry

with new algorithms. Measurement Science Technol-

ogy, 11:603–616.

Smal, I., Niessen, W., and Meijering, E. (2007). Advanced

particle ﬂtering for multiple object tracking in dy-

namic fuorescence microscopy images. Biomedical

Imaging: From Nano to Macro, 4:1048–1051.

Viitanen, T., Kolehmainen, J., Okamoto, Y., and Piche, R.

(2012). Spatter tracking in laser machining. Proceed-

ings of 8th International Symbosium on Visual Com-

puting, pages 626–635.

HighPerformanceParticleTrackingVelocimetryforFluidizedBeds

449