
Using the Base Semantics given by fUML for Verification
Alessandro Gerlinger Romero
1∗
, Klaus Schneider
2
and Maur
´
ıcio Gonc¸alves Vieira Ferreira
1
1
Satellite Tracking and Control Center, Brazilian National Institute for Space Research, S
˜
ao Jos
´
e dos Campos, Brazil
2
Department of Computer Science, University of Kaiserslautern, Kaiserslautern, Germany
Keywords:
Base Semantics, fUML, UML, Alf, Formal Methods, Theorem Proving, Verification.
Abstract:
The lack of formal foundations of UML results in imprecise models since UML only defines graphical nota-
tions, but not their formal semantics. However, in safety-critical applications, formal semantics is a require-
ment for verification. Semantics for the key parts of activities and classes of UML is defined by the semantics
of a foundational subset for executable UML models (fUML). Moreover, the base semantics given by fUML
defines the formal semantics of UML. In this paper, we evaluate a subset of the base semantics given by
fUML covering its formal definition and its use for verification. From the practical perspective, we show with
a simple example how the base semantics can support formal verification through theorem proving. The initial
results show that the base semantics, when mature, can play an important role in the formal verification of
UML models.
1 INTRODUCTION
Simulation and verification of models is the cor-
nerstone of any model-driven development (MDD).
Supporting a large number of MDD methods, Uni-
fied Modeling Language (UML) (OMG, 2011) and
its derivatives have demonstrated a capability for
top-down design refinement for large-scale systems.
However, while UML is expressive, the lack of for-
mal foundations of UML results in imprecise models,
since UML only defines the syntax of diagrams, but
not their formal semantics (Derler et al., 2012; Fecher
et al., 2005).
A major focus of systems and software en-
gineering has considered how to introduce preci-
sion in the approaches based on UML through
formal methods. This introduction can be a re-
quirement when dealing with safety-critical systems;
e.g., the IEC 61508 (functional safety of electri-
cal/electronic/programmable electronic safety-related
systems) defines formal methods as highly recom-
mended techniques for the highest safety integrity
level. Furthermore, DO-178C (software considera-
tions in airborne systems and equipment certification)
addresses formal methods as a complement to testing.
Although there are languages with a formal seman-
tics, there are no modeling languages with widespread
∗
This work was supported by the Brazilian Coordination
for Enhancement of Higher Education Personnel (CAPES).
use in systems and software engineering community
that have the attraction of UML (Graves, 2012). Ac-
cordingly, this paper focuses on the evaluation of
a formal foundation in UML concerning behavioral
definitions.
Behavior is defined in UML (OMG, 2011) mainly
by means of activity diagrams, sequence diagrams,
and state machine diagrams, which do not have for-
mal semantics (Derler et al., 2012) and, in gen-
eral, are also not executable. Behavioral definitions
could evolve with the semantics of a foundational
subset for executable UML models (fUML) (OMG,
2009), which consists of the key parts of activities
and classes. Hence, this version of specification de-
fines semantics, which includes an interpreter and a
formal definition of the semantics called the base se-
mantics. On the contrary, there are research papers
(Benyahia et al., 2010; Perseil, 2011) stating that
fUML is not yet suitable for behavioral modeling of
safety-critical systems. The reasons can be classi-
fied as follows: (1) current tools do neither allow the
use of model-checking nor theorem proving (Perseil,
2011), and (2) the execution model is often nondeter-
ministic (Benyahia et al., 2010). In the following, we
explore reason (1) in detail.
In this paper, we evaluate a subset of the base se-
mantics (we present this one in Section 4) covering
its formal definition and its useage for theorem prov-
ing. The major contributions of this work are: (1) it
5
Gerlinger Romero A., Schneider K. and Gonçalves Vieira Ferreira M..
Using the Base Semantics given by fUML for Verification.
DOI: 10.5220/0004662400050016
In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 5-16
ISBN: 978-989-758-007-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

shows how the base semantics can support theorem
proving, providing one solution for the deficiencies
found by (Perseil, 2011); (2) it detected issues in the
fUML specification (OMG, 2012) (see Appendix),
which suggests to enhance the specification. The ini-
tial results show that the base semantics, when ma-
ture, can play an important role in the formal verifica-
tion of models.
The remainder of this paper is organized as fol-
lows. In Section 2, related works are explored; in
Section 3, the necessary background is presented; in
Section 4, we define and evaluate a subset of the base
semantics for verification; in Section 5, we discuss
the results. Finally, conclusions are shared in the last
section.
2 RELATED WORKS
There is a large number of research papers about se-
mantics for models defined using UML. UML and
fUML share the definitions about activities. There-
fore, every research that has defined semantics for be-
havior based on activities is directly related to fUML.
Considering this relationship, works focused on be-
havioral semantics for UML, and fUML, can be clas-
sified as follows: (1) definition of an operational se-
mantics, (2) translation to other models, and (3) di-
rectly defining a model of computation (MoC).
The first class has led to definitions of the opera-
tional semantics for activities. (Jarraya et al., 2009)
presented a structural operational semantics (SOS)
(Plotkin, 1981) for a subset of activity diagrams of
systems modeling language (SysML) – a derivative
of UML. This subset comprised control nodes and a
generic action. The semantics covered advanced con-
trol flows such as unstructured loops and concurrent
control flows, and model checking was applied for
verification purposes. Focused on reactive systems,
(Kraemer and Herrmann, 2010) presented an opera-
tional semantics for a subset of activity diagrams of
UML. This subset included one action representing
method calls that are executed in one time unit. Fo-
cusing on control flows, this work defined time and
queues for synchronization, and applied model check-
ing for verification. (Grnniger et al., 2010) defined a
formal semantics for a subset of UML activity dia-
grams, using semantics variation points. This work
stated that all definitions, including the abstract syn-
tax, should be encoded in machine-readable form, al-
lowing the use of a theorem prover. (Knieke et al.,
2012) proposed common constructs for the definition
of operational semantics for a subset of activity dia-
grams. The subset covered the actions: CallBehav-
iorAction, SendSignalAction and AcceptEventAction.
In this case, semantics was described through algo-
rithms defined using pseudo-code, and did not com-
prise object flows.
A broad set of works adheres to translation
through definition of a mapping between UML and
a formal language. (Abdelhalim et al., 2012) de-
fined a method that receiving state machine diagrams
and activity diagrams (according to fUML) applied
a transformation to communicating sequential pro-
cesses (CSP). Later, the method used a model checker
to verify the resulting CSP representation. This work
focused on maintaining the behavioral consistency
between state machine diagrams and activity dia-
grams. (Perseil, 2011) suggested that a subset of ac-
tion language for fUML (Alf) (OMG, 2013a) – the
relationship between Alf and fUML is explained in
Section 3 – should be translated to PlusCal, which has
precise semantics defined by a translation to temporal
logic of actions (TLA) so that also the model checker
of TLA can be used for verification. (Maoz et al.,
2011) defined a translation from UML activity dia-
grams to a labeled transition system described using
the language of the SMV model checker. The subset
included control nodes and a generic action.
Concerning MoCs, (Benyahia et al., 2010) shows
that fUML and Alf are not directly applicable to
safety-critical systems because the MoC defined in
the fUML execution model was sequential and non-
deterministic. In spite of variation points provided by
fUML, this work recognized that they were not pow-
erful enough to change the MoC, and an alternative
extension of the core execution model was presented
to accommodate different MoCs. (Gerlinger Romero
et al., 2013) proposed constructs to change the MoC
of the fUML introducing the synchronous-reactive
MoC. (Combemale et al., 2013) presented an alterna-
tive to define domain-specific languages through the
combination of semantics of languages and MoCs.
The case study was fUML combined with two differ-
ent versions of the discrete-event MoC, one sequential
and another concurrent.
However, to the best of our knowledge, we have
not found works about the base semantics defined
in fUML, the relationship between it and other ap-
proaches for semantics definition (Plotkin, 1981;
Hoare, 1969), and how to use it for verification.
3 BACKGROUND
This section presents a review of the OMG (Object
Management Group) specifications related to fUML,
the base semantics, and its purpose.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
6

3.1 OMG Specifications
In UML, actions are the fundamental units of behav-
ior, and are used in activities to define fine-grained
behaviors (OMG, 2011). Considering this, fUML se-
lected part of actions defined in UML to model be-
havior, and part of expressiveness of classes to model
structure. The specification defines four elements for
the language: (1) abstract syntax, (2) model library,
(3) execution model, and (4) base semantics (OMG,
2012). The specification does not define a concrete
syntax, so the only syntax available for defining user
models is the graphical notation provided by UML,
namely activity diagrams, and class diagrams.
The abstract syntax is a subset of UML with ad-
ditional constraints, so a well-formed model is one
that meets all constraints imposed on its syntactic el-
ements by the UML abstract syntax as well as all
additional constraints imposed on those elements by
the fUML abstract syntax. These constraints are
the equivalent of the static semantics according to
fUML (OMG, 2012). Therefore, fUML does not de-
fine static semantics, i.e., context-sensitive constraints
which define a well-formed model.
The model library defines the primitive types,
primitive functions and, a way to interact with the en-
vironment (input and output).
The execution model is an interpreter written in
fUML (circular definition). The interpreter is defined
using core elements (nodes, classes, and edges) of
fUML that together form the base UML (bUML). In-
stead of using activity diagrams, the interpreter is de-
fined as equivalent code in Java. To support that, a
mapping from Java to activities is defined, consider-
ing only bUML. The execution model is defined to
support extensions, what is pursued using two tech-
niques: (1) defining explicit variation points, which
are: event dispatching scheduling (used in the inter-
object communication), and polymorphic operation
dispatching; (2) leaving three semantics elements un-
constrained, namely, timing, concurrency, and inter-
object communication. Base semantics breaks the cir-
cular definition of fUML providing a set of axioms
that constrains the execution.
Base semantics covers elements in bUML, and is
specified in first order logic based on process specifi-
cation language (PSL). PSL provides a way to disam-
biguate common flow modeling constructs in terms of
constraints on runtime sequences of behavior execu-
tion. A desired behavior is specified by constraining
which of the possible executions is allowed (Bock and
Gruninger, 2005; NIST, 2013). PSL and base seman-
tics are defined using Common Logic Interchange
Format (CLIF) (ISO, 2007).
Alf provides a textual concrete syntax for fUML
(OMG, 2013a). It is an action language that includes
primitive types (including real numbers), primitive
actions (e.g., assignments), and control flow mecha-
nisms, among others. It is object-oriented, and it is
an imperative language (like C and Java). The execu-
tion semantics for Alf is given by mapping the Alf
abstract syntax to the abstract syntax of the fUML
(OMG, 2013a).
Fig. 1 shows relationships between these OMG
specifications, where fUML is positioned in the cen-
ter, offering formal semantics for an executable subset
of UML (bottom), and supporting the textual action
language Alf (top).
Figure 1: Relationships between OMG specifications.
3.2 Base Semantics
As discussed in the previous subsection, fUML offers
an interpreter, which can be extended or completely
replaced, e.g., to address scattered scheduling algo-
rithm (Combemale et al., 2013) or nondeterminism
(Benyahia et al., 2010).
The specification states that the conformance for
an interpreter would be demonstrated by a formal
proof that it respects all the definitions of the base se-
mantics ((OMG, 2012); pp. 7). In order to understand
how a formal proof could be evaluated for a fUML
interpreter, Fig. 2 presents the relationships between
abstract syntax, execution model, semantic domain,
and base semantics.
Considering the package Semantics, the execution
model defines the semantic domain (which types an
execution manipulates, e.g., ActivityExecution, Ob-
ject, Reference), and an interpreter (an algorithm) that
UsingtheBaseSemanticsgivenbyfUMLforVerification
7

Figure 2: Relationships between fUML and base semantics.
maps instances of the abstract syntax to the seman-
tic domain (in fact, part of the execution model in
fUML). This semantic mapping defines the meaning
of a given activity.
In Fig. 2, the base semantics depends on the ab-
stract syntax, and is defined to formalize (using first-
order logic) the semantic mapping from abstract syn-
tax to the semantic domain without taking into ac-
count the particular interpreter offered by the execu-
tion model (recall that the base semantics only cov-
ers bUML elements). The technique applied to de-
fine this formal semantic mapping is called embed-
ding (Fikes et al., 2001).
Embedding is a technique to formalize a language,
where the abstract syntax and the semantic domain
are directly used in the axiomatization of the semantic
mapping. This semantic mapping is defined by a set
of axioms and inference rules. Furthermore, a com-
plementary set of inference rules is defined consider-
ing the abstract syntax, i.e., some syntactical patterns
are explicitly defined to support the inference rules of
the semantic mapping.
The base semantics does not formalize the abstract
syntax, which would demand a second order logic
that could only be emulated by CLIF with restrictions
(ISO, 2007).
Therefore, the package Formal Semantics defines
a set of axioms and inference rules that maps a for-
mal version of activities, defined using the embedded
abstract syntax, into a formal version of the semantic
domain.
A formal version of the semantic domain is called
model by logicians. Indeed, (Graves, 2012) recog-
nized that the use of the word model is different in
the modeling community and in the logic community.
For the former, model is a representation of the sys-
tem under consideration (source); whereas model is
a consistent interpretation for a given set of axioms
(result) for the second one.
In summary, CLIF offers the logic syntax, the
base semantics provides a set of axioms and infer-
ence rules that together with embedded user axioms
describing an activity form a mathematical theory. As
envisioned by fUML (OMG, 2012), this mathematical
theory should be used to evaluate formal properties of
an interpreter. Nonetheless, the same theory can be
used to verify properties of fUML models applying
the theorem proving approach.
4 VERIFICATION USING THE
BASE SEMANTICS
This section starts with an example to clarify the con-
cepts introduced in the previous section. Afterwards,
a subset of the base semantics, a rationale for this se-
lection, the relationship with other approaches for se-
mantic definition, and a proof using the presented ex-
ample is shown.
4.1 Example
Considering the representation of a user definition
using abstract syntax (a model according to modeling
community), Fig. 3 shows an activity diagram (I)
considering the fUML abstract syntax. It defines an
activity named Main with a ValueSpecificationAction
that shall produce the value 1 ∈ Z at OutputPin
named variableX. The same activity is presented
using an object diagram (II), which shows instances
of the abstract syntax and their relationships. Part
of the formal description for the same diagram
is exhibited in (III) – BS, which uses the embed-
ded version of the abstract syntax. From the 30
formulas needed to describe the activity, 4 are
presented. For example, the action is represented
as a unary relation (buml:ValueSpecificationAction
Main.ValueSpecificationAction1), meaning that
Main.ValueSpecificationAction1 is a ValueSpeci-
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
8
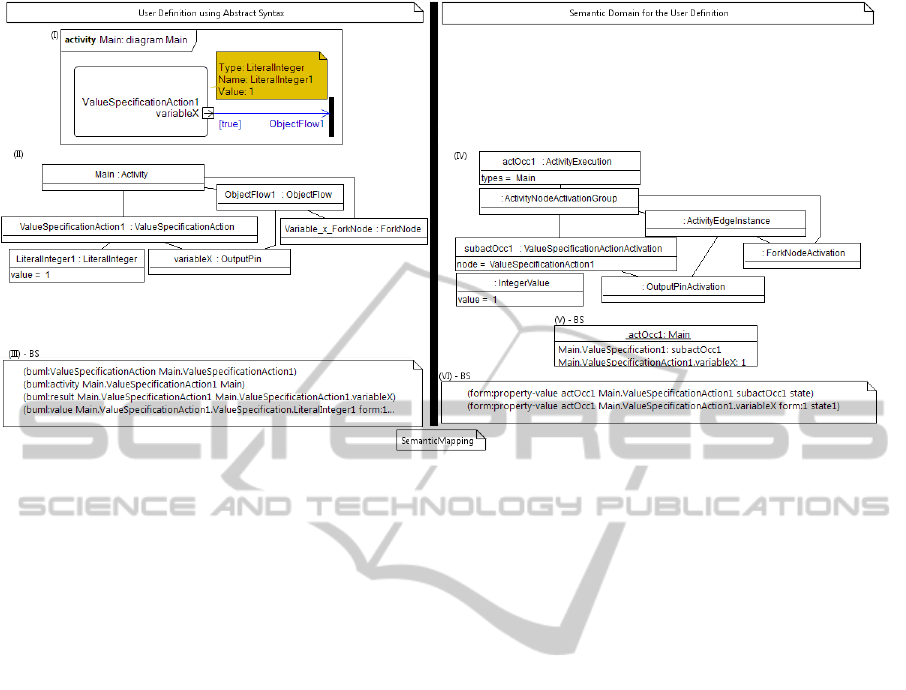
Figure 3: Relationships between fUML and base semantics, considering a user definition.
ficationAction, and the association owned by the
ActivityNode between it and the activity Main is
represented by a binary relation (buml:activity
Main.ValueSpecificationAction1 Main).
Considering the semantic domain for the previous
discussed user definition, Fig. 3 (IV) presents an ob-
ject diagram for one execution, according to execu-
tion model of fUML (OMG, 2012). For example,
one instance of class ActivityExecution identified by
actOcc1 having types as Main; and, one instance of
class ValueSpecificationActionActivation having node
as ValueSpecificationAction1. The object diagram in
(V) – BS Fig. 3 shows the semantic domain according
to the base semantics. In this case, the semantic do-
main is described by an object of type Main identified
by actOcc1 with two slots: Main.ValueSpecification1
equals to subactOcc1 (an occurrence of the ac-
tion), and Main.ValueSpecification1.variableX equals
to 1 ∈ Z (the value of the ObjectNode). Moreover,
(VI) – BS in Fig. 3 uses the CLIF syntax to represent
the semantic domain exhibited in (V) – BS; it is one
model (in the logic meaning) of the deduction process
using the inference rules defined by the base seman-
tics.
The base semantics formalizes the execution of an
activity as defined in the example: occurrences of ac-
tivities are instances of that, occurrences of actions
are values for slots that the owning activity has, and
object nodes assume values for slots from the own-
ing activity (this definition is formalized in the next
subsection). ControlNodes and control tokens are not
embedded in semantic domain from the base seman-
tics.
4.2 The Selected Subset
Fig. 4 shows the abstract syntax for the selected subset
using set-theory (A), as well as, a class diagram (B).
Further, (C) presents the grammar for this subset.
The sets, set operations and relations in (A) – up-
per left corner in Fig. 4 – define the relationship be-
tween the elements of the subset. Moreover, as dis-
cussed in the previous subsection, these relations are
mapped to CLIF using unary and binary relations. In
fact, this defines a mapping from the abstract syntax
of the bUML into the embedded abstract syntax de-
scribed by CLIF.
The class diagram (B) – upper right corner in
Fig. 4 – presents the abstract syntax using the tech-
nique applied by fUML. It shows the selected subset,
and indicates each meta-class and meta-relationship
not formalized using orange color. These elements
are also not embedded in the base semantics (OMG,
2012).
As discussed above, the base semantics does not
define static semantics (OMG, 2012), e.g., it is not
axiomatized that the sets EN (ExecutableNodes), CN
(ControlNodes), and ON (ObjectNodes), subsets of
the set AN (ActivityNode), should be disjoint (EN ∩
CN =
/
0 ∧ EN ∩ ON =
/
0 ∧CN ∩ ON =
/
0).
The grammar (C) – lower left corner in Fig. 4
– defined using BNF (Backus-Naur Form) describes
a text representation for activity diagrams. It is not
used in the fUML, and the goal here is to allow a def-
UsingtheBaseSemanticsgivenbyfUMLforVerification
9
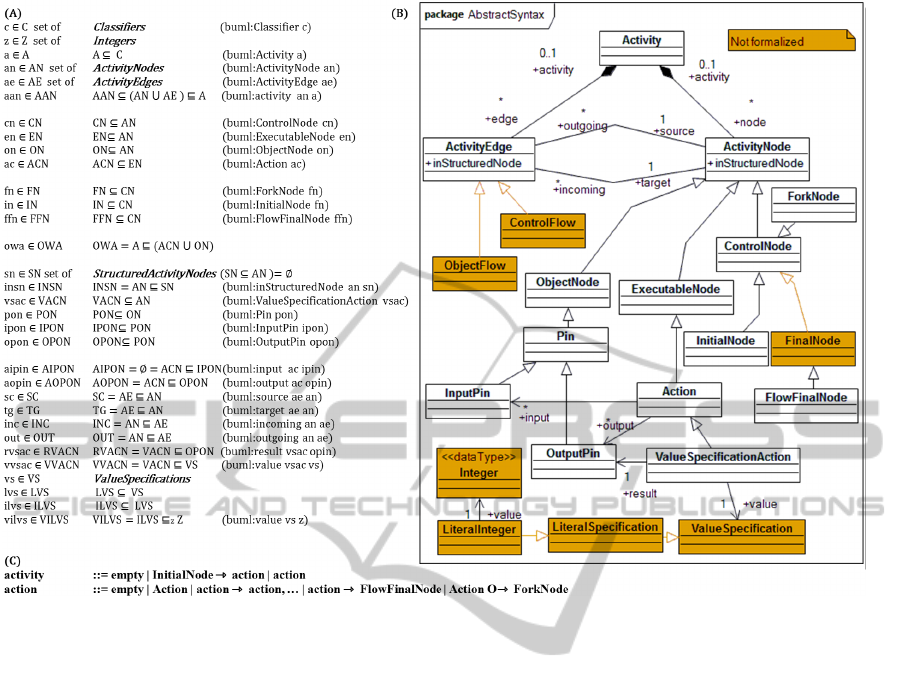
Figure 4: Abstract syntax and grammar for the selected subset.
inition of the formal semantics (Subsection 4.4) using
an operational semantics notation. It uses “→” as a
symbol for ControlFlow, and “O →” as a symbol for
ObjectFlow.
Concerning bUML, the selected subset does not
use a StructuredActivityNode – as defined by A.3.3
Local Variable Declaration ((OMG, 2012); pp. 402)
– to encompass the ValueSpecificationActions. How-
ever, this simplification still reassembles the local
variable declaration in bUML that states: an object
flow should connect the output pin from a ValueSpec-
ificationAction to a ForkNode, which could be used
for other actions ((OMG, 2012); pp. 402). Concern-
ing Alf, the selected subset also applies a simplifica-
tion without using StructuredActivityNodes to encom-
pass sequences of commands (18.3 Block Statements;
(OMG, 2013a); pp. 348). Therefore, the selected sub-
set is able to describe variables in fUML, and se-
quences of statements declaring variables in Alf.
In conclusion, the selected subset is able to model
n(n ∈ N
>0
) specifications of variables of the type in-
teger, including the capacity for describing up to n
concurrent specifications. However, it does neither
cover loops, joins, nor calculations.
4.3 Rationale for Selection
Due to two respective reasons, a subset of the fUML,
and consequently, axioms and inference rules defined
in the base semantics are considered: (1) to show
a complete example considering the semantics and
the theorem proving approach for verification; (2) to
demonstrate the use – due to the issues described in
the appendix, it is impossible, at the moment, to use a
complete version of the base semantics.
In contrast to the base semantics, the selected sub-
set covers all the abstract syntax (see the appendix),
and defined grammar. In fact, the selected subset uses
FlowFinalNode instead of ActivityFinalNode because
of the following proposition.
Proposition AFN: It is not possible to define for-
mal semantics for the control node ActivityFinalNode
with actual base semantics (OMG, 2012).
Proof : UML defines the ActivityFinalNode as “it
stops all executing actions in the activity, and de-
stroys all tokens in object nodes, except in the output
activity parameter nodes” ((OMG, 2011); pp. 340).
The present participle “executing” is used to qualify
the word “actions”, which means: given an action, it
has started at a time t − y, the time is t > t − y, and
it will finish at a time t + x > t, where x, y ∈ N
>0
.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
10

Hence, to formalize ActivityFinalNode, time shall be
defined formally. However, the base semantics does
not formalize time (OMG, 2012), so it is not possible
to define formal semantics for the control node Ac-
tivityFinalNode using actual base semantics (OMG,
2012). Although an alternative definition that could
support the ActivityFinalNode formalization is the use
of states (Grnniger et al., 2010), it would demand
changes, not corrections, in the axioms defined by the
base semantics.
This issue is clearer in the presence of ForkNode
without JoinNode (i.e., in the presence of concurrency
without joining). In this case, it is not possible to
know formally what activities are in execution (see
Fig. 12.49; (OMG, 2011); pp. 341). Therefore, the
selected subset uses FlowFinalNode that has an infor-
mal semantics (OMG, 2011) that does not depend on
time, and this allows a simple formal definition.
4.4 Semantics
Given the abstract syntax, and the grammar, the cur-
rent subsection explores the axioms and inference
rules for the selected subset, which defines the se-
mantic mapping. A file containing the definitions for
the selected subset is available (Gerlinger Romero,
2013b).
Considering semantic domain and semantic func-
tions for the selected subset (Fig. 5 – D), an object
state is defined by an object identifier (obji), the clas-
sifier from this object (OBJIC, a semantic function),
and the properties that the object has (PRV, a seman-
tic function). The semantic function OBJIC is rep-
resented by the base semantics using a ternary re-
lation (form:classifies) between domain, codomain,
and a state identifier. The semantic function PRV
is represented by the base semantics using a quater-
nary relation (form:property-value) between domain,
codomain (property and value), and a state identi-
fier. There are two types of properties: for Exe-
cutableNodes and for ObjectNodes. The former has
as codomain the property identifier, and one occur-
rence of execution (obji) of the action (acn) in a
given instance of an activity (obji). The last one has
as codomain the property identifier, and one integer
value (z) retrieved by the relation v
z
for the domain
defined by an ObjectNode (on) in a given instance of
an activity (obji). The set of all object states is the sys-
tem state (SS), and the set-valued mapping StateMap-
ping maps each system state into state identifiers (st).
As discussed in Subsection 3.2, the base seman-
tics uses the embedding approach (Fikes et al., 2001)
to axiomatize bUML. Accordingly, many inference
rules are devoted to the formalization of the syn-
tactical patterns. These syntactical patterns and the
embedded abstract syntax are used as antecedent in
the inference rules devoted to the semantic mapping.
Hereon, each inference rule that supports semantic
mapping for the selected subset is discussed. On the
other hand, inference rules that support syntactical
conditions are not shown, and when used in the se-
mantic mapping, they appear in italic.
Concerning the inference rule [InitialNode → ac-
tion], displayed in Fig. 5 (E), it checks the following
syntactical pattern: an InitialNode with only one out-
going edge, which is connected to an Action (ac), and
that Action does not have InputPin. If this syntacti-
cal pattern is recognized then the semantic mapping
shall be applied: for all executions (obji) of an activ-
ity (form:classifies) that has the previous syntactical
pattern, there exists an object state (for obji) where
the action (ac) has run. Therefore, the obji acquired
the value (objiac) for the property (obji v ac).
The inference rule [InitialNode → action] is pre-
sented using the base semantics style described by
CLIF (center of E in Fig. 5), and using an operational
semantics style (right of E in Fig. 5). The base se-
mantics style is intended to be used directly by ma-
chines so a significant part of the antecedent is de-
voted to identify the syntactical pattern that this rule
can be applied. The operational semantics notation
avoids this making clear what syntactical pattern the
rule supports, and in this sense, it is intended to ex-
press for humans the formal semantics for a given
language (it is used by machines when a machine-
readable notation is defined including the syntacti-
cal elements). One line shows the relationship be-
tween an antecedent (center) and a condition in the
operational semantic notation (right). A second line
presents the relationship between a consequent (cen-
ter) and a premise in the operational semantic nota-
tion (right). The next rules use the same type of lines
to clarify the relationship.
The next inference rule, [Action] shown in Fig. 5
(F), describes the semantic mapping for the syntac-
tical pattern where an action has neither incoming
edges nor InputPins, which means that the action
shall be executed every time that owning activity runs
(OMG, 2011). This interference rule uses a syntac-
tical antecedent defined as a condition in the oper-
ational semantic notation, which is indicated with a
dashed line in Fig. 5, and states that an action can run
without an incoming control flow. The consequent
is similar from the previous rule stating that the ac-
tivity’s execution (obji) acquired the value (objin) for
the property (obji v n).
An action in the selected subset has only one con-
crete definition, the ValueSpecificationAction. There-
UsingtheBaseSemanticsgivenbyfUMLforVerification
11

Figure 5: Semantics definition (part 1/2).
fore, the [Action
vs
] shown in Fig. 5 (G) describes the
inference rule for it, which defines that the integer
value (v, considering just one) of the ValueSpecifi-
cation is substituted on the OutputPin (opon, repre-
sented in the semantic domain as a property of the ac-
tivity’s execution). Moreover, the antecedent defines
that it shall be evaluated only when the two conditions
are satisfied: There is an execution for the activity
(form:classifies), and for the action (form:property-
value).
The next inference rule, [action → action,...]
shown in Fig. 6 (H), illustrates that a control flow be-
tween actions is decomposed by evaluation of all pos-
sible flows (recursively, and without constraints about
concurrency, e.g., interleaving). It is an unorthodox
rule that is possible because the selected subset does
not change the value from a previous defined prop-
erty. This rule is defined for completeness of the op-
erational semantics notation based on the previous de-
fined grammar, whereas it does not exist in the base
semantics style because it is covered for the (I) [action
→ action].
The rule (I) [action → action] covers control flows
from one action to others, including possible many
ForkNodes between them. These possible ForkNodes
are recognized using the inference rule for this syn-
tactical pattern (form:flow-trans-fork-merge ac1 ac2).
Therefore, the rule [action → action] checks if the ac-
tivity has run, and if the source action has run. In this
case, the target actions have run. It does not matter
how many ForkNodes are between them, or how many
targets have one source. Further, there is no notion of
interleaving, sequence, or any type of constraint about
concurrency in these evaluations. Indeed, fUML is
not deterministic (Benyahia et al., 2010; Gerlinger
Romero et al., 2013), hence multiple traces are ac-
cepted for the same embedded user axioms.
The rest of inference rules, namely [action →
FlowFinalNode] and [Action O → ForkNode], are de-
fined for completeness. The inference rule [action →
FlowFinalNode] states that when an activity has run,
an action has run, and the action is connected to a
FlowFinalNode, then the state is not changed. The
inference rule [Action O → ForkNode] states that an
ObjectNode connected to a ForkNode does not change
the state.
Considering the basic four building blocks (Ini-
tialNode, ValueSpecificationAction, ForkNode and
FlowFinalNode), a permutation (selecting 1, 2, 3, and
4), where order is important and repetition is not al-
lowed, generates 64 possibilities. From these, 12 fol-
low the grammar defined in Fig. 4 – (B), which are
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
12

Figure 6: Semantics definition (part 2/2).
covered by the axioms and inference rules presented.
Therefore, the axioms and inference rules are com-
plete w.r.t. the allowed combinations defined by the
grammar.
In summary, the axioms and inference rules re-
fined from the base semantics (with corrections), and
an illustration using the operational notation for the
semantics definition are presented. The result is that
the base semantics, defined using axiomatization of
the abstract syntax (embedded), semantic domain,
and, semantic mapping, can be related to operational
semantics in general, an exception is concurrency (in
the selected subset).
4.5 Formal Verification of Properties
Using the inference rules presented for the selected
subset, it is possible to conduct proofs in one of the
following two ways: (a) automatically, giving to an
automated theorem prover (ATP) the embedded user
axioms, the axioms and inference rules of the base
semantics, and the user theorems; (b) interactively,
using an interactive theorem prover that receives as
input the axioms, inference rules and theorems; or (c)
manually, e.g., using the operational notation.
Considering the example presented in Fig. 3 Sub-
section 4.1, one can formally verify that for all ex-
ecutions of activity Main, the property variableX
has the value 1. A possible formulation of this
theorem called activityMainAlwaysRunValueSpecifi-
cation1AndValueIsForm1 is shown in Fig. 7. In-
formally, this theorem states: for all activity ex-
ecutions and states (forall (exa f)), if the execu-
tion exa and state f is from the activity Main (if
(form:classifies Main exa f)), then there exists another
state f 2 (exists (f2)) where the value 1 for the property
variableX from execution exa is set (form:property-
value exa Main.ValueSpecificationAction1.variableX
form:1 f2). Moreover, the theorem is described using
CLIF with one extension from HETS (Mossakowski,
2013) to mark that the given text is a theorem (%im-
plied).
Taking into account the simplicity of the example,
the ATP eprover (Schulz, 2013) was applied to auto-
matically perform the verification task, i.e., given all
embedded user axioms (Fig. 3 (III) – BS), and the ax-
ioms and inference rules provided by the base seman-
tics (Fig. 5 and 6), it shall find an application of infer-
ence rules to derive theorem activityMainAlwaysRun-
ValueSpecification1AndValueIsForm1.
As formulas are described by CLIF and eprover
does not support CLIF files (Schulz, 2013), HETS
UsingtheBaseSemanticsgivenbyfUMLforVerification
13

Figure 7: Theorem proved by the ATP eprover (Schulz, 2013).
(Mossakowski, 2013) was used to translate CLIF
files into TPTP files (a format supported by eprover
(Schulz, 2013)). The result of the translation per-
formed by HETS was the input for eprover, which
successfully proved the theorem in this case. The defi-
nitions and results of this proof, including the embed-
ded user axioms and the UML model, are available
(Gerlinger Romero, 2013b).
An alternative to perform this verification task is
using the same set of formulas and an interactive the-
orem prover. The theorem prover can be launched by
HETS (Mossakowski, 2013) after the translation from
CLIF format to the supported format, and should be
driven by the user interested in the verification. This
option is well-suited for the verification tasks not so
simple as the example presented above.
The last alternative (manual proof) demands huge
manual effort, and can be performed stating a post
condition for the activity and using the operational no-
tation. For the example, the post condition can define
that there should exist a state where the property vari-
ableX for the execution of the activity Main has the
value 1. Considering that there exists an execution
for the activity (assumption), manual application of
the sequence of inference rules defined using the op-
erational notation ([Action] and [Action
vs
]) leads to
the defined post condition.
5 DISCUSSION
Concerning verification, there are two main ap-
proaches to perform formal verification: (a) model
checking automatically and exhaustively traverses the
reachable state space of a design and is limited by the
state explosion problem (Jarraya et al., 2009; Krae-
mer and Herrmann, 2010); and (b) theorem proving
which constructs a mathematical proof of a design’s
correctness and is usually limited by the high manual
effort (Grnniger et al., 2010). The formal semantics
considered in this paper supports both approaches,
and in the current paper, the latter approach was ex-
plored and exemplified.
The base semantics uses CLIF to express syntacti-
cal patterns over the embedded abstract syntax, and to
express the semantic mapping from instances of em-
bedded abstract syntax to the semantic domain. The
semantic domain of the execution model is not em-
bedded in the base semantics. Nonetheless, the se-
mantic domain in the base semantics has the features
needed to define the semantic mappings (see Fig. 4)
for the selected subset of bUML.
The base semantics is an axiomatization of the
language defined by bUML, whereas it does not use
the classical axiomatic semantics (Hoare, 1969). It
can be related with operational semantics, as the ar-
ticle illustrates, while it does not apply SOS rules
(Plotkin, 1981; Jarraya et al., 2009). Analyzing con-
currency, rules [action → action,...] and [action →
action], it is clear that axiomatization does not de-
fine all the operational implications. This absence of
some operational details enables us to express the ex-
act meaning of concurrency defined by UML (OMG,
2011). On the other hand, (Jarraya et al., 2009) ap-
plies interleaving using SOS. In the base semantics,
the inference rules do not define the next element
from the grammar to be processed, and instead it
changes the state. An evaluator must analyze the next
applicable rule considering the activity and the actual
state, which is indeed, a characteristic of a deductive
system.
Due to the limitations of the selected subset, the
assertions ascribe particular values to variables (Ob-
jectNode), instead of properties of the values and the
relationship between them (Hoare, 1969). Further, the
properties are verified as total correctness properties,
due to the lack of loops, and advanced control struc-
tures.
There are three major limitations of the base se-
mantics given by fUML that prevent its use: (1)
fUML does not define semantics for time, inter-
communication, and concurrency as well as the base
semantics (OMG, 2012); (2) fUML does not define
how the elements outside bUML (e.g., LoopNode)
can be described by bUML – bUML is used to define
an algorithm to interpret fUML (recall that the base
semantics only covers bUML elements); and, (3) the
lack of maturity of the base semantics (see Appendix).
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
14

6 CONCLUSIONS
The contributions of this work are: (1) it shows how
the base semantics can support theorem proving for
verification as well as its limitations, (2) it illustrates
similarities and differences of the base semantics and
an operational semantics, and (3) it helps in the matu-
ration process of the specification itself (OMG, 2012)
as well as in the motivation for more evaluations about
this section of specification.
Evaluations of the base semantics are a necessity,
e.g., the first syntactical defect described in the ap-
pendix was recognized in version 1.1 RTF from 2012
((OMG, 2012); pp. 383). However, the same de-
fect was detected in version FTF beta 2 from 2009
((OMG, 2009); pp. 289). Further, fUML is a basic
building block for future specifications of OMG. For
example, Request for Proposal – Precise Semantics
for Composite Structures (OMG, 2013b) states that
new axioms must have explicit relationships with the
base semantics, and must be consistent with it. Nev-
ertheless, the base semantics is not consistent (see ap-
pendix) (OMG, 2012).
Although previous work has been done on the se-
mantics of activities of UML, as discussed in Sec-
tion 2, to the best of our knowledge, we introduce
in this paper the first conceptual evaluation of the
formal semantics (base semantics) defined in fUML.
From the practical perspective, we show with a simple
example how the base semantics can support formal
verification (a requirement for safety-critical systems)
through theorem proving. The initial results show that
the base semantics, when mature, can play an impor-
tant role in the formal verification of UML models,
acting as a bridge between the modeling community
and the formal semantics community.
REFERENCES
Abdelhalim, I., Schneider, S., and Treharne, H. (2012). An
optimization approach for effective formalized fUML
model checking. In Eleftherakis, G., Hinchey, M.,
and Holcombe, M., editors, Software Engineering
and Formal Methods (SEFM), volume 7504 of LNCS,
pages 248–262, Thessaloniki, Greece. Springer.
Benyahia, A., Cuccuru, A., Taha, S., Terrier, F., Boulanger,
F., and Grard, S. (2010). Extending the standard
execution model of UML for real-time systems. In
Hinchey, M., Kleinjohann, B., Kleinjohann, L., Lind-
say, P., Rammig, F., Timmis, J., and Wolf, M., editors,
Distributed and Parallel Embedded Systems (DIPES),
volume 329 of IFIP Advances in Information and
Communication Technology, pages 43–54, Brisbane,
Australia. Springer.
Bock, C. and Gruninger, M. (2005). PSL: A semantic do-
main for flow models. Software and Systems Model-
ing, 4(2):209–231.
Combemale, B., Hardebolle, C., Jacquet, C., Boulanger,
F., and Baudry, B. (2013). Bridging the chasm be-
tween executable metamodeling and models of com-
putation. In Czarnecki, K. and Hedin, G., editors, Soft-
ware Language Engineering, volume 7745 of LNCS,
pages 184–203, Dresden, Germany. Springer.
Derler, P., Lee, E., and Sangiovanni-Vincentelli, A. (2012).
Modeling cyber-physical systems. Proceedings of the
IEEE, 100(1):13–28.
Fecher, H., Schnborn, J., Kyas, M., and de Roever, W.-P.
(2005). 29 new unclarities in the semantics of UML
2.0 state machines. In Lau, K.-K. and Banach, R., edi-
tors, International Conference on Formal Engineering
Methods (ICFEM), volume 3785 of LNCS, pages 52–
65, Manchester, England, UK. Springer.
Fikes, R., , and McGuinness, D. (2001). An axiomatic se-
mantics for RDF, RDF-S, and DAML+OIL (march
2001).
Gerlinger Romero, A. (2013a). Files submit-
ted to OMG. http://es.cs.uni-kl.de/ peo-
ple/romero/fUMLOMGIssue20130630.zip Access
date: 28.Oct.2013.
Gerlinger Romero, A. (2013b). Support files
for the modelsward2014. http://es.cs.uni-
kl.de/people/romero/modelsward2014.zip Access
date: 28.Oct.2013.
Gerlinger Romero, A., Schneider, K., and Gonc¸alves Vieira
Ferreira, M. (2013). Towards the applicability of Alf
to model cyber-physical systems. In International
Workshop on Cyber-Physical Systems (IWCPS), pages
1469–1476, Krakw, Poland. IEEE Computer Society.
Graves, H. (2012). Integrating reasoning with SysML. In
INCOSE International Symposium, Rome, Italy.
Grnniger, H., Rei, D., and Rumpe, B. (2010). Towards a se-
mantics of activity diagrams with semantic variation
points. In Petriu, D., Rouquette, N., and Haugen, O.,
editors, Model Driven Engineering Languages and
Systems (MODELS), volume 6394 of LNCS, pages
331–345, Oslo, Norway. Springer.
Hoare, C. (1969). An axiomatic basis for computer pro-
gramming. Communications of the ACM (CACM),
12(10):576–580.
ISO (2007). Information technology – Common Logic
(CL): a framework for a family of logic-based lan-
guages.
Jarraya, Y., Debbabi, M., and Bentahar, J. (2009). On the
meaning of SysML activity diagrams. In Engineering
of Computer Based Systems (ECBS), pages 95–105,
San Francisco, CA, USA. IEEE Computer Society.
Knieke, C., Schindler, B., Goltz, U., and Rausch, A. (2012).
Defining domain specific operational semantics for
activity diagrams. Technical Report IfI-12-04, TU
Clausthal, Clausthal, Germany.
Kraemer, A. and Herrmann, P. (2010). Reactive seman-
tics for distributed UML activities. In Hatcliff, J. and
Zucca, E., editors, Formal Techniques for Distributed
UsingtheBaseSemanticsgivenbyfUMLforVerification
15

Systems (FORTE), volume 6117 of LNCS, pages 17–
31, Amsterdam, The Netherlands. Springer.
Maoz, S., Ringert, J., and Rumpe, B. (2011). An oper-
ational semantics for activity diagrams using SMV.
Aachener Informatik-Berichte AIB-2011-07, Depart-
ment of Computer Science, RWTH Aachen, Aachen,
Germany.
Mossakowski, T. (2013). HETS site for HETS -
v0.99, 02 Mai, 2013. http://www.informatik.uni-
bremen.de/agbkb/forschung/formal methods/CoFI/
hets/index e.htm Access date: 22.Jun.2013.
NIST (2013). PSL psl outer core V2.1. http://
www.mel.nist.gov/psl/download/psl outer core.clf
Access date: 22.Jun.2013.
OMG (2009). Semantics of a foundational sub-
set for executable UML models, V FTF beta
2. http://www.omg.org/spec/FUML/ Access date:
09.Feb.2010.
OMG (2011). OMG Unified Modeling Lan-
guage (OMG UML), Superstructure, V2.4.1.
http://www.omg.org/spec/UML/2.4.1/. Access date:
14.Apr.2013.
OMG (2012). Semantics of a foundational sub-
set for executable UML models, v1.1 RTF beta.
http://www.omg.org/spec/FUML/. Access date:
24.Apr.2013.
OMG (2013a). Concrete Syntax for UML Action Lan-
guage, V1.0.1 Beta. http://www.omg.org/spec/ALF/.
Access date: 27.Apr.2013.
OMG (2013b). Precise Semantics of UML Compos-
ite Structures - Request For Proposal - OMG Doc-
ument: ad/2011-12-07. http://www.omg.org/cgi-
bin/doc?ad/11-12-07/. Access date: 25.Aug.2013.
Perseil, I. (2011). ALF formal. Innovations in Systems and
Software Engineering, 7(4):325–326.
Plotkin, G. (1981). A structural approach to operational se-
mantics. Technical Report FN-19, DAIMI, rhus, Den-
mark.
Schulz, S. (2013). Eprover site for eprover - E
1.6 Tiger Hill. http://www4.informatik.tu-
muenchen.de/
˜
schulz/E/E.html. Access date:
22.Jun.2013.
APPENDIX – BASE SEMANTICS
In this appendix, we present an extract from the is-
sue report submitted (June, 30th, 2013) to OMG con-
cerning the base semantics given by fUML ((OMG,
2012); pp. 351-398). In that report, 42 issues were
found (Gerlinger Romero, 2013a), 5 of them were en-
hancement proposals, and 37 were defects. The main
issues concerning defects were the following ones:
• The base semantics had a defect in Section
10.4.8.3, page 383. There was missing a forall
construction, which lead to a syntax error.
• After having made the necessary corrections, a
model finder (Schulz, 2013) was used to check
if the fUML base semantics together with PSL
(psl outer core; (NIST, 2013)) were consistent.
However, it turned out that both together were in-
consistent.
• A model finder (Schulz, 2013) was also used to
check if the base semantics alone (without PSL)
is consistent. It turned out that the fUML base
semantics was not consistent.
The proposals sent to OMG were:
• A computer-readable version of the base seman-
tics should be made available as a CLIF file.
• The base semantics should declare the PSL ver-
sion used to define it.
• It should not define constraints for actions outside
the bUML: AcceptEventAction and ReadIsClassi-
fiedObjectAction.
• The specification should cover all ActivityNodes
used in bUML. Thus, a declarative definition of
ActivityFinalNode should be added because it is
used in Annex A.3.1 and A.3.2, pages 401 and
402.
• Inference rules that are not used or not needed for
completeness, should be removed.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
16
