Monocular 3D Pose Tracking of a Specular Object

Nassir W. Oumer

Institute of Robotics and Mechatronics, German Aerospace Center, M¨unchner Str. 20, Weßling, Germany

Keywords:

Specular Surface, Pose Tracking, Feature Tracking, Model-based Tracking, On-orbit Satellite Servicing.

Abstract:

A space object such as a satellite consists of highly specular surface, and when exposed to directional source of

light, it is very difﬁcult for visual tracking. However, camera-based tracking provides an inexpensive solution

to the problem of on-orbit servicing of a satellite, such as orbital-life extension by repairing and refuelling, and

debris removal. In this paper we present a real time pose tracking method applied to a such object under direct

Sunlight, by adapting keypoint and edge-based approach, with known simple geometry. The implemented

algorithm is relatively accurate and robust to specular reﬂection. We show the results which are based on real

images from a simulation system of on-orbit servicing, consisting of two six degree of freedom robots, the

Sun simulator and a full scale satellite mock-up.

1 INTRODUCTION

One of the challenges in computer vision is related

to reﬂectance properties of object surfaces under di-

rect source of lighting. A satellite is a such sur-

face made up of mostly non-textured structural ele-

ments and partly covered with a thermal insulation

such as multilayer insulation (known as MLI). Unfor-

tunately this insulation is highly reﬂective and poses

challenges for visual tracking. In spite of these difﬁ-

culties, successful localization of a satellite provides

several beneﬁts for on-orbit servicing. In on-orbit ser-

vicing, a robot mounted on a servicer satellite, ap-

proaches a defective satellite (hereafter called client)

from a certain range, and refuel, repair, maintain or

even remove it from its orbit. Typical on-orbit servic-

ing currently under development is the German on-

orbit servicing mission (DEOS) shown in Fig.1. For

this purpose, we estimate and track relative location

of the client using monocular camera.

The methodology for visual processing of an ob-

ject or a scene depends on the object or scene geome-

try, the environment and reﬂectance property. In com-

puter vision as well as computer graphics, surfaces or

objects are distinguished as a specular and lamber-

tian surface. The reﬂectance property of the Lam-

bertian surface is independent of viewing direction,

while non-lambertian surfaces (Specular) are highly

view point dependent. Most computer vision algo-

rithms assume Lambertian surface and are successful

in solving real world problems such as robot local-

ization, augmented reality and visual servoing. How-

Figure 1: On-Orbit Servcing. Artistic impression of the

German on-orbit servicing mission (DEOS); the robot arm

mounted on a servicer satellite (right) is grasping the client

satellite (left).

SpaceTech GmbH

ever, visual algorithms developed for non-lambertian

surfaces are mostly limited to laboratory and far less

applied to real world problems such as visual tracking

of a satellite under direct sunlight.

In this paper we present a visual tracking method

that exploits edges and keypoints for localization of

a satellite for on-orbit servicing. While state of the

art model-based tracking methods are experimentally

well veriﬁed for Lamabertian surfaces under ordinary

illumination, we are particularly interested to address

a problem associated to specular object that goes be-

yond the theory of specular reﬂection. To that end,

our contributions are mainly; (1) we combine edge

and keypoint tracking methods applied to highly spec-

ular object under direct sunlight illumination, (2) we

generate ground truth trajectory under realistic sim-

ulation of satellite and illumination with high power

spotlight to simulate the Sun’s spectrum, (3) we im-

plement the proposed algorithm and evaluate its per-

458

Oumer N..

Monocular 3D Pose Tracking of a Specular Object.

DOI: 10.5220/0004667304580465

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 458-465

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

formance (accuracy and robustness) under various

motions and different levels of illumination, and (4)

we compare our hybrid tracking method with edge

based tracking, implemented by adapting Lie algebra

tracking method (Drummond and Cipolla, 1999).

In the remaining sections of this paper, we present

related current state of the art approach of combined

edge and feature based tracking, and review computer

vision methods for specular objects in Section 2. Sec-

tion 3 presents our tracking method that integrates

keypoints and edges in 2D-3D registration. Section

4 describes experimental setup used to validate the

proposed method, and compares tracking results with

edge based methods. Finally we summarize and con-

clude the paper in Section 5.

2 PREVIOUS WORK

In this section, we review pose estimation and struc-

ture reconstruction methods that exploit specular cues

of the object, and brieﬂy explore model-based track-

ing methods which utilize edge and point features of

an object.

2.1 Pose Estimation from Specular Cues

In the context of pose estimation and surface recon-

struction, there exist several contributions that deal

with specular objects. The Theory of a specular ge-

ometry describes that image features exist as either

real or virtual (Oren and Nayar, 1995). Real fea-

tures are directly used by vision algorithms such as

matching, tracking and structure from motion. Vir-

tual features (specular cues) are specular reﬂections

of a scene or an object features under change of view-

point. Specular surfaces such as a glass and a smooth

metal create ambiguity (actual scene point or reﬂec-

tion of another scene point) for visual interpretation.

Various methods have been proposed to utilize

these virtual features. For example, shape and re-

ﬂectance parameters can be simultaneously estimated

from multiple views of an object made of single ma-

terial with known lighting (Yu et al., 2004). Phong

reﬂectance model is used to compute reﬂectance of

the object shape modelled with triangular mesh, and

minimize non-linear least square cost function over

the shape and reﬂectance parameters. When the ob-

ject is in motion, specular reﬂections produce 2D im-

age motion (specular ﬂow) (Oren and Nayar, 1995).

The specular ﬂow is mathematically related to the

3D structure of textured object or scene (Roth and

Black, 2006) and provided a parametric mixture mod-

els for recovery of a surface. Most methods of shape

from specular reﬂection assume limited case of sur-

faces, in which its structure is known or qualitatively

sparse, and the environment is calibrated. In contrast

(Vasilyev et al., 2008) presented reconstruction ap-

proach that targets general surfaces under unknown

real-world environments. They recovered 3D shape

from optical ﬂow induced by relative motion between

a specular object, an observer and their environment.

Similarly, (Adato et al., 2010) presented variational

optical ﬂow technique, which accounts for character-

stics of specularity including parabolic singularities

related to surface curvature which are hard to detect.

On the other hand, an object tracking with specu-

lar highlights (Gouiff`es et al., 2006) exploits Phong’s

model by approximatinggeneral photometric changes

with a continuous and differentiable function, approx-

imated with ﬁrst order Taylor series at a pixel point in

the neighbourhood. This approach extends sparse op-

tical ﬂow tracking method such as (Shi and Tomasi,

1994), by compensating for illumination changes and

specular highlights. In the context of pose estima-

tion, unlike classical methods which discard lighting-

information, (Lagger et al., 2008) reﬁned coarse pose

estimates by incorporating lighting information in

texture and specular cues to improveaccuracy of stan-

dard template matching algorithm. In this approach

environment map is retrieved from the specular pixels

of shiny objects and registration is performed in both

image and lighting environment space.

A practical localization and pose estimation

method is demonstrated by (Chang et al., 2009).

They exploited environment map, specular reﬂections

and specular ﬂow, handling partial occlusions, back-

ground clutter and inter-reﬂections. Their method re-

quires to use a calibration object such as a mirror

sphere in the target scene to capture the environment

map. It is, however unsuitable for human inaccessible

environments such as satellite orbits.

Despite existence of several physical and geomet-

ric reﬂectance models of specular objects, they are

rarely exploited for real world problems, mainly be-

cause of their complexity and underlying assumptions

such as placement of a calibration object in the scene.

For a space object such as a satellite, the appropri-

ate reﬂectance model consists of specular lobe, spec-

ular spike and diffuse reﬂections. In the presence

of geometric model of the satellite however, specular

highlights, keypoints and edges of the satellite struc-

ture can be better utilized by integrating into standard

model based tracking.

2.2 Feature-based Tracking

Edges of an image are the most suitable cues for 3D

Monocular3DPoseTrackingofaSpecularObject

459

tracking of a space object such as satellite under di-

rect illumination and specularity. They are relatively

robust to illumination change and specularity. More-

over, an accurate and a robust 3D model based track-

ing can be achieved by integrating keypoints and

edges, also reported by (Pressigout and Marchand,

2007), (Vacchetti et al., 2004), and (Kyrki and Kragic,

2005). On one hand, interest points are well local-

ized in textured objects and robust to some lighting

changes and geometric distortions. However, they are

rarely available, unstable on poorly textured objects

and invariant to scale changes. On the other hand,

edges are more distinctive and informative for ob-

jects with sharp edges and strong contrast changes but

ambiguous in cluttered and textured objects because

of strong texture and background clutter. Moreover,

some edges project close to one another and create

ambiguity. Therefore, the combination of edges and

feature points are complementary, enabling more sta-

ble tracking with less-drift than purely edge or point

feature based methods.

Very good results of combined edge and tex-

ture tracking method, which is robust to occlusion,

shadow, and some specularities, are demonstrated in

(Pressigout and Marchand, 2007). Our method con-

siders the dominant specular nature of the object un-

like (Pressigout and Marchand, 2007), which focuses

mainly on lambertian textured surfaces containing

edges. The satellite surface is mainly textureless, with

some irregularities created by thermal insulation ma-

terial and corners created by intersection of segments

(Fig.2).

Figure 2: Specularities because of the satellite surface and

direct illumination. Our region of interest for tracking is

the nozzle (small circle at the center in frontal view) of the

satellite. The nozzle has usually a cone or paraboloid sur-

face geometry and is feature of most satellites.

3 3D TRACKING

The objective of 3D tracking of an object is to localize

its position and orientation in time. In general, there

exist two basic approaches of 3D tracking; model-

based tracking which utilizes the CAD model of the

object, and model free tracking which does not rely

on a geometric model of the object. If the model of

the object is available, it provides useful prior infor-

mation about the object and helps improve robustness

by reducing inﬂuence of outliers on the tracker.

In this paper, we localize a space object such

as satellite using model-based approach. A simple

model of the object is used for absolute pose tracking,

using full perspective projection camera model. The

perspective projection of a 3D point p = [X,Y, Z, 1]

on image plane under pinhole camera model, is given

x = K[R|t]p (1)

where, x is an image point in homogeneous coordi-

nate, K is a camera matrix, and R and t are rotation

and translation of the object in camera frame respec-

tively. Alignment of model and image edges of non-

textured object is efﬁciently used to recover the ro-

tation and translation of the object, while keypoints

are used for estimating this motion parameters of tex-

tured object. In this section, we present the edge

based and keypoint tracking methods, and formulate

the proposed hybrid feature tracking.

3.1 Edge based 3D Tracking

Edges of an object are widely used feature in model-

based tracking. They are mainly depth discontinu-

ities, including object contours, segments, and primi-

tive shapes such as circles and cylinders. For a close

range (10m to 0.5m) rendezvous of a satellite, its noz-

zle is the most appropriate feature to track, as most

satellites contain this feature to provide thrust for or-

bital control of the satellite. Moreover, the nozzle

is frontal in this close range since the servicer and

the client satellites are well aligned during mid-range

(above 10m) tracking. Consequently the circular ring

of the nozzle is visible in all tracking frames. Hence,

our edge tracking is based on the contours of the noz-

zle in frontal view.

The contours (hereafter all edges are referred to

as contours) are sampled and projected on to the im-

age using hypothetical or predicted pose according to

Eq. (1). Projected model points are associated to each

candidate edge pixel along the respective normals,

also checking against the matching edge directions

(as measured by a Sobel ﬁlter), up to a reasonable

threshold. The state of the art model based tracking

methods (Drummond and Cipola, 2002) and (Com-

port and Marchand, 2004) sample contour points dif-

ferently. The former samples 3D contour points and

project each point to image plane while the latter sam-

ples the contours after projecting on the image plane.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

460

The reader may refer to (Comport et al., 2005) for

comparative study of the two methods.

3.2 Keypoint Tracking

Textured objects consist in distinctive feature points

suitable for tracking. On the contrary textures are

background clutters for purely edge based tracking.

Despite a few in number and sparsely distributed, fea-

ture points of satellite surface are useful for tracking.

Moreover, such keypoints provide additional cues to

estimate correctly the 6D parameter of the motion, as

6 degree of freedom (DOF) motion can not be recov-

ered from certain geometric primitives (e.g circle and

cylinder provide only 5D parameters of 6 DOF mo-

tion of the satellite). Furthermore, when the edges are

weak relative to background clutters, the edge based

tracking gives rise to large errors. Hence, keypoints

are vital to ameliorate robustness and accuracy of vi-

sual tracking.

As 3D keypoints of the satellite are not provided

in our model, we create such model points by back-

projection of detected feature points in the image, at

a known pose estimated using contour based method.

The alternative approach to this method is given by

(Comport et al., 2005), by which they estimate ho-

mography using the pose from edge-based tracker.

Our method is general, in that most satellite surfaces

can be modelled with their primitive shapes such as

cuboid, cylinder, cone, circle and rectangle.

For back-projection of the keypoints, we remodel

the geometry of the frontal surface of the satellite

(see client satellite mock-up in Fig.3), approximated

with right circular cone and cuboid. Although there

exist small unknown curvature at the center of the

cuboid, the model is good approximation to the struc-

ture of the satellite. Accordingly, we compute the 3D

points corresponding to image keypoints through ray

intersection. A ray passing through the image point

x = [u, v]

intersects either a cuboid of known size

with normal N or the right circular cone, parametrized

(X −V)

M(X − V) = 0

A. (X −V) ≥ 0 (2)

M = AA

− cos(θ)

, where A is a direction of the cone axis, θ is an acute

angle of the cone, which is the angle between axis of

the cone and a ray through the point X on the surface

of the cone and the vertex V, and I is identity matrix.

After we create 3D model points, the detected

keypoints are tracked using KLT tracker (Shi and

Tomasi, 1994). Unreliable features are automatically

rejected and substituted by new features during track-

ing. When the 3D model points are not sufﬁcient as

a result of feature rejection, we create model points

from the newly detected features.

3.3 Hybrid Feature Tracking

As stated earlier in this paper, integrating edge and

point features (Fig.4) into 3D tracking corrects draw-

backs of a solely edge-based or feature point track-

ing. In this section, we present the registration of edge

and feature point cues within the same minimization

process, by utilizing 3D point models created by ray

tracing and 3D contour points of a satellite. The 3D

tracking approach is differently handled for the fea-

tures obtained from keypoints and edges; matching

points of the projected contour points are searched

along the edge normals (1D search) while matching

feature points is 2D search. Thus we treat joint opti-

mization of the cost function associated to these fea-

tures in different direction.

Let δp be inter-frame motion. The rigid body

tracking is tantamount to computing the transforma-

tion matrix T in time t for the motion model, provided

the last transformation at time t − 1, according to

= T

t−1

δT(δp

) (3)

where the incremental transform δT is singularity-

free around δT(δp = 0). The tangent space to SE(3)

at T

t−1

is given by the Lie algebra se(3), which pro-

vides δT through the exponential mapping

δT(δp) = exp

∑

i=1

δp

(4)

where G

are the canonical (4× 4) generators of se(3)

(Drummond and Cipolla, 1999).

Each 3D point X, obtained by ray tracing and sam-

pling on the contour, is projected onto image point y

by the respective (3× 4) camera matrix K

y = π(K · T · δT(δp) · X) (5)

where the operator π() transforms from homogeneous

to Euclidean 2D coordinates

π(z) =





. (6)

We minimize the joint objective function

argmin

δT

∑





edge

− y

(δT)





point

− y

(δT)





(7)

where ρ() is a robust function, x

edge

and x

point

are

edge and tracked feature points respectively.

Differentiating Eq.(5) with respect to incremental

pose parameters δp

∂y

∂(δp

)



δp=0

∂π

∂z



z=KTX

· K · J

, (8)

Monocular3DPoseTrackingofaSpecularObject

461

gives rise to screen Jacobian, where J

is the transfor-

mation Jacobian, given by the respective generator

= T

∂

∂(δp

)

δT(δp)



δp=0

= TG

. (9)

The screen Jacobian of each contour point in the

direction of screen normal n is stacked, to form the

Jacobian J

edge

, of maximum size (n

× 6). Similarly,

the Jacobian J

point

associated to re-projection error of

3D point models (from ray tracing) is computed, in

this case without screen normal as these model points

are not contour points. Hence, overall Jacobian ( of

size 3n

× 6) of the minimization is derived by cas-

cading

J =



edge

point



. (10)

Thus, pose parameters δp are updated by minimiz-

ing residuals r, given by

r =



− x

− y



(11)

where x = [u

, v

]

are tracked image feature points,

and y

are projections of 3D points onto the image

plane expressed in standard coordinate.

Several background clutters exist because of spec-

ular reﬂections, resulting very similar edges to the

nozzle edge. Hence, the tracker should be robust to

outliers. The robust function ρ() in Eq.(7) provides

such functionality to reject spurious features during

tracking. For real time efﬁciency we choose the M-

estimator adopted in the context of 2D visual servoing

(Comport et al., 2006). The M-estimator adaptively

thresholds outliers based on robust statistics, while

re-weighting inliers according to the Tukey bi-weight

function

−



− ¯r



if |r

− ¯r| < bδ

(12)

and otherwise the weight is set to zero, where b =

4.6851 is the threshold for Tukey’s function, and the

scale δ is the standard deviation of inlier data, ro-

bustly estimated using the median of absolute devia-

tions (MAD) from the median residual ¯r, and used to

compute the weights. Re-weighted least square min-

imization is performed, by Gauss-Newton update ac-

cording to the Eq.(13)

δp =





−1

Wr (13)

where W is a diagonal matrix containing all weights,

and iterated with the new T matrix, computed by Eq.

(3), until the increment is sufﬁciently small.

This general formulation can be applied also to

cases with reduced degrees of freedom, by suppress-

ing the Jacobian column related to some of the gener-

ators G

. Moreover, for our scenario rotation is con-

trolled quite precisely through attitude measurements

Figure 3: DLR on-orbit servicing simulation system con-

sists of two robots and a satellite mock-up (client). The

servicer (left) and the client with its nozzle(right).

used for control of the satellite, thus we only show re-

sults concerning pure translation and oscillations, by

ﬁxing the rotational part R and using the other three

generators.

4 EXPERIMENTAL RESULTS

In this section, we present the experimental setup and

some of our results at various illumination level and

motion trajectories. As our objective is to address real

world problem of visual tracking, the experiment is

performed with one of the most realistic space simu-

lation system. This system (Fig.3) consists of a high

power ﬂoodlight (the Sun simulator), client satellite

covered with thermal protection (such as multilayer

insulation, MLI) which is highly reﬂective, two 6

DOF Kuka robot system to reproduce relative motion

of servicer and client satellites. The reﬂective surface

of the client, illuminated with direct Sun light pro-

duces strong specular reﬂections (see Fig.2), located

on irregular corners and edges. Although these image

features are short-lived and have unstable shape and

size, we are able to achieve reasonable accuracy and

robustness.

We performed the experimentation with various

motions to validate the method and demonstrate the

practicality. The ground truth data is generated

through robot measurements and hand-eye camera

calibration (DLR CalLab toolbox). The maximum

translational and angular velocities are 5cm/s and

1deg/s respectively. The motion is mainly oscilla-

tory with small rotation. The two satellites are as-

sumed controllable, hence relative attitude measure-

ments can be provided with external system. Conse-

quently we focus on oscillatory motion of the client

in this experiment. However, the implemented algo-

rithm can provide poses for 6 DOF motion. We ini-

tialized the tracker manually, which can be also pro-

vided by an external tracker used for mid-range (≥

10m) localization. The implementation is in C++,

while opencv is used for low-level processing such

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

462

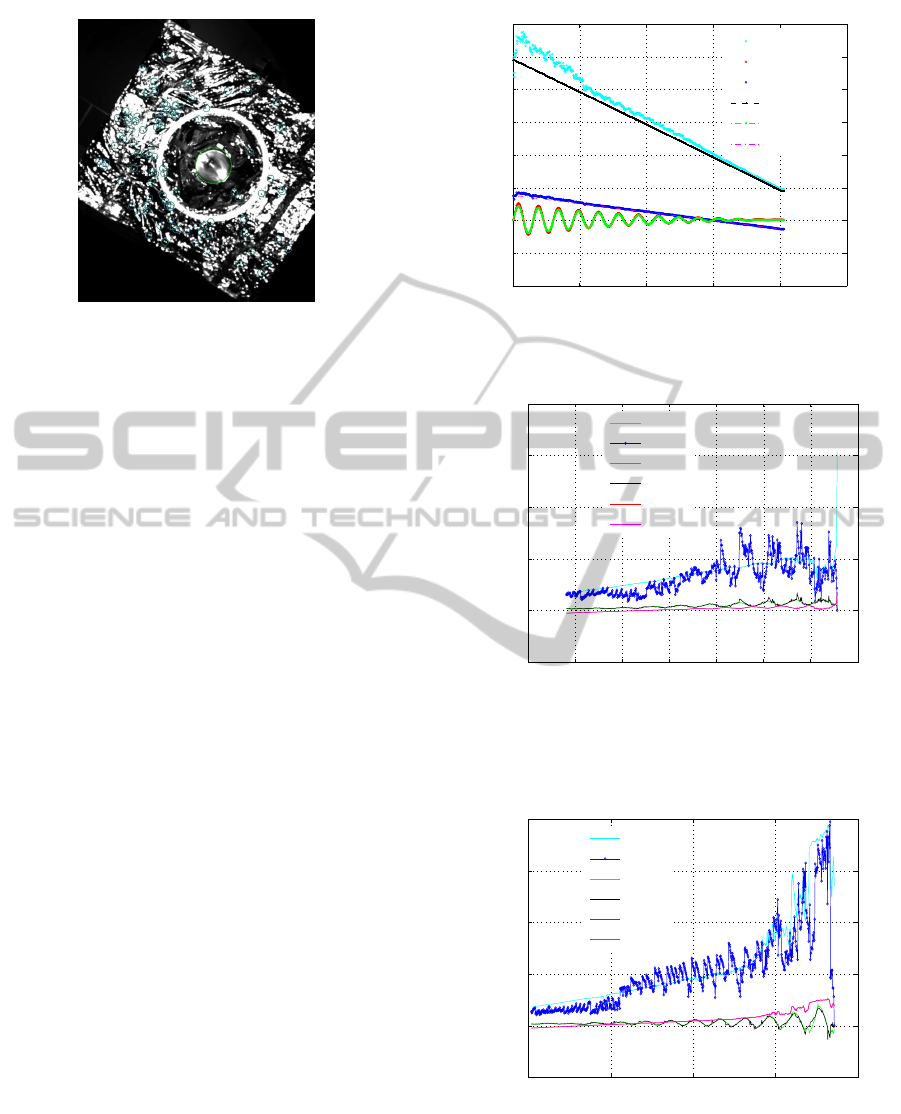
Figure 4: Combined edge and feature point tracking for 3D

localization. Keypoints (small green circles) of irregular

surface and circle of the nozzle (green contour) are tracked.

as edge detection and point feature tracking. The av-

erage processing time for image size of 1024x1024 is

135ms on 2.8GHz processeor.

Hereafter we present experimental results of four

trajectories among our several trajectories (with vari-

ous motion, illumination level and the Sun direction),

and compare combined edge and feature point track-

ing with edge based tracking. Fig.5 illustrates one

of the ground truth and the estimated trajectories. In

the ﬁrst test trajectory, the client moves from 5m to

1m in Z-direction and from 1m to 0 in X-direction

linearly. It rotates around X-axis with sinusoidal os-

cillation and around Z-axis with linear rotation. The

ground truth error associated to hybrid and edge based

tracking is shown in Fig.6; the dominant motion (of

all trajectories) is along camera Z-axis, hence we dis-

cuss errors in this direction and compare translation

errors by combined edge and feature point tracking,

and edge based tracking method. The error of com-

bined edge and keypoint tracking is relatively smaller,

when the client is close to the camera and far away (at

the beginning). However, the edge based tracking out-

performs combined edge and feature point tracking

around the middle of the trajectory (3m to 2m range).

We explain why such error variation occurred, shortly

after we demonstrate results of other trajectories.

Also we observe similar error distribution in Fig.7,

of which the translation motion of the client is simi-

lar to above except the rotation, which is only around

X-axis alternating with sinusoidal motion. In con-

trast, when the client motion is purely translational

without oscillation, the error of hybrid tracking is rel-

atively smaller at the beginning and larger around the

middle of the trajectory, similar to the rest of the ex-

periment. At very closer range however the error of

the hybrid tracking is approximately comparable to

edge based tracking ( Fig.9) unlike that of other ex-

periments. We would like to remark that all the above

0 200 400 600 800 1000

−2

−1

frame

translation [m]

Z−estimated

Y−estimated

X−estimated

Z−true

Y−true

X−true

Figure 5: One of the ground truth trajectories used for vali-

dation and corresponding estimated trajectory of the client.

0.5 1 1.5 2 2.5 3 3.5 4

−0.2

0.2

0.4

0.6

0.8

position [m]

absolute translation error [m]

Z− edge

Z− joint

Y− edge

Y−joint

X− edge

X− joint

Figure 6: Comparsion of ground truth errors of hybrid (joint

keypoint and edge) and edge based tracking. The motion is

linear translation along Z- and X-axis while osscillating si-

nusoidally in X-axis and small linear rotation about Z-axis.

1 2 3 4 5

−0.2

0.2

0.4

0.6

0.8

position [m]

absolute translation error [m]

Z− edge

Z− joint

Y− edge

Y−joint

X− edge

X− joint

Figure 7: Ground truth errors of hybrid and edge based

tracking. The motion is similar to that of Fig.6 excpet the

client rotates only around X-axis alternating sinusoidally.

experiments are performed while the direction of the

Sun simulator is perpendicular to the camera axis. On

the other hand, the ground truth error of a motion tra-

Monocular3DPoseTrackingofaSpecularObject

463

0 1 2 3 4 5

−1

−0.5

0.5

1.5

position [m]

absolute translation error [m]

Z− edge

Z− joint

Y− edge

Y−joint

X− edge

X− joint

Figure 8: Comparsion of ground truth errors of trajectory

similar to that of Fig.7 but with higher illumination and dif-

ferent direction (60 deg) of the Sun simulator.

2 3 4 5 6

−0.1

0.1

0.2

0.3

0.4

position [m]

absolute translation error [m]

Z− edge

Z− joint

Y− edge

Y−joint

X− edge

X− joint

Figure 9: Ground truth errors of purely translational mo-

tion. Edge based tracker provides aprroximately the same

errors as that of hybrid tracking while the former outper-

forms the latter around the middle of trajectory for a such

simple motion.

jectory similar to Fig.7, but the direction of the Sun

simulator about 60 deg to camera axis and illumina-

tion level 10 % higher, is shown in Fig.8. In spite of

the change of the illumination and direction of source

of light, the error of hybrid tracking is comparatively

smaller than that of edge based tracking around simi-

lar regions within the close-range described above.

Combined edge and keypoint tracking outper-

forms edge based tracking in ambiguous region of

the tracking, where the contrast of the nozzle is very

low. The edges extracted from the nozzle of the satel-

lite around 4m are very similar to background edges,

and difﬁcult to track with edge based tracker. In con-

trast, there exist distinctive point features because of

irregular surface of the MLI, which provide important

cues for tracking. Thus, the tracking beneﬁts from

combined keypoint and edges. On the other hand, at

closer range (around 2m) the edge of the nozzle of the

satellite, is sharp with good contrast and can be eas-

Table 1: RMS errors of the edge based and hybrid feature

tracking for various trajectories. The error is in m. The hy-

brid feature tracking outperforms the edge based tracking.

Trajectory Edge Hybrid

1 0.1485 0.1432

2 0.2978 0.2606

3 0.1445 0.1470

4 0.3471 0.3297

ily tracked, however, is not fully visible in the cam-

era ﬁeld of view. The sharp contours of the nozzle

and distinctive feature points at very close range pro-

vide strong cues for accurate and robust tracking. On

the contrary, the accuracy of the combined edges and

point tracking in the range around 4m to 2m drops

compared to edge based tracking. This is simply be-

cause, feature points are not well localized and drift

quickly. The drift also causes the optimization to con-

verge to local minima, degrading the performance of

the overall hybrid tracking. Thanks to model based

absolute pose tracking, the drift does not accumulate

and recovers to the correct pose when good features

and edges are detected in the subsequent frames. In

general, the accuracy of the hybrid tracking is better

than the solely edge-based tracking, as demonstrated

with root mean square errors of each test trajectory in

Table 1.

5 CONCLUSIONS

We implemented a hybrid tracking method that ex-

ploits image edges and feature points, and demon-

strated experimental results under challenging illumi-

nation condition (directional Sunlight) and visually

difﬁcult reﬂective surface (satellite). Simple geomet-

ric features such as depth discontinuities and prim-

itive shapes on the satellite provide strong cues for

real time tracking, and are efﬁcient to compute on

standard processor. Although such features of Lam-

bertian object are salient under normal lighting, they

are often ambiguous against background clutters for

specular objects under direct illumination. The am-

biguity is resolved by combining contours and point

features to ameliorate robustness and accuracy. Our

extensive experimentation using camera images, the

Sun simulator, satellite mock-up and simulated mo-

tion (with robots) shows relatively robust and accu-

rate result compared to a standard edge based track-

ing. The tracking result can be used for approach of a

client satellite for on-orbit servicing such as refuelling

and repairing.

Despite the reported improvements, in a few cases

drift of point features can prohibit the utmost ben-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

464

eﬁt of the hybrid tracking. However, drift free (at

least, reduced drift) feature-based tracking, can be in-

tegrated into edge based tracking. Moreover, our ex-

periment is based on translational motion with small

rotation and oscillation. Large rotation causes large

change of view and the feature points even drift more.

In the future work we will address this large drift

of point features, rotational motion due to tumbling

satellite and illumination changes.

ACKNOWLEDGEMENTS

The author would like to acknowledge Dr. Giorgio

Panin and Dr. Toralf Boge for their invaluable sup-

port.

REFERENCES

Oren Michael and Nayar Shree K. (1995). A Theory of

Specular Surface Geometry. In IJCV’95, International

Journal of Computer vision, volume 24, page. 740–

747.

Lagger Pascal, Salzmann Mathieu, Lepetit Vincet and Fua

pascal (2008). 3D Pose Reﬁnement from Reﬂections.

In CVPR’08, IEEE Conference on Computer vision

ans Pattern Recognition, pages 1-8, Anchorage, AK.

Yu Tianli, Xu Ning and Ahuja Narendra, (2004). Recover-

ing Shape and Reﬂectance Model of Non-lambertian

Objects from Multiple Views. In CVPR’04, Proceed-

ings of IEEE Computer Sosciety Conference on Com-

puter vision ans Pattern Recognition, volume 2, pages

II-226 - II-233.

Roth Stefan and Black Michael J., (2006). Specular Flow

and the Recovery of Surface Structure. In CVPR’06,

Proceedings of IEEE Computer Sosciety Conference

on Computer vision and Pattern Recognition, volume

Vasilyev Yuriy, Adato Yair, Zickler Todd and Ben-Shahar

Ohad, (2008). Dense Specular Shape from Multiple

Specular Flows. In CVPR’08, Proceedings of IEEE

Computer Sosciety Conference on Computer vision

ans Pattern Recognition.

Adato Yair, zickeler Todd and Benn-Shahr Ohad, (2010)

Toward robust Estimation of Specular Flow. In

BMVC’10, Proceedings of the British Machine Vision

Conference, pages 22.1–22.11.

Gouiff`es Mich`ele, Collewet Christophe, Fernandez-

Maloigne Christine, Tr´emeau Alain, (2006) Feature

Points Tracking: Robustness to Specular Highlights

and Lighting Changes. In ECCV’06, 9th European

Conference on Computer Vision, volume 4. pages

82-93.

Shi Jianbo and Tomasi Carlo, (1994) Good Features to

Track. In CVPR’94, IEEE Computer Soc. Conference

Computer Vision and Pattern Recognition, pages 593-

600.

Chang Ju Yong, Raskar Ramesh and Agrawal Amit K.,

(2009) 3D Pose Estimation and Segmentation us-

ing Specular Cues. In CVPR’09, IEEE Computer

Soc. Conference Computer Vision and Pattern Recog-

nition, pages 1706-1713.

Vacchetti Luca, Lepetit Vincent, Fua Pascal, (2004) Com-

bining Edge and Texture Information for Real-Time

Accurate 3D Camera Tracking. In ISMAR ’04, Pro-

ceedings of the 3rd IEEE/ACM International Sympo-

sium on Mixed and Augmented Reality Pages 48-57.

Kyrki Ville, Kragic Danica (2005) Integration of model-

based and model-free cues for visual object tracking.

In ICRA05, Proc. of the IEEE Int. Conf on Robotics

and Automation, pages 1554–1560.

Pressigout Muriel and Marchand Eric, (2007) Real-time

Hybrid Tracking using Edge and Texture Informa-

tion. In Proc. of International Journal of Robotics

Research, volume 26, no.7, pages 689-713.

Drummond Tom and Cipolla Robert, (2002) Real-time vi-

sual tracking of complex structures. In PAMI’02 Proc.

of IEEE Transactions on Pattern Analysis and Ma-

chine Intelligence, Volume 27, issue 7, pages 932 -

946 .

Comport A.I. and Marchand Eric, (2004) Robust model-

based tracking for robot vision. In IROS’04 Proc.

IEEE/RSJ International Conference on Intelligent

Robots and Systems, volume 1, pages 692 - 697.

Comport Andrew.I., Kragic Danica, Marchand Eric and

Chaumette Francois, (2005) Robust Real-Time Vi-

sual Tracking: Comparison, Theoretical Analysis and

Performance Evaluation. In ICRA’05 Proc. IEEE In-

ternational Conference on Robotics and Automation,

pages 2841 - 2846.

Comport Andrew I., Marchand Eric and Chaumette Fran-

cois, (2006) Statistically Robust 2D Visual Servoing.

In IEEE Transactions on Robotics volume 22, no.2,

pages 415-421.

Drummond Tom and Cipolla Robert, (1999) Visual Track-

ing and Control using Lie Algebras. In CVPR’99,

IEEE Computer Society, Computer Vision and Pattern

Recognition, volume 2, pages 2652-2659.

Monocular3DPoseTrackingofaSpecularObject

465