
Likelihood Functions for Errors-in-variables Models
Bias-free Local Estimation with Minimum Variance
Kai Krajsek, Christian Heinemann and Hanno Scharr
IBG-2: Plant Sciences, Forschungszentrum J
¨
ulich, 52425, J
¨
ulich, Germany
Keywords:
Parameter Estimation, Maximum Likelihood Estimation, Error-in-Variables Models, CRLB, Optical Flow.
Abstract:
Parameter estimation in the presence of noisy measurements characterizes a wide range of computer vision
problems. Thus, many of them can be formulated as errors-in-variables (EIV) problems. In this paper we
provide a closed form likelihood function to EIV problems with arbitrary covariance structure. Previous
approaches either do not offer a closed form, are restricted in the structure of the covariance matrix, or involve
nuisance parameters. By using such a likelihood function, we provide a theoretical justification for well
established estimators of EIV models. Furthermore we provide two maximum likelihood estimators for EIV
parameters, a straight forward extension of a well known estimator and a novel, local estimator, as well as
confidence bounds by means of the Cramer Rao Lower Bound. We show their performance by numerical
experiments on optical flow estimation, as it is well explored and understood in literature. The straight forward
extension turned out to have oscillating behavior, while the novel, local one performs favorably with respect
to other methods. For small motions, it even performs better than an excellent global optical flow algorithm
on the majority of pixel locations.
1 INTRODUCTION
Major computer vision problems, e.g. optical flow
estimation (Lucas and Kanade, 1981), camera cali-
bration (Clarke and Fryer, 1998), 3D rigid motion
estimation (Matei and Meer, 2006), or ellipse fit-
ting (Kanatani, 2008) can be described by errors-in-
variables (EIV) models. EIV models are generaliza-
tions of regression models, accounting for measure-
ment errors in the independent, measured variables. It
is well known, that a wide range of least squares esti-
mation schemes are of this type (see (Markovsky and
Huffel, 2007) for a recent overview), e.g. total least
squares estimation (TLS), weighted TLS, or general-
ized TLS.
Characteristic of such models is the coupling of
the variables of interest with the measurement noise.
E.g. spatio-temporal image derivatives needed to esti-
mate optical flow in a differential estimation scheme,
not only suffer from image noise, but also this noise is
correlated by the convolution kernels applied to calcu-
late the derivatives. As a consequence more sophisti-
cated regression techniques than simple least squares
approaches have to be applied in order to obtain re-
liable estimation results. Using such an estimation
scheme well adapted to the requirements of a specific
application can make a significant difference in terms
of accuracy and reliability of the results (see Fig. 1
for an optical flow example).
Most prominent among these regression tech-
niques are maximum likelihood (ML) estimators. ML
estimation is a well established estimation technique
known to be asymptotic efficient, meaning that it is
asymptotically unbiased and has asymptotically the
lowest possible variance for an unbiased estimator
(cmp. Sec. 2).
For identical independent distributed (iid) Gaus-
sian noise in all measurements the ML estimator is
known to be equal to TLS (Abatzoglou et al., 1991;
Huffel and Lemmerling, 2002). Unfortunately, the iid
requirement is not always fulfilled in practice. Thus
applying TLS also leads to biased results. Violation
of the iid assumption can be either due to correlations
between different measurements, as in the OF exam-
ple above, or due to varying noise levels, as e.g. in low
light scenarios, where the noise strongly depends on
image intensities.
Our Contribution. We provide a likelihood
function for EIV models, generalizing and simpli-
fying previous approaches (Matei and Meer, 2006;
Kanatani, 2008; Chojnacki et al., 2001; Leedan and
Meer, 2000). The connection to our approach is dis-
270
Krajsek K., Heinemann C. and Scharr H..
Likelihood Functions for Errors-in-variables Models - Bias-free Local Estimation with Minimum Variance.
DOI: 10.5220/0004667402700279
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 270-279
ISBN: 978-989-758-009-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

a
u
σ
20 40 60 80 100 120 140
0
0.2
0.4
0.6
0.8
1
b
u
σ
20 40 60 80 100 120 140
0
0.2
0.4
0.6
0.8
1
c
u
σ
20 40 60 80 100 120 140
0
0.2
0.4
0.6
0.8
1
d
u
σ
20 40 60 80 100 120 140
0
0.2
0.4
0.6
0.8
1
Figure 1: Results for synthetic sinusoidal pattern moving with velocity u = 0.5. Mean (blue curve) and variance (gray area)
vs. noise level of the image sequence. Left to right: LS (e.g. (Lucas and Kanade, 1981)), TLS (e.g. (Nestares et al., 2000;
Nestares and Fleet, 2003)), equilibration (M
¨
uhlich and Mester, 2004), our approach. We observe less bias for our method
wrt. LS. Lower variance of LS is due to its bias. We further see much less variance compared to TLS and equilibration. For
details see Sec.4.
cussed in detail. Furthermore we derive two schemes
enabling to statistically optimal estimate parameters
and give a method for estimating confidence bounds
in terms of the Cramer-Rao lower bound (CRLB).
Bias and variance behavior are compared, as well as
the stability of our algorithms to TLS (e.g. (Nestares
et al., 2000; Nestares and Fleet, 2003)) and equilibra-
tion (M
¨
uhlich and Mester, 2004) using random EIV
systems of equations and a toy optical flow problem.
In addition we show that, in well-structured image
regions, our estimates compare favorable to one of
the best-performing variational, so-called global al-
gorithms (Sun et al., 2010) on the Middlebury test set
(Baker et al., 2007). This demonstrates that using a
local estimator can be beneficial, when interested in
highest accuracy in the presence of ’good data’. The
derived CRLB allows to detect these good estimates.
Related Work. There is a rich literature on dif-
ferent LS methods, suitable algorithms and their error
bounds. Markovsky and Van Huffel (Markovsky and
Huffel, 2007) give an overview of variants of TLS
estimation, e.g. Weighted TLS, Generalized TLS,
or Structured TLS. Lemmerling et al. (Lemmerling
et al., 1996) show the equivalence of Constrained TLS
and Structured TLS. Yeredor (Yeredor, 2000) formu-
lates a more general criterion called Extended LS
(XLS), where LS, TLS, Constrained TLS and Struc-
tured TLS are special cases of XLS. Robust variants
like robust MSE (Mean Square Error) (Eldar et al.,
2005), or structured robust LS, minimize the worst
case residual over a set of perturbations structured
with constant sets of data matrices and vectors.
Numerous approaches have been proposed to
compensate for the bias in the TLS estimator when
noise is correlated and some of them claim to provide
an ML estimator (Nagel, 1995; M
¨
uhlich and Mester,
2004; Andres et al., 2008) but non of these estimators
delivers an analytical model for the likelihood func-
tion.
Current approaches providing closed form likeli-
hood functions suffer either from nuisance parame-
ters increasing the dimensionality of the likelihood
function with the number of measurements, or im-
pose rather strong restrictions on the error structure
of the measurements, e.g. errors of different measure-
ments are mutually statistically independent. Simon-
celli (e.g. (Simoncelli, 1993)) derived a (conditioned)
likelihood function without noise coupling to the pa-
rameters. Nestares (Nestares et al., 2000; Nestares
and Fleet, 2003) derived a closed form likelihood
function assuming the noise of different measurement
to be statistically independent.
2 MAXIMUM LIKELIHOOD
ESTIMATION
Let us repeat some basic notions of estimation the-
ory needed in the remainder of the paper. Denote
with {g
i
}, i = {1, ...,m}, m observations, with g =
(g
1
;g
2
;...;g
m
) the vector containing all observations
and with u a real valued parameter vector to be es-
timated. An estimator denotes a rule for assigning a
parameter vector ˆu for a given set of observations g.
Furthermore, let us denote with p(g|u) the sampling
distribution of the observations. Considering the sam-
pling distribution as a function of the parameter vector
u for a given set of observations yields the likelihood
function L : u 7→ p(g|u).
Important characterizations of estimators are
given by the terms consistency, (un)biased, variance,
efficiency and the Cramer Rao lower bound (CRLB).
Loosely speaking, an estimator is called consistent if
its estimates converge in a probabilistic sense to the
true parameter for increasing number of observations.
An estimator is called unbiased if the mean of its es-
timates equals the true value of the parameters u
0
, re-
peating the experiment infinitely often. The quality of
an (unbiased) estimator is measured by means of its
variance, i.e. a lower variation around the true value
is considered as more reliable. Naturally one seeks for
the estimator with lowest possible variance, irrespec-
tive of the considered data, known as the minimum
LikelihoodFunctionsforErrors-in-variablesModels-Bias-freeLocalEstimationwithMinimumVariance
271

variance unbiased estimator (MVUE). The CRLB ex-
presses a lower bound on the variance σ
2
u
i
of an un-
biased estimator, given by the inverse of the Fisher
Information I(u
i
)
σ
2
u
i
≥ I
−1
(u
i
) with I(u
i
) = −E[∂
2
u
i
(log(p(g|u)))] (1)
The quotient between the CRLB and the variance
achieved by an estimator is called efficiency. Thus if
an estimator is unbiased and achieves the CRLB, then
it is an MVUE. On the other hand if an estimator has
a lower variance than the CRLB it must be biased.
There is no general rule for deriving an MVUE
or even an efficient estimator. However, if measure-
ments are independent distributed the maximum like-
lihood estimator
ˆu = arg
u
max
∏
i
p(g
i
|u) (2)
is known to be asymptotically efficient, i.e. for m → ∞
it is unbiased and it attains the CRLB. Unfortunately,
for the general case of EIV models, like e.g. in optical
flow estimation, measurements cannot be assumed to
be independent such that asymptotic results cannot be
applied. In this case, the maximum likelihood func-
tion can still be applied within a Bayesian context,
e.g. maximum a posteriori (MAP) or minimum mean
squared estimation. Considering a flat prior distribu-
tion, the likelihood function is proportional to the pos-
terior pdf. If the posterior is not too skewed, the MAP
estimate is a reasonable point estimator of the param-
eters and its variance an estimator of the confidence
of that point estimate.
By deriving the likelihood function for the EIV
models we design an (asymptotically) unbiased, effi-
cient estimator with a natural confidence measure by
means of the CRLB.
3 ERRORS-IN-VARIABLES
PROBLEMS
Notation. Two different notations for EIV-
problems are common in literature, the one using
homogeneous coordinates for the parameter vector of
interest, the other using Cartesian coordinates. We
introduce both notations as they suggest different
estimation schemes, i.e. our Type I and Type II
schemes.
Using homogeneous coordinates for the parameter
vector u, the observation equations can be given by
g
T
0i
u = 0 (3)
with i = 1, ...,m factorizing in i vectors of noise-free
true values g
0i
. As the parameters in u are freely scal-
able they usually are restricted to the unit sphere S
n−1
,
i.e. |u| = 1. Assuming additive noise on the obser-
vations, i.e. g
i
= g
0i
+ η
i
, we observe that the noise
couples to the parameter vector
g
T
i
u − η
T
i
u = 0 . (4)
As u is defined on the unit sphere, at least one compo-
nent is nonzero. If u is known, we can assume u
n
6= 0
and divide (4) by u
n
. This allows (3) and (4) to be re-
formulated using a second frequently used notation,
where parameter vector w is given in Cartesian coor-
dinates
a
T
0i
w + b
0i
= 0 and a
T
i
w + b
i
= ρ
i
(5)
with a
i
, a
0i
, w ∈ R
n−1
, and ρ
i
, b
i
, b
0i
∈ R and i =
1,..., m, and further error components ρ
i
= η
T
i
u/u
n
,
observations
a
i
= ((g
i
)
1
,..., (g
i
)
n−1
)
T
, b
i
= (g
i
)
n
, (6)
true values
a
0i
= ((g
0i
)
1
,..., (g
0i
)
n−1
)
T
, b
0i
= (g
0i
)
n
, (7)
and scaled parameter vector
w = (u
1
/u
n
,..., u
n−1
/u
n
)
T
. (8)
These condition equations can be compactly writ-
ten with the matrix vector notation as
Aw + b = ρ and A
0
w + b
0
= 0 (9)
where we introduced the vectors
b = (b
1
,..., b
m
)
T
, b
0
= (b
01
,..., b
0m
)
T
,
ρ = (ρ
1
,..., ρ
m
)
T
(10)
and the m × n-matrices A and A
0
whose i-th column
contains the vector a
T
i
and a
T
0i
, respectively.
Let us further introduce the vectors a = Vec(A)
and a
0
= Vec(A
0
). Note that some authors, e.g.
(Nestares et al., 2000; Nestares and Fleet, 2003), also
start their analysis with this form (5) of the observa-
tion equations.
3.1 The EIV Likelihood Function
A known way (Gleser, 1981) to derive a likelihood
function L : (w, a
0
) 7→ p(a, b|w,a
0
) for the EIV prob-
lem (5) is to make the variable transformation η
i
→
(a
i
− a
0i
,b
i
− b
0i
) in the noise model p({η
i
}) and use
b
i0
= −a
T
0i
w from the first Equation in (5) to elim-
inate b
i0
. The disadvantage of this likelihood func-
tion is its dependency on the nuisance parameters a
0
growing linearly with the number of observations n.
As the parameters a
0
are unknown they have to be
estimated along with parameters w which makes this
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
272

approach cumbersome for large numbers of observa-
tions. Nestares et al.(Nestares et al., 2000; Nestares
and Fleet, 2003) eliminate the nuisance parameters
by marginalization assuming zero mean Gaussian dis-
tributed noise η
i
∼ N (
~
0,C
η
i
) as well as Gaussian
distributed nuisance parameters. They derive a condi-
tioned prior for the nuisance parameters p(a
0
|w) and
integrate over the parameters a
0
to obtain the likeli-
hood function
p(a,b|w) =
Z
p(a,b|w, a
0
)p(a
0
|w)da
0
(11)
According to Nestares et al. the closed form expres-
sion of the likelihood function requires the covariance
matrix of the noise η
j
to be proportional to the covari-
ance of the true values g
0i
as well as the noise from
different observations to be mutually statistically in-
dependent. Such restriction is in principle not nec-
essary as all nuisance parameters occur linearly and
quadratically in the exponent of the Gaussian. Thus,
they can analytically be marginalized out yielding the
likelihood function for arbitrary covariance structure.
However, it is not recommended to do so for two
reasons. Firstly, it is well known that the integral over
a multivariate Gaussian distribution involves a term
containing the determinant of a matrix whose dimen-
sion is equal to the number of nuisance parameters
and therefore difficult to handle even for moderate
numbers of observations. Secondly, and more impor-
tant, the resulting likelihood function does not fulfill
the requirements for an efficient estimator in a max-
imum likelihood estimation scenario. The asymp-
totic normality property requires measurements to be
identical independent distributed (i.i.d) which is not
fulfilled for the general EIV scenario. Adopting the
Bayesian point of view, we realize that an ML es-
timation might not be reasonable: The marginaliza-
tion of the nuisance parameters leads to a potentially
highly skewed (posterior) probability distribution of
the parameters. As a consequence, most of the prob-
ability mass does not lie under the maximum of the
probability distribution and the MAP estimator fails
to give a reasonable parameter estimate. However,
for other purposes, e.g. within a different estimator
like the minimum mean squared estimator, the EIV
likelihood function may still be useful. However, if
different measurements are mutually statistically in-
dependent, the ML estimator becomes asymptotically
efficient apart from the still cumbersome optimization
problem due to the involved determinant.
3.2 Our Conditional EIV Likelihood
Function
We propose a likelihood allowing for arbitrary Gaus-
sian noise covariance. We model the error compo-
nents ρ = (ρ
1
,..., ρ
m
)
T
, cmp. (5), by a zero mean mul-
tivariate, m-dimensional Gaussian distribution, i.e.
ρ ∼ N (
~
0,C
ρ
). C
ρ
is an m × m covariance ma-
trix. Assuming (a, w) to be given and inserting the
observation equations (5), right, in the error model
yields the conditional likelihood function p(b|a,w) =
N (b|a,w) of the parameters w
p(b|a,w) ∝ exp
−
1
2
(Aw + b)
T
C
−1
ρ
(Aw + b)
(12)
Using this noise model, we circumvent nuisance pa-
rameters and the problems discussed in Sec.3.1.
Using the notation with homogeneous parameter
vector, this function becomes
p(b|a,u) ∝ exp
−
1
2
u
T
G
T
C
−1
ς
Gu
(13)
with matrix G = (A|b) and the following connection
between the covariance matrices (i,k = 1,...,m)
C
ρ
ik
= E [ρ
i
ρ
k
] = E
η
T
i
u/u
n
η
T
k
u/u
n
(14)
=
u
T
E
η
i
η
T
k
u
u
2
n
=
C
ς
ik
u
2
n
(15)
where we defined
C
ς
ik
:= u
T
E
η
i
η
T
k
u in the last
step.
3.3 Our Conditional EIV-ML
Estimators
We propose two different estimation schemes to com-
pute the conditional EIV-ML estimate, using the
above equations:
Type I : For the first algorithm, we maximize (13)
on the unit sphere, i.e. under the condition |u| = 1.
Thus, minimizing the negative conditional log likeli-
hood −log p(b|a,u) constitutes an optimization prob-
lem solved by an iterated sequence of generalized
eigenvalue problems where C
−1
ς
is adapted in each it-
eration starting with the TLS solution. We refer to this
solution strategy as Type I . This is the straight for-
ward extension of the approach for the case of statis-
tically independent measurements presented in (Matei
and Meer, 2006).
Type II : Starting from (12) we derive the condi-
tion equation by setting the gradient wrt. w of the neg-
ative conditional log likelihood −log p(b|a,w) equal
to zero:
AC
−1
ρ
Aw + AC
−1
ρ
b − q = 0 (16)
LikelihoodFunctionsforErrors-in-variablesModels-Bias-freeLocalEstimationwithMinimumVariance
273

Algorithm 1 Calculation of C
ρ
Input: Current solution w, m × m band-matrices of
derivatives F
x
,F
y
,F
t
Output: new m × m covariance matrix C
ρ
calculate gradient operator T = F
x
w
x
+F
y
w
y
+F
t
in
direction of w
calculate C
ρ
= T ∗ T
T
as product of T
with
q
j
=
1
2
(Aw + b)
T
C
−1
ρ
(∂
w
j
C
ρ
)C
−1
ρ
(Aw + b) . (17)
We can solve for w using nonlinear Richardson
iteration (also called Picard or fixed-point iteration
(Kelley, 1995)). To this end, starting with the LS so-
lution for w, we calculate C
ρ
and p from the current
solution and solve (16) for w. The process is iterated
until convergence.
3.4 Implementation Details
C
ρ
may be not that easy to compute, depending on
the problem at hand. For our optical flow example,
coupling of the noise is done by the derivative ker-
nels used to calculate g
i
= (∂
x
,∂
y
,∂
t
)I
|
~x=~x
i
, where I is
the image intensity (cmp. (4)). The partial derivatives
∂
·
can be expressed as convolution kernels or – using
a common matrix-vector-notation, where the image
data is resorted into a vector of length m, and m is
the pixel number of the currently processed neighbor-
hood – as special m × m block-band-matrices
1
called
F
x
,F
y
,F
t
. Pseudo code calculating C
ρ
using this
matrix-vector-notation is given in Algorithm 1. Fig-
ure 2 shows examples of such covariance matrices.
The inverse of C
ρ
is not explicitly needed when
adequate equations are solved instead. E.g. C
−1
ρ
A is
calculated as C
−1
ρ
A = x and thus by solving the equa-
tion system C
ρ
x = A. An overview of the algorithm
can be seen in Algorithm 2.
3.5 Calculation of the CRLB
Computing the CRLB requires the Hessian of the neg-
ative log-likelihood which can be computed straight-
forward from Equation (12) for each subspace in the
decomposition (22). E.g. for the first subspace R
n−1
the Hessian reads
H = AC
−1
ρ
A − Q (18)
1
We neglect the border handling here, for easier under-
standing.
Algorithm 2 Parameter estimation of Type II
Input: LS solution w
old
, observations A,b
Output: new estimate w
new
, CRLB
initialize w
new
= w
old
+ 10ε
while std(w
new
− w
old
) > ε do
w
old
= w
new
calculate C
ρ
with (15) or Algorithm 1
calculate p with (17)
calculate AC
−1
ρ
b and AC
−1
ρ
A
solve for w using (16) and w
new
= w
end while
calculate Q with (19)
calculate H with (18)
Figure 2: Covariance structure of the optical flow likelihood
for a local neighborhood of size 5 × 5 × 3, with different
sizes of the derivative filters; from left to right: 3 × 3 × 3,
5 × 5 ×3 and 7 × 7 × 3. For independently distributed noise
the matrix would be diagonal.
with
(Q)
i j
=
1
2
(Aw + b)
T
C
−1
ρ
(∂
i
∂
j
C
ρ
)C
−1
ρ
(Aw + b) .
(19)
The CRLB is finally obtained by evaluating H at the
true parameter vector u
0
and taking the expectation
of the inverse Hessian w.r.t. the sampling distribu-
tion p(a, b|u
0
). Nestares et al.(Nestares et al., 2000;
Nestares and Fleet, 2003) showed that the Hessian
evaluated at the ML estimate is a reliable estimate of
the CRLB.
3.6 Relation to other ML Estimators
In order to compare different estimators it is sufficient
to compare their condition equations, i.e. the gradient
of the corresponding objective function with respect
to the parameters of interest. If two approaches have
the same objective function gradient, they produce
for each given observation the same estimate. Con-
sequently they produce the same empirical mean and
standard deviation and converge to the same mean and
variance, assuming that the solver does not get stuck
in local minima.
Gleser (Gleser, 1981) proposed the relative like-
lihood function, i.e. a likelihood function depend-
ing also on nuisance parameters, L : (w,a
0
) 7→
p(a,b|w, a
0
). Setting the gradient of the relative neg-
ative log likelihood with respect to the parameters w
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
274
and nuisance parameters a
0
equal zero yields 2n equa-
tions for the 2n unknown (u, a
0
). It is not difficult
but lengthy to show that one can use n equations in
order to eliminate the nuisance parameters a
0
yield-
ing exactly our condition equation (16). Thus, the
relative likelihood involving nuisance parameters is
equivalent to our conditional likelihood for the errors-
in-variables model.
Several publications (Nagel, 1995; Kanatani,
2008; Leedan and Meer, 2000; Chojnacki et al., 2001;
Matei and Meer, 2006) tackle EIV problems in com-
puter vision by maximizing a noise model constrained
to the observation equations for the given problem.
The approaches mainly differ in the way how this op-
timization problem is tackled (cmp. (Matei and Meer,
2006) for a discussion on their close relationship).
For linear observation equations, uncorrelated obser-
vations, i.e. E[η
j
η
i
] = 0 for i 6= j and a Gaussian noise
model η
i
∼ N (
~
0,C
η
i
) such a constrained optimiza-
tion problem can be transformed in an unconstrained
optimization problem with the objective function to
be minimized (see e.g. (Nestares and Fleet, 2003))
J(u) =
n
∑
i=1
u
T
g
i
g
T
i
u
u
T
C
η
i
u
(20)
Setting the derivative of (20) equal zero yields
n
∑
i=1
g
i
g
T
i
u
T
C
η
i
u
u =
u
T
g
i
g
T
i
u
(u
T
C
η
i
u)
2
C
η
i
u . (21)
which is denoted as the heteroscedastic errors-in-
variables (HEIV) equation (Matei and Meer, 2006).
Assuming uncorrelated observations in (13) and set-
ting the gradient of the conditional negative log like-
lihood equal zero yields exactly the HEIV Equa-
tion (21). This proves that the constraint optimiza-
tion problem proposed in (Matei and Meer, 2006;
Kanatani, 2008; Chojnacki et al., 2001) is in fact a
conditional or relative ML estimate.
4 EXPERIMENTS
We demonstrate the usefulness of our approach first
for solving a random equation system and afterwards
for estimating OF as a prototype EIV problem.
Experiment 1. In the first experiment we ran-
domly generated an equation system consisting of 50
observations and three unknown variables to be esti-
mated. We generated a randomized matrix A
0
of size
(# observations)× (# unknowns), A
0
is a 50 × 3 ma-
trix. The right side b
0
of the equation has been solved
using a randomly generated vector w. Afterwards cor-
related noise, randomly generated as well, has been
0 5 10 15 20
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
Bias(x)
x
est
− x
Noise level
OLS
TLS
Our
0 5 10 15 20
−2
−1
0
1
2
3
4
5
Var(x)
Var(x
est
) − Var(x)
Noise level
Figure 3: Solving an equation system with LS, TLS and the
new proposed method of Type II. Bias (left) and variance
(right) for correlated noise are shown.
added to A
0
and b
0
and the equation has been solved
for x as estimator for w. In total, 100 randomly cho-
sen solving vectors w have been used with a total of
20000 runs per noise level.
Results can be seen in Figure 3. The LS shows a
strongly downward biased estimate. Especially for
higher noise levels the estimated solution is much dif-
ferent compared to the true solution. LS nevertheless
shows small variance. This is reasonable as LS has a
strong bias towards the zero parameter vector and thus
frequently estimates a similar wrong solution. TLS
shows better behaviour in estimating the correct so-
lution. Drawback here is that the estimated solution
of TLS is unreliable for a noiselevel of around 12 and
higher. The variance increases strongly. This also ex-
plains the large jumps of TLS in the left plot. The
proposed method shows a more stable behaviour. The
estimation of the solution shows unbiased behaviour
until a high noise level and afterwards a slight bias.
Further, it is more reliable compared to TLS even for
high noise levels. Its variance increases but remains
within a reasonable range.
Experiment 2. In the first OF experiment we use
synthetic, noisy, structured images. We use such a
simplistic toy example to be able to trace back the be-
havior of the estimators to the noise correlation, as in
real data there are more error sources to optical flow
(see e.g. (Weber and Malik, 1995)). We generate a si-
nusoidal pattern moving to the right with a constant
velocity of u = (0.5,0). The observed image is sim-
ulated by adding i.i.d Gaussian noise with standard
deviation σ varying for different instances of the im-
age sequence. We compute the gradient components
g
i
, i ∈
{
x,y,t
}
using derivative filters of size 5 × 5 × 5
as in (Scharr, 2000). The observation equation for this
problem can be stated as g
x
u
x
+ g
y
u
y
+ g
t
= 0 (Lucas
and Kanade, 1981; Nestares et al., 2000; Nestares and
Fleet, 2003). We take constraints from a local neigh-
borhood of size 21 × 21 × 1, i.e. m = 441. Fig. 2 illus-
trates the structure of the covariance matrix of such a
problem for different filter sizes. For i.i.d noise the
matrix would be diagonal.
LikelihoodFunctionsforErrors-in-variablesModels-Bias-freeLocalEstimationwithMinimumVariance
275

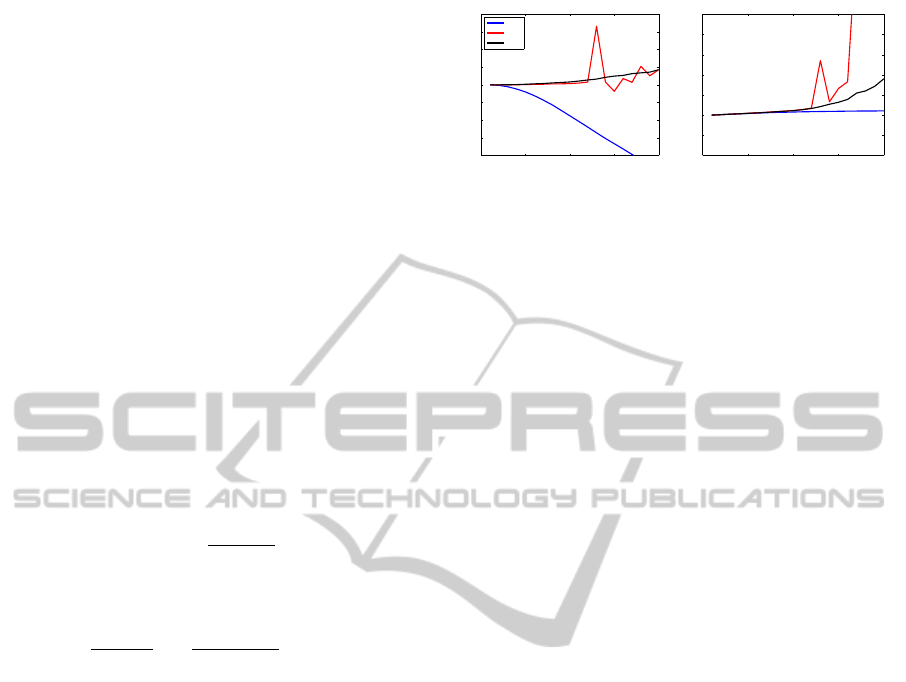
Figure 4: Energy (i.e. the negative log likelihood) vs. time
steps for (left) iteration Type I and (right) iteration Type II
˙
Different colors correspond to different noise levels of the
image sequence.
We use this experiment to test the convergence be-
haviour of algorithms Type I and Type II (see Sec.
3.2). For Type I in some cases we observed an oscil-
lating behavior when nonzero off-diagonal elements
were present in covariance matrix C
ρ
(see Fig. 4,
left), which has been our initial motivation to develop
the Type II algorithm. For Type II we always ob-
served rapid convergence (Fig. 4, right), thus for our
other experiments we use Type II only.
Figure 1 shows bias and variance of optical flow
results u
x
for different noise levels σ. We observe,
that a simple LS estimate (Figure 1a) increasingly un-
derestimates u
x
for increasing noise, but has a smaller
variance than the other estimators for all noise levels.
The TLS estimator (as used e.g. in (Nestares et al.,
2000; Nestares and Fleet, 2003)) shown in Figure 1b
has much less bias, and also a quite small variance up
to a noise level of 60. However, with further increas-
ing noise, the variance quickly rises, such that results
are completely unreliable. The same is true for the
equilibration method (M
¨
uhlich and Mester, 2004) in
Figure 1c. Its bias is even smaller, but results also be-
come unstable for noise levels higher than 80. The
EIV-ML method is shown in Figure 1d. It features
the same low bias as the equilibration method, but re-
mains much more stable for high noise levels, where
it still shows less bias than the LS approach.
Figure 6 illustrates the distribution on the unit
sphere of estimated flows for the same estimators as in
Fig. 1 for the noise level σ = 90. For the LS estimator
(left) variance of the distribution is almost isotropic
and the maximum biased towards the ’north pole’ of
the sphere, i.e. the point of zero motion. For the TLS
estimator (second left) the distribution becomes a belt
around the sphere. The equilibration method (second
right) results in a somewhat compacter distribution,
not spanning the whole sphere, but becoming wider
across the belt. EIV-ML (right) correctly keeps the
maximum very close to the true value and features
an isotropic distribution with a smaller width than the
equilibration method.
Experiment 3. In a last experiment, we calcu-
20 40 60 80 100 120 140 160 180
20
40
60
80
100
120
140
160
180
20 40 60 80 100 120 140 160 180
20
40
60
80
100
120
140
160
180
20 40 60 80 100 120 140 160 180
20
40
60
80
100
120
140
160
180
Figure 5: Accuracy of optical flow estimates in well struc-
tures areas as classified by suitably thresholding the esti-
mated CRLB (no ground truth used!). Left to right: Frame
10 of the Office sequence, ground truth restricted to image
areas with sufficient image structure, flow estimated using
Sun et al.(Sun et al., 2010), and result using our EIV-ML,
see also Table 1.
late optical flow on the well known Office sequence
(Galvin et al., 1998) using our EIV-ML and one of the
best-performing, variational algorithms on the Mid-
dlebury test set
2
(Baker et al., 2007), i.e. the method
of Sun et al.(Sun et al., 2010). Unlike all measures on
Middlebury, we investigate the performance of the al-
gorithms for well-structured image areas, e.g. for sub-
pixel accurate tracking of well structured but slowly
moving features.
In Fig. 5 resulting flows are shown, restricted to
image areas, where the trace of the estimated covari-
ance matrix of the estimator is below a certain thresh-
old (cmp. with Table 1). We see that flows estimated
by EIV-ML in these areas are closer to the ground
truth than the ones derived by the method of Sun et
al.(Sun et al., 2010).
The average error values (end point error) are
shown in Table 1 for different threshold values ap-
plied to the estimated CRLB. Our approach shows
smaller errors than method (Sun et al., 2010), more
clearly the lower the threshold.
For small thresholds it even shows smaller vari-
ance, which is remarkable, as (Sun et al., 2010) uses
a prior and by this reduces variance at the cost of in-
creased bias. The larger variance of our approach for a
larger thresholds is plausible, as adding a prior biases
2
Most sequences of the Middlebury test set include large
motions that cannot be handled by a local method without
further means. We thus do not use them here.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
276

Table 1: Optical flow errors (end point error: mean/variance) on pixels with covariance below the given threshold value for
our approach and Sun et al.(Sun et al., 2010). Density: Percentage of Pixels below Threshold.
Threshold Our Approach Sun et al.(Sun et al., 2010) Density (cmp. (Barron et al., 1994))
0.00001 0.0181 / 0.0620 0.0298 / 0.0697 23.64 %
0.00005 0.0299 / 0.0705 0.0458 / 0.0782 38.53 %
0.0001 0.0397 / 0.0794 0.0559 / 0.0813 48.16 %
0.0005 0.0714 / 0.1224 0.0771 / 0.0821 69.26 %
0.001 0.0844 / 0.1356 0.0867 / 0.0807 78.39 %
Figure 6: Illustration of the distribution of 10
4
estimated samples for different methods and noise level σ = 90. From left to
right: LS, TLS, equilibration (M
¨
uhlich and Mester, 2004), our approach. The black dot indicates ground truth. We observe
less bias for our method wrt. LS. Lower variance of LS is due to its bias. We further see much less variance compared to TLS
and equilibration.
the result and allows the method to reduce variance.
We conclude that for optical flow our local ap-
proach EIV-ML performs better than an excellent
global algorithm up to a factor of 1.6 in well-
structured image areas.
5 DISCUSSION
Our Type II estimator works fine in cases where we
know that one of the sought parameters in u, say u
n
, is
certainly nonzero. The problem can then adequately
be described using Cartesian parameters and we can
relate the homogeneous notation to the Cartesian for-
mulation means of w
j
→ u
j
/u
n
. As this transforma-
tion is one-to-one the justification of this approach
follows directly from the invariance of the likelihood
under re-parameterizations.
However, for some of the major EIV problems
in computer vision, like e.g. orientation estimation
or projective camera calibration, this is not the case.
There we only know that u lies on the unit sphere.
We cannot set any parameter unequal zero ahead of
time. Unfortunately, the estimation scheme Type I
is not always stable and thus no reliable solution.
What one can do instead, is to exploit that estimat-
ing a point on the unit sphere S
n−1
is equivalent to
estimating a point in the projective space RP
n−1
: A
point u with |u| = 1 represents a direction in R
n
. Any
other vector r ∈ R
n
\
~
0 which is parallel or antiparal-
lel to u represents the same orientation such that all
vectors in r ∈ R
n
\
~
0 with the same orientation can
be combined into one equivalence class. The set of
all equivalence classes is denoted as the projective
space RP
n−1
= (R
n
\
~
0)/ ∼ with the equivalence re-
lation x ∼ λx, for any λ ∈ R \ 0 and x ∈ R
n
\
~
0. The
so called cell-decomposition property of projective
spaces (cmp. with (Holme, 2010) p.317) states that
each projective space can be decomposed in disjoint
subspaces
RP
n−1
= R
n−1
∪ R
n−2
∪ ...R ∪ R
0
. (22)
This allows to convert the problem of estimating a
point on the unit sphere S
n−1
(Type I ) to a problem
of estimating a point in n Euclidean spaces. For MAP
estimation, we compute the MAP estimate for each
space and choose the result with the maximum poste-
rior pdf.
To derive the cell-decomposition we assign each
element u ∈ RP
n−1
to the respective subspace R
k−1
iff the last n − k coefficients of u become zero, i.e. we
map u = (u
i
,. .. ,u
k
,0, .. ., 0) by
u → (u
1
/u
k
,. .. ,u
k−1
/u
k
) ∈ R
k−1
(23)
for k ∈
{
2,. .. ,n
}
. For k = 1, i.e. u = (u
1
,0, .. ., 0) we
map u to 1.
Applying our Type II scheme to such problems
by exploiting cell-decomposition is left for future re-
search.
LikelihoodFunctionsforErrors-in-variablesModels-Bias-freeLocalEstimationwithMinimumVariance
277

6 CONCLUSIONS
We introduced a closed form conditional likelihood
function for errors-in-variables problems. It only de-
pends on the parameters of interest, in contrast to
the equivalent likelihood functions as introduced by
Gleser (Gleser, 1981) containing nuisance parame-
ters. Well known estimation schemes known from
literature (Nagel, 1995; Kanatani, 2008; Leedan and
Meer, 2000; Chojnacki et al., 2001; Matei and Meer,
2006) turned out to be special cases of our condi-
tional ML estimator for mutually independent obser-
vations. Therefore error bounds for these estimators
can be calculated as done here. In addition our ap-
proach covers also the case of arbitrary correlations
between measurements.
A straight forward extension of the algorithm from
(Matei and Meer, 2006) iterating SVDs (i.e. Type I )
turned out to have oscillating convergence behavior
when correlated noise is modeled. We did not ob-
serve such behavior for our novel algorithm (i.e. Type
II ). In addition, we experimentally showed for an op-
tical flow application the benefits of having a likeli-
hood function at hand as the likelihood approach dis-
tinguishes good estimates from less reliable estimates.
In such detected, well-structured image regions our
simple local approach even performs better than an
optical flow algorithm with regularization (Sun et al.,
2010) currently among the better performing ones on
the Middlebury test set (Baker et al., 2007). We con-
clude that using a non-regularized estimator can in-
deed be beneficial, when not interested in the whole
image, but the ’good data’ regions. Further we con-
clude that driving regularization by estimated CRLB
may be beneficial and is to be investigated in future
research.
REFERENCES
Abatzoglou, T., Mendel, J., and Harada, G. (1991). The
constrained total least squares technique and its appli-
cations to harmonic superresolution. Signal Process-
ing, IEEE Transactions on, 39(5):1070 –1087.
Andres, B., Kondermann, C., Kondermann, D., K
¨
othe, U.,
Hamprecht, F. A., and Garbe, C. S. (2008). On errors-
in-variables regression with arbitrary covariance and
its application to optical flow estimation. In CVPR.
Baker, S., Roth, S., Scharstein, D., Black, M. J., Lewis, J.,
and Szeliski, R. (2007). A database and evaluation
methodology for optical flow. Computer Vision, IEEE
International Conference on, 0:1–8.
Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).
Performance of optical flow techniques. Int. Journal
of Computer Vision, 12:43–77.
Chojnacki, W., Brooks, M. J., and Hengel, A. V. D. (2001).
Rationalising the renormalisation method of kanatani.
Journal of Mathematical Imaging and Vision, 14:21–
38. 10.1023/A:1008355213497.
Clarke, T. A. and Fryer, J. G. (1998). The Development of
Camera Calibration Methods and Models. The Pho-
togrammetric Record, 16(91):51–66.
Eldar, Y., Ben-Tal, A., and Nemirovski, A. (2005). Ro-
bust mean-squared error estimation in the presence of
model uncertainties. Signal Processing, IEEE Trans-
actions on, 53(1):168 – 181.
Galvin, B., Mccane, B., Novins, K., Mason, D., and Mills,
S. (1998). Recovering motion fields: An evaluation
of eight optical flow algorithms. In British Machine
Vision Conference, pages 195–204.
Gleser, L. J. (1981). Estimation in a multivariate ”errors
in variables” regression model: Large sample results.
The Annals of Statistics, 9(1):24–44.
Holme, A. (2010). Geometry: Our Cultural Heritage.
Springer, 2 edition.
Huffel, S. V. and Lemmerling, P. (2002). Total Least
Squares and Errors-in-Variables Modeling: Analysis,
Algorithms and Applications. Kluwer Academic Pub-
lishers, Dordrecht, The Netherlands.
Kanatani, K. (2008). Statistical optimization for geomet-
ric fitting: Theoreticalaccuracy bound and high order
error analysis. International Journal of Computer Vi-
sion, 80:167–188. 10.1007/s11263-007-0098-0.
Kelley, C. (1995). Iterative Methods for Linear and Non-
linear Equations. Society for Industrial and Applied
Mathematics, Philadelphia.
Leedan, Y. and Meer, P. (2000). Heteroscedastic regression
in computer vision: Problems with bilinear constraint.
Int. J. of Computer Vision, 2:127–150.
Lemmerling, P., De Moor, B., and Van Huffel, S. (1996).
On the equivalence of constrained total least squares
and structured total least squares. Signal Processing,
IEEE Transactions on, 44(11):2908 –2911.
Lucas, B. and Kanade, T. (August 1981). An iterative im-
age registration technique with an application to stereo
vision. In Proc. Seventh International Joint Conf.
on Artificial Intelligence, pages 674–679, Vancouver,
Canada.
Markovsky, I. and Huffel, S. V. (2007). Overview
of total least-squares methods. Signal Processing,
87(10):2283 – 2302. Special Section: Total Least
Squares and Errors-in-Variables Modeling.
Matei, B. C. and Meer, P. (2006). Estimation of nonlin-
ear errors-in-variables models for computer vision ap-
plications. IEEE Trans. Pattern Anal. Mach. Intell.,
28:1537–1552.
M
¨
uhlich, M. and Mester, R. (2004). Unbiased errors-
in-variables estimation using generalized eigensystem
analysis. In ECCV Workshop SMVP, pages 38–49.
Nagel, H.-H. (1995). Optical flow estimation and the
interaction between measurement errors at adjacent
pixel positions. Intern. Journal of Computer Vision,
15:271–288.
Nestares, O. and Fleet, D. (2003). Error-in-variables like-
lihood functions for motion estimation. In Proc. In-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
278

ternational Conference on Image Processing (ICIP
2003), pages 77–80, Madrid, Spain.
Nestares, O., Fleet, D. J., and Heeger, D. J. (2000). Likeli-
hood functions and confidence bounds for Total Least
Squares Problems. In Proc. IEEE Conf. on Computer
Vision and Pattern Recognition (CVPR’2000), Hilton
Head.
Scharr, H. (2000). Optimal Operators in Digital Image Pro-
cessing. PhD thesis, Interdisciplinary Center for Sci-
entific Computing, Univ. of Heidelberg.
Simoncelli, E. P. (1993). Distributed Analysis and Repre-
sentation of Visual Motion. PhD thesis, Massachusetts
Institut of Technology, USA.
Sun, D., Roth, S., and Black, M. J. (2010). Secrets of optical
flow estimation and their principles. In CVPR, pages
2432–2439.
Weber, J. and Malik, J. (1995). Robust computation of op-
tical flow in a multi-scale differential framework. In-
ternational Journal of Computer Vision, 14:67–81.
Yeredor, A. (2000). The extended least squares criterion:
minimization algorithms and applications. Signal Pro-
cessing, IEEE Transactions on, 49(1):74 –86.
LikelihoodFunctionsforErrors-in-variablesModels-Bias-freeLocalEstimationwithMinimumVariance
279
