
Monocular Rear Approach Indicator for Motorcycles
Joerg Deigmoeller
1
, Herbert Janssen
1
, Oliver Fuchs
2
and Julian Eggert
1
1
Honda Research Institute Europe, Carl-Legien-Strasse 30, 63073 Offenbach, Germany
2
Honda R&D Europe (Germany), Carl-Legien-Strasse 30, 63073 Offenbach, Germany
Keywords:
Driver Assistance System, Monocular Camera, Optical Flow.
Abstract:
Conventional rear-view mirrors on motorcycles only allow a limited visibility as they are shaky and cover a
small field of view. Especially at high speeds with strong headwind, it is difficult for the rider to turn his head
to observe blind spots. To support the rider in observing the rear and blind-spots, a monocular system that
indicates approaching vehicles is proposed in this paper. The vision based indication relies on sparse optical
flow estimation. In a first step, a rough separation of background and approaching object pixel motion is done
in an efficient and computationally cheap way. In a post-processing step, pixel motion information is further
checked on geometric meaningful transformations and continuity over time. As a prototype, the system has
been mounted on a Honda Pan-European motorcycle plus monitor in the dashboard that shows the rear-view
image to the rider. If an approaching object is detected, the rider gets an indication on the monitor. The rear-
view on the monitor not only acts as HMI (Human Machine Interface) for the indication, but also significantly
extends the visibility compared to mirrors. The algorithm has been extensively evaluated for relative speeds
from 20 km/h to 100 km/h (speed differences between motorcycle and approaching vehicle), at normal, rainy
and night conditions. Results show that the approach offers a sensing range from 20 m at low speed up to 60
m at night.
1 INTRODUCTION
On motorcycles, the visibility to all sides is signifi-
cantly worse compared to cars. The rear-view is only
possible by means of two mirrors, instead of three,
whereas the field of vision is partially hidden by the
riders body. Additionally, rear-view mirrors have a
tendency to tremble at high velocity or on uneven
ground. Therefore, improved rear-view and rider as-
sistance are of great importance in the motorcycle do-
main to reduce the number of accidents and fatalities.
So far, there exist only special rear view sys-
tems (Quick, 2012) and blind spot assistance systems
for cars. Latter mainly make use of radar ((Audi,
2013),(Mazda, 2011),(Hella, 2012)) or sonar (Bosch,
2012) sensors. Both sensors are not well suited for
motorcycles as they require further treatment or even
additional sensors like gyroscopes to deal with lean-
ing conditions. Additionally, radar is quite heavy and
expensive compared to the overall costs of a motorcy-
cle. Sonar, in turn, only has a range of up to 6 m (at
least for an acceptable sensor size). Therefore, cam-
eras represent a good alternative with respect to costs,
size and sensing range. Despite that, cameras can
cope with leaning conditions and provide a rear-view
image that can be displayed on a dashboard monitor.
Existing work on camera-based assistance sys-
tems are unfortunately only available for cars (Nis-
san, 2012). Commonly, the scaling factor of detected
objects in consecutive video images, i.e. its change of
size overtime is used to decide whether it is approach-
ing or not. For the detection of objects, (Stierlin and
Dietmayer, 2012) and (Mueller et al., 2008) use op-
tical flow information, whereas (Stein et al., 2003))
apply an appearance based method.
More complex approaches using pixel motion in-
formation from monocular images requires an ego-
motion-compensation at first to detect other moving
road users (Ma et al., 2004). This can either be
done by feeding data from an IMU (Inertial Measure-
ment Unit) and refining the ego-motion based on vi-
sual motion information (Rabe et al., 2007) or relying
on vision information only ((Klappstein et al., 2006),
(Scaramuzza and Siegwart, 2008)). Those methods
are mainly used for front-facing cameras.
As soon as the camera is mounted to the rear,
motion segmentation becomes much easier, as back-
ground motion caused by the ego-vehicle and object
motion caused by approaching objects significantly
differ in their scaling factor (see discussion in follow-
474
Deigmoeller J., Janssen H., Fuchs O. and Eggert J..
Monocular Rear Approach Indicator for Motorcycles.
DOI: 10.5220/0004668304740480
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 474-480
ISBN: 978-989-758-009-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ing chapter), because the former is contracting while
the latter is expanding.
Therefore, the method developed within this work
is also based on monocular pixel motion. The deci-
sion was against a stereo system to save one camera.
Additionally, the baseline of a stereo system would be
quite small because of the limited space on a motor-
cycle. This in turn restricts the sensing range signif-
icantly. Another advantage of using motion features
is the independence of an objects appearance, e.g. at
night the appearance changes significantly compared
to day-time as a vehicle can only be identified by its
front-lights.
To the knowledge of the authors, there exists no
such vision-based system for motorcycles yet. As the
main difference in vehicle dynamics between car and
motorcycle is the ability to ride in leaning position,
(Schlipsing et al., 2012) proposed a method to esti-
mate the roll angle of a motorcycle. The idea is to
transfer existing assistance systems from the car do-
main, like lane detection or obstacle detections which
requires such a roll-angle compensation. Obviously,
this represents a convenient solution to make use of
already available technologies. The disadvantage is
that all post-processing depends on the reliability of
the roll-angle compensation, which might not be de-
sirable in sense of error propagation and independent
running applications.
In the remainder of this paper, the approaching ve-
hicle indication is described at first in Section 2. The
implementation of the system on a motorcycle and ex-
perimental results under rainy, dark and high speed
conditions are discussed in Section 3. Finally, the dis-
cussion and conclusion section summarizes the out-
comes and explains remaining challenges.
2 APPROACHING VEHICLE
DETECTION
Mounting a camera to the rear of a vehicle causes a
contracting pixel motion in the image sequence if the
vehicle moves forward. This means that all pixels
move towards a focus of contraction if the scene is
static. The magnitude of each motion vector in the
image mainly depends on the corresponding depth of
a pixel in real world coordinates. If an object is mov-
ing in the scene, the measured pixel motion of the ob-
ject is a combination of the ego-motion and the object
motion. This results in zero motion if the object is
moving with the same speed in the same direction as
the ego-vehicle.
As soon as the object velocity is larger than the
ego-vehicle velocity, the pixel motion pattern of the
object becomes upscaling with a flow field mov-
ing away from a focus of expansion. This means,
during ego-vehicle movement, an approaching ob-
ject causes an expanding flow field while static back-
ground causes a contracting flow field. This makes
both patterns distinguishable by their scaling factor
(greater or lower than 1). In turn, if the object drives
with lower speed as the ego-vehicle, background and
object motion are both contracting, i.e. both scaling
factors are lower than 1.
If the ego-vehicle additionally undergoes a rota-
tional motion, the projected motion pattern on the im-
age plane is overlayed with a vertically translating
component in case of pitching or a rotational com-
ponent in case of rolling, whereas the magnitude of
a motion vector is independent of the corresponding
depth of a pixel. However, scaling factors are not in-
fluenced by rotational motion. The rolling component
is of special interest for this application, as such a mo-
tion occurs only for motorcycles and not for cars.
In the following, potentially approaching object
motion is detected by simply checking the scale fac-
tor in a local neighborhood. This is an efficient pre-
processing step to reduce the number of non-relevant
motion vectors for fitting a geometric motion model
for approaching vehicles in a second step. The main
advantage of this approach is that no ego-motioncom-
pensation needs to be done at all, which avoids the
influence of errors from an additional pre-processing
step.
2.1 Pre-selection of Motion Information
For motion estimation, a sparse pixel motion estima-
tion method has been applied. Sparse means that mo-
tion vectors
~
v
i
= (u
i
,v
i
)
T
with corresponding homo-
geneous pixel coordinates x
i
= (x
i
,y
i
,1)
T
are only
computed at well structured regions. Compared to
dense motion estimations, which compute motion
vectors for every pixel, such methods can save signif-
icant computational effort. The method used here is
the pyramid implementation of the Lucas and Kanade
optical flow estimation (Bouguet, 2000), available in
the OpenCV library (OpenCV, 2013). The big advan-
tage of the pyramid implementation compared to the
standard Lucas and Kanade approach is the ability to
cover large pixel displacements by propagating over
different image resolutions.
To decide whether a motion vector corresponds to
an approaching vehicle or to the background, at least
two neighboring motion vectors are required to com-
pute their scaling factor. As opposed to dense motion
vector fields, the neighborhood within a sparse mo-
tion vector field is not clearly defined.
MonocularRearApproachIndicatorforMotorcycles
475
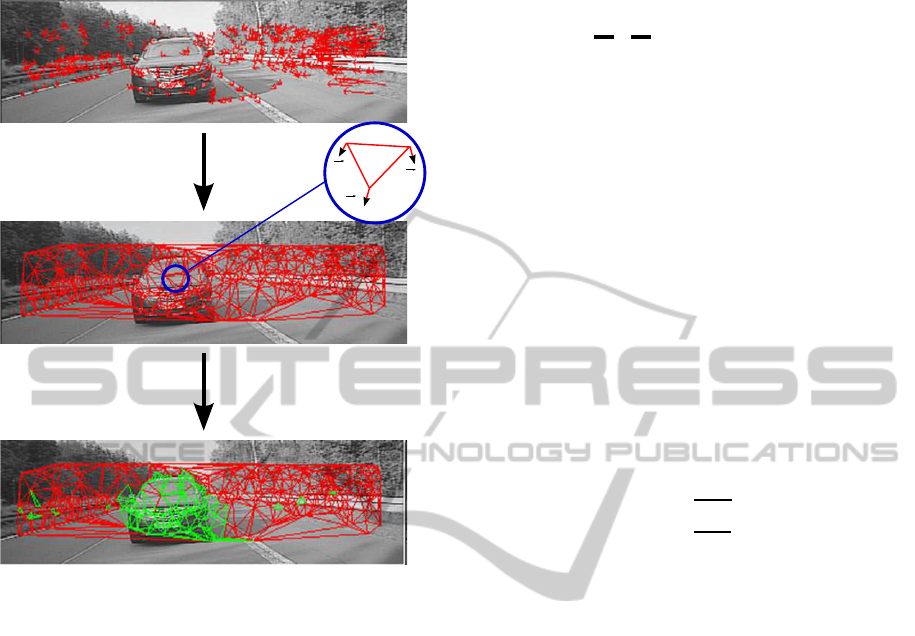
v
v
v
1
2
3
motion
estimation
Delaunay
triangulation
pre-selection
Figure 1: Pre-selection of motion vectors that correspond
to an approaching object, starting with motion estimation,
followed by triangulating the coordinates of motion vectors
and, finally, keeping only those vector triples (green edges)
where all possible combinations of vectors fulfill s
x
> 1 and
s
y
> 1.
Therefore, a Delaunay triangulation (Shewchuk,
2002) is applied to create neighborly relations be-
tween all x
i
in a mesh. For triangulation, the software
Triangle by Jonathan Shewchuk is used (Shewchuk,
1996).
The Delaunay triangulation has the specific prop-
erty that within a circle that is drawn around three co-
ordinates, a triangle does not contain any other co-
ordinate of the complete mesh (see middle image in
Fig. 1). Such a network allows to compare each mo-
tion vector with its closest neighborswithin a triangle.
To make a decision whether a triple of motion vectors
may correspond to an approaching vehicle or not, the
scaling factor of two motion vectors at each edge of a
triangle is computed.
It is assumed that the motion in a close neighbor-
hood mainly consists of a translation T and scaling S,
whereas rotational and shearing as well as perspective
transformations can be neglected. A motion vector
~
v
i
at the homogeneous coordinate x
i
can be expressed as
follows:
~
v
i
= (A
s
− E
′
)
|
{z }
A
′
s
x
i
, where (1)
A
s
=
S T
, S =
s
x
0
0 s
y
T =
t
x
t
y
and E
′
=
1 0 0
0 1 0
E
′
has been subtracted here to allow a direct map-
ping between homogeneous coordinates x
i
and 2D-
vectors
~
v
i
. To estimate the scaling factors s
x
and s
y
,
two motion vectors within a triple are subtracted to
get rid off the translation T:
~
v
i
−
~
v
j
= A
′
s
x
i
− A
′
s
x
j
= A
′
s
x
i
− x
j
y
i
− y
j
0
(2)
Rearranging the equation above and solving for s
x
and s
y
yields:
s
x
s
y
=
u
i
−u
j
x
i
−x
j
+ 1
v
i
−v
j
y
i
−y
j
+ 1
!
(3)
Three motion vectors within a triangle are only
considered for further processing if all possible com-
binations of vector pairs fulfill the constraint to be up-
scale, i.e. s
x
> 1, s
y
> 1. Fig. 1 illustrates all steps for
pre-selecting motion vectors.
2.2 Geometric Model Fitting
After the pre-selection step, it is assumed that if any
motion information remains, it mainly corresponds
to approaching vehicles. Due to wrong or imprecise
measurement it is still possible that some motion vec-
tors may fulfill the constraint to be upscaling even if
they do not follow a meaningful motion.
Therefore, the widely used robust regression
method RANSAC (RANdom SAmple Consensus,
(Fischler and Bolles, 1981), (Ma et al., 2004)) is ap-
plied to fit a geometric model into the remaining mo-
tion vectors to further check for a meaningful trans-
formation. The chosen model is an affine transfor-
mation A, which is a good approximation when real
world coordinates lie on a plane parallel to the image
sensor and move towards the camera:
~
v
′
i
= (A− E
′
)x
i
(4)
Again, E
′
has been subtracted to allow an affine
mapping between x
i
and
~
v
′
i
. The RANSAC method
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
476

finds a model that supports as many motion vectors as
possible, which is defined by the number of motion
vectors in the inlier set or also called consensus set
C(A):
C(A) = {
~
v
i
ε V : min
~
v
′
i
εM(A)
dist(
~
v
′
i
,
~
v
i
) ≤ 1px}, (5)
where V is the whole data set of motion vectors,
M(A) is the manifold of the model A and dist(·,·) is the
Euclidean distance between measured vector
~
v
i
and
model vector
~
v
′
i
. Here, the Euclidean distance is fixed
to an accuracy of 1 pixel.
After fitting the parameters of the affine model,
A is decomposed into its components to identify
whether the motion pattern is upscaling or not:
A =
K T
, where (6)
K =
k
11
k
12
k
21
k
22
, and T =
t
x
t
y
The translational component T can be read off di-
rectly. In turn, scaling components can be separated
from rotational components, if shearing components
are comparably small within K, by taking the square
root of the diagonal entries of K
T
K:
K
T
K ≈ (RS)
T
RS = S
T
R
T
RS
= S
T
ES =
s
2
x
0
0 s
2
y
(7)
where S, R and E are 2 by 2 scaling, rotation and
identity matrices, with R
T
R = E. Only affine motion
patterns that are upscaling are considered for post-
processing.
In this application, there remain two possible mo-
tion patterns after the pre-selection step. First, ap-
proaching vehicles, i.e. motion patterns that are of in-
terest. Second, if the motorcycle is standing still, e.g.
at a traffic light. This type remains because the scal-
ing factor of the background motion hovers around
one (s
x
≈ 1, s
y
≈ 1) due to noise. Therefore, this
motion information can not be identified in the pre-
selection step based on local relations only. Instead,
the global affine transformation clarifies this circum-
stance by its averaged scaling parameters. It has to be
mentioned, that in case of a non-moving motorcycle,
the static scene becomes planar and can be expressed
by an affine transformation. Only if the scaling fac-
tors of the global transformation are below a certain
threshold t
s
, it is assumed that the motorcycleis stand-
ing still.
The RANSAC method is iteratively applied two
times to cover both possible motion patterns of an
approaching vehicle and the non-moving motorcycle.
If the first fit describes the situation of a motorcycle
which is standing still or s
x
and s
y
is even downscal-
ing, corresponding motion vectors are removed and a
second model is computed. In turn, if the first fit con-
tains an upscaling model, no more iteration is done.
The following pseudo-code illustrates this procedure:
FOR i = 0 to 1
doRANSAC() // compute affine model
IF ((s
x
> t
s
) && (s
y
> t
s
))
removeOutlier() // remove motion vectors
// that do not fit to model
break // break loop and do
// post-processing
ELSE
removeInlier() // remove motion vectors
// that fit to model
continue // do second fitting
ENDFOR
2.3 Post-processing
To make the detection of approaching vehicles more
robust, a temporal filtering is applied. To do so, all
values of a 2-dimensional grid I
C
(x
i
,y
i
,t), with size
of the input image, are initialized with zero values.
Values at coordinates (x
i
,y
i
)
T
are set to 1, if they re-
late to a motion vector in the current consensus set at
time t (see Fig. 2):
I
C
(x
i
,y
i
,t) = {
1 if
~
v
′
i
ε M(A)
0 else
(8)
I
C
(x
i
,y
i
,t) is then combined with values I(x
′
i
,y
′
i
,t)
which have been predicted from previous time steps:
I(x
i
,y
i
,t) = α I
C
(x
i
,y
i
,t) + (1 − α) I(x
′
i
,y
′
i
,t), (9)
where α describes the decay over time.
In this application, α is set to 0.1 to make the fil-
tering robust against outliers. To also allow a variance
in position, each coordinate value is blurred by a 3 by
3 Gaussian kernel followed by a median filter of size
3 by 3 to remove noisy areas.
An indication is finally given to the rider if the sum
of values in the filtered 2-dimensional grid I(x
i
,y
i
,t)
exceeds a certain threshold t
a
, i.e.
t
a
>
∑
i
med[G∗ I(x
i
,y
i
,t)], (10)
where G is the Gaussian kernel and med is the me-
dian filtering.
The prediction of coordinate values I(x
i
,y
i
,t) to
the next time step I(x
′
i
,y
′
i
,t + 1) is done with the aid
of the affine transformation A from Equation 6:
MonocularRearApproachIndicatorforMotorcycles
477

predicted and accumulated coordinate values
coordinate values of current time step
Figure 2: Illustration of coordinate values that correspond
to the detected motion vectors (top and middle image) and
prediction plus accumulation over time (bottom image).
x
′
i
y
′
i
= K
x
i
y
i
+ T (11)
3 PROTOTYPE EVALUATION
The prototype motorcycle is a Honda Pan European
with a PlayStation Eye camera (75
◦
diagonal field of
view, 640x480 at 15 frames per second) mounted to
the rear. For the image processing part, the image is
scaled down to 320x240 and is cropped afterwards to
a resolution of 320x108 (mainly sky and lower part
of the road are removed). The algorithm is running
on a Core2-Duo PC (each core running at 1.86 GHz),
that is stored in the side-bag of the motorcycle. The
average computation time at day is 28 ms and 6 ms at
night (almost dark). A display is connected to the PC
which shows the full rear-view image plus the indica-
tion in the upper image part (s. Fig. 3).
Figure 3: Overlay of triangle icon to indicate approaching
vehicle to the rider.
3.1 Recording Set-up
For recording, the prototype and an additional car
were equipped with GPS-sensors to get ground truth
data for relative speed and distance between motorcy-
cle and approaching vehicle. The GPS-data has been
synchronized with the video stream, which has been
captured frame-wise (uncompressed) by the PlaySta-
tion Eye camera.
The test-rides include high-speed conditions (car
is overtaking with up to 200 km/h while the motorcy-
cle is at 100 km/h), bad-weather and night conditions.
The overall recording times were 26 min of maneu-
vers with approaching cars and 1 hour 45 min with-
out any car in the video stream as well as sequences
where the motorcycle is standing still.
3.2 Data Evaluation
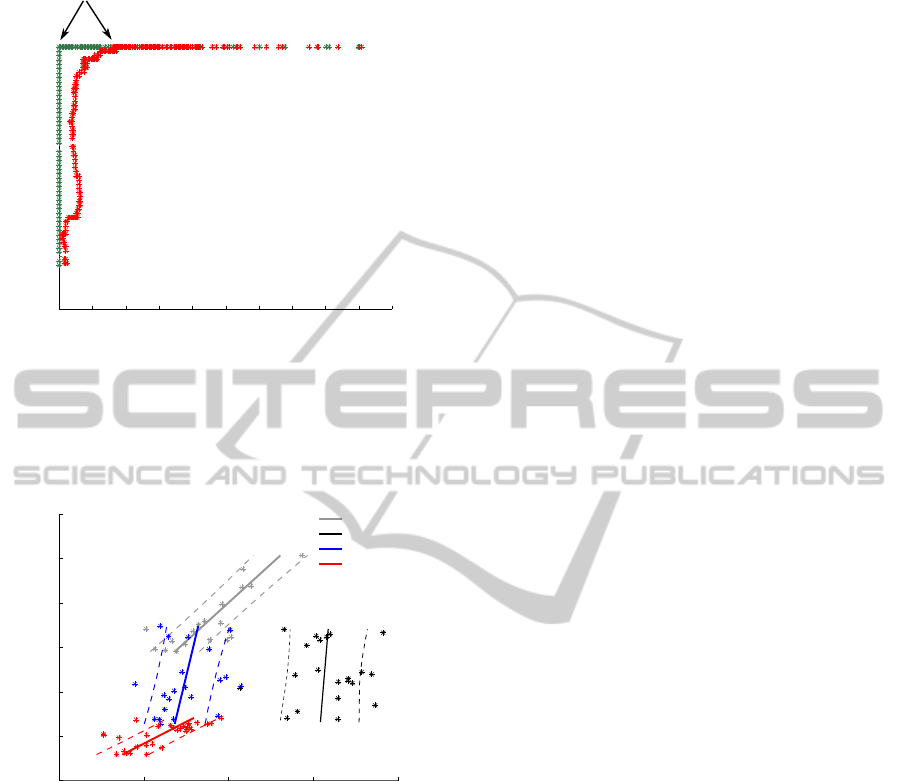
The ROC curves below (Receiver Operator Curve)
show the correct warnings (true positive rate, TPR)
against the false warnings (false positives per hour,
FP/h) for all recorded conditions. The TPR is event
based, which means that as soon as the algorithm de-
tects an approaching vehicle within a positive labeled
sequence, the detection is correct. Each positive la-
beled sequence has a fixed length of 15s (time until
the approaching vehicle reaches the motorcycle). Fi-
nally, the TPR is the ratio between the number of cor-
rectly detected vehicles divided by the total number of
positive labeled sequences. The FP/h is estimated by
counting false warning events, i.e. consecutiveframes
of false warnings are interpreted as single event.
The ROC curves are estimated by increasing the
threshold t
a
(cf. Equation 10) by 0.01 for a range of
t
a
= [0.0 ... 10.0] (see Fig. 4). It can be directly per-
ceived, that the red ROC-curve is a bit jagged instead
of monotonically decreasing. This effect is because of
clustering consecutivefalse positives to a single event.
In special situations, the system still returns false
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
478
0 40 60 80 100 120
20%
40%
60%
80%
100%
0%
true positive rate
false positives per hour
optimal working point
Figure 4: ROC curves of the system for values of t
a
ranging
from 0.0 to 10.0. The red curve represents the performance
of the system for recordings including the stroboscopic ef-
fect. The green curve shows the performance for recordings
without stroboscopic effect. The two arrows indicate the
same optimal working point for each ROC curve.
0
20
40
60
80
100
120
0
20
40
60 80
distance [m]
relative speed [km/h]
high speed
night
rain
approach
Figure 5: Scatter plot of detection distance (distance where
the vehicle has been detected) against relative speed (speed
differences between motorcycle and approaching vehicle)
for the optimal working point chosen from the ROC curves
above.
warnings (see red ROC curve in Fig. 4). Those are
due to the so called stroboscopic effect which hu-
mans also experience, e.g. on television (tyres of ve-
hicles are moving backwards while they are driving
forwards). Objects seem to move in different direc-
tions as in the real world, because of temporal alias-
ing effects caused by periodic motion at a rate close
to the frame rate of the camera. The proposed system
interprets this motion as true motion and warns the
rider in case that the motion is upscaling. The record-
ings contain such effects at an approximate speed of
120 km/h of the motorcycle while it passes a specific
bridge railing with periodic pattern. These bridges ap-
pear several times in the recordings, also because the
route has been driven multiple times.
If sequences including the stroboscopic effect are
removed from the data, the algorithm has an optimal
working range for values of t
a
= [1.7 ... 1.74], i.e.
TPR = 100% and FP/h = 0 (see green ROC curve).
The remaining recording times are 25 min of maneu-
vers with approaching cars and 1 hour 37 min without
any car in the video stream. Choosing the same work-
ing point for the red ROC-curve gives TPR = 100%
and FP/h = 32.
For the optimal working point in the ROC curve,
which corresponds to t
a
= 1.7, an additional scatter
plot is drawn (see Fig. 5). It depicts the distance and
relative speed between vehicle and motorcycle when
the vehicle has been detected for the first time. Each
dot in the plot represents one driven maneuver. The
scatter plot shows four types of maneuvers: overtak-
ing at high speed (up to 100 km/h relative speed),
overtakingat night, overtakingin rainy conditionsand
approaching (car approaches on same lane as motor-
cycle).
For each maneuver,a line has been fit into the data
set (solid line) with standard deviation (dashed lines).
As can be seen, the detection distances increase with
higher relative speed. Rainy conditions obviously do
not significantly worsen the performance of the sys-
tem. This is due to the fact that the lens kept clean for
the whole ride because of the airstream. Surprisingly,
the detection distance at night is nearly constant at
approximately 60 m. The contrast at night around the
vehicle spotlights and the light cone in front of the ve-
hicle allow a very good motion estimation in the im-
ages. As soon as the vehicle is at a certain distance, so
that pixel movement is measurable, the algorithm is
able to immediately identify the moving front-lights.
4 CONCLUSIONS AND
OUTLOOK
Supporting the rider in observing blind spots and im-
proving the surround view compared to mirrors is an
important task to reduce accidents involving motorcy-
cles.
In this paper, a very robust and simple monocu-
lar approaching vehicle detection has been presented,
so that the rider is aware of other traffic participants
behind or in blind spots. The system presented in
this paper relies on pixel motion information only and
hence is independent of the object appearance.
Extensive tests have been carried out under differ-
ent conditions including bad weather and rain. The
MonocularRearApproachIndicatorforMotorcycles
479

sensing distances span a range from 20 m at low rela-
tive speed (20 km/h relative speed) up to 60 m at night
conditions. The quantitative results are very promis-
ing so that the presented approach provides a cheap
and easy to implement support feature for motorcy-
cles.
Next steps will be undertaken to tackle the prob-
lem of the stroboscopic effect. Additionally, the view-
ing conditions concerning display size, display reso-
lution and camera field of view will be optimized to
further increase the riding comfort.
ACKNOWLEDGEMENTS
The authors thank Achim Bendig for the produc-
tive teamwork and setting up the prototype. Spe-
cial thanks also to Nils Einecke for fruitful discus-
sions, and, last but not least, manythanks to Kazuyuki
Maruyama and Mutsumi Katayama for supporting the
project.
REFERENCES
Audi (2013). Audi side assist - innovative driver assis-
tance system. http://www.gizmag.com/audi-digital-
rear-view-mirror-production/23681/.
Bosch (2012). Side view assist. http://www.
bosch-automotivetechnology.com/en/de/homepage/
homepage
1.html.
Bouguet, J.-Y. (2000). Pyramidal implementation of
the lucas kanade feature tracker description of
the algorithm. http://robots.stanford.edu/cs223b04/
algo
tracking.pdf.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM.
Hella (2012). Driver assistance systems. http://www.
hella.com/hella-com/502.html?rdeLocaleAttr=en.
Klappstein, J., Stein, F., and Franke, U. (2006). Monocular
motion detection using spatial constraints in a unified
manner. IEEE Intelligent Vehicles Symposium.
Ma, Y., Soatto, S., Kosecka, J., and Sastry, S. S. (2004). An
Invitation to 3-D Vision. Springer-Verlag, New York,
2nd edition.
Mazda (2011). Mazda’s rear vehicle monitoring sys-
tem to receive euro ncap advanced award. http://
www.mazda.com/publicity/release/2011/201108/
110825a.html.
Mueller, D., Meuter, M., and Park, S.-B. (2008). Motion
segmentation using interest points. IEEE Intelligent
Vehicles Symposium.
Nissan (2012). Multi-sensing system with rear camera.
http://www.nissan-global.com/EN/TECHNOLOGY/
OVERVIEW/rear
camera.html.
OpenCV (2013). Open source computer vision library.
http://opencv.willowgarage.com/wiki/.
Quick, D. (2012). Audi’s digital rear-view mirror
moves from racetrack to r8 e-tron production vehi-
cle. http://www.gizmag.com/audi-digital-rear-view-
mirror-production/23681/.
Rabe, C., Franke, U., and Gehrig, S. (2007). Fast detec-
tion of moving objects in complex scenarios. IEEE
Intelligent Vehicles Symposium.
Scaramuzza, D. and Siegwart, R. (2008). Monocular om-
nidirectional visual odometry for outdoor ground ve-
hicles. Computer Vision Systems, Springer Lecture
Notes in Computer Science.
Schlipsing, M., Salmen, J., Lattke, B., Schroeter, K. G., and
Winner, H. (2012). Roll angle estimation for motorcy-
cles: Comparing video and inertial sensor approaches.
IEEE Intelligent Vehicles Symposium.
Shewchuk, J. R. (1996). Triangle: Engineering a 2d qual-
ity mesh generator and delaunay triangulator. Applied
Computational Geometry: Towards Geometric Engi-
neering.
Shewchuk, J. R. (2002). Delaunay refinement algorithms
for triangular mesh generation. Computational Ge-
ometry: Theory and Applications, 22:1–3.
Stein, G., Mano, O., and Shashua, A. (2003). Vision-based
acc with a single camera: bounds on range and range
rate accuracy. IEEE Intelligent Vehicles Symposium.
Stierlin, S. and Dietmayer, K. (2012). Scale change and ttc
filter for longitudinal vehicle control based on monoc-
ular video. IEEE Intelligent Transportation Systems.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
480
