
Revisiting Pose Estimation with Foreshortening Compensation and Color
Information
Achint Setia, Anoop R. Katti and Anurag Mittal
Department of Computer Science & Engineering, Indian Institute of Technology Madras, Chennai, India
Keywords:
Upper Body Pose Estimation, Foreshortening Compensation, Part Based Model, Loopy Belief Propagation,
Color Similarity.
Abstract:
This paper addresses the problem of upper body pose estimation. The task is to detect and estimate 2D
human configuration in static images for six parts: head, torso, and left-right upper and lower arms. The
common approach to solve this has been the Pictorial Structure method (Felzenszwalb and Huttenlocher,
2005). We present this as a graphical model inference problem and use the loopy belief propagation algorithm
for inference. When a human appears in fronto-parallel plane, fixed size part detectors are sufficient and give
reliable detection. But when parts like lower and upper arms move out of the plane, we observe foreshortening
and the part detectors become erroneous. We propose an approach that compensates foreshortening in the
upper and lower arms, and effectively prunes the search state space of each part. Additionally, we introduce
two extra pairwise constraints to exploit the color similarity information between parts during inference to get
better localization of the upper and lower arms. Finally, we present experiments and results on two challenging
datasets (Buffy and ETHZ Pascal), showing improvements on the lower arms accuracy and comparable results
for other parts.
1 INTRODUCTION
This paper addresses the problem of upper body pose
estimation. The task is to detect and estimate 2D hu-
man configuration in static images for six parts: head,
torso, left and right upper and lower arms. This is
a core problem in computer vision, and it is critical
for many applications such as human computer in-
teraction, image understanding, activity recognition,
etc. There are many representations for pose, among
which the stickman notation (the parts are labeled
with different line segments) is common. An exam-
ple of pose estimation task with stickman notation is
given in Figure 1.
The common approach to pose estimation, in the
last decade, has been the Pictorial Structures(PS)
model (Felzenszwalb and Huttenlocher, 2005) that
is based on local appearance of the parts and kine-
matic constraints (visualized as springs) on the pairs
of parts: parts are parameterized by pixel location
and orientation. The part appearance models are usu-
ally simple linear filters on edges, color and location
(Andriluka et al., 2009; Ramanan and Sminchisescu,
2006), and kinematic constraints are image indepen-
dent deformable costs that force two adjacent parts to
Figure 1: Stickman notation for upper body pose estimation
and the problem of foreshortening in the left lower arm (best
viewed in color).
be together. The framework is powerful and general,
yet it is a simple generative model that allows for ef-
ficient and exact inference of the human pose config-
uration.
In our approach, we use a graphical model repre-
sentation of the upper body where vertices represent
the parts location and edges represent the pairwise
constraints between parts, and we perform inference
using the loopy belief propagation algorithm (Koller
and Friedman, 2009).
Many recent approaches (Sapp et al., 2010b; Ra-
31
Setia A., R. Katti A. and Mittal A..
Revisiting Pose Estimation with Foreshortening Compensation and Color Information.
DOI: 10.5220/0004669300310038
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 31-38
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

manan, 2006; Eichner and Ferrari, 2009; Andriluka
et al., 2009) build upon the PS framework, and use
standard sized template-based part-detectors to ap-
proximately locate parts in the image. These part
detectors are separately trained for each part from
the training dataset. We can observe that parts, par-
ticularly the lower and upper arms, have cylindrical
shape and can depict many shapes depending on their
configurations. When a person appears in fronto-
parallel plane, standard sized part detectors are suffi-
cient for correct localization. But, when certain parts
like lower arms move out of the plane, we observe
foreshortening and the standard detectors produce er-
roneous detections.
One can search for the foreshortening during part
detection, but the state space of each part (number of
different configurations) increases in such a way that
it becomes impractical to compute the pairwise con-
straints. (An example image is shown in Figure 1,
we can observe the wrong estimation of the lower left
arm due to foreshortening.) In our approach, we intro-
duce few levels of foreshortening when we perform
parts detection, and we propose an effective method
to prune the state space of each part. Our method
shows better localization for parts than the standard
sized template-based methods and thus gives better
results on challenging images.
Furthermore, in day to day images, we often ob-
serve color similarity between different parts of hu-
man body in both the presence as well as the absence
of clothes. For instance, left and right upper arms
have similar color irrespective of person clothing and
gender. We propose to exploit these color similarities
by adding two color similarity constraints between the
upper left-right arms pair and the lower left-right arms
pair, and show that these constraints improve pose
estimation when considered simultaneously with the
kinematic constraints.
Our contributions are the following: (1) we com-
pensate foreshortening in the parts, especially lower
and upper arms; (2) we exploit color similarity be-
tween left-right lower and upper arms and show better
results than the simple PS framework; (3) we present
a simple and effective method to reject part candidates
that are unlikely to be true part candidates; (4) we pro-
duce better results for the lower arms and comparable
results for other parts on the two challenging datasets
(Buffy V3.01 and PASCAl Stickmen V1.1).
In the rest of this paper, we first describe the re-
lated work in Section 2, and a brief overview of the
pictorial structures and its limitations in Section 3.
Then, we give detailed description of our framework
in Section 4, followed by the inference step in Sec-
tion 5. Finally, we show our experiments and results
in Section 6, and conclude in Section 7.
2 RELATED WORK
There has been a lot of research on human pose esti-
mation in the last four decades. We focus on the meth-
ods that overlap with our approach. First, (Fischler
and Elschlager, 1973) proposes the pictorial struc-
ture (PS) model, and (Felzenszwalb and Huttenlocher,
2005) proposes an efficient inference method focus-
ing on tree-based models that use Gaussian priors for
the kinematic constraints. (Andriluka et al., 2009)
builds upon the PS framework and uses discrimina-
tively trained part detectors for unary potentials. (Ra-
manan and Sminchisescu, 2006) proposes an advance
method of learning PS parameters that maximizes the
conditional likelihood of the parts, and captures more
complex inter-part interactions than Gaussian priors,
which we also use to train our kinematic constraints.
Along with the kinematic constraints, there have
been a few methods that use inter-part color similar-
ity for better localization of the parts. For instance,
(Eichner and Ferrari, 2009) uses Location Priors in
the window output of a person detector along with
the appearance information to initialize the unary po-
tentials for standard pictorial structure model. (Sapp
et al., 2010b) filters out less probable part locations
by using a cascade of pictorial structures, and uses
richer appearance models only at a later stage on
much smaller set of locations. The disadvantage with
this approach is that one might lose the correct lo-
cations for parts if he considers only the kinematic
constraints in the initial stages of the cascade. We,
on the other hand, directly include the constraints in
the graph and enforce them throughout the inference
stage.
There are few other approaches that use different
methods to get precise location of the parts. For in-
stance, (Gupta et al., 2008) models self-occlusion to
get precise location of the parts, (Karlinsky and Ull-
man, 2012) models the appearance of links that con-
nect two parts, and (Yang and Ramanan, 2011) pro-
poses a general flexible mixture model that augments
standard spring models and is able to capture more
complex configurations of parts.
3 PICTORIAL STRUCTURE (PS)
REVIEW
In this section, we provide a brief overview of the PS
framework (Felzenszwalb and Huttenlocher, 2005)
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
32
followed by shortcomings of the PS and related ap-
proaches.
The human body is treated as an articulated struc-
ture of parts and represented using a graphical model
G = (V,E). Each node in G represents a part location
and each edge represents the kinematic constraint be-
tween physically connected pair of parts. The loca-
tion for i
th
part is given by l
i
= [x
i
,y
i
,θ
i
, f
i
,s
i
], where
(x
i
,y
i
) is the position of the part in image, θ
i
, f
i
,s
i
are
orientation, foreshortening, and scale of the i
th
part
respectively. The configuration, with n parts and an
image I, is represented by L = {l
i
},i = [1 . ..n], and
the posterior probability is written as:
P(L|I,Θ) ∝ exp
∑
i
φ(I|l
i
,Θ) +
∑
(i, j∈E)
ψ(l
i
,l
j
)
!
(1)
Here the unary potentials φ(I|l
i
,Θ) provide the lo-
cal image evidence for the i
th
part located at l
i
with
learned appearance model Θ, and the pairwise poten-
tials ψ(l
i
,l
j
) provide priors on the relative position of
parts enforcing kinematic constraints between them
(e.g. the lower arm must be attached to the upper
arm). The graph G is a tree with only unary and kine-
matic potentials, and the exact inference of the Max-
imum a posteriori (MAP) estimate can be performed
using dynamic programming in O(n×h
2
) time, where
n is the number of parts and h is the number of states
(state space size) for each part. The time complex-
ity is further reduced to O(n × h) by using Gaussian
priors and distance transform for the kinematic con-
straints computation (Felzenszwalb and Huttenlocher,
2005).
Limitations of PS and Related Approaches. The
recent approaches (Sapp et al., 2010b; Ramanan,
2006; Eichner and Ferrari, 2009; Andriluka et al.,
2009; Karlinsky and Ullman, 2012) consider parts
as rigid rectangular templates, and neglect foreshort-
ening in the upper and lower arms. Next, the pair-
wise kinematic constraints are usually modeled as
unimodal Gaussians (Felzenszwalb and Huttenlocher,
2005; Andriluka et al., 2009), which cannot capture
the true multinomial nature of interactions between
parts. Finally, few approaches (Felzenszwalb and
Huttenlocher, 2005; Andriluka et al., 2009) do not
utilize obvious image cues such as color similarity be-
tween the left and right arms during pose estimation.
4 OUR FRAMEWORK
Considering the limitations mentioned in Section 3,
we propose that the foreshortening search and the
color similarity constraints in the upper and lower
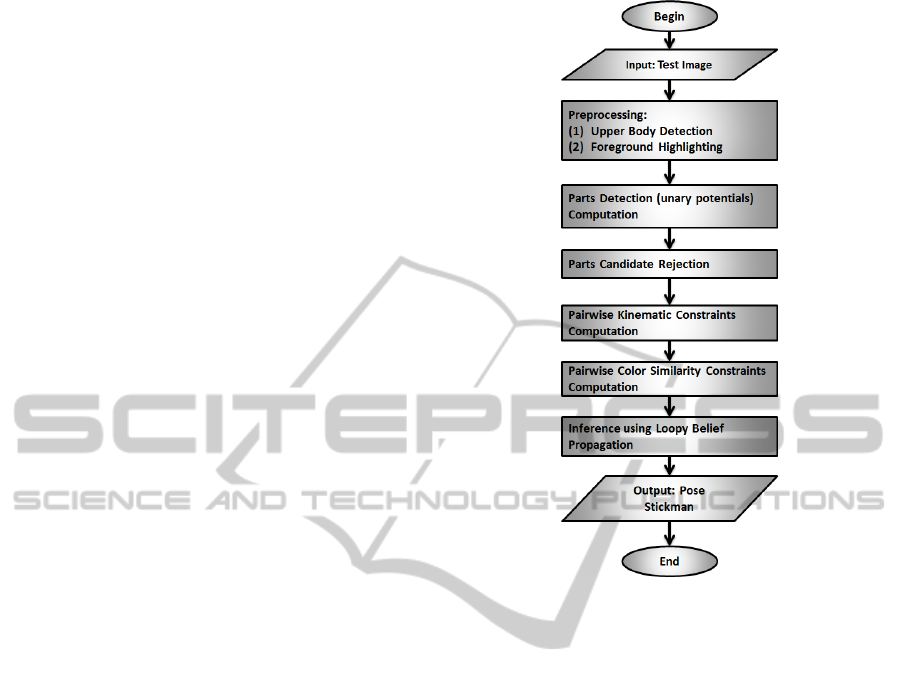
Figure 2: Flowchart of our algorithm.
arms are crucial for better localization of parts in any
upper body pose estimation method.
We implement the following in our framework:
to overcome the foreshortening problem, we add a
foreshortening search parameter f
i
for the upper and
lower arms (details in Section 4.2); to capture more
complex distributions for the kinematic constraints,
we use non-parametric distribution similar to (Ra-
manan, 2006) (details in Section 4.4); and to utilize
image color similarity cues during inference, we add
two new pairwise constraints: (1) upper left and right
arms, (2) lower left and right arms (details in Section
4.5).
Please note that after we add two new color sim-
ilarity constraints, we introduce cycles in the graph
G, and we can not perform MAP estimation using
dynamic programming. Instead, we first reduce the
search space by preprocessing the image (details in
Section 4.3), and then use the loopy belief propaga-
tion framework thus obtaining the approximate final
marginals for each part (details in Section 5).
Now, we represent the color similarity constraints
by edges C, the new posterior probability can be writ-
ten as:
RevisitingPoseEstimationwithForeshorteningCompensationandColorInformation
33

P(L|I, Θ) ∝ exp
∑
i
φ(I|l
i
,Θ) +
∑
(i, j∈E)
ψ(l
i
,l
j
)
+
∑
(i, j∈C)
ω(l
i
,l
j
)
!
(2)
where ω(l
i
,l
j
) is the color similarity measure between
the part patches at locations l
i
and l
j
respectively. We
present the graphs with and without color similarity
constraints in Figure 5.
We present the high level description of our
full upper body pose estimation algorithm through a
flowchart in Figure 2, and we describe each step in the
following sections.
(a) (b)
Figure 3: Preprocessing on the test image (best viewed in
color). (a) Upper body detection with shoulder regions
drawn in green and blue rectangles. (b) Foreground high-
lighting.
4.1 Preprocessing
The starting step of our algorithm is preprocessing on
the test image. In this step, we perform two operations
similar to (Eichner and Ferrari, 2009): upper body
detection, and foreground highlighting.
We use the Calvin upper body detector (Eichner
and Ferrari, 2009) that is based on the Histogram of
Oriented Gradients (HoG) features (Dalal and Triggs,
2005), the part based deformable models (Felzen-
szwalb et al., 2008), and the Haar cascade based face
detector (Viola and Jones, 2001). Next, we perform
foreground highlighting with the help of upper body
detection box and Grabcut (Rother et al., 2004). We
refer the reader to (Eichner and Ferrari, 2009) for
further details on the upper body detection and fore-
ground highlighting.
The upper body detector plays a crucial role in our
algorithm: it finds the locations of upright people in
images, helps reducing search space of body parts,
and provides scale information to normalize the scale
of the test image. Foreground mask further helps in
rejecting part candidates that are unlikely to be body
Figure 4: Foreshortening compensation (best viewed in
color).(a) Correct lower right arm candidate that has suf-
fered from foreshortening. (b) Rotated image at −θ
k
in
the part detection stage. (c) Vertically stretched image by
1/ f
k
. (d) Enlarged positive HoG weights of detector for
lower right arm. (e) Enlarged image patch from (c) notice
now detector will score higher when run on this patch.
parts. We explain the details of part candidates rejec-
tion in Section 4.3, where we utilize both the upper
body detection and foreground information. As an ex-
ample, we show upper body detection and foreground
highlighting on a sample test image in Figure 3.
4.2 Part Detection and Foreshortening
Compensation
After we perform the preprocessing, we have the ap-
proximate scale of the upper body from the upper
body detection box. We resize the test image to the
standard size on which our part detectors are trained,
and fix the scale parameter s
i
= 1 for all parts loca-
tions l
i
= [x
i
,y
i
,θ
i
, f
i
,s
i
] during detection.
Next, we run the trained part detectors separately
for all six parts on the test image. Part detection score
or unary potential at location l
i
for the i
th
part gives
the evidence of how good the match is between the
image patch at location l
i
and the i
th
part. Formally,
we compute part detection score at location l
i
as:
φ(I|l
i
,Θ) = D
i
· H(l
i
,w
i
,h
i
) (3)
where D
i
is the trained part detector for the i
th
part
that has width w
i
and height h
i
, and H(l
i
,w
i
,h
i
) is the
HoG feature vector of the image patch at the location
l
i
having the same dimensions as D
i
.
During detection, as we mentioned before, body
parts have cylindrical shape and they are likely to suf-
fer from foreshortening. Foreshortening is different
from scale as it only affects length of the object while
the width remains the same. (e.g. an arm pointing
towards camera will have shorter length but the same
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
34

width compared to an arm in frontal plane.) To solve
this, we introduce a foreshortening search parameter
f
i
∈ [0.6, 0.8, 1.0] during part detection, and we run
part detectors on the input test image at different ori-
entations and foreshortening levels.
Training separate arm detectors for each orienta-
tion and foreshortening level is a tedious task: one has
to search for the training samples of different orienta-
tions and foreshortening levels in the provided train-
ing set. To avoid this, we use part detectors of fixed
size, but we rotate and stretch the image by −θ
i
and
1/ f
i
respectively and then apply the detector. In this
way, we only have to train a single part detector for
each part.
We present an example in Figure 4 to provide a
clear visualization. Let us assume that the desired
candidate is the right lower arm having orientation
θ
k
and foreshortening level f
k
(marked by red rect-
angle in Figure 4a), and our lower arm detector has
dimensions equal to the red rectangle in Figure 4c.
When checking for θ
k
orientation and f
k
foreshorten-
ing level, we rotate and stretch the image vertically by
−θ
k
and 1/ f
k
respectively. So that the detector gives
an appropriate high score for the desired candidate.
4.3 Parts Candidate Rejection
After we add an additional foreshortening search pa-
rameter f
i
in the part detection step, the state space for
each part increases. For instance, for a typical image
of size 100 × 100, if we compute part detectors for 24
orientations and 4 foreshortening levels, then the state
space for each part is h = 24 × 4 × 10
4
≈ 10
6
. In the
later stage, since we are using non-parametric kine-
matic constraints, pairwise potentials computation re-
quire large number of computations O(h
2
) ≈ 10
12
.
Therefore, it is essential to prune the state space for
each part before one computes pairwise constraints.
We assume that the part detection scores at the
right locations are higher than their neighboring
scores (which generally holds), and we sample only
the local maxima points from the part detector re-
sponse over the location l
i
= [x
i
,y
i
,θ
i
, f
i
] for all six
parts. In this way, the points are not rejected even if
they have low absolute detection scores, which might
occur due to effects like bad illumination, contrast,
blur etc., as long as they possess a higher value within
their neighbourhood. After this pruning, we generally
have thousands of part candidates for each part.
Then, we utilize the upper body detection box to
prune the state space for the head and torso only. We
reject all candidates that do not overlap with the upper
body detection box. We have only a few head and
torso candidates after this step.
For upper arms, it can be noted that if the per-
son is frontal upright in the image, then the shoulders
tend to be in constant regions of upper body detec-
tion box. We call these regions as shoulder regions,
and heuristically define their location relative to up-
per body detection box. If the upper body detection
box is defined as UB = [x
1
,y
1
,w,h], where (x
1
,y
1
) is
the top-left point and w,h are its width and height re-
spectively, we define the left shoulder region (LSh)
and the right shoulder region (RSh) as:
LSh =[x
1
,(y
1
+ 0.4h), 0.4w,0.5h]
RSh =[(x
1
+ 0.6w), (y
1
+ 0.4h), 0.4w,0.5h]
(4)
We exploit these shoulder regions to reduce both the
right and left upper arms candidates: we reject all the
candidates that lie outside the respective shoulder re-
gions, and usually after this, we have only few hun-
dred valid upper arms candidates. As an example in
Figure 3(a), shoulder regions are marked in green and
blue rectangles.
Finally, we use foreground information from the
preprocessing step to reduce the number of candidates
of the lower and upper arms. We keep a part candidate
if it lies on the foreground or it has a score higher
than a threshold t
F
, and reject it otherwise. After this
final step, we usually have less than one thousand part
candidates for the lower arms.
4.4 Kinematic Constraints
Once we have the selected part candidates, we are
ready to compute the kinematic constraints that force
pairs of connected parts to stay together. These can
also be visualized as spring-like connections. For ex-
ample, the upper arms are attached to the torso, the
head is attached to the torso and so on.
We use discrete binning of the relative arrange-
ment of parts for the kinematic constraints similar to
(Ramanan, 2006). These constraints are between two
part patches located at l
i
and l
j
, and have the form:
ψ(l
i
,l
j
) = α
T
i
bin(l
i
− l
j
) (5)
where bin(.) is the vectorized count of spatial and
angular histogram bins, and α
i
is a model parame-
ter that favors certain relative spatial and angular bins
between part patches located at l
i
and l
j
. The reason
for using these over Gaussian priors is that they cap-
ture more complex distributions. We learn α
i
from the
training set with the method specified in (Ramanan
and Sminchisescu, 2006).
4.5 Color Similarity Constraints
While the kinematic constraints are independent of
the image and force pairs of parts to stay together,
RevisitingPoseEstimationwithForeshorteningCompensationandColorInformation
35
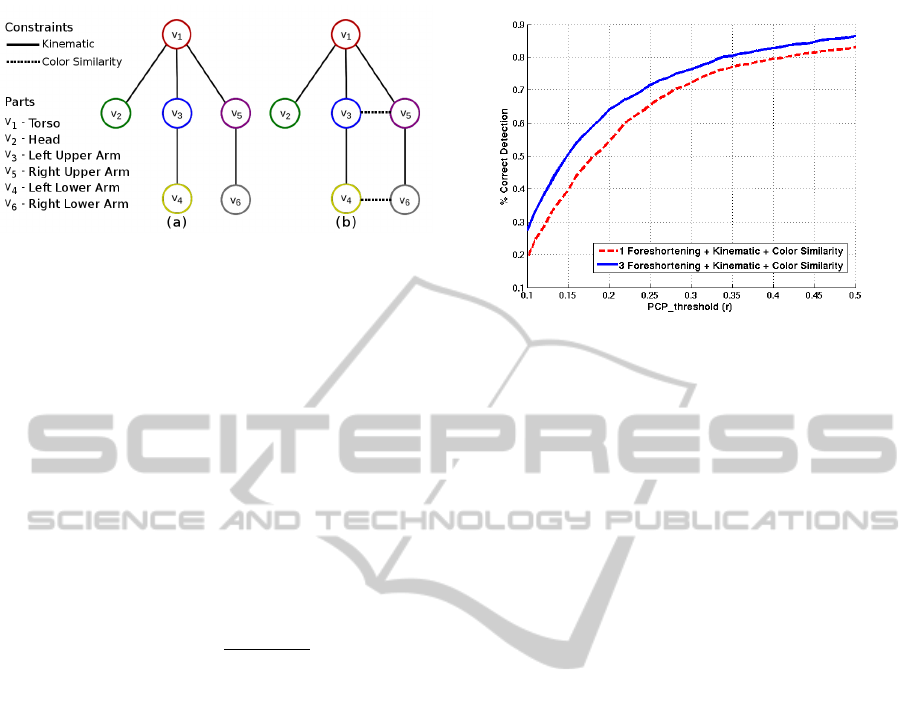
Figure 5: Human upper body pose estimation graph (best
viewed in color). (a) Graph G with only unary potentials
and kinematic constraints ψ(l
i
,l
j
). (b) Graph G
0
with addi-
tional color similarity constraints ω(l
i
,l
j
).
the color similarity constraints force the pair of parts
to have similar color. These constraints encourage
pairs of part candidates that have similar colors and
discourage others that have different colors. For ex-
ample, the true candidates of left and right upper arms
will have similar color and they will definitely differ
from a background candidate in color.
We calculate color similarity between a pair of
part patches located at l
i
and l
j
by taking the neg-
ative of the modified Chi-squared distance (χ
2
) be-
tween their color histograms.
ω(l
i
,l
j
) =
∑
k
(h
l
i
k
− h
l
j
k
)
2
H
k
(6)
where h
l
i
, h
l
j
, and H are the concatenated histograms
of normalized red and green channels over the part
patches located at l
i
, l
j
, and the entire image respec-
tively, and h
l
i
k
, h
l
j
k
, and H
k
are the k
th
bin value of the
corresponding histogram.
We use histograms of normalized red and green
channel because they provide illumination invariance
even if the patches are widely distant and have dif-
ferent illumination properties. And, we divide with
the global histogram because it gives higher weight to
sparsely observed color values than frequently occur-
ring color values.
5 INFERENCE USING LOOPY
BELIEF PROPAGATION
After we compute all the pairwise constraints (kine-
matic and color similarity), we advance to the final
inference step. When there are only unary potentials
(part detection scores) and kinematic constraints, the
graph G is a tree, but as soon as we add two color
similarity constraints, we introduce cycles in G. We
show the graph G having only unary potentials and
Figure 6: PCP curves with 1 and 3 foreshortening levels
with kinematic and color similarity constraints.
kinematic constraints in Figure 5a, and G
0
with addi-
tional color similarity constraints in Figure 5b.
Now since the graph G
0
has cycles, we cannot per-
form MAP estimation using dynamic programming.
Instead, we run the loopy belief propagation algo-
rithm (Koller and Friedman, 2009) on the selected
part candidates with the pairwise constraints. The
loopy belief propagation algorithm optimizes for the
posterior probability marginals of each part: the parts
interact with each other via belief messages. The mes-
sage from a node s with variable X to a node t with
variable Y is given by:
m
st
(Y ) =
∑
X
φ(X) × ζ(X,Y ) × ¯m(X) (7)
where ¯m(X) are the incoming messages at node s ex-
cluding the message from node t, φ(X) is the unary
potentials at node s, and ζ(X,Y ) are the pairwise po-
tentials (kinematic or color similarity) between the
variables X and Y . The algorithm passes the mes-
sages until they converge (have same value in two
consecutive iterations), and in the end, we get ap-
proximate marginals for each part. To get the best
match, we choose the top candidates among the re-
sultant marginals of all six parts for final evaluation.
6 EXPERIMENTS
We evaluate our approach on the Buffy Stickmen
v3.01 (Ferrari et al., 2008) and ETHZ PASCAL Stick-
men v1.1 (Eichner and Ferrari, 2009) datasets. We
provide our implementation details in the following
section.
6.1 Implementation Details
We use separately learned part detectors of (Sapp
et al., 2010a) for all six parts. These are Gentleboost
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
36

Table 1: Experiments on Buffy Stickmen V3.01 at PCP
0.5
(all results are in percentage). Using 3 foreshortening level produces
better results. Color similarity constraints improve the accuracy. See text for details.
Method Torso Head Upper Arms Lower Arms Total
1 foreshortening + kinematic 100 98.5 92 56.6 82.6
1 foreshortening + kinematic + color sim. 100 98.5 92.2 57.3 83.0
3 foreshortening + kinematic 100 98.5 91.3 67.8 86.1
3 foreshortening + kinematic + color sim. 100 98.5 91.9 68.1 86.4
Table 2: Comparison to other methods at PCP
0.5
(all results are in percentage). See text for details.
Results on Buffy Stickmen V3.01 Dataset
Method Torso Head Upper Arms Lower Arms Total
(Andriluka et al., 2009) 90.7 95.5 79.3 41.2 73.5
(Eichner and Ferrari, 2009) 98.7 97.9 82.8 59.8 80.1
(Karlinsky and Ullman, 2012) 99.6 99.6 93.2 60.6 84.5
(Sapp et al., 2010b) 100 96.2 95.3 63.0 85.5
(Sapp et al., 2010a) 100 100 91.1 65.7 85.9
Ours 100 98.5 91.9 68.1 86.4
Results on PASCAL Stickmen V1.1 Dataset
(Sapp et al., 2010b) 99.3 88.1 79.0 49.3 74.0
(Eichner and Ferrari, 2009) 97.2 88.6 73.8 41.5 69.3
(Karlinsky and Ullman, 2012) 98.8 97.3 81.6 47.0 75.5
Ours 96.9 84.5 81.0 45.0 72.1
classifiers (Friedman et al., 2000) on HoG based fea-
tures (Dalal and Triggs, 2005). The filter template
size for arms (upper and lower) is 72 × 36, for head it
is 45 × 45, and for torso it is 100 × 90.
In these datasets, all the images have front up-
right people, so we run the torso detector for only
the vertical orientation, head detector for the verti-
cal and the 2 nearby orientations (0 ± 15
◦
), arm de-
tectors (all 4 types) for 3 foreshortening levels f
i
∈
[0.6,0.8,1.0] and evenly divided 24 orientations θ
i
∈
[0,15,.. . ,360]
◦
. We choose threshold t
F
= 1.0 in the
part candidate rejection stage, and use k = 16 bins
for the histograms in the color similarity computa-
tion. We normalize all unary and pairwise potentials
between [0,1] before the inference stage.
6.2 Results
Evaluation Measure. The criterion for correct pose
estimation from (Ferrari et al., 2008), called the
Percentage of Correctly estimated body Parts (PCP)
is the following: an estimated body part is considered
correct if its segment endpoints lie within r% of
the length of the ground-truth segment from their
annotated location. Commonly r = 50% is chosen
for reporting the results on these datasets.
Results on Buffy Stickmen v3.01. This dataset is
quite challenging due to many uncontrolled condi-
tions such as very cluttered images, dark illumination,
and people wearing clothing of different kind and
color. It has 5 seasons among which images from
seasons 3 and 4 are used for training, and images
from seasons 2,5, and 6 are used for testing. There are
276 testing images, out of which only 259 (93.48%)
give the correct upper body detection. We report our
experiments on the Buffy Dataset in Table 1. We
can see in first and third rows of Table 1 that using 3
foreshortening levels over 1 produces better results
on average: the results are better for the lower arms
since foreshortening is mostly present in them than
the upper arms. Also, we get slightly better results
with two additional color similarity constraints than
using just the kinematic constraints. We plot the two
PCP curves in Figure 6 comparing results with 1 and
3 foreshortening levels, and we compare our results
with others in Table 2(upper). As shown, we perform
comparably well with (Sapp et al., 2010a; Sapp et al.,
2010b), improving over the lower arms accuracy.
Results on ETHZ PASCAL Stickmen v1.1. This
dataset is even more challenging as it has real world
low quality images with different illumination. We
use upper body detections provided by the dataset
and report results (as others) on only 412 test images.
We compare our results with other methods in Table
2(lower). Please note that these results are given in
(Karlinsky and Ullman, 2012) with training on the
PASCAL dataset itself. We did not re-train our part
detectors on this data set, instead we used old our part
RevisitingPoseEstimationwithForeshorteningCompensationandColorInformation
37

Figure 7: Sample results (best viewed in color). Buffy Stickmen V3.01 (left) ETHZ PASCAL Stickmen V1.01 (right).
detectors from Buffy dataset that are trained on sea-
sons 3,4 only. We get detection rate of 71% with our
algorithm, and as we can see, we get comparable re-
sults for the torso and lower arms, and good results
for the upper arms. We show sample results in Figure
7.
7 CONCLUSIONS
In this paper, we have presented a fully automated
upper body pose estimation algorithm. Our algo-
rithm works with uncontrolled images with the only
assumption that the person is upright in the image,
and can easily be extended to the full body pose es-
timation. We have proposed a method to compen-
sate foreshortening in highly variable parts such as
the upper and lower arms, and a method that effec-
tively prunes the search state space of all the parts.
Additionally, we have added pairwise color similarity
constraints between the upper left-right and the lower
left-right arms pairs along with kinematic constraints,
to utilize the image cues for better localization of the
parts, and we have used loopy belief propagation al-
gorithm for the inference. We have shown experimen-
tally that better results can be achieved with our pro-
posed foreshortening compensation and color infor-
mation utilization. We have presented results on the
two challenging datasets with improvements on the
lower arms and comparable results for other parts.
REFERENCES
Andriluka, M., Roth, S., and Schiele, B. (2009). Pictorial
structures revisited: People detection and articulated
pose estimation. In Proc. CVPR 2009. IEEE.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. CVPR 2005.
IEEE.
Eichner, M. and Ferrari, V. (2009). Better appearance mod-
els for pictorial structures. In Proc. BMVC 2009.
British Machine Vision Association.
Felzenszwalb, P., McAllester, D., and Ramanan, D. (2008).
A discriminatively trained, multiscale, deformable
part model. In Proc. CVPR 2008.
Felzenszwalb, P. F. and Huttenlocher, D. P. (2005). Pictorial
structures for object recognition. IJCV 2005.
Ferrari, V., Marin-Jimenez, M., and Zisserman, A. (2008).
Progressive search space reduction for human pose es-
timation. In Proc. CVPR 2008. IEEE.
Fischler, M. A. and Elschlager, R. A. (1973). The repre-
sentation and matching of pictorial structures. IEEE
Transactions on Computers 1973.
Friedman, J., Hastie, T., and Tibshirani, R. (2000). Additive
logistic regression: a statistical view of boosting (with
discussion and a rejoinder by the authors). The Annals
of Statistics.
Gupta, A., Mittal, A., and Davis, L. S. (2008). Constraint in-
tegration for efficient multiview pose estimation with
self-occlusions. PAMI 2008.
Karlinsky, L. and Ullman, S. (2012). Using linking fea-
tures in learning non-parametric part models. In Proc.
ECCV 2012. Springer Berlin Heidelberg.
Koller, D. and Friedman, N. (2009). Probabilistic graphical
models : principles and techniques. MIT Press.
Ramanan, D. (2006). Learning to parse images of articu-
lated bodies. In Proc. NIPS 2006.
Ramanan, D. and Sminchisescu, C. (2006). Training de-
formable models for localization. In Proc. CVPR
2006. IEEE.
Rother, C., Kolmogorov, V., and Blake, A. (2004). ”grab-
cut”: interactive foreground extraction using iterated
graph cuts. ACM Trans. Graph.
Sapp, B., Jordan, C., and Taskar, B. (2010a). Adaptive pose
priors for pictorial structures. In Proc. CVPR 2010.
IEEE.
Sapp, B., Toshev, A., and Taskar, B. (2010b). Cascaded
models for articulated pose estimation. In Proc. ECCV
2010. Springer Berlin / Heidelberg.
Viola, P. and Jones, M. (2001). Rapid object detection using
a boosted cascade of simple features. In Proc. CVPR
2001. IEEE.
Yang, Y. and Ramanan, D. (2011). Articulated pose estima-
tion with flexible mixtures-of-parts. In Proc. CVPR
2011. IEEE.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
38
