Action Categorization based on Arm Pose Modeling
Chongguo Li and Nelson H. C. Yung
Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China
Keywords:
Action Categorization, Arm Pose Modeling, Graphical Model, Maximum a Posteriori.
Abstract:
This paper proposes a novel method to categorize human action based on arm pose modeling. Traditionally,
human action categorization relies much on the extracted features from video or images. In this research,
we exploit the relationship between action categorization and arm pose modeling, which can be visualized in
a probabilistic graphical model. Given visual observations, they can be estimated by maximum a posteriori
(MAP) in that arm poses are first estimated under the hypothesis of action category by dynamic programming,
and then action category hypothesis is validated by soft-max model based on the estimated arm poses. The
prior distribution of each action is estimated by a semi-parametric estimator in advance, and pixel-based dense
features including LBP, SIFT, colour-SIFT, and texton are utilized to enhance the likelihood computation by
the Joint Adaboosting algorithm. The proposed method has been evaluated on images of walking, waving and
jogging from the HumanEva-I dataset. It is found to have arm pose modeling performance better than the
method of mixtures of parts, and action categorization success rate of 96.69%.
1 INTRODUCTION
Human action categorization from visual observa-
tions leads to answering the question of “what is the
person doing?”. Traditionally, action categorization
involves human pose estimation and action recog-
nition, of which they are always treated separately
(Moeslund et al., 2011). In fact, action and pose
are often perceived simultaneously. A research (Yao
et al., 2011) addressed the question of whether pose
estimation is useful for action categorization, and
their experiments confirmed that action categoriza-
tion indeed can benefit from pose estimation. On the
other hand, if action category is incorporated, human
pose estimation can be improved significantly (Li and
Yung, 2012), because action information helps de-
duce possible poses and narrows the pose searching
space.
By and large, arm pose as a subset of human pose
is far more representative of the action taken than
poses by other body parts and therefore dominates
the process of action categorization. It is well-known
that there are general arm poses for different actions
although individual interpretation may be somewhat
different. The difference in interpretation may be due
to individual style, body posture, as well as action tar-
gets. In spite of the differences, arm pose of a specific
action is usually constrained by its prior, which de-
fines the movement trend of the action. If the action
trend matches the prior, then deviation in other details
is tolerable while the action is recognizable. As such,
arm pose modeling and action categorization are com-
plementary from a visual perception point of view.
In this research, arm pose modeling and action
categorization are investigated as two aspects of the
same question. It can be seen as arm pose model-
ing estimates arm positions while action categoriza-
tion assigns the sequence of movements to the most
likely action category, and action priors in turn refine
the estimated arm poses. The relations between action
category, arm poses and visual data can be depicted
as a hierarchical graphical model in which the action
category is treated as the topic variable, the arm pose
modeling is the latent variable, and the visual data is
the observed variable. The topic variable and the la-
tent variable are the objects to be estimated based on
visual observations with the help of pre-learned ac-
tion priors. Given the visual observations, the topic
variable and the latent variable that maximize a pos-
teriori (MAP). In order to infer the MAP efficiently,
the topic variable and the latent variable are observed
alternatively. The best fitted action category and the
corresponding arm poses denote the final results.
The main contributions of the proposed method
are as follows. Firstly, a graphical model is proposed
for action categorization and arm pose modeling, and
two stages inference are adopted. It incorporates the
visual evidence of individual arm parts and their prior
39
Li C. and Yung N..
Action Categorization based on Arm Pose Modeling.
DOI: 10.5220/0004671500390047
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 39-47
ISBN: 978-989-758-004-8
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

distributions of different actions. Secondly, multiple
dense features are used to enhance arm part likeli-
hood, and semi-parametric density estimation is used
for arm pose of actions. Thirdly, it has been evaluated
on the HumanEva-I dataset and shown significant im-
provement over the method of mixtures of parts (Yang
and Ramanan, 2011), as well as 96.69% success rate
on action recognition.
2 RELATED WORKS
Broadly, there are two main directions in this research
area (Moeslund et al., 2011): first, discriminative ap-
proach treats action categorization as a specific la-
beling method; and second, generative model based
approach uses probabilistic models to capture the in-
herent relations between the observation variables and
hidden states of human action.
Discriminative approach for human action is a
classification solution for labeling action and the clas-
sifiers are learned from training datasets. (Schuldt
et al., 2004) proposed a SVM classification schemes
for human action recognition which adopts a local
space-time feature (Laptev, 2005) to capture local
events. It has an average 86.6% recognition accu-
racy on the KTH dataset. A codebook based on es-
timated dynamic pose has been used for action cate-
gorization by SVM classifiers (Xu et al., 2012). It has
91.2% and 81.33% average accuracies on the KTH
(Schuldt et al., 2004) and UCF sports datasets (Ro-
driguez et al., 2008) respectively. But it heavily de-
pends on the accuracy of pose estimation (Yang and
Ramanan, 2011). Action bank (Sadanand and Corso,
2012), a high-level representation of activity in video
with many individual action detectors, is used as fea-
tures for a linear SVM classifier on KTH and UCF
sports with 98.2% and 95% average accuracies re-
spectively. But, this approach needs human to select
templates. Bag of Poses (BoP) (Gong et al., 2013), in-
spired by the idea of Bag of Word, uses weak poses to
form the action vocabulary and SVM for action recog-
nition. It was evaluated on the dataset of HumanEva-I
and IXMAS with 93.9% and 82.2% action recogni-
tion rate respectively. (Fathi and Mori, 2008) con-
structed three levels of classifiers from low-level opti-
cal flow features to the final classifier for action cate-
gorization by AdaBoost. Its average performances on
KTH and Weizmann (Blank et al., 2005) are 90.5%
and 99% respectively.
Generative models for action categorization are
also called parametric time-series methods, which in-
volve learning probabilistic models for various human
actions. (Yamato et al., 1992) proposed an HMM
based method to recognize tennis playing actions.
They used vector quantification to convert grid-based
silhouette mesh features to an observation sequence.
In action categorization, the HMM that best matches
the observation sequence is chosen as the correct ac-
tion sequence. Its recognition rate is higher than 90%
for six tennis strokes. An extension of HMM com-
bines duration modeling, multi-channel interactions
and hierarchical structure into a single model (Natara-
jan and Nevatia, 2012) to capture the duration of sub-
event, the interactions among agents, and the inherent
hierarchical organization of activities. The overall ac-
curacy rates are 90.6% on a gesture dataset (Elgam-
mal et al., 2003) and around 100% on the Weizmann
(Blank et al., 2005). Topic models or hierarchical
Bayesian models, such as probabilistic Latent Seman-
tic Analysis (pLSA) and Latent Dirichlet Allocation
(LDA), are popular in language processing but also
used in action categorization (Niebles et al., 2008).
Spatial-temporal words are extracted from space-time
interest points (Doll
´
ar et al., 2005) and they are as-
signed to one of many topic models by the MAP of
the hierarchical Bayesian model. Its average perfor-
mance were 83.33% and 90% on the KTH and Weiz-
mann datasets respectively.
In summary, methods for human actions recogni-
tion published in the past are reasonably efficient for
some human action datasets. Discriminative methods
rely on the classification scheme to deal with image
features in order to recognize the corresponding hu-
man action, while ignore the semantics of human ac-
tions completely. Generative models try to describe
dependent relations among the related variables of ob-
served image features and action category. Most gen-
erative models for human motion categorization are
directly based on feature words without any seman-
tics of the human body. They attempt to map visual
observations to an action category directly, but ignore
the body configuration altogether. This is obviously
different from the way we recognize actions. We be-
lieve that body configuration is fundamental in action
categorization, and the major constituent that defines
body configuration is arm pose.
3 PROBLEM FORMULATION
3.1 Graphical Models
If an image is viewed as a document and a video as
a set of documents, then the arm pose of an image
can be viewed as the word of a document, and the ac-
tion category simply as the topic of the document. As
shown in Figure 1, for every image in a video, the ac-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
40

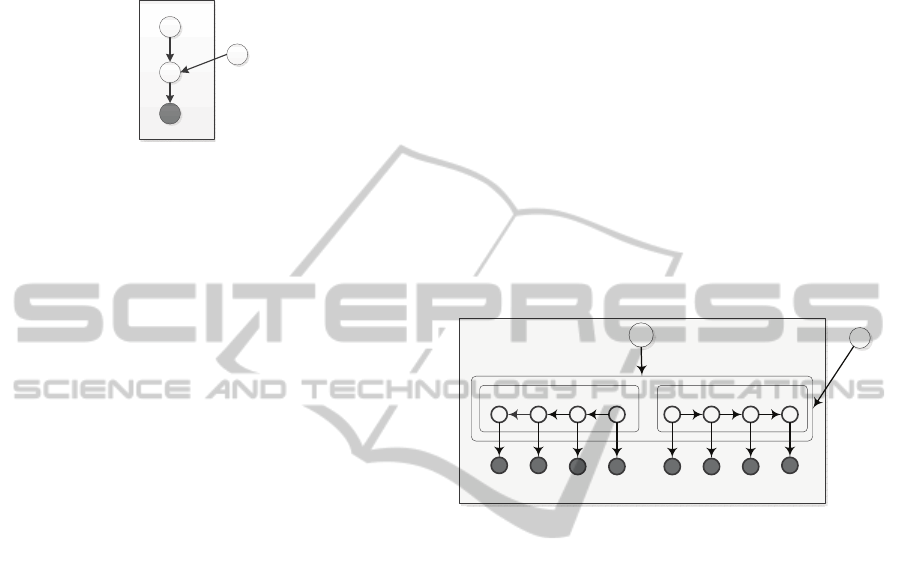
tion category z is viewed as a topic variable for arm
pose, and the arm pose w is viewed as a word i.e. la-
tent variable for the corresponding visual observation
D.
]
Z
E
'
1
Figure 1: Graphical model for action category z and arm
pose w, in which arm pose priors β is fixed and D is the
observation.
Furthermore this latent variable also has a
Bayesian Network structure. The latent variable prob-
abilities β are the arm pose priors for every action,
which we treat as a fixed quantity to be estimated.
So this problem is treated as an estimate of the ac-
tion category z and the arm pose w from the observa-
tions D simultaneously. N is the number of image for
a video and K is the number of action category that
may appear. z ∈ {1, 2, ··· , K} represents the action
category, and it indicates an arm pose prior distribu-
tions as β
z
∈ {β
1
, β
2
, ··· , β
K
}, in which β
K
is a set
of distributions for arm parts of the action category z.
The joint probability of the graphical model as shown
in Figure 1 is:
Pr(D, w, β,z) = Pr(D|w)Pr(w|z, β)
= Pr(D|w)Pr(w|β
z
).
(1)
The arm pose priors β can be learned in a supervised
manner that the action category z and arm pose w are
both observed. During inference, there is an arm pose
model based on a hypothesis of action category where
z is observed, and an action category validation based
on the modeled arm pose where w is derived.
3.2 Bayesian Network of Arm Pose
In Eqt.1, Pr(D|w) and Pr(w|β
z
) are likelihood and
prior of arm pose w respectively. Arm pose w de-
picts the spatial positions of all the arm parts in a
2D image. As proposed in (Li and Yung, 2012),
the arm pose of a person in a 2D image can be de-
fined by seven parameters: shoulder position p, the
corresponding orientations φ and scaling factors ρ
for upper arm, forearm and hand respectively. From
that, the left arm pose θ
L
in a 2D image is given
by θ
L
= [p
L
, φ
LUA
, ρ
LUA
, φ
LFA
, ρ
LFA
, φ
LH
, ρ
LH
], where
LUA, LFA and LH stand for left upper arm, left fore-
arm and left hand respectively. The right arm pose θ
R
can also be defined in the same way. Therefore, for a
person in 2D image, its arm pose parameter is written
as w = [θ
L
;θ
R
].
According to the anatomical structure of human
body, an arm is attached to the torso via the shoul-
der and can be viewed as a chain with upper arm,
forearm and hand. This anatomical chain also can be
mapped to a chain of graphical model. It describes
a conditional dependent relation between every arm
part. A left arm, for example, its parameters of hand
θ
LH
= [φ
LH
, ρ
LH
] depend on the parameters of the
forearm θ
LFA
= [φ
LFA
, ρ
LFA
] which depend on the pa-
rameters of the upper arm θ
LUA
= [φ
LUA
, ρ
LUA
]. The
parameter of its shoulder p
L
only determines the start
position of the upper arm. So there are some condi-
tional independent relations which can be considered
as redundancies among the arm component parame-
ters. Figure 2 depicts the dependent relations between
all variables.
/6
S
/8$
T
/)$
T
/+
T
56
S
58$
T
5)$
T
5+
T
5+
'
5)$
'
58$
'
56
'
/6
'
/8$
'
/)$
'
/+
'
]
Z
E
1
Figure 2: Full graphical model for action category and arm
pose modeling.
As such, the joint probability is decomposed as
Pr(D, w, β,z) = Pr(D|θ
L
, θ
R
)Pr(θ
L
, θ
R
|β
z
)
= Pr(D|θ
L
)Pr(θ
L
|β
z
)Pr(D|θ
R
)Pr(θ
R
|β
z
).
(2)
According to the Bayesian Network in the
full graphical model as shown in Figure 4, the
likelihood Pr(D|θ
L
) and prior Pr (θ
L
|β
z
) of the
left arm can be further decomposed as: Pr(D|θ
L
) =
Pr(D
LH
|θ
LH
)Pr(D
LUA
|θ
LUA
)Pr(D
LFA
|θ
LFA
)Pr(D
LS
|θ
LS
)
and Pr(θ
L
|β
z
) = Pr(θ
LH
|θ
LFA
, β
z
)Pr(θ
LFA
|θ
LUA
, β
z
)
Pr(θ
LUA
|θ
LS
, β
z
).
In the same manner, the likelihood Pr(D|θ
R
) and
prior Pr(θ
R
|β
z
) of the right arm can also be decom-
posed.
3.3 Inference for Arm Pose and Action
Category
The pipeline of action categorization based on arm
pose modeling is illustrated in Figure 3. At the first
stage, the topic variable z i.e. action category is as-
sumed to be observed. According to the Bayesian
rule, the posterior probability of arm pose is propor-
tional to its joint probability:
ActionCategorizationbasedonArmPoseModeling
41

Pr(w|D, β, z) ∼ Pr(D, w, β, z). (3)
For every hypothesis of action category z ∈
{1, 2, ··· , K}, MAP is used for arm pose modeling as
follows,
ˆw
z
= argmax
w
Pr(w|D, β, z) = argmax
w
Pr(D, w, β,z). (4)
There will be a set of results for arm pose mod-
eling, ˆw
z
∈ { ˆw
1
, ··· , ˆw
K
} and the corresponding
joint probabilities Pr(D, ˆw
z
, β, z) ∈ {Pr(D, ˆw
1
, β, z =
1), ··· , Pr(D, ˆw
K
, β, z = K)}. A dynamic program-
ming is used to infer the arm pose parameters, and it
will be descripted in Section 4.3. Then, action catego-
rization is based on the results of arm pose modeling.
At the second stage, the latent variable i.e. arm
pose parameter w is assumed to be observed. For ev-
ery hypothesis of arm pose parameter ˆw
z
and its corre-
sponding probability Pr( ˆw
z
|D, β), the final action cat-
egory ˆz is given by
ˆz = argmax
z
Pr(z| ˆw
z
)Pr( ˆw
z
|D, β), (5)
where Pr( ˆw
z
|D,β)=
Pr( ˆw
z
,D,β,z)
∑
K
k=1
Pr( ˆw
z
,D,β,z=k)
is the probability
of the arm pose ˆw
z
to be the final arm pose modeling,
and Pr(z| ˆw
z
) is the probability that the estimated arm
pose ˆw
z
is classified to action category z. Pr(z| ˆw
z
) is
trained by a soft-max model which will be descripted
in Section 4.4. Then the related arm pose parameter
ˆw
ˆz
is the final result of arm pose modeling for the cur-
rent visual observation D.
4 ARM POSE MODELING AND
ACTION VALIDATION
4.1 Prior Estimation
A Gaussian kernel based non-parametric distribution
(Li and Yung, 2012) is derived for arm priors from a
training data set. If the size of the training data is large
enough, the non-parametric distribution estimate is
suitable to represent the required distribution. How-
ever, in many applications, training data is sparse or
is not easy to collect. Therefore, semi-parametric dis-
tribution estimation (Scarrott and MacDonald, 2012)
is one of the methods used to estimate the required
distribution. Generally, there are more observations
in regions with a high density of data than in regions
with low density of data. In the tails of a distribution
where data are sparse, the non-parametric estimate
performs poorly. In this case, the semi-parametric dis-
tribution estimate takes advantage of both the para-
metric estimate and non-parametric estimate. In the
center of the distribution, a non-parametric estimate
such as Gaussian kernel based estimate is used to es-
timate the cumulative density function (CDF). A para-
metric estimate such as a generalized Pareto distribu-
tion (GPD) is then employed for each tail.
The probability density function of variable x for
the GPD with shape parameter k, scale parameter σ
and threshold parameter µ, is
f (x|k, σ, µ) =
{
1
σ
(1 + k
x−µ
σ
)
−
k+1
k
, k ̸= 0
1
σ
exp(−
x−µ
σ
), k = 0
. (6)
where µ < x when k > 0 or µ < x < −
σ
k
when k < 0.
If k = 0 and µ = 0, the GPD is equivalent to the ex-
ponential distribution. If k > 0 and µ =
σ
k
, the GPD
is equivalent to the Pareto distribution. The param-
eters of generalized Pareto can be estimated by the
maximum likelihood estimation (Davison and Smith,
1990). Finally, the estimated semi-parametric distri-
butions combined with uniform distributions are nor-
malized and discretized as the priors of arm pose.
4.2 Likelihood Computation
The overall likelihood of arm parts comes from two
types of evidence: the evidence from the lines and
regions and the evidence from the pixel-based dense
features.
4.2.1 Likelihood from Lines and Regions based
Features
To derive the likelihood of an image patch containing
an arm part, the boundary and foreground information
for the upper arm and forearm, and skin color for the
hand are selected to be the salient features. Since up-
per arm and forearm are more likely to be covered by
sleeves of clothes, their color or texture information
is unreliable. In this regard, boundary and foreground
features are used for the upper arm and forearm in-
stead, while color information is mainly used for the
hand.
To evaluate the boundary, foreground and skin
color features on a patch, two types of probabilistic
templates are proposed (Li and Yung, 2012). The
features are boundary, foreground and skin color
mask. The probability boundary (pb) approach (Mar-
tin et al., 2004) is used to generate boundary feature
f
pb
, the foreground f
f g
is extracted by the method
(Wang and Yung, 2010), and the skin color mask f
sc
is produced by the method (Conaire et al., 2007). Two
probabilistic templates are proposed to calculate arm
parts’ likelihoods with the derived features. One tem-
plate b
θ...
contains two Gaussian distributions on both
sides for boundary features, and another template g
θ...
contains only Gaussian distributions in the middle for
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
42

&RORU
,PDJH
)HDWXUHV
)HDWXUH
([WUDFWLRQ
$UP3RVH
0RGHOLQJ
$FWLRQ
3ULRUV
$UP3RVH
&DQGLGDWHV
$FWLRQ
9DOLGDWLRQ
$FWLRQ
&DWHJRU\
6RIWPD[
PRGHO
^ƚĂŐĞϭ ^ƚĂŐĞϮ
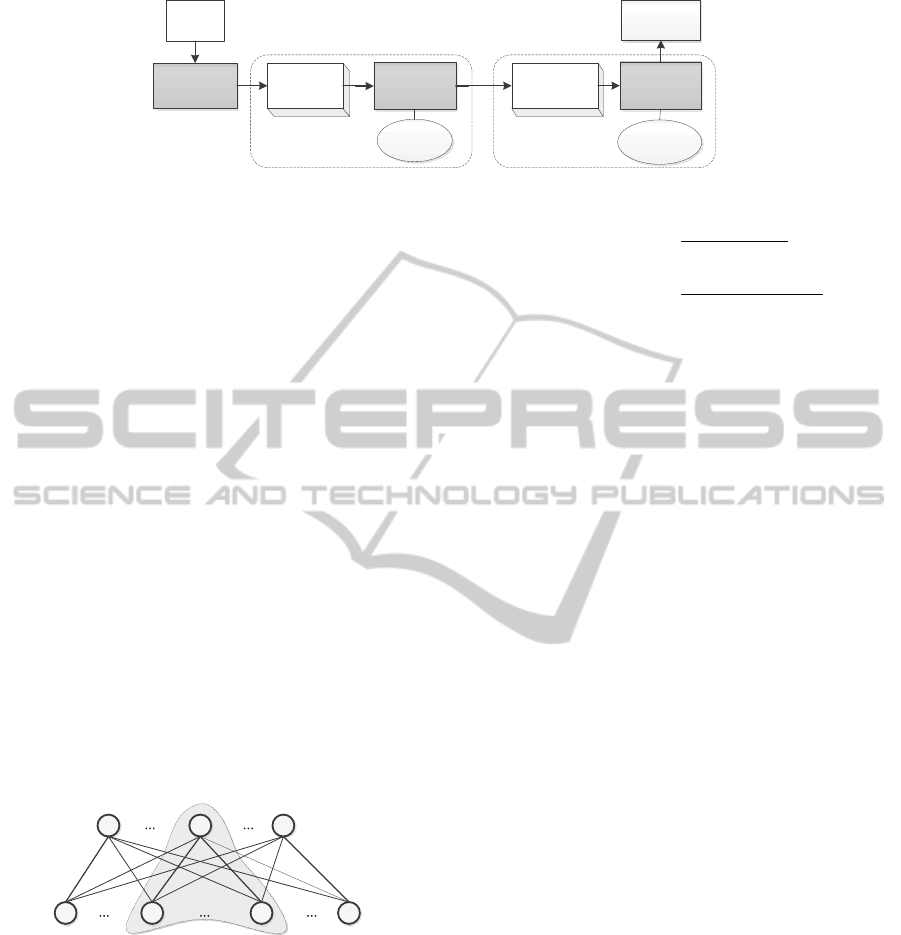
Figure 3: The pipeline for action categorization based on arm pose modeling.
foreground and skin mask, where θ. . . is the parame-
ter of an arm part. All the probabilistic templates are
normalized.
4.2.2 Likelihood from Dense Features
To derive more reliable evidence of the appearance
of arm parts, pixel based dense features are incorpo-
rated. In this proposed method, the combined fea-
ture descriptors used are local binary patterns (LBP),
scale-invariant feature transform (SIFT), colour-SIFT
and texton. To derive the confidence value between
a pixel and a specific class label, the Joint Boosting
algorithm (Torralba et al., 2004) is adopted which is
an efficient approach to train multi-classifiers jointly
by finding common features that can be shared across
classes. The confidence value of class c and the com-
bined feature x
i
for pixel i is derived by a learned
strong classifier in an additive model of the form
H(x
i
, c) =
∑
M
m=1
h(x
i
, c), summing the classification
confidence of M weak classifiers. Actually, it is the
weight of the edge between a category label and the
dense features of a pixel as shown in Figure 4.
T
[

[
S
[
1
[

F
-
F


F[+

-1
F[+

MS
F[+

MT
F[+
M
F
Figure 4: Bipartite graph of pixel based dense features and
category labels, where c
1
, ·· · , c
j
, ·· · , c
J
is the set of labels
with J categories, x
1
, ·· · , x
p
, ·· · , x
N
is the set of dense fea-
tures for N pixels, and the edges between two sets are the
confidence values H from the trained Joint Boosting classi-
fiers. The shaded part is a sub bipartite graph with only one
category label and the dense features of some pixels.
For a given parameter θ of a specific arm part c
j
,
if the involved dense features are represented by X =
{x
p
, ··· , x
q
}, the likelihood based on dense features
can be calculated by
Pr( f
ds
|θ
c
j
) = Pr(X|c
j
) =
∑
x∈X
Pr(x, c
j
)
∑
x∈ds
Pr(x, c
j
)
=
∑
x∈X
exp(H(x, c
j
))
∑
x∈ds
exp(H(x, c
j
))
,
(7)
where f
ds
= {x
1
, x
2
, ··· , x
N
} is the dense features for
all pixels.
4.2.3 The Overall Likelihood
The likelihoods of upper arm (UA), forearm (FA), and
hand ( H) are given as below:
Pr(D|θ
UA
) = Pr( f
pb
, f
f g
, f
ds
|θ
UA
)
= Pr( f
pb
|θ
UA
)Pr( f
f g
|θ
UA
)Pr( f
ds
|θ
UA
),
(8)
Pr(D|θ
FA
) = Pr( f
pb
, f
f g
, f
ds
|θ
FA
)
= Pr( f
pb
|θ
FA
)Pr( f
f g
|θ
FA
)Pr( f
ds
|θ
FA
),
(9)
Pr(D|θ
H
) = Pr( f
sc
|θ
H
)Pr( f
ds
|θ
H
). (10)
The upper arm UA can be the left upper arm LUA
or the right upper arm RUA , and the forearm FA and
hand H also can be one of the two arms. These items
are incorporated in the expansion of Eqt.2 to calculate
the likelihoods for the left and right arms.
4.3 Inference for Arm Pose
When an action hypothesis is given, its pose model-
ing can be derived by MAP based on the extracted
features and the corresponding priors. Dynamic pro-
gramming (Felzenszwalb and Zabih, 2011), one of
message passing methods, is efficient enough to solve
the MAP problem. As shown in Figure 5, there are
three main layers for the lattice of one arm pose es-
timation. The three layers from left to right repre-
sent the parameter states of UA, FA and H. It also
has a start node P
S
which represents the shoulder lo-
cation parameter, and an end node P
E
. Similarly in
every layer, nodes represent all parameter states that
the corresponding arm part may hold. For example,
θ
m
UA
represents the m
th
parameter state for the upper
arm which has M different parameter states in all.
Besides, the node will assign a score S
m
UA
during in-
ference. There are directed edges between nodes of
ActionCategorizationbasedonArmPoseModeling
43

͙
6
S

8$
T

8$
T
P
8$
T
0
8$
T
͙
͙
͙
͙
͙
(
S

)$
T

)$
T
P
)$
T
0
)$
T

+
T

+
T
P
+
T
0
+
T
/D\HURI8SSHU$UP /D\HURI)RUHDUP
/D\HURI+DQG
Figure 5: Lattice structure for dynamic programming.
adjacent layers and their weights represent the condi-
tional probability between arm parts. Dynamic pro-
gramming starts from the start node P
S
, and along the
layer direction to the end node P
E
. The detailed pro-
cedure is as follows.
The score of the start node is initialized as S
P
s
= 0,
then the score of the m
th
node in the second layer, i.e.
upper arm layer, is
S
m
UA
= S
P
s
+ logPr(θ
m
UA
|P
s
) + logPr(D|θ
m
UA
). (11)
After computing the scores of nodes in the layer of
upper arm, the score of the mth node in the third layer,
i.e. forearm layer, is
S
m
FA
= max
n
S
n
UA
+logPr(θ
m
FA
|θ
n
UA
)+logPr(D|θ
m
FA
). (12)
Then, in the same manner, the score of the mth node
in the layer of hand, i.e. the third layer, is
S
m
H
= max
n
S
n
FA
+ logPr(θ
m
H
|θ
n
FA
) + logPr(D|θ
m
H
). (13)
Finally, the score of the end node P
E
is
S
P
E
= max
n
S
n
H
. (14)
During inference, all the nodes record their previ-
ous nodes which contribute to the maximum. So, the
route can be retraced from the end node based on the
records of the previous nodes. Then the nodes in the
corresponding route with the maximum posterior are
the estimated parameters
ˆ
θ
LA
or
ˆ
θ
RA
for the MAP so-
lution. This procedure makes MAP inference possible
and efficient.
4.4 Action Hypothesis Validation
Soft-max regression (Duan et al., 2003) is an efficient
approach for multi-class classification and generalizes
logistic model where the class label can take on more
than one possible value. In our problem, the estimated
parameter of arm pose ˆw
z
is the input to the soft-max
regression model, and it produces the hypothesis of
the probabilities Pr(y = k| ˆw
z
) for the k
th
action cate-
gory. The probability Pr(y = z| ˆw
z
) is used for action
category validation.
Training soft-max regression model is a super-
vised procedure. The training set is {w
k
} which con-
tains the samples of arm pose and their corresponding
action category k ∈ {1, 2, ··· , K}. The i
th
pose sample
of the action category k is represented by w
i
k
and its
hypothesis is
h
ϑ
(w
i
k
) = [Pr(y = 1|w
i
k
;ϑ),· ·· , Pr(y = K|w
i
k
;ϑ)]
T
=
[exp(ϑ
T
1
w
i
k
), ·· · , exp(ϑ
T
K
w
i
k
)]
T
∑
K
j=1
exp(ϑ
T
j
w
i
k
)
,
(15)
where ϑ = [ϑ
1
, ··· , ϑ
K
]
T
is the soft-max model’s pa-
rameter, and
∑
K
j=1
exp(ϑ
T
j
w
i
k
) is used for normaliza-
tion. The model parameter ϑ can be optimized by
gradient descent using training samples and their la-
bels. For an estimated arm pose w, h
ϑ
(w) gives the
probabilities that arm pose w belongs to every action
category.
After the first stage of arm pose modeling, for each
action category z, there is a corresponding estimated
arm pose ˆw
z
. And h
ϑ
( ˆw
z
) can be derived based on the
trained soft-max model. Then Pr(z| ˆw
z
) in Eqt.5 for
action category validation is
Pr(z| ˆw
z
) = h
z
ϑ
( ˆw
z
) =
exp(ϑ
T
z
ˆw
z
)
∑
K
i=1
exp(ϑ
T
z
ˆw
z
)
. (16)
5 EXPERIMENT AND RESULT
The dataset used for evaluating the proposed method
is the HumanEva-I (Sigal and Black, 2006). It con-
sists of mainly frontal images of three actions: Walk-
ing, Jogging and Waving (a subset of Gesture); and
each image is annotated with positions of shoulder,
elbow, wrist and hand endpoint for both arms. There
are four subjects in the dataset and their appearances
vary significantly in style, type, and color of clothing.
The number of frontal images for one action of a spe-
cific subject is about 100, of which half of them are
selected for training and the other half for testing. To
train the potentials of pixel based labeling, the bound-
aries of upper body parts are needed. This includes
upper arms, low arms, hands and torso for both arms,
and they are approximated by rectangles connected by
the annotated joints, and the head is approximated by
a circle. The remaining region is annotated as back-
ground.
5.1 Arm Pose Modeling Result
Percentage of Correctly estimated body Parts (PCP)
(Ferrari et al., 2008) is one of the most popular mea-
sures for 2D pose estimation which is adopted for arm
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
44

Table 1: The average PCP for three actions and each arm part of both arms for proposed method and Yang&Ramanan’s
method.
Average PCP
Actions Arm Parts
Overall
Walking Jogging Waving LUA RUA LFA RFA
Proposed 95.49% 85.85% 81.8% 95.55% 95.42% 77.24% 82.27% 87.62%
Yang&Ramanan 90.97% 85.94% 60.75% 93.83% 85.04% 73.91% 68.85% 80.4%
pose evaluation. To evaluate the performance of our
approach, the approach of mixtures of parts (Yang
and Ramanan, 2011) as one of the state-of-art meth-
ods is selected as reference. It uses mixtures of parts
based on the histogram of oriented gradients (HOG)
descriptor.
According to Figure 6(a), the overall PCP curves
show our method has better performance than the
method of Yang and Ramanan on the testing images
and improves about 7.21% average PCP. In details
for different actions, proposed method improves 4.5%
and 19.05% on walking and waving action. As illus-
trated in Table 1, our method gains 95.49%, 85.85%,
and 81.8% PCP for the actions walking, jogging and
waving respectively. Generally, jogging and walking
actions have smaller variations in space than waving
actions. This proposed adopted the learnt prior to cap-
ture the possible variation for all actions.
0.1 0.2 0.3 0.4 0.5
0
0.2
0.4
0.6
0.8
1
PCP threshold
PCP of all parts
Proposed method
Method of Yang&Ramanan
(a) the overall PCP curves of all
three actions
0.1 0.2 0.3 0.4 0.5
0
0.2
0.4
0.6
0.8
1
PCP threshold
PCP of all parts
Proposed method
Method of Yang&Ramanan
(b) the PCP curves of walking action
0.1 0.2 0.3 0.4 0.5
0
0.2
0.4
0.6
0.8
1
PCP threshold
PCP of all parts
Proposed method
Method of Yang&Ramanan
(c) the PCP curves of jogging action
0.1 0.2 0.3 0.4 0.5
0
0.2
0.4
0.6
0.8
1
PCP_threshold
PCP of all parts
Proposed method
Method of Yang&Ramanan
(d) the PCP curves of waving action
Figure 6: The overall PCP curves for all three actions and
the individual PCP curves for every action in which the blue
curve and the red dotted curve are the results of proposed
method and Yang & Ramanan’s method respectively.
As shown in Table 1, two methods all have bet-
ter performance for upper arm than forearm of both
arms. Proposed method has 95.48% and 79.76% av-
erage PCP for upper arm and forearm, while method
of Yang and Ramanan has 89.44% and 71.38% aver-
age PCP respectively.
5.2 Action Categorization Result
After the arm poses modeling for every possible ac-
tion, the final result of action category is the action
with maximum probability of arm pose modeling for
the current visual observation. Since in this research,
we mainly focus on the arm pose estimation for ac-
tion categorization. The images of walking, waving
and jogging from the HumanEva-I dataset are tested.
Table 2 is the confusion matrix for this three action
categorization. The average recognition rate is about
96.69%, and it has best performance for walking ac-
tion. Figures 7, 8 and 9 illustrate some arm pose mod-
eling for the actions waving, jogging and walking re-
spectively. Recently, the approach of Bag of Poses
(BoP) (Gong et al., 2013) is used for action recogni-
tion by SVM classifiers on this dataset. It has the
recognition rates 94.6%, 91.9%, and 91.8% for Walk-
Figure 7: Some examples of arm pose modeling for waving.
ActionCategorizationbasedonArmPoseModeling
45

Table 2: The confusion matrix for action categorization of
the actions walking, waving, and jogging of the HumanEva-
I dataset.
Acc. Walking Waving Jogging
Walking 99.35% 0.65% 0
Waving 4.28% 94.55% 1.17%
Jogging 3.83% 0 96.17%
Figure 8: Some examples of arm pose modeling for jogging.
ing, Gesture (mainly waving action) and Jogging re-
spectively.
6 CONCLUSIONS
This paper proposed a novel method to implement the
categorization of actions such as waving, walking and
jogging, with the help of arm pose modeling. Un-
like many existing methods, we treat pose modeling
and action recognition interdependently. Proposed
method explored the relationship between arm pose
modeling and action categorization, as well as multi-
ple visual features and priors for arm pose modeling.
We utilized a graphical model to descript relation-
ship between arm pose and action category, and the
inherent dependency between arm parts. Some new
Figure 9: Some examples of arm pose modeling for walk-
ing.
methods of prior distribution estimation, likelihood
calculation, and the inference for arm pose and ac-
tion category were illustrated. This method was eval-
uated on the videos of walking, waving and jogging
from the HumanEva-I dataset. It improved 7.21% av-
erage PCP over the method of Yang and Ramanan for
arm pose modeling, and achieved 96.69% average ac-
tion categorization rate. The result approved that our
arm pose modeling is useful for action categorization,
and the priors of action category can benefit arm pose
modeling conversely. For future research, if there are
enough training samples for prior distribution estima-
tion, the imbalance problem will be alleviated for ac-
tion categorization. Moreover, this paper only shows
its efficiency on three actions and the arm pose model-
ing. More complex actions or modeling for the whole
body pose from different viewpoint will be consid-
ered.
ACKNOWLEDGEMENTS
This research is supported by the Postgraduate Stu-
dentship of the University of Hong Kong.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
46

REFERENCES
Blank, M., Gorelick, L., Shechtman, E., Irani, M., and
Basri, R. (2005). Actions as space-time shapes. In
ICCV, volume 2, pages 1395–1402. IEEE.
Conaire, C. O., O’Connor, N. E., and Smeaton, A. F.
(2007). Detector adaptation by maximising agreement
between independent data sources. In CVPR, pages 1–
6. IEEE.
Davison, A. C. and Smith, R. L. (1990). Models for ex-
ceedances over high thresholds. Journal of the Royal
Statistical Society. Series B (Methodological), pages
393–442.
Doll
´
ar, P., Rabaud, V., Cottrell, G., and Belongie, S. (2005).
Behavior recognition via sparse spatio-temporal fea-
tures. In VS-PETS, pages 65–72. IEEE.
Duan, K., Keerthi, S. S., Chu, W., Shevade, S. K., and Poo,
A. N. (2003). Multi-category classification by soft-
max combination of binary classifiers. In Multiple
Classifier Systems, pages 125–134. Springer.
Elgammal, A., Shet, V., Yacoob, Y., and Davis, L. S. (2003).
Learning dynamics for exemplar-based gesture recog-
nition. In CVPR, volume 1, pages I–571. IEEE.
Fathi, A. and Mori, G. (2008). Action recognition by learn-
ing mid-level motion features. In CVPR, pages 1–8.
IEEE.
Felzenszwalb, P. F. and Zabih, R. (2011). Dynamic pro-
gramming and graph algorithms in computer vision.
PAMI, 33(4):721–740.
Ferrari, V., Marin-Jimenez, M., and Zisserman, A. (2008).
Progressive search space reduction for human pose es-
timation. In CVPR, pages 1–8. IEEE.
Gong, W. et al. (2013). 3D Motion Data aided Human Ac-
tion Recognition and Pose Estimation. PhD thesis,
Universitat Aut
`
onoma de Barcelona.
Laptev, I. (2005). On space-time interest points. IJCV, 64(2-
3):107–123.
Li, C. and Yung, N. (2012). Arm pose modeling for visual
surveillance. In IPCV, pages 340–347.
Martin, D. R., Fowlkes, C. C., and Malik, J. (2004). Learn-
ing to detect natural image boundaries using local
brightness, color, and texture cues. PAMI, 26(5):530–
549.
Moeslund, T. B., Hilton, A., Kr
¨
uger, V., and Sigal, L.
(2011). Visual analysis of humans: looking at peo-
ple. Springer.
Natarajan, P. and Nevatia, R. (2012). Hierarchical multi-
channel hidden semi markov graphical models for ac-
tivity recognition. CVIU.
Niebles, J. C., Wang, H., and Fei-Fei, L. (2008). Unsu-
pervised learning of human action categories using
spatial-temporal words. IJCV, 79(3):299–318.
Rodriguez, M., Ahmed, J., and Shah, M. (2008). Action
mach a spatio-temporal maximum average correlation
height filter for action recognition. In CVPR, pages
1–8.
Sadanand, S. and Corso, J. J. (2012). Action bank: A high-
level representation of activity in video. In CVPR,
pages 1234–1241. IEEE.
Scarrott, C. and MacDonald, A. (2012). A review
of extreme value threshold es-timation and uncer-
tainty quantification. REVSTAT–Statistical Journal,
10(1):33–60.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recogniz-
ing human actions: a local svm approach. In ICPR,
volume 3, pages 32–36. IEEE.
Sigal, L. and Black, M. J. (2006). Humaneva: Synchro-
nized video and motion capture dataset for evaluation
of articulated human motion. Brown Univertsity TR,
120.
Torralba, A., Murphy, K. P., and Freeman, W. T. (2004).
Sharing features: efficient boosting procedures for
multiclass object detection. In CVPR, volume 2, pages
II–762. IEEE.
Wang, L. and Yung, N. H. (2010). Extraction of mov-
ing objects from their background based on multi-
ple adaptive thresholds and boundary evaluation. ITS,
11(1):40–51.
Xu, R., Agarwal, P., Kumar, S., Krovi, V. N., and Corso, J. J.
(2012). Combining skeletal pose with local motion for
human activity recognition. In Articulated Motion and
Deformable Objects, pages 114–123. Springer.
Yamato, J., Ohya, J., and Ishii, K. (1992). Recognizing
human action in time-sequential images using hidden
markov model. In CVPR, pages 379–385. IEEE.
Yang, Y. and Ramanan, D. (2011). Articulated pose estima-
tion with flexible mixtures-of-parts. In CVPR, pages
1385–1392. IEEE.
Yao, A., Gall, J., Fanelli, G., and Van Gool, L. (2011). Does
human action recognition benefit from pose estima-
tion?”. In BMVC, pages 67.1–67.11.
ActionCategorizationbasedonArmPoseModeling
47