
Image Retrieval with Reciprocal and Shared Nearest Neighbors
Agni Delvinioti
1
, Herv
´
e J
´
egou
1
, Laurent Amsaleg
2
and Michael E. Houle
3
1
Inria, Rennes, France
2
CNRS-IRISA, Rennes, France
3
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan
Keywords:
Image Search, Reciprocal Nearest Neighbors, Shared Neighbors, Image Similarity.
Abstract:
Content-based image retrieval systems typically rely on a similarity measure between image vector represen-
tations, such as in bag-of-words, to rank the database images in decreasing order of expected relevance to the
query. However, the inherent asymmetry of k-nearest neighborhoods is not properly accounted for by tradi-
tional similarity measures, possibly leading to a loss of retrieval accuracy. This paper addresses this issue by
proposing similarity measures that use neighborhood information to assess the relationship between images.
First, we extend previous work on k-reciprocal nearest neighbors to produce new measures that improve over
the original primary metric. Second, we propose measures defined on sets of shared nearest neighbors for
reranking the shortlist. Both these methods are simple, yet they significantly improve the accuracy of image
search engines on standard benchmark datasets.
1 INTRODUCTION
During the last decade, significant improvements have
turned content-based image retrieval systems from re-
search laboratory prototypes into large scale, efficient
and effective commercial products. In particular, the
seminal “Video Google” paper (Sivic and Zisserman,
2003), by casting powerful local descriptors such as
SIFT (Lowe, 2004) into a suitable vector represen-
tation, has made possible the use of numerous tech-
niques previously introduced in text-based informa-
tion retrieval, such as inverted files. Many power-
ful systems are now based on this idea, allowing the
quick identification of the images similar to a query,
even within databases comprising millions of images.
On top of that foundation, various techniques have
been presented for enhancing the query result, includ-
ing the use of geometric information for re-ranking
a result shortlist (Fischler and Bolles, 1981; J
´
egou
et al., 2008), (larger) redefinitions of the visual vocab-
ulary (Nister and Stewenius, 2006), alterations of the
distance measure (J
´
egou et al., 2007), and aggrega-
tion of local features in clever ways (Perronnin et al.,
2010; J
´
egou et al., 2010). Although such approaches
do boost the quality of the results, there is still much
room for further improvement.
One significant impediment to neighborhood-
based similarity search is the asymmetry of the k-
nearest neighbor (k-NN) criterion used to identify
similar items. If u is the among the k-NN of v, it is not
necessarily the case that v be among the k-NN of u. A
lack of reciprocity in k-NN relationships can be taken
as an indication that query result sets are likely to con-
tain many noisy data points of low relevance to the
query. The presence of many such false positives may
lower the quality of the overall query result.
This paper proposes two methods that exploit the
fundamental asymmetry of the k-NN measure for the
reranking of image query results. The first contri-
bution is the definition of three robust and stable
extended similarity measures for the comparison of
neighborhoods of the candidates in the shortlist, as
well as reranking criteria based on these measures.
The second contribution is the definition of a max-
imum reciprocal rank criterion for the identification
of a shortlist containing more highly relevant images.
When used either in isolation or in a combined man-
ner, these two contributions are shown to significantly
improve the accuracy of image search engines.
The paper is structured as follows. Section 2 gives
an overview of the research literature most closely
related to this paper. Section 3 details the proposed
reranking approaches. Then, Section 4 gives experi-
mental evidence of the improvements observed when
using our techniques on standard benchmark datasets.
Section 5 concludes the paper.
321
Delvinioti A., Jégou H., Amsaleg L. and Houle M..
Image Retrieval with Reciprocal and Shared Nearest Neighbors.
DOI: 10.5220/0004672303210328
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 321-328
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
In the context of reranking of the results of queries in-
volving image features, Qin et al. in (Qin et al., 2011)
take advantage of k-reciprocal nearest neighbor struc-
ture by applying different distance measures to dif-
ferent parts of the shortlist. Given a query image q,
they separate the database into two disjoint sets, the
close-set containing images highly related to q, and
the far-set comprising the remainder of the database.
The close-set is used to re-rank images from the far-
set according to the degree of connectivity of far-set
images to close-set ones.
While the method is able to take advantage of the
highly related neighbors within the close-set, when
ranking elements of the far-set, the use of arbitrary
threshold values on the (non-reciprocal) primary co-
sine similarity ranking leads to unstable performance
behavior as the neighborhood size k increases. Fur-
thermore, the construction process for the close-set is
quite costly. Overall, their set partition strategy for
exploiting structural information over neighborhoods
turns out to be insufficient for practical applications
on image data.
Houle et al. in (Houle et al., 2010) examines the
use of shared nearest neighbors for secondary rank-
based similarity measures. Experimental evidence in-
dicates that shared-neighbor measures are more stable
and robust than traditional noisy approaches, espe-
cially in high dimensional spaces. Here, the similar-
ity value of an object pair is a function of the number
of data objects in the common intersection of fixed-
sized neighborhoods, determined by a conventional
(primary) similarity measure. The primary similarity
measure can be any function (L
2
, cosine) ranking the
data objects relatively to the query.
The relevant-set correlation (RSC) clustering
model (Houle, 2008) adopts such a shared-neighbor
scheme to account for well-associated items in the
grouping procedure. (Hamzaoui et al., 2013) also
builds on shared-neighbors. They designed a bipar-
tite shared-neighbor clustering algorithm for suggest-
ing additional object-based visual queries suitable for
relevance feedback search.
All three of the aforementioned approaches rely
heavily on some notion of shared neighborhood. Each
attempts to compensate for the difficulties inherent in
high-dimensional search, by extracting adjacency and
structural information among neighborhoods within
the image space, or among object seeds within the ob-
ject space. The three methods all can be regarded as
attempting to “denoise” the primary traditional simi-
larity measure, in a second processing step, in order
to provide more reliable matches.
3 OUR APPROACH
This paper proposes two reranking mechanisms for
the improvement of image query results. Each can be
used in isolation, or in a combined manner. Both ex-
ploit the degree of association between the k-NN sets
of a query image q and any candidate result object.
Both mechanisms to be presented seek to adjust
the contents of the original query result, by measur-
ing the degree to which the neighbor set of a result
object agrees with that of the query object itself. The
first reranking approach involves the use of shared
neighbor information; three neighborhood compari-
son measures are presented in Section 3.1. The sec-
ond approach involves the use of a maximum recipro-
cal rank criterion to construct a result set for query q.
It is defined in Section 3.2.
3.1 Comparing Neighborhoods
In traditional systems, for a query image q, a short-
list N
k
(q) of results is produced from a k-NN can-
didate set, where the membership and order is deter-
mined according to a similarity measure defined in
advance. Such shortlists often contain irrelevant im-
ages, or omit relevant images, in part due to the asym-
metry of the original k-NN ranking criterion.
It is possible to rerank the images in the shortlist
by considering the number of similar images that are
shared by the members of the shortlist. This rerank-
ing strategy borrows from the notion of shared nearest
neighbors studied by Houle et al. (Houle et al., 2010).
3.1.1 Shared Nearest Neighbors
Once a shortlist N
k
(q) has been determined, it is then
possible to parse it to determine the relationship be-
tween the neighborhoods of any two of its elements.
Given two images t and u in the shortlist of q, their
shared neighbor set is defined as the number of im-
ages in the common intersection of their k-NN sets.
The shared neighbor set is more formally defined as
SNN
k
(t, u) = N
k
(t) ∩ N
k
(u); (1)
its cardinality |SNN
k
(t, u)| can be used as the basis of
a query result reranking function.
3.1.2 Metrics for Neighborhoods
Information concerning the pairwise relationships
among all images in the shortlist can in principle be
incorporated into a similarity measure for the purpose
of reranking that shortlist. Two images in the short-
list that share many database images are likely to be
more similar than two other shortlist images sharing
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
322

few relevant images. Comparing the neighborhoods
of the images in the shortlist can therefore serve for
the comparison of the images themselves. In this pa-
per we use three measures for computing the similar-
ity between two neighborhood sets:
• Jaccard: A traditional measure of the similarity
between sets is the Jaccard coefficient:
j
k
(x, y) =
|SNN
k
(x, y)|
|N
k
(x) ∪ N
k
(y)|
(2)
Jaccard values range from 0 to 1, with j
k
(x, y) = 1
implying that the images share precisely the same
set of neighbors, in which case we assume that the
images themselves are very likely to be strongly
related. By taking into account the union of the
neighbor sets, j
k
measures the distribution of the
shared neighbors.
• Set Correlation: Another possible measure is the
set correlation measure defined by Houle (Houle,
2008). For x and y in database D, this measure is:
sc
k
(x, y) =
|D|
|D| − k
|SNN
k
(x, y)|
k
−
k
|D|
(3)
Neighbors appearing in both N
k
(x) and N
k
(y)
support the correlation. In contrast, objects ap-
pearing in only one of two neighborhoods detract
from the correlation. Compared to j
k
, the set cor-
relation measure does not take the union of the
neighborhood sets into account.
• Sigmoid: The Jaccard and Set Correlation mea-
sures both fail to differentiate between the case
where strong (original) similarity scores are ob-
served when k is small, from the case where
weaker similarities are observed when k is large.
In the latter case, neighborhoods typically include
a significant proportion of irrelevant neighbors,
and are therefore less informative and reliable
than when k is small. By construction, j
k
and sc
k
increase with k, and fail to reflect that the associ-
ated neighborhoods become noisy.
For the comparison of neighborhood sets, a sig-
moid function can be used to differentiate strong
from weak similarities while mitigating the influ-
ence of (large) k. The function we define is:
sgm
k
(x, y) =
1
1 + exp(−a ∗ (
|SNN
k
(x,y)|
k
− b))
, (4)
|SNN
k
(x,y)|
k
is the normalized intersection based on
neighborhood size k. The term b = exp
−
k
n
is
a decreasing function of k, which corrects for the
bias associated with large values of k.
The slope of the curve is influenced by the param-
eter a. When a < 1, the resulting mapping is very
gradual. In contrast, higher values for a create a
much sharper mapping as the slope becomes more
steep. The extreme case is when the sigmoid func-
tion approaches a step function. Since our goal is
to benefit on the one hand from the profitable be-
havior of Jaccard and Set Correlation for small k
similarity values, and on the other hand from the
thresholding of similarities when k is large, a nat-
ural choice is to set a = 1.
3.1.3 Extending Neighborhood Measures
The Jaccard and the Set Correlation measures are sen-
sitive to the membership and sizes (k) of the neigh-
borhoods, but not their order; as such, they are oblivi-
ous to the rank which neighborhoods begin to greatly
diverge. On the other hand, the motivation for the
Sigmoid measure comes from the desire to increase
the relative weight of less relevant images (with ini-
tial ranks closer to k) at the expense of highly relevant
images (with initial ranks closer to 1). By determining
the sharpness of the inflection of the sigmoid function,
the shape parameter a allows control of the relative in-
fluence of near and far members of the neighborhood;
however, is very sensitive to the value of k.
In order to cope with the sensitivity of the afore-
mentioned similarity measures, we also propose ro-
bust extensions which account for variation in the
neighborhood size. Each extended measure integrates
contributions from the basic shared neighbor mea-
sure upon which it is based, taken across the range
of neighborhood sizes 1 ≤ k
0
≤ k. For each choice
of neighborhood size k
0
, the basic scores are normal-
ized by a value depending on k
0
, The extended mea-
sures can be viewed as voting processes retaining re-
liable high-quality votes that are likely near the top of
the shortlist, as well as accounting for divergence in
neighborhoods based at items at the bottom of the list.
• Extended Jaccard:
j
k
(x, y) =
k
∑
k
0
=1
j
k
0
(x, y)
1
∑
k
0
l=1
δ
l
(x, y)
, (5)
with
δ
l
(x, y) =
(
1, if |SNN
l
(x, y)| > 0
0, otherwise
(6)
• Extended Set Correlation:
sc
k
(x, y) =
k
∑
k
0
=1
sc
k
0
(x, y)
k
0
(7)
• Extended Sigmoid:
sgm
k
(x, y) =
k
∑
k
0
=1
sgm
k
0
(x, y)
k
0
(8)
ImageRetrievalwithReciprocalandSharedNearestNeighbors
323

The measures can be made even more robust in
practice by allowing k
0
to vary over the range k
0
≤
k
0
≤ k, for some small constant k
0
≥ 1; the extended
measures stated are with k
0
= 1.
3.2 Maximum Reciprocal Rank
In (Qin et al., 2011), Qin et al. use a reciprocal k-NN
criterion for their close-set and then rerank images. In
contrast to their approach, which can be rather costly
and unstable, we propose here a new reranking crite-
rion based on reciprocity of k-NN set membership.
We first define rank
x
(y) as the rank of the image y
when the database is queried for x, according to some
underlying primary similarity measure (possibly but
not necessarily the cosine similarity). Conversely,
rank
y
(x) is the rank of x in the query result based at
y. From the perspective of x, rank
x
(y) will be referred
to as the forward rank of y, while rank
y
(x) is termed
the backward rank of y. We then define the following
reciprocity-based symmetric dissimilarity measure:
r(x, y) = max
x,y∈D
(rank
x
(y), rank
y
(x)). (9)
Based on r(., .), we define R
k
(x), the k-Maximum
Reciprocal Rank Set of an image x ∈ D, to be the k
items of D achieving the smallest maximum recipro-
cal rank values in conjunction with x:
R
k
(x) = k-arg min
y∈D
r(x, y). (10)
R
k
(x) identifies images in the vicinity of x having
a high degree of mutual relevance: these images are
not only reciprocal neighbors of x, but the extent of
reciprocity is strictly bounded by the value of k. This
reciprocity-based neighborhood is a much stronger
indication of mutual similarity than can be determined
by an asymmetric k-NN primary similarity measure.
For these reasons, we propose the use of the
reranked set R
k
(q) as a substitute for the original
neighborhood set N
k
(q) when determining the con-
tents of the shortlist corresponding to the query q.
3.3 Discussion
The extended measures defined in Section 3.1.3 rely
on two different notions of neighborhood. The first
notion corresponds to the direct neighborhood of the
query that is used to determine the shortlist of similar
images. The second notion corresponds to the neigh-
borhood of the images inside that shortlist for build-
ing on their own shared neighbors. This is the indirect
neighborhood of the query.
The criterion for determining the neighborhood of
an image (whether this image be the query or an im-
age from the shortlist) can be based either on a tradi-
tional similarity measure, or on the Maximum Recip-
rocal Rank scheme defined in Section 3.2. It should
therefore be clear that these two mechanisms — based
on shared neighborhoods or on reciprocity of neigh-
borhoods — can be used either independently or in
combination. For example, it is possible to determine
j
k
from N
k
(q) alone, or j
k
from R
k
(q).
In the discussion of the experimentation in the
next section, we will see that query result quality
generally increases when using one of the extended
neighborhood comparison measures for reranking.
When determining neighborhoods using the Maxi-
mum Reciprocal Rank, and then applying our rerank-
ing process, further improvements can be observed.
4 EXPERIMENTS
In this section we report on the performance of the ap-
proaches presented above. We start by examining the
improvements on the quality of the retrievals when
using the extended measures comparing shared neigh-
borhoods. We then compare the performance of these
measures when building the shortlist using R
k
instead
of N
k
. We first describe our experimental setup.
4.1 Experimental Setup
We used the three following popular datasets for our
experiments, all of which are available online.
Holidays (1491 images, 500 queries). This dataset
contains personal holiday photos of high resolution,
provided by INRIA (J
´
egou et al., 2008). The set
is composed of small groups of images showing the
same object or the same scene. Each query image is
applied to the remaining 1490 images in a leave-one-
out fashion.
Oxford5k (5062 images, 55 queries). The set consists
of images corresponding to 11 distinct buildings in
Oxford, England (Philbin et al., 2007). Each query
is specified as the portion of the image contained in
a supplied bounding box. All queries are performed
against the entire database.
Paris6k (6412 images, 55 queries). These images
were taken from Flickr through a search procedure fo-
cusing on particular landmarks in Paris (Philbin et al.,
2008). Again, queries are in bounding boxes, and ran
against the entire database.
SIFT descriptors were extracted from the three
image sets using a Hessian-Affine detector. The fea-
tures describing the Holidays image set were assigned
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
324

0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Oxford5k
baseline
Jaccard
extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Paris6k
baseline
Jaccard
extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Holidays BOF
baseline
Jaccard
extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Holidays VLAD
baseline
Jaccard
extended Jaccard
Figure 1: A comparison of mean average precision (mAP) scores obtained with the baseline measure (cosine + k-NN) with
those obtained with the Jaccard j
k
or the extended Jaccard j
k
shared-neighbor measures. Comparison performed against the
Oxford5k, the Paris6k and the BOF and VLAD versions of the Holidays image sets, while varying k.
to a vocabulary comprising 200k visual words (avail-
able online (J
´
egou et al., 2008)). All the experiments
presented below that use this bag-of-features repre-
sentation of the Holidays image set are indicated by
the label “Holidays BOF”.
Many systems have considered a more sophisti-
cated aggregated representation of the local features,
typically yielding better result quality. We therefore
computed VLAD features over the Holidays image
set (J
´
egou et al., 2010), clustering them to 64 cen-
troids. Another motivation for using VLAD features
is to determine the suitability of our technique when
the dimensionality of the features is relatively low.
Experiments using the VLAD representation are iden-
tified by the label “Holidays VLAD”.
The features computed from the Oxford5k and
Paris6k sets were assigned to two different visual
vocabularies provided by the authors of (Qin et al.,
2011). The Oxford5k feature set was assigned to 1M
visual words, while the Paris6k feature set was as-
signed to 500K visual words.
The baseline for the evaluations is obtained by
computing the mean average precision (mAP) on the
results returned when probing the databases with the
queries. The search process is here a simple k-NN
search based on the cosine similarity. At query time,
L
2
normalization is applied to the cosine similarity,
and a traditional tf-idf weighting scheme is used. We
typically ran many series of retrievals for various val-
ues of k. Note that we do not check the geometrical
consistency of matches in post-processing.
Table 1: Comparing the baseline mAP (cosine+k-NN) with
the mAP obtained using N
k
together with the j
k
, sc
k
and
sgm
k
measures. k = 100 on Oxford5k and Holidays BOF.
Method Oxford5k Holidays BOF
baseline 0.598 0.549
N
k
& j
k
0.699 0.580
N
k
& sc
k
0.697 0.580
N
k
& sgm
k
0.722 0.587
4.2 Jaccard vs. Extended Jaccard
We begin by showing the performance of the basic
and extended versions of the Jaccard measure, j
k
and
j
k
, using N
k
(q) for the generation of the shared neigh-
bor scores SNN
k
. Figure 1 shows the mAP for the
baseline, the Jaccard and the extended Jaccard over
all datasets, k ∈ [1, 100].
Compared to the baseline method, the basic Jac-
card shared-neighbor measure j
k
performed better for
the Paris6k set, as evidenced by an increase in mAP.
For Oxford5k, Holidays BOF and Holidays VLAD,
the performance of the basic Jaccard measure was
worse than the baseline, and degraded as the value
of k increases. A careful analysis of the experimental
logs and the image sets shows that SNN
k
enhances the
results when the diversity of the images contained in
the database is relatively limited. This was the case
for the Paris6k set, as it consists of photos of a small
number of landmarks. This was not at all the case for
the Holidays sets, which contain a wide variety of im-
ages. With Holidays, only very few images are indeed
ImageRetrievalwithReciprocalandSharedNearestNeighbors
325
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Oxford5k
baseline
extended Jaccard
reci + extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Paris6k
baseline
extended Jaccard
reci + extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Holidays BOF
baseline
extended Jaccard
reci + extended Jaccard
0
0.2
0.4
0.6
0.8
1
10 20 30 40 50 60 70 80 90 100
mAP
k
Holidays VLAD
baseline
extended Jaccard
reci + extended Jaccard
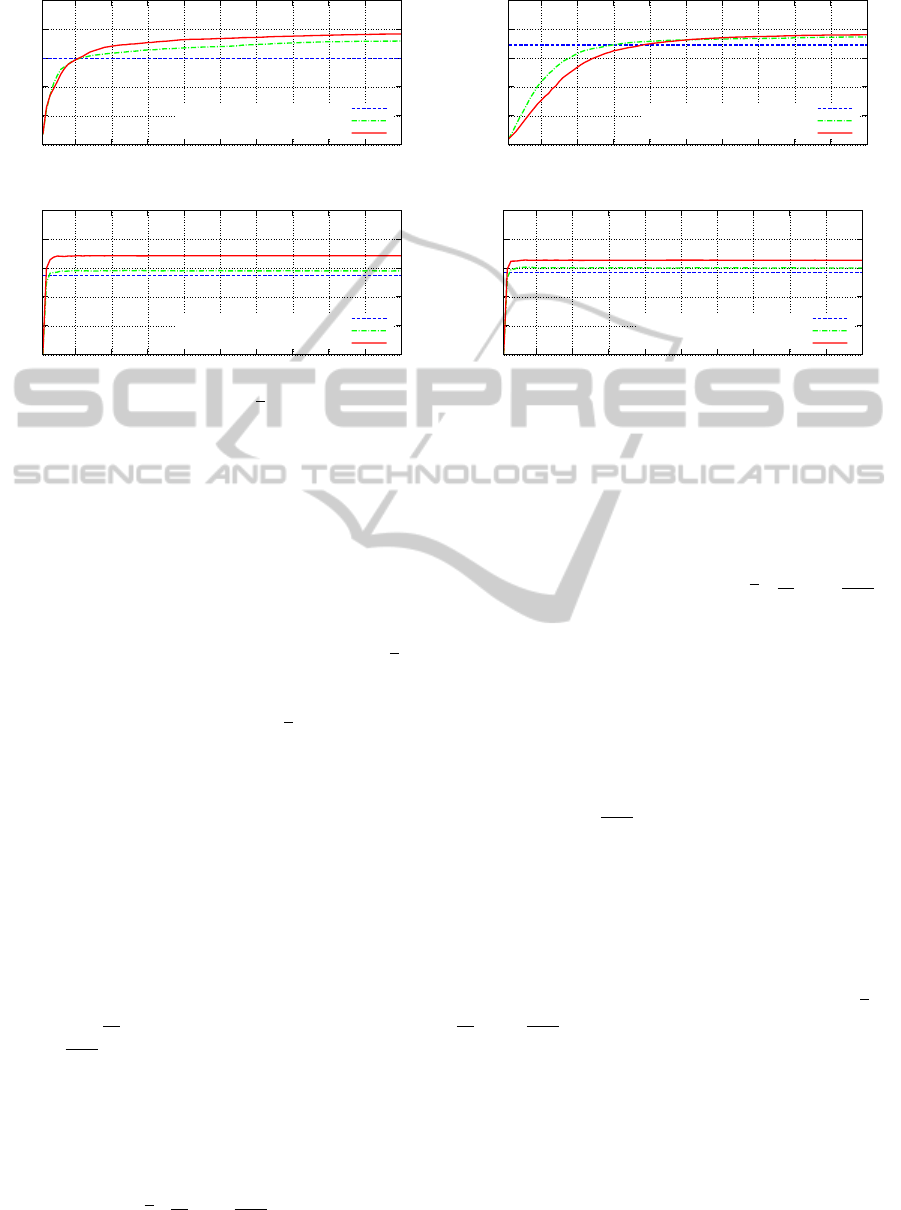
Figure 2: Comparing the behavior of j
k
when the query result shortlist is based on N
k
or R
k
. Comparison performed against
the Oxford5k, the Paris6k and the BOF and VLAD versions of the Holidays image sets, over various choices of k.
similar to each query image, and these images are in
general very well ranked. Therefore, as k increases,
the shortlist contains more and more unrelated im-
ages. This behavior is clearly visible from the Jac-
card performance curves, where the decrease in mAP
is initially very sharp. Note also that this behavior can
be observed on the Oxford5k dataset, although the ef-
fect is far less pronounced.
The extended version of the Jaccard measure, j
k
,
exhibited a much better behavior than the basic Jac-
card. By integrating the basic Jaccard scores across
the full range of neighborhood size, j
k
is better able
to take into account strong shared-neighbor matches
observed from highly relevant items from the short-
list, particularly when k is small. In this way, the use
of the extended Jaccard measure leads to more stable
performance. Note that no improvement over the ba-
sic version was observed when using the Paris6k im-
age set — this is again due to the very low diversity
of the images.
This first experiment showed that the extended
Jaccard measure outperforms both the baseline mea-
sure and the basic Jaccard measure. We also eval-
uated the performances of the Set Correlation mea-
sures sc
k
and sc
k
, as well as the Sigmoid measures
sgm
k
and sgm
k
. Overall, the extended versions of the
three neighborhood comparison measures always out-
performed their non-extended counterparts, and were
always more stable when k is allowed to vary. For
these reasons, in the remainder, we will compare the
performance of the baseline approach only to the ex-
tended versions of the Jaccard, Set Correlation and
Sigmoid measures ( j
k
, sc
k
and sgm
k
, respectively).
4.3 Comparing Extended Measures
The second experiment presented here compared the
performance of the three extended measures against
the baseline when the maximum neighborhood size is
large (k = 100). Table 1 shows that j
k
, sc
k
and sgm
k
all outperformed the baseline despite the high level
of noise in queries involving these two sets. The ta-
ble shows only the results for the Oxford5k and the
Holidays sets, as the performance on the Paris6k set
(with its lower image diversity) was quite similar to
that achieved on the Oxford5k set, and the perfor-
mance on Holidays VLAD was almost identical to the
performance on Holidays BOF. Note that the best per-
formance was consistently achieved by the extended
Sigmoid measure sgm
k
.
4.4 Using Reciprocity
The third experiment of this study investigated the ef-
fect on mAP when the Maximum Reciprocal Rank
criterion is used to reorder the query result short-
list prior to the application of the extended shared-
neighbor measures. More precisely, we applied j
k
,
sc
k
, and sgm
k
to two situations, one in which the co-
sine similarity measure is used to generate the neigh-
borhood sets N
k
, and the other when using the neigh-
borhood set R
k
produced by reordering N
k
according
to the Maximum Reciprocal Rank criterion.
As in the previous experiments, the relationship
between the performances of the basic and extended
measures followed the same trends, across all data
sets tested, and regardless of the method used to con-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
326
0
0.5
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
backward rank
forward rank
Holidays - k = 100
positives
negatives
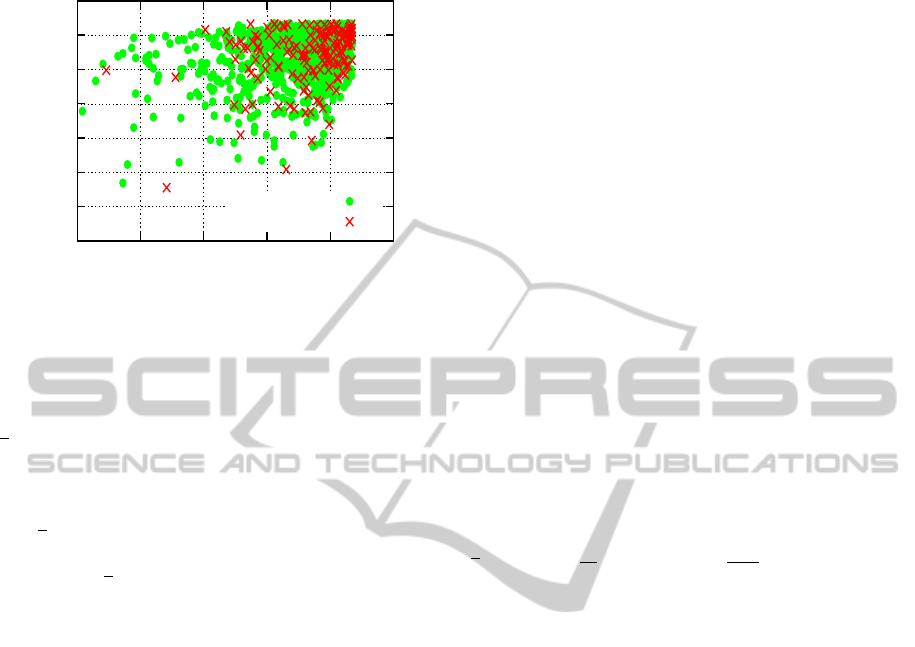
Figure 3: Distribution of contributions to the R
100
, Holi-
days BOF. 500 queries. Positive and negative examples are
determined from the ground truth. log
10
scale for ranks.
struct the initial neighborhoods. Consequently, we
discuss here only the experimental results for j
k
and
j
k
; similar conclusions can be drawn from the exper-
iments for the other two pairs of measures.
Figure 2 plots the mAP for the all datasets consid-
ered. Overall, it shows that the extended Jaccard mea-
sure j
k
using the Maximum Reciprocal Rank criterion
R
k
(indicated as “reci + extended Jaccard”) clearly
outperforms j
k
using the usual k-NN neighborhoods
N
k
(indicated by “extended Jaccard”). The gain is sig-
nificant, even on the challenging Oxford5k image set.
The behavior of the Maximum Reciprocal Rank
rule is illustrated by Figure 3. Here, we plot the for-
ward and backward ranks for the 100 nearest neigh-
bors determined for all 500 queries. Positive exam-
ples (as determined from the ground truth informa-
tion) are indicated using green circles, and negative
examples using red crosses. Note that the density of
the positive examples is high when both the forward
and backward ranks indicate high relevance, whereas
most negative examples have a poor forward or back-
ward rank, or both.
These experiments provide evidence that the use
of reciprocity, as embodied in the Maximum Recip-
rocal Rank rule, clearly allows for the determination
of shortlists of significantly higher quality than can be
constructed according to the primary similarity mea-
sure upon which it is based. Reranking strategies can
then in turn be expected to improve in quality, due to
the higher relevance of the neighborhood sets. Over-
all, the experimental results indicate that the com-
bined use of reciprocity and shared-neighbor informa-
tion can lead to great improvements in the quality of
similarity search and its follow-on applications.
4.5 Summary of Experiments
Table 2 summarizes the results obtained over all ex-
periments performed, including those for which per-
formance curves had not been presented and dis-
cussed above. The table shows the best mAP val-
ues that were observed when running our techniques,
when k was allowed to range between 1 and 200. The
table also compares our proposed approaches to that
of Qin et al. (Qin et al., 2011). Note, however, that
our results differ slightly from those presented by Qin
et al. in their paper when using the Oxford5k and the
Paris6k image sets — despite our best efforts, we
could not reproduce their work exactly, possibly in
part due to differences in the visual vocabularies used.
Note that here k
0
= 1. The best mAP values achieved
are shown in bold font.
Table 3 reports the results obtained when setting
k
0
to specific values larger than 1 and when using R
k
.
Results are reported only for Oxford5k and Paris6k,
where setting k
0
significantly boosts the mAP. This is
not the case for the Holidays set due to the high diver-
sity of its images (and the consequent small number
of true positive results per query). Experiments con-
ducted with N
k
show an improvement in mAP im-
proves for the Paris6k set when k
0
= 60: 0.790 for
j
k
, 0.789 for sc
k
and 0.781 for sgm
k
. All the results
discussed in this paragraph are the best we observed
over all choices of k ≤ 200.
4.6 Lessons
Three main lessons can be drawn from these experi-
mental results:
1. Shared nearest neighbor information is useful. It
is clear from the experiments and from the tables
that taking into account the neighbors shared by
the images in the shortlist dramatically improves
quality. Spectacular improvements are with the
Paris6k image set.
2. Integrating the values of measures over a range
of neighborhood sizes can boost performance of
reranking methods. Another effect of this exten-
sion of reranking measures is that the performance
is more robust to increases in the value of k.
3. Building the shortlist using the Maximum Recip-
rocal Rank clearly improves over the use of the
original k-NN sets.
ImageRetrievalwithReciprocalandSharedNearestNeighbors
327

Table 2: mAP observed for various search strategies and re-ranking
techniques; Holidays, Oxford5k and Paris6k sets. k
0
= 1.
Method
Oxford5k Paris6k Holidays
BOF BOF BOF VLAD
baseline 0.598 0.691 0.549 0.571
(Qin et al., 2011) 0.814 0.803 - -
N
k
& j
k
0.701 0.752 0.582 0.606
N
k
& sc
k
0.700 0.748 0.581 0.602
N
k
& sgm
k
0.724 0.783 0.589 0.607
R
k
& j
k
0.737 0.768 0.685 0.655
R
k
& sc
k
0.734 0.765 0.684 0.654
R
k
& sgm
k
0.746 0.804 0.687 0.660
Table 3: mAP for R
k
with j
k
, sc
k
,
sgm
k
. Varying initial neighborhood
size k
0
. Oxford5k and Paris6k sets.
Oxford5k
Method k
0
= 1 k
0
= 20
R
k
& j
k
0.737 0.779
R
k
& sc
k
0.734 0.777
R
k
& sgm
k
0.746 0.761
Paris6k
Method k
0
= 1 k
0
= 80
R
k
& j
k
0.768 0.820
R
k
& sc
k
0.765 0.820
R
k
& sgm
k
0.804 0.812
5 CONCLUSIONS
This paper presented three measures of the similar-
ity between neighborhoods of images, suitable for use
in shared-neighbor similarity reranking of images in
a query result. Extensions integrating the values of
these measures across a range of neighborhood sizes
were also presented. Experimental evidence shows
that the extended measures improve significantly the
mean average precision scores observed over state-of-
the-art standard image benchmark datasets. This pa-
per also presents a reciprocal rank criterion allowing
the construction of shortlists containing highly rele-
vant images. Both techniques, used in isolation or in
a combined manner, outperform standard techniques.
Overall, compared to the work presented in (Qin
et al., 2011), our approach provides a quite simple
and uniform framework for integrating the structural
information that can be obtained from the neighbor-
hood of images into the overall assessment of simi-
larity to the query point. Furthermore, our reranking
procedure remains free of complex parameter tuning
(since k
0
can be set to a fixed value by default), and
does not involve any optimization process, keeping
its complexity low. The method does require, how-
ever, the computation and storage of ranked neighbor
lists. The memory overhead therefore grows linearly
with the database size, in the same was as for the main
competing method due to Qin et al. (Qin et al., 2011).
REFERENCES
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24(6).
Hamzaoui, A., Letessier, P., Joly, A., Buisson, O., and Bou-
jemaa, N. (2013). Object-based visual query sugges-
tion. Multimedia Tools and Applications.
Houle, M. E. (2008). The relevant-set correlation model for
data clustering. Statistical Analysis and Data Mining,
1(3).
Houle, M. E., Kriegel, H. P., Kr
¨
oger, P., Schubert, E., and
Zimek, A. (2010). Can shared-neighbor distances de-
feat the curse of dimensionality? In Scientific and
Statistical Database Management.
J
´
egou, H., Douze, M., and Schmid, C. (2008). Hamming
embedding and weak geometric consistency for large
scale image search. In ECCV.
J
´
egou, H., Douze, M., Schmid, C., and P
´
erez, P. (2010).
Aggregating local descriptors into a compact image
representation. In CVPR.
J
´
egou, H., Harzallah, H., and Schmid, C. (2007). A con-
textual dissimilarity measure for accurate and efficient
image search. In CVPR.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2).
Nister, D. and Stewenius, H. (2006). Scalable recognition
with a vocabulary tree. In CVPR.
Perronnin, F., Liu, Y., S
´
anchez, J., and Poirier, H. (2010).
Large-scale image retrieval with compressed fisher
vectors. In CVPR.
Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.
(2007). Object retrieval with large vocabularies and
fast spatial matching. In CVPR.
Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman,
A. (2008). Lost in quantization: Improving particu-
lar object retrieval in large scale image databases. In
CVPR.
Qin, D., Gammeter, S., Bossard, L., Quack, T., and Gool,
L. V. (2011). Hello neighbor: accurate object retrieval
with k-reciprocal nearest neighbors. In CVPR.
Sivic, J. and Zisserman, A. (2003). Video google: A text
retrieval approach to object matching in videos. In
ICCV.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
328
