MORPHO-Map

A New Way to Model Animation of Topological Transformations

Annie Luciani

1, 3

, Ali Allaoui

2, 1

, Nicolas Castagné

1, 3

Emmanuelle Darles

, Xavier Skapin

and Philippe Meseure

Laboratoire ICA, Institut Polytechnique de Grenoble, Université Grenoble Alpes, Grenoble, France

Laboratoire XLIM, Université de Limoges-Poitiers, Poitiers, France

ACROE, Ministère de la Culture et de la Communication, Grenoble, France

Keywords: Computer Animation, Topological Transformations, Particle-based Animation, Combinatorial Maps,

Fractures.

Abstract: Animation of topological transformations, such as fractures, cracks, tears, crumbles or fragmentations, is a

new challenge in Computer Graphics and Animation. We propose a new way to model and animate

topological changes, allowing the programmer to design any type of topological changes and animation

mapping. This model is based on organizing the complex modeling activity into three clearly defined

simpler sub-activities: 1) point-based animation, which enables a wide variety of possible temporal

phenomena; 2) topological-based modeling, which makes it possible to manage a wide variety of shape-

independent topologies and topological transformations; 3) free, non predetermined, association between

both, and 4) final output of an animated geometrical model exhibiting any complex behavior. We

experimented the proposed method by modeling tearing effects on deformable garments, on rifts and crack

effects on 3D objects, and finally by modeling imaginary and paradoxical topological transformations

associated with realistic Physics-based animation. Besides improving the consistency and the robustness of

the modeling process of such complex phenomena, our aim is also to offer a user-centered programming

environment to the Computer Graphics and Animation programmers and designers, to enlarge their

modeling and experimentation abilities, and to stimulate their creativity.

1 INTRODUCTION

Computer Animation is currently able to produce

complex animations of rigid solids, deformable

objects or fluids by mixing physical behaviors with

complex shapes. A new challenge is now to handle

extreme deformations leading to dynamical

topological changes, as they occur in very frequent

complex visual phenomena such as breaking,

cutting, tearing or merging. In that context, most of

existing methods are based on creating geometrical

shapes with physical behaviors, for instance by

using finite elements methods and by applying

geometrical and physical transformations via

detected events such as thresholds in stresses.

However, these methods usually imply re-meshing

operations that are even more complex, since they

induce both physical and geometrical re-meshing.

On both physical and geometrical sides, this may

introduce computational drawbacks, such as

temporal instabilities for the first and topological

inconsistencies for the second. That leads to include

all of the necessary optimizations and specific

arrangements to overcome these problems within the

implemented program. As a consequence, the

modeling process is obviously specific to the

phenomenon to be obtained and it cannot be used in

a general way.

We present here an approach based on a clearly-

cut dissociation of the animation stage from the

topological and geometrical stages, in order (1) to be

able to map an existing animation on any shape and

(2) to take topological transformations into account

all along the animation.

The proposed approach is particularly well

adapted for particle-based meshless animation with

no a priori shape, and moreover, for animation

produced by physically based particle modeling.

Thus, the model is composed of two communicating

parts, the first part producing point-based motions

288

Luciani A., Allaoui A., Castagné N., Darles E., Skapin X. and Meseure P..

MORPHO-Map - A New Way to Model Animation of Topological Transformations.

DOI: 10.5220/0004674002880300

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 288-300

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

and the second part being responsible for the

modeling of shapes, including a topological level,

controlled by the previously produced motion.

In addition, particle-based meshless animation,

such as those proposed for instance in (Luciani et al.,

1991), (Pauly et al., 2005), (Wojtan et al., 2009), is

well suited to model transformations or

metamorphosis. Moreover, it is well adapted for

modeling hard topological transformations due to

physical extreme deformations or clearly-cut

changes that occur in fragmentation, breaking,

cracking, tearing, etc.

This paper proposes a new method for generating

complex animations based on three modeling stages:

point-based animation, topological models and

geometrical models, the first level controlling the

topological and geometrical transformations of the

two other levels. These three modeling stages and

their association are supported by a programming

framework, called MORPHO-Map, allowing

programmers to program any kind of topological

models and their association with a point-based

animation, hence to create any variety of animated

shapes transformations.

The paper is organized as follows: Section 2

reviews related works aiming at pinpointing

MORPHO-Map inside the context of Computer

Animation and Topological transformations

modeling; Section 3 presents the theoretical aspects

of MORPHO-Map modeling process; Section 4

details the components of MORPHO-Map modeling

framework; finally, Section 5 illustrates the

modeling MORPHO-Map process by means of

several models: tearing effects on deformable

garments with propagations and ravels, internal

fissures and brittle fractures of 3D rigid objects, and

finally imaginary topological transformations of a

physically-based deformable box.

2 RELATED WORKS

In Computer Animation, it could be useful to

distinguish between three types of approaches: (1)

interactive software implementations, such as Maya

or Blender, and a lot of others; (2) general methods

such as implicit surfaces; and (3) specific algorithms

dedicated to a type of phenomena, for instance

simulations of fluids, fractures, crowds, etc. In the

following, we will examine briefly those main

streams in order to situate our proposition.

Interactive software mainly allow their user to

interactively model shapes, including volumetric

geometry, meshed shapes, skeletons and skinning

processes; those shapes are animated by applying

time-based functions on them, for instance key-

framing, direct and inverse kinematics, motion

blending and retargeting, etc. The modeling activity

is performed through a high-level Human-Computer

Interface. However, these software have been

preferably designed to target solid rigid or

deformable objects, though they sometimes include

specific plug-ins such as particle modeling for

fluids, explosions, vortices, and so on. Consequently

and unfortunately, modeling dynamic topology

changes is not directly accessible to the user, since

topological changes would require to re-design the

geometrical model, for example to redesign the

meshed representation of the objects.

Among methods dedicated to the animation of

soft objects, implicit surfaces avoid any explicit

representation of 2D parametric or meshed surfaces,

3D volumes, etc. An implicit potential function is

associated with each element of a skeleton, for

example a point, to thicken it, either statically

(Desbrun and Cani, 1995) or dynamically (Habibi

and Luciani, 2002). These methods automatically

produce topological changes according to the spatial

proximity of the underlying skeletons. However,

even when they are improved by adding blending

graphs to avoid unwanted blending, the topological

changes are restricted to the specific case of

blending. They do not allow modeling other types of

topological changes such as cracks, fractures,

tearing, breakings, transformations or

metamorphosis, in any place and at any time.

When one wants to handle topology changes

such as fractures as they occur in solids or surfaces,

or during fragmentations, and merging as they occur

in drops of fluids, current methods fall back to

dedicated algorithms.

In regards to solid fragmentations and fractures

modeling, most works root on physically-based

finite elements algorithms including critical physical

re-meshing during simulation (O’Brien et al., 2002),

(Bao et al., 2007), (Molino et al., 2004). Some works

avoid such physical remeshing by using other

methods to determine fracture localization (Glondu

et al., 2013). In all these cases, the geometrical

remeshing of the fragment surfaces, for instance by

means of geometrical replications and refinements

all along the fracture lines (Molino et al., 2004)

(Glondu et al., 2013), remain a specific and quite

complex operation since it must include the

verification of the geometrical consistency of each

created mesh.

In regards to fluid topological transformations,

Computer Graphics works propose specific

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

289

processing for droplets formation and merging

within an algorithmic framework, based on mixing

propagations of wavefronts and Smooth Particles

Hydrodynamics (Losasso et al., 2008) or by

adequately mixing Lagrangian and Eulerian methods

(Irvin et al., 2006).

In all these cases, the algorithms correspond to

one-shot models within which all the aspects

(physics, animation, shape changing) are tightly

integrated and closely tied to each other. They

cannot be used for other types of shapes and

topological transformations, except those taken into

account in the algorithm itself.

Other series of methods are developed in the

domain of topological modeling, such as those based

on the constructive topological modeling approaches

called Combinatorial Maps. Starting from the

modeling of topological relationships by means of

G-Maps (Lienhardt, 1994), some works aimed at

programming evolutions of surfaces or surfaces

metamorphosis (Chen and Lienhardt, 1992) as

needed in geological studies. Some others aimed at

programming evolutions of natural objects (leafs,

plants, etc.) as performed by means of L-systems

(Prusinkiewicz, Lindenmayer, 1990). These methods

enable modeling of a wide variety of topologies and

topological changes. However, control of the

evolutions is directly made within the program

defining the topological model. Thus, the user does

not have access to evolutions coming from external

data, for example from data provided by physical,

biological or genetic externally modeled events.

It appears that none of these tools and methods is

able to propose a generic and modular concept, nor

to support a user-friendly framework allowing to

model freely complex animated transformations.

Indeed, to our knowledge, few works aim at

controlling topological transformations in a generic

way, particularly by Physics. An example of such an

approach can be found in works performed at the

Cornel Fracture Group by physicists (Carter et al.,

1995, 2008) in matter stresses. In these works, two

separated models are used: one for the physical

properties and one for the spatial topological

representations according to operations that are

similar of those mathematically defined in

topological G-Maps (vertex, edge, face and volume

sewing and unsewing).

We propose a modeling framework, called

MORPHO-Map, aiming to overcome some of the

limitations described previously. MORPHO-Map is

based on four principles:

(1) The separation between the animation modeling

stage and its topological and geometrical effects

as those performed in (Meseure et al., 2010)

(Darles et al., 2011) (Fléchon et al. 2013).

(2) The choice of point-based animation, such as

mass-interaction modeling, as proposed in

(Luciani et al., 1991) in order to be as generic as

possible on the side of animation modeling.

(3) The introduction of a topological modeling stage,

and hereto the choice of constructivist

environments such as those based on G-Maps

(MOKA) (CGoGN) in order to offer topological

modeling tools to the programmers that are

generic and robust according to their formal

well-founded theoretical rules. The geometrical

meshed representations will then be obtained by

means of geometrical mappings of topological

models, such as used in (Bézin et al., 2011).

(4) From an existing point-based animation, and an

initial topological model, we define

programming processes allowing the user to

design associations between both, in order to

animate the second with the first, including deep

discontinuous topological evolutions, therefore

enabling the management of any type of shape

transformation and metamorphosis.

A first interest of the very distinction between

the animation stage and the topo-geometrical stage,

as proposed in this article, appears clearly when

using physical modeling to drive the topological

changes processes. Indeed, the current works in

which physical modeling and topological changes

are associated, as those quoted in this state of the art,

are grounded on the strong assumption of a spatial

continuum and of a material contiguity. This

assumption leads naturally to adopt techniques such

as Finite Elements Methods and their two main

derivatives used in Computer Animation: (1)

Meshless (or Meshfree) Methods, as developed from

the Diffuse Element Method (DEM) initiated by

(Nayrolles et al. 1992) and (2) masses-springs

methods mapped onto geometrical meshes. Although

such methods constitute a solid background for

modeling deformations of complex, they introduce

two critical drawbacks when associated:

(1) Modifying the geometry leads to change the

topology of the physical part, and thus may

affect the numerical stability of the physical

model, which is a touchstone aspect in physical

modeling;

(2) The computation of the physical part becomes

more and more cumbersome when the number of

physical constraints (for example the number of

springs in meshed masses-springs methods) or

the number of computation points in meshless

methods increase all along the improvement of

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

290

the geometrical resolution by the refinement

processes, necessary for the final wanted images.

This in contradiction with the fact that physics

simulation must run faster than geometrical and

topological algorithms to ensure numerical

stability and quality of physics behaviors.

Conversely, the formal architecture proposed in

this article, based on a clearly-cut dissociation

between the physical part and the topo-geometrical

part, allows adapting the resolution and the

computation rates of each part to its own true needs.

A second interest of this formal organization of

the modeling process is to be well-suited to support

a modularized modeling pipeline, allowing

Computer Animation users and designers to

experiment the association between point-based

motions and topological and geometrical models, as

freely as possible, to generate a wide variety of

animated evolutionary shapes, and to empower the

user with advanced mastering of modeling,

experimenting and creating using the modeling

processes.

We can notice here that two ways may be

distinguished when aiming at allowing the user to

program topological changes. The first way consists

in specifying topological changes at the

phenomenological level – as we “see” them directly.

In these types of phenomenology-based models,

cracks patterns are phenomenologically predesigned,

for example from images. Then, the patterns can

afterwards be mapped on any shape according to a

logico-geometric process (Desbenoit et al., 2005), or

used to drive optimization processes (Glondu et al.,

2012). The second way, proposed in this article, is

rooted on the possibility to modularize the modeling

process in order to provide elementary combinable

modules, from which the user can program his/her

own topological changes associated to a given

animation.

3 MORPHO-Map PRINCIPLES

MORPHO-Map’s process results in animating

evolutionary meshed shapes exhibiting topological

modifications. The inputs of the process are a set of

moving points called Animation Functions Set and

an initial topological Generalized Map (G-Map).

This section details the MORPHO-Map principles:

(1) to animate a topological model; and (2) to handle

topological transformations of the topological model

and of subsequent modifications of the animation

process.

3.1 MORPHO-Map Inputs

3.1.1 Animation Functions Set

The point-based motion input of MORPHO-Map is

called Animation Functions Set, emphasizing both

the facts that the moving points can possibly be

undifferentiated and unstructured, and that the

motion is globally considered as a whole.

As input of the system, we use a coding format

called Gesture and Motion Signal (GMS) (Luciani et

al., 2006). This format is well adapted since it is

low-level enough to input into MORPHO-Map any

point-based motion: the GMS format encodes the

motion of any number of geometrical points in any

dimension (1D, 2D, or 3D). In addition, this format

allows recording motions generated from the

computation of physics-based mass-interaction

models (Evrard et al., 2006), such as those used in

the experimentations of MORPHO-Map (Section 5).

3.1.2 Topological Generalized Maps Models

In order to benefit from a manageable representation

of the topology and to ensure topological

consistency all along the process, we propose to use

a robust topological constructivist formalism, called

the Generalized Combinatorial Maps or G-Maps

(Lienhardt, 1994).

Figure 1: A 2-dimensional topological generalized map

(left) and its transformation (right). Unsewing pairs of

involutions 

causes a topological split of vertex M,

leading to the creation of a new independent vertex M’.

Within this formalism, a combinatorial map is used

to subdivide a topological space into cells

representing quasi-manifolds. Those cells are

topological vertices, edges, faces, or volumes,

according to their topological dimension (figure 1).

A topological cell is modeled by grouping atomic

elements, called darts, by means of functions called

involutions. For instance, inside a 2D G-Map, a

topological edge is modeled by sewing two darts

with an involution 

. A topological vertex is

modeled by sewing two darts with an involution 

and the connection of two faces is modeled by

sewing two edges by two involutions 

– one for

each pair of darts, and so on. The modeling process

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

291

can continue by creating topological volumes or any

model of any dimension (as long as it is a quasi

manifold). Conversely, cells can be unsewed to

separate entities. In addition, this topological

modeling process allows retrieving adjacency

relationships between cells in a very fast and robust

way.

These principles enable building and

transforming topological models in a constructive

and formally consistent way. Indeed, the G-Map

modeling rules regarding darts and involutions

guarantee that any topological modification respects

topological integrity constraints, and always results

in a consistent topological G-Map structure.

Finally, a geometrical model is obtained from a

topological G-Map by mapping the cells of the G-

Map onto a geometrical space. This process, called

geometrical embedding, can be achieved in a

coherent and flexible manner.

In the work presented in this article, we used the

G-Maps code proposed in the CGoGN C++ library

(CGoGN). In addition to the core features of the G-

Maps formalism, CGoGN offers a flexible attribute

manager allowing to embed any information into

darts or cells. This feature can be used to encode

various properties throughout MORPHO-Map, e.g.

to embed the geometrical mapping and visual

rendering mapping of the topological model. For

instance, it allows associating topological vertices

with geometrical positions, topological faces with

colors, etc.

When starting the MORPHO-Map process, an

initial topological G-Map has to be set up. This

initial G-Map can be designed by the user explicitly

with manipulation of the topological darts. It can

also be created automatically from any geometrical

mesh model, or from the positions of the moving

points at a chosen frame in the animation functions

(Darles and al., 2011). In every case, the user may

modify the initial G-Map until obtaining the needed

topological model, by adding or removing darts or

sewing and unsewing cells.

3.2 Principles for Animation

and Topological Transformations

From both inputs (an Animation Functions Set and

an initial G-Map), MORPHO-Map consists, at each

frame, in (1) computing and animating the

geometrical mapping of the current G-Map; and (2)

transforming the topology of the G-Map to provide a

new G-Map.

3.2.1 Animation Process

The mapping of the G-Map onto the geometrical

space is based on a direct low-level association

between elementary topological cells and

geometrical elements. The geometrical model is

generated at each frame from the current topological

G-Map. Animation consists in computing, at each

frame, from the animation functions, the

displacement (e.g. the new position) of the

geometrical model corresponding to the current state

of the topological G-Map. Hence, there is no need of

any geometrical mesh transformation since

transformations are fully and consistently achieved,

on each frame, at the topological level.

In order to be as general as possible with regards

to the association between the Animation Functions

Set and the topological cells, and further their

corresponding geometrical elements, the animation

process is based upon on the control concept as

follows.

As a starting remark, the number of motions of

the Animation Functions Set and the number of

topological cells (and consequently, the number of

geometrical elements) are usually not the same.

Therefore, the animation control process is based on

a clustering principle, by which subsets of motions

of the Animation Functions Set are freely associated

with subsets of cells of the topological G-map:

Clustering structure := Set of{subset of AFS

points, subset of topological cells}.

The clustering principle enables to define in a

flexible manner how an animation function should

influence the mapping of parts of the topological

model, or conversely how the mapping of a given

topological cell is influenced by a subset of the

Animation Functions Set. Notice that, depending on

the needs, clusters can be defined either manually, or

by using automated algorithms, such as the flood-fill

algorithms proposed in (Jund et al., 2012) or in

(Glondu et al., 2013).

To perform animation, a geometrical mapping is

applied. It consists in controlling the motions of the

subset of geometrical elements corresponding to the

cluster’s topological cells, from the corresponding

cluster of the animation functions With such a

mechanism, the association between the given point-

based motions and the final meshed-shapes is very

adaptable. Several mapping algorithms can be used,

such as, but not exclusively, barycentric mapping,

clusterized Radial Basis Functions, etc.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

292

3.2.2 Topological Transformations

Handling topological transformations is the most

complex part of MORPHO-Map’s pipeline. It

requires mastering deep modifications of the

topological model and consistent handling of their

consequences all over the pipeline, at each temporal

frame, all along the animation.

In MORPHO-Map, topological transformations

are organized into 4 sub-processes:

• Sensing: It consists in extracting information

from the Animation Functions Set, to control

subsequent topological modifications. Sensing

might be local, such as computing distances or

relative velocity vector between two moving

points, or spanned over a subset of the Animation

Functions. Notice that, when the animation is

physically based, distances can represent the

elastic stress in linear elastic material, and

velocities the viscosity forces. Sensing might not

only consider the current motion frame, but also

several frames altogether. Examples of data

extracted during sensing include, but are not

limited to, thresholds: onto a bi-points distance,

onto a set of bi-point distances, onto an organized

sequence of bi-points distances, between bi-point

relative velocity vectors, and so on.

• Selection process: This step outputs the list of cells

on which the topological modifications will be

applied. The Selection of topological cells is

constituted by the information gathered in the

previous sensing step. Selected cells can be of any

dimension: edges, vertices, faces, or volumes.

Moreover, the clusters may be employed to

express selection of cells in the G-Map. For

example, if Sensing has detected a distance

threshold for two Animation Functions, Selection

may consist in retrieving all the topological cells

that belong at the same time to the pair of clusters

of these two Animation Functions.

• Topological modifications: This sub-process

applies the chosen topological modification onto

the previously selected cells. It relies on the G-

Map formalism to output a consistent modified G-

Map. Any topological modification may be

applied. As an example, if Selection outputs a list

of topological volumes, these volumes might be

deleted, unsewn, or split into topological sub-

volumes, and so on.

• Updating: The topological transformations may

require modifying the clusters configuration, to

ensure their consistency with the new topology.

For example, newly created cells, if any, should be

added to some clusters. In this final sub-process,

clusters might be totally reconfigured, or only

locally updated, depending on the depth of the

topological transformations. Updating is achieved

by considering the current state of the Animation

Functions Set and of the G-Map, and potentially

the previous state of the clusters.

On each frame, once these four topological

modification steps have been applied, the pipeline

turns back to the Animation process, and to the

computation of the new geometrical model.

4 MORPHO-Map FRAMEWORK

As explained in the state of the art, modeling

complex animations exhibiting deep topological

transformations is a new challenge, not only for

modeling as such, but also with regards to the tools

able to facilitate the modeling activity. Indeed,

beside the design of human – computer modeling

software and one-shot models development,

modeling activity of complex phenomena, such as

those expected here (fragmentation, tearing,

breaking, and so on) would take advantages of fast

prototyping tools to increase the number of possible

experimentations, and to trigger new modeling

projects. Such experimentations could consist either

in being able to program easily a given dynamic

phenomenon, as those that already exist in the

scientific literature, or to create and model new

dynamic ones.

The principles exposed in section 3 allow for

flexible and comprehensive modeling strategies.

Furthermore, we consider important to offer to the

user a software environment able to support the

corresponding modeling activity. In these regards,

MORPHO-Map modular principles make it possible

to build over new approaches to programming, such

as those proposed in box-and-wires systems, like in

PureData/GEM, or block languages such as Starlogo

TNG. The following presents the MORPHO-Map

software framework, a hybrid user-centric system

between flow programming and sequence diagrams.

4.1 The Component Abstraction for a

Box-and-Wire Programming Style

MORPHO-Map’s framework relies on box-and-wire

principles, by means of a component abstraction

(figure 2). A component encapsulates: (1) an

execution method: the process; (2) parameters of the

process (3) inputs, that are typed and named; (4)

outputs, that are typed and named.

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

293

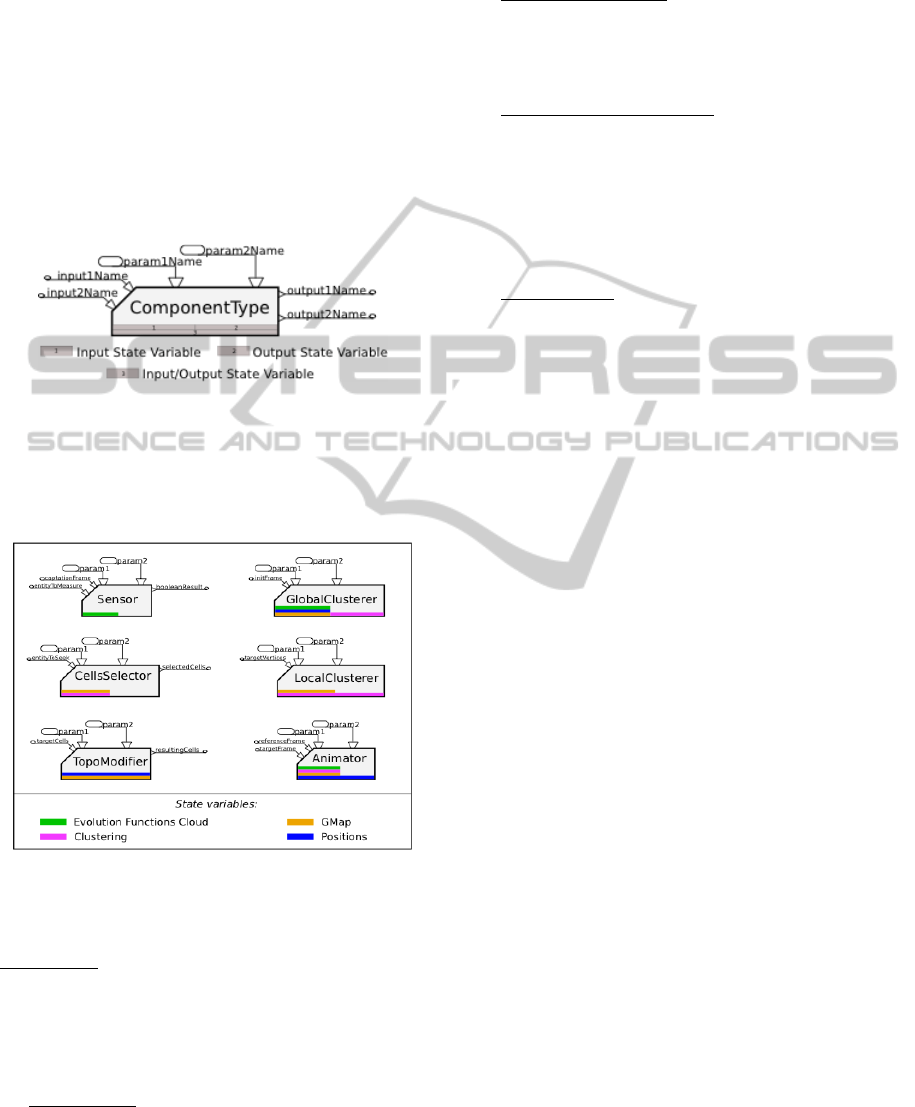
In addition to these notions, the framework relies

on a notion of state variables. State variables

represent all the structured datasets that define the

current state of the system and are needed

transversally throughout the process. The Animation

Functions, the G-Map itself, the clusters and the

resulting geometrical model are hence state

variables in MORPHO-Map’s framework. Any

component may access them any time, as input or

output of its algorithm. The graphical representation

of a component shows the use of state variables by a

component (Figure 2) without the need of heavy

wiring.

Figure 2: Representation of a MORPHO-Map component.

The four MORPHO-Map sub-processes described

above (sensing, selection, topological modifications

and clusters updating) are encapsulated by means of

5 component families (Figure 3).

Figure 3: MORPHOMAP component families. The

“Clusterer” family is decomposed into two sub-families:

the global and the local clusterer.

1. Sensors: A Sensor component specifies the

extraction to achieve from the Animation Functions

Set. Sensors’ inlets indicate where and when to

extract information. Their outlets can output various

data types, from simple types like Boolean to

structured types such as list of real values.

2. Clusterers: They can be global or local. Global

clusterers use a given frame of the Animation

Functions Set to build the clustering from scratch,

ignoring its previous state. Local Clusterers udpate

the clusters at some given location in the G-Map by

considering the previous state of the clusters.

3. Cells Selectors: Their inlets are usually

connected to the outputs of a Sensor and indicate

which animation function should be sought in the

clustering. Their outlets consist of at least one vector

of darts representing the selected cells.

4. Topological Modifiers: They usually take as

input the output of cells selectors. Their outlets are

cells representative of the topological modifications

to be applied (e.g. after splitting a face, the newly

created edge will be returned). As they take dart

vectors as input, they process the modification onto

the G-Map by batch, e.g. by deleting in one step all

the volumes they receive as input.

5. Animators: Their inputs are the target frame

(e.g. the current frame) and the reference frame

(generally the previous frame). Their role is to

compute the new geometrical model from the

information embedded into the G-Map, from the

displacements provided by the Animation Functions

Sets, and from the clusters.

With these five components families, the user

directly manipulates the key concepts of the

previously defined generic modeling process,

including topological changes and their animation.

4.2 Control of the Execution Flow

Given the complexity of the process to manage, i.e.

“animation with topological transformations”,

modeling requires control over the execution flow.

For instance, all the sub-processes dealing with

topological modifications (sensing, selection,

modification and updating) may be applied globally

one after another, in which case each of them acts all

over the state variables in one run. Conversely, it is

possible to obtain a totally different though equally

relevant animation, by looping over all the steps on

each frame, each loop being applied to the handling

of a given single subset of the topological model.

Thus, beside the above component families,

MORPHO-Map enables a precise control over the

execution flow of the components’ algorithms, by

means of the notion of Processes Line and of

Control Flow Components.

A Processes Line is a vector of components

instances, identified by a name. A model is made of

two sorts of Processes Lines: initialization lines and

loop lines. Hence, designing a model consists in

instantiating components, placing them into

Processes Lines, and interconnecting their inlets and

outlets. Once modeling has been achieved, executing

the complete model consists in executing the

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

294

initialization lines first, then executing, in a loop, all

the loop-lines until the last frame is reached.

Executing a Processes Line consists in executing

each of its component instances, in the order given

by the vector.

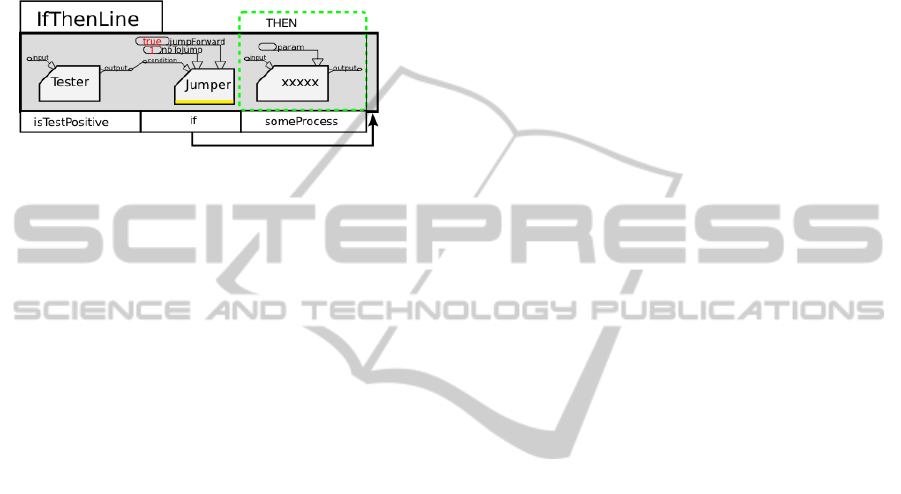
Control Flow Components are components that

have power to alter the sequential execution of a

Processes Line.

Figure 4: Writing an ”if then” statement.

The Jumper is a first useful example of Control

Flow Component (Figure 4). It implements a

conditional “goto” that sets the next component to

execute by “jumping” forward or backward in the

Processes Line. The Jumper gives the possibility to

implement control structures such as “if then”

statements, but also such as loops when associated

with a “popper” component that pops a single

element from a list. If the jump is defined forward, it

operates an “if then” statement (figure 4). If the

jump is defined backward, it operates a “do while”

loop. For the sake of simplicity in modeling, more

integrated control flow components are also

provided, such as a If statement, and DoWhile,

WhileDo and ForEach loops.

Hence, by associating inter-connectable

components with means to control the execution

flow, and facing the intrinsic complexity of the

modeling of animation with topological

modifications, MORPHO-Map has been designed as

a hybrid system that combines the object oriented

aspects and flexible connectivity of flow

programming with basic sequential programming.

4.3 MORPHO-Map Ide

Researchers, programmers and Computer Animation

designers interact with MORPHO-MAP within a

dedicated Integrated Development Environment.

This IDE is organized in three sub-spaces: a script

editor to support the modeling activity, an output

window that displays both the graphical

representation of the Processes Lines and the patch

of components, and a 3D Open-GL scene window

that displays all of the computed data.

The modeling part of the IDE features seven

predefined Processes Lines, each of them

corresponding to a particular step of the modeling

process. The first two lines are dedicated to the

modeling of the initial state of all the state variables,

and the five others are dedicated to the modeling of

the looped animation process, including modeling of

the topological modifications. These are:

(1) the “Initial Geometry” line, where the

components that build the G-Map and its

geometrical embedding are inserted;

(2) the “Initial Clustering” line, which figures one

Global Clusterer component that defines the

initial clustering;

(3) The “Frame Updaters” line, which updates the

current frame and starts each loop;

(4) and (5) dedicated to the “Modification Process”,

allowing to express the part of the model that

deals with topological modifications and the

update of the state variables in case of a

modification;

(6) The “Animation” line, on which the animation

process is designed;

(7) Finally, an “Export” line, which is, after each

step, in charge of a small amount of post

processing on the geometrical mesh and is able

to export the mesh to various formats, adapted to

the 3D software that may be used for various

renderings.

A typical modeling walk-through in the MORPHO-

Map IDE consists in:

(1) Choosing the motion to input, and, when the user

decides to employ a predefined G-Map instead of

generating it automatically, selecting this G-Map

within the initialization lines.

(2) Designing all the Processes Lines. This mainly

consists in instantiating components, providing

their parameters, and inter-connecting their inlets

and outlets.

(3) Executing the animation – that is launching the

execution of the Processes Lines – and

controlling the results.

Any modeled Processes Line is automatically

stored into a database by the IDE. This allows easy

reuse of pre-modeled parts of the final model, and

sharing within groups of users.

Finally, the MORPHO-Map IDE enables the user

to act at three levels of modeling according to

his/her aim or level of expertise, allowing both

flexibility and progressive learning of the system

and its core features.

The first level consists in editing an existing

model at a basic level: the user only acts on

parameters values, without any change in its

structure (connections, types of components).

The second level consists either in building an

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

295

entire model or an entire Processes Line from

scratch, or in editing an existing model or Process

Line by changing its structure.

The third level consists in designing a new

component for any component family, and adding it

to the available component series. This is achieved

by means of an XML specification describing the

structure of the component (inlets and outlets names

and types, state variables processed) and a C++ code

snippet describing its algorithm. This third level is of

importance since the question of animation with

topological modifications is an open issue that may

require by principle being able to add new features

and algorithms at the component level.

5 RESULTS

In this section, we illustrate the MORPHO-Map

modeling and simulation processes with animations

of shapes exhibiting topological changes through

three types of models: tearing effects on deformable

garments exhibiting tears and ravels; internal

fissures and clearly-cut cracks in 3D solid objects;

and non realistic imaginary shape metamorphosis.

All the animation functions used in the presented

examples have been produced by Physics-based

particle modeling methods as proposed in (Luciani

et al., 1991) (Evrard et al., 2006).

5.1 A Modeling Process for Tearing

Effects

We illustrate here the modeling process with a

model of fabric exhibiting tearing effects.

Figure 5: The initial topological state with the Processes

Initialisation Lines corresponding to the initial clustering.

The topological model consists of a grid of quads. In

the example given here, the given point-based

animation, used as an Animation Functions Set, has

been produced by a physically-based particle

animation of a deformable fabric. In this example,

clusters are defined in such a way that each point of

the Animation Functions Set is associated with a

unique quad, and contributes to the animation of the

four vertex of this quad. Figure 5 shows the initial

state with (1) the initial state geometry and initial

clustering (2) their corresponding Initialization Lines

with their two components.

The initial association between the animation

functions set and the G-Map is supported here by a

component called “FloodKeepAtLeast”, which is a

simple example of the topology-based flood

algorithm proposed by (Jund et al., 2012).

The topological modification process consists, at

each frame, in unsewing pairs of quads whenever the

distance of their two associated points in the

animation functions is beyond a given threshold.

Sensing consists in computing the distance

between each relevant pair of points of the

animation functions, and in comparing it to a given

threshold. If the distance exceeds the threshold, the

pair is output by the sensing component, and passed

to Selection. Then, Selection consists in searching,

among the edges of the G-Map, those for which both

vertices are associated with the received pair of

points, i.e. which clusters contain both Animation

Functions. Then, Topological Modification consists

in unsewing the two adjacent faces of this edge.

Finally, Cluster Updating is performed.

The animation process employed is the simplest

that can be used to compute the displacement of

each vertex from its associated animation functions.

When quads are sewn, the displacement of a vertex

shared by several quads is calculated from the

contributions of the animation function associated

with each quad. When they are unsewed, the

displacement of each vertex depends only on the

displacement of its unique associated animation

function.

Figure 6 shows the whole Processes Lines

following the initialization lines presented before

Figure 6: The whole Processes lines.

5.2 Tears Effects on Deformable Fabric

Figure 7 (next page) shows the results of the

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

296

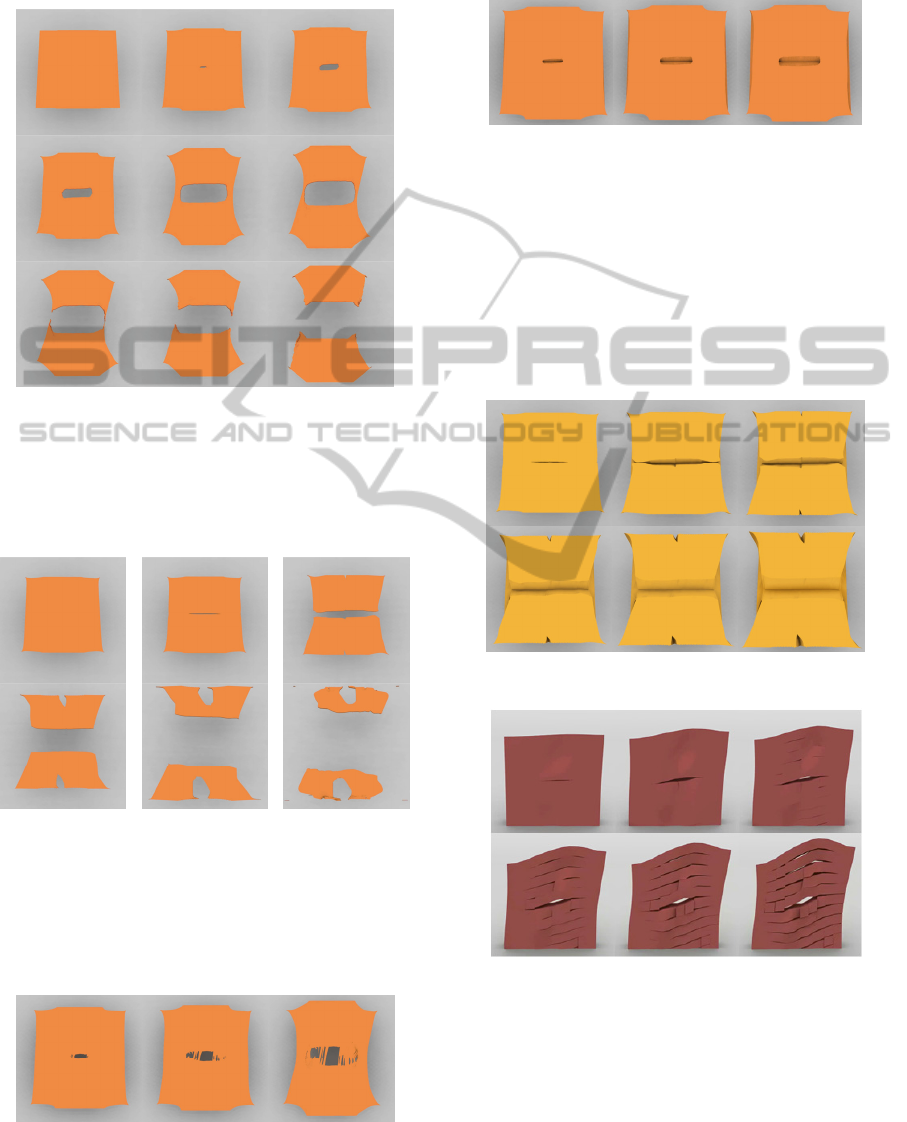
modeling of a tearing effect in a fabric, starting by a

hole with frays, just before the final separation in

two parts.

Figure 7: Tears effect in a deformable fabric: from a hole

to a fracture with frays just before separation.

Figure 8 shows another tearing effect, starting with a

smooth crack on the middle, and forming other tears

on the external sides.

Figure 8: Two tears in a highly deformable fabric.

The images of the MORPHO-Map model shown in

Figure 9 figurate out that this model is able to

exhibit several micro tears surrounding a central

tear, resulting from the propagation of the fabric

deformation within the frailty zone.

Figure 9: Several successive tears resulting from the

propagation of the deformation all along the frailty zone.

Figure 10 shows a type of tear presenting a lot of multiple

very fine serrations or ravels, which appear all along the

tear.

Figure 10: A tear with multiple fine serrations and ravels

along the tear.

5.3 Cracking Effects on Deformable 3D

Thick Plates

The following figures show the formation of cracks

in deformable 3D thick plates.

Notice the final shapes after the crack, which

result from a soft material in figure 11 and from a

harder material in figure 12.

Figure 11: Cracks in a soft thick 3D plate.

Figure 12: Cracks in a hard thick 3D plate.

Figure 13 shows three variants of a similar

MORPHO-Map model in which we obtain various

types of tearing, from the same Animation

Functions, by changing the topo-geometric

parameters, for instance by decreasing the distance

threshold. We may notice that the material on the

left corresponds to the material used in Figure 12,

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

297

and it is more brittle than the material on the right.

Figure 13: From left to right, three tearing effects obtained

with the same Animation Functions Set and the same

MORPHO-Map model. Variations are due only to the

changes of the Sensing process parameters.

5.4 Cracking Effects on a Rigid 3D

Object

This paragraph illustrates another type of

MORPHO-map model that differs from the models

of surfaces and plates previously presented in two

aspects: (1) the clustering process, e.g. the mapping

of the animation on the 3D G-Map and (2) the type

of topological modifications.

Figure 14: Clustering and animation mapping for a 3D

object.

The mapping of the animation on the G-Map is

based on the topologically-based flood process

proposed by (Jund et al., 2012). In that case, a very

small number of Animation Functions are associated

with parts of a solid object – the dragon. Figure 14

shows a case with only eight control Animation

Functions and their eight respective zones of

influences. Notice that, similarly to the clustering

employed for the fabric animation presented

previously, zones of influence can overlap. The

dragon used in this example is the final geometrical

meshed object.

Figure 15: Emergence of internal rifts from the clustering

and animation functions shown in Figure 14.

Using this clustering, sensors detect elongations

between each pair of animated points and, according

to the sensed data, the topology of the zone of

influence zone is changed. Results presented in

Figure 15 show how progressive internal rifts are

emerging.

Figure 16 shows another model generating

clearly-cut cracks on a 3D object – here we use the

dragon again. The animation is produced by an

existing Physics-based model, composed of two

tetrahedra, modeled by 4 masses, elastically linked

to each other. Each tetrahedron controls the

movement of a part of the dragon, as shown in

Figure 16-Up-Left. Both tetrahedrons interact

through a cohesive interaction (Darles et al., 2011).

When the cohesive interaction function is disrupted,

the dragon also breaks itself in two pieces. The

motions of each piece remain controlled by the

movement

of its associated tetrahedron.

Figure 16: Modeling crack in a 3D rigid object.

Figure 17 shows other results, with the same

Animation Functions Set as for the dragon cracking,

i.e. produced by the motion of two coupled

tetrahedra. On the upper lines of Figure 17,

tetrahedra are more deformable than for the dragon,

and then, their motions control the fracture of a

deformable bar. On the bottom lines of Figure 17,

the same tetrahedra motions control the

displacements of two rigid objects, a tore and a cone.

Before the tetrahedra dissociation, the movements of

the tore and the cone are elastically linked, whereas

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

298

they are free afterwards.

Figure 17: Modeling the animation of other objects with

the same Animation Functions Set. Top lines: the crack of

a deformable bar. Bottom lines: the separation of the

motions of two 3D rigid objects.

5.5 Creating Imaginary Effects

By manipulating the components and the Processes

Lines of the MORPHO-Map environment, it is also

possible to create new evolutionary shapes. Hence,

stimulating the creativity could lead to non-realistic

modeling. Figure 18 shows a deformable box

animated by a previously computed Physics-based

masses-interactions simulation, which

metamorphoses itself into two deformable boxes

with creation of internal deformable sheets. Note

that the motion may remain coherent despite the

metamorphosis of the object.

Figure 18: Physically-based animation of a non realistic

imaginary topological metamorphosis of a deformable

box.

6 CONCLUSIONS

Managing the evolution of the topology in an

animation process is a new challenge in computer

animation. A wide variety of metamorphoses and

transformations may exist, depending on the physics

of the matter but also on the spatial shape of that

matter. Rather than considering an object as a whole,

processing closely its matter and its shapes, we

suggest here to separate both parts. This lead us to

define a more generic modeling process composed

of three stages: (1) generation of motion; (2)

modeling of the topology and its mapping on a

meshed geometrical model; (3) free control of the

transformation of the topology by the motion.

As the transformation and metamorphosis of the

shapes exhibit strong topological modifications, we

propose to introduce an explicit modeling stage

dedicated to topology, before the classical shape

modeling itself. Thus, the topological modifications

are directly handled in this stage by using motion

data extracted from a pre-existing animation. Such

segmentation of the animation process of complex

evolutionary shapes allows modeling any kind of

animated topological transformations in a generic

and modular way. Supported by a modular pipeline

and a graphical IDE, it makes the experimentation of

the modeling of complex phenomena possible by

any kind of programmers or designers.

Finally, we assume that the work presented here

open new ways of modeling and new

experimentations, by anyone. Moreover, with the

development of new ways of programming, many

users other than programmers, interested in

experiencing modeling and animation of complex

shapes, may have in hand, with MORPHO-Map, a

versatile programming tool, not limited to specific

algorithms dedicated to a restricted class of effect.

Our experience with art students who are, nowadays,

very skilled and curious of new types of

programming, makes it possible to say that such

tools will be used in a creative way to imagine

realistic or non-realistic animations.

In addition, the different levels of modeling

allowed by the MORPHO-Map framework

(changing the parameters of a previous MORPHO-

Map structure available in the database, designing a

new MORPHO-Map structure using existing

Processes Lines, programming new MORPHO-Map

components, such as new clustering processes, new

selectors, or new topological modifiers), allow new

users to progressively evolve in the practice of

computer modeling.

A number of evolutions are then possible, to

MORPHO-Map-ANewWaytoModelAnimationofTopologicalTransformations

299

provide a more user-centered modeling tool,

alongside dedicated algorithms and interactive user

interfaces that are less expandable. Our main goal is,

from now on, to go toward new types of

programming and modeling of such complex

phenomena, such as visual or creative programming.

ACKNOWLEDGEMENTS

These research works have been supported by the

French National Research Agency under the contract

ANR-09-CONT-007 named DYNAMé, the French

Ministry of Research and the French Ministry of

Culture.

REFERENCES

Bao, Z., Hong, J.M., Teran, J. and Fedkiw, R., 2007.

Fracturing Rigid Materials. In IEEE Transactions on

Visualization and Computer Graphics-13, pp 370-378.

Bézin, R., Crespin, B., Skapin, X., Terraz, O., Meseure, P.,

2011. Topological Operations for Geomorphological

Evolution. In Proceedings of VRIPHYS 2011.

Carter, B.J., Ingraffea, A.R., Bittencourt, T.N., 1995

(reprint 2008). Topology-controlled Modeling of

Linear and Nonlinear 3D Crack Propagation in Geo-

Materials. In Fracture of Brittle, Disordered

Materials, G. Baker and B.L. Karihaloo Eds, Taylor &

Francis Pub.

Chen X., Lienhardt P, 1992. Modeling and programming

evolutions of surfaces. In Computer Graphics Forum,

Vol. 2, no. 5.

CGoGN http://cgogn.u-strasbg.fr/Wiki/index.php/

CGoGN.

Darles, E., Kalantari, S., Skapin, X., Crespin, B., Luciani,

A., 2011. Hybrid physical – topological modeling of

physical shapes transformations. In Proc. of CASA

2011 - Digital Media and Digital Content

Management, pp. 154–157.

Desbenoit, B., Galin, E., Akkouche, S. 2005. Modeling

Cracks and Fractures. In The Visual Computer

(Proceedings of Pacific Graphics). 21(8-10), 717-726.

Desbrun, M., Cani-Gascuel, M-P., 1995. Animation of soft

substances with implicit surfaces. In SIGGRAPH, ser.

Comput. Graph., pp. 287–290.

Evrard, M., Luciani, A., Castagné, N., 2006. MIMESIS :

Interactive interface for mass-interaction modeling. In

Proc. of CASA 2006, pp. 177–186.

Fléchon, E., Zara F., Damiand, G., Jaillet, F. 2013. A

generic topological framework for physical simulation.

In proceedings of the 21st International Conference on

Computer Graphics, Visualization and Computer

Vision, pp 104-113.

Glondu, L., Muguercia, L., Marchal, M., Bosch, C.,

Rushmeier, H., Dumont, G., Drettakis, G. 2012.

Example-Based Fractured Appearance. In

Eurographics Symposium on Rendering 2012. Vol.

31(4).

Glondu, L., Marchal, M., Dumont, G., 2013. Real-Time

Simulation of Brittle Fracture using Modal Analysis.

In IEEE Transactions on Visualization and Computer

Graphics, Vol. 19(2), pp.201-209.

Habibi A., Luciani A., 2002. Dynamic particle coating. In

Transactions on Visualization and Computer

Graphics. Vol. 8. pp. 383-394.

Irving, G., Guendelman, E., Losasso, F., Fedkiw, R., 2006.

Efficient Simulation of Large Bodies of Water by

Coupling Two and Three Dimensional Techniques. In

Proc. of SIGGRAPH 2006, ACM TOG n°25, pp. 805-

811.

Jund, T., Allaoui, A., Darles, E., Skapin, X., Meseure, P.,

Luciani, A., 2012. Mapping volumetric meshes to

point-based motion models. In Proc. of VRIPHYS

2012, pp. 11–20.

Lienhardt, P. 1994. N-dimensional generalized

combinatorial maps and cellular quasi-manifolds. In

Int. J. Comput. Geom. Appl., vol. 4, no. 3, pp.275–324.

Losasso, F., Talton, J., Kwatra, N., Fedkiw, R., 2008.

Two-way Coupled SPH and Particle Level Set Fluid

Simulation. In IEEE Transactions on Visualization

and Computer Graphics, n° 14, pp. 797-804.

Luciani, A., Evrard, M., Couroussé, D., , Castagné, N., ,

Cadoz, C., Florens, J-L., 2006. A basic gesture and

motion format for virtual reality multisensory

applications. In Proc. of the First International

Conference on Computer Graphics Theory and

Applications (GRAPP), pp. 349–356.

Luciani, A., Jimenez, S., Florens, J-L., Cadoz, C., Raoult,

O. 1991. Computational physics: a modeler-simulator

for animated physical objects. In Proceedings of

EUROGRAPHICS’91, pp. 425–436.

Molino, N., Bao, Z. and Fedkiw, R., 2004. A Virtual Node

Algorithm for Changing Mesh Topology During

Simulation. In Proceedings of SIGGRAPH 2004,

ACM TOG n°23, pp385-392.

Meseure, P., Darles, E., Skapin, X., 2010. A Topology-

Based Mass/Spring System. In Proc. of CASA 2010.

MOKA. http://sourceforge.net/projects/moka-modeller/

Nayrolles, B., Touzot, G., Villon, O. 1992. Generalizing

the finité element method : Diffuse approximation and

diffuse elements. Computational Mechanics - 10, pp

307-318.

O’Brien, J.F., Bargteil, A.W., Hodgins, J.K., 2002.

Graphical modeling and animation of ductile fracture.

In Proceedings of SIGGRAPH 2002, pp. 291–294.

Pauly, M., Keiser, R., Adams, B., Dutré, P., Gross, M.,

Guibas, L.J., 2005. Meshless animation of fracturing

solids. In Proceedings of SIGGRAPH 2005, pp 957-

964.

Prusinkiewicz, P., Lindenmayer, A., 1990. The

algorithmic beauty of plants: the virtual laboratory.

Springer Verlag.

Wojtan, C., Thurey, N., Gross, M., Turk, G., 2009.

Deforming meshes that split and merge. In ACM

Transactions on Graphics, vol. 28, no. 3, pp. 76-86.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

300