Perception-prediction-control Architecture for IP Pan-Tilt-Zoom
Camera through Interacting Multiple Models
Pierrick Paillet
1
, Romaric Audigier
1
, Frederic Lerasle
2,3
and Quoc-Cuong Pham
1
1
CEA, LIST, LVIC, Point Courrier 173, F-91191, Gif-sur-Yvette, France
2
CNRS, LAAS, 7 Avenue du Colonel Roche, F-31400, Toulouse, France
3
Universit´e de Toulouse, UPS, LAAS, F-31400, Toulouse, France
Keywords:
Tracking, Pan-Tilt-Zoom Camera, PTZ, Delay, Latency, Prediction, Zoom Control, Interacting Multiple
Models
Abstract:
IP Pan-Tilt-Zoom cameras (IP PTZ) are now common in videosurveillance areas as they are easy to deploy and
can take high resolution pictures of targets in a large field of view thanks to their pan-tilt and zoom capabilities.
However the closer the view is, the higher is the risk to lose your target. Furthermore, off-the-shelf cameras
used in large videosurveillance areas present important motion delays. In this paper, we suggest a new motion
control architecture that manages tracking and zoom delays by an Interacting Multiple Models analysis of the
target motion, increasing tracking performances and robustness.
1 INTRODUCTION
Human tracking with fixed cameras is a well-known
problem in Computer Vision and especially in video
surveillance. Unlike static cameras, PTZ are able to
pan and tilt aroundtheir center and take close-up shots
of the target, matching perfectly needs to cover large
areas such as building halls and outdoor surround-
ing. These devices are mostly deployed in sparse net-
works, allowing to watch over a large videosurveil-
lance area such as shopping center or station with
fewer devices thus reducing cost.
However, these active cameras introduce multiple
challenging drawbacks: mobile background, blurring
in-going images during motion and important control
delays due to network transmissions and actuators.
Zoom control may be slower as more actuators are
involved than pan or tilt motion. Consequently state-
of-the-art methods mainly use one (or more) PTZ co-
operating with a fixed camera which assures a robust
tracking apart from PTZ motion. Then PTZ are driven
by the tracking result to other tasks such as acquiring
high resolution pictures of the targets faces (Wheeler
et al., 2010), with an additional faces tracking even-
tually to refine position (Bellotto et al., 2009). Two
PTZ may also play alternatively the fixed camera role
for more flexibility, as in (Everts et al., 2007), by re-
ducing zoom when it conducts tracking task. How-
ever none of these approaches solved the single PTZ
tracking problem. A second, wide angle camera with
a joined field of view (FoV) is required to deal with
global target motion.
For the few state-of-the-art algorithms that use
only one PTZ, a specific strategy is needed to keep the
target into the FoV, through a pan-tilt control to center
the camera on the target and a zoom strategy to main-
tain the target at a given size. Some used PTZ proto-
types to build an ad-hoc law of control (Ahmed et al.,
2012; Bellotto et al., 2009) or had access to inter-
nal elements such as motor-units to fit PID controllers
(Al Haj et al., 2010; Iosifidis et al., 2011). However
off-the-shelf PTZ elements are not accessible and the
camera has to be considered as a black box. Further-
more, their large execution delay prevents feedback
control strategies such as used in (Singh et al., 2008).
Another approach, mainly used in multi-PTZ track-
ing, balances motion delays by anticipating the posi-
tion of the target with a perception-prediction-action
(PPA) loop. Constant motion models are mostly used
to anticipate target position, such as constant-velocity
(Liao and Chen, 2009; Varcheie and Bilodeau, 2011),
maximum-likelihood estimation (Choi et al., 2011),
general velocity-direction estimation (Natarajan et al.,
2012) or Kalman filtering (Wheeler et al., 2010).
However as no other camera can reliably track the
target during PTZ motion, prediction accuracy is cru-
cial in such strategies. All state-of-the-art predictions
314
Paillet P., Audigier R., Lerasle F. and Pham Q..
Perception-prediction-control Architecture for IP Pan-Tilt-Zoom Camera through Interacting Multiple Models.
DOI: 10.5220/0004674103140324
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 314-324
ISBN: 978-989-758-009-3
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Block diagram of system architecture synoptic: ours (left) vs. (Varcheie and Bilodeau, 2011) (right). Improved
elements are highlighted in red.
are efficient if target motion is nearly linear, but have
troubles when unexpected yet common events appear
(e.g. when target turns back or avoids obstacles). In
such situation an enhanced prediction model taking
into account multiple plausible dynamic behaviours
is needed. To our best knowledge, Varcheie et al.
(Varcheie and Bilodeau, 2011) is the only single PTZ
tracking system managing PTZ delays in that way, but
with a basic linear prediction based on the 2D appar-
ent target speed whereas target dynamic models are
more accurate in 3D than in 2D.
Two main strategies coexist to control zoom dur-
ing tracking. The first one, based on geometry, tries
to maintain the target at a given size in the image
to avoid appearance change, such as in (Dinh et al.,
2009; Bellotto et al., 2009; Varcheie and Bilodeau,
2011). While simple and effective, this strategy does
not take into account situations where intuitively a
lower zoom would be safer, such as complex target
motion. On the contrary, (Shah and Morrell, 2005;
Tordoff, 2002) use the probability of their tracking fil-
ter, e.g. the confidence on tracking position, to select
the zoom level. However this last strategy zooms out
only when tracking is already failing. In this paper
we construct a strategy that combines zoom control
with the target position prediction to analyze target
behaviour and anticipate potential tracking failure sit-
uation.
This paper presents a visual servoing strategy ap-
plied on an off-the-shelf PTZ camera to track a given
person, enhanced by two main improvements: an In-
teracting Multiple Model Kalman Filter (IMM KF)
increasing prediction robustness to target unexpected
motion and a zoom control strategy based on the dy-
namic models probabilities used in the IMM KF. Our
approach also uses PTZ delays to reinforce predic-
tion accuracy by an online evaluation during camera
latency. The efficiency of this combination is illus-
trated and compared to state-of-the-art method.
We present in section 2 our global algorithm ar-
chitecture. Our main contributions, IMM KF and its
application to PPA and zoom strategy, are described in
section 3. Finally both quantitativeand qualitative on-
line evaluations on unexpected motions and tracking
scenarios are shown in section 4, with a comparison to
(Varcheie and Bilodeau, 2011). Section 5 concludes
the paper and presents some future works.
2 DESCRIPTION OF OUR
ARCHITECTURE
2.1 Camera Control Model
Four delays could be denoted during a complete
perception-prediction-action iteration, similarly to
(Varcheie and Bilodeau, 2011), illustrated in Fig-
ures 1 and 2:
• Image capture and transmission through network,
with delay τ
1
depending on traffic.
• Object tracking with our software implementa-
tion, taking τ
2
seconds.
• A latency, as motion order is transmitted to PTZ
through network and from internal camera soft-
ware to hardware. However no motion is made
and images can be still acquired and handled dur-
ing τ
3
.
• An effective PTZ motion, taking τ
4
seconds to
complete depending on the motion amplitude.
According to our experiments, we observed that τ
1
≪
τ
2
,τ
3
and τ
4
. Similarly to (Kumar et al., 2009; Mian,
Perception-prediction-controlArchitectureforIPPan-Tilt-ZoomCamerathroughInteractingMultipleModels
315

2008), our AXIS 233D PTZ camera
1
shows a global
motion delay τ
3
+ τ
4
of 400 to 550 ms for a 20
o
pan-
tilt motion, but τ
3
seems to be independent of the am-
plitude motion, around 300 ms. This analysis suits on
IP PTZ available in our laboratory (AXIS 233D and
Q6034) even if delays may differ and seems simple
enough to match most of PTZ cameras.
Two more challenges may arise with off-the-shelf
camera: internal camera information may not be cor-
related to real position when it moves and frames are
mainly blurred during motion, causing tracking and
3D re-projection error. This leads to use position ser-
voing instead of speed control to command the PTZ
and a global image motion detection to evaluate mo-
tions delays τ
3
and τ
4
.
2.2 Architecture Synoptic
The block-diagram of the system architecture is
showed in Figure 1 and highlights differences with
(Varcheie and Bilodeau, 2011) which shares a similar
approach.
In nominal mode, i.e. if no previous order has
been already issued, the new image acquired at time
t
k
by the PTZ and sent through the network is pro-
cessed by a tracking module that detects and extracts
3D target position. Even if it requires a geometrical
calibration, a tracking on the ground plane is chosen
as target dynamic models are more accurate in 3D
than in 2D and 3D information ensures consistency
between collaborating networked devices. In this sys-
tem, only two elements of information are needed
from the tracking module: a 3D target position esti-
mation on the ground plane Y
t
, and the posterior state
density probability p(X
t
|Y
t
) associated to that posi-
tion. The complete description of the tracking algo-
rithm is out of the paper scope, but most of current
tracking algorithms can be used.
The new observation updates a prediction module
that then anticipates target position to take into ac-
count known processing delays τ
1
+ τ
2
and the esti-
mated time
ˆ
τ
3
+
ˆ
τ
4
needed to center the PTZ on the
position. This predicted position is finally checked in
a motion trigger and if some conditions are fulfilled
(cf section 3.3), PTZ motion is allowed.
In the same time, a trajectory analyzer is also up-
dated with tracking probability and prediction module
confidence to evaluate how reliable is the tracking, se-
lecting relevant zoom level that could balance resolu-
tion and risk of target loss. To reduce PTZ latency τ
3
we strive to reduce the number of pan-tilt-zoom or-
ders. Also the camera zoom is never increased alone,
but only if a pan and/or tilt motion is also triggered
1
http: //www.axis.com/fr/products/cam
233d/index.htm
Figure 2: Perception-prediction-action cycle synoptic:
Naive one (up) vs. ours (down). Tracking result position
is quoted with red ellipse, predicted position on which PTZ
would be centered is in green and further predictions are in
blue.
by the predicted position. However if trajectory ana-
lyzer detects a potential failure situation, it triggers a
zoom decreasing order and avoid failure. If triggered,
a pan-tilt-zoom order is given to center the PTZ on the
predicted position with the required zoom.
Once an order has been issued and until the PTZ
motion is detected, i.e. during the camera latency τ
3
,
the interruption mode is activated. Following static
images are handled by the tracking module, new pre-
dictions are then evaluated but still at t
k+1
, the same
time used to make the first prediction which triggered
the motion. Made on a shorter period with new target
information, this second prediction is more reliable
than the previous one.
If the distance between the new prediction and the
position where PTZ is supposed to be centered at t
k+1
is too large, then a third prediction is made and an
interruption order is issued to drive the PTZ to this
latter predicted position. Figure 2 shows a complete
motion and interruption cycle.
Most of other state-of-the-art strategies do not
evaluate the prediction accuracy once the motion or-
der has been issued. This interruption module in-
creases the system reactivity and decreases the risk
of losing the target. Furthermore, this also makes use
of intermediate frames and reduces the time between
consecutive frames when an order is issued, increas-
ing tracking robustness.
3 IMM-BASED CONTROL
STRATEGY
As explained in introduction, state-of-the-art predic-
tion methods model human behaviour with only lin-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
316

ear motion, but have troubles when this hypothesis
is challenged. To overcome this limitation, an In-
teracting Multiple Models Kalman Filter (IMM KF),
based on a probabilistic competition between multi-
ple Kalman filters with different dynamics, is used as
prediction module. Well known from filtering com-
munity (Lopez et al., 2010; Rong Li et al., 2005), it
has never been studied in PTZ camera state-of-the-
art algorithms. One great IMM KF advantage is its
ability to deal with different dynamics for a low com-
putational cost, as just a few more Kalman filters run,
possibly in a parallel architecture.
In the same time, IMM architecture also gives for
each model a probability that its dynamic is in use at a
given iteration. Well fitted, this property gives infor-
mation about the target behaviour, in particular how
reliable is our prediction. A probabilistic based zoom
control is then built from this information and track-
ing posterior state probability to adapt zoom level to
the system tracking confidence, and particularly de-
crease zoom if a risk situation is detected.
3.1 Target Motion Prediction
An IMM KF is used as prediction module, which con-
sists in recursively approximating the posterior den-
sity state of our system by a set of combined Kalman
filters corresponding to admissible dynamics.
Notations are following: N (X,
ˆ
X,P) the Gaussian
distribution, defined by (
ˆ
X,P) its mean and covari-
ance. Dynamic models form a set M of cardinality
M. For each time t
k
, X
k
denotes the state vector,m
i
k
the
event that model i ∈ M is in use during the sampling
period ]t
k−1
,t
k
] and p(m
i
k
) = µ
i
k
its probability density
function. By definition of IMM methods, models up-
date follows a homogeneousfinite-state Markov chain
with given transition probabilities π
ij
= P(m
j
k+1
|m
i
k
),
∀(i, j) ∈ M × M . For each Kalman Filter evalu-
ated according to model i, (
ˆ
X
i
k|k
,P
i
k|k
) denoted the
state mean and covariance at t
k
, and (ˆz
i
k
,S
i
k
) the pre-
dicted measurement and measurement prediction co-
variance.
At initial time, µ
i
0
,
ˆ
X
i
0|0
and P
i
0|0
are given, then the
IMM recursion for times t
k
to t
k+1
consists in a five
step cycle:
1 / Models propagation: Probabilities are updated ac-
cording to Markovian transition.
∀ j ∈ M , µ
j
k+1|k
←
∑
i∈M
π
ij
µ
i
k
µ
j|i
k+1
←
1
µ
j
k+1|k
π
ij
µ
i
k
(1)
2 / Model-conditioned initial mixed state estimation:
∀ j ∈ M ,
ˆ
X
j|0
k|k
←
∑
i∈M
µ
j|i
k+1
ˆ
X
i
k|k
P
j|0
k|k
←
∑
i∈M
µ
j|i
k+1
(P
i
k|k
+
[
ˆ
X
i
k|k
−
ˆ
X
j|0
k|k
].[
ˆ
X
i
k|k
−
ˆ
X
j|0
k|k
]
T
)
3 / Model-conditioned filtering:(
ˆ
X
j|0
k|k
,P
j|0
k|k
) are then
used as inputs in the j
th
Kalman filter with observa-
tion Y
k+1
, and produce outputs (
ˆ
X
j
k+1|k+1
,P
j
k+1|k+1
)
and (ˆz
j
k+1
,S
j
k+1
).
4 / Models probabilities update: according to poste-
rior probability.
∀ j ∈ M , L
j
k+1
← N (ˆz
j
k+1
,0,S
j
k+1
)
µ
j
k+1
=
µ
j
k+1|k
.L
j
k+1
∑
∀i∈M
µ
i
k+1|k
.L
i
k+1
5 / Final state fusion: according to Bayes Theorem.
ˆ
X
k+1|k+1
=
∑
j∈M
µ
j
k+1
ˆ
X
j
k+1|k+1
(2)
IMM KF parameters need to be adapted to our
specific system, namely which models to use, their
number and the finite-state Markov chain for interac-
tion. Too similar models or too many models will de-
crease precision as no model will prevail over the oth-
ers, so our IMM KF uses only five dynamics to model
human behaviour: a linear motion with a constant-
velocity model and four nearly constant-turn models
chosen such that, for ∆t = 200ms, rotations corre-
spond to quarter-turns and half-turns in each direc-
tion. Here only linear Kalman models with the same
dimension have been chosen, extensions exist (Lopez
et al., 2010; Rong Li et al., 2005) but have higher
computational complexity.
Almost no assumption is made on the Markov
model as sudden motion change should be allowed:
the target has half chances to remain in the same dy-
namic, and half to change with equal probability of
switching to any model, i.e. ∀i ∈ M , π
ii
= 0.5 and
∀i, j ∈ M , i 6= j,π
ij
= 0.125 in our case.
During the tracking process, the normal IMM KF
cycle is interrupted at step 3/ to evaluate the predicted
position
ˆ
X
k+1|k
. Then once the new target observation
Y
k+1
is knownin the following iteration, we simply re-
sume IMM algorithm steps to where we stopped. De-
noting ∀i ∈ M ,(
ˆ
X
i
k+1|k
,P
i
k+1|k
) the result of prediction
equation in each model-conditioned Kalman filter:
i
k
0
← argmax
i∈M
(µ
i
k
)
ˆ
X
k+1|k
=
ˆ
X
i
k
0
k+1|k
Perception-prediction-controlArchitectureforIPPan-Tilt-ZoomCamerathroughInteractingMultipleModels
317

The most probable model leads to better prediction re-
sults than a probabilistic mean like in equation (2) as
no observation could balance the predefined transition
matrix bias introduced in equation (1).
3.2 Probabilistic Zoom Level Selection
Zoom control has to balance the target resolution and
the risk of losing the target as it may easily leave of
the FoV. We chose here a careful strategy that values
tracking continuity over target resolution.
State-of-the-art zoom strategies (Shah and Mor-
rell, 2005; Tordoff, 2002) based on tracking probabil-
ities are more robust to tracking failure than strategies
which maintain the target at a given size. But none of
them takes into account unexpected target behaviour
that may deceive the system prediction. As showed in
Figure 3.C
2
, the tracking posterior probability is still
high even if target is on the edge of the image, so the
zoom will be corrected only after that target goes out
of FoV. In order to prevent this situation, a trajectory
analyzer evaluates the system confidence at each iter-
ation C
k
in the predicted position where the tracking
drives the camera on:
C
k
= P(m
l
k
).P(X
k
|Y
k
)
(3)
where P(X
k
|Y
k
) is the posterior state density at itera-
tion k given by our tracking module and P(m
l
k
) is the
linear model probability.
As long as the target moves, the IMM KF de-
scribed in the previous section 3.1 gives the proba-
bility P(m
l
k
) that linear motion hypothesis is relevant.
This model is prevalent most of time as illustrated in
Figures 3 and 4 but its probability falls when an un-
expected motion occurs as other models are needed to
describe real target motion. On the contrary, the other
dynamic models do not have so much motion infor-
mation as target never do exactly the specific rotations
we set in our IMM KF. So the probability P(m
l
k
) re-
flects well how confident the algorithm is about the
prediction model in use.
However, IMM KF probabilities accuracy drops
to an equiprobable state between every models when
the target does not move, as no dynamic can be eval-
uated. This situation is also showed in Figure 5 when
the target stopped its motion, linear model probability
drops to
1
5
as a five model IMM KF is used. So we in-
troduce an exponential speed based term that filters in
equation 3 the linear model probability if not relevant:
C
k
=
P(m
l
k
)
1+α.e
β.
¯
V
2
.P(X
k
|Y
k
)
(4)
where
¯
V denotes the mean of the Euclidean norm of
the target speed during a temporal window (1s for in-
stance). This window reduces speed estimation noise
and detects more robuslty that the target stopped. Pa-
rameters α and β are set such that if the target is
stopped, C
k
is only defined by P(X
k
|Y
k
) and if she
moves, the exponential term has no influence :
if
¯
V = 0 m/s ⇐⇒
P(m
l
k
)
1+α.e
β.
¯
V
2
= 1
if
¯
V ≥ 0.2 m/s ⇐⇒ |α.e
β.
¯
V
2
| ≤ 0.01
In our application, IMM probabilities are considered
as reliable if target speed is over 0.2 m/s, so parame-
ters becomes α = −
4
5
and β = −110s
2
/m
2
.
This confidence score selects one of the three rel-
ative target heights to maintain the target on, namely
20%, 30% and 40% of the image height, depending
on the context. If C
k
< 50%, the required height is re-
duced and on the contrary, if C
k
> 85% it is increased.
Also, as will be explained in the next section 3.3, a de-
creasing zoom level triggers a motion in order to react
as soon as possible to a potential risk situation.
3.3 Pan-Tilt-Zoom Control
The PTZ camera is driven by the information de-
scribed in the two last sections. Pan-tilt coordinates
are evaluated from the predicted 3D position thanks to
calibration and the zoom level selected by the track-
ing confidence score is converted to focal value and
then to zoom value by geometric evaluation.
However the motion strategy has to face opposite
goals. First it aims to center the PTZ on the target
to assure best resolution and tracking continuity but
moving the PTZ to this parameters set on every iter-
ation is not cost efficient, off-the-shelf PTZ latencies
accumulate. So, as in (Chang et al., 2010), the target
is keeped inside a 2D allowed area around the image
center where target motion does not trigger PTZ mo-
tion, limiting it to large motions. Margins to the im-
age edges are fitted such that the target is kept into the
FoV during latency delay τ
3
. However, 3D tracking
allows a direct tracking continuity, instead of (Chang
et al., 2010).
A 3D area is also defined around the image center
projected on the ground, typically a two-by-two meter
square. The image center corresponds to the last tar-
get position where the PTZ has been moved, so this
second area guarantees that a target at long distance
observed with a small zoom level is still kept close to
the image center.
The zoom control strategy is more complexe. In
one hand the best resolution available is desirable to
take advantage of the device. But in the other hand its
motion is much slower than pan and/or tilt only mo-
tion, sometimes taking one or more seconds to com-
plete in such a way that the target already left the FoV
when the required zoom level is reached. As no other
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
318

Table 1: Architecture differences for the PPA strategies evaluated.
Module 1
st
Strategy 2
nd
Strategy 3
rd
Strategy
Prediction linear dynamic Kalman filter IMM KF (section 3.1) Speed average
Trigger Motion Areas (section 3.3) Appearance score
Zoom control Confidence-dependent size (section 3.2) Maintain target size
Interruption Yes No
device may track the target during motion, a strategy
that values tracking robustness over target resolution
is prefered.
For each PTZ, maximum feasible zoom modifi-
cation that would not delay the motion for a given
pan-tilt amplitude is evaluated in an off-line module
and stored. Then during tracking, once the required
target size is selected in the trajectory analysis step,
zoom amplitude needed to reach this objective is lim-
ited to the pan-tilt motion used by motion order. It
leads to reach the required target size in few iterations
but keeps our tracking system as fast as possible.
Furthermore, if the tracking confidence score falls
below a threshold, reducing the required target height,
a motion is also triggered to reduce the risk. But if
the tracking confidence remains upon that threshold,
zoom level is not set up until one of the previous ge-
ometrical condition triggers a complete pan-tilt mo-
tion. This avoids supplementary motion needed only
to increase resolution but which adds more delays and
risks to lose the target.
4 EXPERIMENTS AND
EVALUATIONS
4.1 Scenarios
We conduct our experiments on three perception-
prediction-action (PPA) strategies illustrated on Ta-
ble 1. The first two strategies mainly differ on the
prediction module and allow us to evaluate our con-
tributions over the common Kalman filter on unex-
pected target behaviour. Last strategy is based on
(Varcheie and Bilodeau, 2011), illustrated in Figure 1,
as it shares a similar PPA loop. Its prediction step is a
speed average model and the motion trigger is based
on target appearance score given by the tracking mod-
ule. However to evaluate the strategies influence apart
from tracking algorithm results, the same tracking
module and appearance model is used for all con-
figurations. Here a sampling-importance-resampling
particle filter drived by a HOG-based human detec-
tor (Dalal and Triggs, 2005) is used, with a target ap-
pearance model based on HSV color and SURF inter-
est points (P´erez et al., 2002) instead of the one from
(Varcheie and Bilodeau, 2011).
No public dataset is available for testing a com-
plete PTZ tracking system because of its dynamic na-
ture. Instead, four scenarios were selected and played
each five times for every strategy to reduce variance
due to online evaluation and the particle filter stochas-
tic nature. This dataset represents more than 7000
frames over 45 sequences, taken by day in a build-
ing hall. Details about motions for each scenario are
shown in Table 2 and illustrated in Figures 3 to 4.
We tried to keep the same experimental conditions for
all sequences from a scenario. Trajectories have been
marked on the ground and sequences have been made
in a row with the same targets. Once recorded, we
extracted ground truths manually for further perfor-
mance evaluation.
The first two scenarios include one specific unex-
pected motion or trajectory break such as half turns
(HT) or quarter-turns (QT), happening when the tar-
get is near the allowed area center. These scenarios
specifically evaluate the system behaviour on unex-
pected motions and the influence of the prediction
step achieved by the Kalman filter versus IMM KF. A
third scenario is conducted to show performances of
our method with more than one person in the scene.
Finally a longer scenario, illustrated in Figure 4, of-
fers more varied background, complex lighting con-
dition (shadows, over exposition), target acceleration
and stop in addition to the previous trajectory breaks.
In all scenarios except during the last scenario accel-
eration, targets are asked to walk normally, around
1m/s.
4.2 Metrics
We use four metrics inspired by CLEARMOT
(Bernardin and Stiefelhagen, 2008) and Varcheie et
al. (Varcheie and Bilodeau, 2011):
Precision (P) is the ratio of frames where target
is well tracked in the sequence. Centralization (C)
evaluates how close the target is to the image center.
Track fragmentation (TF) indicates lack of continuity
of the track and Focusing (F) evaluates the size of the
Perception-prediction-controlArchitectureforIPPan-Tilt-ZoomCamerathroughInteractingMultipleModels
319

Table 2: Quantative evaluations for the different strategies over different scenarios.
Sc.n
o
Motion type Duration Occlusion Strategy P C TF F Fps Failure
1 linear, QT 10 s 0 % 1 59 % 95 % 19 % 42 % 6.8 2 / 5
2 77 % 94 % 0 % 39 % 7 0 / 5
2 linear, HT 20 s 0 % 1 58 % 93 % 20 % 42 % 5.9 4 / 5
2 87 % 95 % 1 % 38 % 5.4 0 / 5
3 linear, stop 25 s >40 % 1 75 % 92 % 2 % 32 % 7.2 1 / 5
4 people >5s 2 75 % 95 % 2 % 32 % 6.4 2 / 5
4 linear, QT, stop >40 % 1 85 % 89 % 13 % 40 % 6.3 1 / 5
HT, acceleration 42 s <1s 2 93 % 91 % 0 % 39 % 6.5 0 / 5
3 61 % 85 % 11.3 % 40 % 5.3 2 / 5
Figure 3: System behaviour as target turns back (HT) during the 2
nd
scenario. Red boxes are ground truth and purple ones are
tracking results. First curve indicates zoom value during tracking, linear model and tracking probabilities are shown for IMM
based strategy.
target in the image. Those metrics are defined by:
P =
#TP
NF
, TF =
#T
out
NF
,
C =
∑
i∈TP
D
i
#TP
, F =
∑
i∈TP
H
i
#TP
,
TP denotes true positive frames set, i.e. frames where
target bounding box and ground truth surface cover-
age is higher than 50%, # denotes the cardinality and
NF is the total number of frames. D
i
is the Euclidean
distance between the 2D target position and the im-
age center, T
out
is the number of frames where target
is outside the FoV and H
i
is the ratio between the size
of the target and the image height. Finally, frame rate
(Fps) and the number of sequences where target is fi-
nally lost at the end (Failure) are also evaluated.
4.3 Unexpected Trajectory Break
Evaluation
Results on Table 2 shows that IMM KF based strategy
improves tracking performance compared to Kalman
based strategy when an unexpected motion occurs,
improving precision (P) by 10 to 20 percentage points
thus reducing fragmentation (TF) and failures to al-
most 0. IMM KF prediction accuracy is better and the
system can react quicker to the unexpected motion as
other dynamics can explain such trajectory than just
moving forward.
Figure 3 illustrates a typical failure with a Kalman
based strategy. In both configurations (Figure 3.B and
3.C) prediction drives the camera too far as it does not
realize that target turns back. But this event is taken
into account quicker with IMM KF (Figure 3.D
2
) and
failure is avoided thanks to a quick zoom out, allow-
ing a larger area to look for the target. On the con-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
320

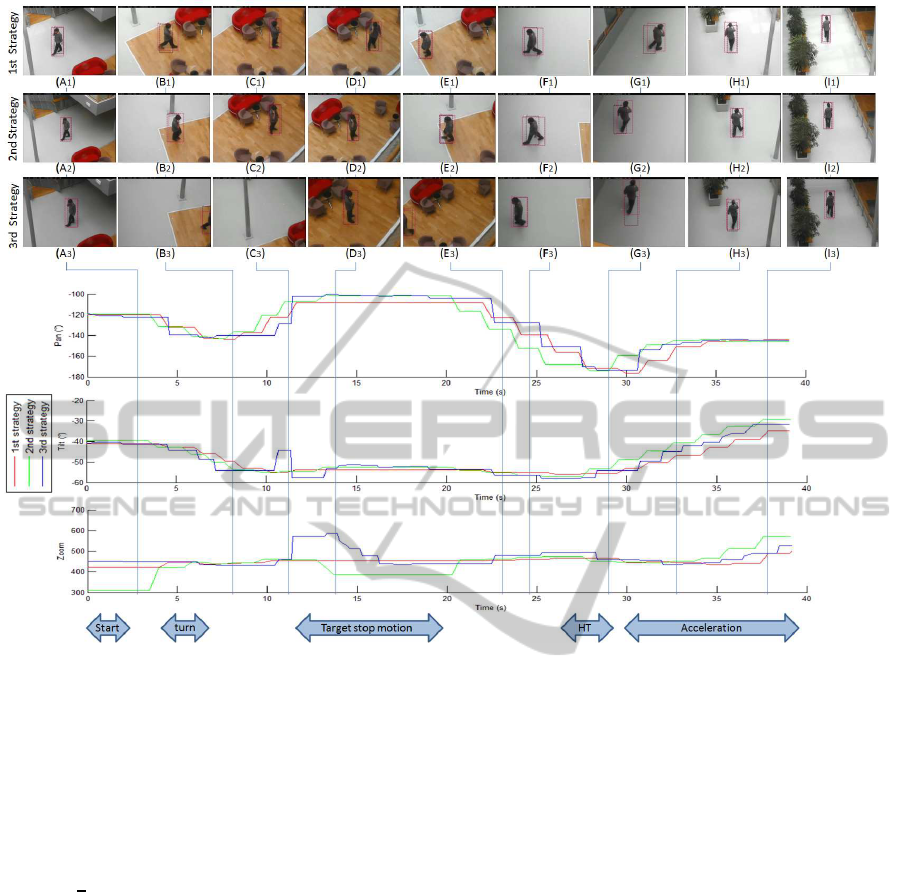
Figure 4: 4
th
scenario. Pan-Tilt-Zoom parameters are shown for every strategy. The red boxes are ground truths and the purple
ones our tracking results.
trary, even if PTZ camera is also driven by Kalman
prediction (Figure 3.D
1
) the dynamic change is not
fully taken into account and finally moves the cam-
era according to previous target behaviour, losing the
target.
Figure 3 also shows how linear model probability
evolves during tracking. It rises from an equiproba-
ble value (
1
5
for a five model IMM) to almost 1 when
the target moves, increasing zoom level as well. But
when the half turn occurs, linear model probability
falls quickly, leading to decrease zoom level (between
Figure 3.C
2
and 3.D
2
) to avoid target to go out of FoV,
even if tracking probability is still good.
On Table 2, quarter turns show similar results on
tracking performance but lead less often to failure
than half turn. This is due to a less abrupt change
of direction, so the target may not leave the PTZ FoV
before Kalman prediction assimilates the event.
4.4 More Complex Scenarios
Evaluation
The 3
rd
scenario (Figure 6) where a target is tracked
among many people, shows similar results for both
first and second strategies as the trajectory is quite
simple. However IMM KF approach causes more
camera motions, reducing its framerate (Fps), as oc-
clusions lead the system to detect an risk situation
and zooming in or out (between the 7
th
and 12
th
sec-
onds). System failures are mainly due to a shift be-
tween target and occluding people while they remain
at the same place for a long period, as we see on the
tracking probability curve in Figure 6.
The second strategy still performs better on the
last scenario, illustrated in Figure 4, increasing preci-
sion by 10% thus reducing fragmentation and failures
on unexpected trajectory breaks that perturb Kalman
prediction. This scenario includes many large camera
motions, so the zoom control does not slow down the
framerate as in the previous scenario. The stop and
the half turn in trajectory are well detected, as shown
between Figures 5.D
2
and 5.G
2
, leading to a decreas-
Perception-prediction-controlArchitectureforIPPan-Tilt-ZoomCamerathroughInteractingMultipleModels
321

Figure 5: Linear model and tracking probabilities, Target mean speed, expected target height in image and zoom value for the
2
nd
strategy during 4
th
scenario.
Figure 6: System behaviour during the 3
rd
scenario. Red boxes are ground truths and purple ones are tracking results. First
curve indicates zoom value during tracking, linear model and tracking probabilities are shown for IMM based strategy.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
322

ing zoom level between the 12
th
and 14
th
seconds.
In particular, the decreasing confidence score (eq. 4)
triggers a motion that center the target (Figure 4.D
2
),
unlike Kalman-based strategy (Figure 4.D
1
). Then,
once the trajectory analyser detects that such unex-
pected motion is a target stop the zoom level rises
again thanks to the exponential speed based term.
However the system can not zoom closer until a pan-
tilt motion allows zoom control (green plot on the
second graphic on Figure 5, between the 15
th
and
20
th
seconds). This is the main drawback from our
method, as we chose to preserve the tracking con-
tinuity over target resolution. Furthermore, the
IMM KF based strategy is also better than the one
based on (Varcheie and Bilodeau, 2011), as shown
on Table 2. Precision is increased by over 30 per-
centage point when centralization is also increased
by 5 percentage point, thus reducing tracking failure
and increasing framerate (Fps). The main drawback
of Varcheie-based third strategy is the motion trigger
that leads to small accumulated motions, decreasing
framerate. For instance many small motions are trig-
gered as the target stops between Figures 4.C
3
and
4.D
3
, while the first strategy does not and the second
only once, to adjust zoom parameter after detecting
the target stop. Furthermore, camera view angle and
scene context may quickly change target appearance
during the 4
th
scenario, preventing motion trigger in
the third strategy, decreasing performances (P) and
(C). Target also goes out of the FoV as trigger con-
dition is not met (Figures 4.B
3
and 4.E
3
) increasing
fragmentation (TF). Finally speed average prediction
may drive the PTZ in a wrong direction, because of
a distractor detection when target goes away from the
FoV, such as in Figure 4.C
3
.
5 CONCLUSIONS
Only a few state-of-the-art systems track a person
with a single IP PTZ camera. This device is subject
to large and variable motion delays, especially off-
the-shelf PTZ that can not be entirely modeled. That
slows down the algorithm and increases the risk of
losing the target during camera motion. Our ap-
proach is focused on managing these delays through a
perception-prediction-action strategy relying on three
innovativefeatures. First, an improvedprediction step
updates and anticipates target position such that the
camera is centered on the target at the end of its mo-
tion. We improved prediction performances with an
Interacting Multiple Model Kalman filter which is
more resilient to abrupt motion change, improving
pan-tilt control accuracy. This prediction filter also
gives a probabilistic estimation of the prediction re-
liability that allows a trajectory enhanced zoom con-
trol. Camera motion order is therefore more accurate
and possibly corrected by an interruption module that
takes advantage of camera control latency. Further-
more, this strategy can be used with most of track-
ing algorithms that return a target position probability
and requires almost no computational time to process.
Experiments we led demonstrate that our strategy
performs well on typical tracking situations. Espe-
cially our IMM KF based prediction is more efficient
than the one based on Kalman filter and leads less of-
ten to failure in case of unexpected trajectory breaks.
Then we also show that our innovations improve ro-
bustness to context and motion change compared to
the state-of-the-art method (Varcheie and Bilodeau,
2011) which shares a similar perception-prediction-
action strategy. Further investigations will focus
on increasing zoom control performance, in particu-
lar to increase reactivity to target behaviour. Then we
will apply our monocular approach to collaborative
PTZ network with partially common FoV.
REFERENCES
Ahmed, J., Ali, A., and Khan, A. (2012). Stabilized ac-
tive camera tracking system. In Journal of Real-Time
Image Processing.
Al Haj, M., Bagdanov, A., Gonzalez, J., and Roca, F.
(2010). Reactive object tracking with a single ptz cam-
era. In Pattern Recognition (ICPR), 2010 20th Inter-
national Conference on, pages 1690–1693.
Bellotto, N., Sommerlade, E., Benfold, B., Bibby, C., Reid,
I., Roth, D., Fernandez, C., Van Gool, L., and Gonza-
lez, J. (2009). A distributed camera system for multi-
resolution surveillance. In Distributed Smart Cam-
eras, 2009. ICDSC 2009. Third ACM/IEEE Interna-
tional Conference on, pages 1–8.
Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-
tiple object tracking performance: the clear mot met-
rics. J. Image Video Process., 2008:1:1–1:10.
Chang, F., Zhang, G., Wang, X., and Chen, Z. (2010). Ptz
camera target tracking in large complex scenes. In In-
telligent Control and Automation (WCICA), 2010 8th
World Congress on.
Choi, H., Park, U., Jain, A., and Lee, S. (2011). Face track-
ing and recognition at a distance : A coaxial & con-
centric ptz camera system. In IEEE Transactions on
Circuits and systems for video technology.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Computer Vision and
Pattern Recognition, IEEE Computer Society Confer-
ence on.
Dinh, T., Qian, Y., and Medioni, G. (2009). Real time
tracking using an active pan-tilt-zoom network cam-
era. In IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS).
Perception-prediction-controlArchitectureforIPPan-Tilt-ZoomCamerathroughInteractingMultipleModels
323

Everts, I., Sebe, N., and Jones, G. (2007). Cooperative ob-
ject tracking with multiple ptz cameras. In 14th Inter-
national Conference on Image Analysis and Process-
ing.
Iosifidis, A., Mouroutsos, S., and Gasteratos, A. (2011). A
hybrid static/active video surveillance system. Inter-
national Journal of Optomechatronics.
Kumar, P., Dick, A., and Sheng, T. (2009). Real time target
tracking with pan tilt zoom camera. In Proceedings of
the 2009 Digital Image Computing: Techniques and
Applications.
Liao, H.-C. and Chen, W. (2009). Eagle eye : A dual PTZ
camera system for target tracking in a large open area.
In 11th International Conference on Advanced Com-
munication Technology.
Lopez, R., Danes, P., and Royer, F. (2010). Extending the
imm filter to heterogeneous-order state space models.
In 49th IEEE Conference on Decision and Control
(CDC).
Mian, A. (2008). Realtime face detection and tracking us-
ing a single pan, tilt, zoom camera. In 23rd Inter-
national Conference on Image and Vision Computing
New Zealand (IVCNZ).
Natarajan, P., Hoang, T., Low, K., and Kankanhalli, M.
(2012). Decision-theoretic approach to maximiz-
ing observation of multiple targets in multi-camera
surveillance. In Proceedings of the 11th International
Conference on Autonomous Agents and Multiagent
Systems.
P´erez, P., Hue, C., Vermaak, J., and Gangnet, M. (2002).
Color-based probabilistic tracking. In Proceedings of
the 7th European Conference on Computer Vision.
Rong Li, X., Zhao, Z., and Li, X. (2005). General model-
set design methods for multiple-model approach. In
IEEE Transactions on Automatic Control.
Shah, H. and Morrell, D. (2005). A new adaptive zoom al-
gorithm for tracking targets using pan-tilt-zoom cam-
eras. In Conference Record of the 39th Asilomar Con-
ference on Signals, Systems and Computers.
Singh, V., Atrey, P., and Kankanhalli, M. (2008). Coopeti-
tive multi-camera surveillance using model predictive
control. Machine Vision and Applications.
Tordoff, B. J. (2002). Active Control of Zoom for Computer
Vision. PhD thesis, University of Oxford.
Varcheie, P. and Bilodeau, G. (2011). Adaptive fuzzy parti-
cle filter tracker for a ptz camera in an ip surveillance
system. In IEEE Transactions on Instrumentation and
Measurement.
Wheeler, W., Weiss, R., and Tu, P. (2010). Face recogni-
tion at a distance system for surveillance applications.
In 4th IEEE International Conference on Biometrics:
Theory Applications and Systems (BTAS).
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
324