
Regional SVM Classifiers with a Spatial Model for Object Detection
Zhu Teng
1
, Baopeng Zhang
1
, Onecue Kim
2
and Dong-Joong Kang
2
1
School of Computer and Information Technology, Beijing Jiaotong University, No.3 Shang Yuan Cun,
Hai dian District Beijing, China
2
Department of Mechanical Engineering, Pusan National University, Busandaehak-ro 63beon-gil Geumjeong-gu,
Busan, South Korea
Keywords: Regional SVM, Object Detection, Spatial Model.
Abstract: This paper presents regional Support Vector Machine (SVM) classifiers with a spatial model for object
detection. The conventional SVM maps all the features of training examples into a feature space, treats
these features individually, and ignores the spatial relationship of the features. The regional SVMs with a
spatial model we propose in this paper take into account a 3-dimentional relationship of features. One-
dimensional relationship is incorporated into the regional SVMs. The other two-dimensional relationship is
the pairwise relationship of regional SVM classifiers acting on features, and is modelled by a simple
conditional random field (CRF). The object detection system based on the regional SVM classifiers with the
spatial model is demonstrated on several public datasets, and the performance is compared with that of other
object detection algorithms.
1 INTRODUCTION
Detecting an object of a category is very challenging
in the computer vision area due to the significant
changes in object color, illumination, viewpoint,
large intra-class variability in shape, appearance,
pose, and complex background clutter and
occlusions. As it is one of the most significant tasks
in this field, it has been studied by many researchers
for decades, and many successful results have been
reported. A detector that localizes objects in an
image was realized by some learning algorithms in
many studies. The learning method used in object
detection can be a boosting algorithm (Alexe et al.,
2010), a Support Vector Machine (SVM) (Scholkopf
and Smola, 2002), a transformation of any of them
(Opelt et al., 2006) or a combination of some of
them (Song et al., 2011). In this paper, we propose
the multiple regional SVM classifiers to enhance the
performance of the SVM classifier and focus on
modelling the spatial relationship of these regional
SVM classifiers.
The spatial relationship has been taken into
consideration in many works. In (Tagare et al.,
1995), the spatial relation of similar patches was
described, and a model of the spatial relation
between parts was learnt in (Kumar and Hebert,
2006, David J. Crandall, 2006, David Crandall,
Figure 1: Spatial relationship. View the cell features of
training examples in a 3D space. The spatial relationship
along z axis is encoded by the regional SVM classifiers,
and the spatial relationship along axis x and axis y is
delineated by the spatial model.
372
Teng Z., Zhang B., Kim O. and Kang D..
Regional SVM Classifiers with a Spatial Model for Object Detection.
DOI: 10.5220/0004679003720379
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 372-379
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 2: The training of regional SVMs. There are m feautres in an image, so m regional SVMs should be learnt. In each
feature space of regional SVMs, a red point denotes for a positive feature, a blue square indicates a negative feature, and
there are 2n features for each feature space.
2005). Others encoded the spatial relationship in a
graphical model such as the Bayesian model
(Bogdan et al., 2010), a pictorial structure (Fischler
and Elschlager, 1973), a tree model (Long (Leo) Zhu,
2010), etc. Most of these approaches require the
association of a label to a part in order to learn the
model, and it becomes unsound if some of the parts
are missing or undetected. In addition, sometimes
good part structures should be carefully selected
(Felzenszwalb et al., 2010). In contrast, we explore
the spatial relationship of regional SVM classifiers
acting on cell features, which is a lower level
description compared with the part description, and
it requires no labels of parts.
We describe the spatial relationship in Fig. 1.
Assume the cell features (split training examples
into cells) for training are viewed in a 3D space, the
spatial relationship along the axis z is incorporated
into the regional SVM classifiers, and the spatial
relationship along the axis x and axis y (or on the x-
y plane) is described as a pairwise relationship of
regional SVM classifiers modelled by a simple
conditional random field (CRF).
The contributions of this paper include: 1)
construction of regional SVM classifiers to boost the
performance of SVM classifier; 2) modelling of the
pairwise relationship of regional SVM classifiers by
CRF. The conventional SVM training maps all the
features of positive and negative training images into
a feature space and finds a decision plane. In
contrast, we build several regional SVMs, and the
training data for each SVM are the features from
different instances at the same location. The number
of regional SVMs is determined by the number of
cells in one instance. The training time of multiple
regional SVMs is largely decreased compared with
that of the conventional SVM, and above all,
regional SVM classifiers improve the performance
because each regional SVM classifier encloses a
spatial relationship among examples.
The rest of the paper is arranged as follows. The
regional SVMs are described in Section 2, and the
spatial model based on CRF that expresses the
pairwise relationship of regional SVM classifiers is
illustrated in Section 3. Experiments and discussions
are presented in Section 4, and conclusions follow in
Section 5.
2 REGIONAL SVM CLASSIFIERS
We will first give the main idea of the regional
SVMs in Section 2.1. The prediction using the
learned regional SVM classifiers is illustrated in
Section 2.2.
NI
1
NI
2
…
NI
n
PI
1
PI
2
…
P
I
n
RegionalSVMClassifierswithaSpatialModelforObjectDetection
373

2.1 Definition of Regional SVMs
The regional SVMs are constructed by multiple local
SVMs, each encoding the patterns of features from
different spatial districts. The features from different
images with the same relative location are collected
for each individual SVM of regional SVMs. The
feature utilized here is cell-based features (such as
HOG (Dalal and Triggs, 2005, Felzenszwalb et al.,
2008) or LBP (Ojala et al., 1996), that is, several
features can be extracted from a single image. The
number of SVMs in the regional SVMs is the
number of cell features in one single image. The
implementation for an individual SVM of regional
SVMs is the same as that for the conventional SVM.
Assume we have n positive images and n
negative images, denoted by {PI
1
,PI
2
,…,PI
n
} and
{NI
1
,NI
2
,…,NI
n
}, respectively. We also presume
there are m features extracted from one image.
Features for the i
th
positive image and the i
th
negative
image are described by
},...,,{
21
iii
PI
m
PIPI
XXX
and
},...,,{
21
iii
NI
m
NINI
XXX
, respectively.
The conventional SVM maps all the features of
positive and negative images into a feature space,
and then the conventional SVM model is trained
using the feature set
]},1[],,1[|,{ mjniXX
ii
NI
j
PI
j
. The regional
SVMs we propose train m SVMs (as shown in Fig.
2). Each SVM of regional SVMs delineates the
characteristics of the object with different spatial
locations. The training set for the i
th
SVM
(
mi ,...,1
) is defined as
},...,,,,...,,{
2121 nn
NI
i
NI
i
NI
i
PI
i
PI
i
PI
i
XXXXXX
.
The union of the training data of all the regional
SVMs is the same with the training data of the
conventional SVM, but the patterns for each SVM of
the regional SVMs are reconstituted. To train each
individual SVM of the regional SVMs, the LibSVM
(Chang and Lin, 2011) is employed in our program.
2.2 Prediction of Regional SVM
Classifiers
The prediction of the regional SVMs for a detection
window is reached by all the SVM models
constructed in the training of regional SVMs. The
relative location of each feature in the detection
window can be perceived, and as we denote the
features in the detection window by
},...,,{
dw
m
dw
2
dw
1
xxx
, the subscripts 1,2,…,m
indicate the relative location of features in the
current window. The decision on the detection
window is made with Eq. (1), which suggests that
the detection window contains an object if the
confidence is positive; otherwise, the detection
window is determined to be a non-object window.
m
1f
f
s
1i
dw
f
f
i
f
i
f
i
m
1f
f
dw
f
T
f
dw
)b)x,K(xαysgn(
)b)φ(xsgn(wconfidence
(1)
where
f
i
f
i
y
,
f
i
x
, and
f
b are parameters of the f
th
SVM model in the regional SVMs. s indicates the
number of support vectors and K is the kernel
function, we use the linear kernel in the program.
We can see from Eq. (1) that the prediction of a
detection window in the regional SVMs is associated
with both the relative location of the feature to be
tested in the detection window and the regional
SVM classifier, as each cell feature of the detection
window is estimated by the corresponding regional
SVM classifier. In other words, if the same feature
has different locations in different windows, the
prediction result of the feature in different windows
could also be different.
3 A SPATIAL MODEL BASED ON
CRF
In this section, we introduce the spatial model that
encodes the pairwise relationship (spatial
relationship along axes x and y in Fig. 1) of regional
SVM classifiers acting on features. The spatial
model is built based on the CRF (Koller and
Friedman, 2009) and predicts a binary label Y that
suggests the category of a detection window, given
an observed feature vector X. The pairwise
relationship is incorporated in the feature vector X.
The model we employ in our formulation is a
simple CRF. The conditional probability P(Y|X) is
formulated by Eq. (2) and θ is the parameter we
want to estimate.
)1(
)
1
()
1
1
()|(
Y
T
e
T
e
Y
T
e
YP
X
X
X
X
θ
θ
θ
(2)
The parameter estimation approach we use to
learn the model of the conditional probability
P(Y|X) is the maximum likelihood estimation.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
374

Figure 3: Pairwise relationship of regional SVM classifiers
acting on cell features.
Assume that the training dataset is denoted by
}1),,{(
0
CcyD
cc
c
x , given
0
C training
examples, in the learning process, we need to
estimate θ* that minimizes the negative log
likelihood of the training data L
2
-regularization
expressed in Eq. (3).
0
2
1
2
11
* arg min log( ( : ))
2
arg min log( ( | ; ))
2
n
ci
i
C
n
ci
ci
LD
Py
c
x θ
θ
θ
θθ
(3)
Our learning problem is transformed to an
optimization problem, and to perform this
optimization, the stochastic gradient descent
algorithm (Koller and Friedman, 2009) is utilized.
The update rule is presented in Eq. (4).
2
2
:[log((|;)]
2
[ (1 ) log( ) log(1 ) ]
2
1
()]
1
TT
T
kc
kc
T
kc
Py
ye e
y
e
cc
c
c
xx
c
x
x
[x
θ
θθ
θ
θ
θθ θ θ
θθ
θθ
(4)
To this point, we explained the parameter estimation
process of our spatial model, and the only thing we
have not yet reported is how to express the feature
x
c
. The feature x
c
in our spatial model is required to
enclose the pairwise relationship of regional CRF
classifiers acting on cell features in one detection
window or one training example (we will call it the
specified window hereafter). It is defined as a row of
confidences that the regional SVM classifiers predict
on each cell feature in the specified window, so the
feature x
c
represents the specified window. Since the
number of the regional SVM classifiers (denoted by
m) is equal to the number of cell features defined in
a specified window, the feature x
c
for the specified
window has a size of 1*m
2
to describe the pairwise
relationship between regional SVM classifiers acting
on cell features (as shown in Fig. 3). We use SVM
i
(
i
w ,
i
b ) to denote the i
th
SVM of the regional SVM
classifiers, and represent the feature of the j
th
cell of
the specified window as
sw
cj
x
, and assume there are
m cells in one specified window. A feature matrix
X
cij
, which has the size of m*m, can be calculated by
Eq. (5). The feature x
c
of our spatial model is gained
by reshaping matrix X
cij
to a row vector.
),(
ji
cellSVMconfidence
cij
X
(5)
After learning all the parameters of the spatial
model, a prediction approach is required in order to
make a decision on a new feature x
cnew
. We judge
the new feature as positive if the possibility of Y=1
is larger than the possibility of Y=0; otherwise, the
new feature is settled as negative. The verdict rule is
articulated by Eq. (6) and the derivation of this
verdict rule is explained in Eq. (7).
(1 )
T
cnew
ysigne
cnew
x
(6)
(1|)(0|)
10
T
cnew cnew
Py Py
e
cnew cnew
X
xx
(7)
4 EXPERIMENTS
Two kinds of experiments are reported in this
section. The comparison between the regional SVMs
and the SVM is demonstrated with experiments in
Section 4.1. The experiments for the spatial model
and detecting objects in images are revealed in
Section 4.2. All of the experiments are executed on
an Intel(R) i5 2.80GHz desktop computer.
4.1 Performance Comparison between
Regional SVMs and the
Conventional SVM
The performance of regional SVMs and the SVM
(Hsu et al., 2003) is estimated and compared on two
public datasets, MIT pedestrian dataset and UIUC
Image Database for Car Detection. Two kinds of
widely used features are involved, and the training is
executed in a 5-fold cross validation, so the final
accuracy is the average accuracy of the five runs.
Experimental setting. The HOG feature is
employed in the experiment on the MIT pedestrian
dataset. The cell size of the HOG feature is 8*8
pixels. We operate the LBP feature in the
experiment of the UIUC Image Database for Car
Detection, and the cell size of the LBP feature is
defined as 16*16 pixels. The CRF based spatial
model is not used in this experiment for a fair
comparison.
RegionalSVMClassifierswithaSpatialModelforObjectDetection
375

Table 1: Comparison results between regional SVMs and the SVM on the MIT Pedestrian Dataset for human detection.
MIT pedestrian dataset 5-fold cross validation HOG feature
1000 examples 800 examples 600 examples 400 examples 200 examples
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
acc 0.6241 0.7528 0.6256 0.7487 0.6210 0.7431 0.6185 0.7307 0.6342 0.7170
time 4931 s 29.41s 3151s 22.49s 1721s 15.51s 748.2s 7.672s 110.7s 3.566s
Note: The bold number indicates the best performance.
Table 2: Comparison results between regional SVMs and the SVM on the UIUC Image Database for car detection.
UIUC Image Database for Car Detection 5-fold cross validation LBP feature
1000 examples 800 examples 600 examples 400 examples 200 examples
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
SVM Regional
SVMs
acc 0.6837 0.7464 0.6848 0.7389 0.6886 0.7368 0.6998 0.7435 0.7154 0.7350
time 286.6s 20.44s 180.5s 14.01s 101.5s 7.394s 43.38s 3.640s 9.723s 1.258s
Note: The bold number indicates the best performance.
Figure 4: Comparisons of several shots that are processed by our object detection system with and without the spatial model
on the UIUC Car Dataset. Top row: Results of our object detection system without the spatial model. Bottom row: Results
of our object detection system with the spatial model.
Table 1 epitomizes the accuracy and time cost of
two methods testing on the MIT Pedestrian Dataset.
We see that the accuracy of the regional SVM
classifiers is improved by at least 10%, compared
with the results processed by the SVM. The
performance is enhanced a little in the experiment of
200 examples, but not as much as the other
experiments with more examples, because of the
limited number of training samples. Generally, for
the regional SVMs, the more training examples used
in the experiment, the better the accuracy
performance. The computational time we reveal in
the table contains the training time and predicting
time for five runs of cross validations. It is clear
from Table 1 that the training of regional SVMs is
dozens of times faster than that of the SVM despite
of the number of training examples that are used.
Table 2 discloses the results on the UIUC Image
Database. With the results of Table 2, a similar
conclusion can be reached. To summarize, the
regional SVMs is superior to the SVM algorithm on
both the accuracy performance and time
performance.
4.2 Object Detection in Images
The object detection experiments are first executed
on the UIUC Image Database for Car Detection,
which contains training images, single-scale test
images, and multi-scale test images. Since multi-
scale test images are more difficult than the single-
scale test images, we use the single-scale test images
as the validation dataset and examine our algorithm
on the multi-scale test images. The feature we use to
represent images is a 31-dimensional HOG feature,
and we employ a pyramid framework to detect
multiple scales of objects. The confidences gauged
by regional SVMs and the spatial model are fused by
the weighted average, and the weights are reckoned
on the validation dataset. The training process is
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
376
performed twice to explore hard negative examples.
In the first iteration, cropped training images with a
fixed size are used to train initial regional SVMs,
and then hard negative examples are explored by
detecting the original training negative files rather
than cropped training negative examples
(Felzenszwalb et al., 2010). The hard negative
examples are added to the negative training set to
conduct the second round of training. The process of
detecting objects using our proposed algorithm
consists of four steps (given a test image): 1)
pyramid feature extraction; 2) predictions by
regional SVMs; 3) confidences estimated by the
spatial model; 4) non-maximum suppression. The
non-maximum suppression is employed to deal with
the situation in which multiple overlapping
detections for each instance of an object are
obtained. The bounding box with the highest
confidence is reported among bounding boxes
overlapping at least 50%.
Fig. 4 presents comparisons of several shots that
are processed by our object detection system with
and without the spatial model. It is clear that the
spatial model greatly improves the performance. The
performance on the entire dataset is assessed by the
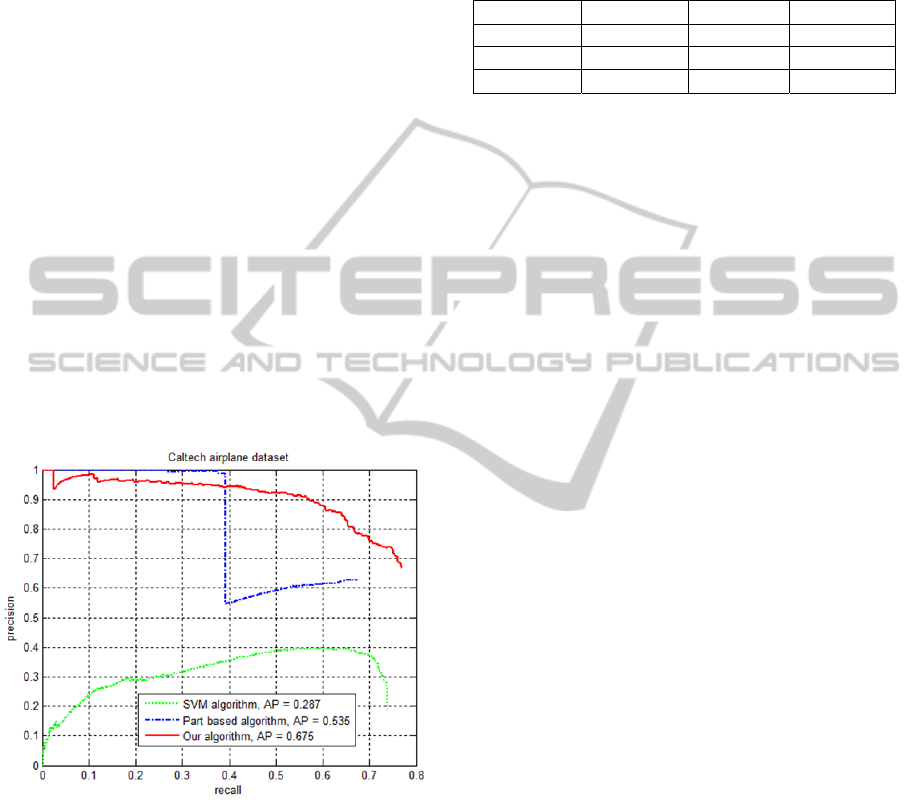
Figure 5: Precision-recall curve on the Caltech Airplanes
Dataset.
precision, recall and F-measure of the testing results,
and Table 3 presents the results of ours compared
with the Neighborhood Suppression Algorithm
(NSA) and the Repeated Part Elimination Algorithm
(RPEA) of (Agarwal et al., 2004), which have also
evaluated the performance on the multi-scale test
images of the UIUC Database. The results of Table
3 demonstrate that our algorithm achieves a
performance (F-measure) that is almost 20% better
than the performance of the NSA and RPEA. Note
that the best F-measure of these two algorithms
reported in (Agarwal et al., 2004) is referred to in
Table 3.
Table 3: Performance on the multi-scale test images of the
UIUC Image Database for Car Detection.
N
SA RPEA Ours
Recall 38.85% 39.57% 66.91%
Precision 49.09% 49.55% 60.00%
F-measure 43.37% 44.00% 63.27%
We also evaluate our proposed algorithm on the
Caltech Airplanes dataset consisting 1074 images,
which are divided into a training set (500 images),
an validation set (74 images) and a test set (500
images). The training process is similar to that
applied on the Car Dataset and the performance is
evaluated by the precision-recall curve (Everingham
and Zisserman, 2007) as shown in Fig. 5 (some of
the detection results are shown in Fig. 6). The
comparison methods include the SVM method that
employs the HOG feature and part-based algorithm
(Felzenszwalb et al., 2010), and our algorithm gives
the best average precision (AP) (Everingham and
Zisserman, 2007) and a relatively better performance.
5 CONCLUSIONS
This paper presents the regional SVM classifiers
with a spatial model to describe the 3D (axes x, y, z
in Fig. 1) spatial relationship of features, which is
ignored by the conventional SVM. Regional SVM
classifiers encode the spatial relationship along axis
z, and the spatial model incorporates the spatial
relationship along axes x and y. We demonstrate
regional SVM classifiers with the spatial model
using diversified features in various categories, and
the experiments establish that the regional SVM
classifiers do enhance the performance of the SVM
classifier and the spatial model improves the
performance of the object detection system. The
experiments on the benchmark datasets show that
our system has a relatively better performance
compared with other object detection algorithms.
ACKNOWLEDGEMENTS
This work was financially supported by the Basic
Science Research Program through the National
Research Foundation of Korea (NRF) funded by the
Ministry of Education, Science and Technology
RegionalSVMClassifierswithaSpatialModelforObjectDetection
377

Figure 6: Results on the Caltech Airplanes dataset. Top row: processed by the conventional SVM; Middle row: processed
by the part-based algorithm (Felzenszwalb et al., 2010); Bottom row: processed by our algorithm.
(2011-0027213 and 2011-0017228), and also
partially supported by Natural Science Foundation
of China (61300175 and 61301185) and
Fundamental Research Funds for the Central
Universities of the Ministry of Education of China
with grant number 2012JBM033.
REFERENCES
Moore, R., Lopes, J., 1999. Paper templates. In
TEMPLATE’06, 1st International Conference on
Template Production. SCITEPRESS.
Smith, J., 1998. The book, The publishing company.
London, 2
nd
edition.
Bernhard Scholkopf, Alexander J. Smola, 2002. Learning
with kernels: Support Vector Machines,
Regularization, Optimization, and Beyond, The MIT
Press.
Andreas Opelt, Axel Pinz, Andrew Zisserman, 2006.
Incremental learning of object detectors using a visual
shape alphabe, In Proc. IEEE Conf. Computer Vision
and Pattern Recognition, vol. 1, pp. 3-10.
Zheng Song, Qiang Chen, Zhongyang Huang, Yang Hua,
Shuicheng Yan, 2011. Contextualizing Object
Detection and Classification, In IEEE Conf. on
Computer Vision and Pattern Recognition (CVPR).
Tagare H., Vos F., Jaffe C.C., Duncan J.S., 1995.
Arrangement: A spatial relation between parts for
evaluating similarity of tomographic section, In IEEE
Trans. PAMI, 17 (9), 880-893.
Bogdan Alexe, Thomas Deselaers, Vittorio Ferrari, 2010.
What is an object? In Proc. CVPR.
Martin A. Fischler, Robert A. Elschlager, 1973. The
representation and matching of pictorial structures, In
IEEE Transactions on Computers, Vol. c-22, No. 1.
Long (Leo) Zhu, Yuanhao Chen, Alan Yuille, William
Freeman, 2010. Latent Hierarchical Structural
Learning for Object Detection, In Proc. IEEE
Computer Vision and Pattern Recognition (CVPR).
Sanjiv Kumar, Martial Hebert, 2006. Discriminative
random fields: A discriminative framework for
contextual interaction in classification, In Int. J.
Comput. Vis., vol. 68, no. 2, pp.179 -201.
David J. Crandall and Daniel P. Huttenlocher, 2006.
Weakly Supervised Learning of Part-Based Spatial
Models for Visual Object Recognition, In Proc.
ECCV, pages I: 16-29.
David Crandall, Pedro Felzenszwalb, Daniel Huttenlocher,
2005. Spatial Priors for Part-Based Recognition using
Statistical Models, In Proc. IEEE Conf. Computer
Vision and Pattern Recognition.
Navneet Dalal and Bill Triggs, 2005. Histograms of
Oriented Gradients for Human Detection, In Proc.
IEEE Conf. Computer Vision and Pattern Recognition.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
378

T. Ojala, M. Pietikäinen, and D. Harwood, 1996. A
Comparative Study of Texture Measures with
Classification Based on Feature Distributions, In
Pattern Recognition, vol. 29, pp. 51-59.
Daphne Koller, Nir Friedman, 2009. Probabilistic
Graphical Models: Principles and Techniques -
Adaptive Computation and Machine Learning, The
MIT Press.
Pedro F. Felzenszwalb, Ross B. Girshick, David
McAllester, and Deva Ramanan, 2010. Object
Detection with Discriminatively Trained Part-Based
Models, In IEEE Trans. PAMI, Vol. 32, No. 9.
P. Felzenszwalb, D. McAllester, and D. Ramanan, 2008.
A Discriminatively Trained, Multiscale, Deformable
Part Model, In Proc. IEEE Conf. Computer Vision and
Pattern Recognition.
C.-C. Chang and C.-J. Lin, 2011. LIBSVM : a library for
support vector machines, In ACM Transactions on
Intelligent Systems and Technology, 2:27:1--27:27.
Software available at http://www.csie.ntu.edu.tw/
~cjlin/libsvm.
Chih-Wei Hsu, Chih-Chung Chang, and Chih-Jen Lin,
2003. A Practical Guide to Support Vector
Classification, Technical Report, Taipei.
M. Everingham, A. Zisserman, C.K.I., Williams and L.
Van Gool, 2007. The PASCAL Visual Object Classes
Challenge 2007 (VOC 2007) Results. Available at:
http://pascallin.ecs.soton.ac.uk/challenges/VOC/voc20
07/.
Shivani Agarwal, Aatif Awan, and Dan Roth, 2004.
Learning to detect objects in images via a sparse, part-
based representation, In IEEE Transactions on Pattern
Analysis and Machine Intelligence, 26(11):1475-1490.
RegionalSVMClassifierswithaSpatialModelforObjectDetection
379
