
Active Shape Models with SIFT Descriptors and MARS
Stephen Milborrow and Fred Nicolls
Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa
Keywords:
Facial Landmark, Active Shape Model, Multivariate Adaptive Regression Splines.
Abstract:
We present a technique for locating landmarks in images of human faces. We replace the 1D gradient pro-
files of the classical Active Shape Model (ASM) (Cootes and Taylor, 1993) with a simplified form of SIFT
descriptors (Lowe, 2004), and use Multivariate Adaptive Regression Splines (MARS) (Friedman, 1991) for
descriptor matching. This modified ASM is fast and performs well against existing techniques for automatic
face landmarking on frontal faces.
1 INTRODUCTION
In this paper we use the Active Shape Model (ASM)
of (Cootes et al., 1995) for locating facial land-
marks, but use a simplified form of SIFT (Lowe,
2004) descriptors for template matching, replacing
the 1D profiles used in the classical model. Ad-
ditionally, we use Multivariate Adaptive Regression
Splines (MARS) (Friedman, 1991) to to efficiently
match these descriptors around the landmark. We also
introduce techniques for significantly decreasing their
computational load, making SIFT based ASMs use-
able in practical applications.
First a brief overview of ASMs. For details
see (Cootes and Taylor, 2004). A landmark represents
a distinguishable point present in most of the images
under consideration, for example the nose tip (Fig-
ure 1). A set of landmarks forms a face shape. The
ASM starts the search for landmarks from the mean
Figure 1: A landmarked face (Milborrow et al., 2010).
training face shape aligned to the position and size of
the image face determined by a global face detector.
It then repeats the following two steps until conver-
gence:
(i) Suggest a new shape by adjusting the current
positions of the landmarks. To do this at each land-
mark it samples image patches in the neighborhood of
the landmark’s current position. The landmark is then
moved to the center of the patch which best matches
the landmark’s model descriptor. (The landmark’s
model descriptor is generated during model training
prior to the search.)
(ii) Conform the suggested shape to a global
shape model. This pools the results of the individ-
ual matchers and corrects points that are obviously
mispositioned. The shape model is necessary because
each matcher sees only a small portion of the face and
cannot be completely reliable (Figure 2).
The entire search is repeated at each level in an im-
age pyramid, typically four levels from coarse to fine
resolution. In this paper our focus is on step (i), the
template matching step. We leave step (ii) unchanged.
Figure 2: 15 × 15 patches of the nose tip in Figure 1. The
left patch is at half image scale; the right is at full scale.
380
Milborrow S. and Nicolls F..
Active Shape Models with SIFT Descriptors and MARS.
DOI: 10.5220/0004680003800387
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 380-387
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
Numerous proposals have been made to replace the
1D profiles of the classical ASM. We mention just a
few SIFT based schemes, emphasizing facial applica-
tions. (Zhou et al., 2009) use SIFT descriptors with
Mahalanobis distances. They report improved eye
and mouth positions on the FGRCv2.0 database. (Li
et al., 2009) use SIFT descriptors with GentleBoost.
(Kanaujia and Metaxas, 2007) use SIFT descriptors
with multiple shape models clustered on different face
poses. (Belhumeur et al., 2011) use SIFT descriptors
with SVMs and RANSAC. They report excellent fits,
albeit at speeds orders of magnitude slower than ours.
(Shi and Shen, 2008) use SIFT descriptors in hier-
archical ASM models for medical images. SIFT de-
scriptors for face data are also used in (Querini and
Italiano, 2012; Rattani et al., 2007; Zhang and Chen,
2008; Zhang et al., 2011).
Multivariate Adaptive Regression Splines
(MARS) is a general purpose regression technique
introduced by Jerome Friedman in a 1990 pa-
per (Friedman, 1991). MARS has been shown to
perform well in diverse applications e.g. (Leathwick
et al., 2005; Vogel et al., 2010), although it is
apparently not well known in the image processing
community. For our purposes the principal advantage
of MARS over related nonparametric regression
methods like SVMs is its prediction speed. Also
making it attractive are short training times and
interpretability of the models it creates
3 SIFT DESCRIPTORS
A descriptor for template matching captures some dis-
tinguishing quality of the image feature in question.
In the ASM context, we want descriptors to capture
the nature of say the inner corner of the left eye. A
simple example is the “gradient descriptor”, which
takes the form of an array with the same dimensions
as the image patch; each element of the array is the
gradient or gradient magnitude at the corresponding
pixel in the patch. Typically the descriptor is normal-
ized to unit length. The classical ASM uses 1D gradi-
ent descriptors. Gradients are invariant to affine light-
ing changes, but not to other changes, so researchers
have devised more sophisticated techniques.
In this section we give an overview of the SIFT
descriptors which form the basis of the “HAT” de-
scriptors used in our version of the ASM. The next
section will then describe how HAT descriptors dif-
fer from SIFTs. We chose SIFT descriptors for in-
vestigation because of their well known good sensi-
Figure 3: An area in the patch maps to a cell in the his-
togram array.
tivity and specificity properties. Details can be found
in David Lowe’s paper (Lowe, 2004). Precedents for
the orientation histograms used in SIFT can be found
in e.g. (Belongie et al., 2002; Freeman and Roth,
1995).
The SIFT descriptor takes the form of an array of
histograms (Figure 3). The descriptor is generated
from a rectangular patch around the image point of in-
terest. Ignoring interpolation for now, coordinates in
the patch map to cells in the histogram array. We use a
15 × 15 patch and an array of 4 × 5 histograms. These
dimensions were determined during our ASM train-
ing; other values are also in common use. The low
spatial resolution of the histogram array helps provide
immunity to small changes within the patch while still
picking up overall structure.
Each histogram describes the distribution of gra-
dient orientations in its region of the patch. We use
8 bins per histogram, thus 360/8 = 45 degrees per
bin. The gradient magnitude at a pixel is added to the
histogram bin designated for its orientation, down-
weighted for smoothness by the Gaussian distance
of the pixel from the center of the patch. The ar-
ray of histograms is stored internally as a vector with
4 × 5 × 8 = 160 elements.
In the non-interpolated setup just described, a
small change in the patch position may cause a large
change to the descriptor as the mapping for a pixel
jumps abruptly from one histogram to another. We
thus linearly interpolate, or “smear out”, a pixel’s
contribution across adjacent histograms. The contri-
bution of a pixel which maps to the border between
histogram cells is divided equally between the his-
tograms. A pixel which maps to the center of a cell
affects only the histogram in that cell.
Likewise a small change in the orientation at a
pixel can cause an abrupt jump in assignment from
one histogram bin to another. We therefore also inter-
polate orientations across histogram bins. A gradient
with a 45
◦
orientation is shared equally between the
ActiveShapeModelswithSIFTDescriptorsandMARS
381

bin for 0−45
◦
and the bin for 45−90
◦
.
Our tests verified that the Gaussian spatial down-
weighting and all three interpolations (horizontally
and vertically across histograms, and across bins
within a histogram) are necessary for optimum fits in
ASMs, although computationally demanding.
Finally, we take the square root of each element of
the descriptor vector and normalize the resulting vec-
tor to unit length. Taking the square root reduces the
effect of extreme values such as the bright spots on the
nose tip in Figure 1. Normalizing to unit length gives
invariance to linear changes in image contrast. (In-
variance to the absolute illumination level is already
achieved because we are using gradients not gray lev-
els.) Actually, taking the square root is what we use
in our ASM; SIFT descriptors in their original form
use a slightly more complicated scheme.
4 HAT DESCRIPTORS
This section presents the descriptors used in our
model. They are essentially unrotated SIFT descrip-
tors with a fixed scale. In this paper it is convenient to
use the term Histogram Array Transforms (HATs) for
these descriptors.
HAT descriptors can be generated much more
quickly than descriptors in the standard SIFT frame-
work. Speed is important because to locate the land-
marks in a face we need to evaluate something like
25 thousand descriptors. (Using typical parameters:
68 landmarks × 4 pyramid levels × 4 model itera-
tions × 5 × 5 search grid = 27k.)
4.1 No Automatic Scale Determination
Readers familiar with SIFT will be aware that the
overview of descriptors in Section 3 does not mention
the overall SIFT framework in which the descriptors
are used (Lowe, 2004). This framework first does a
time consuming scale-space analysis of the image to
discover which points in the image are “keypoints”.
It also discovers the intrinsic scale of each of these
keypoints.
In contrast, in ASMs the keypoints are pre-
determined — they are the facial landmarks — and
the face is prescaled to a constant size before the ASM
search begins. (Our implementation scales to an eye-
mouth distance of 100 pixels.) Thus we do not need
SIFTs automatic determination of scale. The ASM
descriptor patches are a fixed size. The ASM uses a
simple 4 octave image pyramid and the search pro-
ceeds one pyramid level at a time. SIFT’s sub-octave
DOG pyramid where multiple levels are analyzed si-
multaneously is unnecessary.
4.2 No Patch Orientation
In the SIFT framework once the intrinsic scale of a
descriptor has been determined there is an additional
preprocessing step (omitted in Section 3): the local
structure of the image around the point of interest is
analyzed to determine the predominant gradient ori-
entation, and the descriptor is formed from a patch
rotated to this direction. The orientation is computed
by looking for peaks in an orientation histogram (in-
dependent of the histograms in the descriptor array).
In our ASM, however, before the search begins
we rotate the entire image so the eyes are horizon-
tal (after locating the eyes with the OpenCV eye de-
tectors (Castrill
´
on Santana et al., 2007)). Thus the
automatic orientation described in the previous para-
graph is unnecessary, and in our experiments actually
reduced the quality of fit. We also found it unneces-
sary to orientate the descriptors to the shape bound-
ary as is often done in ASMs. Some rotational varia-
tion will still remain (not every face is the same, and
the eye detectors sometime give false positives on the
eyebrows or fail to find eyes, causing mis-positioning
of the ASM start shape), and so we must also rely on
the intrinsic invariance properties of the descriptors.
4.3 Precalculation of Mapping from
Patch to Histogram Array
When generating a SIFT or HAT descriptor, each
pixel in the patch must be mapped to a position in the
array of histograms. Calculating this mapping takes
time, especially for scaled and rotated patches, and
must be done each time we generate a descriptor.
But HATs do not use such scaling or rotation, and
the mapping therefore depends only on the histogram
array dimensions (4 × 5) and the image patch width
(15 pixels), which remain constant through the ASM
search. Thus we can precalculate the mapping indices
just once for all descriptors (or once per pyramid level
if we use different patch sizes at different pyramid lev-
els). In our software this precalculation reduced total
ASM search times by 40%.
4.4 Descriptor Caching
In an ASM search we repeatedly revisit the same im-
age coordinates while iterating the models. Addi-
tionally, at coarse pyramid levels the search areas of
nearby points overlap. We therefore save HAT de-
scriptors for reuse. In practice we get a cache hit rate
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
382

of over 65% (over 65% of the requests for a descriptor
can be satisfied by using a saved descriptor). Caching
reduces search time by a further 70%.
5 DESCRIPTOR MATCHING
METHODS
Once we have the descriptor of an image patch, we
need a measure of how well the descriptor matches
the facial feature of interest. This section reviews
some standard techniques for descriptor matching,
leading to the MARS models used in our ASM. (Note
that at each landmark the ASM looks only for the sin-
gle best match in the search region, and so we need
be concerned only with the relative quality of match.)
A simple approach is to take the Euclidean dis-
tance between the descriptor and the mean training
descriptor for the landmark in question. This gives
every histogram bin equal weight, but that is inappro-
priate because pixels on certain edges will be more
important than pixels elsewhere. Furthermore, a high
variance bin is likely to add more noise than informa-
tion.
The Mahalanobis distance gives more important
bins more weight (it considers a bin important if it has
low variance in the training set), and takes into con-
sideration interaction between bins. The Mahalanobis
distance is the optimal measure to the extent that the
distribution of the bins’ values is Gaussian, which is
at most only approximately true for count data like
histogram bins (Figure 4). Calculating the Maha-
lanobis distance is slow (proportional to the square of
the number of elements in the descriptor; in our case
160 × 160 = 26k).
Within the standard SIFT framework for key-
point matching, descriptors are matched using near-
est neighbors, but that would be very slow for ASMs,
and for all landmarks would require a large amount of
memory.
Another tack is regression, using sample descrip-
tors on and around the correct position of the land-
marks in training images to train a model that es-
timates match quality as a function of the elements
of the descriptor. Linear regression would be a first
choice, but this assumes that the effect of a bin on
the match is proportional to its value, and a straight-
forward application of linear regression makes the as-
sumption that it is unnecessary to account for interac-
tions between bins. These assumptions may be sim-
plistic given that we are looking for a pattern of pixels.
To test that there is enough data to make more com-
plicated regression assumptions, we trained Support
Vector Machines (SVMs) for matching HAT descrip-
tors, which did indeed outperform the other methods
mentioned above. However, SVMs are slow. At each
landmark the SVM after training typically has over a
thousand support vectors. To evaluate a descriptor we
have to take the dot product of the descriptor vector
with each of these vectors (160 × say 1000 = 160k
operations).
We thus turned to Multivariate Adaptive Re-
gression Spline (MARS) models (Friedman, 1991).
MARS models give ASM results that are almost as
good as SVMs and are much faster. In our software,
MARS decreased total search time by over 80%. An
overview of MARS will be given in the next section.
We mention also that in our tests linear SVMs
gave slightly worse fits than the RBF SVMs we used
above. Random Forests (Breiman, 2001) gave not
quite as good fits and took roughly the same time (but
we did not do extensive tuning of Random Forests).
Single CART style trees (Breiman et al., 1984) did
not give good fits.
We generated regression training data as follows.
This regimen was reached after some experimentation
but we do not claim it is optimal. At the landmark of
interest in each training face, we generated (i) three
negative training descriptors at x and y positions ran-
domly displaced by 1 to 6 pixels from the “true” (i.e.,
manually landmarked) position of the landmark, and
(ii) a positive training descriptor at the true position of
the landmark. To bypass issues with imbalanced data,
we duplicated this positive descriptor thrice so there
were equal numbers of positive and negative training
descriptors. We regressed on this data with the posi-
tive training descriptors labeled with 0 and the nega-
tive training descriptors all labeled with 1 irrespective
of their distance from the true position of the land-
0.0 0.5 1.0 1.5 2.0 2.5
bin 5
(hist 0 bin 5)
0.0 0.5 1.0 1.5 2.0 2.5
bin 10
(hist 1 bin 2)
0.0 0.5 1.0 1.5 2.0 2.5
bin 12
(hist 1 bin 4)
0.0 0.5 1.0 1.5 2.0 2.5
bin 13
(hist 1 bin 5)
Figure 4: Non-Gaussianity is evident in the distribution of values across the training set in example histogram bins. Without
the square root mentioned in Section 3, these would be even more non-Gaussian (the square root pulls in the long right tail).
These examples are for the bottom left eyelid in the full scale image.
ActiveShapeModelswithSIFTDescriptorsandMARS
383

mark.
6 MARS
We give a brief overview of MARS by way of
an example. The MARS formula to estimate the
descriptor match at the bottom left eyelid in the full
scale image is
match = 0.026 (1)
+ 0.095 max(0, 1.514 − b
5
) (2)
+ 0.111 max(0, 2.092 − b
10
) (3)
+ 0.258 max(0, b
12
− 1.255) (4)
− 0.108 max(0, 1.574 − b
13
) (5)
· · · (6)
where the b
i
are HAT descriptor bins 0 ...159. There
happen to be 17 terms in the formula; we have shown
just the first few. The MARS model building algo-
rithm generated the formula from the training data.
There is a similar formula for each landmark at each
pyramid level.
The bins enter the formula via the max functions
rather than directly as they would in a linear model.
The max functions are characteristic of MARS. They
allow nonlinear dependence on the value of a bin and
contain the effect of a bin to a range of its values. The
effect of two of the bins is shown in Figure 5. The
same bin can appear in multiple terms, allowing com-
plex non-monotonic regression surfaces (but always
piecewise linear).
MARS has included only certain histogram bins
in the formula (there are 160 bins but only 17 terms
in our example). HAT descriptors lend themselves to
this kind of variable selection. The innate structure
of the image feature makes some bins more important
than others. Furthermore, the trilinear interpolation
Figure 5: The effect of bins 10 and 12 in terms (3) and (4) in the MARS formula above (with the other bins fixed at their
median values). The estimated quality of match is increased by low values in bin 10 and/or high values in bin 12. From
Figure 4, high values in bin 12 are uncommon. Low values are common but uninformative.
0.00 0.05 0.10 0.15
0.0 0.2 0.4 0.6 0.8 1.0
me17
proportion
BioID
HatAsm
Stasm 3.1
Cootes et al. 2012
Belhuemer et al.
0.00 0.05 0.10 0.15
0.0 0.2 0.4 0.6 0.8 1.0
me17
proportion
XM2VTS
HatAsm
Stasm 3.1
0.00 0.05 0.10 0.15
0.0 0.2 0.4 0.6 0.8 1.0
me17
proportion
PUT
HatAsm
Stasm 3.1
0.00 0.05 0.10 0.15
0.0 0.2 0.4 0.6 0.8 1.0
me17
proportion
Helen
HatAsm
Stasm 3.1
Figure 6: me17 distributions comparing our HatAsm to Stasm Version 3.1.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
384
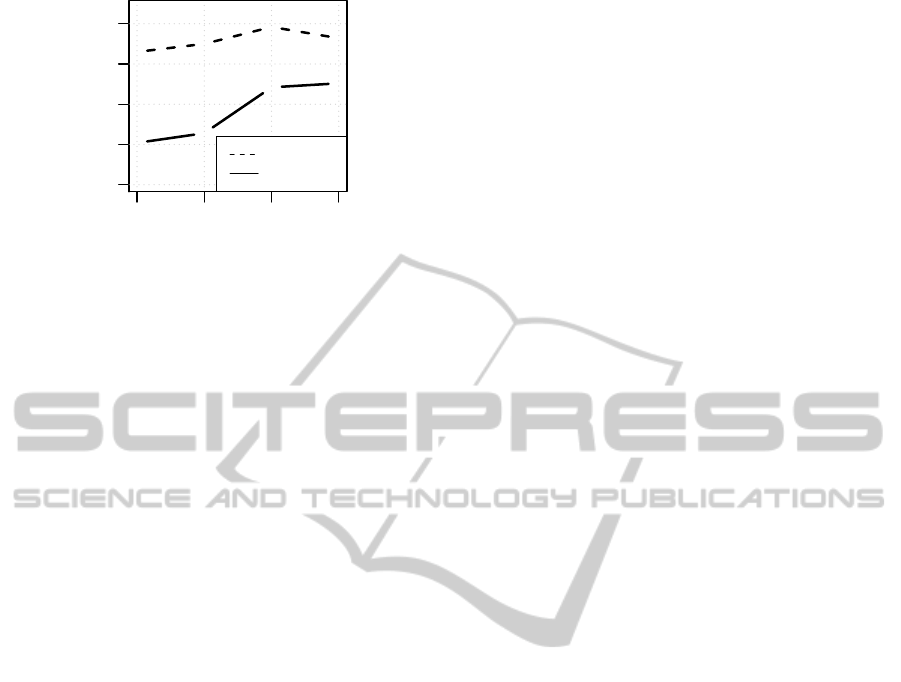
●
●
●
●
0 50 100 200
search time in ms
●
●
●
●
●
●
●
●
Stasm 3.1
HatAsm
BioID 55
XM2VTS 101
PUT 280
Helen 280
Figure 7: Search times (excluding face detection). The
databases are arranged in order of mean inter-pupil dis-
tance (shown after the database name on the horizontal
axis). Times were measured on a 3.4 GHz i7 with the same
datasets as Figure 6. Our software allows 64 bit executables
and use of OpenMP, but for impartial comparison we used
32 bit Microsoft VC10 builds without OpenMP for testing
both implementations.
induces collinearities between nearby bins. When
matching, it may therefore make little difference if we
use a bin or its neighbor. The MARS model building
algorithm will arbitrarily (depending on noise) pick
one or the other. Once the bin is in the formula, the
other bin can be ignored as it brings little new infor-
mation. Usually the final formula is so short that eval-
uating it is quicker than it would be to say take the
Euclidean distance between two descriptors. Exploit-
ing structure in the data saves unnecessary calculation
and reduces noise from uninformative variables.
Further details on MARS can be found in (Fried-
man, 1991) and perhaps more accessibly in (Hastie
et al., 2009). We compiled the MARS formulas as
C++ code directly into our application. We performed
MARS model selection (i.e. optimization of the num-
ber of terms) not by using the standard MARS Gen-
eralized Cross Validation but by optimizing descrip-
tor match performance on a tuning set. With smaller
training sets (less than a thousand faces) our experi-
ence has been that linear models can perform as well
as MARS. MARS also allows interactions between
variables, but interactions do not appear to give better
fits in this setting unless large data sets are used (ten
thousand faces).
7 EXPERIMENTS
To summarize, our model differs from the classical
ASM simply in that it incorporates HAT descriptors
and uses MARS to measure descriptor matches. In
this section we refer to this model as a “HatAsm”
model.
We compare the model primarily to the open
source Stasm landmarker (Milborrow and Nicolls,
2008). (Stasm outperformed other public landmark-
ers in three of the four tests in a comprehensive 2013
study (C¸ eliktutan et al., 2013). Stasm uses a combina-
tion of 1D and square gradient descriptors with Ma-
halanobis distances.) We used the version of Stasm
current at the time of writing (Version 3.1), which was
trained on the MUCT data (Milborrow et al., 2010).
For these tests we trained our ASM on the same data
(using the training regimen described at the end of
Section 5). We also used the same OpenCV frontal
face detector (Lienhart and Maydt, 2002) as Stasm
to find the face and for initialization the ASM start
shape. After preliminary experimentation on inde-
pendent data, for the tests here our model uses 1D
gradient descriptors at the coarsest pyramid level and
on the jaw points at all pyramid levels, and HAT de-
scriptors otherwise.
We present results in terms of the me17 mea-
sure (Cristinacce and Cootes, 2006), which is the
mean distance between 17 internal face points (Fig-
ure 1) located by the search and the corresponding
manually landmarked points, divided by the distance
between the manual eye pupils. Depending on the ap-
plication, other fitness measures may be more appro-
priate, but the me17 is widely used and forms a con-
venient baseline. Tests using other distance measures
gave results similar to those shown here.
Figure 6 shows results on four different datasets
disjoint from the training data. (As is common prac-
tive, we show results as the cumulative distribution
of fits. The quicker an S curve starts and the faster
it reaches the top, the better the model.) Our imple-
mentation outperforms Stasm 3.1 on all sets except
arguably on the BioID data.
The BioID graph also shows the results of (Bel-
humeur et al., 2011). Apart from the poor perfor-
mance above the 75th percentile, the Belhumeur et al.
results are to our knowledge the best published re-
sults on this set (excluding papers which report re-
sults on subsets or re-marked versions of the BioID
data). However, their landmarker takes on the order
of a second per landmark, whereas ours processes the
entire face in about 50ms. We also show the results
of (Cootes et al., 2012), who estimate the position of
a point by combining the positions estimated by Ran-
dom Forest regressions on nearby patches. The im-
proved results near the top of their curve are perhaps
due to their use of a commercial face detector which
almost certainly outperforms the OpenCV detector.
Both our HatAsm and Stasm are limited to near-
ActiveShapeModelswithSIFTDescriptorsandMARS
385

frontal views by their reliance on a frontal face detec-
tor, so are inappropriate for the Helen set (Le et al.,
2012) with its wide range of poses, but our imple-
mentation fares significantly better.
Figure 7 compares search times. Our implemen-
tation is faster than Stasm. The (Cootes et al., 2012)
Random Forest technique (not shown in Figure 7) is
faster than ours, but they fit only 17 points (we fit 76).
Details. The HatAsm and Stasm 3.1 curves in-
clude all faces in the BioID (Jesorsky et al., 2001),
XM2VTS (Messer et al., 1999), and PUT (Kasinski
et al., 2008) sets, and the designated test of the Helen
set (Le et al., 2012). Faces not found by the face de-
tectors are included in these curves, with an me17 of
infinity. For the PUT set several extra points needed
for calculating me17s were manually added before
testing began. For the Helen set we approximated the
pupil and nose points needed for me17s from neigh-
boring points, introducing noise to the results (but
equally for both implementations). The Belhumeur et
al. and Cootes et al. curves were transcribed from fig-
ures in their papers. All other curves were created by
running software on a local machine.
Publication Note. Techniques in this paper have
now been integrated into Stasm to form Stasm Ver-
sion 4.0. Documented source code is available at
www.milbo.users.sonic.net/stasm.
8 DISCUSSION AND FUTURE
DIRECTIONS
We have shown that HAT descriptors together with
MARS work well with ASMs. HAT descriptors out-
perform gradient based descriptors. HAT descriptors
with MARS bring significant computational advan-
tages over SIFT descriptors with Mahalanobis dis-
tances or SVMs.
An obvious next step would be to investigate other
modern descriptors such as GLOH (Mikolajczyk and
Schmid, 2005), SURF (Bay et al., 2006), or HOG
(Dalal and Triggs, 2005) descriptors (our HAT de-
scriptors are the same as one variant of HOGs, R-
HOGs). Evidence from other domains indicate that
such alternatives per se may not give fit improvements
over HATs.
In (Milborrow et al., 2013) we extend the model
to non-frontal faces.
In recent years researchers have paid considerable
attention to improving the way the template and shape
models work together. Instead of the rigid separation
between template matching and the shape model of
the classical ASM, one can build a combined model
that jointly optimizes the template matchers and shape
constraints. An early example is the Constrained Lo-
cal Model of (Cristinacce and Cootes, 2006). An
informative taxonomy is given in (Saragih et al.,
2010). Such an approach would probably improve
HAT based landmarkers. The advantages of HATs
are diminished by the classical ASM shape model (the
improvement of HATS over square gradient descrip-
tors is significantly larger before the shape constraints
are applied). The match response surfaces over the
search regions are smoother for HATs than for square
gradient descriptors, and this might ease the difficult
optimization task.
REFERENCES
Bay, H., Tuytelaars, T., and Gool, L. V. (2006). SURF:
Speeded Up Robust Features. ECCV.
Belhumeur, P. N., Jacobs, D. W., Kriegman, D. J., and Ku-
mar, N. (2011). Localizing Parts of Faces Using a
Consensus of Exemplars. CVPR.
Belongie, S., Malik, J., and Puzicha., J. (2002). Shape
Matching and Object Recognition Using Shape Con-
texts. PAMI.
Breiman, L. (2001). Random Forests. Machine Learning.
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone,
C. J. (1984). Classification and Regression Trees.
Wadsworth.
Castrill
´
on Santana, M., D
´
eniz Su
´
arez, O.,
Hern
´
andez Tejera, M., and Guerra Artal, C. (2007).
ENCARA2: Real-time Detection of Multiple Faces at
Different Resolutions in Video Streams. Journal of
Visual Communication and Image Representation.
C¸ eliktutan, O., Ulukaya, S., and Sankur, B. (2013). A
Comparative Study of Face Landmarking Techniques.
EURASIP Journal on Image and Video Processing.
http://jivp.eurasipjournals.com/content/2013/1/13/
abstract. This study used Stasm Version 3.1.
Cootes, T., Ionita, M., Lindner, C., and Sauer, P. (2012). Ro-
bust and Accurate Shape Model Fitting using Random
Forest Regression Voting. ECCV.
Cootes, T. F. and Taylor, C. J. (1993). Active Shape Model
Search using Local Grey-Level Models: A Quantita-
tive Evaluation. BMVC.
Cootes, T. F. and Taylor, C. J. (2004). Technical Re-
port: Statistical Models of Appearance for Computer
Vision. The University of Manchester School of
Medicine. http://www.isbe.man.ac.uk/∼bim/Models/
app
models.pdf.
Cootes, T. F., Taylor, C. J., Cooper, D. H., and Graham, J.
(1995). Active Shape Models — their Training and
Application. CVIU.
Cristinacce, D. and Cootes, T. (2006). Feature De-
tection and Tracking with Constrained Local Mod-
els. BMVC. mimban.smb.man.ac.uk/publications/
index.php.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
386

Dalal, N. and Triggs, B. (2005). Histograms of Oriented
Gradients for Human Detection. CVPR.
Freeman, W. T. and Roth, M. (1995). Orientation His-
tograms for Hand Gesture Recognition. AFGR.
Friedman, J. H. (1991). Multivariate Adaptive Regres-
sion Splines (with discussion). Annals of Statistics.
http://www.salfordsystems.com/doc/MARS.pdf.
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Ele-
ments of Statistical Learning: Data Mining, Inference,
and Prediction (Second Edition). Springer.
Jesorsky, O., Kirchberg, K., and Frischholz, R. (2001). Ro-
bust Face Detection using the Hausdorff Distance.
AVBPA.
Kanaujia, A. and Metaxas, D. N. (2007). Large Scale
Learning of Active Shape Models. ICIP.
Kasinski, A., Florek, A., and Schmidt, A. (2008). The PUT
Face Database. IPC.
Le, V., Brandt, J., Lin, Z., Boudev, L., and Huang,
T. S. (2012). Interactive Facial Feature Localization.
ECCV. http://www.ifp.illinois.edu/ vuongle2/helen.
Leathwick, J., Rowe, D., Richardson, J., Elith, J., and
Hastie, T. (2005). Using Multivariate Adaptive Re-
gression Splines to Predict the Distributions of New
Zealand’s Freshwater Diadromous Fish. Freshwa-
ter Biology, 50, 2034-2052. http://www.botany.
unimelb.edu.au/envisci/about/staff/elith.html.
Li, Z., Imai, J.-i., and Kaneko, M. (2009). Facial Feature
Localization using Statistical Models and SIFT De-
scriptors. Robot and Human Interactive Communica-
tion.
Lienhart, R. and Maydt, J. (2002). An Extended Set of Haar-
Like Features for Rapid Object Detection. IEEE ICP.
Lowe, D. G. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. IJCV.
Messer, K., Matas, J., Kittler, J., Luettin, J., and Maitre, G.
(1999). XM2VTS: The Extended M2VTS Database.
AVBPA.
Mikolajczyk, K. and Schmid, C. (2005). A Performance
Evaluation of Local Descriptors. PAMI.
Milborrow, S., Bishop, T. E., and Nicolls, F. (2013). Mul-
tiview Active Shape Models with SIFT Descriptors for
the 300-W Face Landmark Challenge. ICCV.
Milborrow, S., Morkel, J., and Nicolls, F. (2010).
The MUCT Landmarked Face Database. Pat-
tern Recognition Association of South Africa.
http://www.milbo.org/muct.
Milborrow, S. and Nicolls, F. (2008). Locating Facial Fea-
tures with an Extended Active Shape Model. ECCV.
Querini, M. and Italiano, G. F. (2012). Facial Biometrics
for 2D Barcodes. Computer Science and Information
Systems.
Rattani, A., Kisku, D. R., Lagorio, A., and Tistarelli, M.
(2007). Facial Template Synthesis based on SIFT Fea-
tures. Automatic Identification Advanced Technolo-
gies.
Saragih, J., Lucey, S., and Cohn, J. (2010). Deformable
Model Fitting by Regularized Landmark Mean-Shifts.
IHCV.
Shi, Y. and Shen, D. (2008). Hierarchical Shape Statisti-
cal Model for Segmentation of Lung Fields in Chest
Radiographs. MICCAI.
Vogel, C., de Sousa Abreu, R., Ko, D., Le, S., Shapiro,
B. A., Burns, S. C., Sandhu, D., Boutz, D. R., Mar-
cotte, E. M., and Penalva, L. O. (2010). Sequence
signatures and mRNA concentration can explain two-
thirds of protein abundance variation in a human cell
line. Molecular Systems Biology.
Zhang, J. and Chen, S. Y. (2008). Combination of Local
Invariants with an Active Shape Model. BMEI.
Zhang, L., Tjondronegoro, D., and Chandran, V. (2011).
Geometry vs. Appearance for Discriminating between
Posed and Spontaneous Emotions. NIP.
Zhou, D., Petrovska-Delacr
´
etaz, D., and Dorizzi, B. (2009).
Automatic Landmark Location with a Combined Ac-
tive Shape Model. BTAS.
ActiveShapeModelswithSIFTDescriptorsandMARS
387
