Floor Plan Generation and Room Labeling of Indoor Environments from

Laser Range Data

Eric Turner and Avideh Zakhor

Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, CA, U.S.A.

Keywords:

Floor Plan, Watertight Modeling, Range Data, LiDAR.

Abstract:

Automatic generation of building ﬂoor plans is useful in many emerging applications, including indoor naviga-

tion, augmented and virtual reality, as well as building energy simulation software. These applications require

watertight models with limited complexity. In this paper, we present an approach that produces 2.5D extruded

watertight models of building interiors from either 2D particle ﬁlter grid maps or full 3D point-clouds captured

by mobile mapping systems. Our approach is to triangulate a 2D sampling of wall positions and separate these

triangles into interior and exterior sets. We partition the interior volume of the building model by rooms, then

simplify the model to reduce noise. Such labels are useful for building energy simulations involving thermal

models, as well as for ensuring geometric accuracy of the resulting 3D model. We experimentally verify the

performance of our proposed approach on a wide variety of buildings. Our approach is efﬁcient enough to be

used in real-time in conjunction with Simultaneous Localization and Mapping (SLAM) applications.

1 INTRODUCTION

Indoor building modeling and ﬂoor plan generation

are useful in many ﬁelds such as architecture and civil

engineering. Green buildings and sustainable con-

struction have increased the use of building energy

simulation and analysis software, requiring building

geometry as input. Even though existing energy simu-

lation tools can accurately model the thermodynamic

properties of building interiors, their performance is

hindered by overly complex geometry models (Craw-

ley et al., 2000). Indoor models can also be used

for positioning in wide-area augmented reality appli-

cations, whereby low-complexity models enable low

memory use for mobile client-side processing.

In this paper, we present a technique for gener-

ating aesthetically pleasing, minimalist 2.5D models

of indoor building environments. Such models are in-

tended to capture the architectural elements of a build-

ing such as ﬂoors, walls, and ceilings while ignoring

transient objects such as furniture. We generate our

models by ﬁrst computing a 2D ﬂoor-plan of the en-

vironment, then using estimated height information to

extrude the ﬂoor-plan into a 3D building model.

Generating 3D models by extruding 2D ﬂoor-

plans typically yield clean and aesthetically pleasing

results. Even though such models may not capture the

ﬁne details of the environment, they still offer many

advantages. As shown later, it is possible to gener-

ate sizable 2.5D extruded models at real-time speeds,

enabling human operators to capture and navigate en-

vironments thoroughly and adaptively.

We also propose a technique to partition the inte-

rior environment rooms, yielding secondary features

of buildings, such as locations of doorways. Room

labeling is useful for many applications, such as fast

rendering of models (Funkhouser et al., 1992). Fur-

thermore, since energy simulation engines model heat

and air ﬂow within the building environment, they

need accurate partitions of the interior spaces to rep-

resent distinct thermal zones (Crawley et al., 2000).

In addition to exporting room labels, our proposed

technique uses the computed labels to further improve

the geometry of the model. Speciﬁcally, knowledge

of room partitions can be exploited to reduce noise

in the computed geometry while preserving ﬁne de-

tails in doorways. Furthermore, since input height es-

timates are often noisy, using room labels to group

these heights can provide substantial error reduction

in the resulting extruded 3D meshes.

This paper is organized as follows. In Section 2,

we describe related work to this research. Section 3

describes our proposed algorithm to generate ﬂoor

plans from the speciﬁed input. In Section 4, we de-

scribe our approach to room labeling. In Section 5,

we show how room labeling is used to reduce noise

Turner E. and Zakhor A..

Floor Plan Generation and Room Labeling of Indoor Environments from Laser Range Data.

DOI: 10.5220/0004680300220033

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 22-33

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

in the model. Section 6 describes how 2D ﬂoor plans

are extruded into 2.5D models with height informa-

tion. Section 7 demonstrates experimental results on

a wide variety of building models. Lastly, in Section 8

we describe potential future work in this area.

2 BACKGROUND

Modeling and navigation of indoor environments is a

well-studied ﬁeld. Due to cost of full 3D laser range

ﬁnders, the majority of indoor modeling systems use

2D LiDAR scanners. Examples of such systems in-

clude autonomous unmanned vehicles (Shen et al.,

2011; Brunskill et al., 2007) or systems worn by a hu-

man operator (Chen et al., 2010; Fallon et al., 2012).

Most simultaneous localization and mapping

(SLAM) systems use a horizontally-oriented 2D Li-

DAR scanner, which estimates the trajectory of the

system, creating a 2D map of the environment (Thrun

et al., 2005). The constructed 2D grid map is stored

as a set of points in R

that represent the primary

features of the environment, such as walls and build-

ing architecture. Particle ﬁltering approaches to local-

ization typically result in real-time mapping (Hahnel

et al., 2003; Grisetti et al., 2007) and can therefore

beneﬁt from a real-time ﬂoor plan generation algo-

rithm that delivers a live map of the environment.

These mapping systems can also use additional

scanners to create a dense 3D point-cloud representa-

tion of the environment geometry (Smith et al., 2011;

Kua et al., 2012), which can be used to develop full

3D models (Chauve et al., 2010; Holenstein et al.,

2011). Many applications are unable to use these 3D

models due to their complexity and number of ele-

ments. For example, building energy simulations re-

quire watertight meshes that are also highly simpliﬁed

in order to perform effectively (Crawley et al., 2000).

To address this issue, a number of simpliﬁed

building modeling algorithms have been developed,

most of which assume vertical walls, rectiﬁed rooms,

and axis-alignment (Xiao and Furukawa, 2012). Un-

der these assumptions, fundamental features of the

building can be identiﬁed, while ignoring minor de-

tails such as furniture or other clutter (Adan and Hu-

ber, 2011). One of the major limitations of these

techniques is that they are developed only for axis-

aligned models. Often, such techniques correctly re-

construct major rooms while fundamentally changing

the topology of minor areas, such as ignoring door-

ways, shapes of rooms, or small rooms entirely.

In this paper, we show that simple models can be

generated with only 2.5D information, while preserv-

ing connectivity and geometry of building features,

including doorways. Our approach generates a 2D

ﬂoor plan of the building, then uses wall height infor-

mation to generate a 3D extrusion of this ﬂoor plan.

Such blueprint-to-model techniques have been well-

studied (Or et al., 2005; Lewis and Sequin, 1998),

but rely on the original building blueprints as input.

Our technique automatically generates the ﬂoor plan

of the building and uses this information to create a

2.5D model of the environment.

Prior work on automatic ﬂoor plan generation use

dense 3D point-clouds as input, and take advantage of

the verticality of walls to perform histogram analysis

to sample wall position estimates (Okorn et al., 2009;

Turner and Zakhor, 2012), which are in the same for-

mat as a grid map for particle ﬁltering (Grisetti et al.,

2005). In situations where dense 3D point-clouds are

available, we apply similar techniques to convert them

to a 2D wall sampling.

A novel contribution of this paper is the use of

room labeling to enhance building models, e.g. for

thermal simulations of interior environments (Craw-

ley et al., 2000). One motivation for existing work has

been to capture line-of-sight information for fast ren-

dering of building environments (Funkhouser et al.,

1992). This technique requires axis-aligned rectilin-

ear building geometry, which often is not a valid as-

sumption. Others have partitioned building environ-

ments into submap segments with the goal of efﬁcient

localization and tracking (Brunskill et al., 2007). This

approach is meant to create easily recognizable sub-

sections of the environment, whereas our proposed

room labeling technique uses geometric features to

capture semantic room deﬁnitions for both architec-

tural and building energy simulation applications.

3 FLOOR PLAN GENERATION

In this section, we present a technique to automati-

cally generate accurate ﬂoor plan models at real-time

speeds for indoor building environments. Section 3.1

describes the type of input for our approach, which

can be generated from either 2D mapping systems

or dense 3D point-clouds of environments. In Sec-

tion 3.2, we discuss the way these input data are used

to compute the interior space of the 2D ﬂoor-plan,

which deﬁnes the resultant building geometry.

3.1 Input Data

The input data used during ﬂoor plan generation con-

sist of points in the (x,y) horizontal plane, which

we call wall samples. These points depict loca-

tions of walls or vertical objects in the environ-

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData

Figure 1: Example input wall samples of hotel hallways

and lobby generated from a particle ﬁlter system. (a) Wall

samples of full model; (b) close up of wall in model.

ment. We assume that interior environments satisfy

“2.5-Dimensional” geometry: all walls are vertically

aligned, while ﬂoors and ceilings are perfectly hori-

zontal. In many application scenarios only 2D scan-

ners operating in one plane are used, so this assump-

tion is needed to extract 3D information about the en-

vironment. Many mapping systems use a horizontal

LiDAR scanner to estimate a map of the area as a set

of wall sample positions, while reﬁning estimates for

scanner poses. These mobile mapping systems often

have additional sensors capable of estimating ﬂoor

and ceiling heights at each pose (Chen et al., 2010;

Shen et al., 2011). The input to our algorithm is a

set of 2D wall samples, where each sample is associ-

ated with the scanner pose that observed it, as well as

estimates of the ﬂoor and ceiling heights at the wall

sample location.

An alternate method of computing wall samples is

to subsample a full 3D point-cloud to a set of repre-

sentative 2D points (Turner and Zakhor, 2012; Okorn

et al., 2009). This process cannot be done in a stream-

ing fashion, but can provide more accurate estimates

for wall positions than a real-time particle ﬁlter. Such

an approach is useful when representing dense, highly

complex point clouds with simple geometry. Under

the 2.5D assumption of the environment, wall sam-

ples can be detected by projecting 3D points onto the

horizontal plane. Horizontal areas with a high density

of projected points are likely to correspond to vertical

surfaces. Wall samples are classiﬁed by storing these

projected points in a quadtree structure with resolu-

tion r. A resolution of 5 cm typically results in sufﬁ-

cient detail in even the most cluttered environments.

Each leaf node in this quadtree contains the 3D points

that are projected onto its r × r area. A vertical his-

togram is computed using the original heights of these

points. This histogram has bin-size r, and if a suf-

ﬁcient vertical coverage H is represented by at least

ceil(H/r) bins, then the average (x,y) position of

the leaf is considered a wall sample. The value of H

may vary depending on application, but a length of 2

meters works well to capture permanent wall features

while ignoring furniture and other interior clutter.

The result is a set of wall samples P ⊆ R

, where

each wall sample p ∈ P is represented by its 2D po-

sition, the minimum and maximum height values of

the points that sample represents, and the poses of

the scanners that observed the sample location. As

we discuss later, these scanner poses provide crucial

line-of-sight information that facilitate ﬂoor plan re-

construction. An example of such input for a hotel

hallway is shown in Figure 1. As shown, even though

the walls are well sampled, noise in the localization

estimate causes noisy wall samples with outliers.

3.2 Triangulation

We generate a ﬂoor plan by partitioning space into in-

terior and exterior domains. The interior represents

all open space in the environment, such as rooms and

hallways, while the exterior represents all space out-

side of the building, space occupied by solid objects,

or space that is unobservable. Once this partitioning

is completed, as described below, the boundary lines

between the interior and exterior are used to represent

the exported walls of the ﬂoor plan.

The input samples are used to deﬁne a volumetric

representation by generating a Delaunay Triangula-

tion on the plane. Each triangle is labeled either in-

terior or exterior by analyzing the line-of-sight infor-

mation of each wall sample. Initially, all triangles are

considered exterior. Each input wall sample, p ∈ P,

is viewed by a set of scanner positions, S

⊆ R

. For

every scanner position s ∈ S

, the line segment (s, p)

denotes the line-of-sight occurring from the scanner

to the scanned point during data collection. No solid

object can possibly intersect this line, since otherwise

the scan would have been occluded. Thus, all trian-

gles intersected by the line segment (s, p) are rela-

beled to be interior.

In order to prevent ﬁne details from being re-

moved, we check for occlusions when carving each

line segment (s, p). If another wall sample p

is lo-

cated in between the positions of s and p, then the

line segment is truncated to (s, p

). Thus, no features

captured by wall samples are ever fully carved away,

preserving environment details. This process carves

away the interior triangles with each captured scan.

Since these scans are captured on a mobile scanner,

the scanner poses are ordered in time. In order for

the system to traverse the environment, the line seg-

ment between adjacent scanner poses must also in-

tersect only interior space. In addition to carving via

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

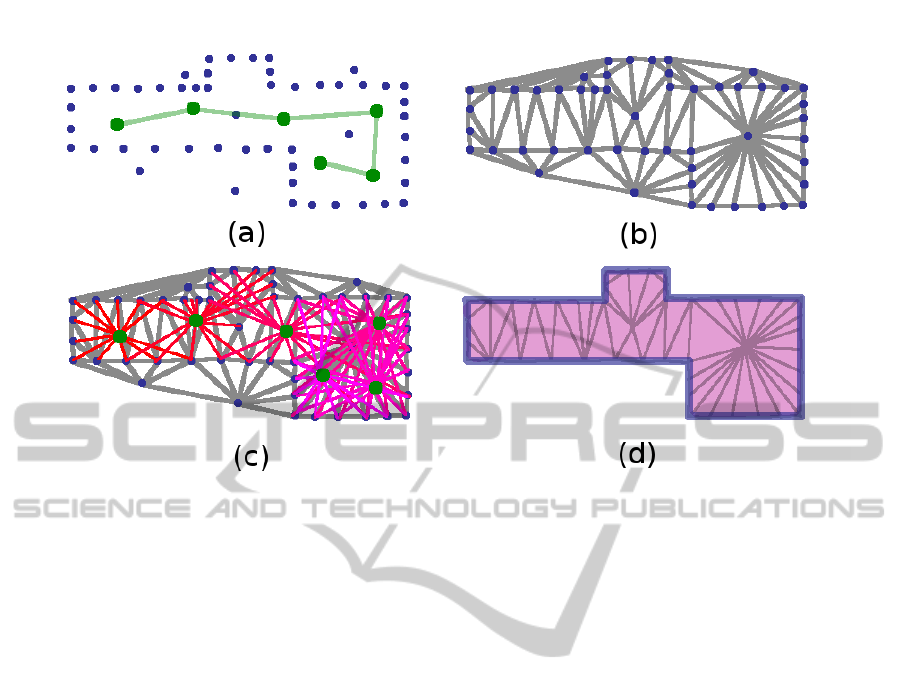
Figure 2: Example of carving process to ﬁnd interior triangles: (a) wall samples (in blue) with path of scanner (in green); (b)

Delaunay Triangulation of wall samples; (c) laser scans from each pose (in red); (d) triangles that intersect with laser scans

(in pink), used as interior triangles, with building model border (in blue).

scanner-to-scan lines, the same carving process is per-

formed with scanner-to-scanner line segments.

Figure 2 demonstrates an example of this process.

Figure 2a shows the input wall samples, in blue, as

well as the path of the mobile mapping system, in

green. These points are triangulated, as shown in Fig-

ure 2b. The line-of-sight information is analyzed from

each pose of the system, demonstrated by the laser

scans from each pose to its observed wall samples in

Figure 2c. The subset of triangles that are intersected

by these laser scans are considered interior. The inte-

rior triangles are shown in pink in Figure 2d, denot-

ing the interior volume of the reconstructed building

model. The border of this building model is shown in

blue, denoting the estimated walls of the ﬂoor plan.

4 ROOM LABELING

Once the volume has been partitioned into interior

and exterior domains, the boundary between these do-

mains can be exported as a valid ﬂoor plan of the en-

vironment. Keeping volumetric information can also

yield useful information, such as a partitioning of the

interior into separate rooms.

We deﬁne a room to be a connected subset of the

interior triangles in the building model. Ideally, a

room is a large open space with small shared bound-

aries to the rest of the model. Detected rooms should

match with real-world architecture, where separations

between labeled rooms are located at doorways in the

building. Since doors are often difﬁcult to detect, or

not even present, there is no strict mathematical def-

inition for a room, so this labeling is heuristic in na-

ture.

We model room labeling as a graph-cut problem.

First, a rough estimate for the number of rooms and a

seed triangle for each room is computed. A seed tri-

angle is representative of a room, where every room

to be modeled has one seed triangle. These seeds

are used to partition the remainder of interior trian-

gles into rooms. This process typically over-estimates

the number of rooms, so prior knowledge of architec-

tural compliance standards is used to evaluate each

estimated room geometry. Using this analysis, the

number of ill-formed rooms is reduced, providing an

update on the original seed points. This process is

repeated until the set of room seeds converges.

4.1 Forming Room Seeds

We use the Delaunay property of the triangulation

to identify likely seed triangle locations for room la-

bels. If we assume that the input wall samples repre-

sent a dense sampling of the building geometry, this

property implies that the circumcircles of none of the

interior triangles intersect the boundary walls of the

carved ﬂoor plan, forcing these circles to represent

only interior area. This make-up allows each trian-

gle’s circumradius to provide an estimate of the local

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData

Figure 3: Example room seed partitioning: (a) interior triangulation; (b) the room seed triangles, and their corresponding

circumcircles; (c) room labels propagated to all other triangles.

feature size at its location on the ﬂoor plan bound-

ary polygon. Given the example interior triangulation

shown in Figure 3a, the highlighted triangles in Fig-

ure 3b show the chosen seed locations.

Triangles with larger circumradii are likely to be

more representative of their rooms than those with

smaller circumradii. We form the initial set of room

seeds by ﬁnding all triangles whose circumcircles are

local maxima. Speciﬁcally, given the set of interior

triangles T , each triangle t ∈ T has circumcircle c

which is tested against every other circumcircle in T

that is intersected by c

. If c

has the largest radius

of any intersecting circumcircle, then t is considered

a seed for the room labeling. This process selects the

largest triangles that encompass the space of rooms as

the seeds for room labeling. Figure 3b shows example

seed triangles and their corresponding circumcircles.

The result is an estimate of the number of rooms and

a rough location for each room.

4.2 Partitioning Room Labels

Let K be the number of room seeds found, with the

seed triangles denoted as t

, t

, ..., t

. We wish to par-

tition all triangles in T into K rooms. This step can be

performed as a graph-cut on the dual of the triangu-

lation. Speciﬁcally, each triangle t ∈ T is a node in

the graph, and the edge weight between two abutting

triangles is the length of their shared side. Performing

a min-cut on this graph partitions rooms to minimize

inter-room boundary length. In other words, rooms

are deﬁned to minimize the size of doors. This pro-

cess propagates the room labels to every triangle, and

the boundaries between rooms are composed of only

the smallest edges in the triangulation T . The result

of this process is shown in Figure 3c.

4.3 Reﬁning Rooms

Room labels partition T into a set of rooms R =

, R

, ..., R

}, where each room R

contains a dis-

joint subset of T and has seed triangle t

. The initial

room seeds over-estimate the number of rooms, since

a room may have multiple local maxima. This case is

especially true for long hallways, where the assump-

tion that one triangle dominates the area of the room is

invalid. An example is shown in Figure 3c, where two

lower rooms, shown in green and purple, are prop-

erly labeled, but their adjoining hallway is broken into

three subsections. The solution is to selectively re-

move room seeds and redeﬁne the partition.

A room is considered a candidate for merging if

it shares a large perimeter with another room. Ide-

ally, two rooms sharing a border too large to be a door

should be considered the same room. By Americans

with Disabilities Act Compliance Standards, a swing-

ing door cannot exceed 48 inches in width (ADA,

1990). Accounting for the possibility of double-

doors, we use a threshold of 2.44 meters, or 96 inches,

when considering boundaries between rooms. If two

rooms share a border greater than this threshold, then

the seed triangle with the smaller circumradius is dis-

carded. This process reduces the value of K, the num-

ber of rooms, while keeping the interior triangulation

T unchanged. With a reduced set of room seeds, ex-

isting room labels are discarded and the process of

room partitioning is repeated. This iteration repeats

until the room labeling converges.

Another way room labels are reﬁned is by com-

paring the path of the mobile mapping system to the

current room labeling for each iteration. The mobile

scanning system does not necessarily traverse every

room, and may only take superﬁcial scans of room ge-

ometry passing by a room’s open doorway. Since the

room is not actually entered, the model is unlikely to

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

Figure 4: Room labeling reﬁnement example: (a) initial room labels; (b) converged room labels.

capture sufﬁcient geometry, and so only a small hand-

ful of wall samples are acquired for such a room. It

is desirable to remove this poorly scanned area from

the model rather than keeping it as part of the out-

put. After each round of room partitioning, if none

of the triangles in a room R

are intersected by the

scanner’s path, then we infer that room has not been

entered. The elements of R

are removed from the in-

terior triangulation T . Since the topology of the build-

ing model is changed, the set of room seeds is recom-

puted in this event and room labeling is restarted. This

process will also remove areas that are falsely identi-

ﬁed as rooms, such as ghost geometry generated by

windows and reﬂective surfaces, which cause rooms

to be replicated outside the actual model.

Figure 4 shows an example of the room reﬁne-

ment process for the hallways and classrooms in an

academic building. Figure 4a shows the initial room

seeds that were found based on circumcircle analy-

sis of Section 4.1. The hallways of this building are

represented by several room labels, but after room la-

bel reﬁnement as shown in Figure 4b, the hallways

are appropriately classiﬁed. Additionally, rooms that

are insufﬁciently scanned and represented with trian-

gulation artifacts are removed from the model in the

manner described above.

5 SIMPLIFICATION

The interior building model is represented as a trian-

gulation of wall samples, which densely represent the

building geometry. In many applications, it is use-

ful to reduce the complexity of this representation, so

that each wall is represented by a single line segment.

This step is often desirable in order to attenuate noise

in the input wall samples or to classify the walls of a

room for application-speciﬁc purposes. The goal is to

simplify the wall geometry while preserving the gen-

eral shape and features of the building model.

We opt to simplify walls using a variant of

QEM (Garland and Heckbert, 1997). Since this mesh

is in the plane, only vertices incident to the model

boundary are considered for simpliﬁcation. The error

matrix Q

of each boundary vertex v is used to com-

pute the sum of squared displacement error from each

adjoining line along the boundary polygon. Since er-

ror is measured via distance away from a line in 2D,

each Q

has size 3 × 3, and is deﬁned as:

∑

l∈lines(v)

(1)

where E

is deﬁned from the line equation ax +

by + c = 0, with a

+ b

= 1:





ab ac

ab b

ac bc c





(2)

The simpliﬁcation of the boundary proceeds in a

similar manner to QEM, but if a wall vertex v is con-

tained in multiple rooms or if it is connected by an

edge to a vertex that is contained in multiple rooms,

then it is not simpliﬁed. This constraint is used to

preserve the ﬁne details of doorways between rooms,

while freely simplifying walls that are fully contained

within one room. Wall edges are iteratively simpliﬁed

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData

Figure 5: Example of creating a 3D extruded mesh from 2D wall samples: (a) walls of generated ﬂoor plan with estimated

height ranges; (b) ﬂoor and ceiling heights are grouped by room; (c) simpliﬁcation performed on walls; (d) ﬂoor and ceiling

triangles added to create a watertight mesh.

until no simpliﬁcation produces error of less than the

original wall sampling resolution, r. Thus, walls are

simpliﬁed while preserving any geometry features of

the building interior.

Since we are interested in preserving the 2D tri-

angulation T of the building model, in addition to the

boundary polygon, every edge simpliﬁcation is per-

formed by collapsing an interior triangle. This com-

putation simpliﬁes the boundary polygon of the model

while still preserving the room labeling of the model’s

volume. These triangle collapses do not preserve the

Delaunay property of the triangulation, but do pre-

serve the boundaries between room volumes, which

is more desirable in the output.

6 HEIGHT EXTRUSION

As mentioned in Section 3.1, each input wall sam-

ple also references the vertical extent for the observed

scans at that location. This information can be used

to convert the labeled 2D interior building model to

a 2.5D extruded model, by using the minimum and

maximum height values for each scan as an estimate

of the ﬂoor and ceiling heights, respectively.

Since these wall samples are collected using 2D

planar scanners in an environment containing clut-

ter, the minimum and maximum heights associated

with each point are noisy. Figure 5a shows an ex-

ample room with these initial heights. To produce

aesthetically-pleasing models, each room uses a sin-

gle ﬂoor height and a single ceiling height. This as-

sumption is reasonable since the goal of this process-

ing is to produce a simpliﬁed building mesh. This step

demonstrates the utility of room labeling to modeling.

The height range for each room is computed from the

median ﬂoor and ceiling height values of that room’s

vertices. An example is shown in Figure 5b and the

corresponding result from the simpliﬁcation process

from Section 5 is demonstrated in Figure 5c.

The 2D triangulation of a room is then used to cre-

ate the ﬂoor and ceiling mesh for that room, with the

boundary edges of the triangulation extruded to cre-

ate rectangular vertical wall segments. The result is a

watertight 3D mesh of the building, capturing the per-

manent geometry in an efﬁcient number of triangles.

Figure 5d shows an example of this watertight ex-

truded geometry, including the effects of wall bound-

ary simpliﬁcation on the resulting extruded mesh.

7 RESULTS

Our approach works well on a variety of test cases,

spanning several model types including ofﬁces, ho-

tels, and university buildings. For the largest mod-

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

(a) (b)

Figure 7: Ofﬁce building: (a) Input represented by 12,823 wall samples; (b) generates ﬂoor plan with 19 rooms. Extruded 3D

mesh represented with 6,084 triangles. Total processing time required is 7.5 seconds.

(a) (b)

Figure 8: Apartment complex ofﬁce: (a) Input represented by 3,462 wall samples; (b) generates ﬂoor plan with 5 rooms.

Extruded 3D mesh represented with 512 triangles. Total processing time required is 1.2 seconds.

(a)

(b)

Figure 6: Comparison of models from (a) our approach with

(b) existing approach (Turner and Zakhor, 2013).

els, total processing time to compute an extruded 3D

model from 2D wall samples is under 10 seconds.

Most of this time is spent on carving interior trian-

gles, which can be performed real-time in a streaming

manner during data acquisition, which typically lasts

several minutes.

Our 2.5D approach produces simpliﬁed models

when compared to surface reconstruction techniques

that preserve ﬁne detail with more complex output.

Speciﬁcally, our method omits interior clutter such

as furniture since it uses wall samples as input. Fig-

ure 6 compares the models resulting from our 2.5D

method with that of an existing 3D building model-

ing technique (Turner and Zakhor, 2013) for the hotel

hallways shown in Figure 1. The two methods result

in 2,944 triangles and 4.1 millions triangles, respec-

tively.

Next, we show sample models resulting from our

proposed method in ﬁve different environments. For

all the models shown in Figures 7 through 11, the

scale is in units of meters, and the resolution is 5

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData

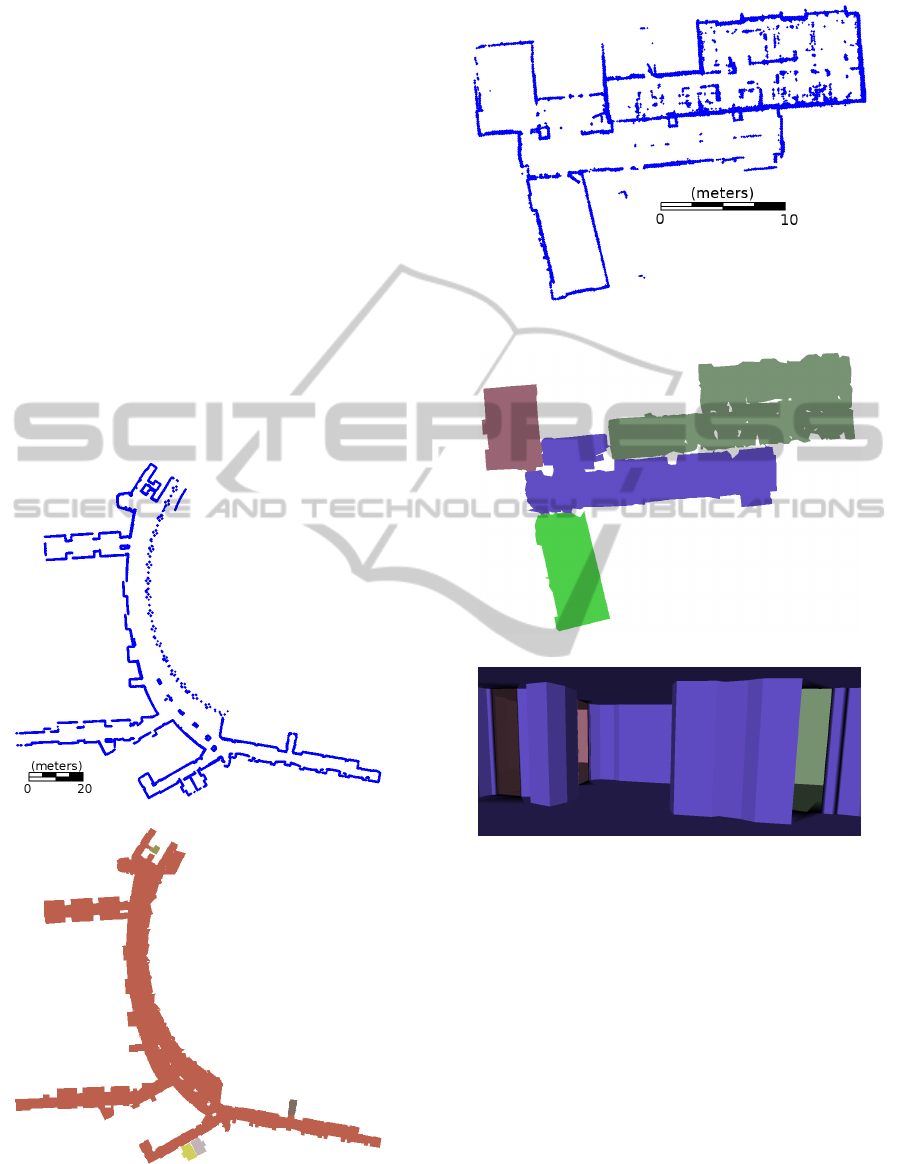
cm. Figure 7 corresponds to an ofﬁce building, in-

cluding cubicles and individual ofﬁces. The largest

room in this model, shown in teal, primarily contains

cubicles. The cubicle walls do not meet our height

threshold of H = 2 meters, so they are not captured

by the wall samples. Since cubicles are not an ar-

chitectural feature of the environment, this effect is

desirable. The room shown in purple in the lower-

left corner of this model also shows an example error

in the building reconstruction. The adjacent room to

the right was brieﬂy seen through a window, but its

area was considered part of this purple room rather

than being removed in the manner described in Sec-

tion 4.3, resulting in a small extrusion remaining in

the model. Figure 8 shows a small test model of an

apartment ofﬁce complex and Figure 9 denotes a ho-

tel lobby, hallways, and side rooms. The vast majority

of this model is labeled as one room, consisting of the

(a)

(b)

Figure 9: Hotel lobby and hallways: (a) Input represented

by 33,582 wall samples; (b) generates ﬂoor plan with 5

rooms. Extruded 3D mesh represented with 5,012 triangles.

Total processing time required is 8.5 seconds.

(a)

(b)

(c)

Figure 10: University ofﬁce area: (a) Input represented by

12,183 wall samples; (b) generates ﬂoor plan with 4 rooms;

tal processing time required is 7 seconds.

hallways of the building. Since no part of these hall-

ways are separated by doors, this result is desirable.

This model is also the largest example output, cover-

ing over 260 meters of hallways. An interior of the

3D extruded model for this dataset is shown in Fig-

ure 6a. Figure 10 represents an academic research

lab, including conference rooms and student cubicles.

The upper portion of the center room, shown in blue,

is a kitchenette area, with a counter-top. Since the

counter was not sufﬁciently captured by the wall sam-

ples, it is not represented in the 2.5D extrusion of the

model. Figure 11 shows the hallways of an academic

building.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

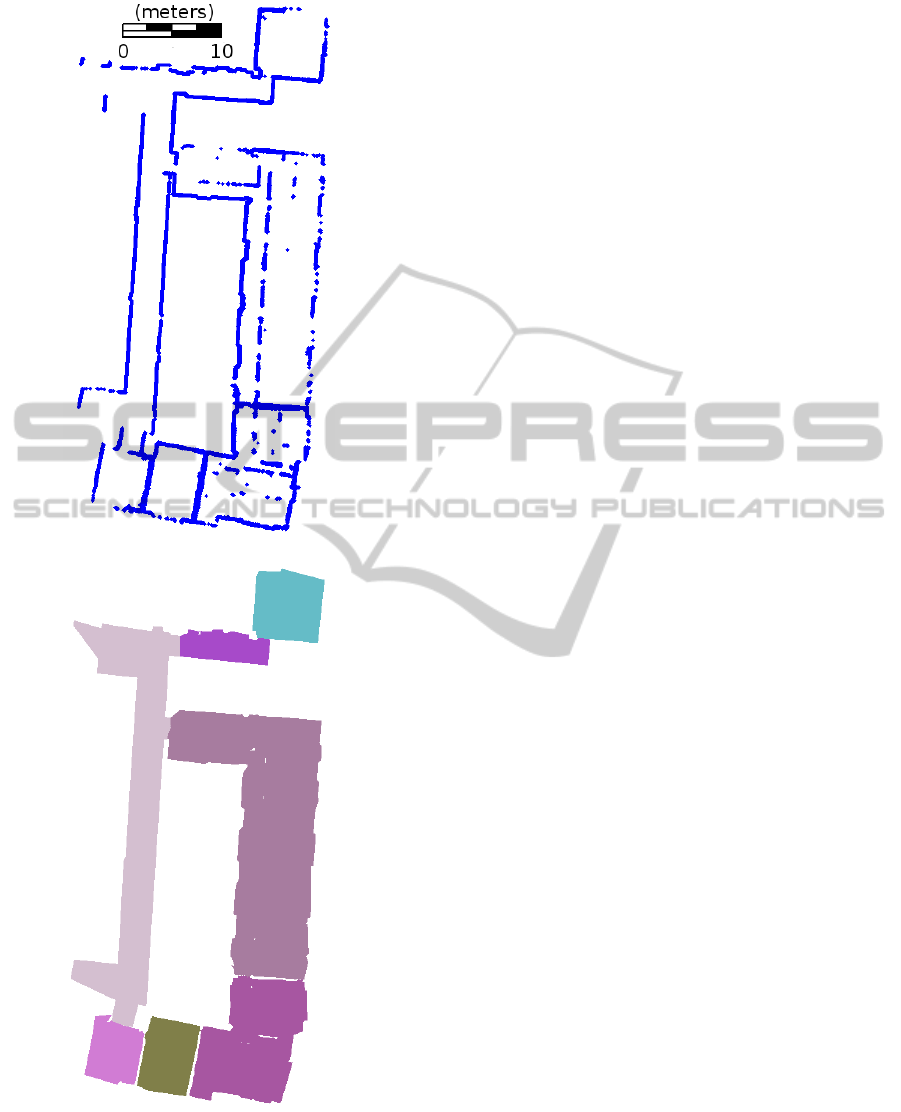
(a)

(b)

Figure 11: University ofﬁce building: (a) Input represented

by 12,125 wall samples; (b) generates ﬂoor plan with 7

rooms. Extruded 3D mesh represented with 3,604 triangles.

Total processing time required is 4.5 seconds.

Since these models were generated with a sys-

tem that captures imagery in addition to laser range

points, these models can also be texture-mapped with

the scenery of the environment (Cheng et al., 2013).

Figure 12 depicts the hallways of an academic build-

ing with and without texturing.

8 CONCLUSIONS

We demonstrate an efﬁcient approach to automati-

cally generate ﬂoor plans of building interiors at real-

time speeds. Classifying and labeling the rooms

within each generated ﬂoor plan allows for simpliﬁ-

cation schemes that can preserve ﬁne details at door-

ways. These room labels allow for accurate 2.5D ex-

trusion from noisy ﬂoor and ceiling height estimates

of the input points. The resulting model is suitable

for visualization, simulation, and navigation applica-

tions. Current limitations of this algorithm include the

verticality assumption made about observed building

features. If the horizontal cross-section of an environ-

ment changes dramatically between different heights,

the modeling techniques presented in this paper does

not accurately portray the actual geometry. Such lim-

itations could be overcome by observing more infor-

mation about each wall sample than just (x, y) posi-

tion and height ranges. If 3D normal estimates could

be made about surfaces, this information may allow

better ﬁltering of outlier wall samples, or to infer

building geometry that was poorly scanned.

REFERENCES

(1990). Americans with Disabilities Act. U.S. Architectural

and Transportation Barriers Compliance Board, 1331

F Street N.W. Suite 1000 Washington D.C. 20004-

1111. ANSI A117.1-1980.

Adan, A. and Huber, D. (2011). 3d reconstruction of inte-

rior wall surfaces under occlusion and clutter. Interna-

tional Conference on 3D Imaging, Modeling, Process-

ing, Visualization and Transmission, pages 275–281.

Brunskill, E., Kollar, T., and Roy, N. (2007). Topologi-

cal mapping using spectral clustering and classiﬁca-

tion. International Conference on Intelligent Robots

and Systems, pages 2491–3496.

Chauve, A.-L., Labatut, P., and Pons, J.-P. (2010). Ro-

bost piecewise-planar 3d reconstruction and comple-

tion from large-scale unstructured point data. CVPR.

Chen, G., Kua, J., Shum, S., Naikal, N., Carlberg, M., and

Zakhor, A. (2010). Indoor localization algorithms for

a human-operated backpack system. 3D Data Pro-

cessing, Visualization, and Transmission.

Cheng, P., Anderson, M., He, S., and Zakhor, A. (2013).

Texture mapping 3d planar models of indoor envi-

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData

(a)

(b)

Figure 12: Interior view of 3D extruded reconstructed model: (a) without and (b) with texture-mapping (Cheng et al., 2013).

ronments with noisy camera poses. SPIE Electronic

Imaging Conference.

Crawley, B. B., Kawrie, L. K., Pedersen, C. O., and Winkel-

mann, F. C. (2000). Energyplus: Energy simulation

program. ASHRAE, 42(4):49–56.

Fallon, M. F., Johannsson, H., Brookshire, J., Teller, S.,

and Leonard, J. J. (2012). Sensor fusion for ﬂexible

human-portable building-scale mapping. Intelligence

Robots and Systems, pages 4405–4412.

Funkhouser, T. A., Sequin, C. H., and Teller, S. J. (1992).

Management of large amounts of data in interactive

building walkthroughs. Proceedings of the 1992 Sym-

posium on Interactive 3D Graphics, pages 11–21.

Garland, M. and Heckbert, P. S. (1997). Surface simpliﬁca-

tion using quadric error metrics. SIGGRAPH, pages

209–216.

Grisetti, G., Stachniss, C., and Burgard, W. (2005). Im-

proving grid-based slam with rao-blackwellized parti-

cle ﬁlters by adaptive proposals and selective resam-

pling. Proceedings of IEEE International Conference

of Robotics and Automation, pages 2443–2448.

Grisetti, G., Stachniss, C., and Burgard, W. (2007).

Improved techniques for grid mapping with rao-

blackwellized particle ﬁlters. IEEE Transactions on

Robotics, 23(1):34–46.

Hahnel, D., Gurgard, W., Fox, D., and Thrun, S. (2003).

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

An efﬁcient fastslam algorithm for generating maps of

large-scale cyclic environments from raw laser range

measurements. International Conference on Intelli-

gent Robots and Systems, 1:206–211.

Holenstein, C., Zlot, R., and Bosse, M. (2011). Water-

tight surface reconstruction of caves from 3d laser

data. IEEE/RSJ International Conference on Intelli-

gent Robots and Systems.

Kua, J., Corso, N., and Zakhor, A. (2012). Automatic loop

closure detection using multiple cameras for 3d indoor

localization. IS&T/SPIE Electronic Imaging.

Lewis, R. and Sequin, C. (1998). Generation of 3d building

models from 2d architectural plans. Computer-Aided

Design, 30(10):765–779.

Okorn, B., Xiong, X., Akinci, B., and Huber, D. (2009).

Toward automated modeling of ﬂoor plans. 3DPVT.

Or, S.-H., Wong, K.-H., kin Yu, Y., and yuan Chang, M. M.

(2005). Highly automatic approach to architectural

ﬂoorplan image understanding and model generation.

Pattern Recognition.

Shen, S., Michael, N., and Kumar, V. (2011). Autonomous

multi-ﬂoor indoor navigation with a computationally

constrained mav. IEEE International Conference on

Robotics and Automation, pages 20–25.

Smith, M., Posner, I., and Newman, P. (2011). Adaptive

compression for 3d laser data. The International Jour-

nal of Robotics Research, 30(7):914–935.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

Robotics. The MIT Press.

Turner, E. and Zakhor, A. (2012). Watertight as-built archi-

tectural ﬂoor plans generated from laser range data.

3DimPVT.

Turner, E. and Zakhor, A. (2013). Watertight planar sur-

face meshing of indoor point-clouds with voxel carv-

ing. 3DV 2013.

Xiao, J. and Furukawa, Y. (2012). Reconstructing the

world’s museums. EECV 2012 Lectures in Computer

Science, 7572:668–681.

FloorPlanGenerationandRoomLabelingofIndoorEnvironmentsfromLaserRangeData