Haptic Rendering using Support Plane Mappings
Konstantinos Moustakas
Electrical and Computer Engineering Department, University of Patras, Rio-Patras, Greece
Keywords:
Haptic rendering, Collision detection, Implicit representation, Support plane mapping.
Abstract:
This paper presents a haptic rendering scheme based on distance maps over implicit surfaces. Using the
successful concept of support planes and mappings, a support plane mapping formulation is used so as to gen-
erate a convex conservative representation and efficiently perform collision detection. The proposed scheme
enables, under specific assumptions, the analytical reconstruction of the rigid 3D object’s surface, using the
equations of the support planes and their respective distance map. As a direct consequence, the problem of
calculating the force feedback can be analytically solved using only information about the 3D object’s spatial
trasnformation and position of the haptic probe. Moreover, several haptic effects are derived by the pro-
posed mesh-free haptic rendering formulation. Experimental evaluation and computational complexity analy-
sis demonstrates that the proposed approach can reduce significantly the computational cost when compared
to existing methods.
1 INTRODUCTION
Human perception combines information of various
sensors, including visual, aural, haptic, olfactory, etc.,
in order to perceive the environment. Virtual real-
ity applications aim to immerse the user into a vir-
tual environment by providing artificial input to its
interaction sensors (i.e., eyes, ears, hands, etc.). The
visual and aural inputs are the most important fac-
tors in human-computer interaction (HCI). However,
virtual reality applications will remain far from be-
ing realistic without providing to the user the sense
of touch. The use of haptics augments the standard
audiovisual HCI by offering to the user an alternative
way of interaction with the virtual environment (Bur-
dea and Coiffet, 2003). However, haptic interaction
involves complex and computationally intensive pro-
cesses, like collision detection or distance calculation
[5], that place significant barriers in the generation of
accurate and high fidelity force feedback.
1.1 Related Work
Seen from a computational perspective, haptic render-
ing can be decomposed in two different but heavily
interrelated processes, namely collision detection and
force calculation. Initially, collisions have to be iden-
tified and localized and then the resulting force feed-
back has to be estimated so as to accurately render the
force that will be fed back to the user using specific
assumptions on the physical model involved.
Concerning collision detection, most approaches
presented in the past are based on building a Bound-
ing Volume Hierarchy (BVH) around the object con-
sisting of primitive objects like spheres (Hubbard,
1996), OBBs (Gottschalk et al., 1996) or volumes
based on complex dynamically transforming geome-
tries k-DOPs (Klosowski et al., 1998). The hierar-
chy of the processed mesh is built, based on topolog-
ical criteria. The root of the tree built, contains the
entire object, while the leafs just contain single tri-
angles. Different algorithms for building this hierar-
chy have been proposed in the past (Gottschalk et al.,
1996; van den Bergen, 1997). In these methods, if
intersection is detected between the BV of the root
and an object, the algorithm checks for intersection
between the child nodes of the tree and the object and
so on, until the leaf nodes are reached and the accurate
points of a potential collision are found.
The intersection tests between BVs are based
on the Separating Axis Theorem for convex objects
(Gottschalk et al., 1996), (Coming and Staadt, 2008).
The theorem states that for a pair of disjoint convex
objects there exists an axis, such that the projections
of the objects on this axis do not overlap. Intersec-
tion tests for BVs exploit this theorem by testing the
existence of a Separating Axis in a set of candidate
axes. The basic difference among different types of
445
Moustakas K..
Haptic Rendering using Support Plane Mappings.
DOI: 10.5220/0004680604450452
In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 445-452
ISBN: 978-989-758-002-4
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

BVs is the number of axes needed to be tested. There
is a trade-off between the bounding efficiency and the
computational cost of the intersection test. BVs with
low efficiency, such as spheres, can be tested very fast
for intersection while more efficient bounding vol-
umes, such as the OBBs, require much more com-
putation.
Despite the accuracy of these methods, which are
extensively used in the literature, the computational
cost of performing the intersection tests between the
objects is very high, especially when these consist of
a large number of triangles or when they participate in
multiple simultaneous collisions. Recently, methods
for collision detection based on distance fields were
introduced (Osher and Fedkiw, 2002; Fuhrmann et al.,
2003; Teschner et al., 2004), which decrease the com-
putational cost dramatically. These methods require,
at a preprocessing stage, to generate distance fields for
the objects, which are stored in arrays. In particular, a
bounding box is assumed for each object. A 3D grid
is defined inside each box and a distance value is as-
signed to every point of the grid, which indicates the
distance of the specific point from the mesh. Nega-
tive values indicate that the point lies inside the mesh.
These distance values are usually obtained using level
set (Osher and Sethian, 1988) and fast marching algo-
rithms (Sethian et al., 1999).
Concerning haptic rendering research can be di-
vided into three main categories (Lin and Otaduy,
2008): Machine Haptics, Human Haptics and Com-
puter Haptics (Srinivasan and Basdogan, 1997). Ma-
chine Haptics is related to the design of haptic de-
vices and interfaces, while Human Haptics is devoted
to the study of the human perceptual abilities related
to the sense of touch. Computer Haptics, or alterna-
tively haptic rendering, studies the artificial genera-
tion and rendering of haptic stimuli for the human
user. It should be mentioned that the proposed frame-
work takes into account recent research on human
haptics, while it provides mathematical tools target-
ing mainly the area of computer haptics.
The simplest haptic rendering approaches focus
on the interaction with the virtual environment us-
ing a single point. Many approaches have been pro-
posed so far both for polygonal, non-polygonal mod-
els, or even for the artificial generation of surface ef-
fects like stiffness, texture or friction, (Laycock and
Day, 2007). The assumption, however, of a single
interaction point limits the realism of haptic inter-
action since it is contradictory to the rendering of
more complex effects like torque. On contrary, mul-
tipoint, or object based haptic rendering approaches
use a particular virtual object to interact with the en-
vironment and therefore, besides the position of the
object, its orientation becomes critical for the render-
ing of torques. Apart from techniques for polygonal
and non-polygonal models (Laycock and Day, 2007),
voxel based approaches for haptic rendering (Peter-
sik et al., 2001) including volumetric haptic rendering
schemes (Palmerius et al., 2008) have lately emerged.
Additionally, research has also tackled with partial
success the problem of haptic rendering of dynamic
systems like deformable models and fluids (Barbic
and James, 2009).
1.2 Motivation and Contribution
In general, with the exception of some approaches re-
lated to haptic rendering of distance or force fields
(Barlit and Harders, 2007), one of the biggest bot-
tlenecks of current schemes is that haptic rendering
depends on the fast and accurate resolution of colli-
sion queries. The proposed approach aims to widen
this bottleneck by providing a free-form implicit hap-
tic rendering scheme based on support plane map-
pings. In particular, a 3D object is initially modelled
using the associated support plane mappings (van den
Bergen, 2003). Then the distance of the object’s sur-
face from the support plane is mapped at discrete sam-
ples on the plane and stored at a preprocessing step.
During run-time and after collision queries are re-
solved, estimation of the force feedback can be an-
alytically estimated, while several haptic effects, like
friction, texture, etc. can be easily derived. This re-
sults in constant time haptic rendering based only on
the 3D transformation of the associated object and the
position of the haptic probe.
The rest of the paper os organized as follows. Sec-
tion 2 briefly describes the support plane mapping for-
mulation, concept and haptic rendering scheme. In
Section 3 several haptic effects are derived using the
proposed formulation, while in Section 4 the compu-
tational complexity and simulation results of the ap-
proach are analyzed. Finally, conclusions are drawn
in Section 5.
2 SUPPORT PLANE MAPPINGS
Support planes are a well studied subject of compu-
tational geometry and have been employed in algo-
rithms for the separation of convex objects (Dobkin
and Kirkpatrick, 1985; Chung and Wang, 1996;
van den Bergen, 2003). From a geometrical perspec-
tive, a support plane E of a 3D convex object O is a
plane such that O lies entirely on its negative half-
space H
−
E
. Support planes have become useful in
previous algorithms based on the concept of support
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
446

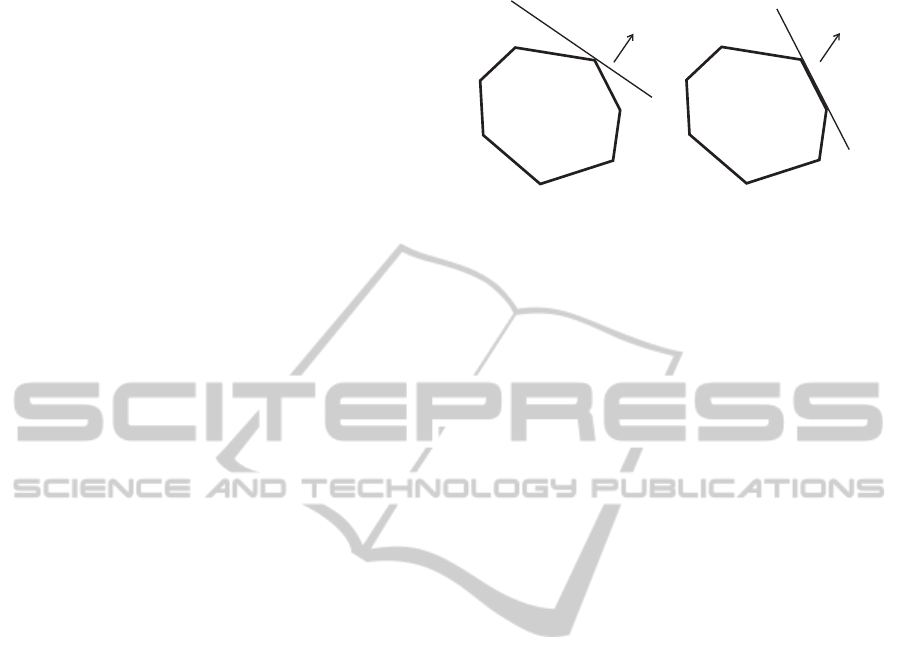
mappings. A support mapping is a function that maps
a vector v to the vertex of vert(O) of object O that is
“most” parallel to v (van den Bergen, 2003; Ericson,
2005). As a direct consequence, a support plane can
be defined as the plane that passes through s
O
(v), the
support mapping of v, and is parallel to v.
2.1 Collision Detection using SPMs
The importance of support planes is intuitively appar-
ent: they provide an explicit way of deciding whether
another object could possibly intersect with the one
that the support planes refers to. Based on this sim-
ple but important feature of support planes, a slightly
more generalized formulation can be derived intro-
ducing the concept of support plane mappings (Vo-
giannou et al., 2010) by the following definitions:
Definition 2.1. E is a Support Plane (SP) of the object
O if
1. x ∈ H
−
E
, ∀x ∈ O
2. E and O have at least one common point.
Definition 2.2. Let the object O and E
O
be a set
of Support Planes of O. A Support Plane Mapping
(SPM) of O is defined as
M
O
(v) = E ∈ E
O
: v · n
E
= max{v · n|n ∈ n
E
O
}
where n
E
denotes the normal of support plane E and
n
E
O
the set of all normals in E
O
.
The difference between the above definitions and
previous work is that the above definitions do not
make any assumption about the convexity of O or,
concerning only the SPM, about the set of Support
Planes E
O
. For example, a Support Plane Mapping
can be constructed using the infinite set of all sup-
port planes of object O and the support mapping s
O
.
This kind of SPM is referred as the Vertex-based SPM
(Figure 1-(a)) of O, since s
O
maps to vert(O). The
Vertex-based SPM is actually an alternative defini-
tion for generating support planes (Dobkin and Kirk-
patrick, 1985). Since there is no restriction on the
used set of Support Planes E
O
, another approach to
construct a SPM would be to use the set of support
planes that lie on at least one face of O. This kind of
mapping is referred as the Face-based SPM (Figure
1-(b)) of O. Note that both Vertex-based and Face-
based SPMs are uniquely defined for each object.
In practice we are mostly interested for having
enough support planes to surround the given object.
Therefore we define the fully bounding SPM of an
object O as a SPM such that the planes of the re-
spective E
O
form a finite sub-space G =
T
i
H
−
E
i
for
every E
i
∈ E
O
, that fully bounds O. This sub-space
O
E
v
HE
-
HE
+
(a)
HE
-
O
E
HE
+
v
(b)
Figure 1: Support Plane Mappings. In (a) the Support
Plane E is generated using a vertex-based mapping, i.e.
E = M
O
(v), and the normal is parallel to the direction of
the input vector v. In (b) E comes from a face-based map-
ping and it lies on a face of O.
G serves, implicitly, as a convex bounding represen-
tation of the object. Note that both Vertex-based and
Face-based SPMs are fully bounding SPMs. Based on
this formulation of support plane mappings, conser-
vative collision rejection can be performed following
the procedure described in (Vogiannou et al., 2010).
2.2 Scalar and Vectorial Haptic Support
Plane Maps
After collision is detected, the force feedback pro-
vided to the user through the haptic device has to be
calculated. In the present framework, force feedback
is obtained directly from the model adopted for col-
lision detection, thus handling collision detection and
haptic rendering in an integrated way, as described in
the sequel.
Let the parametric form of the support plane equa-
tion S
SP
(η, ω) be:
S
SP
(η, ω) =


x
0
+ ηu
1
+ ωv
1
y
0
+ ηu
2
+ ωv
2
z
0
+ ηu
3
+ ωv
3


, ∀η,ω ∈ ℜ (1)
where u and v constitute an orthonormal basis of the
support plane and (x
0
, y
0
, z
0
) its origin.
Assuming now a dense discretization of the η, ω
space, we can define a discrete distance map of the
support plane SP and the underlying manifold mesh
surface S
mesh
, by calculating the distance of each point
of SP from S
mesh
:
D
SP
(η, ω) = ICD(S
SP
, S
mesh
) (2)
where ICD calculates the distance of every point sam-
ple (η, ω) of the support plane SP, alongside the nor-
mal direction at point (η, ω), from the mesh S
mesh
and
assigns the corresponding values to the distance map
HapticRenderingusingSupportPlaneMappings
447

D
SP
(η, ω). The distance map is used in the sequel to
analytically estimate the force feedback.
It should be mentioned that the above procedure
results in scalar distance maps that accurately encode
the surface if and only if there is a one to one mapping
of all surface parts with at least one support plane. If
such a mapping does not exist, then vectorial distance
maps can be used that include information about the
distance of all sections of the ray cast in the normal
direction of the support plane to the object mesh as
illustrated in Figure 2.
Figure 2: Vectorial distance maps.
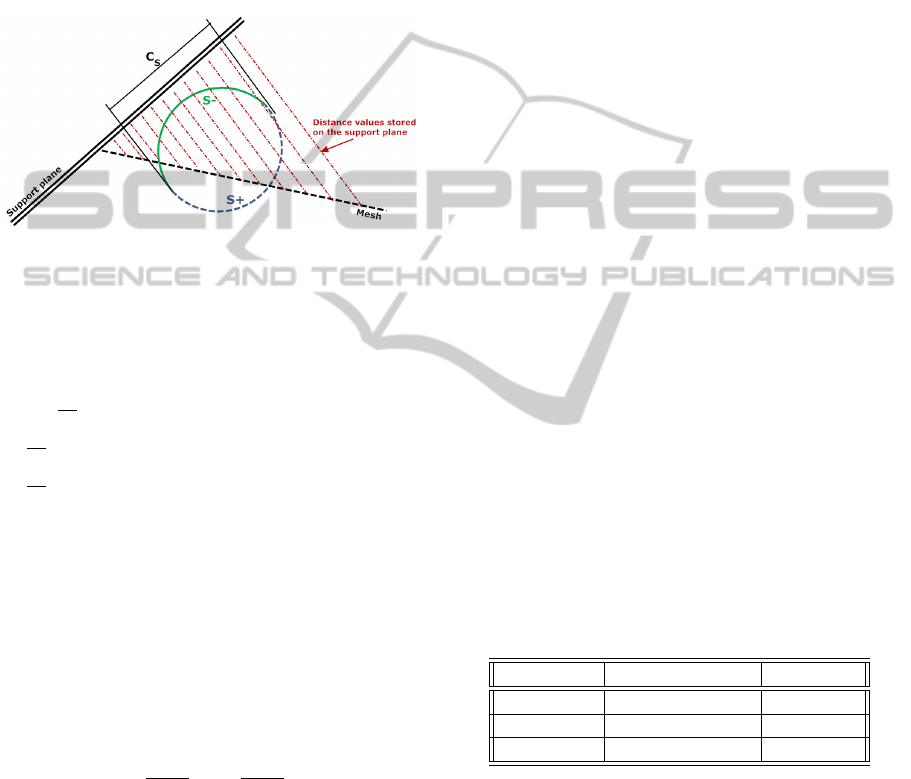
2.3 Haptic Rendering using SPMs
Referring to Figure 3, let point H
p
be the position of
the haptic probe and S
mesh
represent the local surface
of the object.
Figure 3: Distance calculation using distance maps over
support planes.
Let also S
SP
represent the distance of point H
p
from the support plane, which corresponds to point
P
M
on the SP. If collision is detected, the absolute
value of the force fed onto the haptic device is ob-
tained using a spring model as illustrated in Figure 3.
In particular:
k
F
k
= k ·
|
S
SP
− D
SP
(P
M
)
|
(3)
where k is the spring constant. D
SP
(P
M
) is the dis-
tance of point P
M
from the mesh and is stored in
the distance map of the support plane. Notice that
the term
|
S
SP
− D
SP
(P
M
)
|
is an approximation of the
actual distance of H
p
from the mesh that becomes
more accurate if the support plane surface approxi-
mates well the mesh.
The direction of the force should in general be
perpendicular to the local area, where collision is de-
tected. An obvious solution to the evaluation of the di-
rection of this force would be to detect the surface el-
ement (i.e. triangle), where the collision occurred and
to provide the feedback perpendicularly to it. This
approach is not only computationally intensive, but
also results in non-realistic non-continuous forces at
the surface element boundaries. In the present frame-
work the analytical approximation of the mesh sur-
face is used utilizing the already obtained SP approx-
imation and the distance map. Based on this approx-
imation the normal to the object’s surface can be ap-
proximated rapidly with high accuracy. In particular,
if D
SP
(η, ω) is the scalar function of the distance map
on the support plane, as previously described, the sur-
face S
mesh
of the modelled object can be approximated
by equation (4) (Figure 3):
S
mesh
(η, ω) = S
SP
(η, ω)− D
SP
(η, ω)n
SP
(4)
where S
SP
is the surface of the support plane, D
SP
the
associated distance map and n
SP
its normal vector that
can be easily evaluated through n
SP
= u × v.
Now the calculation of the force feedback de-
mands the evaluation of the normal vector n
S
on the
object’s surface. that is obtained through equation (5).
In the following the brackets (η, ω) will be omitted
for the sake of simplicity.
n
S
=
∂S
mesh
∂η
×
∂S
mesh
∂ω
(5)
where
∂S
mesh
∂η
=
∂S
SP
∂η
−
∂D
SP
∂η
n
SP
− D
SP
∂n
SP
∂η
(6)
Since n
SP
is constant over SP, equation (6) becomes:
∂S
mesh
∂η
= u −
∂D
SP
∂η
n
SP
(7)
A similar formula can be extracted for
∂S
mesh
∂ω
:
∂S
mesh
∂ω
= v −
∂D
SP
∂ω
n
SP
(8)
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
448

All above terms can be computed analytically, except
from
∂D
SP
∂η
and
∂D
SP
∂ω
that are computed numerically.
Substituting now equations (4), (6), (7), (8) in
equation (5) the normal direction n
S
can be obtained.
Since, the direction of the normal along the sur-
face of the modelled object is obtained using equation
(5), the resulting force feedback is calculated through:
F
h
= k
|
S
SP
− D
SP
(P
M
)
|
n
S
k
n
S
k
(9)
3 HAPTIC EFFECTS
The analytical estimation of the force feedback based
only on the object 3D transformation, the probe posi-
tion and the distance maps, provides the opportunity
to develop closed form solutions for the rendering of
physics-based or symbolic force effects; the follow-
ing sections indicatively describe some of them.
3.1 Force Smoothing
By applying a local smoothing operation to the dis-
tance map, the resulting force feedback is smooth
in the areas around the edges, without being over-
rounded as is the case with the force shading method
(Ruspini et al., 1997). A typical example of distance
map preprocessing so as to achieve force smoothing
using a Gaussian kernel is given by the following
equation:
D
0
SP
(η, ω) = D
SP
(η, ω)∗ G
σ
(η, ω) (10)
where G
σ
is a 2D Gaussian kernel and “∗” denotes
convolution. It is evident that different smoothing
operators can be easily applied. A very useful op-
erator that can be implemented is the force smooth-
ing only in areas that are not smooth due to the fi-
nite tessellation (sampling) and not in object and sur-
face boundaries, following the popular in computer
graphics “crease angle” concept. A haptic “crease
angle” rendering can be easily performed by apply-
ing anisotropic diffusion or even an edge-preserving
smoothing operator on the distance map.
3.2 Friction and Damping
The force calculated from equation (9) is always per-
pendicular to the object’s surface. If no friction com-
ponent is added, the resulting force feedback will be
like touching a very slippery surface. In order to avoid
this defect, a friction component is added to the force
of equation (9). In particular:
F
f riction
= − f
C
· (1 + k
f
|
S
SP
− D
SP
(P
M
)
|
) ·
n
f


n
f


(11)
where f
c
is the friction coefficient and n
f
the direc-
tion of the motion of the processed point, i.e. n
f
=
P
t
− P
t−∆t
, where P
t
is the current position of the
processed point and P
t−∆t
its position at the previ-
ous frame. Term k
f
|
S
SP
− D
SP
(P
M
)
|
is used in order
to increase the magnitude of the friction force when
the penetration depth of the processed point increases.
The variables S
SP
and D
SP
(P
M
) are defined in equa-
tion (3), while factor k
f
controls the contribution of
the penetration depth to the calculated friction force.
In a similar sense, damping can be considered by
including the term F
damping
= −k
d
·
˙
P
M
in the force
feedback formula.
Finally, the force fed onto the haptic device yields
from the addition of the reaction, the friction and the
damping force:
F
haptic
= F
reaction
+ F
f riction
+ F
damping
(12)
3.3 Texture
Similarly using the proposed framework for haptic
rendering, haptic texture can be also simulated eas-
ily by applying appropriate transformations on the
acquired distance map. An example for simulating
surface roughness is provided below, where Gaussian
noise is added on the distance map. No computational
cost is added, since the procedures for calculating the
force direction are not altered due to the existence of
haptic texture. The only difference lies in the evalu-
ation of the magnitude of F
texture
, which now yields
from:
F
texture
= k
|
S
SP
− (D
SP
(P
M
) + n
g
)
|
n
S
k
n
S
k
(13)
where n
g
denotes the gaussian noise.
3.4 Non-infinite-small Haptic
For the case of an infinite-small interaction point, then
the aforementioned equations can be directly applied.
However, in practise, for the haptic proxy a rigid body
is considered, not only for performing 6DoF haptic
rendering, but also for 3DoF force feedback estima-
tion, so as to allow for noise-less (small force discon-
tinuities) interaction by averaging the forces applied
by the mesh to the proxy. A typical proxy object is the
sphere. An analysis on how to directly use a spheri-
cal probe with the proposed framework is described
HapticRenderingusingSupportPlaneMappings
449

in the sequel. It should be emphasized that the analy-
sis could be potentially generalized for any object that
can be represented in an implicit form.
Referring to Figure 4 that for simplicity depicts
the 2D case, let C
S
denote the support set of the pro-
jection of the sphere on the support plane. Moreover,
let S
+
and S
−
denote the surface of the sphere that is
further and closer to the support plane than the sphere
center respectively.
Figure 4: Distance calculation using distance maps over
support planes.
Then the force feedback that is due to S
+
can be
estimated from the following formula:
F
S
+
=
1
N
+
R
S∈C
S
k · max

S
+
(η, ω) − S
SP
(η, ω) , 0

· n
S
dS
=
1
N
+
R R
η,ω∈C
S
k · max

S
+
(η, ω) − S
SP
(η, ω) , 0

· n
S
dηdω
=
1
N
+
∑ ∑
η,ω∈C
S
k · max

S
+
(η, ω) − S
SP
(η, ω) , 0

· n
S
(14)
where N
+
is the number of the (η, ω) points
on the distance map that satisfy the relation
S
+
(η, ω) > S
SP
(η, ω), are thus contributing to the es-
timation of the force feedback.
An identical derivation can be formulated for F
S
−
that estimates the force due to the surface S
−
of
the sphere. The final force can be easily obtained
through:
F =
N
+
N
total
F
+
+
N
−
N
total
F
−
(15)
The careful reader would notice that using the
above approach only the surface of the sphere con-
tributes to the estimation of the force feedback. A
similar equation, using the sphere volume that is col-
liding with the object, for the estimation of the force
feedback, can be easily derived by using a formula-
tion similar to the one of equation (14) and a triple
integral adding one more dimension along the normal
direction of the support plane.
4 COMPLEXITY AND
EXPERIMENTAL RESULTS
In the following an analysis of the computational
complexity of the proposed scheme in comparison to
the typical state-of-the-art mesh-based haptic render-
ing scheme is discussed.
Moreover, even if an experimental analysis of the
proposed support plane mapping based haptic ren-
dering approach, in terms of timings for simulation
benchmarks would not be fair for the state-of-the-art
approaches, since it would encode the superiority of
SPM based collision detection and would not directly
highlight the proposed haptic rendering approach, two
experiments are presented where the proposed hap-
tic rendering scheme is compared to the state-of-the-
art mesh-based haptic rendering in terms of timings
in computationally intensive surface sliding experi-
ments.
4.1 Computational Complexity
After collision is reported, a typical force feedback
calculation scheme would need to identify the collid-
ing triangle of the involved 3D object in O(n) time,
where n is the number of triangles, or in O(logn) time
if bounding volume hierarchies are used. Then the
force can be calculated in constant O(1) time. In or-
der to avoid force discontinuities, for example force
shading, and if there is no adjacency information then
the local neighbourhood of the colliding triangle can
be found again in O(n) time, where n is the number
of triangles, or in O(logn) time if bounding volume
hierarchies are used. Finally, the mesh-based haptic
rendering scheme has no additional memory require-
ments per se.
Table 1: Computational complexity comparison.
Process Mesh-based Free-form
Force O(n) or O(logn) O(1)
Smoothing O(n) or O(logn) O(1)
Memory - O(m · s)
On the other hand, concerning the proposed free-
form implicit haptic rendering scheme, after a col-
lision is detected, the resulting force feedback can
be calculated in constant time O(1) using equation
(9). In order to avoid depth discontinuities the dis-
tance map can be smoothed, in an image processing
sense, at a preprocessing phase. Even if this step is
performed during run-time it would take O(k) time,
where k is the local smoothing region or the filter-
ing kernel window. On the other hand the proposed
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
450

scheme has O(m · s) memory requirements, where m
is the number of support planes and s the number of
samples per support plane. Taking now into account
that the more support planes are used the smaller their
size and the less samples are necessary for a spe-
cific sampling density we can safely assume that the
memory requirements are linear to the total number of
samples that depends on the sampling density used.
Table 1 summarizes the computational complexity
analysis of the proposed free-form haptic rendering
scheme, when compared to the mesh-based approach.
4.2 Experimental Results
Concerning the quantitative results, interaction with
two objects was considered, namely the Galeon and
Teeth models of 4698 and 23000 triangles respec-
tively. The objects are illustrated in Figure 5 and
Figure 6 respectively. Moreover, CHAI-3D was used
for interfacing with the haptic devices (Conti et al.,
2005).
Figure 5: Galeon model, 4698 triangles.
Figure 6: Teeth model, 23000 triangles.
Moreover, the force estimation algorithms were
applied on a predefined trajectory of the haptic probe,
so as to assure fair comparison. In particular, initially
the trajectory of the haptic probe in the 3D space has
been recorded while being in sliding motion over the
objects’ surface. Then this trajectory has been used as
input for both algorithms so as to extract the timings
mentioned below.
Table 2 and Table 3 present the mean timings
and their standard deviation of the force estimation
throughout the simulation using the mesh-based,and
the proposed free-form haptic rendering scheme for
the case of the Galeon and the Teeth models respec-
tively.
Table 2: Galeon model: Interaction timings.
Process Mean time (ms) σ
Mesh-based 1.2 0.22
Free-form 0.028 0.006
Table 3: Teeth model: Interaction timings.
Process Mean time (ms) σ
Mesh-based 4.2 0.82
Free-form 0.036 0.005
It should be emphasized that the above timings
need to be taken into account under the exact ex-
perimental setting. In particular, concerning the pro-
posed approach 1000 support planes were used for the
case of the Galeon and 1500 for the case of the Teeth
model. Distances are estimated for all support planes
and forces are calculated for the closer one. This pro-
cedure, could be optimized by partitioning the space
in a preprocessing step and knowing beforehand to
which support plane, each point in space “belongs
to”, thus reducing the search from O(n) to O(logn).
Moreover, concerning the mesh-based approach force
shading has been also implemented.
It is evident that the proposed scheme reduces sig-
nificantly the computational cost in the performed
simulations. This significant gain comes at an ex-
pense of two limitations. Firstly, special care has to
be taken at the preprocessing step so that the models
are well approximated using the support planes and
the distance maps. For example if the objects demon-
strate large complex concavities the use of vectorial
distance maps is inevitable. Secondly, the proposed
scheme cannot be, in its current form, directly ap-
plied to deformable models. An extension to piece-
wise or free-form deformable models, where defor-
mations can be analytically expressed seems possible
and remains a direction for future work.
5 CONCLUSIONS
The proposed approach introduces an implicit free-
form haptic rendering scheme of rigid bodies based
on distance maps over support plane mappings and
therefore exploits the superiority and bounding effi-
ciency of SPMs for collision detection and extends
it for direct closed-form haptic rendering. Moreover,
the derivation of analytical expressions of widely used
HapticRenderingusingSupportPlaneMappings
451

haptic effects becomes straightforward. The proposed
approach is seen to be highly efficient when compared
to the state-of-the-art mesh-based haptic rendering at
a cost, however, of increased memory requirements.
REFERENCES
Barbic, J. and James, D. (2009). Six-dof haptic rendering of
contact between geometrically complex reduced de-
formable models: Haptic demo. In In Proc. of Euro-
haptics, pages 393–394.
Barlit, A. and Harders, M. (2007). Gpu-based distance map
calculation for vector field haptic rendering. In Euro-
haptics, pages 589–590.
Burdea, G. and Coiffet, P. (2003). Virtual Reality Technol-
ogy. Wiley-IEEE Press, 2nd edition.
Chung, K. and Wang, W. (1996). Quick Collision Detec-
tion of Polytopes in Virtual Environments. In ACM
Symposium on Virtual Reality Software and Technol-
ogy 1996, pages 1–4.
Coming, D. and Staadt, O. (2008). Velocity-aligned dis-
crete oriented polytopes for dynamic collision detec-
tion. IEEE TVCG, 14(1):1–12.
Conti, F., Barbagli, K., Morris, D., and Sewell, C. (March,
2005). Chai 3d: An open-source library for the rapid
development of haptic scenes. In IEEE World Haptics,
Pisa, Italy.
Dobkin, D. P. and Kirkpatrick, D. G. (1985). A linear algo-
rithm for determining the separation of convex poly-
hedra. Journal of Algorithms, 6(3):381 – 392.
Ericson, C. (2005). Real-Time Collision Detection. The
Morgan Kaufmann Series in Interactive 3D Technol-
ogy. Morgan Kaufmann.
Frisken, S. F., Perry, R. N., Rockwood, A. P., and Jones,
T. R. (2000). Adaptively sampled distance fields: a
general representation of shape for computer graph-
ics. In Computer graphics and interactive techniques,
pages 249–254.
Fuhrmann, A., Sobottka, G., and Gross, C. (September
2003). Distance fields for rapid collision detection in
physically based modeling. In Proceedings of Graph-
iCon 2003, pages 58–65.
Gottschalk, S., Lin, M., and Manocha, D. (1996). OBB-
Tree: A Hierarchical Structure for Rapid Interference
Detection. In Computer Graphics, ACM SIGGRAPH,
pages 171–180.
Hubbard, P. (1996). Approximating Polyhedra with Spheres
for Time-Critical collision detection . ACM Transac-
tions on Graphics, 15(3):179–210.
Klosowski, J., Held, M., Mitchell, J., Sowizral, H., and
Zikan, K. (1998). Efficient Collision Detection us-
ing Bounding Volume Hierarchies of k-DOPs. IEEE
Transaction on Visualization and Computer Graphics,
4(1):21–36.
Laycock, S. and Day, A. (2007). A survey of haptic render-
ing techniques. Computer Graphics Forum, 26(1):50–
65.
Lin, M. and Otaduy, M. (2008). Haptic rendering: Foun-
dations, algorithms and applications. page A.K.Peters
publishing.
McNeely, W., Puterbaugh, K., and Troy, J. (1999). Six
degree-of-freedom haptic rendering using voxel sam-
pling. In Computer graphics and interactive tech-
niques, pages 401–408.
Osher, S. and Fedkiw, R. (2002). Level Set Methods and
Dynamic Implicit Surfaces. Springer-Verlag.
Osher, S. and Sethian, J. A. (1988). Fronts propagat-
ing with curvature-dependent speed: algorithms based
on hamilton-jacobi formulations. J. Comput. Phys.,
79(1):12–49.
Palmerius, K., Cooper, M., and Ynnerman, A. (2008).
Haptic rendering of dynamic volumetric data. IEEE
Transactions on Visualization and Computer Graph-
ics, 14(2):263–276.
Petersik, A., Pflesser, B., Tiede, U., and Hohne, K. (2001).
Haptic rendering of volumetric anatomic models at
sub-voxel resolution. In In Proc. of Eurohaptics,
Birmingham, UK, pages 182–184.
Ruspini, D., Kolarov, K., and Khatib, O. (1997). The haptic
display of complex graphical environments. In Com-
puter Graphics (SIGGRAPH 97 Conference Proceed-
ings), pages 345–352.
Sethian, J., Ciarlet, P., Iserles, A., Kohn, R., and Wright, M.
(1999). Level Set Methods and Fast Marching Meth-
ods : Evolving Interfaces in Computational Geome-
try, Fluid Mechanics, Computer Vision, and Materials
Science. Cambridge University Press.
Srinivasan, M. and Basdogan, C. (1997). Haptics in virtual
environments: Taxonomy, research status and chal-
lenges. Computers and Graphics, pages 393–404.
Tang, M., Curtis, S., Yoon, S.-E., and Manocha, D. (2008).
Interactive continuous collision detection between de-
formable models using connectivity-based culling. In
SPM 08: Proceedings of the 2008 ACM Symposium
on Solid and Physical Modeling, pages 25–36.
Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann,
G., Raghupathi, L., Fuhrmann, A., Cani, M.-P.,
Faure, F., Magnenat-Thalmann, N., Strasser, W., , and
Volino, P. (2004). Collision detection for deformable
objects. In Eurographics.
van den Bergen, G. (1997). Efficient Collision Detection
of Complex Deformable Models using AABB Trees.
Journal of Graphics Tools, 2(4):1–13.
van den Bergen, G. (2003). Collision Detection in Interac-
tive 3D Environments. The Morgan Kaufmann Series
in Interactive 3D Technology. Morgan Kaufmann.
Vogiannou, A., Moustakas, K., Tzovaras, D., and Strintzis,
M. (2010). Enhancing bounding volumes using sup-
port plane mappings for collision detection. Computer
Graphics Forum, 29(5):1595–1604.
Wald, I., Boulos, S., and Shirley, P. (2007). Ray tracing
deformable scenes using dynamic bounding volume
hierarchies. ACM Transactions on Graphics, 26(1).
Zhang, X., Redon, S., Lee, M., and Kim, Y. (2007). Con-
tinuous collision detection for articulated models us-
ing taylor models and temporal culling. ACM Trans.
Graph, 26(3).
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
452