Segmentation of Optic Disc in Retina Images using Texture

Suraya Mohammad

, D. T. Morris

and Neil Thacker

School of Computer Science, University of Manchester, Kilburn Building, Oxford Road, Manchester, U.K.

ISBE, Medical School, University of Manchester, Stop ford Building, Oxford Road, Manchester, U.K.

Keywords:

Optic Disc Segmentation, BRIEF, Texture.

Abstract:

The paper describes our work on the segmentation of the optic disc in retinal images. Our approach comprises

of two main steps; a pixel classiﬁcation method to identify pixels that may belong to the optic disc boundary

and a circular template matching method to estimate the circular approximation of the optic disc boundary.

The features used are based on texture, calculated using the intensity differences of local image patches. This

was adapted from Binary Robust Independent Elementary Features (BRIEF). BRIEF is inherently invariant

to image illumination and has a lower degree of computational complexity compared to other existing texture

measurement methods. Fuzzy C-Means (FCM) and Naive Bayes are the clustering and classiﬁer used to

cluster/classify the image pixels. The method was tested on a set of 196 images composed of 110 healthy

retina images and 86 glaucomatous images. The average mean overlap ratio between the true optic disc region

and segmented region is 0.81 for both FCM and Naive Bayes. Comparison with a method based on the Hough

Transform is also provided.

1 INTRODUCTION

The evaluation of retinal images is a diagnostic tool

widely used to gather important clinical information,

such as for diabetic retinopathy and glaucoma assess-

ment, due to its noninvasive nature. These diseases

are two of the main cause of visual impairment world-

wide (Congdon et al., 2003). Both are asymptomatic

in nature, therefore early detection is vital to prevent

complete visual loss. Segmentation of the optic disc

represents the starting point of many automatic com-

puter based methods used to assist the ophthalmolo-

gist in detecting these two diseases.

The Cup-to-Disc (CDR) ratio is commonly used

clinically to asses glaucoma progression. CDR is ob-

tained by measuring the ratio between the vertical di-

ameter of the optic disc cup and the optic disc rim. As

for diabetic retinopathy assessment, the identiﬁcation

of the optic disc is important to reduce misclassiﬁca-

tion in the automatic detection of other lesions.

Some of the difﬁculties experienced in the seg-

mentation of the optic disc may be appreciated by Fig-

ure 1 which shows an image of a healthy retina (Fig-

ure 1(a)) and a glaucomatous retina (Figure 1(b)). On

a healthy retina, the optic disc appears as bright and

yellowish, normally with a circular or slightly ellip-

tical shape. However these features and its size may

vary between images. The contrast around the optic

disc boundary is also not constant, normally brighter

(a) (b)

Figure 1: Healthy and glaucomatous retina images.

on the temporal side and less so on the nasal side.

In addition, part of the optic disc boundary may be

obscured by the outgoing blood vessels. Sometimes

there exist bright regions near the edge of the disc

caused by peripapillary atrophy (Figure 1(b)). This

is more common in glaucomatous images compared

to normal images. Retinal images also suffer from

non uniform illumination due to how the image is cap-

tured. This non-uniform illumination results in shad-

ing artefacts and vignetting (Hoover and Goldbaum,

2003), hindering both quantitative image analysis and

the reliable operation of subsequent global operators

(Winder et al., 2009).

In this paper we present an automated segmenta-

tion of the optic disc combining pixel classiﬁcation

and circular template matching. We used texture fea-

tures based on Binary Robust Independent Elemen-

tary Feature (BRIEF) (Calonder et al., 2010) to clas-

293

Mohammad S., T. Morris D. and Thacker N..

Segmentation of Optic Disc in Retina Images using Texture.

DOI: 10.5220/0004680802930300

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 293-300

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

sify the image pixels. BRIEF is inherently invariant

to image illumination, which in our opinion will han-

dle the illumination issue faced by the retinal images.

It is also has a lower degree of computational com-

plexity compared other texture measurements. Naive

Bayes and Fuzzy C Means (FCM) are used as the clas-

siﬁer and the clustering method respectively to clas-

sify/cluster the image pixels. To obtain the ﬁnal circu-

lar approximation of the optic disc circular template

matching is used. This is to approximate the optic

disc boundary in the case of (1) not all of the optic disc

boundary is detected and (2) there exist large gaps due

to vessel passing in and out of the eye.

We validate our result with a retina image data

set consisting of both normal and glaucomatous im-

ages. We also compare our result with another

commonly known template matching approach, the

Hough Transform.

2 LITERATURE REVIEW

A number of studies have reported work on optic disc

segmentation. Among the existing techniques, the de-

formable or active contour (snake) has been used in

(Joshi et al., 2011; Lowell et al., 2004; Morris and

Donnison, 1999; Muramatsu et al., 2011). The main

advantage of using this approach is the ability to ob-

tain an accurate optic disc boundary. This is possible

because the active contour has the ability to change

shape depending on the properties of the image, de-

sired contour properties and/or knowledge based con-

straints (Kass et al., 1988). There are two types of

active contour currently used for optic disc segmen-

tation, region based active contour or gradient-based

active contour.

The gradient based active contour normally relies

on the image gradient or edges to inﬂuence the en-

ergy forces to evolve to the true optic disc bound-

ary. The presence of the blood vessels, atrophy, low

contrast optic disc boundary and strong optic cup

boundary may prevent the snake from evolving to the

true optic disc boundary. Thus several preprocessing

steps are often implemented prior to snake implemen-

tation, such as by performing blood vessel removal

through morphological ﬁltering as in (May, 2008) or

histogram equalisation followed by thresholding and

pyramid edge detection to enhance the edge (Morris

and Donnison, 1999).

Region based active contour models on the other

hand make use of statistical information from the

background and foreground regions to minimise the

energy function to best separate the regions (Joshi

et al., 2011). The region based active contour is more

robust against local gradient variations. However in

the case where the object to be segmented and the

background regions are heterogeneous and have simi-

lar statistical model, erroneous segmentation may oc-

cur. Thus additional information such as local infor-

mation from multiple image channels is used in (Joshi

et al., 2011).

Another technique used for optic disc segmenta-

tion is circular and elliptical template matching. The

Hough Transform is one of the commonest circular

and elliptical template matching techniques used for

optic disc segmentation. The matching is performed

on an edge map extracted from the underlying image.

The optic disc boundary found through this method is

an approximation and may be not as precise as that

obtained from deformable contour. One main advan-

tage of the Hough Transform technique is that it is

relatively unaffected by noise and gaps in the edge

feature (Lowell et al., 2004). Thus it is very useful

when attempting to determine the optic disc contour

which has no clearly deﬁned edges and is broken by

ingoing and outgoing blood vessels. However obtain-

ing good edge descriptors is vital for the success of

the Hough transform. Otherwise unacceptable results

may be given such as hitting either the curved blood

vessel segments or the strong cup boundary (Lowell

et al., 2004).

Recently pixel classiﬁcation has been used to seg-

ment the optic disc. Pixel classiﬁcation is where ev-

ery pixel in the retina image will be classiﬁed into a

class, such as optic disc or background. In (Mura-

matsu et al., 2011), Fuzzy C Means (FCM) and Ar-

tiﬁcial Neural Networks (ANN) are used to cluster

and classify image pixels as optic disc or background

pixels. For FCM Clustering, two pixel features were

used, the median pixel value in the red channel and

the mean pixel’s values in the blood vessel erased im-

age. Both are calculated over the surrounding 15x15

pixels. As for ANN three different pixel features were

used. They are the pixel value in the red channel of

the original image, and the blood vessel erased image

and the presence of edges in the surrounding 3x3 pix-

els. They compared the result of the pixels classiﬁca-

tion with the result obtained by the snake method and

show that pixel classiﬁcation is able to demonstrate

comparable performance to the snake approach.

Retinal images are acquired with a digital fun-

dus camera, which captures the illumination reﬂected

from the retinal surface. Due the small size of the

objects and the complexities of the optic system in-

volved during the imaging process, retinal images are

often affected by non uniform illumination. Figure

2 shows an example of a retina image with uneven

illumination. The retina images affected by this are

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

294

Figure 2: Samples of a retina image suffers from non uni-

form illumination.

normally brighter in the central region and darker in

the periphery. The exact properties of illumination

change may vary from image to image. Uneven illu-

mination may alter the local statistical characteristics

of the image intensity such as the mean and median

and thus limits the reliable operation of any global

image processing (Winder et al., 2009).

The existence of a large number of works on retina

image illumination correction emphasize the impor-

tance of correcting the image illumination prior to

further processing. This is normally done by pre-

processing the images. The main aim of this pre-

processing is to obtain images with a common stan-

dardised value to be used for subsequent processing or

analysis. Some of the preprocessing methods used to

correct the uneven illumination are brieﬂy described

next.

Illumination equalisation technique is used

(Hoover and Goldbaum, 2003) for illumination cor-

rection. In this method each pixel is adjusted based

on the desired intensity and its local average intensity.

Work by (Cree et al., 1999) and (Foracchia et al.,

2004) use a method based on the image formation

model to correct the illumination. This method is

based on the principle of the image formation model

which states that a captured image is made up of two

independent functions: the underlying image and

the degradation model. Thus to correct the image, a

degradation model of the image is estimated and then

used to restore the underlying image.

Shade correction is another technique used to cor-

rect the non uniform illumination. It is based on the

same principle as the image formation model above.

The background image is approximated either (1) by

smoothing the original image with mean/median ﬁl-

ter as in (Spencer et al., 1996) or (2) using alternating

sequential ﬁlters as in (Walter and Klein, 2002). Then

the ﬁltered image is subtracted from the original im-

age to recover a more uniformly illuminated image.

The above approaches estimate the correction

from the whole image, thus the result can be a gener-

alised smoothing (Foracchia et al., 2005). To rectify

this later techniques have used speciﬁc retinal features

to contribute to the overall image correction. Vessel

pixels are proposed in (Wang et al., 2001) and back-

ground pixels are used in (Foracchia et al., 2005; Joshi

and Sivaswamy, 2008; Grisan et al., 2006) to estimate

the illumination correction. Once the estimate is ob-

tained, it will be used to normalise the original image.

Although the preprocessing steps have been

shown to improve performance in some automatic de-

tection system (Youssif et al., 2007), but in some other

experiment they are not (Ricci and Perfetti, 2007).

Retinal images consist of many features e.g., optic

disc and various types of lesions, and these features

can be very important especially as diagnostic evi-

dence for many diseases. Thus care must be taken

while performing this preprocessing step, so that the

this features are preserved. Small structures such as

the thinnest blood vessel may become lost and image

noise may be ampliﬁed(Ricci and Perfetti, 2007).

Our work contributes to the use of pixel classiﬁ-

cation for optic disc segmentation. Instead of using

pixel features based on statistical pixel features such

as mean and median, we used texture. We have cho-

sen to characterise texture using BRIEF which is al-

ready invariant to image illumination. Since the retina

image suffers from non-uniform illumination we be-

lieve this texture measurement is worth doing. And in

doing so, we avoid doing the preprocessing explained

above.

3 METHODS

The objective of this work is to implement optic

disc segmentation. The proposed method combines

pixel classiﬁcation using texture and circular template

matching. The procedure is illustrated in Figure 3 and

consists of 3 main steps:

1. Feature Extraction. Regions surrounding each

pixel from each colour (red, green and blue) chan-

nel are transformed into their BRIEF representa-

tion or descriptor. In addition to all the three chan-

nels, to ensure that we utilise the available colour

information in the retina image, we also combine

the BRIEF descriptor from those separate chan-

nels into an RGB descriptor. To form the RGB

descriptor, the descriptors are concatenated into

a single binary string. For example assuming a

16 bits descriptor is used to represent a pixel in

each colour channel, then the resulting descriptor

for that pixel in the RGB channel is 48 bits long.

These representations are then used for classiﬁca-

tion.

2. Classiﬁcation: Naive Bayes and Fuzzy C Means

(FCM) are the selected classiﬁer and clustering

SegmentationofOpticDiscinRetinaImagesusingTexture

295

Figure 3: Flow Chart of the methods

methods used to classify/cluster each pixel into

one of two classes, ’optic disc’ and ’background’.

3. Circular Template Matching. This last stage is

to obtain the ﬁnal circular approximation of the

optic disc. This will handle the gaps caused by

ingoing and outgoing blood vessels near the optic

disc boundary and will approximate the optic disc

boundary if not all of the boundary is detected.

3.1 Binary Robust Independent

Elementary Feature (BRIEF)

BRIEF (Calonder et al., 2010) uses binary vectors to

represent image patches. It takes a smoothed image

patch and computes the result of the binary test be-

tween sets of pairs of pixel intensities. The location

of the pixels pairs are predeﬁned either randomly or in

systematic pattern and lies within the patch. The fea-

ture descriptor for a patch is then deﬁned as a vector

of n binary tests.

Two important considerations when computing

BRIEF descriptors are the smoothing kernel to be

used and the spatial arrangement of the pixel pairs.

Smoothing is introduced to suppress noise, thus in-

creasing the stability and repeatability of the descrip-

tors (Calonder et al., 2012). However smoothing may

cause loss of spatial image detail,because of that we

adopted the method used in (Tar and Thacker, 2011),

i.e. we estimate the noise level beforehand and use

it as a threshold when calculating the BRIEF descrip-

tors. In this works, the test locations (the pixel pairs)

are deﬁned randomly within the patch.

The formal deﬁnition of the BRIEF descriptor

used in our work is as follows:

A test τ deﬁned on patch p of size SxS as

τ(p;x

, y

) =



1 if (p(x

) - (p(y

)) >Threshold

0 otherwise

(1)

where p(x

) and p(y

) are the pixel intensities at loca-

tions x

and y

The BRIEF descriptor is deﬁned as the n bit vector

∑

1≤i≤n

i−1

τ(p;x

, y

) (2)

We choose S = 27 and n = 16. Other combinations

of S and n were considered and tested with a smaller

number of training cases. The above mentioned pa-

rameters were selected as they gave the best result.

The threshold is set to 3 times the estimated image’s

noise magnitude.

3.2 Naive Bayes Classiﬁer

Naive bayes (Duda et al., 2001) is used as a sample of

supervised learning. It has the advantages of simplic-

ity, computational efﬁciency, and good classiﬁcation

performance and in some cases is able to outperform

more sophisticated classiﬁers.

Since the BRIEF features are binary, given a ﬁnite

set of features then Bayes theorem can be expressed

as:

P(ω

|x) =

P(x|ω

)P(ω

)

P(x)

(3)

Where ω

is the i

class. P(ω

) is a priori probability

of class ω

, P(x|ω

) is the likelihood of feature vector

x given a class ω

and P(ω

|x) is the posterior prob-

ability of class ω

given observation x, i.e. the result

of the Bayes rule. P(x) is the normalisation constant.

We estimate P(ω

) and P(x|ω

) from the training data.

The decision rule used for classiﬁcation is based on

maximum a posterior (MAP), i.e. choose the class

with the highest P(ω

|x).

We used Naives Bayes with two fold cross valida-

tion. BRIEF features from the optic disc and back-

ground are used to train the Naive Bayes.

3.3 Fuzzy C Means (FCM)

FCM clustering is selected as a sample of unsuper-

vised learning. One of the advantages of unsupervised

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

296

learning is that it is not dependent on the training data,

and thus it is generalisable to new cases. FCM is a

method of clustering where each point may belong to

one or more clusters with different degree of mem-

bership (Bezdek, 1981). The features with close sim-

ilarity in an image are grouped into the same clusters.

Similarity is deﬁned as the distance from feature vec-

tors to the cluster’s centre.

FCM is based on minimisation of the objective

function in equation 4, by iteratively updating the

membership u

and cluster centre v

J =

∑

k=1

∑

i=1

− v

(4)

where N is the number of data points, C is the number

of clusters, x

is the kth data point, v

is the ith cluster

centre, u

is the degree of membership of kth in the

ith cluster and m is a constant greater than 1 (normally

2), used to determine the fuzziness of the clusters. In

this study the number of cluster is chosen as two, optic

disc and background cluster.

The membership degree, u

and the cluster centre

are deﬁned by:

∑

j=1

(

− v

)

m−1

(5)

∑

k=1

∑

k=1

(6)

Given the desired number of clusters and initial

value of cluster centres, the FCM will converge to a

solution for v

that represents a local minimum or sad-

dle point of the cost function J (Bezdek, 1981).

3.4 Circular Template Matching

To approximate the circular boundary of the optic disc

we use circular and elliptical template matching. The

templates are of various diameters and orientations

(see examples in Figure 4), and these templates will

be cross correlated with the classiﬁcation result im-

ages. The matching process is done in parallel in the

four classiﬁcation images from the red, green, blue

and RGB channel.

The correlation coefﬁcient was used to present an

indication of the match between the template image

and the classiﬁcation image. The ﬁnal decision of the

good match is taken as the one with the highest corre-

lation value.

Figure 4: Samples of the template used.

4 TESTING AND RESULT

The image database used in this study is made up

of 196 images. 110 images are normal and 86 are

glaucomatous images. These images were kindly pro-

vided by Manchester Royal Eye Hospital.

The algorithm performance was evaluated by

measuring the overlap area, using an overlapping

score (O) between the ground truth optic disc region

and the approximated regions obtained from the de-

scribed approach, deﬁned as below:

O =

Area(G ∩ S)

Area(G ∪ S)

(7)

where O is the overlap area, G is the ground truth re-

gion and S is the segmented region by the proposed

approach. An overlap area of ’1’ indicates perfect

agreement between ground truth and the proposed

approach. For the determination of CDR value, the

vertical length of the disc region is often measured.

Therefore average errors in the largest vertical length

of the disc region are also calculated.

The results are shown in Table 1 and Table 2. The

average overlap area between the ground truth and

the segmentation result by FCM and Naive Bayes are

0.85 and 0.84 for the normal set respectively. For the

glaucomatous set of images the overlapping score for

FCM and Naive Bayes is 0.77. In the classiﬁcation

image result using FCM, the optic disc boundary is

more pronounced thus giving a slightly better perfor-

mance.

As expected the average overlapping area result in

the glaucomatous set is slightly lower than the normal

set. The reason is that glaucoma deforms the optic

disc shape making it less conforming to the standard

shape of our templates. In addition, a larger number

of images in this set show signs of atrophy. Atrophy

shares similar characteristic to the optic disc, thus at-

rophy regions are misclassiﬁed as optic disc pixels. In

the case of severe atrophy the image is either over seg-

mented or under segmented. Samples of segmented

optic discs are shown in Figure 5.

A good segmentation result is obtained in an im-

age with a good contrast and clear optic disc bound-

ary. The system also managed to get good approxima-

tion in an image with incomplete optic disc boundary

and the presence of mild atrophy. Poor segmentation

SegmentationofOpticDiscinRetinaImagesusingTexture

297

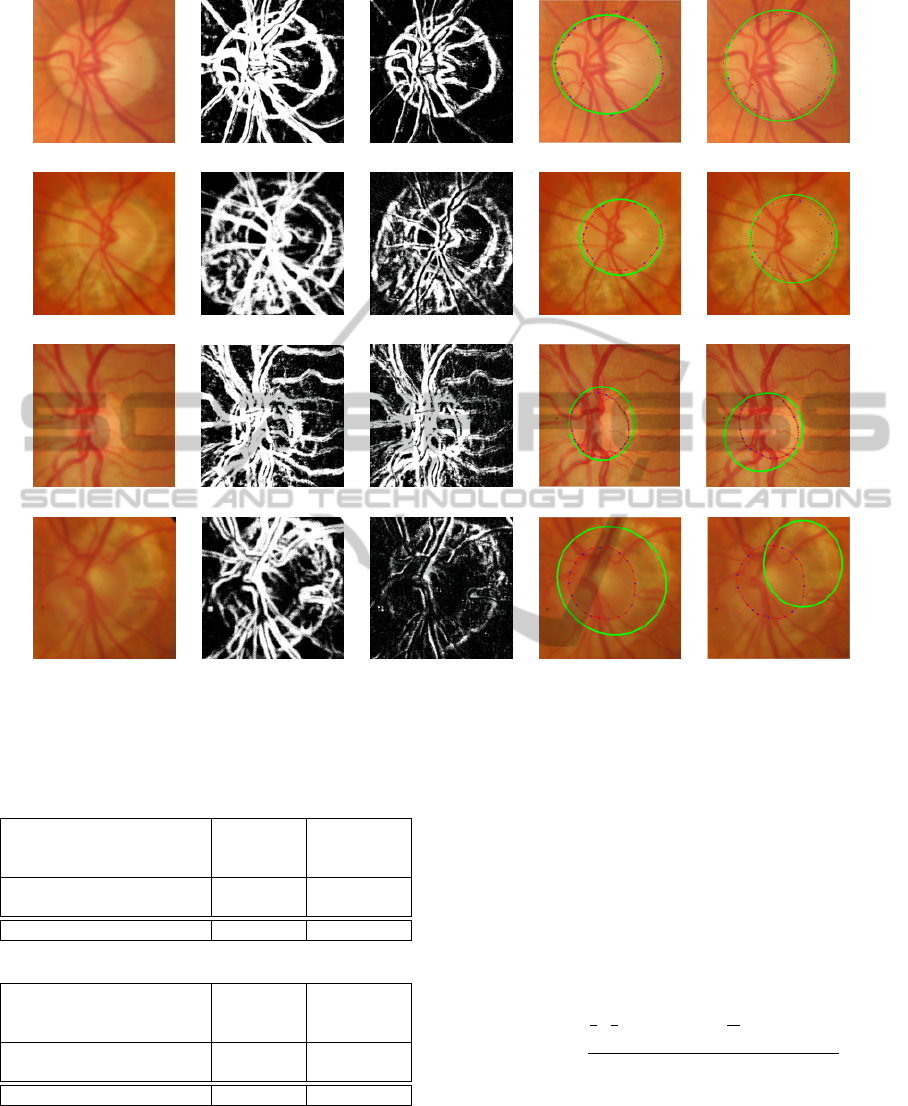
Figure 5: This ﬁgure illustrates the process of segmenting the optic disc, performed on the colour combination channel. The

ﬁrst and fourth rows are images from the normal images set. The second and third row are images from the glaucomatous

set. From left to right: Original image, classiﬁcation image using FCM, classiﬁcation image using Naive Bayes, optic disc

boundary approximation using FCM and optic disc boundary approximation using Naive Bayes. The dotted line is the ground

truth and the green line is the approximated boundary.

Table 1: Disc segmentation result by the Fuzzy C Means.

Average

overlapping

ratio

Vertical

length

error (%)

Horizontal

length error

(%)

Normal 0.85 3.1 4.3

Glaucoma 0.77 5.8 6.0

All 0.81 4.5 5.2

Table 2: Disc segmentation result by the Naive Bayes.

Average

overlapping

ratio

Vertical

Length

error (%)

Horizontal

Length

Error (%)

Normal 0.84 4.9 5.2

Glaucoma 0.77 7.1 8.6

All 0.81 6 6.9

results are normally obtained from an image with ei-

ther severe atrophy (Figure 5:row 4), or with quite a

number of thick vessels passing in and out of the optic

disc (Figure 5:row 3) and those with irregular shape.

We also compared our result to another common

template matching approach that is the Hough trans-

form as implemented in (May, 2008). The Hough

Transform is performed based on the edges obtained

by the Canny edge detector. Vessel removal is imple-

mented prior to the edge detector. The evaluation used

in their work is based on calculating the discrepancy

(D) between two closed boundary curves or contour

described as:

D(G

, S

) =

{

∑

i=1

d(g

, S) +

∑

i=1

d(s

, G)}

(8)

and S

are the contours of the segmented area in

the ground truth and segmented images. d(a

, B) is

the minimum distance from point i on the contour A

to any point on the contour B. G

is the diameter of

the ground truth contour. A low discrepancy value

implies a better segmentation performance.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

298

The comparison result is shown in Table 3. As can

be seen, our approach shows improvement in min-

imising the discrepancy over the Hough Transform

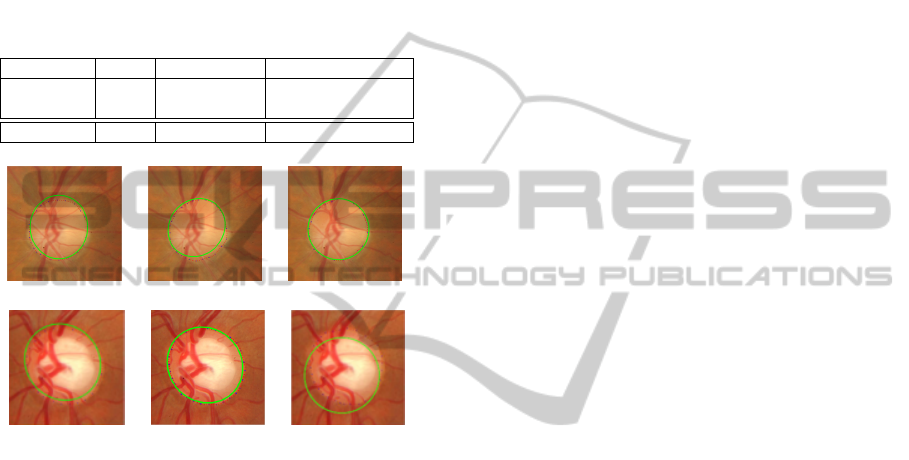
method. Figure 6 shows a sample image where the

optic disc is successfully segmented by all three meth-

ods (Row 1) and an image where our approach shows

a better segmentation result compared to the Hough

Transform (Row 2). In this particular case, the Hough

Transform is trapped by the strong optic cup bound-

ary.

Table 3: Average Discrepancy (D) by the three methods.

FCM Naive Bayes Hough Transform

Normal 0.06 0.06 0.10

Glaucoma 0.09 0.09 0.13

All 0.08 0.08 0.12

Figure 6: Comparisons of disc outlines determine by the

three method. From left to right: Optic disc boundary ap-

proximation based on clustering result by FCM clustering

and optic disc boundary approximation based on classiﬁca-

tion result by Naive Bayes and optic disc approximation by

the Hough Transform. The dotted line is the ground truth

and the green line is the approximated boundary.

5 CONCLUSIONS AND FUTURE

WORKS

A method for optic disc segmentation is presented in

this paper. We demonstrate that the proposed method

is at least as reliable as other algorithms for the op-

tic disc segmentation with the advantages of com-

putational simplicity. An interesting property of our

method is the use of an illumination invariant texture

measurement to address the illumination issue of the

retina images. Furthermore, by making use of ma-

chine learning techniques in our approach, we can ex-

ploit the knowledge of the characteristics of the optic

disc in the segmentation process.

Nonetheless, the method has several limitations

which we aim to address in future research. We used

training data to model the optic disc characteristic

with the hope of better discrimination between optic

disc and background pixels (including vessels and at-

rophy pixels). However, some miss classiﬁcation be-

tween pixels on the vessel boundaries, atrophy and

optic disc boundary do occur in some of the images.

Thus in future we intend to (1) implement a rotation

invariant version of BRIEF as an attempt to reduce

miss classiﬁcation of vessels and (2) ensure that data

used for training the Naive Bayes includes sufﬁcient

number of atrophy pixels so that the result may im-

prove. At the moment the pixels used in the training

data were randomly selected.

Another problem is the use of circular/elliptical

template matching. Quite often, this approach fails to

get good segmentation in cases where the optic disc

is not of ’standard’ shape. Therefore we are currently

looking at ways to trace the boundary from the classi-

ﬁcation image guided by the obtained circumference

given by the template matching approach.

REFERENCES

Bezdek, J. C. (1981). Pattern recognition with fuzzy objec-

tive function algorithms. Kluwer Academic Publish-

ers.

Calonder, M., Lepetit, V., Ozuysal, M., Trzcinski, T.,

Strecha, C., and Fua, P. (2012). Brief: Computing

a local binary descriptor very fast. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

34(7):1281–1298.

Calonder, M., Lepetit, V., Strecha, C., and Fua, P. (2010).

Brief: binary robust independent elementary features.

In Computer Vision–ECCV 2010, pages 778–792.

Springer.

Congdon, N. G., Friedman, D. S., and Lietman, T. (2003).

Important causes of visual impairment in the world

today. JAMA: the journal of the American Medical

Association, 290(15):2057–2060.

Cree, M. J., Olson, J. A., McHardy, K. C., Sharp, P. F.,

and Forrester, J. V. (1999). The preprocessing of

retinal images for the detection of ﬂuorescein leak-

age. Physics in Medicine and Biology, 44(1):293–308.

Cited By (since 1996):18.

Duda, R., Hart, P., and Stork, D. (2001). Pattern classiﬁca-

tion. Wiley, pub-WILEY:adr, second edition.

Foracchia, M., Grisan, E., and Ruggeri, A. (2004). Detec-

tion of optic disc in retinal images by means of a geo-

metrical model of vessel structure. IEEE Transactions

on Medical Imaging, 23(10):1189–1195.

Foracchia, M., Grisan, E., and Ruggeri, A. (2005). Lu-

minosity and contrast normalization in retinal images.

Medical Image Analysis, 9(3):179–190.

Grisan, E., Giani, A., Ceseracciu, E., and Ruggeri, A.

(2006). Model-based illumination correction in reti-

nal images. In Biomedical Imaging: Nano to Macro,

2006. 3rd IEEE International Symposium on, pages

984–987. IEEE.

SegmentationofOpticDiscinRetinaImagesusingTexture

299

Hoover, A. and Goldbaum, M. (2003). Locating the optic

nerve in a retinal image using the fuzzy convergence

of the blood vessels. Medical Imaging, IEEE Trans-

actions on, 22(8):951–958.

Joshi, G. D. and Sivaswamy, J. (2008). Colour retinal image

enhancement based on domain knowledge. In Com-

puter Vision, Graphics & Image Processing, 2008.

ICVGIP’08. Sixth Indian Conference on, pages 591–

598. IEEE.

Joshi, G. D., Sivaswamy, J., and Krishnadas, S. (2011). Op-

tic disk and cup segmentation from monocular color

retinal images for glaucoma assessment. Medical

Imaging, IEEE Transactions on, 30(6):1192–1205.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International journal of com-

puter vision, 1(4):321–331.

Lowell, J., Hunter, A., Steel, D., Basu, A., Ryder, R.,

Fletcher, E., and Kennedy, L. (2004). Optic nerve

head segmentation. Medical Imaging, IEEE Trans-

actions on, 23(2):256–264.

May, M. (2008). Automatic Detection of the Optic Disc

Within Retinal Images. Master’s thesis, University of

Manchester, UK.

Morris, D. and Donnison, C. (1999). Identifying the neu-

roretinal rim boundary using dynamic contours. Im-

age and Vision Computing, 17(3):169–174.

Muramatsu, C., Nakagawa, T., Sawada, A., Hatanaka, Y.,

Hara, T., Yamamoto, T., and Fujita, H. (2011). Au-

tomated segmentation of optic disc region on retinal

fundus photographs: Comparison of contour model-

ing and pixel classiﬁcation methods. Computer meth-

ods and programs in biomedicine, 101(1):23–32.

Ricci, E. and Perfetti, R. (2007). Retinal blood vessel

segmentation using line operators and support vector

classiﬁcation. Medical Imaging, IEEE Transactions

on, 26(10):1357–1365.

Spencer, T., Olson, J., McHardy, K., Sharp, P., and For-

rester, J. (1996). An image-processing strategy for the

segmentation and quantiﬁcation of microaneurysms in

ﬂuorescein angiograms of the ocular fundus. Comput-

ers and Biomedical Research, 29(4):284–302.

Tar, P. and Thacker, N. (2011). A quantitative representation

for segmentation of martian images. Technical report,

ISBE, Medical School, University of Manchester.

Walter, T. and Klein, J.-C. (2002). A computational ap-

proach to diagnosis of diabetic retinopathy. In Pro-

ceedings of the 6th Conference on Systemics, Cyber-

netics and Informatics (SCI2002), pages 521–526.

Wang, Y., Tan, W., and Lee, S. C. (2001). Illumination nor-

malization of retinal images using sampling and inter-

polation. In Medical Imaging 2001, pages 500–507.

International Society for Optics and Photonics.

Winder, R., Morrow, P., McRitchie, I., Bailie, J., and Hart,

P. (2009). Algorithms for digital image processing in

diabetic retinopathy. Computerized Medical Imaging

and Graphics, 33(8):608 – 622.

Youssif, A. A., Ghalwash, A. Z., and Ghoneim, A. S.

(2007). A comparative evaluation of preprocessing

methods for automatic detection of retinal anatomy. In

Proceedings of the Fifth International Conference on

Informatics and Systems (INFOS 07), pages 24–30.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

300