An Inverse Distance-based Potential Field Function for Overlapping

Point Set Visualization

Jevg

enijs Vihrovs, Kri

anis Pr

usis, K

arlis Freivalds, P

eteris Ru

cevskis and Valdis Krebs

Institute of Mathematics and Computer Science, University of Latvia, Rain¸a bulv

aris 29, LV-1459, Riga, Latvia

Keywords:

Information Visualization, Implicit Surfaces.

Abstract:

In this paper we address the problem of visualizing overlapping sets of points with a ﬁxed positioning in a

comprehensible way. A standard visualization technique is to enclose the point sets in isocontours generated

by bounding a potential ﬁeld function. The most commonly used functions are various approximations of

the Gaussian distribution. Such an approach produces smooth and appealing shapes, however it may produce

an incorrect point nesting in generated regions, e.g. some point is contained inside a foreign set region. We

introduce a different potential ﬁeld function that keeps the desired properties of Gaussian distribution, and

in addition guarantees that every point belongs to all its sets’ regions and no others, and that regions of two

sets with no common points have no overlaps. The presented function works well if the sets intersect each

other, a situation that often arises in social network graphs, producing regions that reveal the structure of their

clustering.

1 INTRODUCTION

Point sets emerge from the study of many real-world

data structures, from social networks to geographical

maps. The sets identify important groups of objects

inside the structure, for instance, scientiﬁc article co-

authorship (Santamara and Thern, 2008) or social cir-

cles in organizations (Krebs, 2007). Overlaps often

occur naturally in such graphs, with sets sharing com-

mon intermediary vertices. For example, human and

biological networks rarely cluster in clean ways, and

one vertex may belong to many groups.

After the identiﬁcation of different point sets in

the given data, there is still the problem of presenting

this information in a quickly and easily comprehensi-

ble way. In order for the visualization of overlapping

point sets to be effective, it should adhere to various

criteria. Firstly, it should be unambiguous: the user

should be able to identify the sets and their points,

as well as their overlaps, without any misunderstand-

ings. It should also represent the geometrical layout

of the points themselves as closely as possible. In this

paper we deal with visualizing point sets that have an

arbitrary, but ﬁxed positioning.

The common approach in visualization is to en-

close the points of each set in a region that represents

this set, forming an Euler diagram. There are several

works that list the desirable properties of visualiza-

Figure 1: An example of the proposed visualization. There

are three overlapping point sets, which correspond to vertex

clusters in the given graph. In this example edges do not

affect the visualization.

tions that produce such regions (Rosenthal and Lin-

sen, 2009; Dinkla et al., 2012). Here we present a

brief summary.

P1 Each point of a set is contained inside the region

of this set.

P2 Each point not present in a set is not contained

inside the region of this set.

P3 The regions of two different sets must have over-

laps only where there is a point that belongs to

both of the sets.

P4 The regions must have a strict boundary that sep-

Vihrovs J., Pr¯usis K., Freivalds K., Ru

cevskis P. and Krebs V..

An Inverse Distance-based Potential Field Function for Overlapping Point Set Visualization.

DOI: 10.5220/0004681100290038

In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 29-38

ISBN: 978-989-758-005-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

arates the included and excluded space.

P5 The boundary of the region should stay close to

the points of the set.

P6 The boundaries of the regions should be sufﬁ-

ciently smooth.

P7 The region of one set should be connected.

A widely used visualization method is to compute

the regions by bounding a potential ﬁeld function.

The advantages are the smooth shape borders and the

ﬂexibility of the result, as the function parameters can

be adjusted to obtain a better visualization. The main

problems are ensuring the correct membership of the

points (P1, P2) and region overlapping (P3), as well

as maintaining each region connected (P7). Tradition-

ally, most potential functions are based on the Gaus-

sian distribution function (Blinn, 1982; Gross et al.,

1997; Sprenger et al., 2000) or quadratic polinomial

functions (Watanabe et al., 2007; Collins et al., 2009).

These functions naturally satisfy properties P4-P6.

The main problem with such functions is main-

taining the membership properties P1-P3. If each set

region is calculated ignoring the inﬂuence of the for-

eign points, then P1 holds, but P2 and P3 are com-

pletely ignored. To mitigate this, the foreign points

are assigned a negative potential, thus repelling the

inﬂuence of the points of the given set. This im-

proves P2 and P3 (though does not fully satisfy ei-

ther), but violates P1, as negative potentials can over-

whelm positives ones even directly at a point. To limit

the effect this has on P1, smaller weights are often

used for negative potentials. However, this weak-

ens the improvements to P2 and P3. In particular,

only when negative and positive potentials are equal

does the following hold: if two sets share no common

point, their regions do not overlap, which is important

in cases with no overlapping sets.

In this work we address this problem and propose

a different potential ﬁeld function that always pro-

duces visualization with correct point membership,

and visually still behaves much like the mentioned

potential functions. It is very similar to Gaussian-

based methods in isocontour appearance and satisﬁes

the same properties P4-P6. In addition, when using

our function with equal negative and positive weights

as described earlier, it is guaranteed to satisfy proper-

ties P1, P2 concerning the membership of the points.

Thus it also guarantees the property P3 for every two

sets with no common points. We show the results of

the visualization on different artiﬁcial and real-world

examples and compare them to other potential func-

tions. The function has also two parameters that allow

to adjust the size and appearance of the produced re-

gions.

Maintaining property P7 is a topological problem,

and cannot be solved by a speciﬁc potential func-

tion design. Still, it can be ensured using standalone

techniques such as including the edges of each set’s

spanning tree when computing the potential function

(Collins et al., 2009), but usually at the cost of ignor-

ing correct overlap properties P2 and P3. We show

how this method works with the proposed function.

However, as the proposed function is designed to im-

prove properties P1-P3, this leads to unusual visual

behavior. Without this property the region of each

set can consist of multiple disconnected shapes. In

our examples, we use color-coding to differentiate be-

tween set regions.

2 RELATED WORK

There have been a substantial number of works that

deal with overlapping point set visualization. The

problem is highly relevant in visualizing graph vertex

clusters in graph drawing, and many approaches are

described in the context of graph clusters (Gansner

et al., 2010; Balzer and Deussen, 2007; Van Ham and

Van Wijk, 2004; Heer and Boyd, 2003).

The main tasks pursued in most visualizations are

maintaining connectivity of the regions of a set (P7)

and point region membership (P1-P3). The connectiv-

ity is very important in the sense that it allows the user

to quickly identify a particular set. The correctness

of the sets’ overlaps may be crucial in understanding

the membership of the points and the relationships

of the sets. Both these properties may be conﬂict-

ing: if the positioning of the points is ﬁxed, it is fre-

quently not possible to ensure connectivity and elimi-

nate all unnecessary region overlaps. It is also impor-

tant whether the layout of the points can be changed

or not; various algorithms of point positioning may

greatly improve the readability of the visualization.

The most straightforward approach for obtaining

the region of a set is to obtain its convex hull, used,

for example, in (Heer and Boyd, 2003; Santamara and

Thern, 2008). Here, the boundaries of the convex

hulls are smoothed by using B

ezier curves. However,

the convex hull approach ignores the P2 and P3 prop-

erties, and many points may happen to reside inside

foreign set regions. This is addressed in (Byelas and

Telea, 2009), which describes visualization of UML

diagrams. The areas where foreign elements overlap

the convex hull are excluded from the region heuristi-

cally, and afterwards the resulting polygon is shrunk

inwards to better represent the layout of the elements

in the set. The borders of the regions are also softened

which achieves a more natural look of the shapes.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

A more sophisticated method that also computes

discrete hulls is proposed in (Simonetto et al., 2009).

The intersection graph of the sets (which is planar) is

built and positioned using a force-directed algorithm

(Di Battista et al., 1998). Then a polygonal skeleton is

built around the graph vertices, and the points are in-

serted inside the corresponding polygons; these poly-

gons are then expanded by applying the force-directed

layout algorithm several more times. The resulting

visualization has correct point membership, and each

set region is connected, thus all the constraints P1-P3,

and P7 are fully satisﬁed. Still, this visualization can

be applied only when the positioning of the points is

not important.

Another method is to use the Voronoi diagram of

the given points to create the space partitioning for

the visualization. A simple application of such ap-

proach for visualizing self-organizing maps can be

found in (Matsumoto et al., 2008). The result fully

ensures all the membership constraints P1-P3, and is

very simple to implement. However, the regions have

many sharp edges and all borders are shared (P6 does

not hold). Another problem is the long and sharp re-

gion parts that do not contain any set vertices, which

are common in Voronoi diagrams, as these parts dis-

tort the regions and lessen readability, violating P5.

GMap (Gansner et al., 2010) mitigates this by insert-

ing many artiﬁcial points in the diagram around the ar-

eas of interest. A particular technique for smoothing

the boundaries of the regions is described in (Rosen-

thal and Linsen, 2009), which also uses Voronoi dia-

grams. They create the region boundaries by using the

Voronoi diagram to obtain a hull of the set and then

drawing a distance ﬁeld around this hull. This does

not, however, work on boundaries between adjacent

or intersecting regions. A problem with all Voronoi-

based methods is that they do not ensure region con-

nectivity.

The approach used in this work is to compute the

regions for point sets by using a potential ﬁeld func-

tion. The value of inﬂuence of a point in the given

space is deﬁned by the potential function, and the to-

tal inﬂuence of a point set in some location is the sum

of inﬂuences for all the points in the set. Then the

region for a set is obtained by thresholding the total

inﬂuence of this set.

The properties of such visualization depend on the

choice of the potential ﬁeld function. Most standard

potential functions are based on the Gaussian distribu-

tion. Its main advantage is the contour smoothness of

the regions, they look similar to hand-drawn. One of

the ﬁrst analyses of such a potential function appears

in (Blinn, 1982). It also describes how the “blobbi-

ness” of the visualization can be adjusted using the

parameters of the function.

Another type of potential functions are polyno-

mial approximations of Gaussians that are faster to

compute and produce nearly identical results, e.g.

(Balzer and Deussen, 2007). Also used are bounded

quadratic functions (Watanabe et al., 2007; Collins

et al., 2009), they generate similar results.

This approach has been widely applied in point set

visualization. Some works visualize and cluster point

sets in 3D (Sprenger et al., 2000; Balzer and Deussen,

2007). The latter also focuses on hierarchical depic-

tion of a clustered graph. To avoid incorrect overlaps

of different set regions, one can assign negative poten-

tial to point of foreign sets, which is noted in (Blinn,

1982), and used in (Gross et al., 1997; Watanabe et al.,

2007; Collins et al., 2009).

Bubble Sets (Collins et al., 2009) directly focus

on 2D point set visualization; while it also uses a po-

tential ﬁeld function and negative inﬂuences for for-

eign set points, it maintains P7 by using the edges of

a spanning tree of each set in addition to the vertices

when computing the potential functions. However,

these edges from different sets can overlap, violating

P3.

Other novel methods include Euler diagrams with

connected regions (Riche and Dwyer, 2010), as well

as Kelp diagrams (Dinkla et al., 2012), which focus

primarily on region connectivity in visualizing points

with ﬁxed geometrical layout.

3 THE POTENTIAL FUNCTION

We are given a set of points and the subsets we have to

visualize, along with a geometrical positioning of the

points in an Euclidean space. For clarity, we will call

the given points the vertices (from the use cases of

representing social graphs), to avoid confusion with

spatial points. For each set, we independently com-

pute a function which assigns a real number to each

point denoting the set’s inﬂuence on it. Vertices be-

longing to the set positively inﬂuence the value of

the function, whereas other vertices inﬂuence it neg-

atively. The amount a vertex inﬂuences a point is de-

termined by their distance.

After calculating the function for a set, the shape

for this set is extracted using a ﬁxed threshold. We de-

scribe the potential function in Sect. 3.1. In Sect. 3.3,

we discuss the speciﬁcs of the implementation.

3.1 Function Description

Suppose we are given N non-empty sets S

...S

where ∀i : S

⊆ V , and V is the set of all the vertices.

AnInverseDistance-basedPotentialFieldFunctionforOverlappingPointSetVisualization

Some vertices can also belong to no set. These ver-

tices in any case negatively inﬂuence the value of the

function for all sets.

For the visualization, we need the vertices to be

geometrically positioned. The positioning can be ex-

pressed by a function P : V → R

that assigns a po-

sition to each vertex in a n-dimensional Euclidean

space. Clearly, in practice, the visualization can be

meaningful to users when n ≤ 3. For use case with-

out a predeﬁned layout, constructing the function P

is itself a separate, well-studied problem(Di Battista

et al., 1998). In this work, we do not propose any

new positioning methods, and the visualization itself

does not require any special positioning. For clus-

tered graphs, we will often use a positioning based on

a force-directed layout algorithm.

The ﬁeld function approach works as follows:

ﬁrst, deﬁne the inﬂuence of a vertex v with respect

to a point p, which is a function I(v, p). Then the in-

ﬂuence of a vertex set S on a point p is deﬁned as the

sum of the inﬂuence of its vertices:

I(S, p) =

∑

v∈S

I(v, p). (1)

The potential ﬁeld function for set S

at a point p is

deﬁned as the difference between the inﬂuence of this

set and the total inﬂuence of all other vertices:

(p) = I(S

, p) − w · I(V \ S

, p) (2)

All the vertices that belong to the i-th set inﬂuence

the value of the function positively, whilst all other

vertices inﬂuence it negatively. The nonnegative pa-

rameter w is the weight of negative inﬂuence, which

is usually less than 1 (i.e. the weight of the positive

inﬂuence).

To obtain a shape that represents the i-th set, use a

nonnegative threshold t. The region of the vertex set

is deﬁned to be the set of points such that for any point

p in the set the inequality F

(p) > t holds. By adjust-

ing the value of t the shapes can be made smaller or

larger. In practice, it can be difﬁcult to estimate the

shape size from t, therefore we adjust the desired ra-

dius of the shape of a single vertex R

and set t to be

the inﬂuence of a single vertex at distance R

Since the inﬂuence of the vertices belonging to S

is taken with a positive sign and the inﬂuence of other

vertices with a negative sign, vertices not belonging

to the set repel its shape.

As the function I(v, p) we use the following:

I(v, p) = max(kP(v) − pk

−b

− m,0) (3)

where b and m are nonnegative constants (parame-

ters). We also use the weight w = 1 (we show later this

contributes to an important property of the function).

When kP(v) − pk = 0, inﬂuence I(v, p) is deﬁned as

lim

x→0

= +∞.

There can also be a situation when two or more

vertices have equal positions, where by (3) it is not

clear what value should F

take. For example, there

can be one vertex v

from set i and two other v

, v

from set j in the same point p. For all three vertices

the inﬂuence in this point is equal to inﬁnity, so F

formally is undeﬁned. In this case F

should be equal

to −∞, since for all other points q the value of F

−I(v

,q) = I(v

,q) − I(v

,q). So in such

situations, if the number of set i vertices in point p

is less than the number of foreign set vertices in this

point, then F

(p) should be equal to −∞, and +∞ or 0

if it is greater or equal respectively. This may not be

very important as it affects only individual points but

should be noted during implementation.

Parameter b regulates the slope of the function.

When b grows larger, the function decreases much

faster when distance is greater than 1. Visually this

adjusts how strongly the blobs of the vertices interact

with each other. Fig. 2 shows the graphs of the func-

tion with different b values (m = 0). The threshold

b was chosen so that for each function the radius of

a single blob would be constant. When m is small,

the blobs of nearby vertices meld together. When b is

large, they appear as overlapping circles.

distance

b = 0.2

b = 1

b = 2

b = 20

(a) (b)

Figure 2: Graphs of the inﬂuence function with different b

values. This example shows how b affects blob interaction:

(a) b = 0.2; (b) b = 1; (c) b = 2; (d) b = 20. The radius of

a single blob R

is the same in all examples.

The value m is subtracted to set function values

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

to 0 starting from a certain distance. The purpose of

this is to limit the maximum effect radius of a sin-

gle vertex, preventing large concentrations of vertices

from accumulating a large radius of the correspond-

ing region with respect to other regions that contain

less vertices. This is shown in Fig. 3: m normalizes

the radiuses of the small and large set regions. Again,

as with threshold, we regulate m with the use of the

value R

, which is deﬁned as the distance at which

the value of inﬂuence of a single vertex is equal to 0.

It is clear that R

should be greater than R

; we mostly

set the value of R

to be a multiple of R

(a) (b)

Figure 3: The effect of parameter m on the consistency of

region radiuses: (a) R

is unbounded (m = 0), the larger set

region has a much larger radius then the smaller set region;

(b) R

= 2.5R

, the radiuses of the regions are almost the

same.

3.2 Properties and Comparison

In this section we discuss how the presented func-

tion deals with properties P1-P3 and how it com-

pares to already known functions. As inﬂuence func-

tion I(v, p) we also consider the Gaussian distribu-

tion function e

−

2σ

and quadratic polynomial func-

tion (max(r − x,0))

, where x = kP(v) − pk. For

Gaussian distribution function, standard deviation pa-

rameter σ also adjusts blobbiness. Overall the pro-

posed function keeps the desired properties of these

functions, and in addition guarantees correct point re-

gion membership because the potential function di-

verges to plus inﬁnity at x = 0.

A simple example in Fig. 4 shows that the pro-

posed function maintains the visual appearance of

Gaussian distribution and quadratic polynomial po-

tential functions. Of course, each function has its pa-

rameters that adjust the blobbiness and size of the re-

gions, so each can be used to produce different visu-

alizations with the same example case. However, the

ﬁgure shows that all three functions can be adjusted

to produce similar-looking results.

Further we examine how these functions satisfy

(a) (b)

(c)

Figure 4: A simple example of how the proposed function

maintains the appearance of common potential functions:

(a) Gaussian distribution; (b) quadratic polynomial; (c) pro-

posed function.

the membership properties P1-P3. In contrast to other

functions, the proposed function guarantees proper-

ties P1, P2. It also ensures property P3 for sets with

no common points.

The property P1 is easy to establish for any po-

tential function by taking w = 0 in (2), i.e. ignoring

foreign vertex inﬂuence for the current set. This intro-

duces many unwanted region intersections, thus prop-

erties P2 and P3 are not maintained. This is shown

in Fig. 5 (a) with Gaussian distribution (of course

it happens with any potential function): the blue and

red regions almost completely overlap (they should

not since the two sets do not have any vertex in com-

mon), besides the blue region swallows all vertices of

the red region.

This means that if we want to remove unnecessary

region overlaps or ensure correct vertex membership,

we have to adjust the value of w. Fig. 5 (b) shows

the same example with Gaussian distribution and w =

0.5. The vertex membership is correct, but the regions

still overlap. Fig. 5 (c) uses Gaussian with w = 1,

i.e. the negative potential has the same weight as the

positive. In this case the two regions do not overlap,

but the red region swallows the single blue vertex.

That is, in fact, an important property when w = 1,

which holds for any potential function. If two sets

have no vertices in common, then their regions do not

overlap (this is actually a special case of the P3 prop-

erty). The proof is trivial: suppose the total positive

inﬂuences of the two sets at some spatial point are I

and I

. Only one of the values I

− I

and I

− I

can

be positive, thus only one can be greater than thresh-

old t. Other set vertices do not change this property,

since for each spatial point the inﬂuence from them is

subtracted from both of the given set total inﬂuences.

This property is very important if we need to visu-

alize sets with no intersections: then no two regions

will have any overlaps. Therefore we would want to

keep it while also ensuring correct vertex member-

AnInverseDistance-basedPotentialFieldFunctionforOverlappingPointSetVisualization

ship. We examine this property for a small example

with a ﬁxed R

Using a Gaussian function with a ﬁxed parameter

σ, as it is shown in Fig. 5 (a)-(c), all of the mentioned

properties at once are not achievable. In the given ex-

ample, we can change σ (from 2.5 to 3.5), and obtain

a correct visualization, see Fig. 5 (d); however, this

is an unstable improvement and slightly adjusted ver-

tex positions again produce an incorrect visualization

even with the new σ, see Fig. 5 (e). In addition, σ also

regulates blobbiness and it is not desirable to adjust it

in order to maintain correctness.

With the proposed function all of the above is

guaranteed in the visualization, see Fig. 5 (f). Firstly,

we keep weight w = 1, so non-intersecting sets will

have no overlaps between their regions. Secondly,

the potential function is based on inverse distance and

reaches positive inﬁnity at distance 0, regardless of

the function parameters. Thus properties P1 and P2

are ensured: each vertex will always be inside the re-

gions of the sets it belongs to and will not be inside

the regions of the sets it doesn’t belong to. This al-

lows using the parameters b and m to adjust the visual

quality of the result, while the membership of the ver-

tices will always be correct.

The only case when P1 and P2 do not hold is in

the same case if several different set vertices are in the

same position p. However, it is obviously impossible

to satisfy these properties with any visualization in

this case.

Using a quadratic polynomial function produces

results similar to those of using a Gaussian function,

see Fig. 6. Parameter r can be adjusted to regulate the

blobbiness. The red region swallows the blue vertex

in Fig. 6 (a), when r = 1.4R

. Again, it can be solved

by adjusting r to 1.02R

(see Fig. 6 (b)), and again

this solution is unstable and doesn’t work when the

vertex positions are changed slightly (see Fig. 6 (c)).

The example uses the same R

in all cases, but

a vertex positioning producing similar results can be

obtained for any R

. In practice, changing the radius

of the blobs is also unwanted if we need to obtain

shapes of particular size. With the proposed function

there is no need for ﬁne-tuning to obtain a correct ver-

tex membership visualization.

It should be noted that the situation with P3 is dif-

ferent if two sets do have some vertices in common.

As it was shown that any vertex belonging to a set will

reside inside the region of this set, a vertex belonging

to two sets will also always reside in some intersec-

tion of their regions. However, among all overlaps of

the regions, there can be some that contain no vertices

from any of the given sets. These overlaps may be un-

wanted since they do not hold any semantic meaning

(a) (b)

(f)

Figure 5: Comparison with the Gaussian distribution func-

tion. The example shows two non-intersecting sets: 1 vertex

(blue); 3 vertices (red). In this example the threshold radius

is the same for all six cases. (a) Gaussian, σ =

/2.5,

w = 0. (b) Gaussian, σ =

/2.5, w = 0.5. (c) Gaussian,

σ =

/2.5, w = 1. (d) Gaussian, σ =

/3.5, w = 1. (e) Dif-

ferent vertex positioning, Gaussian, σ =

/3.5, w = 1. (f)

The proposed function, b = 2, R

= 2R

(a) (b)

(c)

Figure 6: Quadratic polynomial function (max(r − x, 0))

results with the same example and the same R

: (a) r =

1.4R

; (b) r = 1.02R

; (c) Different vertex positioning, r =

1.02R

of set relationship, see Fig. 7 (a). Still, such over-

laps can also contribute to the smooth region borders,

see Fig. 7 (b); without them, the image would not

look natural. Generally, this problem has a topologi-

cal nature and most probably cannot be solved solely

through potential function design.

3.3 Implementation

In this section we discuss the implementation

speciﬁcs of the proposed potential function. We use a

radial sweep algorithm to ﬁnd the region boundaries

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

(a) (b)

Figure 7: Unnecessary region overlaps (with the proposed

potential function): (a) the highlighted overlap is unwanted;

(b) the highlighted overlaps are not necessary, but manda-

tory for smooth shape borders. Vertices that have black bor-

ders in each example belong to all sets.

for each set (marching squares could be used as well),

which are simpliﬁed using the Douglas-Peucker algo-

rithm (Douglas and Peucker, 1973). For high-quality

images (as in this paper) we also interpolate these

polygons with splines (Hobby, 1986).

One aspect of the implementation of our poten-

tial function is the possibility of inﬁnity values. In

fact, due to datatype restrictions (for example, ﬂoat-

ing point) such values could be achievable not only

exactly at a vertex, but also within some ε-distance

from the vertex. This problem can be solved by ad-

justing the used datatype for our function speciﬁcs:

• if the operation would cause the value of a vari-

able to overﬂow, it should take the special ∞-value

with an appropriate sign (the ﬂoating point stan-

dard guarantees this);

• if an ∞-value is added a value which is not an ∞-

value with the opposite sign, the result should re-

main the same ∞-value (the ﬂoating point stan-

dard guarantees this);

• if an ∞-value is added to an ∞-value with the op-

posite sign, the result should be 0 (this is different

from the ﬂoating point standard).

Still, in our implementation we used the standard

ﬂoating point datatype, as it is fully sufﬁcient in prac-

tice and produces no visible errors, because such ε-

regions are negligible in size.

Another aspect of the implementation is choosing

appropriate values for b, m and t. Recall the following

auxiliary parameters we used in the previous section:

— the desired radius of the shape of a single ver-

tex; R

— the distance where the inﬂuence of a sin-

gle vertex reaches 0. These parameters can be used in

the implementation to adjust the look of the visualiza-

tion. We advise to set R

to be some multiple of R

for example, R

= 2R

. We use the following rules to

compute the actual parameters for the function:

• b = 2, but adjust in real-time if needed.

• m = R

−b

• t = R

−b

− m, provided R

> R

The running time of the implementation is mainly

dependent on the particulars of the radial sweep or

marching squares algorithm used. The only time-

consuming part connected with the function is the

calculation of the inﬂuence on the given scalar ﬁeld,

which is essentially O((set count) · (vertex count) ·

(ﬁeld size)). There are a few worthy optimizations

to this:

• since F

(p) = I(S

, p) − I(V \ S

, p), ﬁrst calculate

only I(S

, p): if it is less than the used threshold t,

there is no need to calculate I(V \ S

, p);

• if the distance kP(v)− pk is greater than R

, then

the inﬂuence is 0 and there is no need to take v

into account for point p;

• to avoid expensive exponentiation in kP(v) −

−b

, the value of b = 2 can be used, leaving only

the inverse of the easily computable squared dis-

tance between v and p.

4 CASE STUDIES

In this section we demonstrate our visualization on

several real-world examples and compare it to the

Gaussian distribution-based visualization. We show

that in cases where the Gaussian distribution works

well, so does the proposed function. In addition, we

show that our function can be used to achieve a good

result where that is not possible using the Gaussian

distribution. We focus on the Gaussian distribution

function, as quadratic polynomial potential functions

produce essentially the same results.

The ﬁrst example shows that the proposed func-

tion can be used to obtain similar results to those of

the Gaussian distribution function, see Fig. 8. The lat-

ter works well in this example, and we have produced

essentially the same result using our function. The

example itself demonstrates a small company with

four work locations. The central red cluster corre-

sponds to the company headquarters. Each vertex

in the graph represents an employee, colored accord-

ing to the location they work at. Graph edges de-

note frequent, work-related communications between

employees. Cluster overlaps reveal which employees

frequently interact with other locations. Besides the

comparison of the functions, this example shows how

this visualization can be used to depict graph overlap-

ping clustering (Krebs, 2007).

AnInverseDistance-basedPotentialFieldFunctionforOverlappingPointSetVisualization

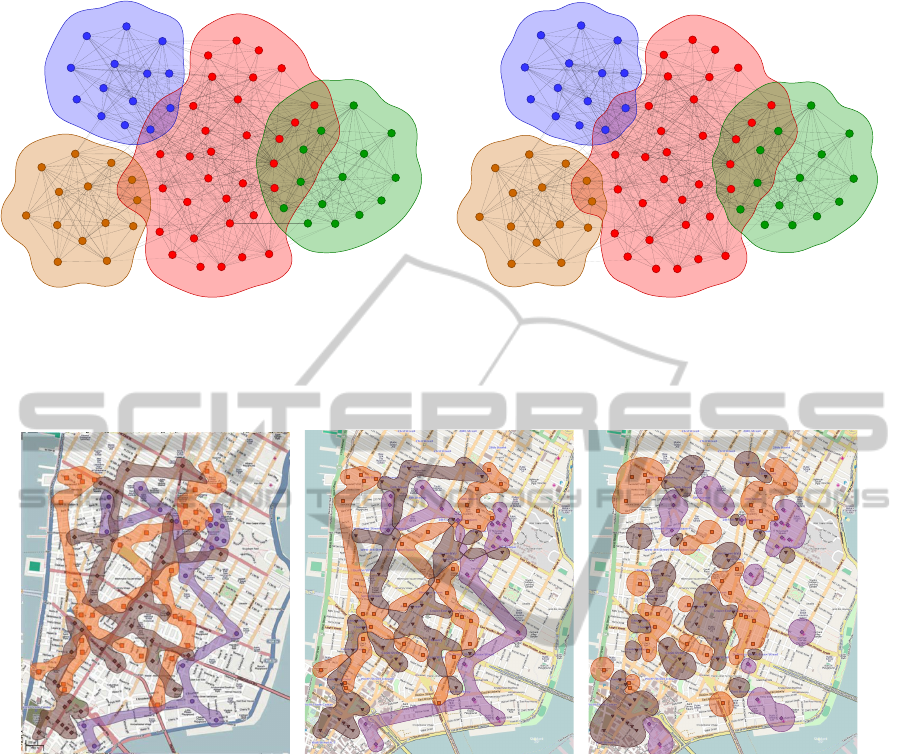
(a) (b)

Figure 8: This ﬁgure illustrates a visualization of a simple real-world overlapping set example: (a) Gaussian distribution; (b)

the proposed function. There are no difﬁculties in ensuring correct point membership for both functions in this case. The

example shows that our function is able to produce results that are very similar to the visualization with Gaussian distribution

function. Both cases illustrate that this visualization method works well with graph clustering.

(a) (b) (c)

Figure 9: Hotels (orange), subway stations (brown), and medical clinics (purple) in Manhattan: (a) Bubble Sets (Collins et al.,

2009); (b) our function with spanning tree edges added to the visualization; (c) our function without any modiﬁcations. This

example shows how region connectivity can be ensured while using our function.

In the second example we compare our visual-

ization with Bubble Sets (Collins et al., 2009), see

Fig. 9 and illustrate how their method of ensuring re-

gion connectivity works with the proposed method.

The example depicts the locations of hotels, subway

stations and clinics in Manhattan. Case (a) shows

the Bubble Sets result. It uses a quadratic polyno-

mial function as the potential ﬁeld function, and en-

sures region connectivity by assigning potential to the

edges of a (not necessary the minimum) spanning tree

of the set vertices in addition to the vertices them-

selves. When computing the inﬂuence of an edge on

a point the standard point-segment distance is used.

As a result the regions have unwanted overlaps, many

of which, however, contribute to region connectivity.

In case (b) we have applied the same spanning tree

method with our function. In addition to maintain-

ing connectivity, in our visualization there are also no

region overlaps. The function properties lead to in-

teresting behavior at edge intersection points, where

each of the regions is connected by a single point. We

leave it to the reader to decide whether such a result

is aesthetically pleasing. In case (c) we apply our vi-

sualization without any modiﬁcations.

In the last example we visualize a part of the hu-

man disease network described in (Goh et al., 2007),

see Fig. 10. In this graph, diseases are linked by

common genetic associations, with the sets denoting

various types of disease. This graph contains no set

overlaps, so using equal weights for positive and neg-

ative inﬂuence ensures that there are no region over-

laps. We show that our visualization works better than

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

(a) (b)

(e)

Figure 10: A part of the human disease network (Goh et al., 2007). Case (a) is recreated from the diseasome poster available

at http://diseasome.eu/poster.html and uses a Gaussian distribution function with no negative weights. In this case there are

many unnecessary region overlaps. Cases (b) and (c) show the Gaussian distribution function with negative weights. In (b),

we tried to preserve the blobbiness of the shapes in (a), however this results in some regions disappearing completely. In (c)

this is remedied at the cost of the blobbiness of the regions. Cases (d) and (e) show the results of the proposed method. (d)

closely resembles the results of the Gaussian function in (c). However, (e) combines the smooth regions of (a) with correct

overlaps, a result not achievable using a Gaussian function.

the Gaussian in this example. We were also interested

in improving the visualization performed by Mathieu

Bastian and S

ebastien Heymann from Gephi (avail-

able online at http://diseasome.eu/poster.html).

AnInverseDistance-basedPotentialFieldFunctionforOverlappingPointSetVisualization

5 CONCLUSIONS

We presented a new potential ﬁeld function for over-

lapping point set visualization in the form of Euler di-

agrams. In contrast to the most widely used potential

functions, the proposed function ensures correct point

membership in the set regions. Moreover, it retains all

desired Gaussian-based potential ﬁeld function prop-

erties, e.g., the set region shapes are smooth and vi-

sually pleasing. Set regions are easily identiﬁable and

closely match the layout of the points. The smooth-

ness and size of the regions can be also adjusted using

the parameters of our function.

We have applied our function on different real-

world examples and compared the result to the ear-

lier methods. The proposed function is very effective

in cases with no intersecting sets, since then the re-

gions are guaranteed not to overlap. It also works

well with overlapping sets, with regions creating an

easily comprehensible Euler diagram, retaining cor-

rect point membership. We have demonstrated that

our function works well in cases where it is not possi-

ble to obtain a good result using the Gaussian poten-

tial function. We have also illustrated how the overall

approach can be successfully used to visualize over-

lapping graph clustering.

REFERENCES

Balzer, M. and Deussen, O. (2007). Level-of-detail visual-

ization of clustered graph layouts. 2007 6th Interna-

tional AsiaPaciﬁc Symposium on Visualization, pages

133–140.

Blinn, J. F. (1982). A generalization of algebraic surface

drawing. ACM Trans. Graph., 1(3):235–256.

Byelas, H. and Telea, A. (2009). Towards realism in draw-

ing areas of interest on architecture diagrams. Journal

of Visual Languages Computing, 20(2):110–128.

Collins, C., Penn, G., and Carpendale, S. (2009). Bubble

sets: Revealing set relations with isocontours over ex-

isting visualizations. IEEE Transactions on Visualiza-

tion and Computer Graphics, 15(6):1009–1016.

Di Battista, G., Eades, P., Tamassia, R., and Tollis, I. G.

(1998). Graph Drawing: Algorithms for the Visual-

ization of Graphs. Prentice Hall PTR.

Dinkla, K., van Kreveld, M. J., Speckmann, B., and West-

enberg, M. A. (2012). Kelp diagrams: Point set mem-

bership visualization. Computer Graphics Forum,

31(3pt1):875–884.

Douglas, D. H. and Peucker, T. K. (1973). Algorithms for

the reduction of the number of points required to rep-

resent a digitized line or its caricature. Cartograph-

ica The International Journal for Geographic Infor-

mation and Geovisualization, 10(2):112–122.

Gansner, E. R., Hu, Y., and Kobourov, S. (2010). GMap: Vi-

sualizing graphs and clusters as maps. 2010 IEEE Pa-

ciﬁc Visualization Symposium PaciﬁcVis, pages 201–

208.

Goh, K.-I., Cusick, M. E., Valle, D., Childs, B., Vidal, M.,

and Barabsi, A.-L. (2007). The human disease net-

work. Proceedings of the National Academy of Sci-

ences of the United States of America, 104(21):8685–

8690.

Gross, M. H., Sprenger, T. C., and Finger, J. (1997). Vi-

sualizing information on a sphere. In In Proceedings

of the 1997 Conference on Information Visualization,

pages 11–16.

Heer, J. and Boyd, D. (2003). Vizster: visualizing online

social networks. IEEE Symposium on Information Vi-

sualization 2005 INFOVIS 2005, 5(page5):32–39.

Hobby, J. D. (1986). Smooth, easy to compute interpolat-

ing splines. Discrete and Computational Geometry,

1(2):123–140.

Krebs, V. (2007). Managing the 21st century organization.

IHRIM Journal, XI(4):2–8.

Matsumoto, Y., Umano, M., and Inuiguchi, M. (2008). Vi-

sualization with Voronoi tessellation and moving out-

put units in self-organizing map of the real-number

system. Neural Networks, 1:3428–3434.

Riche, N. H. and Dwyer, T. (2010). Untangling Euler dia-

grams. IEEE Transactions on Visualization and Com-

puter Graphics, 16(6):1090–1099.

Rosenthal, P. and Linsen, L. (2009). Enclosing surfaces

for point clusters using 3D discrete Voronoi diagrams.

Computer Graphics Forum, 28(3):999–1006.

Santamara, R. and Thern, R. (2008). Overlapping clustered

graphs: Co-authorship networks visualization. Lec-

ture Notes in Computer Science, 5166:190—199.

Simonetto, P., Auber, D., and Archambault, D. (2009).

Fully automatic visualisation of overlapping sets.

Computer Graphics Forum, 28(3):967–974.

Sprenger, T. C., Brunella, R., and Gross, M. H. (2000). H-

BLOB: a hierarchical visual clustering method using

implicit surfaces. In Visualization 2000. Proceedings,

pages 61 –68.

Van Ham, F. and Van Wijk, J. J. (2004). Interactive visu-

alization of small world graphs. IEEE Symposium on

Information Visualization, pages 199–206.

Watanabe, N., Washida, M., and Igarashi, T. (2007). Bub-

ble clusters: an interface for manipulating spatial ag-

gregation of graphical objects. In Proceedings of the

20th annual ACM symposium on User interface soft-

ware and technology, UIST ’07, pages 173–182, New

York, NY, USA. ACM.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications