
2D Shape Matching based on B-spline Curves and Dynamic
Programming
Nacéra Laiche and Slimane Larabi
Computer Science Department, USTHB University, BP 32, EL ALIA, Algiers, Algeria
Keywords: B-spline Curve, Curvature Points, Dynamic Programming (DP), Shape Matching.
Abstract: In this paper, we propose an approach for two-dimensional shape representation and matching using the B-
spline modelling and Dynamic Programming (DP), which is robust with respect to affine transformations
such as translation, rotation, scale change and some distortions. Boundary shape is first splitedinto
distinctpartsbased on the curvature. Curvature points are critical attributes for shape description, allowing
the concave and convex parts of an objectrepresentation, which are obtained by the polygonal
approximation algorithm in our approach. After thateach part is approximated by a normalized B-spline
curve usingsome global features including the arc length, the centroid of the shape and moments.Finally,
matching and retrieval of similar shapes are obtained using a similarity measure defined on their normalized
curves with Dynamic Programming.Dynamic programming not only recovers the best matching, but also
identifies the most similar boundary parts. The experimental results on some benchmark databases validate
the proposed approach.
1 INTRODUCTION
One of the most popular image information
incomputer vision is the shape. The objectshape
provides a powerfulvisual featurefor shape
representation, recognition, matching, classification..
Many approaches have been proposed for shape
modelling; most of them focus either on shape
boundaries or on interior region of shape. Region-
based methods which are easy to compute take into
account global information such as: area, circularity
and Fourier descriptor (Zhang and Lu, 2002).
Moments based shape descriptors are the most
popular region-based methods (Kim and Kim,
2000). There are different shape moments such as
the geometric moments, Legendre moments (Yang
et al, 2006) and Zernike moments (Singh and Pooja,
2011). Although these methodsachieve reasonable
results, they are not robust in case of occlusion and
do not allow partial matching (Dao and De Amicis,
2006).
On the other hand, boundary-based methods
which use curvature focus on the extraction of
features from the boundary contour. Fourier
descriptor (Zhang and Lu, 2002), chain codes
(Dubois and Glanz, 1986) and wavelet descriptors
are some of the effective boundary-based shape
methods. Curvature scale space (Mokhtarianet al.,
1996) is a rich descriptor which represents the shape
curve by convolving the curve with a Gaussian
function at different scalesand extracts the inflexion
points along the resulting curves.
In shape context descriptor (Belongie et al.,
2002), the authors describe a shape as a set of
sample pointswith the geometric relationship
between them. A shape context at a sample point
captures the distribution of the rest points relatively
to it.
Another shape descriptor is the Medial Axis
Transform, which is presented by Blum (Blum,
1967) and later Sebastian and al (Sebastian et al,
2004) used this descriptor for shape recognition.
In the literature, the notion of a part-based
representation has played an important role in object
recognition. For example, in (Latecki and Lakamper,
2000), the authors used a discrete curve evolution
technique to decompose a boundary shape into parts.
Then a shape similarity measure based on the
correspondence of visual parts is defined in order to
achieve the matching of two shapes.
In another work (Alajlan et al., 2007), the
proposed descriptor is based on triangle area
484
Laiche N. and Larabi S..
2D Shape Matching based on B-spline Curves and Dynamic Programming.
DOI: 10.5220/0004681304840491
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 484-491
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

representation (TAR) to measure concavity and
convexity of each boundary point at multi scales.
Daliri and al in (Daliri et al., 2010) proposed a
representation for shape-based recognition based on
the extraction of the perceptuallyrelevant fragments.
According to this method, each shape is described
by a set of symbols based on the extracted segments
which is mapped to an invariant dimensional space
that is used for recognition.
Other techniques consist of approximate the
shape contour by the polygonal approximation
(Arkin et al., 1991; Carmona-poyato et al.,2010), B-
spline (Paglieroni, 1985), and height functions
(Wang et al., 2012).
The B-splines possess attractive properties such
as continuity, smoothness and affine transformation
invariance that make them suitable for shape
representation. In (Cohen et al., 1995), the authors
used the B-splines to represent and match 2D objects
like handwriting and aircrafts.Wang and Teoh
(Wang and Teoh, 2004)consider the B-splines
curves and their curvature scale space for 2D shape
matching algorithm. In another work (Mongkolnam
et al., 2007) propose a technique for representing
structural features of images based on B-splines
curves and chain code.
In the above references, the B-splines are used to
extract features from boundary or to curve
representation. However, few works have used the
B-spline representation in a 2D image analysis
(Mongkolnam et al., 2007).
In this paperwe propose a recognition system
which is invariant to translation, rotation, scale
change and small amount of deformation. After
decomposing2D objects into meaningful parts, curve
normalization based on the B-splines model and
invariant moments areapplied in order to ensure the
affine invariant shape representation. The matching
algorithm that follows matches the obtained curves
using the dynamic programming (DP).DP selects
among all possible matching curves the most
promising one with the minimal distance.Two
shapes are considered similar when the cost with
both shape representations is minimal.
Our contributions of this work are:
First, we propose a part-based method for
shape representation based on the curvature
points and normalized curves.
Second, we propose to explore directly the
obtained curvesto matching and retrieving.
2 PROPOSED APPROACH
In our approach to represent 2D shape we have to
segment the contour shape into elementary parts.
The segmented boundaries are firstmodelled by B-
spline curves. Then, the obtained curvesare
normalized in several steps in order to eliminate
translation, scaling and rotation transformations. So
some global features are associated to a shape
S
as
the centriod of shape, the minimum area rectangle
and moments.
The centroid of the shape
GG
yx , is
normalized so as to coincide with the origin. It
is defined by the first moment order as:
00010010
/,/ MMyMMx
GG
(1)
where
),( jifjiM
q
ij
p
pq
(2)
and the intensity function
f
:
.),(,1),( Sjijif
(3)
The minimum area rectangle enclosing a
silhouette is defined as the smallest rectangle
minimizing the area between the shape and its
convex hull (Philip et al., 2002). It is unique
for each shape and it is invariant to rotation. In
our approach, the shape is reoriented so that
the width of the rectangle is parallel to theY
axis.
(a) (b)
Figure 1: (a) The minimum rectangle. (b) Centroid shape.
The different steps of the proposed algorithm for
shape representation and recognition will be
explained in the following sections and are
summarized in Fig. 2.
3 B-SPLINE MODELLING
It is assumed that the contour shape is extracted and
represented by a set of ordered points. Our goal is to
2DShapeMatchingbasedonB-splineCurvesandDynamicProgramming
485
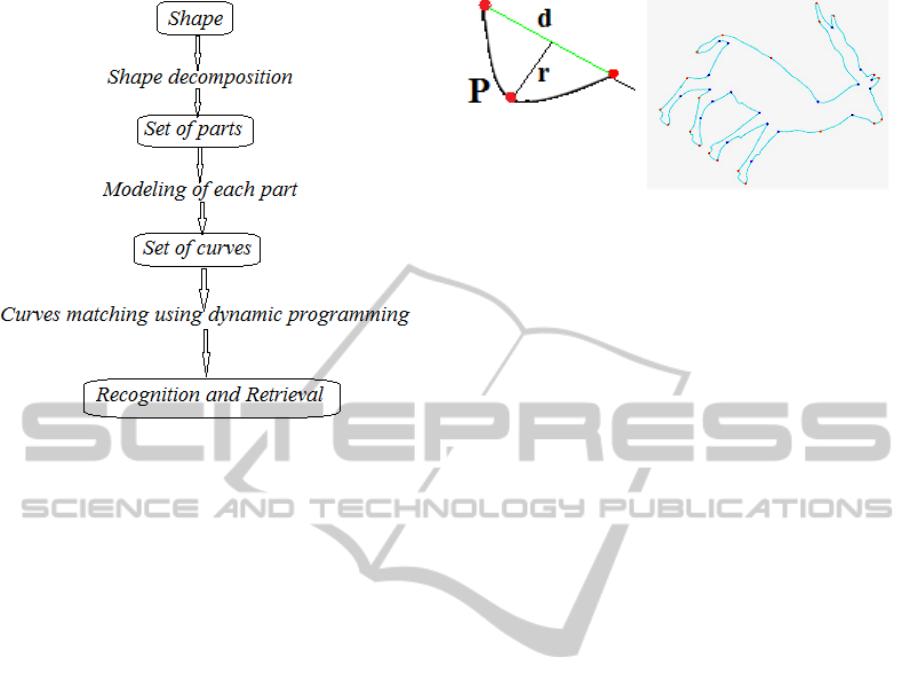
Figure 2: A bloc- diagramof the proposed algorithm for
shape representation and retrieval.
give a rough description of the shape using the B-
spline model.
First, we have to locate the partitioning points
allowing us to decompose shape.
Second, we have to approximate each part by a
normalized curve.
3.1 Shape Decomposition
Curvature points play an important role in shape
representation, reflecting the concave and convex
parts of a shape. There are various methods for
locating curvature points such as Chetverikov
algorithm (Chetvericov, 2003). In our paper, the
curvature points are extracted using Peuker Douglas
algorithm, which will be used in decomposition
process.
For a givenboundary shape
S
represented by an
ordered points, split it into
n
different parts:
i
ni
i
SS
1
.
i
S is called a partof
S
. To determine
the number of parts, we select the concave points
from the extracted curvature points.
Only concave points having a high degree of
concavity are selected to segment the shape
boundary into a set of convex parts (see Fig. 3(b)).
The concavity degree
dr /
of a point p is
computedas the ratio of the distance
r
from p to
associated chord of length
d
(Fig. 3(a)).
(a) (b)
Figure 3: (a) Concavity degree. (b) Decomposition of deer.
3.2 Curves Construction
Each part
i
S is approximated by a parametric curve
using the B-spline model. This curve is defined
relatively to the coordinates system attached to the
minimum rectangle enclosing the shape. A B-spline
curve is used because B-spline has important
properties such as smoothness, continuityand
theirlocal control. In our approach a cubic B-spline
is chosen instead of a higher order because it is less
wiggly.
The B-spline curve
)(tS
of order 3 is defined by:
m
i
ii
PtNtS
0
3,
)()(
(4)
Where
)(
3,
tN
i
is the splines basis functions of order
3 in the parameter
1,0
t
(Cohen et al., 1995) and
),(
iii
yxP
;
0
i
to
m
are the B-splines
coefficients (control points)
.
The conventional method toestimate the control points
uses an iterative process for adjusting the number of
the control points to maintain an error bound (Wang
et al., 2006). In our work,
the control points as chosen
as the high curvature points.
3.3 Curves Normalization
In order to simplify comparison of curve shapes, we
normalize the measured B-splines curves without
changing the shape.
A curve translation procedure is used as the first
step of normalization. The centroid of the shape is
normalized so as to coincide with the origin (see Fig.
4):
GG
yyyxxx
','
(5)
Where
),( yx
represents a curve point and
)','( yx
the corresponding normalized curve point.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
486
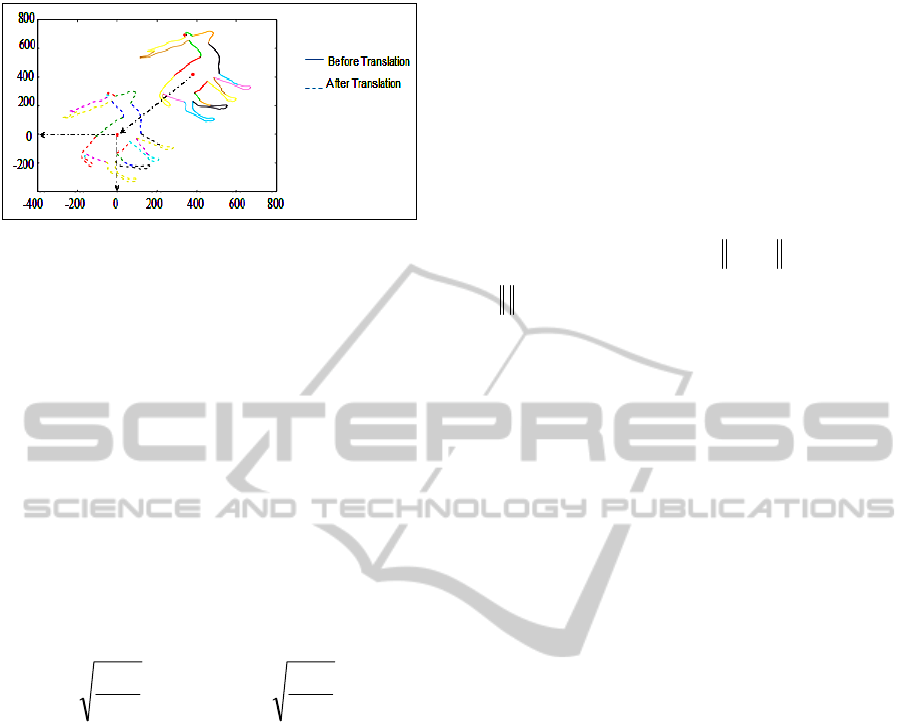
Figure 4: Curve shape translation.
In the second step of normalization, we have to
eliminate scaling transformation based on the
geometric momentsof a shape of an object. There are
several ways to normalize the shape size.Adjusting
the dimensions of the minimum rectangle, width and
high or its area. However in our approach, moments
of order up to two are used instead of area because
when small deformations occur, area can be altered.
The transformation carried out on the curve
points
),( yx
obtained through the B-spline model is
defined by
21
/''',/''' kyykxx
(6)
Where the scaling factors
1
k
and
2
k
represent the
normalized moment of order two:
L
M
kand
L
M
k
02
2
20
1
(7)
With
L
is the length of the B-spline curve.
4 SHAPE MATCHING
This section describesa dynamic-programming for
establishing correspondences between normalized
curves of two shapes. Dynamic programming is an
appropriate method for finding associations between
segments. It has been used for deformable-template-
based segmentation (McNeill and Vijayakumar,
2006).The idea behind our matching process is that
if two shapes match, then they share some similar
curves. However, it seems appropriate to apply the
dynamic programming to establish the best matching
pair of curvesby using a suitable distance measure.
4.1 Similarity between Curves
Measuring the similarity between curves is a key
element in object recognition. There are several
distances to measure resemblance. Frechet and
Euclidean distance are used for boundary based
approaches. In our approach, the Hausdorf distanceis
used for matching two different curves.
Given two normalized curves
C
and
'C
of a
query shape
Q
and a reference shape
M
respectively, the Hausdorffdistance is defined as:
( , ') max( ( , '), ( ', ))CC hCC hC C
(8)
Where
'minmax)',(
''
cccch
Cc
Cc
(9)
and
. is a norm defined on the curve, such as the
2
L
norm.
This similarity measurement is used for dynamic
programming for curve-based shape matching.
4.2 Matching using Dynamic
Programming
Our aim is to find the best match between a given
shape and the query shape by matching their
different curves. For this, we use the Dynamic
programming (DP). The proposed algorithm tries to
build a DP table of cots of partial matches in order to
find the minimum cost with the two shapes.
Given two shapes
Q
(query shape) and
M
(model
shape), the DP table has
q
rows and
m
columns,
where
q
and
m
correspond to the B-splines curves
of
Q
and
M
respectively.
The dynamic programmingalgorithmcan be defined
as follows:
Let
),(
ji
CCD denotes the optimal cost of
matching
i
CC ,....,
1
, the first i curves of Q with
j
CC ,....,
1
, the first
j
curvesof M. It can be
defined as:
).,(),(
),,(),(
),,(),(
min),(
11
1
1
jiji
jiji
jiji
ji
CCCCD
CCCCD
CCCCD
CCD
(10)
Where
),(
ji
CC
denotes the cost of matching
curves
i
C and
j
C defined by the Eq. (8).
Two shapes are considered similar when the cost
with both shape representations is minimal.
2DShapeMatchingbasedonB-splineCurvesandDynamicProgramming
487

5 EXPERIMENTAL RESULTS
Several experiments have been carried out to test the
effectiveness of the proposed approach.
The well known MPEG-7 database (Latecki et al,
2000) is used in our tests. The database contains
1400 images from 70 classes with 20 images per
class (see Fig. 5).
Figure 5: Some examples from MPEG-7 database.
The first experiment illustrates some retrieval
results from different classes of MPEG-7 database.
Each shape has been matched against all the shapes
in the database and itself. The obtained results of
matching have been ranked using the minimal cost
given by the dynamic programming that reflects the
similarity between the different normalized curves.
For each query, the first twenty closest shapes are
shown in Fig. 5.
The queries shapes are in the first row (at the left
of each row). The twenty top similar shapes that
have been matched by the proposed algorithm are
shown in the rest rows.
In order to evaluate the effectiveness of the
matching, we have reported under each query shape
the obtained hit rate(see Fig. 7). This hit rate is
defined as the ratio of the number of retrieved
shapes belonging to a certain class to the number of
shapes in that class.
A qualitative analysis of the retrieval results is
performed.
The retrieval results for the query shape of deer-5
Figure 6: Query shapes and their retrieval results from
MPEG-7 database (Latecki et al, 2000). Left column
shows query shapes and the right rows show the first 20
ranked nearest neighbours for each query shape.
are compared with the results produced in (Qi et al.,
2010) using the methods developed by Wei in (Wei
et al., 2009) and the weight-based method in (Jain
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
488

100.00 100.00 100.00 90.00 95.00 88.00
Figure 7: Some query shapes with their recognition rates.
and Vailaya, 1998).
These methods are based on extracting global
features such as moments, centroid distances, Zenike
moments and edge directions.
Query Retrieval Results
(a)
(b)
(c)
Figure 8: Top ten retrieval results of shape deer-5 using
the weight-based (a). (b) The two-component solution. (c)
The proposed approach.
As we can see, the retrieval results of the method
proposed by Qi et al. and illustrated by Fig. 8(b)
provide 50% precision rate for the top ten retrieval.
However, the method of Jain and Vailaya achieve
60% and the proposed approach with 70%.
5.1 Dealing with Occlusion
The goal of the second test is to show the robustness
of the proposed approach to deal with occluded
shapes. For this, we have used shapes of Kimia-99
database (Sebastian et al., 2004) (see Fig. 9). This
database consists of nine categories with eleven
shapes per category.
In this experiment, we retrieve the top 15 most
similar for each query.
Figure 9: Kimia-99 database.
Table 1 shows an example of this retrieval. The left
column represents the query shape. As each class
contains 11 shapes, this figure shows that in most
cases, most of the shapes from the query class are
among the first 11 retrieved shapes.
6 CONCLUSIONS
In this paper, we have presented a new approach for
shape representation based on the B-spline model
and dynamic programming. A boundary shape is
represented as a sequence of normalized B-splines
curves of its meaningful parts. These parts are
obtained using curvature points.
A key characteristic of our approach is that
describes the different partsconstituting the outer
closed boundary of the shape. This can be used
directly in matching process using the Hausdorff
distance and dynamic programming.
The obtained results show the robustness of the
approachto several kinds of geometric
transformations and occlusion.
2DShapeMatchingbasedonB-splineCurvesandDynamicProgramming
489

Table 1: A tabulation of the top 15 matches for some
occluded query shapes.
Query Retrieval results
REFERENCES
Alajlan, N., El Rube, I., Kamel, M. S., Freeman, G., 2007.
Shape retrieval using triangle-area representation and
dynamic space warping.In Pattern Recognition.,40,
1911-1920.
Arkin, E., Chew, L., Huttenlocher, D., Mitchell, J., 1991.
An efficient computable metric for comparing
polygonal shapes. In IEEE Transactions on Pattern.
Analysis and Machine Intelligence. PAMI 13 (3), 209-
216.
Belongie, S., Malik, J., Puzicha, J., 2002.Shape matching
and object recognition using shape contexts. In IEEE
TRANS. PAMI 24 (24), 509-521.
Blum, H., 1967. A transformation for extracting new
descriptors of shape.In Models for the perception of
speech and visual form. MITPress, 362-379.
Carmona-poyato, A., Madrid-Cuevas, F. J., Medina-
Carnicer, R., Munoz-Salinas, R., 2010.Polygonal
approximation of digital planar curves through break
point suppression. In: PatternRecognition 43, 14-25.
Chetvericov, D., 2003. A Simple and efficient algorithm
for detection of high curvature points in planar
curves.In 10
th
International Conference. CAIP, 25-27.
Chong, C. W., Raveendran, P., Mukundan, R., 2003.
Translation invariants of Zernike moments. In: Pattern
Recognition.1765-1773.
Cohen, F. S., Huang, Z., Yang, Z. Invariant matching and
identification of curves using B-spline curve
representation. In IEEE Transactions on Image
Processing. 4(1) (1995) 1-10.
Daliri, M. R., Torre, V., 2010. Classification of silhouettes
using contour fragments. In Computer Vision and
Image Understanding.113, 1017-1025.
Dao, M. S., Amicis, R., 2006 .A new method for
boundary-based shape matching and retrieval. In:
Proceedings of te International Conference on Image
Processing,8-11.
Dubois, S. R., Glanz, FH., 1986. An autoregressive model
approach to two dimensional shape classification. In:
IEEE Trans Pattern Anal Mach Intell, 8, 55-65.
Hwang, S. K., Kim, W. Y., 2006. A novel approach to the
fast computation of Zernike moments. In: Pattern
Recognition. 39, 2065-2076.
Jain. A. K., Vailaya. A., 1998. Shape-based retrieval: A
case study with trademark image databases. In: Pattern
Recognition, 31 (9), 1369-1390.
Kim. H., Kim. J., 2000.Region-based shape descriptor
invariant to rotation, scale and translation, In: Signal
Processing: Image Communication, 16, 87-93.
Latecki, L. J, Lakamper, R. 2000. Shape similarity
measure based on correspondence of visual parts. In:
IEEE TPAMI. 22 (10), 1182-1190.
McNeill, G., Vijayakumar, S., 2006. Hierarchical
procrustes matching for shape retrieval. In: CVPR:
IEEE International Conf on Computer Vision and
Pattern Recognition, pp. 885-894.
Mokhtarian, F., Abbasi, S., Kittler, J. (1996).Efficient and
robust retrieval by shape content through curvature
scale space, In International Workshop on Image
Databases and Multimedia Search, pp. 35-42.
Mongkolnam, P. Nukoolkit, C., Dechsakulthorn, T. 2007.
Represent image contents using curves and chain code.
In:IAPR Conference on Machine and Vision
Applications, MVA .355-358.
Paglieroni, D., Jain, A.K., 1985. A Control point theory
For boundary representation and matching. In: Proc.
ICASSP. 1851-1854.
Philip, J., Schneider, D., Eberly, H. Geometric tools for
computer graphics, Ed. Textbook Binding, 2002.
Preparata, F., Shamos, M., 1985.Computational
Geometry: An introduction, Springer, Berlin,
Germany.
Qi, H., Li, K., Shen, Y., Qu, W., (2010). An effective
solution for trademark image retrieval by combining
shape description and feature matching. In: Pattern
Recognition, 43(6) 2017-2027.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
490

Sebastian, T. B., Klein, P. N., Kimia, B. B., 2004.
Recognition of shapes by editing their shock graphs.
InIEEE TRANS. PAMI 26 (5), 550-571.
Singh, C., Pooja, 2011. Improving image retrieval using
combined features of Hough transform and Zernike
moments. In Elsevier, Optics and Lasers in
Engineerin, 49 (12), 1384-1396.
Wang. J., Bai. X., You.X., Liu.W., 2012.Shape matching
and classification using height functions. In: Pattern
Recognition Letters, 33, 134-143.
Wang, W., Pottmann, H., Liu Y., 2006. Fitting B-spline
curves to point clouds by curvature-based squared
distance minimization”. In ACM Transactions on
Graphics, 25(2), 214-38.
Wang, Y., Teo, E. K. 2004. A novel 2D shape matching
algorithm based on B-spline modeling. Singapore.
Wei, C. H., Li, Y., Chau, W. Y., Li, C. T. (2009).Trade-
mark image retrieval using synthetic features for
describing global shape and interior structure. In:
Pattern Recognition, 42 (3) 386-394.
Yang, G. Y., Shu, H. Z., Toumoulin, C., Han, G. N., Luo,
L. M., 2006. Efficient Legendre moments computation
for grey level images. In: Pattern Recognition. 39, 74-
80.
Zhang, D. S. Lu, G? 2002. Generic Fourier for shape-
based image retrieval. In ICME: IEEE. International
Conference on Multimedia and Expo, pp. 425-428.
2DShapeMatchingbasedonB-splineCurvesandDynamicProgramming
491
