Appearance-based Eye Control System by Manifold Learning

Ke Liang

, Youssef Chahir

, Mich

ele Molina

, Charles Tijus

and Franc¸ois Jouen

CHArt Laboratory, EPHE Paris, 4-14 rue Ferrus 75014 Paris, France

Computer Science Department, GREYC-UMR CNRS 6072, University of Caen, Caen, France

PALM Laboratory EA 4649, University of Caen, Caen, France

Keywords:

Appearance Eye Descriptor, Appearance-based Method, Manifold Learning, Spectral Clustering, Human-

computer Interaction.

Abstract:

Eye-movements are increasingly employed to study usability issues in HCI (Human-Computer Interacetion)

contexts. In this paper we introduce our appearance-based eye control system which utilizes 5 speciﬁc eye

movements, such as closed-eye movement and eye movements with gaze ﬁxation at the positions (up, down,

right, left) for HCI applications. In order to measure these eye movements, we employ a fast appeance-based

gaze tracking method with manifold learning technique. First we propose to concatenate local eye appearance

Center-Symmetric Local Binary Pattern(CS-LBP) descriptor for each subregion of eye image to form an eye

appearance feature vector. The calibration phase is then introduced to construct a trainning samples by spectral

clustering. After that, Laplacian Eigenmaps will be applied to the trainning set and unseen input together to

get the structure of eye manifolds. Finally we can infer the eye movement of the new input by its distances

with the clusters in the trainning set. Experimental results demonstrate that our system with quick 4-points

calibration not only can reduce the run-time cost, but also provide another way to mesure eye movements

without mesuring gaze coordinates to a HCI application such as our eye control system.

1 INTRODUCTION

As gaze tracking technology improves in the last 30

years, gaze tracker offers a powerful tool for diverse

study ﬁelds, in particular eye movement analysis and

human-computer interaction (HCI), such as eye con-

trol system or eye-gaze communication system. Eye

control helps users with signiﬁcant physical disabili-

ties to communicate, interact and to control computer

functions using their eyes (Jacob & Karn, 2003). Eye

movements can be measured and used to enable an in-

dividual actually to interact with an interface. For ex-

ample, users could position a cursor by simply look-

ing at where they want it to go, or click an icon by

gazing at it for a certain amount of time or by blink-

ing.

Nowadays most commercial gaze trackers use

feature-based method to estimate gaze coordinates,

which relies on video-based pupil detection and the

reﬂection of infra-red LEDs. In general, there are two

principal methods: 1) Pupil-Corneal Reﬂection(P-

CR) method (Morimoto et al., 2000)(Zhu and Ji,

2007), and 2) 3D model based method(Shih and Liu,

2004)(Wang et al., 2005). IR light and extraction of

pupil and iris are important for these feature-based

methods, and the calibration of cameras and geome-

try data of system is also required.

Appearance-based methods do not explicitly ex-

tract features like the feature-based method, but rather

use the cropped eye images as input with the intention

of mapping these directly to gaze coordinates(Hansen

and Ji, 2010). The advantage is that they do not re-

quire calibration of cameras and geometry data like

feature-based method. Moreover, they can be less ex-

pensive in materials than feature-based method since

they don’t have to work on the same quality im-

ages like feature-based method does. But they still

need a relatively high number of calibration points

to get accurate precision. Different works can be

seen in multilayer networks(Baluja and Pomerleau,

1994)(Stiefelhagen et al., 1997)(XU et al., 1998),

or Gaussian process(Nguyen et al., 2009)(Williams

et al., 2006), or manifold learning(Martinez et al.,

2012)(Tan et al., 2002). Williams et al. (Williams

et al., 2006) introduces the sparse, semi-supervised

Gaussian Process (S

GP) to learn mappings from

semi-supervised training sets. Fukuda et al. (Fukuda

et al., 2011) propose a gaze-estimation method that

uses both image processing and geometrical process-

ing to reduce various kinds of noise in low-resolution

148

Liang K., Chahir Y., Molina M., Tijus C. and Jouen F..

Appearance-based Eye Control System by Manifold Learning.

DOI: 10.5220/0004682601480155

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 148-155

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

eye-images and thereby achieve relatively high accu-

racy of gaze estimation.

Manifold learning is widely applied to solve many

problems in computer vision, in pattern recognition

etc (Lee and Kriegman, 2005)(Rahimi et al., 2005)

(Weinberger and Saul, 2006)(Zhang et al., 2004).

Manifold learning, often also referred to as non-

linear dimensionality reduction, is also one of the

approaches applied in appearance-based gaze track-

ing(Tan et al., 2002), and one of the reason to ap-

ply manifold learning techiques is to reduce com-

putational costs. Manifold learnig means the pro-

cess of estimating a low-dimensional structure which

underlies a collection of high-dimensional data, also

preserves characteristic properties of the set of high-

dimensional data. Here we are interested in the

case where the mainifold lies in a high dimensional

space R

, but will be homeomorphic with a low

dimensional space R

(d < D). Laplacian eigen-

maps(Belkin and Niyogi, 2001)(Belkin and Niyogi,

2003) most faithfully preserves proximity relations of

a high-dimensional non-linear data set in the low di-

mensional space, by using spectral graph technique.

Here our emphasis is on creating a pratical, real-

time eye control system with our appearance-based

method. Our contributions are:

• A subregion CS-LBP concatenated histogram is

used as eye appearance feature which not only re-

duce the dimension of raw images, but also can be

robust against the changes in illumination.

• During the calibration phase, we use spectral clus-

tering to build on-line the subject’s eye move-

ments model by selecting and trainning a limited

number of eye feature samples.

• To infer its movement for an unseen eye input,

Laplacian Eigenmaps is introduced to analyse the

similarities and the manifold structure for the

training samples and the unseen input.

• The system requires only a remote webcam and

without IR light.

The rest of the paper is organized as follows. Sec-

tion2 describes the eye manifold learning to the pro-

posed eye feature. Section 3 presents a global view of

our eye control system. Section 4 shows the experi-

mental setup and results. Finally section 5 concludes

the paper.

2 EYE APPEARANCE

MANIFOLD LEARNING

2.1 Eye Appearance Descriptor

Let an eye image I be a two-dimensional M by N

array of intensity values, and it may also be consid-

ered as a vector of dimension M × N. The proposed

gaze tracker captures left and right eyes together and

combines them into one image. Our eye image of

size 160 by 40 becomes a vector of dimension 6400.

Appearance-based gaze tracking methods mostly rely

on the eye images as input. Extracting eye appearance

descriptor not only helps to reduce the dimension of

eye images, but also preserves the feature and varia-

tion of eye movemnts.

There exist a number of eye appearance feautre

extraction methods for gaze tracking system, like

multi-level HOG (Martinez et al., 2012), eigeneyes

by PCA (Noris et al., 2008), and subregions feature

vector (Lu et al., 2011). Lu et al. have proven the efﬁ-

ciency of using 15D subregions feature vector in (Lu

et al., 2011). To compute this feature vector, the eye

image I

is divided into N

subregions of size w × h.

Let S

denote the sum of pixel intensities in j−th sub-

region, then feature vector X

of the image I

is repre-

sented by

,...,S

]

∑

j ∈ N

(1)

Here we introduce our subregion methods with

Center-Symmetric Local Binary Pattern (CS-LBP) to

calculate low dimensional feature vector for raw eye

image content. Local Binary Pattern (LBP) opera-

tor has been highly successful for various computer

vision problems such as face recognition, texture

classiﬁcation etc. The histogram of the binary pat-

terns computed over a region is used for feature vec-

tor. The operator describes each pixel by the relative

graylevels of its neighboring pixels. If the graylevel

of the neighboring pixel is higher or equal, the value

is set to one, otherwise to zero.

We calculate the CS-LBP(Heikkil

a et al., 2009)

histogram, which is a new texture feature based on the

LBP operator, for each subregion in Fig.1(a) and con-

catenate them to form the eye appearance feature vec-

tor. Instead of describing a center pixel by comparing

its neighboring pixels with it in LBP, CS-LBP com-

pares the center-symmetric pairs of pixels in Fig.1(b).

The CS-LBP value of a center pixel in position

(x,y) is calculated as follows:

CS − LBP

R,N,T

(x,y) =

N/2−1

∑

i=0

s(n

− n

i+(N/2)

)

Appearance-basedEyeControlSystembyManifoldLearning

149

(a) (b)

Figure 1: a) 40 subregions of an eye image sample b) CS-

LBP for a neighborhood of eight pixels.

where s(t) =



1 t > T

0 else

, n

and n

i+(N/2)

are the

gray values of center-symmetric pairs of pixels of N

equally spaced pixels on a circle with radius R , and

the threshold T is a small value. From this equation,

the value of CS-LBP may be any integer from 0 to

N/2

− 1, and the histogram dimension will be 2

N/2

CS-LBP is fast to compute and its histogram has been

proven to be robust against the changes in illumina-

tion as a texture descriptor(Heikkil

a et al., 2009).

2.2 Spectral Clustering

Graph Laplacians are the main tools in spectral graph

theory. Here we focus on two kinds of graph Lapla-

cian:

• Unnormalized graph Laplacian.

= D −W

where W is the symmetric weight matrix with pos-

itive entries for edge weights between vertices. If

i j

= 0, then vertices i and j are not connected.

D is the degree matrix: d

∑

j=1

i j

and d

i j

= 0

∀i 6= j.

• Normalized graph Laplacian.

sym

= D

−1/2

1/2

= I − D

−1/2

W D

1/2

normalized

= D

−1

= I − D

−1

W = I − L

Where L

sym

is a symmetric matrix, and L

closely related to a random walk. There are 3

properties:

1) λ is an eigenvalue of L

with eigenvector v if

and only if λ and v solve the generalized eigen-

problem Lv = λDv.

2) L

is positive semi-deﬁnite with the ﬁrst en-

genvalue λ

= 1 and the constant one vector 1

the corresponding eigenvector.

3) All eigenvectors are real and it holds that: 1 =

|λ

| ≥ |λ

| ≥ ... ≥ |λ

| .

(a) (b)

Figure 2: (a) Eye capture for 8 visual patterns in the screen

(b) 4-points calibration (up-right, up-left, down-left, down-

right) (c) Eye manifolds in the phase of 8-points calibration

(d) Eye manifolds in the phase of 4-points calibration (up-

right, up-left, down-left, down-right).

Laplacian eigenmaps use spectral graph tech-

nique to compute the low-dimensional representation

of a high-dimensional non-linear data set, and they

most faithfully preserves proximity relations, map-

ping nearby input patterns to nearby outputs. The

algorithm of Laplacian eigenmaps has a similar struc-

ture as LLE. First, one constructs the symmetric undi-

rected graph G = (V, E), whose vertices represent in-

put patterns and whose edges indicate neighborhood

relations (in either direction). Second, one assigns

positive weights W

i j

to the edges of this graph; typ-

ically, the values of the weights are either chosen

to be constant, say W

i j

= 1/k, or a heat kernel, as

i j

= exp(−

||x

−x

) where l is a scale parameter.

In the third step of the algorithm, one obtains the em-

beddings ψ

∈ R

by minimizing the cost function:

∑

i j

||ψ

− ψ

j j

This cost function encourages nearby input patterns to

be mapped to nearby outputs, with “nearness” mea-

sured by the weight matrix W . To compute the em-

beddings, we ﬁnd the eigenvalues 0 = λ

≤ λ

≤

... ≤ λ

and eigenvectors v

,...,v

of the generalized

eigenproblem: Lv = λDv. The embeddings Ψ : ψ

→

(i),...,v

(i)).

Spectral clustering refers to a class of techniques

which rely on the eigen-structure of a similarity ma-

trix to partition points into disjoint clusters with

points in the same cluster having high similarity and

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

150

points in different clusters having low similarity. We

follow the works of (Shi and Malik, 2000). Their al-

gorithm of spectral clustering computes the normal-

ized graph Laplacian L

, and its ﬁrst k generalized

eigenvectors v

,...,v

as embeddings, and then utilise

k-means to cluster the points.

From the section 2.1 we’ve introduced our subre-

gion CS-LBP methods to extract the eye appearance

feature descriptor. Here we’d like to at ﬁrst obtain eye

manifold distribution by using Laplacian Eigenmaps,

and then we apply the normalized spectral clustering.

The Fig.2 (a,b) shows eye samples of the subject’s

eye movements when the subject follows the visual

pattern(green points) shown in the screen. The Fig.2

(c,d) demonstrate the distribution of embeddings in

the subspace. (c) gives the distribution of a dataset

of 240 points which contains only the eye samples on

the 8 points in the screen , while (d) contains only

120 eye samples from the 4 points in the corner(up

right, up left, down left, down right). For a given

number C of visual patterns, generally we can get l

clusters U = {U

,...,U

} associated with weights

W = {w

,w2,...,w

} by the size of cluster, where

C ≤ l < n.

3 EYE CONTROL SYSTEM

In this section we introduce our eye control system

which aims to recognize 5 speciﬁc eye movements,

such as closed-eye movement and eye movements

with gaze ﬁxation at the up-right, up-left, down-right

and down-left of the screen. The four eye gaze move-

ments are used to select events and the closed-eye

movements can be used as control signal like a ’click’

of the mouse. The system has two components: cal-

ibration phase and prediction phase which are shown

in Fig. 3.

3.1 Calibration Phase

As an appearance-based approach, the system needs

an eye-gaze mapping calibration which can be consid-

ered as the collection and analysis phase of labelled

and unlabelled eye data. This on-line calibration pro-

cedure aims to provide a model of the subject’s eye

movement in a given region (for example, the screen

of laptop etc) with limited number of eye samples.

The system utilizes 4 points (up-right, up-left,

down-right and down-left of the screen) as calibra-

tion points (Fig. 2b). In order to achieve an efﬁcient

calibration, we apply spectral clustering (Sec. 2.2)

to all the unlabelled eye samples and get the clusters

of their manifolds during the calibration procedure.

Figure 3: Flowchart of system.

A labelled data set then can be built by selecting the

center samples of each clusters, and can be used as

training model for a new inputs. The manifold struc-

ture of labelled data set might be shown in Fig. 2d.

3.2 Prediction Phase

The prediction phase executes a classiﬁcation task for

new eye feature inputs. In order to map feature vec-

tor X ∈ R

to gaze region output Y ∈ R, which rep-

resents a set of categories, we have a trainning set

D = {(X

)|i = 1,2,...,n}, where X

denotes an in-

put vector of dimension M

and Y

denotes the number

of category, n is the number of observations. Given

this trainning set D, we wish to make predictions for

the new inputs X

which is not in the training set.We

apply Laplacian Eigenmaps to the trainning set and

the new input together.

We propose a 24-points visual pattern scenario

Fig. 4(a) in a given region which size is 754

× 519 pixels. With the screen in which pixel is

0.225mm/pixel, the real size is about 17cm × 11.6cm.

The subject is asked to gaze each point one by one.

Fig. 4(b,c,d) shows the distribution of 3D eye man-

ifolds projected by laplacien eigenmaps. Notice that

there are some degrees of similarity between the man-

ifold surface and position plane of the 24 points. From

Appearance-basedEyeControlSystembyManifoldLearning

151

(a) (b) (c) (d)

Figure 4: Projection of 990 eye gaze samples on 24 points in the screen (a) by Laplacian Eigenmaps. b) c) 3D eye manifolds

= {v

} d) 3D eye manifolds e

= {λ

,λ

(a) (b) (c) (d) (e) (f)

Figure 5: Projection of the trainning samples plus new eye input of different movements by by Laplacian Eigenmaps (l=700).

(Red point represents the new input data, black points represents the trainning samples).

their manifold structure we can infer the eye move-

ment of the new input by the distance of similarity

with the training datas given a threshold T

corner

For an input like eye blinkings or closed-eye

movements, which are very different with the train-

ning samples, their manifold structure is completely

changed as shown in Fig. 5f. The scale of trainning

set becomes more smaller than the scales in the other

case such as Fig. 5 (a,b,c,d), while the eye blink-

ing image is added into the trainning set. Laplacian

Eigenmaps helps to give prominence to the differ-

ence. We take advantage of this difference in scale

to recognize eye blinkings by the distance of similar-

ity with the training datas given a threshold T

blinks

4 EXPERIMENTATION

This section evaluates our proposed methods pre-

sented in the previous sections. Our experimenta-

tion is tested on MacBook Pro 8,1 with Intel Core

i5-2415M CPU. Microsoft LifeCam HD-5000 is used

for image acquisition of gaze tracking system in the

experiments. The USB color webcam captures 30

frames per second with a resolution of 640 × 480.

4.1 Eye Detection and Tracking

The distance between the subject and the camera is

about 40 - 70 cm. To the entire RGB image cap-

tured from camera, we ﬁrstly use a face components

detection model, which is based on Active Shape

Model(T.F.Cootes et al., 1995), to localize the eye

regions and the corners. We introduce then Lukas-

Kanade method to track the corner points in the fol-

lowing frames. Finally we combine the left and right

eye regions to the eye appearance pattern, which is

converted to grayscale and used as the input data for

gaze estimation process. The process of eye detection

and tracking is shown in Fig. 6. The eye appearance

pattern is an image of 160×40. Fig. 7 shows eye sam-

ples of ﬁve subjects. As introduced in section 2.1, the

pattern is divided into 40 subregions and we calculate

CS-LBP histogram for each subregion. The size of

the feature vector is 640.

4.2 Eye Manifolds

In this section we evaluate eye manifold structure for

different persons, and in different conditions.

Taking eye samples of ﬁve subjects such as Fig. 7

who follow the 16 points outside-round the screen, we

can see that the distributions of their eye manifolds

are relatively similar (Fig. 8), despite the difference

between their eyes’ form. If taking eye samples at

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

152

Figure 6: Eye localization and tracking

Figure 7: Five eye samples in different light condition. The

subjects have head-free movement and the distance between

the subject and the camera is about 40 - 70 cm.

(a) (b) (c) (d)

Figure 8: Each line of ﬁgures represents the eye mani-

fold distribution for each subject mentioned above. α =

0.8 l = 100 a)b) 750 eye samples c)d) 120 eye samples.

four points on the corners, the distibution shows the

different clusters distinctly such as Fig. 8(c)(d). The

curve in Fig. 13 shows the exponential growth of time

cost for spectral clustering with the growth number of

eye samples.

Here we analyse the structure of eye manifolds

projected by laplacien eigenmaps in 2 different condi-

tions as the illumination changes and the head move-

ment. We also compare our subregion CS-LBP de-

scriptor with the original subregion method, which

calculates the feature vector as the equation(1) shown

in Sec. 2.1.

• Illumination changes

Here the subject follows the 4 points in the screen

(Fig. 2b) 2 times within 20 seconds, while the

indoor-illumination changes as Fig. 9. We extract

the eye appearance descriptor from the 500 eye

images by our proposed CS-LBP descriptor, alos

by the original subregion descriptor as a compar-

ative method. From the observations (Fig. 10)

of projection by Laplacian Eigenmaps, CS-LBP

descriptor gives the translation of eye movement

stucture for the changes of illumination, while

subregion descriptor is totally disturbed by the

changes illumination.

• Head movements

Different humans vary widely in the tendency to

move the head for a given amplitude of gaze shift.

We are interested in the difference of eye manifold

structure between a limited natural head move-

ment as Fig. 11 and the movement keeping the

head still. Here the subject is asked to follow a

point which moves along the edge line of screen.

The size of screen is 33cm × 22cm. The distance

between the subject and the screen is about 60 cm.

From the result as shown in Fig. 12, we can see

that both the descriptors can keep the structure of

eye movement while moving the head slightly, but

the scale of structure changes.

4.3 Calibration Phase and Prediction

Phase

The calibration phase will vary depending on appli-

cation. Generally the conventional calibration proce-

dure makes each calibration point appear in the screen

for one second, and the subject is expected to follow

it. The 30Hz camera can capture 120 images for 4

senconds. So in this case we can get 120 eye samples

for unlabelled data set.

But for our eye-control application, the calibration

phase can be done more quickly et efﬁciently, because

the position of the four calibration points are just at

the corner of the screen. The more efﬁcient way to

calibrate is just that let the subject look at the corner

by himself and the camera captures the images during

Appearance-basedEyeControlSystembyManifoldLearning

153

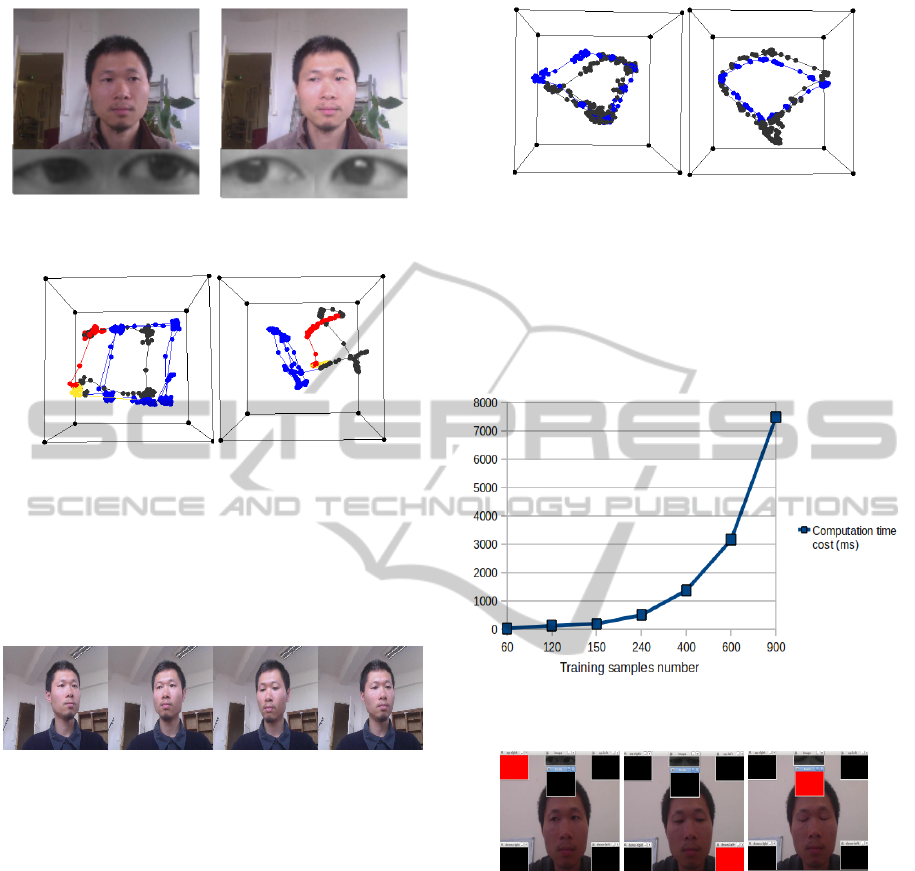
Figure 9: Demonstration of the changes of illumination by

2 sample frames.

(a) (b)

Figure 10: Comparison of using CS-LBP and subregion

methods as eye descriptor in the condition of changes of

illumination (500 eye samples). The different colors show

the changes of illumination. a) CS − LBP

1,8,0.01

fea-

ture vector projected in 3D by Laplacian Eigenmaps(l =

10000). b) original subregion feature vector by Laplacian

Eigenmaps(l = 700).

Figure 11: Demonstration of the free-head movement while

the suject follows the points in the screen. The distance

between the subject and the screen is about 60 cm.

the time. It might take one or two seconds and we can

get 30 or 60 unlabelled eye samples.

In our experimentation, the prediction phase uti-

lize a trainning set of 12 samples (3 samples for each

corner). In order to predict an unseen input, we com-

pute the 3D manifold for the set of 13 eye features (12

trainning samples + 1 new input) by Laplacian Eigen-

maps and compare the scale of structure and their dis-

tances as shown in Fig 5. The thresholds T

blinks

and

corners

take empirical values as 2 and 900. The ex-

perimentation movie in the attachment shows that the

system can predict the eye movements for four direc-

tions, at the same time, it is also able to recognize the

closed-eye movements as well as eye blinkings(Fig.

14).

Fig. 13 demonstrates the consuming time of

Laplacian Eigenmaps for different numbers of train-

ning samples. The consuming time for 60 eye sam-

(a) (b)

Figure 12: Comparison of using CS-LBP and subregion

methods as eye descriptor for the head movement (520 eye

samples). Blue points represent the stucture with ﬁxed head

and black points represent the structure with slight head

movements. a) CS − LBP

1,8,0.01

feature vector

projected in 3D by Laplacian Eigenmaps(l = 9000). b) orig-

inal subregion feature vector by Laplacian Eigenmaps(l =

900).

Figure 13: Consuming time of spectral clustering to differ-

ent numbers of eye samples.

Figure 14: Demonstration of eye control system interface.

Red labels present the result of prediction: up-left, down-

right and closed eye movement.

ples is about 41 ms, and 137ms for 120 eye samples.

So with 12 trainning samples provides a possiblity for

the real-time application.

5 CONCLUSIONS

We presented our appearance-based eye movements

tracker and the application for an eye control system.

We used subregion CS-LBP concatenated histogram

as eye appearance feature, which not only can reduce

the dimensionality of eye images, but also can be ro-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

154

bust againt the changes in illumination. Addition-

ally, we introduced Laplacian Eigenmaps and spec-

tral clustering which help to learn about the “mani-

fold structure” of eye movement and give an efﬁcient

calibration phase. With limited number of trainning

samples, the system can provides a quick prediction

even when the number of calibration samples is lim-

ited. The efﬁciency and reasonable accuracy can help

to provide a real-time application.

ACKNOWLEDGEMENTS

This work is supported by company UBIQUIET, and

the French National Technology Research Agency

(ANRT).

REFERENCES

Baluja, S. and Pomerleau, D. (1994). Non-intrusive gaze

tracking using artiﬁcial neural networks. Advances in

Neural Information Processing Systems.

Belkin, M. and Niyogi, P. (2001). Laplacian eigenmaps

and spectral techniques for embedding and clustering.

NIPS, 15(6):1373–1396.

Belkin, M. and Niyogi, P. (2003). Laplacian eigenmaps

for dimensionality reduction and data representation.

Neural Comput., 15(6):1373–1396.

Fukuda, T., Morimoto, K., and Yamana, H. (2011). Model-

based eye-tracking method for low-resolution eye-

images. 2nd Workshop on Eye Gaze in Intelligent Hu-

man Machine Interaction.

Hansen, D. W. and Ji, Q. (2010). In the eye of the beholder:

A survey of models for eyes and gaze. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

32(3):478–500.

Heikkil

a, M., Pietik

ainen, M., and Schmid, C. (2009). De-

scription of interest regions with local binary patterns.

Pattern Recogn., 42(3):425–436.

Lee, K.-C. and Kriegman, D. (2005). Online learning

of probabilistic appearance manifolds for video-based

recognition and tracking. In Proceedings of the 2005

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition (CVPR’05) - Volume 1

- Volume 01, CVPR ’05, pages 852–859, Washington,

DC, USA. IEEE Computer Society.

Lu, F., Sugano, Y., Okabe, T., and Sato, Y. (2011). Infer-

ring human gaze from appearance via adaptive linear

regression. In Metaxas, D. N., Quan, L., Sanfeliu,

A., and Gool, L. J. V., editors, ICCV, pages 153–160.

IEEE.

Martinez, F., Carbonne, A., and Pissaloux, E. (2012). Gaze

estimation using local features and non-linear regres-

sion. ICIP(International Conference on Image Pro-

cessing).

Morimoto, C. H., Koons, D., Amir, A., and Flickner, M.

(2000). Pupil detection and tracking using multiple

light sources. Image and Vision Computing, pages

331–335.

Nguyen, B. L., Chahir, Y., and Jouen, F. (2009). Eye gaze

tracking. RIVF ’09.

Noris, B., Benmachiche, K., and Billard, A. (2008).

Calibration-free eye gaze direction detection with

gaussian processes. Proceedings of the International

Conference on Computer Vision Theory and Applica-

tion.

Rahimi, A., Recht, B., and Darrell, T. (2005). Learning

appearance manifolds from video. In Proceedings

of the 2005 IEEE Computer Society Conference on

Computer Vision and Pattern Recognition (CVPR’05)

- Volume 1 - Volume 01, CVPR ’05, pages 868–875,

Washington, DC, USA. IEEE Computer Society.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. IEEE Transactions on Pattern Analysis

and Machine Intelligence.

Shih, S.-W. and Liu, J. (2004). A novel approach to 3d gaze

tracking using stereo cameras. IEEE Trans. Systems,

Man, and Cybernetics.

Stiefelhagen, R., Yang, J., and Waibel, A. (1997). Track-

ing eyes and monitoring eye gaze. Proc. Workshop

Perceptual User Interfaces.

Tan, K. H., Kriegman, D. J., and Ahuja, N. (2002).

Appearance-based eye gaze estimation. Proc. Sixth

IEEE Workshop Application of Computer Vision ’02.

T.F.Cootes, C.J.Taylor, D.H.Cooper, and J.Graham (1995).

Active shape models– their training and application.

Computer vision and image understanding, 61(1):38–

59.

Wang, J.-G., Sung, E., et al. (2005). Estimating the eye

gaze from one eye. Computer Vision and Image Un-

derstanding.

Weinberger, K. Q. and Saul, L. K. (2006). Unsupervised

learning of image manifolds by semideﬁnite program-

ming. Int. J. Comput. Vision, 70(1):77–90.

Williams, O., Blake, A., and Cipolla, R. (2006). Sparse and

semi-supervised visual mapping with the s3p. Proc.

IEEE CS Conf. Computer Vision and Pattern Recog-

nition.

XU, L.-Q., Machin, D., and Sheppard, P. (1998). A

novel approach to real-time non-intrusive gaze ﬁnd-

ing. Proc. British Machine Vision Conference.

Zhang, J., Li, S. Z., and Wang, J. (2004). Manifold learning

and applications in recognition. In in Intelligent Mul-

timedia Processing with Soft Computing, pages 281–

300. Springer-Verlag.

Zhu, Z. and Ji, Q. (2007). Novel eye gaze tracking tech-

niques under natural head movement. IEEE TRANS-

ACTIONS on biomedical engineering.

Appearance-basedEyeControlSystembyManifoldLearning

155