A Combined Calibration of 2D and 3D Sensors

A Novel Calibration for Laser Triangulation Sensors based on Point

Correspondences

Alexander Walch and Christian Eitzinger

Machine Vision Department, Profactor GmbH, Steyr-Gleink, Austria

Keywords:

Laser Triangulation Sensor, Calibration of Laser Stripe Proﬁler, Colored Point Cloud, Camera Calibration.

Abstract:

In this paper we describe a 2D/3D vision sensor, which consists of a laser triangulation sensor and matrix

colour camera. The outcome of this sensor is the fusion of the 3D data delivered from the laser triangulation

sensor and the colour information of the matrix camera in the form of a coloured point cloud. For this reason

a novel calibration method for the laser triangulation sensor was developed, which makes it possible to use

one common calibration object for both cameras and provides their relative spatial position. A sensor system

with a SICK Ranger E55 proﬁle scanner and a DALSA Genie color camera was set up to test the calibration

in terms of the quality of the match between the color information and the 3D point cloud.

1 INTRODUCTION

Laser triangulation sensors are a widespread instru-

ment to gain 3D information in machine vision appli-

cations. They consist of a matrix camera and a laser

stripe projector.

The matrix camera is directed onto the plane de-

ﬁned by the laser and is parameterized in a way that

only data from points intersecting with this laser plane

are captured.

To gain more 3D information than only one pro-

ﬁle, laser triangulation sensors are often used to scan

objects moved by a conveyor belt or they are mounted

on a linear axis.

However, for many inspection tasks it is necessary

to obtain information about their textures, in addition

to the 3D shape of the objects.

On the one hand such a system is presented in

(Munaro et al., 2011), where a colour camera is used

for both tasks and additionally two lasers were used

to reduce occlusion. For that reason one area in the

middle of the image sensor of the camera was used

to obtain colour information and the surrounding ar-

eas of the sensor serve as laser triangulation sensor,

together with the two lasers.

On the other hand there already exist different

methods to calibrate pure laser triangulation sensors.

Some of them, such as the calibration method pro-

vided by the manufacturer of the Ranger E55, only

describe a mapping between the image plane and the

laser plane of triangulation sensor. This methods lack

of information about the spatial position of the sensor.

In case of a linear motion of the sensor, it requires to

mount the laser in an orthogonal position to the di-

rection of motion. In (McIvor, 2002) a calibration is

presented, which uses a 3D calibration object and the

used mathematical model fully describes the laser tri-

angulation sensor including its extrinsic parameters.

In this paper we describe in section 2.3 a cali-

bration which only uses data received from the laser

plane and does not use the laser triangulation sensors

camera as a matrix camera as in (Munaro et al., 2011)

and (Bolles et al., 1981). Hence it is also applicable

in camera setups which use bandpass ﬁlters to block

out the surrounding light.

All necessary data for the calibration are obtained

from one single scan of the calibration object. This

makes the calibration process more efﬁcient, espe-

cially because additionally to the laser triangulation

sensor, we also calibrate the second camera, which

provides colour images.

On the contrary to the algorithm, which is de-

scribed in (McIvor, 2002) the distance the objects are

moved between two captured proﬁles does not need to

be known, but is a parameter of the calibration, which

is determined.

Furthermore the novel calibration is easy to imple-

ment because either the direct-linear-transformation-

algorithm (Abdel-Aziz and Karara, 1971) is used to

determine the camera parameters or closed form solu-

Walch A. and Eitzinger C..

A Combined Calibration of 2D and 3D Sensors - A Novel Calibration for Laser Triangulation Sensors based on Point Correspondences.

DOI: 10.5220/0004682900890095

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 89-95

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

tions of the arising non-linear optimization problems

are presented in this paper.

Since the calibration object of the laser triangula-

tion sensor is also suitable for the calibration of ma-

trix cameras (as described in section 2.4), customized

sensor systems can be built, which combine the high

3D data aquisition rate of specialised proﬁle scanner

cameras like the SICK Ranger with additional texture

information.

In section 3 a setup of the 2D/3D sensor is pre-

sented, which was used to perform experiments and to

evaluate the calibration. Additionally results of exper-

iments, which were performed with a simulated laser

triangulation sensor, are visualised.

Finally in section 4 we discuss the results of the

experiments and make some proposals for improve-

ments and future work.

2 CALIBRATION OF THE 2D/3D

VISION SENSOR

2.1 The Calibration Object

The calibration object delivers the needed informa-

tion to determine the parameters of the mathematical

models of the cameras. For this reason it contains

points with well known coordinates in an arbitrary,

predeﬁned coordinate system. An necessary property

of these corners is that they can be found in the raw

data of the cameras.

The object, which is used to calibrate the 2D/3D

sensor, consists of 2 nonparallel planes with checker-

board patterns (3D calibration object). Its advan-

tage is that ﬁnding its points, the inner corners of

the checkerboards , is a well researched problem and

there already exist algorithms, which provide their

pixel coordinates on the image of the color camera

and also in the raw data provided from the SICK

Ranger seen on ﬁgure 1.

For the calibration of the matrix camera the row

and column coordinates of the found corners on

the colour image are used, but a scan of the cali-

bration object of the laser triangulation sensor con-

tains more information. The pixel coordinates c =



, c



of a corner are 3-dimensional, be-

cause the laser triangulation sensor yields its raw data

in form of a range image on which every row corre-

sponds to one proﬁle of the scanned object.

• c

: The x-coordinate of a corner on the range im-

age of the proﬁle scanner (corresponding to the x-

coordinate on the image plane of the matrix cam-

era).

Figure 1: In addition to the range images, laser triangula-

tion sensors often provide intensity images, which do not

contain 3D information, but the intensity of the reﬂected

laser light. This images can be used to ﬁnd the c

and c

coordinate of the corners.

• c

: The y-coordinate of a corner on the range

image, corresponding to the number of scanned

proﬁles until the particular corner intersected the

laser plane.

• c

: The range value, which represents the height

of the corner and corresponds to the y-coordinate

on the image plane.

Since the same points are used for the calibration of

both cameras, both mathematical models are located

in the same coordinate system and it’s therefore easy

to combine the colour information with the 3D point

cloud.

2.2 Correcting the Lens Distortion

The lens distortion of the matrix camera as well as

the lens distortion of the laser triangulation sensor

is corrected with the same algorithm, described in

(Tardif et al., 2006), which is separated from the rest

of the calibration. The used method belongs to the

plumbline algorithms, which use the fact that straight

lines remain straight under perspective transforma-

tions, and only takes account of the radial lens dis-

tortion.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

Hence points of the calibration object, which are

located in the real world on straight lines, are taken to

determine the parameters of the lens distortion model.

All data received from the cameras are rectiﬁed with

this algorithm before they are used for further compu-

tations. Therefore we assume, in the algorithms pre-

sented below, that the lens distortion is already cor-

rected. Hence we can use the pinhole camera model

to describe the cameras of the sensor.

2.3 The Laser Triangulation Sensor

2.3.1 The Mathematical Model

At least for the calibration of the laser triangulation

sensor, we require a linear relative motion between

the sensor and the calibration object. Furthermore

we assume that the absolute distances, which the cali-

bration object is moved between two scanned proﬁles

are unknown, but constant. Then the process of map-

ping a corner with the laser triangulation sensor from

world coordinates C into pixel coordinates c can be

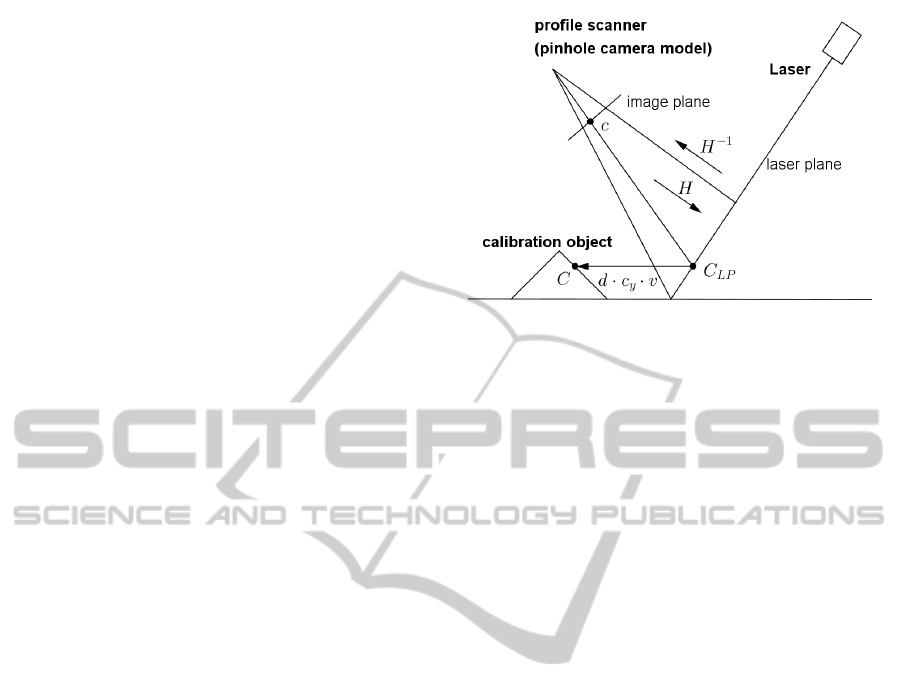
described mathematically as follows.

First the position where the corner intersects the

laser plane during a scan is computed. The coordinate

of this point of intersection on the laser plane is

received by projecting the corner along the direction

of motion onto the laser plane:

= Pr

· LP

−1

·C

(1)

where

LP =





(2)

is a basis of R

, with v

, v

are parallel to the laser

plane, d represents the direction of motion of the pro-

ﬁl scanner and



1 0 0

0 1 0



(3)

is the projection matrix along the third coordinate.

When the corner reaches the coordinates C

on the

laser plane, it is illuminated by the laser and therefore

seen by the camera of the sensor.

Since the camera only detects points which inter-

sect the laser plane, its projection matrix is reduced to

a invertible homography H

−1

, which fulﬁlls the fol-

lowing constraint:









∝ H

−1





(4)

The last unknown pixel coordinate c

of the corner

can be computed by dividing the distance of the cor-

ner to the laser plane along the direction of motion

through the distance v.

Figure 2: The mathematical model of the laser triangulation

sensor.

According to this description of mapping the

world coordinates of a corner of the calibration ob-

ject onto its pixel coordinates, the used mathematical

model consists of 14 degrees of freedom (DF):

v . . . distance between two

proﬁles 1 DF

n . . . normal unit vector of the

laser plane 2 DF

. . . the distance of the laser

plane from the origin of

the coordinate system 1 DF

d . . . direction of motion 2 DF

H . . . homography which maps

points from the image

onto the laser plane 8 DF

The aim of the calibration of the laser triangula-

tion sensor is to determine the parameters, which are

needed to transform the data provided by the sensor

into the world coordinate system in which the cali-

bration object is located.

2.3.2 Computing the Range Values of the

Checkerboard Corners

While the scan number c

and the x-coordinate on im-

age plane c

of the pixel coordinates c are received by

applying a standard image processing algorithm for

corner detection on the range image, we still have to

determine the range value c

For this reason we do not read out c

, but ﬁt a sur-

face into the scanned checkerboard plane in a row-

column-enviroment of c on the range image. The

range value is then determined by the height of the

corresponding surface at the corner coordinates c

and

Besides of being more robust against noise, this

method avoids two other problems, which occur dur-

ACombinedCalibrationof2Dand3DSensors-ANovelCalibrationforLaserTriangulationSensorsbasedonPoint

Correspondences

Figure 3: The laser line position above was determined by

computing the center of gravity of the intensity of the re-

ﬂected light. The missing reﬂections of the laser at the dark

areas cause a wrong estimation of the laser line position.

ing the determination of the range values of the

checkerboard corners:

1. If the corner is found on a black square of the

checkerboard, there might be no range value re-

ceived at its position, because the intensity of the

reﬂected laser light was too low and the laserline

could not be detected by the laser triangulation

sensor.

2. All corners are located at bright/ dark transitions

of the checkerboard pattern. At those locations the

estimation of the laser stripe position (and con-

sequently the corresponding range values) on the

image plane gets biased, due to the change of the

intensity of the reﬂected laser light. This situation

is visualized in ﬁgure 3.

Since the surfaces are only used to locally describe

the range image, the lens distortion has a negligible

inﬂuence on the surface ﬁt.

2.3.3 Computation of the Direction of Motion

The computation of the direction of motion d is based

on the transformation of the world coordinates C of

the corners into pixel coordinates c

and c

described

in section 2.3.1. Since we are interested only in the

determination of the direction of motion in this part

of the calibration, we can simplify the problem by as-

suming that the laser plane is orthogonal to the direc-

tion of motion.

This rotation of the laserplane causes only a scaling

of the coordinates C

of the projected corners in LP

coordinates, followed by a scaling of the columnes

of the homography H

−1

with the result that the real

world corner coordinates still are mapped onto their

pixel counterparts. We also do not care about the ori-

entation of v

and v

within the laser plane, because a

transformation of these vectors can be undone in the

same way with no effect on the computation of the di-

rection of motion d.

For this reason we choose LP as an orthonormal ba-

sis, what makes the computation of its inverse easy.

As d should be a unit vector, it only depends on two

angles α, β (spherical coordinates) and can be ex-

pressed as:

d =







cos(α)cos(β)

cos(α)sin(β)

sin(α)







(5)

⇒ Depending on d, v

and v

can be chosen:







−sin(α) cos(β)

−sin(α) sin(β)

cos(α)







, v







−sin(β)

cos(β)







(6)

The process of mapping a corner from world coordi-

nates can be condensed to one projective transforma-

tion T by using the projective counterparts

and

−1

of Pr

and LP

−1









∝ H

−1

{z }





(7)

The composed matrix T is determined with the help

of the direct linear transformation algorithm.

As a consequence the computation of the vector,

which represents the direction of motion, is reduced to

the decomposition of the matrix T into the two factors

−1

and

−1





−sin(α) cos(β) −sin(α)sin(β) cos(α) 0

−sin(β) cos(β) 0 0

0 0 0 1





(8)

Calculating this decomposition yields the following

result for the sperical coordinates of the direction of

motion d:

cos(β) = ±



1,2

1,3

2,2

2,3



1,2

1,3

2,2

2,3



1,1

1,3

2,1

2,3



sin(β) =



1,2

1,3

2,2

2,3



1,3

1,2

2,3

2,2



· cos(β)

cos(α) = ±

2,3

(

2,2

sin(β)+T

2,1

cos(β)

)

sin(α) =

−cos(α)

(

2,2

sin(β)+T

2,1

cos(β)

)

2,3

(9)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

• The computed vector d is only determined up to a

multiplication with ±1. The correct factor can be

found by considering the order in which the cor-

ners of the checkerboard pattern intersected the

laser plane.

• Permuting the rows on the left repectivly right

side of equation 7 will cause a permutation of

the rows respectively columns of matrix T . With

this strategy the gimbal lock problem, which oc-

curs at α = ±

, and numerical instabilities can be

avoided.

2.3.4 Computation of the Laser Plane and the

Distance between Two Proﬁles

The computation of the position of the laser plane is

based on the known number of scanned proﬁles c

until a corners of the calibration object intersects the

laser plane. Subtracting the vector v · c

· d from C

yields a point, which is located on the laser plane (see

ﬁgure 2) and therefore satisﬁes the following equa-

tion:

C − vc

d, n

= d

(10)

Since every corner of the calibration object must hold

this equation, the unknown parameters v, d

and

n are obtained by solving a non-linear optimization

problem.

Using the normalized data C





respectively c

, related to the coordinates C respec-

tively c

and by means of the method of Lagrange

multipliers, a necessary condition for the normal unit

vector n

in form of the following eigenvalue problem

is received (For reasons of simplicity there are no in-

dices of summation in the equations, but summation

always relate to the world and pixel coordinates of the

corners 1. . . N):

A · n

= λn

λ = Lagrange multiplier

i, j

∑

−

∑

(11)

The unit eigenvector belonging to the smallest eigen-

value of matrix A is then the normal vector of the laser

plane. Since scaling and shifting the corners has no

inﬂuence on the orientation of the laser plane, n

also the normalvector of the laser plane related to the

original corners coordinates C.

∑

(

)

(12)

LPn



∑

− v

d), n



(13)

Under taking into account the transformation between

the coordinates C and C

, the searched parameters v

and d

can be obtained from v

and d

LPn

2.3.5 Computation of the Homography

The last parameter to determine is the homography H,

which maps points from the image plane of the laser

triangulation camera onto the laser plane. On the one

hand the coordinates, where the corners appeared on

the image plane are





, on the other hand their

projections on the laser plane H ·





must

coincide with the coordinates C

(see ﬁgure 2).

Since the direction of motion is already known and

also a basis of the laser plane is obtained in the form

of two eigenvectors of equation (11), the coordinates

can be computed by means of equation (1).

The searched homography can then be determined

according the following equation system:





∝ H ·









(14)

This linear optimization problem can be solved by

means of the direct linear transformation algorithm.

2.4 Calibration of the Color Camera

Because the lens distortion is corrected with a sepa-

rated algorithm, as described in section 2.2, the pin-

hole camera model is used again to describe the color

camera. Due to the 3D calibration object, the direct

linear transformation algorithm can be used to deter-

mine the needed projection matrix. The advantage of

this algorithm is that only one image of the calibration

object is needed, which keeps the calibration process

efﬁcient.

In case of an installation of the 2D/3D sensor

above a conveyor belt it is necessary to take the cir-

cumstance into account that the calibration object,

and therefore also the world coordinate system, is

moved during the calibration process.

However the color camera can be shifted to the

correct position by taking advantage of the direction

of motion vector d and the distance v, which are

gained during the calibration of the laser triangulation

sensor.

ACombinedCalibrationof2Dand3DSensors-ANovelCalibrationforLaserTriangulationSensorsbasedonPoint

Correspondences

3 RESULTS

3.1 Combining the 3D Point Cloud with

the Color Information

One possibility to evaluate the precision of the color

mapping is to take advantage of the known positions

of the calibration object corners. Starting in the range

image, provided by the laser triangulation sensor, the

pixel coordinates of the corners are transformed into

world coordinates. The yielded reconstructed corner

coordinates are then mapped, by means of the projec-

tion matrix of the color camera, onto the color im-

age, which was used to calibrate the color camera.

That projected corners should coincide with the cor-

ners of the checkerboards, which are shown in the im-

age. The color mapping error then can be assessed by

computing the Euclidean distance between the pro-

jected corners and the corners on the image, which

are found by a corner detection algorithm.

Such an evalution is visualized on the ﬁgures 4

with a mean distance between the projected and found

corners of 0.417 pixels and maximum and minimum

distances amounting to 1.475 pixels and 0.012 pixels.

However that evaluation also reﬂects the errors of the

corner coordinate detection in the range image as well

as in the color image.

3.1.1 An Example of a Colored Point Cloud

In this section we present an example of a colored

point cloud. The scanned object was a multimeter,

whose colored point cloud is visualised in ﬁgure 5.

4 CONCLUSIONS AND FUTURE

WORK

The inovation of the presented 2D/3D vision sensor

was the novel calibration of laser triangulation sen-

sors, which does not treat the sensor as matrix camera

with an additional laser, but as one composed sensor.

All needed data are gained through one single scan

of the calibration object and the subsequent computa-

tion of the sensor parameters is based on closed-form

solutions.

A calibration object was proposed and it was de-

scribed how to extract the corner coordinates from its

scan.

The quality of mapping the color onto the 3D

point cloud was examined in section 3.

However in the presented calibration the direct-

linear-transformation algorithm is used, which mini-

mizes an algebraic cost function instead of a geomet-

ric interpretable error. Furthermore the computation

is done in three separated steps, whereby the cali-

bration parameters are not optimized simultaneously

what would be preferable.

For this reason it is planned to add another calibra-

tion step, which minimizes the reconstruction error of

the corners and optimizes all calibration parameters

simultaneously by means of a gradient methode.

The convergence of this algorithm can be ensured

since the outcome of the calibration method presented

above serves as starting guess for this iterative algo-

rithm and the calibration parameters are only reﬁned.

(a) The projections of the reconstructed corners of the calibration object.

(b) An enlarged view of the region within the rectangular.

Figure 4: The circles on the image mark the corners, which

are found with a corner detection algorithm. The projected

3D corners are visualized with the crosses.The projected

corners do not perfectly coincide with the found corners

marked by the circles.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

(a) The raw data provided from a laser triangulation sensor in form of a

range image.

(b) The image of the color camera.

Figure 5: An example of a colored point cloud in form of a

scanned multimeter.

ACKNOWLEDGEMENTS

The authors have been supported by the EC project

FP7-ICT-270138 DARWIN.

The presented 2D/3D vision sensor was examined

as a part of the DARWIN project. Moreover we want

to thank our colleagues of the machine

REFERENCES

Abdel-Aziz, Y. and Karara, H. (1971). Direct linear trans-

formation into object space coordinates in close-range

photogrammetry. In Proc. of the Symposium on Close-

Range Photogrammetry.

Bolles, R., Kremers, J., and Cain, R. (1981). A simple sen-

sor to gather three-dimensional data. Technical Report

249, SRI, Stanford University.

McIvor, D. A. M. (2002). Calibration of a laser stripe pro-

ﬁler. Optical Engineering 41.

Munaro, M., Michieletto, S., So, E., Alberton, D., and

Menegatti, E. (2011). Fast 2.5d model reconstruction

of assembled parts with high occlusion for complete-

ness inspection. Fast 2.5D model reconstruction of

assembled parts with high occlusion for completeness

inspection.

Tardif, J.-P., Sturm, P., and Roy, S. (2006). Self-calibration

of a general radially symmetric distortion model. In

Proc. of the 9th European Conference on Computer

Vision, Graz, Austria.

ACombinedCalibrationof2Dand3DSensors-ANovelCalibrationforLaserTriangulationSensorsbasedonPoint

Correspondences