
A Bayesian Framework for Enhanced Geometric Reconstruction of
Complex Objects by Helmholtz Stereopsis
Nadejda Roubtsova and Jean-Yves Guillemaut
Centre for Vision, Speech and Signal Processing, University of Surrey, Guildford, U.K.
Keywords:
3D Reconstruction, Helmholtz Stereopsis, Complex Reflectance
Abstract:
Helmholtz stereopsis is an advanced 3D reconstruction technique for objects with arbitrary reflectance proper-
ties that uniquely characterises surface points by both depth and normal. Traditionally, in Helmholtz stereopsis
consistency of depth and normal estimates is assumed rather than explicitly enforced. Furthermore, conven-
tional Helmholtz stereopsis performs maximum likelihood depth estimation without neighbourhood consid-
eration. In this paper, we demonstrate that reconstruction accuracy of Helmholtz stereopsis can be greatly
enhanced by formulating depth estimation as a Bayesian maximum a posteriori probability problem. In re-
formulating the problem we introduce neighbourhood support by formulating and comparing three priors: a
depth-based, a normal-based and a novel depth-normal consistency enforcing one. Relative performance eval-
uation of the three priors against standard maximum likelihood Helmholtz stereopsis is performed on both
real and synthetic data to facilitate both qualitative and quantitative assessment of reconstruction accuracy.
Observed superior performance of our depth-normal consistency prior indicates a previously unexplored ad-
vantage in joint optimisation of depth and normal estimates.
1 INTRODUCTION
As evidenced by the formidable volume of past and
active research, reconstruction of 3D geometry is both
challenging and much desirable for practical applica-
tions. A tremendous progress has been made in the
field with sub-millimetre accurate geometries being
obtained when capture conditions and surface prop-
erties are tailored for reconstruction. All prior al-
gorithms rely on multiple images to resolve inherent
depth ambiguity, while differing in acquisition and
view correlation employed to formulate ambiguity re-
solving constraints. Also variable is the degree of
neighbour support used when characterising a surface
point by its depth, normal or both.
The oldest of 3D reconstruction techniques
is conventional stereopsis thoroughly surveyed in
(Scharstein and Szeliski, 2002) and (Seitz et al., 2006)
for single- and multi-view respectively. Conventional
stereopsis computes disparity through feature-point
intensity matching between acquired views in the
presence of sufficient texture. In this approach, sur-
face points are characterised by depth, which is re-
ciprocal to disparity. Conventional intensity-based
stereo strongly relies on the inter-viewpoint constancy
of feature appearance (i.e. Lambertian reflectance)
failing when the assumption is violated. Alternative
SIFT features are robust to intensity variations, al-
though they only facilitate sparse representation.
Another reconstruction approach called photo-
metric stereopsis (Woodham, 1989) permits an arbi-
trary reflectance model as long as it is a priori known.
Photometric constraints are linked to the response of a
point to varying illumination at a constant viewpoint.
The sought surface orientation is the one best recon-
ciling intensity predictions and measurements. Essen-
tially, the reflectance issue of conventional stereo is
not solved by photometric stereo but rather the bur-
den of it is shifted to the calibration phase of which
a surface-orientation-dependent reflectance model is
required. Reflectance modelling is a tedious task, of-
ten impossible to the desired accuracy for real objects.
With an accurate model, photometric stereo directly
outputs highly descriptive surface normals. Individual
normals however need to be integrated into a surface
often resulting in drift (global shape distortion) due to
accumulation of numerical integration errors. Unlike
conventional stereo, photometric stereo with its single
viewpoint avoids the task of feature-point matching.
There are few techniques bypassing the need for
reflectance modelling. One old example is the shape-
from-silhouette algorithm (Baumgard, 1974) which
335
Roubtsova N. and Guillemaut J..
A Bayesian Framework for Enhanced Geometric Reconstruction of Complex Objects by Helmholtz Stereopsis.
DOI: 10.5220/0004683503350342
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 335-342
ISBN: 978-989-758-009-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

computes a rough 3D outline of the object, its visual
hull (Laurentini, 1994), by intersecting visual cones
of multiple views. Visual hull is used for initialisa-
tion by many advanced reconstruction algorithms. A
more recent highly promising photometric technique
of Helmholtz stereopsis (HS) (Zickler et al., 2002) ad-
dresses the fundamental problem of reflectance mod-
elling by enforcing consistency of reflectance-model-
independent Helmholtz reciprocity observation: i.e.
swapping the sensor and the light source does not alter
reflectance response. Besides its independence of the
reflectance model, HS has the unique feature of point
characterisation by both depth and normal. However,
in its conventional formulation, HS is sequential with
depth estimates uniquely determining the normals.
Such unidirectional indexation of normals by depth
estimates means that the typically noisy HS depth
maps result in normal inaccuracies and hence in local
and global reconstruction errors (although a certain
degree of robustness to normal errors has been ob-
served). Conceptually, the depth-normal dependency
need not be unidirectional: depth and normal estima-
tion can be unified in a single framework enforcing
consistency and comparable accuracy levels of both
estimates.
Conventional HS essentially performs maximum
likelihood estimation (MLE). Even in the absence of
noise, inherent point depth ambiguities exist, for in-
stance, due to coincidental symmetries in the acquisi-
tion set-up configuration relative to the sampled sur-
face. Since local evidence is ambiguous, neighbour-
hood support is clearly needed and warranted as there
is always a degree of local smoothness in real objects.
Yet, to our knowledge, MAP optimisation in the con-
text of HS has not been previously attempted. In this
paper, we propose a novel MAP formulation embed-
ding HS into a Bayesian framework with a prior that
for the first time explicitly enforces consistency be-
tween depth and normals. We show that, with the con-
sistency prior, MRF optimisation of MAP HS indeed
results in superior reconstruction accuracies. Un-
like alternative depth-based or normal-based priors,
the depth-normal consistency prior capitalises on the
unique ability of HS to provide both depths and nor-
mals and, combining the two, produces the most cor-
rect geometries coherent in both depth and integrated
normal representation. These conclusions are based
on the quantitative and qualitative evaluation compar-
ing conventional ML HS to MAP optimisation with 1.
classical depth-based; 2. normal-based and 3. novel
depth-normal consistency priors.
2 RELATED WORK
Helmholtz reciprocity states that a light ray and its re-
verse will undergo the same processes of reflection,
refraction and absorption (Helmholtz, 1925). Let ˆv
1
be the unit vector directed from the surface point to
the camera and ˆv
2
the corresponding vector from the
surface point to the light source. The implication
of Helmholtz reciprocity, first observed by Zickler
et al. (Zickler et al., 2002) in the context of multi-
view reconstruction, is that interchanging the light
source and camera in the set-up, thereby swapping
the vector definitions, has no effect on the point’s re-
flective behaviour. Mathematically, Bidirectional Re-
flectance Distribution Function (BRDF) f
r
is recipro-
cal: f
r
( ˆv
2
, ˆv
1
) = f
r
( ˆv
1
, ˆv
2
). The following standard
image formation equations for reciprocal images I
1
and I
2
respectively:
i
1
= f
r
( ˆv
2
, ˆv
1
)
ˆn · ˆv
2
r
2
, i
2
= f
r
( ˆv
1
, ˆv
2
)
ˆn · ˆv
1
r
1
(1)
express a surface point’s image intensities i
1
and i
2
as
a function of BRDF, surface normal ˆn, the two recip-
rocal unit vectors and the radiation fall-off factor r.
Reciprocity of BRDF in conjunction with Equation 1
result in the following constraint ˆw notably without
any dependency on the BRDF:
i
1
ˆv
1
r
1
− i
2
ˆv
2
r
2
· ˆn = ˆw · ˆn = 0. (2)
With a single ˆw per reciprocal pair, 3 or more re-
ciprocal pairs result in constraint matrix W to which
singular value decomposition (SVD) can be applied:
SV D(W ) = U ΣV
∗
where U,V are unitary and Σ is a
rectangular diagonal matrix. The last column of V
gives the normal at the sampled point. The last diag-
onal value of Σ, the SVD residual σ
3
, tends to 0 when
there is a mutual constraint consistency. For outlier
elimination, Zickler et al. also involve σ
2
in their con-
sistency measure: the SVD coefficient
σ2
σ3
tends to in-
finity for consistent W (those of true surface points).
The requirement of multiple reciprocal pairs and
the need for careful offline calibration led to discus-
sions on acquisition impracticality of HS. In response,
Zickler in (Zickler, 2006), firstly, devises an auto-
calibration algorithm using specular highlights and
intensity patches, two inherent easily identifiable re-
gions of interest. Unlike conventional stereo, inten-
sity matching in HS is not conditional on the valid-
ity of the Lambertian assumption making intensity
patches stable calibration markers.
The inherent appearance predictability of an in-
tensity patch of one reciprocal image based on the
other is also employed in (Tu et al., 2003) to formu-
late prediction error for registration in full 3D HS.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
336

Work on full 3D HS is scarce. The work of De-
launoy et al. (Delaunoy et al., 2010) and the more re-
cent publication of Weinmann et al. (Weinmann et al.,
2012) are two notable examples. Both are variational
approaches requiring computationally intensive opti-
misation over the entire surface with long execution
times. The method of Weinmann et al. is more cum-
bersome due to fusion with structured light at acquisi-
tion. The impracticalities are however outweighed by
the impressive degree of demonstrated reconstruction
detail.
To address the issue of multiple constraint require-
ment, Zickler et al. in (Zickler et al., 2003) propose
binocular HS i.e reconstruction from a single recipro-
cal pair. The method is a differential approach where
the (single) constraint is formulated as a PDE of depth
over the surface coordinates. The PDE requires ini-
tialisation and results in a family of solutions the am-
biguity of which is resolved through multi-pass op-
timisation. Although interesting as an exercise on
acquisition simplification, additional computational
complexity is perhaps not outweighed by the advan-
tages.
Binocular HS and full 3D HS methods exploit
the advantages of optimisation over a set of sur-
face points. In the original HS, the depth label at
each point is computed independently of its neigh-
bours (without a Bayesian prior). Logically, there
is a strong correlation between neighbouring surface
points. By formulating a prior, the problem is turned
into a MAP one, solvable by numerous mature MRF
optimisation techniques (Szeliski et al., 2008). The
value of MRF optimisation for other 3D reconstruc-
tion approaches has been established. In conventional
stereo, the top-performers are global optimisation al-
gorithms solved through MRF-based graph-cuts and
belief propagation (Scharstein and Szeliski, 2002).
(Wu et al., 2006) is an interesting work where MRF
optimisation is performed in the context of photo-
metric stereo with a normal-based (rather than depth-
based) prior achieving remarkable robustness in the
face of noisy input, complex geometries, shadows,
transparencies etc..
Conventional HS will similarly benefit from
MRF-based optimisation, since geometries obtained
by ML HS lack in smoothness and fine structural
detail due to inherent depth ambiguities, intensity
measurement noise, sensor saturation and calibra-
tion/discretisation errors. Aimed at tackling the issues
of conventional HS, the contributions of this paper are
twofold. Firstly, we devise a MAP framework allow-
ing to apply MRF-based optimisation in the context of
HS. Secondly, we introduce a novel smoothness prior
enforcing coherence of depth and normal estimates of
HS and show superiority of the prior over the purely
depth-based or normal-based ones.
3 METHODOLOGY
In reconstruction by HS, we begin with N recipro-
cal image pairs (N ≥ 3) and a discrete volume V
of N
X
× N
Y
× N
Z
voxels v(x, y, z) containing the ob-
ject. Each v(x, y, z) is sampled by projection onto
the reciprocal images to acquire a set of N intensity
2-tuples
{
(i
1
, i
2
)
1
, .., (i
1
, i
2
)
N
}
and formulate N con-
straints ˆw as in Equation 2. Only those v(x, y, z) ∈
V containing surface points will have N mutually
consistent constraints. In standard HS, voxel sets
R
p(x,y)
= {v(x, y, z) : x = x
∗
, y = y
∗
} with constant
2D coordinates x
∗
and y
∗
are sampled exhaustively
over V . Each R
p(x,y)
defines the depth search space
for random variable p(x, y) with the optimal depth
value z
p(x,y)
= z
∗
p(x,y)
corresponding to the surface
point P(x, y, z
∗
p(x,y)
). In our work, the object’s vi-
sual hull (VH) restricts the search space to R
V H
p(x,y)
=
{v(x, y, z) : x = x
∗
, y = y
∗
, v(x
∗
, y
∗
, z
p(x,y)
) ∈ V H} (im-
plicit in Equations 4 and 5) limiting sampling in both
2D ( R
p(x,y)
∩V H =
/
0 for some p(x, y)) and depth.
We postulate that depth estimation of HS is in
fact a labelling problem where each random variable
p(x, y) is assigned depth label z
∗
p(x,y)
. The optimal
solution to such a labelling problem is known (Li,
1994) to be one maximising the a posteriori probabil-
ity (MAP) i.e. the likelihood of a parameter assum-
ing a certain value given the observation. The prob-
lem is typically translated into the equivalent one of
posterior energy minimisation where the total energy
is a sum of likelihood (data) and prior energy terms.
Likelihood is related to the noise model of the obser-
vation representing its quality, viewed independently
of the other observations. The prior term (typically lo-
cal smoothness) is the knowledge of the problem en-
capsulating interaction between observations. In our
work, the interaction is contained within the Marko-
vian neighbourhood of p(x, y) restricted by VH:
N (p(x, y)) = {p(x + k, y + (1 − k)) :
k ∈ {0, 1}, R
V H
p(x+k,y+(1−k))
6=
/
0} (3)
In this paper, we formulate depth estimation of HS
as a MAP problem in Equation 4. For each ran-
dom variable p(x, y) and given p(x
0
, y
0
) ∈ N (p(x, y)),
we define normalised data and smoothness costs,
E
d
(x, y, z
p(x,y)
) and E
s
(x, y, z
p(x,y)
, x
0
, y
0
, z
p(x
0
,y
0
)
) re-
spectively, weighted by the normalised parameter α.
The total optimisation is over all random variables
within VH. The solution to the labelling problem is
ABayesianFrameworkforEnhancedGeometricReconstructionofComplexObjectsbyHelmholtzStereopsis
337

the label configuration f
∗
= {z
∗
p(x,y)
∈ [Z
1
, .., Z
N
Z
] : x ∈
[X
1
, .., X
N
X
], y ∈ [Y
1
, ..,Y
N
Y
]} selected from a set of S
such configurations.
f
∗
MAP
= argmin
f ∈S
∑
p(x,y)
((1 − α)E
d
(x, y, z
p(x,y)
) +
+
∑
p(x
0
,y
0
)∈N (p(x,y))
αE
s
(x, y, z
p(x,y)
, x
0
, y
0
, z
p(x
0
,y
0
)
)) (4)
In contrast to our approach, conventional HS solves a
simpler maximum likelihood (ML) optimisation prob-
lem, without the smoothness prior, resulting a sub-
optimal solution because each random variable is op-
timised independently:
f
∗
ML
= argmin
f ∈S
∑
p(x,y)
E
d
(x, y, z
p(x,y)
) (5)
Sub-optimality leads to noisy depth maps and hence
lacking surface smoothness and structural detail. The
global shape may be reasonable, but the recon-
struction finesse of conventional HS is limited be-
cause noisy depth labels index approximate normals.
Through Bayesian formulation in Equation 4, we en-
deavour to obtain cleaner depth maps improving accu-
racy by more accurate normal indexing. A Bayesian
framework is clearly more suitable because of the
strong statistical dependency between neighbouring
depth estimates. The following sections define data
energy and three investigated smoothness priors.
3.1 Data Term
Depth hypothesis z of each p(x, y) has got a likeli-
hood E
d
(x, y, z) defined through the SVD coefficient
σ
2
(v(x,y,z))
σ
3
(v(x,y,z))
associated with the corresponding voxel.
The coefficient tends to infinity as z approaches the
correct depth z
∗
. Since MRF optimisation is formu-
lated as a minimisation, E
d
(x, y, z) is a decaying func-
tion of
σ
2
(v(x,y,z))
σ
3
(v(x,y,z))
. Throughout the paper, we adhere
to the exponential formulation with the decay factor
µ = 0.2 × log(2):
E
d
(x, y, z) = e
−µ×
σ
2
(v(x,y,z))
σ
3
(v(x,y,z))
(6)
As it indicates likelihood, the function is bounded in
the range [0, 1].
3.2 Smoothness Term
Unlike conventional data-based HS, we introduce
priors. We devise three prior types reflecting the
unique ability of HS to generate both depth and nor-
mal estimates.
1. Depth-based Prior. The prior is known from
conventional stereo. In this work, we define depth-
based smoothness cost E
s d
(x, y, z, x
0
, y
0
, z
0
) of voxel
v(x, y, z) relative to v(x
0
, y
0
, z
0
) by the discontinuity-
preserving truncated squared difference of the neigh-
bouring depth hypotheses normalised by the total
number of labels (N
Z
):
E
s d
(x, y, z, x
0
, y
0
, z
0
) = λ × min(S
max
, (z − z
0
)
2
) (7)
where S
max
= (0.5 × N
Z
)
2
is the truncation value and
λ = (N
Z
)
−2
is the normalising constant. With penal-
ties for much different labels at neighbouring sur-
face points, the prior encourages piece-wise constant
depth and biases towards a fronto-parallel represen-
tation. Discontinuities are preserved by truncation
moderating depth fluctuation penalties.
2. Normal-based Prior. Surface characterisation
through normals is typical of photometric techniques.
A suitable normal-based prior would enforce locally
constant normals encouraging locally flat, though not
necessarily fronto-parallel, surfaces. Hence, this prior
is less restrictive of reconstructed surfaces than the
depth-based one. The complication in formulating
normal-based priors arises because 1. normals are
continuous 3D quantities that cannot be labels in our
discrete framework and 2. normal correlations are
irregular expressions not optimisable by graph cuts
(Kolmogorov and Zabih, 2004). In this work, dis-
crete depths are still the labels, but rather than depth
information, we use the corresponding normal sim-
ilarity to assess label compatibility. Sequential tree
re-weighted message passing (TRW-S) (Wainwright
et al., 2005), (Kolmogorov, 2006) MRF optimisation
is used consistently throughout the paper because it
does not require regularity of prior.
Given photometric normal ˆn(x, y, z) =
(n
x
, n
y
, n
z
)> and ˆn(x
0
, y
0
, z
0
) = (n
0
x
, n
0
y
, n
0
z
)> of
voxels v(x, y, z) and v(x
0
, y
0
, z
0
) respectively, we
formulate the smoothness-based constraint:
E
s n
(x, y, z, x
0
, y
0
, z
0
) =
π
−1
arccos
ˆn(x, y, z) · ˆn(x
0
, y
0
, z
0
)
(8)
The cost function of Equation 8 is the normalised
correlation angle between normals.
3. Depth-normal Consistency Prior. The depth-
based prior seeks to clean up depth maps by enforcing
their smoothness, while the normal-based approach
promotes gradual spatial evolution of the normal field.
Both approaches are one-sided: the depth is optimised
indexing the normals or vice versa. Depth and nor-
mal estimation processes are however not indepen-
dent and must be consistent with each other. We
formulate a prior explicitly enforcing consistency be-
tween depths and normals, for the first time perform-
ing joint depth map and normal field optimisation.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
338

Figure 1: Real data: object appearance.
Each depth transition between v(x, y, z) and
v(x
0
, y
0
, z
0
) uniquely defines local geometric normal
ˆn
g
(x, y, z, x
0
, y
0
, z
0
), always contained in the transition
plane (xz or yz). If the depth transition is correct, the
geometric normal correlates well with the projections
of the photometric normals of v(x, y, z) and v(x
0
, y
0
, z
0
)
(their normal estimates), respectively ˆn
ph pr j
(x, y, z)
and ˆn
ph pr j
(x
0
, y
0
, z
0
), onto the corresponding depth
transition plane. Mathematically, the correlation de-
gree can be expressed by the correlation angle. For
example, for v(x, y, z) we have:
φ
ph−g
= π
−1
arccos( ˆn
ph pr j
(x, y, z) · ˆn
g
(x, y, z, x
0
, y
0
, z
0
))
(9)
Since the range of the arc-cosine function is [0, π], the
orientation of the geometric normal must be forced to
be consistent with the photometric normals (i.e. out of
the surface, z > 0). Hence, the depth-normal consis-
tency prior E
s dn
(x, y, z, x
0
, y
0
, z
0
) is formulated as fol-
lows:
E
s dn
(x, y, z, x
0
, y
0
, z
0
) =
1
2
(φ
ph−g
+ φ
0
ph−g
) (10)
4 EVALUATION
We perform evaluation of the proposed method on
both real and synthetic data to enable qualitative and
quantitative analysis. Throughout, our method with
its 3 prior options is compared against the standard
HS approach without MRF optimisation. For real
data, the quality of results is assessed visually as there
is no ground truth. Synthetic input imagery, on the
other hand, is generated from an a priori known mesh
and hence permits quantitative assessment of both lo-
cal and global shape deviations of the reconstructions.
4.1 Real Data
Real data is composed of 4 sets (Figure 1) from
(Guillemaut et al., 2008), each posing different chal-
lenges. The billiard ball and the teapots are specular
smooth objects. The teapots are more complex with
wider specularities and 2D texture (e.g. stripes, flow-
ers). The terracotta doll is Lambertian but has many
fine geometric details (e.g. dimples, clothing).
Figure 2 contrasts estimated depth maps and the
corresponding integrated surfaces of the proposed
MAP HS formulation against standard (ML) HS.
MAP optimisation priors are compared by qualita-
tively accessing both local and global accuracy of
the generated depth maps and surfaces. The relative
weight α is tuned for each prior independently but the
optimal setting per prior tends to be consistent across
all datasets. Surface integration is performed from
the normal fields in the frequency domain using the
Frankot-Chellappa (FC) algorithm (Frankot and Chel-
lappa, 1988).
The results in Figure 2 show that, relative
to ML HS, MAP optimisation clearly produces
smoother reconstructions (teapot/ball surface in Fig-
ures 2(e),(f),(g)) with finer structural detail (the doll’s
dimples/eyebrows in Figure 2(h); the corresponding
normal fields in Figure 2(m) are rectified to reveal
structural detail). On the relative performance of the
priors, the key observation is that only the depth-
normal consistency prior generates geometrically cor-
rect depth maps. Global accuracy of the depth-based
prior ranges from poor (ball, Figure 2(a)) to rea-
sonable (teapots, Figures 2(b),(d)) and high (doll,
Figure 2(c)). The depth maps of the depth-based
prior are however universally noisy. Correspond-
ing normal-based prior results are consistently heav-
ily distorted. Correct reconstruction is only possible
from a geometrically (globally and locally) accurate
depth map. While this is evident for the doll dataset,
in other cases distorted depth maps of the normal-
based approach may, in the front view, seem to pro-
duce decent reconstructions (Figures 2(f),(g)). The
deceiving appearance results from optimisation ac-
cidentally finding well-correlating normals at wrong
depths. These integrate into locally smooth surfaces,
yet distort the global shape for all four datasets (Fig-
ures 2(i),(j),(k),(l)). As the depth map accuracy as-
sessment suggests, the best global shape reconstruc-
tion belongs to the depth-normal consistency prior op-
timisation.
HS is known (Guillemaut et al., 2004) to be sensi-
tive to calibration and discretisation errors whereby,
due to projection mismatches, intensity measure-
ments i
1
and i
2
within a reciprocal pair are inconsis-
tent. The grave form of inconsistency when, within
a single reciprocal pair, a point is projected into dif-
ferent intensity fields, results in reconstruction of 2D
(imprinted) texture as geometric detail. Along with
sharpening true geometries, optimisation is seen to
strengthen the effect of calibration errors: e.g. printed
stripes and flowers on the teapots (Figure 1) appear
embedded into geometry (Figure 2(f),(g)). Perform-
ing patch-based intensity averaging during input data
ABayesianFrameworkforEnhancedGeometricReconstructionofComplexObjectsbyHelmholtzStereopsis
339

(a) depth maps, α
d
= 0.9, α
n
= 0.1, α
dn
= 0.8 (b) depth maps, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(c) depth maps, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(d) depth maps, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(e) FC reconstruction, front view, α
d
= 0.9, α
n
= 0.1, α
dn
= 0.8
(f) FC reconstruction, front view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(g) FC reconstruction, front view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(h) FC reconstruction, front view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(i) FC reconstruction, side view, α
d
= 0.9, α
n
= 0.1, α
dn
= 0.8
(j) FC reconstruction, bottom view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(k) FC reconstruction, bottom view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(l) FC reconstruction, side view, α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
(m) Normal fields (doll), α
d
= 0.9, α
n
= 0.5, α
dn
= 0.8
Figure 2: Depth maps, normal fields (doll) and final reconstruction by integration using the FFT-based Frankot-Chellappa (FC)
algorithm. In each sequence of 4 images (left to right) standard (ML) HS is compared against proposed MAP HS formulation
using MRF optimisation with depth-based (d), normal-based (n) and depth-normal consistency (dn) priors (data-smoothness
weighting α as indicated in each case). Sampling resolution ∆x × ∆y × ∆z and sampled volumes |V | = N
X
× N
Y
× N
Z
are as
follows. Doll: 1.0mm ×1.0mm×0.5mm, |V | = 160×82 ×60; teapot no.1: 1.0mm × 1.0mm×0.25mm, |V | = 150×200 × 320;
teapot no.2: 1.0mm × 1.0mm × 0.25mm, |V | = 120 × 190 × 480; billiard : 1.0mm × 1.0mm × 0.25mm, |V| = 60 × 60 × 100.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
340
(a) Improved depth maps (b) Improved FC reconstructions
Figure 3: Mitigation of saturation and mis-calibration artefacts through patch-based averaging. Settings: MAP HS with
depth-normal consistency prior, patch-based averaging and α
dn
= 0.5.
0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
normalised noise variance
RMS geometric error [m]
standard HS
MRF depth−based prior
MRF normal−based prior
MRF depth−normal consistency prior
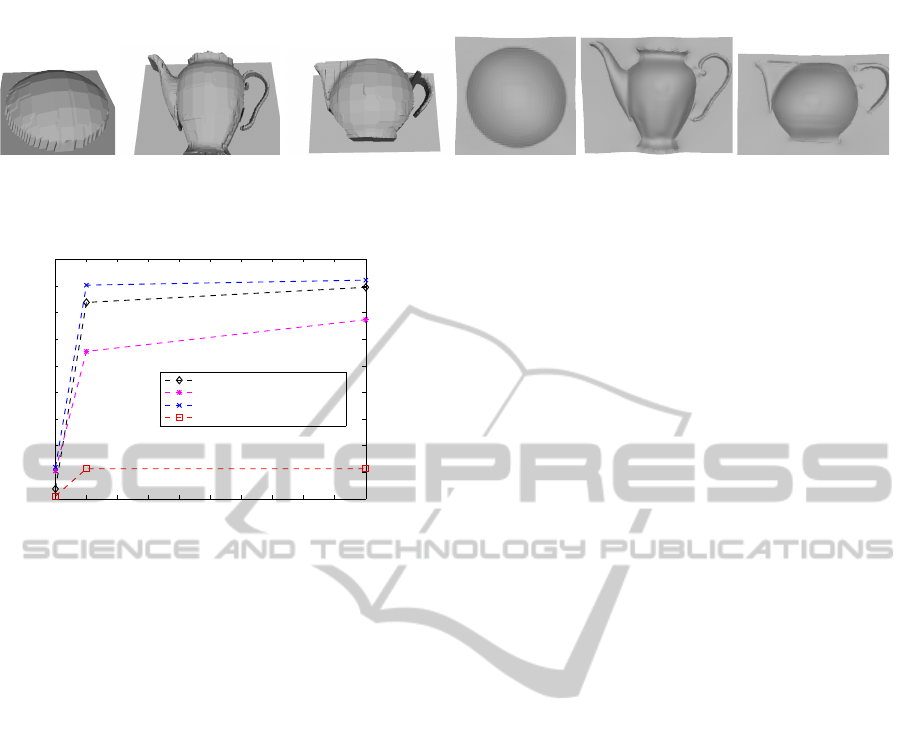
Figure 4: Quantitative evaluation on synthetic data. RMS
geometric error as a function of normalised intensity noise
variance for our MRF (MAP) HS formulation with different
priors and standard (ML) HS.
sampling to bring inconsistent measurements into
closer correspondence would counteract the problem
(Guillemaut et al., 2004). The measure mitigates sat-
uration artefact as well since, instead of the indiscrim-
inative sensor upper limit, the intensities in Equation
2 acquire more meaningful values through regional
support of patch-based averaging. In Figure 3(a) we
show how patch-based averaging effectively elimi-
nates depth errors in the saturated and pattern regions,
hence eliminating/substantially mitigating saturation
and embedded 2D texture artefacts (Figure 3(b)).
4.2 Synthetic Data
Our synthetic object of choice is a sphere (radius =
200 mm). The mesh of the sphere is rendered in
POV-Ray (POV-Ray, 2013) with reflectance consist-
ing of diffuse and specular components and under
controlled camera/light source configurations to pro-
duce 8 noise-free reciprocal pairs. For robustness as-
sessment, two additional image sets are produced by
corrupting the original set by Gaussian zero-mean in-
tensity noise with the variance levels of respectively
0.001 and 0.01. Reconstruction quality is quantified
by the geometric error: the reconstructed mesh is
sampled for each point seeking the closest distance on
the target ground truth mesh. Figure 4 shows the RMS
error as a function of noise variance comparing stan-
dard ML HS and our MRF (MAP) formulation with 3
different priors (sampled volume |V | = 82 × 82 × 251
at resolution 5mm × 5mm × 1mm). The input inten-
sity range is [0, 65535]. Hence, the normalised noise
variance of 0.001 and 0.01 translates into the abso-
lute intensity standard deviations of 2072 and 6554
respectively. Surface integration is performed us-
ing unscreened Poisson surface reconstruction (Kazh-
dan et al., 2006) because the method outputs surfaces
characterised in the absolute world coordinate system
facilitating their easy comparison unlike FC surfaces
in their individual relative reference frames needing
alignment.
In Figure 4 MRF optimisation with the depth-
normal consistency prior clearly outperforms the
other approaches by an order of magnitude mar-
gin achieving reconstruction accuracies of roughly
0.5mm and 5mm for noise-free and noise-corrupted
sets respectively. The accuracy of the other methods
is the order of a few mm and a few cm for the two
respective cases. For the noise-free case, standard HS
comes closest to the depth-normal prior with the 2mm
error. The second observation to be made is that the
normal-based prior is utterly ineffective with the ac-
curacy always below standard HS, consistent global
shape distortion and the greatest performance deteri-
oration with increased noise levels owing to the high
susceptibility of normals as continuous 3D quanti-
ties to input noise via SVD. Even for the noise-free
case, the error with the normal-based prior is high be-
cause there is no theoretical guarantee that the best
correlating normals correspond to the correct depth
positions. The depth-based prior appears to facilitate
an improvement compared to standard HS for noise-
corrupted data. On visual inspection however, the
depth-based reconstruction is seen to retain the global
shape distortion of the standard HS result, albeit mit-
igated as its lower RMS indicates. In the noisy case,
only our depth-normal consistency prior produces a
global shape visually acceptable as a sphere.
5 CONCLUSIONS
We have proposed a novel MRF optimisable MAP
ABayesianFrameworkforEnhancedGeometricReconstructionofComplexObjectsbyHelmholtzStereopsis
341

formulation of HS, instead of its standard ML form.
To this end, we formulated and compared a depth-
based, a normal-based and a specially tailored depth-
normal consistency prior. We conclude that correctly
utilising the given of piece-wise surface smoothness
in the MAP formulation greatly improves both local
and global reconstruction accuracy relative to ML re-
sults. Both quantitative and qualitative results indi-
cate our depth-normal consistency prior to be the cor-
rect formulation of the smoothness term, which by
enforcing consistency between depth and normal in-
formation produces the best results in terms of both
local smoothness and global object shape. The re-
sults generated with the prior are uniquely consistent
in both depth and integrated normal domain with the
normals being indexed from a geometrically correct
depth map. The computational overhead for the prior
is dependent on the size of the sampled voxel volume
and for the presented real data ranges from 2 min-
utes (billiard ball) to 4 hours (teapot no. 2). In our
future work we are confident the run-times will be re-
duced substantially by embedding MRF optimisation
of Bayesian HS into a coarse-to-fine framework using
octrees and/or by parallelising and porting prior cost
pre-computation (the bottleneck of the pipeline) onto
the GPU. In addition, we shall explore the potential
of our MRF framework in resolving ambiguities in
the sensor saturation region and at grazing sampling
angles.
REFERENCES
Baumgard, B. (1974). Geometric Modeling for Computer
Vision. PhD thesis, University of Stanford.
Delaunoy, A., Prados, E., and Belhumeur, P. (2010). To-
wards full 3D Helmholtz stereovision algorithms. In
Proc. of ACCV, volume 1, pages 39–52.
Frankot, R. and Chellappa, R. (1988). A method for enforc-
ing integrability in shape from shading algorithms.
PAMI, 10(4):439–451.
Guillemaut, J.-Y., Drbohlav, O., Illingworth, J., and
ˇ
S
´
ara,
R. (2008). A maximum likelihood surface normal es-
timation algorithm for Helmholtz stereopsis. In Proc.
of VISAPP, volume 2, pages 352–359.
Guillemaut, J.-Y., Drbohlav, O.,
ˇ
S
´
ara, R., and Illingworth,
J. (2004). Helmholtz stereopsis on rough and strongly
textured surfaces. In Proc. of 3DPVT, pages 10–17.
Helmholtz, H. (1925). Treatise on Physiological Optics,
volume 1. Dover (New York).
Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Poisson
surface reconstruction. In Proc. of SGP, pages 61–70.
Kolmogorov, V. (2006). Convergent tree-reweighted
message passing for energy minimization. PAMI,
28(10):1568 – 1583.
Kolmogorov, V. and Zabih, R. (2004). What energy func-
tions can be minimized via graph cuts? PAMI, 26:65–
81.
Laurentini, A. (1994). The visual hull concept
for silhouette-based image understanding. PAMI,
16(2):150–162.
Li, S. (1994). Markov random field models in computer
vision. In Proc. of ECCV, volume B, pages 361–370.
POV-Ray (2013). POV-Ray - The Persistence of Vision
Raytracer. http://www.povray.org/.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. IJCV, 47(1-3):7–42.
Seitz, S., Curless, B., Diebel, J., Scharstein, D., and
Szeliski, R. (2006). A comparison and evaluation of
multi-view stereo reconstruction algorithms. In Proc.
of CVPR, volume 1, pages 519– 528.
Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Kol-
mogorov, V., Agarwala, A., Tappen, M., and Rother,
C. (2008). A comparative study of energy min-
imization methods for markov random fields with
smoothness-based priors. PAMI, 30(6):1068–1080.
Tu, P., Mendonc¸a, P. R., Ross, J., and Miller, J. (2003). Sur-
face registration with a helmholtz reciprocity image
pair. In Proc. of IEEE Workshop on Color and Photo-
metric Methods in Computer Vision.
Wainwright, M. J., Jaakkola, T. S., and Willsky,
A. S. (2005). Map estimation via agreement on
trees: Message-passing and linear-programming ap-
proaches. IEEE Transactions on Information Theory,
51(11):3697–3717.
Weinmann, M., Ruiters, R., Osep, A., Schwartz, C., and
Klein, R. (2012). Fusing structured light consistency
and helmholtz normals for 3D reconstruction. In Proc.
of BMVC, pages 108.1–108.12. BMVA Press.
Woodham, R. J. (1989). Shape from shading, chapter Pho-
tometric method for determining surface orientation
from multiple images, pages 513–531. MIT Press,
Cambridge, MA, USA.
Wu, T.-P., Tang, K.-L., Tang, C.-K., and Wong, T.-T.
(2006). Dense photometric stereo: A Markov Ran-
dom Field approach. PAMI, 28(11):1830–1846.
Zickler, T. (2006). Reciprocal image features for uncali-
brated Helmholtz stereopsis. In Proc. of CVPR, pages
1801– 1808.
Zickler, T., Belhumeur, P. N., and Kriegman, D. J. (2002).
Helmholtz stereopsis: Exploiting reciprocity for sur-
face reconstruction. IJCV, 49(2–3):215–227.
Zickler, T. E., Ho, J., Kriegman, D. J., Ponce, J., and Bel-
humeur, P. N. (2003). Binocular Helmholtz stereopsis.
In Proc. of ICCV, volume 2, pages 1411–1417.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
342
