Template-based Treemaps to Preserve Spatial Constraints

Natallia Kokash

, Bernard de Bono

and Joost Kok

Leiden Institute of Advanced Computer Science (LIACS), Leiden, The Netherlands

Imperial College London, London, U.K.

Keywords:

Information Visualization, Treemaps, Constraints, Templates.

Abstract:

Treemapping is a method for displaying hierarchical data using nested rectangles. Each branch of the tree

is given its rectangle, which then is tiled with smaller rectangles representing sub-branches. A node’s shape

has an area proportional to a speciﬁed dimension of the data. To create a treemap, one must deﬁne a tiling

algorithm, i.e., a way to divide a rectangle into sub-rectangles of speciﬁed areas. There are several problems

with existing tiling algorithms: (i) they allow tiles to shift when the main window or some of the tiles are

resized affecting the user perception of the information; (ii) they do not allow users to place selected elements

into desired positions w.r.t. each other. In this paper, we present a method for creating treemaps with cus-

tomized layouts. The method is based on reusable templates and supports zooming into speciﬁc areas of the

treemap without affecting its initial layout. We illustrate the use of template-based treemaps to the visualiza-

tion of biomedical data. Furthermore, we present an algorithm for automated generation of layouts satisfying

positional constraints for a particular class of constraints.

1 INTRODUCTION

Treemaps (Johnson and Shneiderman, 1991) are an

effective technique to visualize two-dimensional hier-

archical data by using nested shapes in a space-ﬁlling

layout. The standard shape is the rectangle, but other

shapes and variations, e.g., circular treemaps (Fischer

et al., 2012; Wetzel, 2006) and Voronoy diagram-

based subdivisions (Balzer and Deussen, 2005), have

been used. Each shape represents a geometric region,

which can be subdivided recursively into smaller re-

gions. At each level of recursion, some attribute of

interest is displayed, e.g., with the help of shape color.

Nodes in a treemap, also called tiles, represent

individual data items in a dataset. Node size, color

and text label can be used to represent attributes of

the data item. One-layered treemaps can display data

attributes but are not very good at emphasizing the

place of an item in the overall hierarchical structure.

To compensate for that, a small ﬁxed margin with

structural labels are typically used. In treemaps dis-

playing hierarchical structures, it is possible to nav-

igate among different layers and zoom into selected

tiles (Blanch and Lecolinet, 2007). A more complete

overview of treemap development history and appli-

cations can be found in (Shneiderman, 2009).

To create a treemap, one must deﬁne a tiling algo-

rithm - a way to divide a rectangle into sub-rectangles

of speciﬁed areas. In most tiling algorithms, the node

position does not precisely represent any character-

istic of the data. This can reduce the clarity of the

representation by violating user expectations to locate

certain item in a certain place. The same data can be

represented in arbitrarily different looking treemaps

depending on the treemap dimensions and ordering

of nodes. Even if the same tiling algorithm is used

for the identical datasets, their visual representations

may vary drastically. The ability of the tiling algo-

rithm to preserve locations of individual data items

upon changes of visualization and dataset parameters

is referred to as stability. Most of the tiling algorithms

target at optimizing metrics other than stability. An

average aspect ratio (the longest side of a rectangle

divided by its shortest side), and whether the natural

order of the dataset is preserved in its visualization

are two important characteristics (Wattenberg, 2005).

Among the most commonly used tiling algorithms

are slice and dice (Johnson and Shneiderman, 1991),

squarify (Bruls et al., 2000), strip (Bederson et al.,

2002), and their numerous variations. These al-

gorithms do not guarantee the complete adherence

to two-dimensional spatial constraints. For exam-

ples, Figure 1 shows how the representation of the

same hierarchical structure using the squarify algo-

Kokash N., de Bono B. and Kok J..

Template-based Treemaps to Preserve Spatial Constraints.

DOI: 10.5220/0004684900390049

In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 39-49

ISBN: 978-989-758-005-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Unstable treemap layouts.

rithm (Bruls et al., 2000) changes when the propor-

tions of the display area are changed.

The need for a tiling algorithm that allows users

to control treemap layouts has been pointed out

in (de Bono et al., 2012). This work applies treemaps

to automatically generate biomedical maps from pub-

licly available data sources by overlaying the informa-

tion about blood vessels, proteins, gene expressions,

cells, drug and disease mechanisms, etc. over graph-

ical schematics of human body anatomy. In these

treemaps,

• it is expected that spatial relations and constraints

on relative node positioning among body parts are

always preserved,

• there should be a possibility to ﬁlter the dataset by

showing only selected tiles of interest to a certain

user without affecting the visual stability of the

corresponding treemap.

The concepts of a constrained treemap layout and

custom user templates have emerged, but no generic

methods to build such templates have been developed.

In this paper, we address the problem of build-

ing customized and controlled treemap layouts. First,

we describe our effort to control tile positions using

a constraint solver (Section 2). Then we introduce

a concept of a template: a hierarchical structure that

allows users to pose constraints on relative tile posi-

tioning (Section 3). We present a graphical tool to cre-

ate such templates and a tool to draw treemaps with

customized layouts by binding such templates with

treemap datasets using an example from the biomed-

ical domain (Section 4). Furthermore, we introduce

a problem of automated generation of templates to

satisfy spatial constraints and provide an algorithm to

generate such templates for a particular class of con-

straints (Section 5). Finally, we provide an overview

of the state of the art on data visualization using

treemaps (Section 6), conclude the paper and discuss

future work (Section 7).

2 CONSTRAINING TREEMAP

LAYOUTS

The work on treemap generalization (de Bono et al.,

2012; Tsiaras et al., 2009) inspired us to apply a

(a) Basic layout (b) Width > height

Figure 2: Layouts found by the constraint solver.

constraint solver to build layouts for a general set

of geometric constraints. We encoded the conditions

for a desired treemap layout and employed Z3 SMT

solver (de Moura and Bjrner, 2008) to ﬁnd solutions

for data with constraints on the aspect ratio of treemap

tiles. As a tiling algorithm is typically a recursive

procedure, it is sufﬁcient to show how tiles are allo-

cated on one level. Our general approach is outlined

in Figure 1. This listing shows a pseudocode for a

constraint satisfaction problem (CSP) that for a given

display area deﬁned by its left top corner coordinates

and dimensions and a list of n elements that should

be placed in this area returns positions and dimen-

sions of treemap rectangles. The constraints deﬁne

bounds on element positions and dimensions, and re-

quire that any two rectangles should not intersect. The

sum of areas of all rectangles should be equal to the

main area. Finally, any custom constraints on element

positions, dimensions, adjacency etc. can be deﬁned.

We applied the presented algorithm to ﬁnd a

treemap layout for a simple tree consisting of a root

node with three children elements. A custom con-

straint here is a requirement that the width of rectan-

gles should be larger than their height. The solution

for the CSP with no custom constraints is shown in

2(a). It is found in less than a second, while to ﬁnd

a solution for the layout with the additional constraint

(Figure 2(b)) the solver needed several minutes. Thus,

while it is feasible to build treemap layouts with any

desired properties using a constraint solver, the ap-

proach is too slow for ad-hoc visualization. Even

in trivial cases, the SMT solver may fail to satisfy

the constraints due to their non-linear nature or large

search space. The stability of the layouts is not guar-

anteed either.

From this we conclude that the search space for

possible layouts should be restricted to some geomet-

rical pattern. For example, the strip (Bederson et al.,

2002) algorithm allows only layouts composed of hor-

izontal or vertical stripes at each level. Although this

algorithm produces ordered treemaps, it is not sufﬁ-

cient for our goals due to its instability (elements may

jump from one line to another when element sizes are

changed) and inability to impose two-dimensional po-

sitioning constraints.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

/*Define terms representing the position and dimensions of the main tile */

← 0; y

← 0; w

← area.width; h

← area.height;

/*Define arrays x,y, h,w of terms representing the positions and dimensions of its children, 0 < i ≤ n */

/*The dimensions of each child should not exceed the dimensions of the main rectangle */

for 0 < i ≤ n do

assertCnstr ((x

≥ 0) ∧ (y

≥ 0) ∧ (w

> 0) ∧ (h

> 0));

assertCnstr (((x

+ w

) ≤ (x

+ w

)) ∧ ((y

+ h

) ≤ (y

+ h

)));

end

/*Rectangles should not intersect */

for 0 < i ≤ n do

for 0 < j ≤ n do

assertCnstr (((x

+ w

≤ x

) ∨ (x

+ w

≤ x

)) ∧ ((y

+ h

≤ y

) ∨ (y

+ h

≤ y

)));

end

/*Define area constraints for each child rectangle */

for 0 < i ≤ n do assertCnstr ((h

∗ w

) = w

∗ h

∗ s

.size/ totalSize);

/*The sum of areas of all rectangles should be equal to the main area */

totalArea ← 0;

for 0 < i ≤ n do totalArea ← totalArea + h

* w

;

assertCnstr (totalArea = w

∗ h

);

/*Add custom constraints here, solve the CSP */

Algorithm 1: Generic constraint-based tiling algorithm.

The template-based treemapping algorithm we

propose uses the multi-level splitting of a given area

into columns and rows. Two-dimensional constraints

on positions of treemap elements are satisﬁed by plac-

ing such elements into areas corresponding to differ-

ent branches of a template.

3 DEFINING TEMPLATES

In this section, we describe our method to create tem-

plates for treemap tile allocation.

A template is deﬁned in the form of a tree where

each node has an assigned attribute to represent a ver-

tical split or a horizontal split operation. Leaf nodes

of the tree correspond to the treemap tiles and deﬁne

their relative positions. Internal nodes of the tree de-

ﬁne the way the available area is subdivided. Color

or image can be assigned to each node of the tem-

plate (typically, only appearance of leaf nodes mat-

ters). Additionally, one may want to use only part

of the area allocated to the parent rectangle to place

children elements. This can be accomplished with the

help of vertical ratio and horizontal ratio parameters

of a template node. If not the entire area of the tile

is occupied, we can use vertical alignment and hor-

izontal alignment properties with values top, middle,

down and left, center, right, respectively, to position

nested elements within the tile.

A layout deﬁned by a template is build by splitting

the available area at each level using the operation de-

ﬁned in template nodes. All the leaf tiles of the tem-

plate that appear on the top level of such a treemap

will always remain at the same relative positions to

(a) Template

(b) Deﬁned layout

Figure 3: Template builder.

each other. Figure 3 shows our template builder fea-

turing a sample template with 6 tiles. At the ﬁrst level,

the entire area is split into 2 columns. At the second

level, the second column is split into 2 rows. At the

third level, the bottom row is split into 2 columns and,

ﬁnally, its ﬁrst column is split into 3 rows. Figure 3(b)

shows the rendering of the template.

The graphical editor prototype we used

to create this template is available at

Template-basedTreemapstoPreserveSpatialConstraints

http://nkokash.com/apinatomy. The deﬁned tem-

plates can be exported to ﬁles and reconstructed from

such ﬁles when bound to treemap items. The number

of leaf items in the template should coincide with the

number of the children of the tile it is assigned to.

The customized treemap can be stored and further

reused without the need to reassign templates.

Algorithm 2 computes positions and dimensions

of tiles representing children of each treemap item.

Each slice is allocated the area proportional to the to-

tal area of all its items w.r.t. to the total area of all

items in the parent rectangle. The allocation of the

corresponding area is controlled either by the width

or by the height of the strip while its other dimension

remains unchanged at this level. The leaf nodes of

the template tree deﬁne the layout for a single level

of a treemap. In order to keep the algorithm simple,

we omit the processing of scaling and alignment at-

tributes.

4 TEMPLATE-BASED

TREEMAPS

In this section, we illustrate the application of tem-

plates to control the positions of tiles in a treemap

representing human anatomy.

Our example is explained in Figure 4 which de-

picts a longitudinal section through the middle of the

male human body showing the external and internal

surfaces, and organs. From this view, we obtain an

idealized radially symmetric body plan, apportioned

over cylindrical regions. Each of the organs in the

plan is composed of multiple tissues and sub-organs,

the structural information about them is obtained from

the Foundational Model of Anatomy (FMA) ontol-

ogy

. As the visualization of the full ontology may

obscure the details a user is interested to see, it is es-

sential for the visualization tool to support data ﬁl-

tering across multiple levels and contextual zooming

into selected areas. The user should be able to create a

custom view with the internal structure of the selected

body parts placed in a way that simpliﬁes the analysis

of these data.

We reproduce this view on human anatomy in our

prototype. The ﬁrst level of the “Body” treemap con-

sists of 24 equal-size tiles. The template that controls

this layout consists of 4 rows, each in its turn contains

6 columns. We illustrate how the template-based al-

gorithm works by assigning the template created in

the previous section to the item “6000002: Liver Pan-

Foundational Model of Anatomy -

http://sig.biostr.washington.edu/projects/fm/.

creas Duodenum”. Its initial layout (tiles are placed in

a grid) is shown in Figure 5(a). Figure 5(b) shows the

allocation of the tile children according to the prede-

ﬁned template. Note that in contrast to the Figure 3(b)

where we emphasized the splitting deﬁned in the tem-

plate, the treemap layout is formed to preserve the ra-

tio among item sizes (all equal in this case). To en-

large a certain area of a template-based treemap, it is

sufﬁcient to update the size dimension of the item.

Figure 5(c) demonstrates that the tile relative posi-

tions are preserved after tile resizing. Moreover, if

one decides to ﬁlter the treemap to remove items that

are not of interest for data analysis, the remaining tiles

will occupy the available area and their relative posi-

tions will be preserved as well.

The “Body” treemap prototype can be seen at

http://nkokash.com/apinatomy. Several views are

available to illustrate the difference of our approach to

the existing treemapping algorithms, which become

apparent once one modiﬁes the treemap by removing

or including new items or resizing selected tiles. For

example, Figure 5(d) shows two versions of the cus-

tom treemaps for the body anatomy. The left treemap

includes 24 upper level tiles with some details about

the structure of selected parts, including “6000002:

Liver Pancreas Duodenum”. The right image shows a

modiﬁcation of this treemap where some tiles are re-

moved and the sub-parts of others are shown in more

detail. The overall layout remains stable.

Publicly available ontologies and other resources

maintained by biomedical communities provide a rich

source of information about human body which how-

ever is hard to perceive and process in the existing

form. Treemapping templates we introduced in this

paper provide a quick way to extend these data with

the information about spacial representation of related

concepts in a schematic way. Thus, our approach may

ﬁnd multiple applications in the area of biomedical

data analysis, e.g., for the generation of teaching ma-

terials or reasoning about large amounts of intercon-

nected data.

5 TEMPLATE GENERATION

We illustrated how a user can control treemap layout

using manually deﬁned templates. In this section, we

consider the problem of generating such templates au-

tomatically.

Multiple variations in the nature and description of

tile positioning constraints are possible. We introduce

here a CSP which consists in ﬁnding a treemap layout

satisfying requirements in the form “item x should be

placed left (right) and/or above (below) item y”. More

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

Input: TreemapItem template - reference to the template associated with a treemap item;

Rect currRect - a rectangle deﬁning the available area for this item;

Output: List hRect i ﬁnalRects - a list of tile dimensions for item children;

List hTreemapItem i ﬁnalTiles - a list of tiles;

void TemplateBased (TreemapItem template, Rect currRect, List hRect i ﬁnalRects, List hTreemapItem i ﬁnalTiles)

begin

if template.Children.Count > 1 then

float prevX = currRect.X, prevY = currRect.Y;

foreach TreemapItem subTemplate in template.Children do

float fraction = subTemplate.FinalSize / template.TotalChildrenSize;

float dWidth = currRect.Width, dHeight = currRect.Height;

if template.Split == ”horizontal” then dHeight *= fraction else dWidth *= fraction;

Rect rect = new Rect (prevX, prevY, dWidth, dHeight);

TemplateBased (subTemplate, rect, ﬁnalRects, ﬁnalTiles);

if template.Split == ”horizontal” then prevY += dHeight else prevX += dWidth;

end

else

/*Leaf tile occupies all available area */

ﬁnalRects.add(currRect);

ﬁnalTiles.add(template);

end

Algorithm 2: Template-based tiling algorithm.

(a) Schematic body plan (b) Visualizing medical ontologies using treemaps

Figure 4: Longitudinal section through the middle of the male human body.

formally, let S be a list of elements with a given di-

mension s.size,s ∈ S. Assume also that for each s ∈ S,

we generate rectangles identiﬁed by their top left cor-

ner coordinates, width and height. Thus, we can refer

to s.x, s.y, s.w and s.h as to the x and y coordinates

of the rectangle top left corner, its width and height,

respectively. We write

→ s

, i 6= j iff s

.x + s

.w ≤ s

and

↑ s

, i 6= j iff s

.y + s

.h ≤ s

.y;

Our goal is to generate a treemap layout that satisﬁes

a system of constraints

C = {s

, s

∈ S,R ∈ {→, ↑}}.

Easy to notice that a set of one-dimensional con-

straints, either {s

→ s

, s

∈ S} or {s

↑ s

, s

∈

S}, can be satisﬁed by separating elements s

and s

into subsets and placing elements of each subset into

a treemap region separated from the regions for other

subsets by vertical or horizontal lines, respectively.

To refer to the transitive constraint satisfaction, we

can write s

⇒ s

iff there exists s

∈ S such that s

→

and s

→ s

; Analogously, s

 s

iff there exists

∈ S such that s

↑ s

and s

↑ s

. Clearly, the system

Template-basedTreemapstoPreserveSpatialConstraints

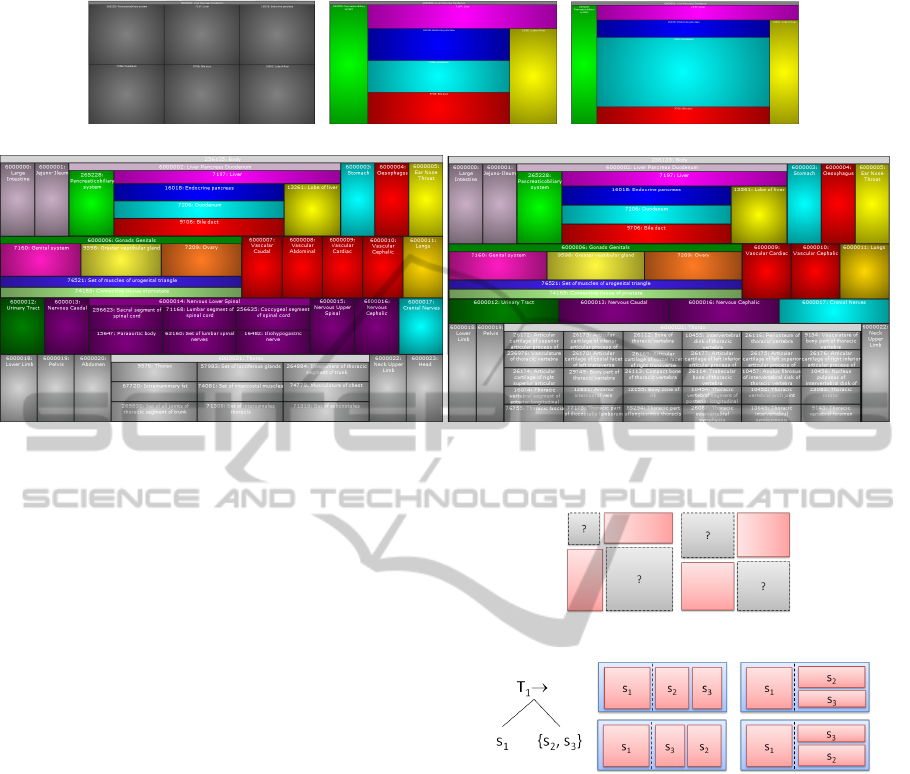
(a) Default layout (b) With assigned template (c) Zooming

(d) Examples of customized treemaps

Figure 5: Body treemap: customizing tile “6000002: Liver Pancreas Duodenum”.

of constraints is not satisﬁable if there exist s

such

that s

⇒ s

∧ s

⇒ s

or s

 s

∧ s

 s

We say that a system of constraints

C = C

∧C

where

= {s

⇒ s

, s

∈ S}

and

= {s

 s

, s

∈ S}

is orthogonal iff for any s

such that

⇒ s

) ∈ C

it follows that

 s

) /∈ C

The orthogonality of vertical and horizontal con-

straints suggest that they can be satisﬁed in a tem-

plate obtained by dividing the area into subregions

using vertical and horizontal splits. The satisfaction

of non-orthogonal systems of constraints is problem-

atic since we are not able to guarantee the existence

of the solution in the form of the rectangular treemap

without gaps. Figure 6 shows two possible layouts

for a dataset with two elements with non-orthogonal

constraints. Such constraints require elements to be

placed diagonally and remaining empty areas to be

ﬁlled with other tiles. It is easy to see that there may

be no items of suitable areas in the dataset to ﬁll these

areas without gaps. An appropriate layout, if it exists,

can be searched for in the form of a CSP as described

in Section 2.

For a dataset with orthogonal constraints, we look

for a suitable layout by constructing and evaluating

Figure 6: Satisfying non-orthogonal constraints.

Figure 7: Building and rendering slicing trees.

all possible slicing trees (Chen et al., 2002; Lai and

Wong, 2001). A slicing tree can be represented us-

ing an inﬁx expression with operands referring to free

tile sets or sub-trees and an operator deﬁning the type

of the split operation. The deﬁnition of a slicing tree

essentially coincides with the deﬁnition of our tem-

plate: a template can be seen as a slicing tree for the

complete dataset with additional visual attributes. Ev-

ery internal node of a slicing tree represents a vertical

slice satisfying → constraint or a horizontal slice sat-

isfying ↑ constraint. Leaf elements (or atoms in cor-

responding expressions) represent dataset items dis-

played as treemap tiles.

To construct a template for a given set of orthogo-

nal constraints, we dynamically build a set of trees

that satisfy constraints one by one (Algorithm 3).

Thus, given a constraint c = s

, we check whether

items s

and s

are already in the set of slicing trees

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

obtained at the previous step. If both items are found,

we check whether the constraint c is satisﬁed. As-

sume that function search(Tree tree, Item s) returns a

path from the item s to the tree root. Using this func-

tion, we ﬁnd paths path1 and path2 from items s

and

to the tree root. The constraint c is satisﬁed if the

operator of the node where both paths deviate coin-

cides with the operator in the constraint and the left

handed item s

is located to the left from the deviation

point, that is, the next node of the path1 is the left

child of the node at the deviation point.

If only one of the items is in the partial tree (say,

), we can insert the second item s

in such a way that

the constraint c is satisﬁed. This can be achieved ei-

ther by inserting the missing item in any branch of the

tree that is already separated from the existing item

using the splitting operator in c, or by creating a new

split at the root of the tree or right to the existing item.

If none of the items in the constraint are in the tree, we

create all the permutations containing one of the items

and then add the second item to each of these trees as

in the previous case.

Let us consider an example. Assume we have a

dataset

S = {s

,1 ≤ i ≤ 6}

with the following sets of orthogonal constraints

= {s

→ s

}

and

= {s

↑ s

For brevity, we use ﬁgure brackets {...} to refer to all

possible two-dimensional permutations of elements

we do not need to unfold at a particular step. Figure 7

shows a slicing tree with the ﬁrst constraint satisﬁed

and the corresponding treemap layouts. Inﬁx expres-

sions can be used to describe both initial constraints

and the slicing trees at any intermediate step:

= s

→ {s

}, c

= s

↑ s

= s

→ s

, c

= s

↑ s

= s

↑ s

The ﬁrst set of slicing trees T

is equivalent to c

Next, we join a constraint c

. Since none of its items

is in T

, this case folds into case 4 of the algorithm,

i.e., all permutations are generated:

= T

 c

= (s

→ {s

}) → (s

→ s

)

= (s

→ s

) → (s

→ {s

}),

= (s

→ {s

}) ↑ (s

→ s

= (s

→ s

) ↑ (s

→ {s

}),

= s

→ {s

,(s

→ s

)},

= {s

,(s

→ s

)} → {s

Note that the positions of both items from c

are pre-

deﬁned in the generated trees. Thus, at this step the

Figure 8: Automatically generated constraint-satisfying

layouts

case 1 of the algorithm is applied and we eliminate

trees that do not satisfy c

, leaving options T

and

, where T

is further unfolded and ﬁltered to leave

only trees satisfying c

= T

 c

= (s

→ s

) ↑ (s

→ {s

}),

= ((s

→ s

) ↑ s

) → {s

= (s

→ (s

↑ s

)) → {s

The items of constraint c

are already positioned,

so we again ﬁlter the set T

according to the option 1

of the algorithm, leaving T

as the only valid alterna-

tive:

= T

 c

= (s

→ s

) ↑ (s

→ {s

}).

After joining the remaining constraint c

= s

↑ s

according to the case 3 (s

is in the tree T

while s

is a new item), we obtain the following set of slicing

trees:

= T

 c

= (s

→ s

) ↑ ((s

→ {s

}) ↑ s

= (s

→ s

) ↑ (s

→ ({s

} ↑ s

)),

= (s

→ s

) ↑ (s

→ {(s

↑ s

),s

}).

If there are items in the data set without positional

constraints, they can be inserted to any place in the ﬁ-

nal slicing trees. Together with two-dimensional per-

mutations of elements {s

} in the generated solu-

tions, 12 layouts shown in Figure 8 satisfy our ini-

tial constraints. In total we get 11 unique layouts as

layouts 2(d) and 3(a) in Figure 8 represent identical

treemaps because permutations of elements we did

not unfold in slicing trees T

and T

yield the same

layouts.

Assuming that we target at ﬁnding all accept-

able layouts, in the worst case we need to generate

all two-dimensional permutations of the given set of

tiles. Having in mind that to generate such permuta-

tions each of the items is placed to the left and right

Template-basedTreemapstoPreserveSpatialConstraints

Input: List hConstraint i constraints - a list of constraints;

Output: List hTree i slicingTrees - a list of slicing trees satisfying constraints;

List hTree i defineLayout (List hConstraint i constraints)

begin

List hTree i slicingTrees = new List hTree i (new Tree (constraints[0]));

constraints.remove(0);

foreach c in constraints do

List hTree i newSlicingTrees = new List hTree i ();

foreach tree in slicingTrees do newSlicingTrees.addAll(generateTrees (tree, c));

slicingTrees = newSlicingTrees;

end

List hTree i generateTrees (Tree tree, Constraint c)

begin

List hConstraint i path1 = search (tree, c.left); List hConstraint i path2 = search (tree, c.right);

/*1. Both items are already in the tree */

if (path1 != null) and (path2 != null) then

/*Find the last common node in the paths */

int i = 0; while path1[path1.length - 1 - i] == path2[path2.length - 1 - i] do i++;

Constraint node = path1[path1.length - i];

/*If the operator in this node coincides with the operator in the constraint and the rest of path1

is in its left branch, the constraint is satisfied. Otherwise, the constraint is violated and the

slicing tree is eliminated. */

if (node == c.operator) and (node.left == path1[path1.length - 1 - i]) then return tree; else return null;

end

List hTree i slicingTrees = new List hTree i;

/*2. Left item is in the tree */

if (path1 != null) and (path2 == null) then

if path1[0] == c.left then

foreach node in path1 do

/*for all ancestors with the same split type located on the same side with the existing item

if (node.operator == c.operator) and (node.parent.left == node) then slicingTrees.addAll(insert (node.right,

c.right));

end

else

/*...analogously, but insert the missing element into the left branch of each ancestor with the

same operator that has the existing item on the right */

end

slicingTrees.add(new Tree (tree, c.constraint, c.right)); slicingTrees.add(new Tree (insert (path1[0], c.right));

end

/*3. Right item is in the tree */

if (path1 == null) and (path2 != null) then

/*...Analogously to the case 2 */

/*4. None of the items is in the tree */

if (path1 == null) and (path2 == null) then

List hTree i newSlicingTrees = insert (tree, c.left);

foreach tree in newSlicingTrees do

/*...Analogously to the case 2 */

end

return slicingTrees;

end

List hTree i insert (Tree tree, Constraint c)

begin

List hTree i slicingTrees = new List hTree i;

slicingTrees.add(new Tree (tree, Operator.uparrow, c)); slicingTrees.add(new Tree (tree, Operator.rightarrow, c));

slicingTrees.add(new Tree (c, Operator.uparrow, tree)); slicingTrees.add(new Tree (c, Operator.rightarrow, tree));

if tree.right != null then

slicingTrees.addAll(c, tree.right); slicingTrees.addAll(tree.right, c);

end

if tree.left != null then

slicingTrees.addAll(c, tree.left); slicingTrees.addAll(tree.left, c);

end

return slicingTrees;

end

Algorithm 3: Template generation algorithm.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

branches of the slicing tree for both vertical and hori-

zontal split operators, the following dynamic formula

applies F(n) = 4 ∗ n ∗ F(n − 1) and the algorithm’s

performance can be estimated as Θ(4

∗n!). However,

in practice we need only one suitable layout, and if no

speciﬁc constraints on the tile positions are given, it

is deﬁned in Θ(n). In the case of constrained layouts,

each new constrained item needs to be added to the

slicing trees generated at the previous step and this

may lead to the generation of two-dimensional per-

mutations of the current element with all previously

inserted items. Thus, the complexity can be estimated

as Θ(4

∗ m!), where m is the number of unique data

items with constrained positions. A more detailed

analysis of the algorithm’s performance as well as its

possible optimizations will be studied in future work.

6 RELATED WORK

In this section, we overview related work and com-

pare our method to existing approaches.

Various extensions and modiﬁcations of classic al-

gorithms exist that target at improving treemap per-

formance metrics. Spatially ordered squariﬁed lay-

out (Wood and Dykes, 2008) provides a more consis-

tent arrangement of nodes w.r.t. the simple unordered

squariﬁed layout while maintaining low aspect ratios.

Buchin et al. (Buchin et al., 2011) describe algorithms

for transforming a rectangular layout without hierar-

chical structure, together with a clustering of the rect-

angles of the layout, into a spatial treemap that re-

spects the clustering and, to the extent possible, the

adjacency of the input layout. Berg et al. (de Berg

et al., 2011) study tiling algorithms with bounded as-

pect ratios. They show that one cannot bound the as-

pect ratio if the regions are restricted to be rectangles.

Tak and Cockburn (Tak and Cockburn, 2013) intro-

duce a new metric to capture more efﬁciently the no-

tion of spatial stability and introduce tiling algorithms

designed to perform well according to this metric. We

ﬁnd our method complimentary to such algorithms as

we target a different problem. Template-based lay-

outs can be used in combination with other tiling algo-

rithms which arrange free items from a dataset to opti-

mize a certain metric while our approach is employed

to create custom layouts where relative tile positions

carry meaningful information, such as in the case of

our body anatomy scenario. If multiple suitable lay-

outs are found by the template generation algorithm

as in our example in Section 5, any of the available

treemapping metrics (e.g., average aspect ratio, lay-

out distance change function) can be used to select

the optimal layout. Constraints on item adjacency

as in (Shneiderman and Wattenberg, 2001) will re-

quire only a minor modiﬁcation of the proposed tem-

plate generation algorithm and are likely to reduce its

search space.

Treemaps are commonly used in combination

with nodelinks such as overlaying trees or graphs.

Linsen and Behrendt (Linsen and Behrendt, 2011)

present a joint 3D map nodelink and treemap interac-

tive visualization tool. While it is not an issue to sup-

port 3D layouts (one of our early prototypes featured

a 3D view where a treemap was used as a “chess-

board” to place 3D objects), zooming facilities in our

approach are more naturally supported. We can en-

large multiple selected areas of a treemap while re-

taining contextual information around enlarged tiles.

As pointed out in (Tu and Shen, 2008), such context-

retaining multi-focus zooming is not supported by ex-

isting tools. The authors tackle this problem by con-

structing a dependency graph that reﬂects relative po-

sitions of tiles and provide an algorithm to enlarge se-

lected areas while retaining initial relative positions

of selected tiles. Non-focused items are evenly dis-

tributed in remaining area. The algorithm is non-

trivial, requires solving systems of linear equations

and introduces a signiﬁcant computational overhead.

An extension of treemapping algorithms has been

studied in the attempt to generalize them for directed

acyclic graphs (DAG) (Tsiaras et al., 2009). It has

been shown that such layouts are not always possible,

and when they are possible, the tiling algorithm is NP

complete. Heuristics have been proposed for several

special cases. The DAGs can be modiﬁed by replicat-

ing nodes with two or more parents. If all such nodes

are replicated, the DAG is converted to a rooted tree.

What is the minimal number of replications needed

to be able to build a DAG map is an open question.

While the objective of this work is different from ours,

the idea to encode desired characteristics of a treemap

layout as constraints was inspired by this paper.

de Bono et al. (de Bono et al., 2012) describes lim-

itations of existing treemapping tools for biomedical

data visualization. This work focuses on the concep-

tual templates tailored for the representation of body

anatomy. In our work, we introduce a generic method

to build custom templates and apply them to control

treemap layouts in any application domain.

Vliegen et al. (Vliegen et al., 2006) apply

treemaps with various tiling algorithms for visual-

izing business data. The best results are obtained

using the hybrid approaches. In our approach, we

allow users to customize the appearance of each

tile independently by assigning a template. The

design guidelines for creating effective rectangular

treemaps (Kong et al., 2010) can help users to deﬁne

Template-basedTreemapstoPreserveSpatialConstraints

templates in our framework for the best visual per-

ception of data depending on their quantitative char-

acteristics. The tree-like templates introduced in our

work can be targeted not at satisfying relative posi-

tioning constraints but at optimizing the layout dis-

tance change function or some other metric, including

custom ones.

The complete coverage of all available area may

not be required for biomedical data visualization or

other application domains. In relation to this, many

other variations of CSPs can be deﬁned and solved to

generate visually appealing treemap layouts. More-

over, such CSPs may require only approximate or

fuzzy solution as the visualization does not always

need to strictly correspond to the data attributes it dis-

plays. For example, a treemap-based tool for the vi-

sualization of mutual fund portfolios (Csallner et al.,

2003) introduces a so called distorted treemap, which

trades proportionality of a mapped attribute to a more

inclusive visualization. The distorted treemap is a

compromise between showing all the data elements

and a classic treemap that preserves value propor-

tions. Consequently, such treemap can show one

more attribute than a classic treemap, though the node

area is no longer proportional to the visualized at-

tribute. This direction of work was not covered in our

approach and requires further investigation.

7 CONCLUSIONS AND FUTURE

WORK

In this paper, we introduced a method and tools to

build custom templates and apply them to customize

treemaps layouts. We illustrated the application of our

approach to control the positions of tiles in a sample

treemap. We also presented a method for automatic

generation of treemap templates for a class of prob-

lems with positional constraints. Our method gener-

ates stable layouts with an easy way to zoom in se-

lected areas, including multi-foci case.

Our future work includes analysis of the problems

of automated template generation for other classes

of constraints as well as application of the presented

method to the visualization of various data sets. Scal-

ability and usability of the proposed methods will be

studied more extensively. Since building custom tem-

plates for large data sets (e.g., human brain ontology)

is time-consuming and requires specialized knowl-

edge, a shared platform for template storage and reuse

will be useful. We are also planning to extend our

method to deﬁne templates for generating 3D images

from biomedical ontologies.

REFERENCES

Balzer, M. and Deussen, O. (2005). Voronoi treemaps. In

Proc of InfoVis’05, pages 49–56. IEEE.

Bederson, B. B., Shneiderman, B., and Wattenberg, M.

(2002). Ordered and quantum treemaps: Making ef-

fective use of 2d space to display hierarchies. ACM

Trans. Graph., 21(4):833–854.

Blanch, R. and Lecolinet, E. (2007). Browsing zoomable

treemaps: Structure-aware multi-scale navigation

techniques. TVCG, 13:1248–1253.

Bruls, M., Huizing, K., and van Wijk, J. (2000). Squari-

ﬁed treemaps. In Proc. of the Joint Eurographics and

IEEE TCVG Symposium on Visualization, pages 33–

42. IEEE.

Buchin, K., Eppstein, D., L

ofﬂer, M., N

ollenburg, M., and

Silveira, R. I. (2011). Adjacency-preserving spatial

treemaps. In Proc. of WADS, pages 159–170.

Chen, L.-Q., Xie, X., Ma, W.-Y., Zhang, H., Zhou, H.-Q.,

and Feng, H. (2002). Dress: A slicing tree based web

page representation for various display sizes. Tech-

nical report MSR-TR-2002-126, Microsoft Research

Asia.

Csallner, C., Handte, M., Lehmann, O., and Stasko, J. T.

(2003). FundExplorer: Supporting the diversiﬁcation

of mutual fund portfolios using context treemaps. In

Proc. of InfoVis’03, pages 203–208. IEEE.

de Berg, M., Speckmann, B., and van der Weele, V. (2011).

Treemaps with bounded aspect ratio. Proc. of the 22nd

Int. Conf. on Algorithms and Computation, pages

260–270.

de Bono, B., Grenon, P., and Sammut, S. (2012). Ap-

inatomy: A novel toolkit for visualizing multiscale

anatomy schematics with phenotype-related informa-

tion. Hum Mutat, 33(5):837–848.

de Moura, L. M. and Bjrner, N. (2008). Z3: An efﬁcient

SMT solver. In Proc. of the 14th Int. Conf. on Tools

and Algorithms for the Construction and Analysis of

Systems (TACAS 2008), volume 4963 of LNCS, pages

337–340. Springer.

Fischer, F., Fuchs, J., and Mansmann, F. (2012). Clockmap:

Enhancing circular treemaps with temporal glyphs for

time-series data. In EuroVis 2012 Short Papers), pages

97–101.

Johnson, B. and Shneiderman, B. (1991). Tree-maps: a

space-ﬁlling approach to the visualization of hierar-

chical information structures. In Proc. of the 2nd Con-

ference on Visualization ’91, pages 284–291. IEEE.

Kong, N., Heer, J., and Agrawala, M. (2010). Perceptual

guidelines for creating rectangular treemaps. TVCG,

16:990–998.

Lai, M. and Wong, D. (2001). Slicing tree is a complete

ﬂoorplan representation. In Proc. of the Conf. on

Design, Automation and Test in Europe (DATE’01),

pages 228–232. IEEE.

Linsen, L. and Behrendt, S. (2011). Linked treemap: a 3d

treemap-nodelink layout for visualizing hierarchical

structures. Computational Statistics, 26(4):679–697.

Shneiderman, B. (2009). Treemaps for space-constrained

visualization of hierarchies. Web document.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

Shneiderman, B. and Wattenberg, M. (2001). Ordered

treemap layouts. In Proc of InfoVis’01, pages 73–78.

IEEE.

Tak and Cockburn (2013). Enhanced spatial stability with

hilbert and moore treemaps. TVCG, 19:141–148.

Tsiaras, V., Triantaﬁlou, S., and Tollis, I. G. (2009).

Dagmaps: Space ﬁlling visualization of directed

acyclic graphs. J. Graph Algorithms Appl., 13(3):319–

347.

Tu, Y. and Shen, H.-W. (2008). Balloon focus: a seam-

less multi-focus+context method for treemaps. TVCG,

14(6):1157–1164.

Vliegen, R., van Wijk, J. J., and van der Linden, E.-J.

(2006). Visualizing business data with generalized

treemaps. TVCG, 12:789–796.

Wattenberg, M. (2005). A note on space-ﬁlling visualiza-

tions and space-ﬁlling curves. In Proc. of InfoVis’05,

pages 181–186. IEEE.

Wetzel, K. (2006). Pebbles - using circular treemaps to vi-

sualize disk usage. Web document.

Wood, J. and Dykes, J. (2008). Spatially ordered treemaps.

TVCG, 14:1348–1355.

Template-basedTreemapstoPreserveSpatialConstraints