Converting Underwater Imaging into Imaging in Air

Tim Dolereit

1,2

and Arjan Kuijper

Fraunhofer Institute for Computer Graphics Research IGD, Joachim-Jungius-Str. 11, 18059 Rostock, Germany

University of Rostock, Institute for Computer Science, Albert-Einstein-Str. 22, 18059 Rostock, Germany

Fraunhofer Institute for Computer Graphics Research IGD, Fraunhoferstr. 5, 64283 Darmstadt, Germany

Keywords:

Underwater Image Formation, Underwater Camera Model, Camera Calibration, Underwater Stereo Vision.

Abstract:

The application of imaging devices in underwater environments has become a common practice. Protecting

the camera’s constituent electric parts against water leads to refractive effects emanating from the water-glass-

air transition of light rays. These non-linear distortions can not be modeled by the pinhole camera model. For

our new approach we focus on ﬂat interface systems. By handling refractive effects properly, we are able to

convert the problem to imaging conditions in air. We show that based on the location of virtual object points

in water, virtual parameters of a camera following the pinhole camera model can be computed per image ray.

This enables us to image the same object as if it was situated in air. Our novel approach works for an arbitrary

camera orientation to the refractive interface. We show experimentally that our adopted physical methods can

be used for the computation of 3D object points by a stereo camera system with much higher precision than

with a naive in-situ calibration.

1 INTRODUCTION

The almost standard installation of visual sensors on

autonomous underwater vehicles (AUV) or remotely

operated vehicles (ROV) and the possibility to also

equip divers with them, makes underwater imaging an

efﬁcient sampling tool. Some of the key advantages

of underwater imaging are its non-destructive behav-

ior toward marine life and its repeatable application.

Imaging underwater imposes different constraints

and challenges than imaging in air. One of the main

problems is the refraction of light passing bounding,

transparent interfaces between media with differing

refractive indexes (water-glass-air transition). In this

paper we focus on ﬂat interface systems. Such sys-

tems can be cameras watching through a viewing win-

dow, an aquarium, etc. or cameras inside a special

housing immersed in water. A severe effect induced

during this transition is that objects seem to be closer

to the observer and hence bigger than they actually are

(see ﬁgure 1). This refraction induced deviation in di-

mension is dependent on the distance of the imaged

objects to the refractive interface and the incidence

angle of light rays entering the camera through this

interface. This dependency acts in a non-linear way

and poses a problem to every discipline relying upon

metric image information.

Figure 1: left - exemplary magniﬁcation and distortion un-

derwater, right - perspective imaging in air.

If it is the task to gain metric information from

the recorded images, the cameras have to be cali-

brated and the refractive effects have to be handled

in a way to prevent the calibration of getting cor-

rupted. The mapping of a camera from the im-

aged three-dimensional scene of the world to the two-

dimensional image plane can be well approximated

using the linear pinhole camera model of perspec-

tive projection. This is represented by a set of intrin-

sic camera parameters (focal length, image principal

point, skew factor). As no camera, respectively no

real lens is expected to fulﬁll this linear mapping per-

Dolereit T. and Kuijper A..

Converting Underwater Imaging into Imaging in Air.

DOI: 10.5220/0004685600960103

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 96-103

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

fectly, some non-linear terms are incorporated into the

calibration process accounting for radial and tangen-

tial distortions. Because of the well known fact, that

underwater images have multiple viewpoints (Treib-

itz et al., 2012), calibration of cameras imaging un-

derwater scenes is theoretically not possible with the

pinhole camera model. Nevertheless, many works

have been published using a standard in air calibration

technique. Despite the fact that the imaging model

does not match the imaging conditions, they have to

deal with an often cumbersome handling of calibra-

tion targets by divers underwater. This is accompa-

nied by a severe loss of expensive underwater dive

time, which is supposed to be used for the actual tasks

that have to be performed.

In this paper we present a method to convert un-

derwater imaging to the conditions in air. After ap-

plication of this novel approach it is possible to use

well known computer vision algorithms suitable for in

air usage based on the pinhole camera model. Using

our approach, the camera parameters can now be cal-

ibrated with a standard technique in air, followed by a

step in which the corrected parameters can be derived.

To achieve this, we compute virtual camera parame-

ters following the pinhole model per image ray based

on rules of physical optics. These parameters vary for

image rays with differing properties. Once computed,

the set of virtual parameters is reusable for every new

view acquired with the calibrated camera. As a re-

sult, we get a virtual center of projection, a virtual fo-

cal length and an orientation of the virtual camera to

the refractive interface for each ray respectively. This

essentially converts the underwater imaging problem

into imaging in air as will be explained in the later

sections. Our approach works for cameras oriented

arbitrarily to the refractive interface.

In section 2 a brief overview on related works is

given. Section 3 describes the problems we have to

deal with. A short overview of our approach is pre-

sented and our imaging setup is explained. Section 4

deals with the computations needed in our approach.

In section 5 an experiment on stereo 3D reconstruc-

tion incorporating the results of section 4 is described.

Our results – outperforming a naive in-situ calibration

– are presented in section 6 and section 7 deals with

conclusions and future works.

2 RELATED WORK

In this section a brief overview on underwater imag-

ing using ﬂat interface systems and handling refrac-

tion in relation to camera calibration is given. A com-

prehensive overview on camera models in underwater

imaging can be found in (Sedlazeck and Koch, 2012).

The ﬁrst kind to handle refraction is by simply

using the pinhole camera model. Refractive effects

are either completely ignored (Gracias and Santos-

Victor, 2000; Pessel et al., 2003; Kunz and Singh,

2010; Brandou et al., 2007; Pizarro et al., 2009;

Silvatti et al., 2012) or expected to be absorbed by

the non-linear distortion terms (Shortis and Harvey,

1998; Shortis et al., 2009; Meline et al., 2010; Eu-

stice et al., 2008). Further similar approaches using

in-situ calibration strategies are mentioned in (Bran-

dou et al., 2007; Beall et al., 2010; McKinnon et al.,

2011; Johnson-Roberson et al., 2010; Sedlazeck et al.,

2009).

The second kind to handle refractive effects is to

model them explicitly and incorporate them into the

camera model and calibration process. The reasoning

concerning the applicability of the pinhole model in

imaging through refractive media by many authors is

that it is invalid. For that reason, refraction is mod-

eled physically correct (Agrawal et al., 2012; Chang

and Chen, 2011; Chari and Sturm, 2009; Gedge et al.,

2011; Ishibashi, 2011; Ke et al., 2008; Kunz and

Singh, 2008; Kwon and Casebolt, 2006; Li et al.,

1997; Maas, 1995; Sedlazeck and Koch, 2011; Jordt-

Sedlazeck and Koch, 2012; Telem and Filin, 2010;

Treibitz et al., 2012; Yamashita et al., 2006).

A different way to handle refraction is by approx-

imation. Belonging into this category, (Ferreira et al.,

2005) assume only low incidence angles of light rays

on the refractive surface. The approach with the most

similar aim is perhaps the work of (Lavest et al.,

2003). They try to infer the underwater calibration

from the in air calibration in form of an approxima-

tion of a single focal length and radial distortion. The

inapplicability of the pinhole model is not considered.

In contrast to the above methods, we try to in-

fer the underwater camera parameters following the

pinhole camera model ray-based for multiple view-

points from in air camera parameters. Furthermore,

no cumbersome in-situ handling of calibration targets

is needed.

3 PROBLEM STATEMENT

The main contribution of this paper is a way to re-

late an image of an object immersed in water with

an image of the same object as if it was situated in

air. This makes the application of the well known pin-

hole camera model of perspective projection possible.

As already stated in other works like (Treibitz et al.,

2012), we also assume that the pinhole camera model

is not valid in underwater imaging setups. As can be

ConvertingUnderwaterImagingintoImaginginAir

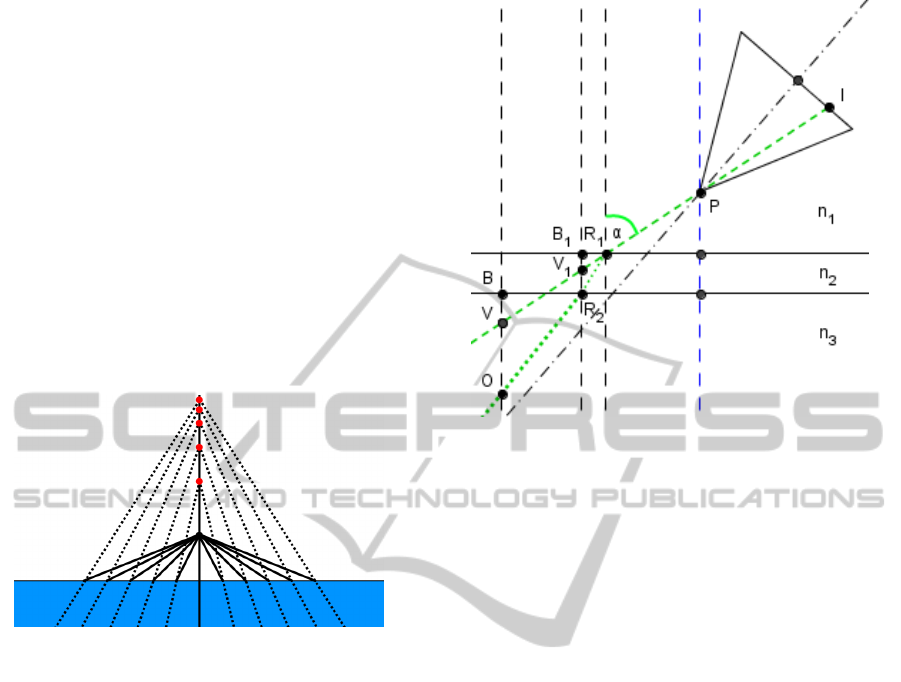
seen in ﬁgure 2, the extension of the refracted image

rays (dashed lines) into air leads to several intersec-

tion points, depending on the respective incidence an-

gles and representing multiple virtual viewpoints (red

dots). Because of refraction, there is no collinearity

between the object point in water, the center of pro-

jection of the camera (black dot) and the image point.

On the contrary, all rays following the pinhole cam-

era model intersect in a single point, namely the cen-

ter of projection. This occurrence of multiple virtual

viewpoints in underwater imaging makes it impossi-

ble to infer a single focal length adjustment that can

represent the imaging situation in terms of the pin-

hole camera model correctly. Nevertheless, a relation

between the two imaging situations can be assembled

for the single image rays. It follows the rules of phys-

ical optics and is presented in the following sections.

Figure 2: Multiple viewpoints in underwater imaging.

3.1 Overview

The main idea of our approach is, that the imaging

camera with a constant focal length is working based

on the pinhole camera model. In essence, it does not

know anything about refraction. Hence (see ﬁgure 3),

one can assume that the camera is imaging a virtual

object point V, which is situated collinear to the cam-

era’s center of projection P and the image point I. The

real object point O is not situated collinear, as a re-

sult of refraction known from Fermat’s and Snell’s

law. We assume that the camera’s intrinsics and non-

linear distortion terms in air are known. For now, it is

expected that lens distortion is not inﬂuenced by re-

fraction and hence can be eliminated by standard in

air distortion correction algorithms in advance. A set

of parameters accounting for refraction is assumed to

be known as well. These comprise the indexes of re-

fraction of the involved media, which are expected to

stay constant. Further known parameters are the per-

pendicular distance from the refractive interface to the

center of projection, the camera’s orientation towards

this interface and the interface thickness.

Stepping back to the assumption of the underwater

camera imaging a virtual object point, we show how

Figure 3: Geometric construction of the location of the vir-

tual object point.

to infer virtual camera parameters following the pin-

hole camera model for the corresponding image ray

using the virtual object point’s location. These vir-

tual parameters belong theoretically to a virtual cam-

era imaging an underwater object point, as if the wa-

ter was eliminated, to the same image point as the real

underwater camera does. The image point in the vir-

tual camera, its center of projection and the real un-

derwater object point are collinear (see ﬁgure 4). As

already mentioned before, refraction leads to the per-

ception of an object being closer as it really is and

hence being magniﬁed. This corresponds directly to

the location of the virtual object point. As a conse-

quence, the virtual camera’s focal length differs from

the one of the real camera, because it has to compen-

sate for this magniﬁcation. A well known limit case

from physics is a ray with an incidence angle of 90 de-

grees. Only in this case the focal length can simply be

multiplied by the refractive index of water to result in

the corresponding virtual focal length (rule of thumb

for underwater magniﬁcation). For incidence angles

differing from this perpendicularity the computation

gets more complicated. The virtual parameters don’t

just comprise focal length but also a new location of

the center of projection and a new orientation to the

refractive interface. The image’s principal point is ex-

pected to stay constant and the skew factor is ignored.

The biggest problem is to ﬁnd the location of the

virtual object point V. More precisely, if one can ﬁnd

a rule to locate the virtual object point on the image

ray relative to its real location on the refracted ray (see

ﬁgure 3), one can infer the virtual camera parameters

as will be shown. The result is a set of virtual parame-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

ters per image ray. This can lead to a huge number of

parameters, because the number of image rays corre-

sponds to the number of image pixels. These parame-

ters only depend on ray direction which stays constant

from image to image, as long as the camera’s posi-

tion to the refractive interface stays ﬁxed. They are

independent of the imaged scene. Hence, it is possi-

ble to compute all parameters for a single image in a

pre-computation step and reuse them for consecutive

images. The number of parameters can be decreased

if rays with the same properties are summarized. The

only signiﬁcant properties are the incidence angle to

the refractive interface and the ray’s angle to the opti-

cal axis of the camera.

3.2 Imaging Setup

For our experiments we generate an ideal imaging

setup by using simulated underwater images rendered

with Blender. Simulated images seem to be adequate

for our effort to show the applicability of our theoret-

ical approach for computation of virtual camera pa-

rameters. Advantages are the already known needed

parameters and perfect perspective projection under

the inﬂuence of refraction. The imaged scene and

the general camera setup is not restricted. For con-

venience in evaluation we use a simple checker pat-

tern on a plane with known dimensions and location

as imaging target. The plane is located in a way that

most of the image regions are covered by the pattern.

This is especially useful to evaluate our algorithms in

outer image regions, where distortions due to refrac-

tion get severe.

4 VIRTUAL CAMERA

PARAMETERS

4.1 Location of Virtual Object Points

Refraction occurs on the way of the light from the

emitting object point on the transition from water to

glass and from glass to air according to Snell’s law in

a plane through the refractive interface’s normal and

the light ray. The way of the light depends on the dis-

tances it has to pass in the respective media, due to

the fact that light always takes the path for which it

needs the shortest time to travel (Fermat’s law). Most

of the times we do not know where the imaged ob-

ject is located. But we do know the camera’s center

of projection and its orientation to the refractive in-

terface. Hence, when looking along the path of light

from camera direction, we can get an image ray from

pixel coordinates and also know its incidence angle

to the refractive interface. Like can be seen in ﬁg-

ure 3, the virtual object point V lies somewhere on

the extended image ray. We start with the formula for

refraction on a single interface:

− n

(1)

with g being the object distance, b being the image

distance and r being the curvature radius of the inter-

face. For a ﬂat interface system we get r = ∞. After

reorganization we end up with

b = −

∗ g. (2)

This is what most physics textbooks teach for the case

of an incidence angle of 90 degree. In this case, there

is no refraction just a magniﬁcation. Other incidence

angles are not considered explicitly in most cases.

This formula is used as approximation for small de-

viations from 90 degree. It is obviously independent

of the incidence angle and depends on distances and

the speed of light in the involved media. We assume

that these dependencies do not change if the incidence

angle varies and just a change in direction of the im-

age ray and the refracted ray is happening. When

we consider both media transitions with its refractions

= 0) using formula (2), we get

V =



−



(3)

for the distance from the incidence point R

to the vir-

tual object point V on the extended image ray. For a

geometrical representation with an arbitrary but ﬁxed

real object point we have all we need to illustrate the

location of the virtual object point. As can be seen

in ﬁgure 3 it is located directly above the real object

point on the perpendicular of the interface. If we vary

the incidence angle or the object position this stays

apparently the same. This statement coincides with

parts of the work of (Bartlett, 1984). The location

of the virtual object point is a controversial topic in

physics. For our purposes we assume that the virtual

object point is always located exactly above the real

object point on the perpendicular of the ﬂat refractive

interface. That this assumption holds is shown in an

experimental way in a later section. Based on this

assumption, one can relate the distances from the in-

terface (perpendicular) to the virtual point and to the

real point incorporating all three involved media by

BV = BO ∗

cosα

− sinα

+ B

∗

cosα

− sinα

(4)

like in (Bartlett, 1984) by simple trigonometric rules.

This relationship stays the same for arbitrary loca-

tions of the real object point on the same refracted

ConvertingUnderwaterImagingintoImaginginAir

ray, which can be utilized for depth-independent cal-

culations in the following sections.

After revisiting this concept to determine the lo-

cation of the virtual object point, we show how to use

it to infer the virtual camera parameters in the next

subsection.

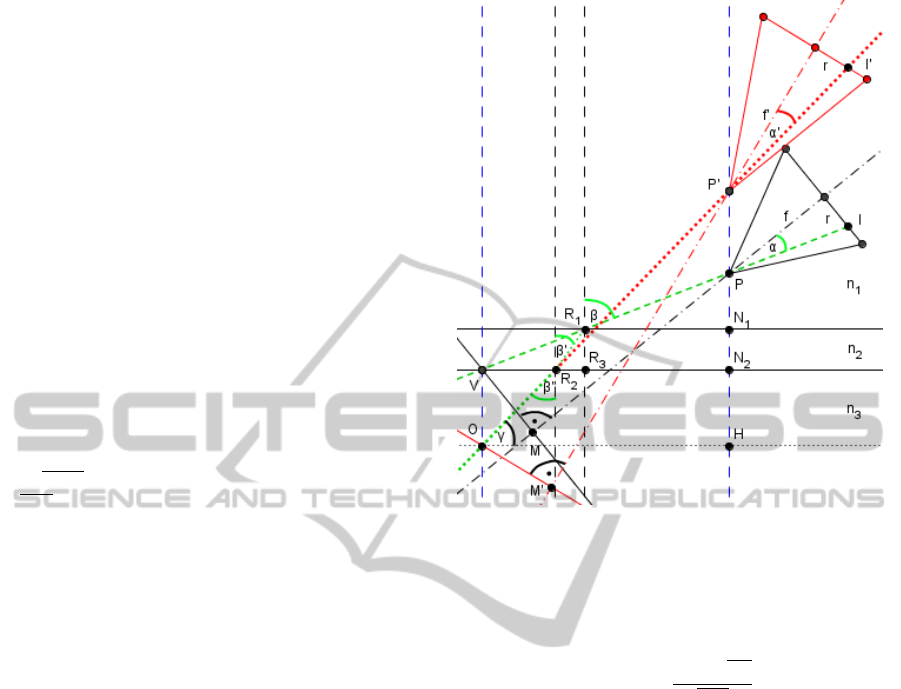
4.2 Parameter Computation

The computation of the virtual camera parameters

is illustrated geometrically in ﬁgure 4. As refrac-

tion happens in a plane and following the results of

(Agrawal et al., 2012), the virtual center of projection

P’ lies on the ﬂat interface’s normal through the real

center of projection P (axial camera). The point is de-

termined by the intersection of the rearward extended

refracted ray (green dotted line turning into red) and

that normal. As we know the angle β from the dot

product of the image ray and the interface’s normal

in the camera’s coordinate system as well as the dis-

tances N

corresponding to the interface thickness

and PN

corresponding to the perpendicular displace-

ment of the center of projection from the interface, we

can compute nearly all we need for parameter compu-

tation by simple trigonometric rules. Further refrac-

tive angles β

and β

can be determined by Snell’s law.

Because of perpendicularity, the virtual center of pro-

jection P’ turns to an easy computable distance. Now

the location of the virtual object point V is incorpo-

rated. Since it is located directly above the real object

point and their relationship is depth-independent we

deﬁne it to be located exactly on the surface between

water and glass. This ﬁxation makes further simple

trigonometric calculations possible.

As we know the angle α of the image ray to the

optical axis of the camera from image coordinates and

focal length, we know all the angles and distances il-

lustrated in ﬁgure 4 except for the virtual focal length

f’ and the virtual camera’s orientation. This orienta-

tion is conditioned by the angle α

in an ambiguous

way. For determination of this focal length and ori-

entation we need the rules for magniﬁcation of lenses

from physical optics. In ﬁgure 4 both, the real (black

triangle) and the virtual camera (red triangle) are il-

lustrated. We want our real object O to appear at the

exact same pixel position on the virtual camera’s im-

age sensor (I’) as is the virtual object point V on the

real camera’s sensor (I). It hast to be in the correct

magniﬁcation which is realized by the virtual focal

length and correct positioning of the virtual camera’s

optical axis. The virtual optical axis is determined by

angle α

. From α

and r the virtual focal length f ’

can be easily calculated. For the calculation of α

found out that the distances perpendicular to the re-

Figure 4: Geometric construction of the virtual parameters.

spective optical axis (MV and M’O) have to be equal,

so that magniﬁcation works properly. Furthermore,

by knowing angle α and the distances VP and OP’

one can calculate α

= arcsin

sinα ∗ VP

. (5)

In contrast to refraction, which happens in a plane, the

real and the virtual optical axis needs not to be located

in that plane. The virtual optical axis has an ambigu-

ous location, because it is just determined based on an

angle α

to the respective ray. Hence, it can be located

on a position anyway around the ray. This is not really

a problem because of the fact that the pixel position

of the ray in the respective image is not altered by

this and the virtual parameters are calculated for this

ray only. An arbitrary but matching virtual orienta-

tion can be computed with angle α

and the deﬁnition

of the dot product as the angle between two vectors.

One being the refracted ray and the other being the

optical axis with two degrees of freedom. Based on

the vector of the optical axis both missing coordinate

axes can be computed in a similar way.

These virtual parameters essentially convert un-

derwater imaging into imaging in air. If the camera

is oriented perpendicular it leads to some simpliﬁca-

tions during computation.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

100

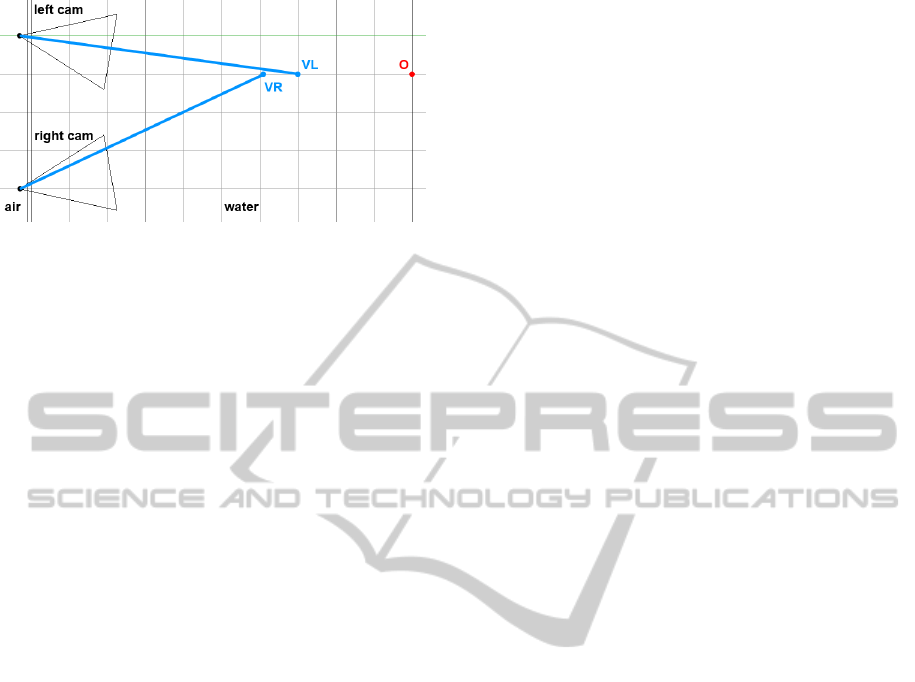
Figure 5: Stereo setup with different virtual object points.

5 3D-RECONSTRUCTION

In this experiment we use the concept for the relation

between the location of virtual object points and real

object points in a stereo 3D reconstruction problem.

This should underline the applicability of this con-

cept. Furthermore, the results are compared with the

results of a stereo 3D reconstruction based on a naive

in-situ stereo camera calibration ignoring refraction.

A stereo camera system is generated with Blender

as can be seen in ﬁgure 5. The cameras are located

40 cm apart in a horizontal converging formation of

10 degree per camera. The perpendicular distance to

the ﬂat refractive interface with a thickness of 1cm

amounts to 2cm for each camera. The refractive in-

dexes are respectively 1 for air, 1.6 for glass and 1.33

for water. The focal length of both cameras is 27mm,

with an image resolution of 1920x1080, square pix-

els and a horizontal sensor size of 22.3mm. Hence,

all needed parameters are known in advance (corre-

sponding to camera calibration in air) and radial im-

age distortion can be set to zero. Both cameras image

a plane with a checker pattern at a certain distance.

The checker corners on that plane are used as feature

points and their respective 3D locations are known.

We tried to cover as much of the overlapping image

region with the pattern. For each corresponding fea-

ture pair the respective image ray is calculated in a

left-handed world coordinate frame with its origin on

the foot of perpendicular of the left camera on the

water-sided interface. The z-axis is pointing into the

water, the y-axis points upward and the x-axis to the

left. The two rays are emitted from a different virtual

object point (VL and VR). However, both rays corre-

spond to the same real object point O. The two virtual

object points are not likely to intersect in the same z-

value as long as their respective rays have different

incident angles. What we are able to do is to com-

pute the intersection of just the x- and y-values of both

rays. The results are differing in their z-values as can

be seen exemplary in ﬁgure 5. Now we use formula

(4) to compute the z-value of the real object point.

The two new z-values should be nearly the same and

we take their mean as object depth. The x- and y-

values stay the same. With this easy method we have

inferred the 3D coordinates of our object from just a

virtual object point and refraction is handled physi-

cally plausible.

6 RESULTS

The results of our computation of virtual camera pa-

rameters are tested in an experimental way. The

rendering sequence to check if our computed virtual

camera parameters match the situation works as fol-

lows. We render an underwater image of our target

with Blender with known parameters. We compute

the virtual parameters for one feature point. After-

ward, we use these parameters in Blender to render

a new image of our target, but this times in air. The

result should be an image with the feature point at ex-

actly the same image location and in the same mag-

niﬁcation as in the underwater image. This feature

point is now the result of a perspective projection and

refraction is eliminated for this particular image pixel.

The camera is imaging a plane with a checker pattern

in an underwater environment. The refractive indexes

are respectively 1 for air, 1.6 for glass and 1.33 for

water. The interface has a thickness of 1cm and the

camera is placed 2cm in perpendicular direction away

from it with a horizontal angle of 10 degree. Its fo-

cal length is 27mm. This matches the left camera in

ﬁgure 5. Because of the required exact placement and

conﬁguration of the virtual camera, this can not be

evaluated in the desired accuracy with real image se-

tups in a reasonable way.

One rendered result can be seen in ﬁgure 6. The

corresponding feature points are marked with a cir-

cle. Manual visual evaluation results in a difference

of zero pixel between both feature points. The green

lines are drawn supplementary to illustrate the distor-

tions in the underwater image and the truly straight

chessboard lines in the in air image. Because of the

already mentioned ambiguous orientation of the vir-

tual camera, the in air rendered image is rotated. The

pixel position is not affected by this as can bee seen

and as was explained before. The virtual focal length

for this case is 36.632mm, the virtual center of pro-

jection is at a distance of 2.608cm from the refractive

interface and the camera’s rotation matrix amounts to

R =





0.9718 0.2121 0.1027

−0.0909 −0.0644 0.9938

0.2174 −0.9751 0.0433





Further tests on several random feature points re-

ConvertingUnderwaterImagingintoImaginginAir

101

Table 1: 3D reconstruction errors

IN-SITU(1m) IN-SITU(2m) OUR(1m) OUR(2m)

3D Error 6.831cm 13.559cm 0.32cm 1.074cm

x-Error 6.571cm 12.92cm 0.08cm 0.15cm

y-Error 0.076cm 0.152cm 0.035cm 0.077cm

z-Error 1.714cm 3.65cm 0.285cm 1.042cm

Figure 6: Comparison of the rendered underwater image

(top) and the inferred in air rendering (bottom) with the cor-

responding ray (image pixel) marked by the red circle.

sulted in a mean deviation of at most 1 pixel. This

shows that our method is well applicable for our sce-

nario.

For stereo 3D reconstruction we used 204 feature

points on a plane at a distance of 1m and 228 fea-

ture points on a plane at a distance of 2m from the

refractive interface. The planes are parallel to the in-

terface and all 3D locations of the feature points are

known in advance. The results of our method and the

results of a stereo 3D reconstruction based on a naive

in-situ stereo camera calibration ignoring refraction

are compared in table 1. The denoted errors are the

3D mean euclidean distance as well as the euclidean

distances per coordinate direction between measured

and real 3D points. Our results are signiﬁcantly better

than those of the in-situ method. The huge error in x-

direction of the in-situ method amounts from false rel-

ative orientation parameters from in-situ stereo cam-

era calibration. The ignored magniﬁcation by refrac-

tion leads to a shift of the camera behind its real po-

sition and to a smaller angle in the converging cam-

era setup. This false camera conﬁguration somehow

compensates the triangulation error in z-direction at

the cost of a shift in x-direction leading to an overall

severe error in 3D location. On the contrary, our val-

ues match the 3D locations at this comparatively large

imaging distances pretty well in all dimensions.

7 CONCLUSIONS

We presented a new method to convert an underwater

image to imaging conditions in air with the aid of a

set of virtual camera parameters for each image ray.

Rays with the same properties can be summarized.

Our method is based on rules of physical optics. The

virtual parameters can be computed for one image in

a pre-processing step. They can be reused for every

consecutive image from that camera. With known vir-

tual parameters, computer vision algorithms relying

on the pinhole camera model can now be executed

for the underwater images. In an experimental way,

we show that our method matches our imaging condi-

tions. Our results are tested on simulated image data

allowing for ground truth comparison. This proce-

dure shows that our theoretical results are correct and

applicable. Our underwater imaging model makes it

possible to infer parameters of an underwater camera

from its calibration in air. Hence, we avoid a cumber-

some and expensive in-situ calibration.

In a further experiment we show that our used

concepts can be incorporated into stereo 3D recon-

struction. The results are signiﬁcantly better than the

results of a naive in-situ stereo calibration with fol-

lowing triangulation. This experiment underlines the

applicability of our method for underwater imaging.

Further validation on real image data and a compar-

ison with naive in-situ, as well as with more mature

calibration approaches is needed and is part of our fu-

ture work.

REFERENCES

Agrawal, A., Ramalingam, S., Taguchi, Y., and Chari, V.

(2012). A theory of multi-layer ﬂat refractive geom-

etry. In 2012 IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 3346 – 3353.

Bartlett, A. A. (1984). Note on a common virtual image.

American Journal of Physics, 52(7):640 – 643.

Beall, C., Lawrence, B. J., Ila, V., and Dellaert, F.

(2010). 3D reconstruction of underwater structures.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

102

In 2010 IEEE/RSJ International Conference on Intel-

ligent Robots and Systems (IROS), pages 4418 – 4423.

Brandou, V., Allais, A. G., Perrier, M., Malis, E., Rives,

P., Sarrazin, J., and Sarradin, P. M. (2007). 3D re-

construction of natural underwater scenes using the

stereovision system IRIS. In OCEANS 2007 - Europe,

pages 1–6.

Chang, Y.-J. and Chen, T. (2011). Multi-view 3D recon-

struction for scenes under the refractive plane with

known vertical direction. In ICCV’11, pages 351 –

358.

Chari, V. and Sturm, P. (2009). Multiple-view geometry of

the refractive plane. In Proceedings of the 20th British

Machine Vision Conference, London, UK.

Eustice, R. M., Pizarro, O., and Singh, H. (2008). Visu-

ally augmented navigation for autonomous underwa-

ter vehicles. IEEE Journal of Oceanic Engineering,

33(2):103–122.

Ferreira, R., Costeira, J. P., and Santos, J. A. (2005). Stereo

reconstruction of a submerged scene. In Proceedings

of the Second Iberian conference on Pattern Recogni-

tion and Image Analysis - Volume Part I, IbPRIA’05,

pages 102–109.

Gedge, J., Gong, M., and Yang, Y. (2011). Refractive epipo-

lar geometry for underwater stereo matching. In 2011

Canadian Conference on Computer and Robot Vision

(CRV), pages 146–152.

Gracias, N. and Santos-Victor, J. (2000). Underwater video

mosaics as visual navigation maps. Computer Vision

and Image Understanding, 79:66 –91.

Ishibashi, S. (2011). The study of the underwater camera

model. In OCEANS, 2011 IEEE - Spain, pages 1–6.

Johnson-Roberson, M., Pizarro, O., Williams, S. B., and

Mahon, I. (2010). Generation and visualization

of large-scale three-dimensional reconstructions from

underwater robotic surveys. Journal of Field Robotics,

27(1):21–51.

Jordt-Sedlazeck, A. and Koch, R. (2012). Refractive cali-

bration of underwater cameras. In Proceedings of the

12th European conference on Computer Vision - Vol-

ume Part V, ECCV’12, pages 846–859.

Ke, X., Sutton, M. A., Lessner, S. M., and Yost, M. (2008).

Robust stereo vision and calibration methodology for

accurate three-dimensional digital image correlation

measurements on submerged objects. Journal of

Strain Analysis for Engineering Design, 43(8):689–

704.

Kunz, C. and Singh, H. (2008). Hemispherical refrac-

tion and camera calibration in underwater vision. In

OCEANS 2008, pages 1–7.

Kunz, C. and Singh, H. (2010). Stereo self-calibration for

seaﬂoor mapping using AUVs. In Autonomous Under-

water Vehicles (AUV), 2010 IEEE/OES, pages 1–7.

Kwon, Y.-H. and Casebolt, J. B. (2006). Effects of light

refraction on the accuracy of camera calibration and

reconstruction in underwater motion analysis. Sports

Biomechanics / International Society of Biomechanics

in Sports, 5(2):315–340.

Lavest, J. M., Rives, G., and Lapreste, J. T. (2003). Dry

camera calibration for underwater applications. Mach.

Vision Appl., 13(5-6):245 – 253.

Li, R., Li, H., Zou, W., Smith, R. G., and Curran, T. A.

(1997). Quantitative photogrammetric analysis of

digital underwater video imagery. IEEE Journal of

Oceanic Engineering, 22(2):364–375.

Maas, H.-G. (1995). New developments in multimedia

photogrammetry. Symposium A Quarterly Journal In

Modern Foreign Literatures, 8(3):150 – 5.

McKinnon, D., He, H., Upcroft, B., and Smith, R. N.

(2011). Towards automated and in-situ, near-real time

3-d reconstruction of coral reef environments. In

OCEANS’11 MTS/IEEE Kona Conference.

Meline, A., Triboulet, J., and Jouvencel, B. (2010). A cam-

corder for 3D underwater reconstruction of archeolog-

ical objects. In OCEANS 2010, pages 1–9.

Pessel, N., Opderbecke, J., and Aldon, M. J. (2003). An ex-

perimental study of a robust self-calibration method

for a single camera. In Proceedings of the 3rd Inter-

national Symposium on Image and Signal Processing

and Analysis, 2003. ISPA 2003, volume 1, pages 522–

527.

Pizarro, O., Eustice, R. M., and Singh, H. (2009). Large

area 3-D reconstructions from underwater optical

surveys. IEEE Journal of Oceanic Engineering,

34(2):150–169.

Sedlazeck, A. and Koch, R. (2011). Calibration of hous-

ing parameters for underwater Stereo-Camera rigs. In

Proceedings of the British Machine Vision Confer-

ence, pages 118.1 – 118.11.

Sedlazeck, A. and Koch, R. (2012). Perspective and non-

perspective camera models in underwater imaging -

overview and error analysis. In Outdoor and Large-

Scale Real-World Scene Analysis, volume 7474 of

Lecture Notes in Computer Science. Springer Berlin

Heidelberg.

Sedlazeck, A., Koser, K., and Koch, R. (2009). 3D recon-

struction based on underwater video from ROV kiel

6000 considering underwater imaging conditions. In

OCEANS 2009 - EUROPE, pages 1–10.

Shortis, M., Harvey, E., and Abdo, D. (2009). A review

of underwater stereo-image measurement for marine

biology and ecology applications. In Oceanography

and Marine Biology, volume 20092725, pages 257–

292. CRC Press.

Shortis, M. R. and Harvey, E. S. (1998). Design and cali-

bration of an underwater stereo-video system for the

monitoring of marine fauna populations. Interna-

tional Archives Photogrammetry and Remote Sensing,

32(5):792–799.

Silvatti, A. P., Salve Dias, F. A., Cerveri, P., and Barros,

R. M. (2012). Comparison of different camera calibra-

tion approaches for underwater applications. Journal

of Biomechanics, 45(6):1112–1116.

Telem, G. and Filin, S. (2010). Photogrammetric modeling

of underwater environments. ISPRS Journal of Pho-

togrammetry and Remote Sensing, 65(5):433–444.

Treibitz, T., Schechner, Y., Kunz, C., and Singh, H. (2012).

Flat refractive geometry. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 34:51–65.

Yamashita, A., Kato, S., and Kaneko, T. (2006). Robust

sensing against bubble noises in aquatic environments

with a stereo vision system. In Proceedings 2006

IEEE International Conference on Robotics and Au-

tomation, 2006. ICRA 2006, pages 928–933.

ConvertingUnderwaterImagingintoImaginginAir

103