Energy based Descriptors and their Application for Car Detection

Radovan Fusek, Eduard Sojka, Karel Mozd

n and Milan

Surkala

Technical University of Ostrava, FEECS, Department of Computer Science

17. listopadu 15, 708 33 Ostrava-Poruba, Czech Republic

Keywords:

Object Detection, Image Features, Recognition.

Abstract:

In this paper, we propose a novel technique for object description. The proposed method is based on inves-

tigation of energy distribution (in the image) that describes the properties of objects. The energy distribution

is encoded into a vector of features and the vector is then used as an input for the SVM classiﬁer. Generally,

the technique can be used for detecting arbitrary objects. In this paper, however, we demonstrate the robust-

ness of the proposed descriptors for solving the problem of car detection. Compared with the state-of-the-art

descriptors (e.g. HOG, Haar-like features), the proposed approach achieved better results, especially from the

viewpoint of dimensionality of the feature vector; the proposed approach is able to successfully describe the

objects of interest with a relatively small set of numbers without the use of methods for the reduction of feature

vector.

1 INTRODUCTION

In the feature-based detectors, the selection of rele-

vant features that are able to reliably describe the ob-

jects of interest is a key point. In the recent years,

the object detectors that are based on the edge anal-

ysis that provide the valuable information about the

objects of interest have been used in many detection

tasks. In this area, the Histograms of Oriented Gradi-

ents (HOG) (Dalal and Triggs, 2005) are considered

as the state-of-the-art method. In HOG, a sliding win-

dow is used for recognition. In the process of ob-

taining HOG descriptors, the window is divided into

small connected cells. The histograms of gradients

are calculated for each cell. It is desirable to normal-

ize the histograms across a large block of image. As a

result, a vector of values is computed for each position

of window. This vector is then used for recognition,

e.g. by the Support Vector Machine (SVM) classi-

ﬁer (Boser et al., 1992). The HOG descriptors are

very useful in many detection tasks. Dalal and Triggs

(Dalal and Triggs, 2005) proposed the human detec-

tion algorithm based on the HOG descriptors and a

linear SVM classiﬁer. Zhu at al. (Zhu et al., 2006)

presented the nearly real-time human detector using

the cascade of rejectors with the HOG features. F.

Suard at al. (Suard et al., 2006) proposed the method

for pedestrian detection using the HOG descriptors

with the SVM classiﬁer. Boosting HOG features for

the vehicle detection in airborne videos are presented

in (Cao et al., 2011).

In general, the methods that describe the edges by

making use of their orientations, gradient magnitudes,

positions, or length suffer from a high dimensionality

of feature vectors. Furthermore, the training and clas-

siﬁcation phase can be slowed down by this drawback

(a big number of training samples are required). The

images that are affected by rain, noise, lack of light,

misty and cloudy weather are frequent in the outdoor

applications. These images cause a great difﬁculty

in obtaining relevant features for the object descrip-

tion without the use of image ﬁltering. The mentioned

problems created a motivation for developing new de-

scriptors. The preliminary versions of the presented

method were used for face detection in (Fusek et al.,

2013a), and for pedestrian detection in (Fusek et al.,

2013b).

In essence, the method was inspired by the fea-

tures that are based on HOG. We divide the image

inside the sliding window into regions, and within

the regions we deﬁne the sources of energy. By the

transfer of energy, we will mean the transfer of heat.

After the temperature transfer inside the sliding win-

dow, we investigate the movement of thermal energy

from the sources. The values that we calculate are

used for composing the feature vector of sliding win-

dow and the vector is then used as an input for the

SVM classiﬁer. In contrast with the HOG descriptors,

the proposed method captures the object information

by the energy distribution in object areas instead of

492

Fusek R., Sojka E., Mozd

n K. and Šurkala M..

Energy based Descriptors and their Application for Car Detection.

DOI: 10.5220/0004685804920499

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 492-499

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the distribution of gradient magnitudes and directions.

Using the proposed method, we are able to describe

the object areas that are useful for recognition. The

ﬁrst advantage is that the feature vectors of relatively

small dimensions are sufﬁcient for successful recog-

nition. The next advantage is a very good resistance

to the noise. The ﬁltering step is directly included in

the calculation of proposed approach. We will show

the robustness of the presented method for solving the

problem of car detection.

2 RELATED WORKS

The vehicle detection systems have been very use-

ful in the recent years. Especially nowadays in the

cities, the increasing number of vehicles brings a ma-

jor problem. The car detection systems can be impor-

tant, especially for drivers who are looking for vacant

spaces in the parking lots, for trafﬁc analysis, for in-

telligent scheduling, and so on.

The information about the presence of vehi-

cles can be provided by the intrusive (magnetome-

ters, piezoelectric cables, micro-loop probes) and

non-intrusive sensors (microwave radar, laser radar)

(Mimbela et al., 2007). On the other hand, the

camera-based system that is able to provide very valu-

able information about the situation can be used and

the object detection methods that were proposed in

the last years (based on the image information) can

be used for vehicle detection.

For instance, Viola and Jones (Viola and Jones,

2001; Viola and Jones, 2002) proposed the very pop-

ular object detector. Haar-like features, integral im-

ages, and AdaBoost algorithm were used in their de-

tection framework. Several improvements of this de-

tection framework exist. The extension of the feature

set of their method has been presented by Lienhart

(Lienhart and Maydt, 2002). The improvement of the

weak classiﬁers combined with Real Adaboost for the

fast multi-view face detection system has been pre-

sented by Wu at al. (Wu et al., 2004). The tree struc-

ture for the construction of detector using the Vec-

tor Boosting algorithm has been presented by Huang

at al. (Huang et al., 2007). The method for detect-

ing multi-view cars has been presented by Zheng and

Liang (Zheng and Liang, 2009). The authors pro-

posed a novel set of image strip features for car de-

tection. Their strip features are calculated using the

integral image. Combined with the RealBoost frame-

work, the authors reported good performance. Never-

theless, the authors mentioned that the strip features

discard some statistical information compared with

the more complex descriptors such as HOG (Dalal

and Triggs, 2005). The trainable object detector for

detecting faces and cars at any size, location and pose

was presented by Schneiderman and Kanade (Schnei-

derman and Kanade, 2004). Their classiﬁer is based

on the statistics of localized parts that represent vari-

ous local properties. Papageorgiou and Poggio (Papa-

georgiou and Poggio, 2000) described the object de-

tector for face, people and cars using Haar wavelets

with the support vector machine.

Detectors that are focused on detecting the cars

in parking lot are also very useful. Several methods

aimed at detecting the cars in parking lot have been

presented. Three-layer Bayesian hierarchical frame-

work for the parking lot occupancy problem was pre-

sented in (Huang and Wang, 2010). The system for

parking lot vehicle detection based on the fuzzy c-

means clustering classiﬁer was reported in (Ichihashi

et al., 2010). The detection system consisting of

shadow removal, lens distortion correction, and park-

ing space extraction was presented in (Fabian, 2008).

In this paper, we also focus on detecting the cars in

parking lot, nevertheless, we use the classical sliding

window detection approach, therefore, for compari-

son, we use the classical image features (e.g. HOG,

Haar-like features) that are usually used in the sliding

window methods.

3 PROPOSED METHOD

For determining the proposed descriptors that are

based on distribution of energy (temperature), we use

the sliding window (similarly as in HOG); the win-

dow is divided into a chosen number of areas (e.g.

squares) called blocks (Fig. 2). For the image in-

side the sliding window, the distribution of tempera-

ture can be solved by making use of physical laws.

We suppose that the image is a plate that is cre-

ated from a material with a certain thermal conduc-

tivity. The value of conductivity depends on the local

size of the gradient of brightness or colour function

(the higher is the gradient size, the lower is the con-

ductivity). Inside each block, a source of temperature

is deﬁned through which the thermal energy can ﬂow

into the image; we use the gravity centers of blocks as

the positions of sources. The method that we propose

is based on determining the distribution of tempera-

ture in the image inside the sliding window after the

temperature transfer, which can be performed during

a chosen time. At the time t = 0, the temperature of

the plate is zero. At the same time (t = 0), the source

of heat with a constant temperature is attached to the

gravity centers of all blocks in one position of slid-

ing window. From the time t = 0, the temperature of

EnergybasedDescriptorsandtheirApplicationforCarDetection

493

sliding window

block

feature vector of sliding window

...

... ...

...

block

feature vector of block

source

block

...

Figure 2: The vector of features.

block

source

cell

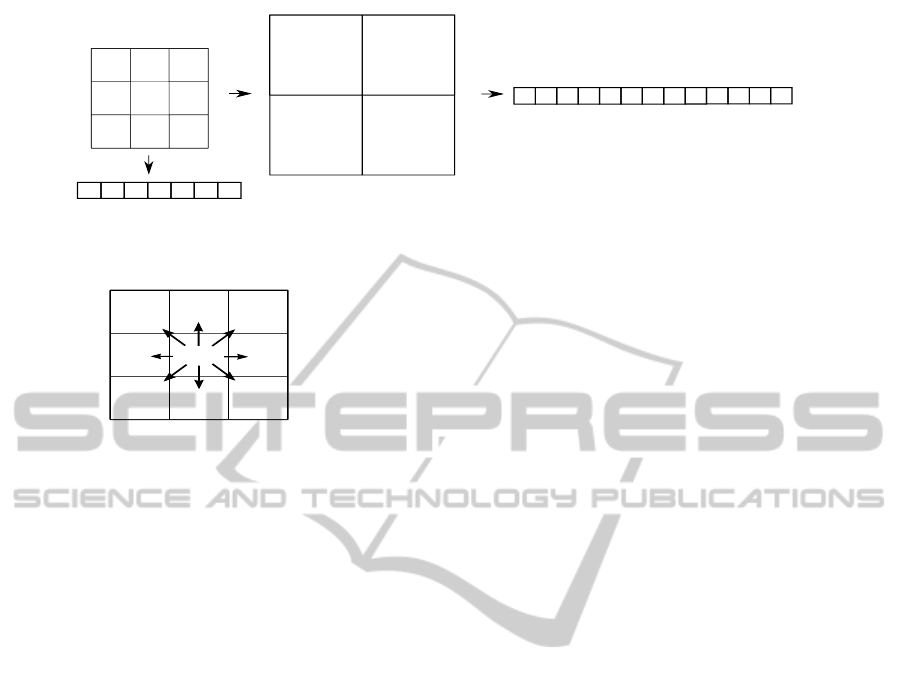
Figure 1: The block divided into cells. The source of tem-

perature is placed to the gravity center of block. In this

particular case, by appropriately placing of cells, we inves-

tigate the 8-neighborhood of source.

source points is held on the value of 1 (theoretically,

this temperature can be held to inﬁnity). After a cer-

tain chosen time t, the temperature of the image plate

inside the sliding window is examined.

For the purpose of investigating the distribution at

a chosen time t, each block is divided into cells that

are placed into the neighborhood of source (Fig. 1).

Let I(x, y, t) be the function of temperature that was

determined. We can compute the mean temperature in

every cell; Iµ

stands for the mean temperature of the

i-th cells at the time t. We use the mean cell tempera-

tures as the values in the feature vector, i.e. the size of

feature vector equals to the number of cells within the

blocks. The ﬁnal vector of features is composed from

all mean temperatures Iµ

inside each block (Fig. 2).

It is important to mention that the transfer of temper-

ature from the sources is not restricted by the block

size but it is computed in the entire sliding window,

and the blocks and cells are only formed only for dis-

tribution measurement. We note that the heat from

one source can be transported to all blocks in the win-

dow.

Before continuing to further technical details, we

regard as desirable to discuss the rationale behind the

method proposed above. The main idea of presented

approach is that the properties of the objects of inter-

est can be described by distribution of energy (tem-

perature). The usefulness of temperature distribution

can be illustrated as follows. Say that the values for

recognition are obtained as the sample values of a

function that is deﬁned over the area of image. If it

is a function of the gradient size of brightness, it is

obvious that it is difﬁcult to hit (by the samples) the

places that are important for recognition (thin edges).

Therefore, in the proposed method, we use the func-

tion of temperature distribution in which the infor-

mation about its changes is not so important. It is

sufﬁcient to obtain the information about the areas in

which the values of distribution function are approx-

imately constant (by sampling, the information about

the areas can be easily obtained). Clearly, the infor-

mation about the areas also contains the information

about the edges in the original image. Since the object

boundary creates the thermal insulator, the area of ob-

ject contains a certain distribution of temperature that

reﬂects the shape of object. This distribution can be

investigated and used for recognition.

In the real images (Fig. 3(a)), the objects of in-

terest consist of more complicated areas but the gen-

eral idea from the previous paragraph can be used

again. Suppose that the several temperature sources

are located into this image (sliding window); say in

the form of a regular grid (Fig. 3(b)). The values of

temperatures that are transfered from the sources cre-

ate separate segments (Fig. 3(c)). The temperature

distributions inside the segments are used to encode

the information about the appearance of object. For

the purpose of encoding the distribution of tempera-

ture, we investigate the mean temperature of all cells

inside the sliding window in several suitably chosen

times of temperature transfer.

It is clear that the real images contain the areas of

different sizes. At different times, we get various in-

formation about objects (Fig. 4). For the description

of small areas by the temperature distribution, a lower

time (lower number of iterations) during which the

temperature transfer is carried out is required; small

areas are ﬁlled with a certain distribution of tempera-

ture (that is sufﬁcient for the description of these ar-

eas) in a relatively short period of time. On the other

hand, the temperature sources that are located into the

big areas require more time to affect the whole areas

of the objects. For instance, the shape of the side win-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

494

hood

side window

roof

windshield

(a) (b) (c)

Figure 3: The real-life image (a). The regular grid of sources (b). The visualization of distribution of temperature from these

sources (c). The value of temperature is depicted by the level of brightness.

orig. t = 50 t = 100 t = 150 t = 200 t = 250

Figure 4: The visualization of distribution of temperature at different times. The value of temperature is depicted by the level

of brightness.

dows is visible at the time t = 50, however, the shape

of the hood is recognizable at the time t ≥ 150 (Fig.

4). For this reason, we compute the temperature dis-

tribution at different times. For example, we can com-

pute two different distributions; one at the time t

and

the second at t

. In this particular case, the ﬁnal fea-

ture vector includes the information from both these

distributions. We can take the values of both distri-

butions and compose them sequentially one after an-

other into the ﬁnal vector. The next possibility is to

combine the values from both distributions together

(e.g. by averaging them). In the ﬁrst case, the size

of the ﬁnal vector is two times larger than is the size

in the second case. We regard the second approach as

often more suitable for recognition due to the fact that

the dimensionality of ﬁnal vector is not increased.

It is important to mention that the classical HOG

descriptors are not rotationally invariant. Since the

proposed descriptors are similar to the HOG descrip-

tors in the sense that in both approaches the features

are computed in a grid, this limitation also occurs in

the proposed descriptors. Similarly as in HOG, the

scale invariance is achieved by rescaling the images.

For practical realization of the method, it is impor-

tant to mention that the thermal ﬁeld over the one po-

sition of sliding window can be solved by making use

of the following equation (Perona and Malik, 1990)

∂I(x, y, t)

∂t

= div(c∇I), (1)

where I represents the temperature at a position (x, y)

and at a time t, div is a divergence operator, ∇I is the

temperature gradient and c stands for the thermal con-

ductivity. For the source points and the arbitrary time

t ∈ [0, ∞), we set I(x

, y

, t) = 1, where (x

, y

) are the

coordinates of source points (i.e. we hold the tem-

perature constant during the whole process of trans-

fer, which is in contrast with the usual diffusion ap-

proaches). In all remaining points, we take into ac-

count the initial condition I(x, y, 0) = 0. We solve the

equation iteratively. The conductivity in Eq. 1 is de-

termined by

c = g(

), (2)

where E is an edge estimate. We deﬁne the edge es-

timate E as the gradient of original image E = ∇B,

where B is the brightness function. The function g(·)

has the form of (Perona and Malik, 1990)

∇B

) =

1 +



∇B



, (3)

where K is a constant representing the sensitivity to

the edges (Perona and Malik, 1990). Once the tem-

perature ﬁeld over the input image is obtained (at a

chosen time t), the mean cell temperature Iµ

can be

obtained by making use of the formula

Iµ

I(x, y, t)dxdy

|M|

, (4)

where M stands for the cell area, and |M| is its size.

In the next step, the SVM classiﬁer is trained over

the proposed descriptors. Let us consider a training

data set (x

, y

) where x is the vector of proposed de-

scriptors from training samples and y is the class label

(+1 for cars, -1 for non-cars). The linear SVM de-

termine the hyperplane w · x + b where w is a weight

vector, x is the vector of features and b is a constant.

The goal is to ﬁnd the optimal decision function that

EnergybasedDescriptorsandtheirApplicationforCarDetection

495

maximizes the distance between the nearest point x

and the hyperplane. In the case when it is difﬁcult

to separate the samples in a linear manner, the non-

linear SVM can be used. The non-linear SVM maps

the original space into a high-dimensional space us-

ing a kernel function that separate training samples.

The optimal hyperplane for the non-linear SVM is ob-

tained by the function f (x):

f (x) =

∑

i=0

k(x, x

) + b, (5)

where N represents the number of training patterns, y

is a class indicator (+1 for cars, -1 for non-cars) for

each training pattern x

, α

and b are learned weights

and k(., .) is a kernel function. In our case, we use the

Gaussian radial basis function kernel:

k(x, y) = e

|x−y|

2σ

. (6)

4 EXPERIMENTS

For the training phase, we collected the data set con-

sisting of 5000 samples (2500 non-cars, 2500 cars).

We experimented with the parameters of our descrip-

tors and we suggest the following conﬁguration. The

conﬁguration is denoted as Energy

288

with the size

of block: 15 × 15 pixels, size of temperature sources:

5×5 pixels, number of cells inside the block: 8, itera-

tions (time) for the temperature transfer: 50, 100, 150.

This conﬁguration consists of 288 descriptors. Each

training sample was resized to the size of 90× 90 pix-

els, for the proposed detector. The example of visu-

alizations of temperature distribution is shown in Fig.

5 (the visualizations of Energy

288

conﬁguration at the

time t = 150).

For comparison, we use the detectors that are

based on the HOG features, LBP (Local Binary Pat-

terns) features (Liao et al., 2007), and Haar features

(Viola-Jones detection framework).

For the HOG based detectors, we created two

conﬁgurations: HOG

900

and HOG

300

. HOG

900

was

designed with the following settings; size of block:

32 × 32, size of cell: 16 × 16, horizontal step size:

16, number of bins: 9. This conﬁguration consists of

900 descriptors. Since the proposed method produces

the relatively small number of descriptors, we de-

signed the conﬁguration of HOG

300

that was used for

the purpose to test these descriptors with the smaller

number of features than the HOG

900

conﬁguration.

The HOG

300

conﬁguration was designed with the fol-

lowing settings; size of block: 32 × 32, size of cell:

16 × 16, horizontal step size: 16, number of bins: 3.

This conﬁguration consists of 300 descriptors. For the

HOG descriptors combined with SVM, we used the

same training data set that we used for the proposed

method (2500 non-cars, 2500 cars), and each sample

was resized to the size of 96 × 96. For the detectors

that are based on the Viola-Jones detection framework

with the Haar features and with the features that are

based on LBP, we created the cascade classiﬁers. The

ﬁnal strong classiﬁers consist of 20 stages for LBP

and also for Haar features.

To calculate the performance of approaches, we

used Matthew’s correlation coefﬁcient (MCC) that is

typically used in machine learning to assess the per-

formance of a binary classiﬁer; MCC is useful if two

classes have a different size (in our case, the num-

bers of TP, TN, FP, FN are different). The values of

MCC are between -1 and +1. The higher value repre-

sents better predictions. We collected 28 testing im-

ages from the parking lot to evaluate the approaches.

The testing images were not used in the training phase

and the images were taken in several year seasons (in

different weather and lighting conditions). The exam-

ple of testing images is shown in Fig. 6.

The performance results obtained during our test

are shown in Table 1. In fact, the table is divided into

two parts. The ﬁrst part shows the results of images

captured in good lighting conditions. The second part

shows the results for winter, rain, and night, i.e. difﬁ-

cult conditions.

The HOG descriptors were successful in the sunny

weather and good lighting conditions. Nevertheless,

the HOG based detectors failed in the bad lighting

conditions especially at night, in winter and in rain.

In such cases, the numbers of false positives were in-

creased. In poor lighting situations, the HOG based

detectors detect the places in the images as occupied

although the cars are not present in these places. The

artifacts (noise) created in the bad-lit conditions have

a negative effect to the HOG descriptors, despite the

fact that we used the median ﬁlter on each image.

Using the HOG descriptors, we achieved the best re-

sult with HOG

900

conﬁguration (in this case, MCC

= 0.90). The feature vector of HOG

300

conﬁgura-

tion (with such a small number of descriptors) was

not able to describe the appearance of cars correctly

and this conﬁguration achieved MCC = 0.83 only.

In the good conditions, the Haar based detector

also achieved the high accuracy (MCC = 0.94). In

the worst lighting conditions, the Haar based detector

(like the HOG based detectors) failed in some cases

(MCC = 0.88). Haar based detector and the LBP

based detector missed some of the cars in the difﬁcult

conditions (e.g. in night) and the LBP based detector

even missed some of the cars in the good conditions.

The detectors that are based on these features (Haar,

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

496

Figure 5: The visualization of distribution of temperature. The value of temperature is depicted by the level of brightness.

summer winter night

Figure 6: The parking lot in different conditions.

Table 1: The detection performance (occupancy detection).

sunny winter/rain/night overall performance

TP TN FP FN MCC TP TN FP FN MCC MCC

Energy

288

408 363 13 0 0.97 251 510 17 6 0.93 0.95

HOG

300

405 334 42 3 0.89 252 433 93 6 0.76 0.83

HOG

900

407 356 20 1 0.95 254 453 73 4 0.81 0.90

Haar 405 354 22 3 0.94 242 501 25 16 0.88 0.91

LBP 372 360 11 41 0.87 217 523 4 40 0.87 0.88

LBP) need to increase the amount of training data to

achieve better detection results.

The proposed detector achieved very satisfactory

results in the various weather and lighting conditions

across all testing images. In the sunny weather with

the good conditions, the descriptors reached the very

high MCC results. In winter seasons, during nights

and rain, the presented descriptors achieved much bet-

ter results than the HOG, LBP, Haar feature based

detectors. In general, in night images, the noise has

the negative effect on image quality and especially on

the quality of object edges. The proposed descriptors

that are based on the temperature distribution gain the

noise resistance properties from the diffusion equa-

tion and the noisy images do not cause the problem in

obtaining the relevant features for the object descrip-

tion. In the conﬁguration of Energy

288

of our descrip-

tors, we achieved the best MCC = 0.95 with the 288

descriptors. The HOG

900

conﬁguration needed three-

times more descriptors than the proposed approach to

achieve MCC = 0.90.

Finally, the proposed method shows that the cars

can be described with a reasonable number of features

with very good detection results without need for the

methods for reducing the feature space. The example

of detection results of our approach is shown in Fig.

5 CONCLUSIONS

This paper proposed the efﬁcient method for comput-

ing the image descriptors that are useful for object de-

tection. The proposed descriptors are based on the

distribution of temperature and the vector of these de-

scriptors is used as an input for the SVM classiﬁer.

In this paper, we used the descriptors for detecting

the cars. The results that we demonstrated are very

promising and our future work will focus on the de-

tection of other objects of interest using this method

and we will also focus on the time complexity of com-

putation of the proposed features.

ACKNOWLEDGEMENTS

This work was supported by the SGS in VSB Techni-

cal University of Ostrava, Czech Republic, under the

grant No. SP2013/185.

EnergybasedDescriptorsandtheirApplicationforCarDetection

497

Figure 7: The detection results of our approach.

REFERENCES

Boser, B. E., Guyon, I. M., and Vapnik, V. N. (1992).

A training algorithm for optimal margin classiﬁers.

In Proceedings of the 5th Annual ACM Workshop

on Computational Learning Theory, pages 144–152.

ACM Press.

Cao, X., Wu, C., Yan, P., and Li, X. (2011). Linear svm clas-

siﬁcation using boosting hog features for vehicle de-

tection in low-altitude airborne videos. In Image Pro-

cessing (ICIP), 2011 18th IEEE International Confer-

ence on, pages 2421 –2424.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In Computer Vision and

Pattern Recognition, 2005. CVPR 2005. IEEE Com-

puter Society Conference on, volume 1, pages 886 –

893 vol. 1.

Fabian, T. (2008). An algorithm for parking lot occupation

detection. In Computer Information Systems and In-

dustrial Management Applications, 2008. CISIM ’08.

7th, pages 165 –170.

Fusek, R., Sojka, E., Mozdren, K., and Surkala, M. (2013a).

Energy-transfer features and their application in the

task of face detection. In Advanced Video and Signal

Based Surveillance (AVSS), 2013 10th IEEE Interna-

tional Conference on, pages 147–152.

Fusek, R., Sojka, E., Mozd

n, K., and

Surkala, M. (2013b).

Energy-transfer features for pedestrian detection. In

Bebis, G., Boyle, R., Parvin, B., Koracin, D., Li, B.,

Porikli, F., Zordan, V., Klosowski, J., Coquillart, S.,

Luo, X., Chen, M., and Gotz, D., editors, Advances

in Visual Computing, volume 8034 of Lecture Notes

in Computer Science, pages 425–434. Springer Berlin

Heidelberg.

Huang, C., Ai, H., Li, Y., and Lao, S. (2007). High-

performance rotation invariant multiview face de-

tection. IEEE Trans. Pattern Anal. Mach. Intell.,

29(4):671–686.

Huang, C.-C. and Wang, S.-J. (2010). A hierarchical

bayesian generation framework for vacant parking

space detection. Circuits and Systems for Video Tech-

nology, IEEE Transactions on, 20(12):1770 –1785.

Ichihashi, H., Katada, T., Fujiyoshi, M., Notsu, A., and

Honda, K. (2010). Improvement in the performance

of camera based vehicle detector for parking lot. In

FUZZ-IEEE, pages 1–7. IEEE.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

498

Liao, S., Zhu, X., Lei, Z., Zhang, L., and Li, S. Z. (2007).

Learning multi-scale block local binary patterns for

face recognition. In ICB, pages 828–837.

Lienhart, R. and Maydt, J. (2002). An extended set of haar-

like features for rapid object detection. In Image Pro-

cessing. 2002. Proceedings. 2002 International Con-

ference on, volume 1, pages I–900–I–903 vol.1.

Mimbela, L., Klein, L., Kent, P., Hamrick, J., Luces, K.,

and Herrera, S. (2007). Summary of Vehicle Detec-

tion and Surveillance Technologies used in Intelligent

Transportation Systems. Federal Highway Adminis-

tration’s (FHWA) Intelligent Transportation Systems

Program Ofﬁce.

Papageorgiou, C. and Poggio, T. (2000). A trainable system

for object detection. Int. J. Comput. Vision, 38(1):15–

33.

Perona, P. and Malik, J. (1990). Scale-space and edge detec-

tion using anisotropic diffusion. IEEE Trans. Pattern

Anal. Mach. Intell., 12:629–639.

Schneiderman, H. and Kanade, T. (2004). Object detection

using the statistics of parts. Int. J. Comput. Vision,

56(3):151–177.

Suard, F., Rakotomamonjy, A., Bensrhair, A., and Broggi,

A. (2006). Pedestrian detection using infrared images

and histograms of oriented gradients. In Intelligent

Vehicles Symposium, 2006 IEEE, pages 206 –212.

Viola, P. and Jones, M. (2001). Rapid object detection using

a boosted cascade of simple features. In Computer Vi-

sion and Pattern Recognition, 2001. CVPR 2001. Pro-

ceedings of the 2001 IEEE Computer Society Confer-

ence on, volume 1, pages I–511 – I–518 vol.1.

Viola, P. and Jones, M. (2002). Robust real-time object

detection. International Journal of Computer Vision,

57(2):137–154.

Wu, B., Ai, H., Huang, C., and Lao, S. (2004). Fast rotation

invariant multi-view face detection based on real ad-

aboost. In Automatic Face and Gesture Recognition,

2004. Proceedings. Sixth IEEE International Confer-

ence on, pages 79–84.

Zheng, W. and Liang, L. (2009). Fast car detection using

image strip features. In Computer Vision and Pattern

Recognition, 2009. CVPR 2009. IEEE Conference on,

pages 2703–2710.

Zhu, Q., Yeh, M.-C., Cheng, K.-T., and Avidan, S. (2006).

Fast human detection using a cascade of histograms

of oriented gradients. In Computer Vision and Pat-

tern Recognition, 2006 IEEE Computer Society Con-

ference on, volume 2, pages 1491 – 1498.

EnergybasedDescriptorsandtheirApplicationforCarDetection

499