Visualization of Varying Hierarchies by

Stable Layout of Voronoi Treemaps

Sebastian Hahn

, Jonas Tr

umper

, Dominik Moritz

and J

urgen D

ollner

Hasso-Plattner-Institute, Potsdam, Germany

Keywords:

Hierarchical Visualization, Voronoi Treemaps, Stable Layout, Changing Hierarchies.

Abstract:

Space-restricted techniques for visualizing hierarchies generally achieve high scalability and readability (e.g.,

tree maps, bundle views, sunburst). However, the visualization layout directly depends on the hierarchy, that

is, small changes to the hierarchy can cause wide-ranging changes to the layout. For this reason, it is difﬁcult

to use these techniques to compare similar variants of a hierarchy because users are confronted with layouts

that do not expose the expected similarity. Voronoi treemaps appear to be promising candidates to overcome

this limitation. However, existing Voronoi treemap algorithms do not provide deterministic layouts or assume a

ﬁxed hierarchy. In this paper we present an extended layout algorithm for Voronoi treemaps that provides a high

degree of layout similiarity for varying hierarchies, such as software-system hierarchies. The implementation

uses a deterministic initial-distribution approach that reduces the variation in node positioning even if changes

in the underlying hierarchy data occur. Compared to existing layout algorithms, our algorithm achieves lower

error rates with respect to node areas in the case of weighted Voronoi diagrams, which we show in a comparative

study.

1 INTRODUCTION

Space-restricted visualization of hierarchical data has

been a well investigated research ﬁeld for the last

decades. Although most of the existing techniques per-

form well with respect to scalability, readability, and

the aspect ratio of the items (i.e., the graphical repre-

sentation of hierarchy nodes), the stability of the lay-

out represents a major challenge. If the depiction of

similar hierarchies (e.g., varying hierarchies) does not

expose similar layouts, the usability is substantially re-

stricted. Users need to analyze and correlate the visual-

ization results to compare the hierarchy visualization

and to detect changes.

Guerra-G

omez et al. (Guerra-G

omez et al., 2013)

deﬁne ﬁve types of tree-comparison problems. In our

case, we need to discern two comparison problems:

The layout algorithm faces a type 3 problem (“positive

and negative changes in leaf node values with aggre-

gated values in the interior nodes and with changes in

topology”); the user faces a type 1 problem (“positive

and negative changes in leaf node values with aggre-

gated values in the interior nodes [...] and no changes

in topology”). That is, the layout algorithm has to deal

with both topological as well as value changes and

(a) (b)

Figure 1: Chromium Compositor project (approx. 500 ﬁles):

Visualization of its hierarchy for two revisions. Despite a

number of changes in 1 month (May 2013) – 314 ﬁles

changed, 30 ﬁles added, and 18 ﬁles deleted – the layout

is stable and we notice signiﬁcant coherence between the

two images (the nodes’ unique ids are mapped to color).

shall produce a layout that exhibits only few topologi-

cal changes but still represents value changes.

In other words, we refer to such a layout algo-

rithm’s ‘tolerance’ against changes in varying input

hierarchy-data with respect to the arrangement and

layout of resulting visual representations as layout

stability. Layout stability is considered essential for

effectively and efﬁciently performing visual analysis

tasks such as comparing hierarchies and attributes of

such hierarchies’ nodes, and tracking changes to hi-

Hahn S., Trümper J., Moritz D. and Döllner J..

Visualization of Varying Hierarchies by Stable Layout of Voronoi Treemaps.

DOI: 10.5220/0004686200500058

In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 50-58

ISBN: 978-989-758-005-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Create Voronoi treemap

Calculate

Power Diagram

AdaptPositionsWeights AdaptWeights

Calculate

Power Diagram

Calculate

Power Diagram

Create random

distribution

Create deterministic

stable distribution

break

Improve distribution

done

a.) b.) c.) d.)

Figure 2: Process of computing a Voronoi treemap with weighted sites.

erarchies over time (Nocaj and Brandes, 2012b; Card

et al., 2006; Hadlak et al., 2010). A key reason for this

fact is that users explore visual representations and

create their own mental maps (Kitchin, 1994). Such

maps signiﬁcantly aid their orientation in the visual-

ized information space by providing a reference sys-

tem similar to road maps in the physical world. As

with navigation in the physical world, such map is use-

less if changes to the input data result in items not be-

ing placed as expected. Thus, users can only use their

mental map if the context – the spatial position of hier-

archy nodes – is more or less stable, i.e., within some

small frame of placement error. Otherwise, a new men-

tal map has to be constructed. For example, in software

visualization, large sequences of versioned module hi-

erarchies (e.g., source-code trees) demand for a degree

of coherence in corresponding visual representations

to facilitate comprehension of the underlying software

evolution.

Voronoi treemaps appear to be promising candi-

dates to increase layout stability for visualizing vary-

ing hierarchies. Due to the way Voronoi diagrams are

constructed, changes in the input data (a point distribu-

tion) typically only induce locally constrained changes

to the output. One of the main disadvantages of exist-

ing layout algorithms for Voronoi treemaps (Balzer

et al., 2005; Nocaj and Brandes, 2012a) consists in

using a random initial distribution, which can result

in essentially different depictions of similar hierar-

chies. We present an approach for deterministically

computing an initial point distribution as input for the

Voronoi Treemap computation stage instead of the ran-

dom initial distribution used by Nocaj and Brandes

(see Fig. 2a). As the distribution algorithm is toler-

ant against changes in the input hierarchy, we ensure

that hierarchy nodes are position-stable in the result-

ing layout, and achieve a high degree of layout sta-

bility for varying hierarchies. Further, our approach

reduces the error of achieved target areas for weighted

Voronoi treemaps. For it, we show three optimizations

to the latest algorithm: (see Fig. 2b) a less restrictive

but holding criteria for the prevention of empty cells,

(see Fig. 2c) a different calculation for increasing and

decreasing the cell sizes through the iterative process,

and (see Fig. 2d) a more precise break condition. We

show an application of our Voronoi treemap layout

algorithm in the ﬁeld of software visualization, exem-

pliﬁed for the case of a sub-module of the open-source

web browser Chromium

, the Chromium Compositor

(cc) project (as shown in Fig. 1).

This paper is structured as follows. Section 2 gives

a brief overview about related and previous work on

layout stability, mental maps and treemaps, as well as

techniques used for shape transformations. A theoret-

ical model for varying hierarchical data is given in

Section 3. Section 4 describes the workﬂow and pro-

posed algorithms to render Voronoi treemaps layout

stable with respect to varying hierarchical data. In Sec-

tion 5 our improvements to the latest Voronoi treemap

algorithm by Nocaj and Brandes (Nocaj and Brandes,

2012a) are shown to reduce the number of iterations

and to increase precision of target-area sizes. The eval-

uation of our improvements to the Algorithm of Nocaj

and Brandes is presented in Section 6. Finally, Sec-

tion 7 concludes this paper and gives an outlook on

possible future work.

2 RELATED WORK

Since the invention of Treemaps by Johnson and

Shneiderman (Johnson and Shneiderman, 1991),

space-restricted hierarchical visualization has been im-

proved along the dimensions of item ordering, aspect-

ratio, readability, and stability. While the original

Slice’n dice treemap layout (Shneiderman, 1992) cre-

ates representations with good stability, its items can

have imbalanced aspect ratios that aggravate overall

readability and size comparison between items. Other

layout techniques such as Squariﬁed (Bruls et al.,

2000) or Strip (Shneiderman and Wattenberg, 2001)

focus on creating items with an aspect-ratio close to

one, but are less layout stable (Sud et al., 2010).

http://www.chromium.org, last accessed 07/25/2013

VisualizationofVaryingHierarchiesbyStableLayoutofVoronoiTreemaps

As outlined above, for our visual-analysis tasks,

in particular the recognition of a hierarchies’ nodes,

the memorability of item positions is a primary goal.

The InfoSky, presented by Andrews et al., uses a force-

based node placement and additively weighted power

diagrams for the visualization of hierarchically struc-

tured documents (Andrews et al., 2002). Kuhn et al.

present a non-space-restricted approach that creates

a so-called software landscape or software map by

applying a mountain metaphor to create a consistent

visualization (Kuhn et al., 2008). For it, a multidimen-

sional scaling (MDS) algorithm creates a distribution

of the hierarchy nodes in visual space. Afterwards, a

hill shading based on the lines of code of each artifact

is applied. This use of MDS leads to a high degree

of consistency over several variants of a hierarchy but

does not allow for visualizing the hierarchy’s structure.

To achieve higher layout stability, Tak and Cockburn

present a rectangular-based treemap layout-algorithm –

Hilbert and Moore treemaps (Tak and Cockburn, 2013)

– that uses the space-ﬁlling property of Hilbert and

Moore curves. By this, the approach prevents spa-

tial discontinuity with respect to the items’ siblings.

Reusing an initial reference layout for subsequent lay-

out computations based on Voronoi treemaps (Nocaj

and Brandes, 2012b) also partially addresses this is-

sue. It assumes, though, as input a single version of the

same hierarchy (or sub-hierarchies thereof). Whenever

this hierarchy changes, the reference layout becomes

invalid and thereby unusable. To achieve layout sta-

bility in Voronoi treemaps, the use of deterministic

algorithms for computing an initial point distribution

instead of random ones is essential. Due to the fact that

Voronoi treemaps can be used with arbitrary convex

root polygons, generalizable polygon coordinates are

needed. A common way to achieve this is the use of

generalized barycentric polygon coordinates, or Wach-

spress coordinates (Wachspress, 1975). These coordi-

nates, which are well deﬁned for convex polygons, al-

low the description of a point inside the polygon with

respect to a polygon’s vertices. Floater et al. further

present an algorithm using Wachspress coordinates to

transform the coordinates of points from inside an ini-

tial polygon into a target polygon (Floater et al., 2006).

Our goal combines the above challenges: We want

to create a visualization that allows for implicitly

identifying unchanged and changed hierarchy nodes

across multiple variants of a hierarchical dataset. That

is, the stability property of our computed layout shall

enable users to distinguish (un)changed nodes by their

relatively (un)stable spatial position and, thereby, also

the recognizability of structural patterns (groups of un-

changed hierarchy nodes). By this, they are effectively

able to identify trends in the visualization of those

data, to compare depictions of different states.

3 VARYING HIERARCHICAL

DATASETS

There exists a wide range of varying hierarchical

datasets. To illustrate this diversity, we pick two exam-

ples, illustrating a set of change operations that induce

the variation of the datasets, before we deﬁne a formal

model of the datasets that we consider in this paper.

File-Systems on Hard disks

Files on a hard

disk are structured strongly hierarchical (excluding

links) using folders. In addition to this parent-child-

relationship meta information on ﬁles, e.g., the at-

tributes size and modiﬁcation date, exist. A folder’s

size is then the aggregation of the sizes of all ﬁles con-

tained in such folder. Furthermore, a ﬁle system can

be modiﬁed by editing ﬁles, and through it modify-

ing their ﬁle size (operation changeAttribute), deleting

ﬁles as well as folders, and adding new ﬁles or folders.

Tree of Life

The tree of life shows a hierarchi-

cal structure of different organisms (the tree’s leafs)

grouped by species. As in the ﬁle-system example, at-

tributes exist for the leafs. A typical attribute here is

an organism’s population. Analogous to the ﬁle sys-

tem, these attributes change over time, too (changeAt-

tribute). Organism or even species become extinct

(delete) while others evolve (add).

A Formal Model

We deﬁne a formal model for vary-

ing hierarchical dataset

H = (N, E)

, which contains a

set of nodes

N = {n

, ..., n

}

and a set of versioned

edges E = {E

, ..., E

} as follows:

E = {k

, ..., k

} k = (n

, n

) (1)

are considered as edges between nodes de-

scribed by a tuple of nodes (a parent

and a child

node

) with the following properties: (a) Only one

tuple exists in E where

= null

and through this the

child of that

is considered as root node. (b) Every

child node has only one unique parent node. (c) There

are no (transitive) cycles in E.

Hence, a tuple

T = (N, E

∈E)

deﬁnes one variant

of our hierarchical dataset. We say that subsequent

variants of such tuples are similar to each other, i.e.,

∀

i∈[0, j−1]

: T

∼T

j+1

. We further deﬁne a function

uid :

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

N ×E → N

that yields a unique identiﬁer per path

p : N ×E → N ×... ×N such that:

∀

∈N,E∈E

: p(n

, E) 6= p(n

, E) ⇔ (2)

uid(n

, E) 6= uid(n

, E)

Here,

p(n, E)

returns the path from node

to the

root node

deﬁned by

. Note that each variant

E ∈

can deﬁne a different path

for a node

n ∈ N

. In

other words, our data model considers nodes that are

moved in

as different nodes and they will have more

than one unique identiﬁer

uid

. Last, there exists a set

of functions

attr

: N ×E → R

returning numerical

attributes per node n ∈ N and versioned edges E.

4 A STABLE INITIAL

DISTRIBUTION

Nocaj and Brandes construction of Voronoi cells is de-

terministic – except that they start with nondetermin-

istic initial positions for the Voronoi sites. To achieve

stability, we thus need to ﬁnd a method that is able

to create deterministic initial positions. That is, our

approach has to fulﬁll the following requirements:

•

The initial-distribution algorithm for the Voronoi

sites has to be deterministic.

•

If change operations such as add or delete occur

to a parent node, they should not affect positions

of its children already positioned in an earlier evo-

lution step.

•

The placement of sites relative to each other has to

be stable, even if polygon’s shape of their parent

has changed.

•

changeAttribute operations on nodes should only

cause small changes in the resulting layout.

Voronoi treemaps allow for using arbitrary convex

polygons as root item, within which any subsequent

direct and indirect child items are contained. For each

created shape that represents a child node, the algo-

rithm can further be applied recursively to this node’s

children.

We start with a target polygon having a given num-

ber of vertices (corners

) that represent the root item

in which a set of Voronoi sites

(S)

should be dis-

tributed. Next, we calculate a regular polygon with the

same number of vertices (Fig. 3a). Given a set of nodes

(S)

, which are assumed to have a uniquely identiﬁer,

we are able to deﬁne consistent Cartesian coordinates

in a unit square for each node. In our case, we compute

such unique identiﬁer (

uid

) as a hash

<< x, y >>

(an

integer) from a node’s path

. We then encode the ﬁrst

and last half of this hash with

x ∈[0..1]

and

y ∈ [0..1]

Next, these two coordinates are transformed into the

incircle of the regular polygon (Fig. 3b and 3c) by cal-

culating polar coordinates (see Equations in (3)).

c = numberOfPolygonVertices

apothem = cos





<<x, y>> = hash









−



0.5



r = apothem ·

+ y

φ = ±arccos





(3)

As a last step, we compute Wachspress coordinates

(Wachspress, 1975) for the regular polygon and the

sites distributed within. They then describe the sites

position inside a convex polygon as weighted terms of

the polygon’s vertices. By using the vertices’ weights,

each point of the distributed sites is transformed into

the target polygon (Fig. 3d) (Floater et al., 2006).

Since it is guaranteed both that the target polygons in

Voronoi treemaps are convex at any time, and that the

incircle and Wachspress coordinates are well deﬁned

for convex polygons, the whole workﬂow effectively

ensures that the distributed points are always placed

inside the respective target polygon.

As an additional beneﬁt, we do not need to recom-

pute the Wachspress coordinates’ weights of a poly-

gon if the target polygon’s vertices change their po-

sition slightly while polygons number of vertices re-

mains constant. This can happen, e.g., when changes

in the item’s occur. It thereby allows for a fast recalcu-

lation of the target distribution. The Wachspress coor-

dinates only need to be recomputed if the number of

vertices of the target polygon increase or decrease.

5 OPTIMIZED LAYOUT

COMPUTATION

After the initial distribution, the actual Voronoi

treemap is computed (Fig. 2 b,c,d). Although the orig-

inal algorithm (Nocaj and Brandes, 2012a) describes

a rather fast way for computing Voronoi treemaps, we

identiﬁed several optimizations for achieving more

precise results with respect to the size of target area

size of created Voronoi cells. These optimizations con-

cern the functions used in the iterative positioning

process (Fig. 2 b,c) as well as the break condition

(Fig. 2 d) that decides weather a distribution is suf-

ﬁciently precise.

VisualizationofVaryingHierarchiesbyStableLayoutofVoronoiTreemaps

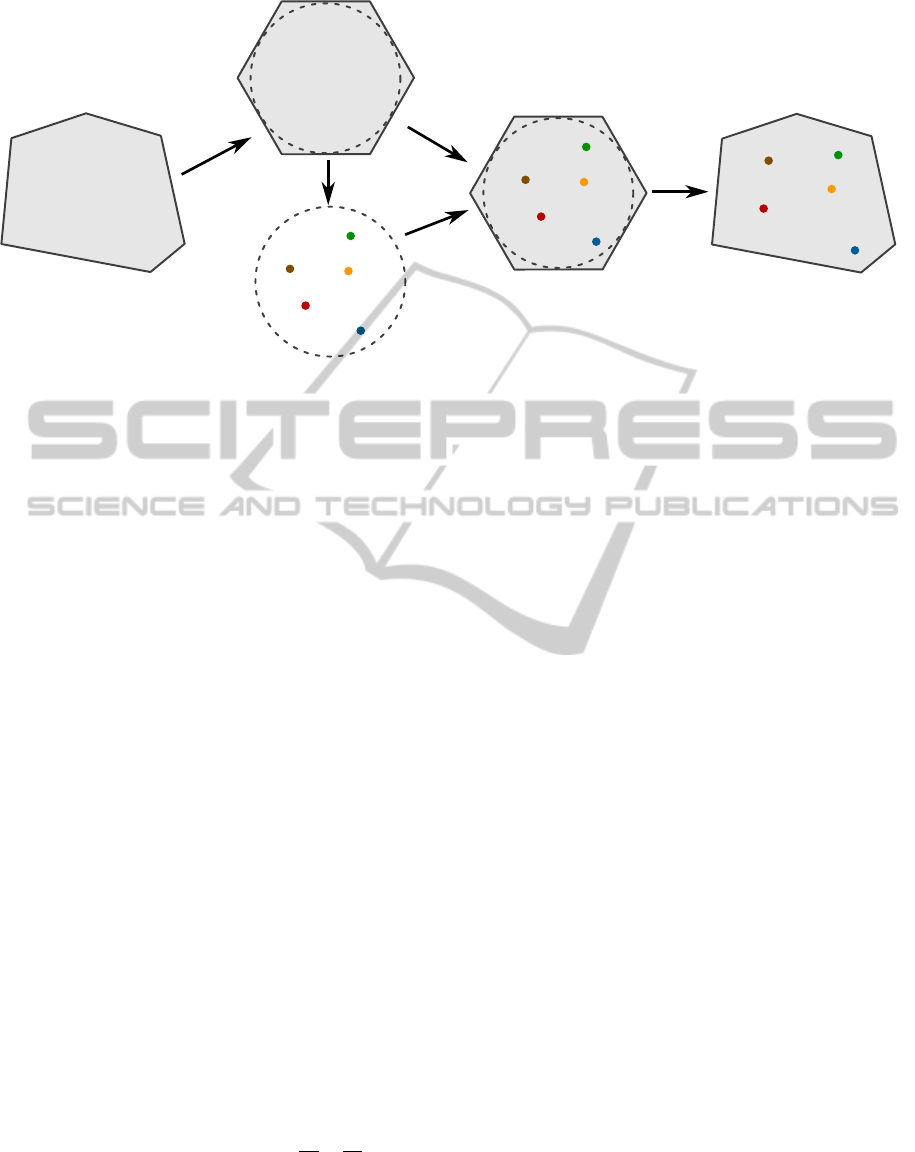
c=6

(a)

(c)

(d)

(b)

Regular

Target

Polygon

Incircle

Figure 3: Workﬂow for computing a deterministic initial site distribution within a target polygon (left). (a) A regular polygon

with the same number of vertices as the target polygon is created. (b) Sites are distributed by our deterministic approach into a

unit circle and (c) transformed into the incircle of a regular polygon. (d) The regular polygon and the sites distributed within

are transformed into the target polygon by using Wachspress coordinates.

5.1 Precision of Target-Area Size

As the initial positioning of the Voronoi sites does

not necessarily reﬂect the targeted weights, Nocaj and

Brandes propose an iterative optimization based on

Lloyd’s algorithm. Lloyd’s algorithm, also known as

Voronoi relaxation, in its original form is used to cal-

culate Voronoi diagrams where the sites’ location co-

incide with the centroids of its Voronoi cell(Du et al.,

1999).

Nocaj and Brandes use power diagrams to iter-

atively adapt the sites’ weights and positions dur-

ing each iteration. For it, the current areas (current

size of a cell) of the cells are iteratively adapted

towards the target areas (cell size that should be

achieved). That is, they loop through the functions

AdaptPositionsWeights

and

AdaptPositions

un-

til a break condition is satisﬁed.

As pointed out by Nocaj and Brandes, empty cells

have to be prevented during the iterative optimization

of weights and positions: A centroid is required for

optimizing a site’s position, but cannot be computed

for empty cells. Such a site’s empty cell can emerge if

the site is encircled by a circle deﬁned by the weight of

another site. Consequently, empty cells can be avoided

by limiting the site’s weights such that the constraint

in Equation 4 is satisﬁed.

∀s,t ∈ S, s 6= t : ||s −t||> max(

√

) (4)

However, Nocaj and Brandes propose a criterion

that is too strong in several cases. They limit the new

site’s weight to the minimum of the distance of the

cell that it belongs to and its maximum weight in Al-

gorithm 1. This often results in many cells being too

small and thus – counterintuitively – especially cells

that should be very small are far too large.

We propose a weaker limit for a site’s weight as

follows: A site’s weight in

AdaptPositionsWeights

is limited to the minimum distance to any other site,

just like Nocaj and Brandes did in

AdaptWeights

. In

most cases, this criterion is weaker, but it always sat-

isﬁes the constraint in Equation 4. Our Algorithm 3

uses the same method to determine the distance to the

nearest neighbor as proposed by Nocaj and Brandes

in Algorithm 2. The distances can be calculated by

means of a Voronoi diagram in O(nlog n).

During our experiments, we noticed that the

method of Nocaj and Brandes often results in oscil-

lating site locations, weights, and areas during the iter-

ative optimization. To overcome this problem

adapt

is limited to

1 ± ρ

if its ﬁrst derivative (increas-

ing/decreasing the weight) starts oscillating as de-

scribed in Algorithm 4.

Note that even though the distance is described in Al-

gorithm 3 and 4 as being the distance between two

sites, it can also be computed as twice the distance

to the cell from a site. It is not necessary to know

which site is the nearest neighbor. Also note that most

distances can be calculated as the squared distances

which does not require calculating any square roots.

The effects of our optimizations are shown in

Fig. 4 and are evaluated and discussed in detail in Sec-

tion 6.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

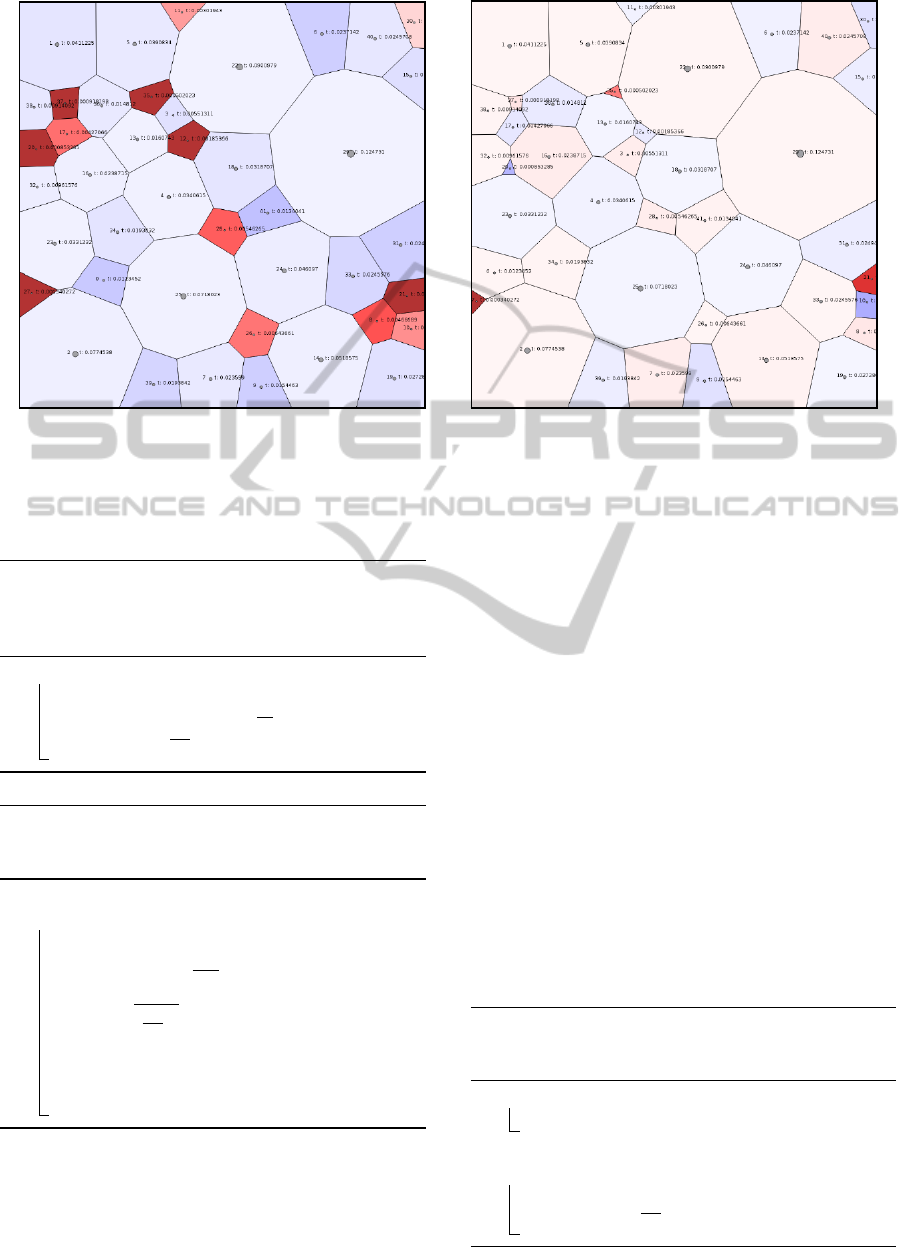
(a) Approach of Nocaj and Brandes (b) Our Approach

Figure 4: Errors in target-area size shown by color (red = too big, white = correct, blue = too small), i.e., color encodes how

much the actual size of a target area deviates from its expected size (given by the respective attribute value mapped to area

size). Comparison between the results from the algorithm of Nocaj and Brandes (left) and our approach (right). In comparison

to Nocaj and Brandes, our optimizations yield higher precision with respect to the error in target-area size .

Algorithm 1: AdaptPositionsWeights

(p, V (S), S,W)

used to adapt the positions and

weights in an iterative optimization algorithm

proposed by Nocaj and Brandes.

1 foreach site s ∈ S do

2 a ← centroid(V

)

3 distanceBorder ← min

x∈V

||x −s||

4 w

← (min(

√

, distanceBorder))

Algorithm 2: AdaptWeights( p, V (S), S,W)

used

to adapt the weights in an iterative optimization algo-

rithm proposed by Nocaj and Brandes.

1 NN ← Nearestneighbor(S)

2 foreach site s ∈ S do

3 A

current

← A(V

); // current area

4 A

target

← A(Ω) ·

v(s)

v(p)

; // target area

5 f

adapt

←

target

current

6 w

new

←

√

· f

adapt

7 w

max

← ||s −NN

8 w

← (min(w

new

, w

max

))

9 w

← max(w

, ε)

5.2 Break Condition

The iterative optimization to calculate Voronoi dia-

grams where the cells have a target area requires a

break condition (see Fig. 2d) that is satisﬁed when the

iterative optimization has ﬁnished. Nocaj and Brandes

propose to cancel the optimization process when the

sum of area errors is below a certain threshold. They

deﬁne the area error as the difference between the cur-

rent area and target area of a Voronoi cell. Furthermore

the maximum number of iterations is limited.

Unfortunately the area error often does not con-

verge to zero and the minimum error that is reached in

a reasonable number of iterations highly depends on

the number of sites and the target areas of the Voronoi

cells. Consequently, the threshold is often reached af-

ter only a few iterations or not reached at all and the

maximum number of iterations is reached. In the ﬁrst

case more iterations would reduce the sum of area

errors. In the second case fewer iterations would prob-

ably not imply a much higher sum of area errors.

Algorithm 3:

Optimized version of

AdaptPositionsWeights(p, V (S), S,W )

with

less-restrictive empty cell prevention.

1 foreach site s ∈ S do

2 a ← centroid(V

)

3 NN ← Nearestneighbor(S)

4 foreach site s ∈ S do

5 w

max

← ||s −NN

6 w

← (min(

√

, w

max

))

VisualizationofVaryingHierarchiesbyStableLayoutofVoronoiTreemaps

Algorithm 4:

Optimized version of

AdaptWeights(p, V (S), S,W )

that prevents

“oscillation”.

1 fs ← initialize with zeros

2 NN ← Nearestneighbor(S)

3 foreach site s ∈ S do

4 A

current

← A(V

)

5 A

target

← A(Ω) ·

v(s)

v(p)

6 f

adapt

←

target

current

7 if fs

6= 0 and sgn( f

adapt

−1) 6= sgn(fs

−1)

then

8 f

adapt

← min(1 + ρ, max( f

adapt

, 1 −ρ))

9 w

new

←

√

· f

adapt

10 w

max

← ||s −NN

11 w

← (min(w

new

, w

max

))

12 w

← max(w

, ε)

13 fs

← f

adapt

We propose a threshold for the difference between

the maximum area error (the maximum error of each

individual cell,

target

−A

current

) of different itera-

tions which could be seen as the slope of the maxi-

mum area error. More formally, the optimization pro-

cess if canceled when

diff

< threshold

diff

is deﬁned

in Equation 5 where

−l

is the maximum error

itera-

tions ago in a list

iterations,

is the middle

entry of

and

is the maximum error in the current

iteration.

diff

= max(e

−l

, e

) −e

(5)

A disadvantage of this method is that the area er-

ror of the resulting Voronoi diagram does not have an

upper bound. However, we know that more iterations

would probably not reduce the area error.

6 COMPARATIVE EVALUATION

To evaluate the optimizations of our approach (

Alg

)

(presented in Section 5) in comparison to the algo-

rithms of Nocaj and Brandes (

Alg

) (Nocaj and

Brandes, 2012a), we tested both algorithms distribut-

ing different numbers of sites within the same parent

polygon. For it, we computed distributions of 10, 50

and 250 sites with random polygon weights with 1000

iterations per distribution. To achieve comparable re-

sults we use the same seed to compute the weights

for each run. The dependent variables of our study are:

Time needed to compute the distribution within 1000

iterations, maximum error of the target sizes and the

sum of target-size errors. Table 1 shows the evaluation

setup with (in)dependent variables in detail.

Table 1: Dependent and independent variables for the com-

parative study (example for 10 sites).

Seed Alg Time Max Err Sum Err

Alg

err

max

err

sum

Alg

err

max

err

sum

Alg

err

max

err

sum

Alg

err

max

err

sum

... ... ... ... ...

Alg

2n−1

err

max

2n−1

err

sum

2n−1

Alg

err

max

err

sum

The mean computation time of

Alg

compared

Alg

shows equal results with each number of

sites (Table 2 shows the mean computation times

in detail), our algorithms shows better error rates in

both the maximum area error and the sum of area er-

rors for every number of distributed sites (shown in

Fig. 5 a,b). A paired t-test shows that our method sig-

niﬁcantly decreases both, the maximum area error (10

Sites:

p = 2 ·10

−6

; 50 Sites:

p = 8 ·10

−8

; 250 Sites:

p = 0, 01

) as well as the sum of all area errors (10

Sites:

p = 4 ·10

−4

; 50 Sites:

p = 2 ·10

−6

; 250 Sites:

p = 8 ·10

−8

Table 2: Mean computation times for the comparative eval-

uation. The computation times of our algorithm are equal

compared to the ones of Nocaj and Brandes.

Number Of Sites Alg Mean Time

10 Alg

355 ms

10 Alg

353 ms

50 Alg

1686 ms

50 Alg

1701 ms

250 Alg

8937 ms

250 Alg

8914 ms

7 CONCLUSIONS AND

FUTURE WORK

We have presented an extension to an existing layout

algorithm for Voronoi treemaps by using a determin-

istic initial distribution for the Voronoi sites. Since

the resulting layouts are stable with respect to vary-

ing input hierarchies and varying size of items, this

enables the use of Voronoi treemaps for comparing hi-

erarchy variants. Such data sets emerge, e.g., from ver-

sioned source-code trees of software systems. Fig. 6

shows an example of such a varying hierarchy, depict-

ing the cc project from the Chromium Git repository

(branch: master) over several revisions (annotated with

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

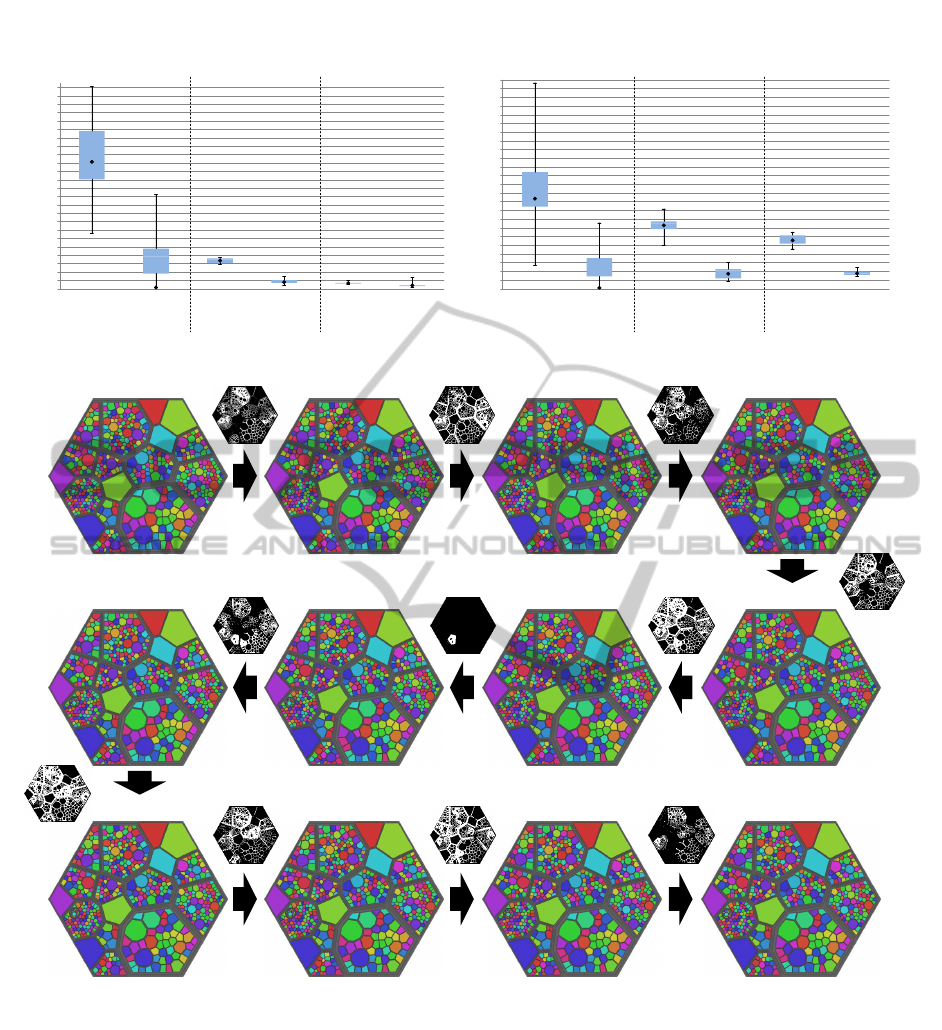
0,002

0,004

0,006

0,008

0,01

0,012

0,014

0,016

0,018

0,02

0,022

0,024

0,026

0,028

0,03

0,032

0,034

0,036

0,038

0,04

0,042

0,044

0,046

0,048

Noc+Bran

Our Approach

Noc+Bran

Our Approach

Noc+Bran

Our Approach

Max_ERROR

10 Sites 250 Sites 50 Sites

(a) Maximum target error rates

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

0,1

0,11

0,12

0,13

0,14

0,15

0,16

0,17

0,18

0,19

0,2

0,21

0,22

0,23

0,24

Noc+Bran

Our Approach

Noc+Bran

Our Approach

Noc+Bran

Our Approach

Sum_ERROR

10 Sites 250 Sites 50 Sites

(b) Sum of all node target error rates

Figure 5: Results of the maximum target error rate (a) and the sum of all target error rates (b) evaluated by a comparative study

between (Nocaj and Brandes, 2012a) and our optimization approach to improve the precision of the target areas for different

numbers of sites (10, 50, 250) with randomized weights distributed in their parent node.

Hash: c28df4c Hash: c9f0d06 Hash: d293572 Hash: b38864d

Hash: 045098d Hash: 3d8ab9f Hash: 41512b0 Hash: f826b5f

Hash: a9f0cfd Hash: a4a08d0 Hash: 953e094 Hash: 22898ed

Figure 6: Visualization of the hierarchical folder structure (with about 500 nodes) of 12 revisions from the cc project of the

Chromium Git repository (master). The area of the cells is mapped to the corresponding ﬁle size of the represented node.

The nodes’ unique identiﬁer – created from the paths to the root node – is shown as color. For each adjacent layouts, which

represent successive revisions, a difference mask is shown. Unchanged areas are represented by black pixels, while white

pixels indicate differences between the two respective layouts. Although several changes (operations: changeAttribute in 169

ﬁles, 5 ﬁles added, 2 ﬁles deleted) are present in the input data, the resulting layouts are appears as stable and exhibit only few,

local differences. Through it, the layout is memorable over all revisions.

the commit-hashes). Our comparison of target-error

rates further show that we achieve a lower target-error

rate than existing layout algorithms. We conclude that

the resulting layout represents attributes of the input

data more accurately than previous techniques.

As future work, we plan to apply keyframe ani-

mations to blend between the display of the hierarchy

variants. We then plan to evaluate how well users can

track existing hierarchy items in the visualization and

whether the placement of items can be further opti-

VisualizationofVaryingHierarchiesbyStableLayoutofVoronoiTreemaps

mized with respect to user expectations. Since com-

puting layouts for large graphs is still too slow for

interactive use, it would likely beneﬁt by porting the

layout algorithm to GPUs. Moreover, we want to add

support for move and rename as possible change oper-

ations.

ACKNOWLEDGEMENTS

The authors would like to thank the anonymous re-

viewers for their valuable comments. This work was

funded by the Research School on ”Service-Oriented

Systems Engineering” of the Hasso-Plattner-Institute

and the Federal Ministry of Education and Research

(BMBF), Germany, within the InnoProﬁle Transfer re-

search group ”4DnD-Vis” (www.4dndvis.de).

REFERENCES

Andrews, K., Kienreich, W., Sabol, V., Becker, J., Droschl,

G., Kappe, F., Granitzer, M., Auer, P., and Tochtermann,

K. (2002). The infosky visual explorer: exploiting hi-

erarchical structure and document similarities. Infor-

mation Visualization, 1(3-4):166–181.

Balzer, M., Deussen, O., and Lewerentz, C. (2005). Voronoi

treemaps for the visualization of software metrics. In

Proceedings of the 2005 ACM symposium on Software

visualization, pages 165–172. ACM.

Bruls, M., Huizing, K., and Van Wijk, J. J. (2000). Squariﬁed

treemaps. In Data Visualization 2000, pages 33–42.

Springer.

Card, S. K., Sun, B., Pendleton, B. A., Heer, J., and Bodnar,

J. W. (2006). Time tree: Exploring time changing hi-

erarchies. In Visual Analytics Science And Technology,

2006 IEEE Symposium On, pages 3–10. IEEE.

Du, Q., Faber, V., and Gunzburger, M. (1999). Centroidal

voronoi tessellations: Applications and algorithms.

SIAM review, 41(4):637–676.

Floater, M. S., Hormann, K., and K

os, G. (2006). A general

construction of barycentric coordinates over convex

polygons. advances in computational mathematics,

24(1-4):311–331.

Guerra-G

omez, J. A., Pack, M. L., Plaisant, C., and Shneider-

man, B. (2013). Visualizing Change Over Time Using

Dynamic Hierarchies: TreeVersity2 and the StemView.

IEEE Transactions on Visualization and Computer

Graphics, 19(12):2566–2575.

Hadlak, S., Tominski, C., Schulz, H.-J., and Schumann, H.

(2010). Visualization of attributed hierarchical struc-

tures in a spatiotemporal context. International Jour-

nal of Geographical Information Science, 24(10):1497–

1513.

Johnson, B. and Shneiderman, B. (1991). Tree-maps: A

space-ﬁlling approach to the visualization of hierar-

chical information structures. In Visualization, 1991.

Visualization’91, Proceedings., IEEE Conference on,

pages 284–291. IEEE.

Kitchin, R. M. (1994). Cognitive maps: What are they and

why study them? Journal of Environmental Psychol-

ogy, 14(1):1 – 19.

Kuhn, A., Loretan, P., and Nierstrasz, O. (2008). Consistent

layout for thematic software maps. In Reverse Engi-

neering, 2008. WCRE’08. 15th Working Conference

on, pages 209–218. IEEE.

Nocaj, A. and Brandes, U. (2012a). Computing voronoi

treemaps: Faster, simpler, and resolution-independent.

In Computer Graphics Forum, volume 31, pages 855–

864. Wiley Online Library.

Nocaj, A. and Brandes, U. (2012b). Organizing search re-

sults with a reference map. Visualization and Com-

puter Graphics, IEEE Transactions on, 18(12):2546–

2555.

Shneiderman, B. (1992). Tree visualization with tree-maps:

2-d space-ﬁlling approach. ACM Transactions on

graphics (TOG), 11(1):92–99.

Shneiderman, B. and Wattenberg, M. (2001). Ordered

treemap layouts. In Proceedings of the IEEE Sym-

posium on Information Visualization 2001, volume

73078.

Sud, A., Fisher, D., and Lee, H.-P. (2010). Fast dynamic

voronoi treemaps. In Voronoi Diagrams in Science and

Engineering (ISVD), 2010 International Symposium

on, pages 85–94. IEEE.

Tak, S. and Cockburn, A. (2013). Enhanced spatial stability

with hilbert and moore treemaps. IEEE Transactions

on Visualization and Computer Graphics, 19(1):141–

148.

Wachspress, E. (1975). A Rational Finite Element Basis.

Academic Press rapid manuscript reproductions. Aca-

demic Press.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications