
Surface Area Analysis for People Number Estimation
Hiroyuki Arai, Naoki Ito and Yukinobu Taniguchi
NTT Media Intelligence Laboratories, NTT Corporation, 1-1 Hikari-no-oka, Yokosuka, Kanagawa, Japan
Keywords:
Projective Geometry, Camera Calibration, Surface Area, People Number Estimation, Congestion Monitoring.
Abstract:
An important property of surface areas of objects as observed by a calibrated monocular camera is introduced;
also improved techniques to apply the property to people number estimation are proposed. Standard surface
area (SSA) is defined as the surface area of the reverse projection of an image-pixel onto a plane at specific
height in the real world. SSA is calculated for each pixel according to camera calibration parameters. When
the target object is bound to a certain plane, for example the floor plane, the sum of SSA along with the
foreground pixels of one target object becomes constant. Therefore, simple foreground detection and SSA
summation yield the number of target objects. This basic idea was proposed in a prior article, but there were
two major limitations. One is that the original model could not be applied to the area directly below the
camera. The other is that the silhouette of the target object was limited to a simple rectangle. In this paper we
propose improved techniques that remove the limitations. Slant silhouette analysis removes the first limitation,
and silhouette decomposition the second. The validity and the effectiveness of the techniques are confirmed
by experiments.
1 INTRODUCTION
Crowd estimation or crowd level monitoring is impor-
tant, especially in the fields of safety management and
marketing. Crowd levels at a train station should be
carefully monitored because crowded situations may
cause an accident, for example a fall. In the field of
marketing, audience acceptance of digital-signage is
becoming more and more important. The number of
people who remain in front of the screen is thought to
be a key audience rating metric.
Existing image processing techniques to esti-
mate the number of people are roughly divided into
3 types. The first covers “shape-detection based”
techniques, for example, detection of human body,
upper-body or head region(Sheng-Fuu Lin and Chao,
2001)(Min et al., 2008). The second consists of
“tracking based” techniques (Rabaud and Belongie,
2006), (Zhao et al., 2007),(Sidla et al., 2006),(An-
tonini and Thiran, 2006), for example, tracking peo-
ple by trajectory clustering in the spatio-temporal do-
main. The last, “feature-based” techniques, relate im-
age features to the number of people by case-learning
(Marana et al., 1998),(Cho et al., 1999),(Kong et al.,
2006),(Wen et al., 2011).
Crowd estimation schemes based on image pro-
cessing are expected to meet the following require-
ments, especially for the application of audience esti-
mation. 1)Must be stable even if crowds are present.
2)Must have low computation cost. 3)Must be easy
to set up (because many systems will be needed). If
crowds are present, shape-detection becomes unsta-
ble because many confusing shapes appear in each
image, and tracking also becomes unstable because
too many feature points appear around each other.
Fortunately, feature-based techniques are more sta-
ble than the other two, because the basic operations
used to get the feature vector, such as edge detection
or foreground detection, can be done even if crowds
are present. Feature-based techniques also satisfy
the computation cost requirement. However, existing
feature-based techniques demand a large amount of
ground-truth data. Given the very large number of
cameras needed, preparing enough data would take
far too long and be too expensive.
To satisfy all the above requirements, an a pri-
ori algorithm that can estimate the number of people
by analyzing foreground images was proposed(Arai
et al., 2009). The basic idea is that, after the cam-
era is calibrated, a rough estimation of the number
of people can be made by determining the number of
foreground pixels and their positions in the image. To
realize this idea, the concept of ”standard surface area
(SSA)” which quantitatively represents the extension
of each pixel in the real world was introduced. The
prior article showed that the sum of SSA in the case of
86
Arai H., Ito N. and Taniguchi Y..
Surface Area Analysis for People Number Estimation.
DOI: 10.5220/0004687000860093
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 86-93
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
a rectangle silhouette standing on the floor becomes
invariant. By using this property of SSA and an oc-
clusion model that estimates the influence of occlu-
sion on foreground image, the number of people can
be estimated from foreground images.
According to this technique, a system for mea-
suring the advertizing effectiveness of digital signage
was developed. However, while in operating the sys-
tem, several problems were revealed. The original
technique, implemented in the system, has two im-
portant limitations. One is that it can not be applied
to the area directly below the camera. The other is that
the silhouette of the target object is limited to a sim-
ple rectangle. The first limitation is especially serious,
because many cameras will be fixed to the ceiling to
cover the areas underneath them. Although the sec-
ond limitation is not so serious in the case of people
number estimation, because the silhouette of standing
or walking people can be roughly approximated to the
rectangle model, the ability to handle arbitrary silhou-
ettes is expected to improve measurement precision,
and lead to new applications.
In this paper, we extend the theory proposed in
prior article and introduce improved techniques, slant
silhouette analysis and silhouette decomposition, to
be able to realize directly downward capture and arbi-
trary silhouettes.
Section 2 provides the theoretical background of
the method. The slant silhouette analysis is detailed
in Section 3. Section 4 describes the silhouette de-
composition technique. Experiments to confirm the
validity of the theory and the effectiveness of the es-
timation technique are shown in Section 5. Our con-
clusion is given in Section 6.
2 FUNDAMENTAL THEORY OF
NUMBER ESTIMATION
This section describes the basic theory of the geomet-
rical properties of SSA and the concept of number
estimation. Here, some part of the theory has been
modified (simplified) from the former article().
2.1 Preconditions
The algorithm, described below, is valid given the fol-
lowing assumptions,
(a) camera has been calibrated,
(b) target object, for example human body, can be ap-
proximated as a rigid silhouette of known size.
(c) imageresolution is high enough so that each target
object occupies many pixels in the image
(d) target objects are randomly positioned on the
floor.
2.2 Basic Idea for Number Estimation
The basic idea is to quantitatively relate each fore-
ground pixel to some part of the surface area of the
target object. To simplify the explanation of this idea,
we consider the case of one person standing at known
position (X,Y) on the floor and assume that the hu-
man body can be approximated as a rectangle silhou-
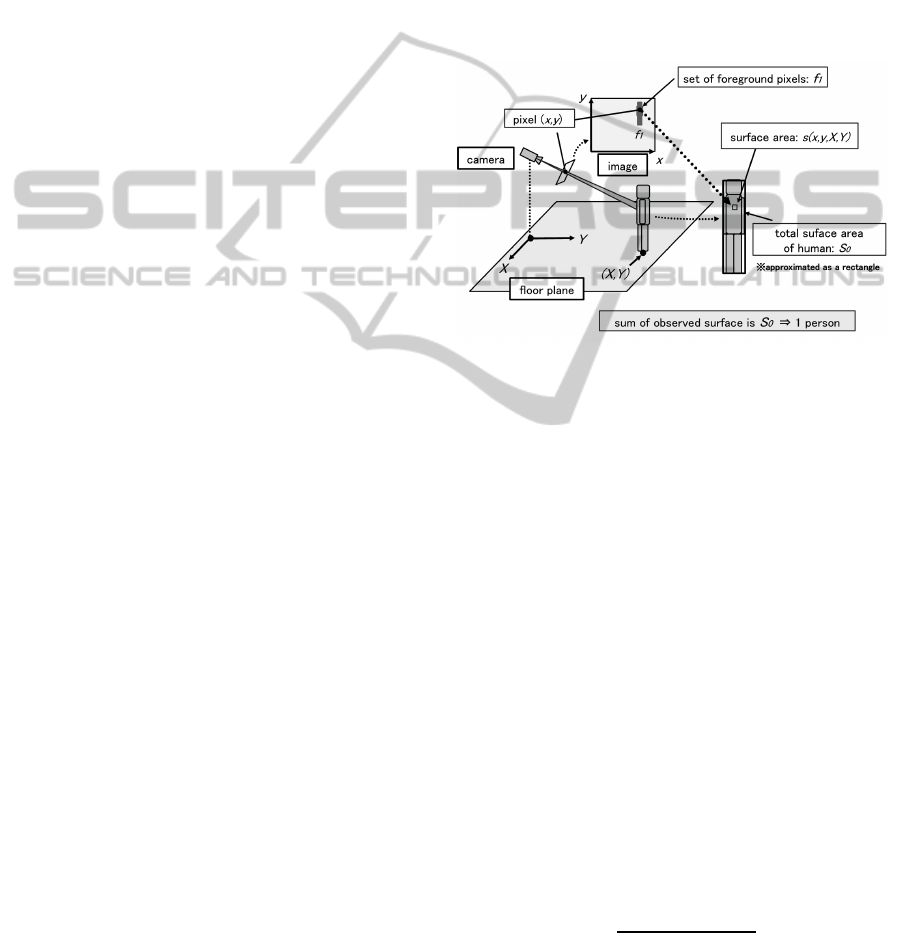
ette with known size, see Figure 1.
Figure 1: Basic idea: correspondence of pixel to partial sur-
face area of human body.
Let s(x,y,X,Y) denote the partial surface area of
the rectangle(person) standing at (X,Y) on the floor,
that corresponds to pixel(x,y), f
1
denotes the total set
of foreground pixels that correspond to the rectangle,
and S
0
represents the entire surface area of a single
rectangle silhouette in the real world; the relationship
between them can be written as follows,
∑
(x,y)∈ f
1
s(x,y, X,Y) = S
0
. (1)
s(x,y, X,Y) can be calculated by analyzing the reverse
projection of pixel (x, y) onto the rectangle standing at
(X,Y) on the floor. If the person is perfectly detected
as foreground in the image, the sum of s(x,y,X,Y)/S
0
along with the foreground pixels becomes 1, because
the sum of s(x,y,X,Y ) approaches S
0
which means
the entire surface of the rectangle in the real world.
Therefore, pixel(x,y) brings proof of s(x,y,X,Y)/S
0
for one person’s existence at (X,Y). By simple ex-
tension, the number of people N can be estimated as
follows,
N =
∑
(x,y)∈F
s(x,y, X,Y)
S
0
, (2)
here, F is the set of foreground pixels for all people in
the image, and S
0
is the surface area, in the real world
measure, of the silhouette of a single person.
SurfaceAreaAnalysisforPeopleNumberEstimation
87

2.3 Definition of Standard Surface Area
The assumption that the positions of the people (X,Y)
are known is not realistic, especially in the case
of crowded scenes. As the position of the person
changes, the corresponding surface area in the real
world changes, see Figure 2.
Figure 2: Variation in pixel correspondence to surface area
in real world.
Therefore, equation(2) cannot be applied naively.
To handle position variation, the concept of ”standard
surface area:SSA” is introduced. Pixel (x,y) can cor-
respond to any of the many positions at which a per-
son could stand, and its surface area directly depends
on the height of the projection on the human body.
SSA is defined as follows,
ˆs(x,y) = s(x,y,X
η
,Y
η
),
{X
η
,Y
η
| η = Z{(x,y),(X
η
,Y
η
)}}, (3)
here Z{(x,y),(X,Y)} is a function that calculates the
Z-position(height) of the projection of pixel (x,y) at
position (X,Y) on the floor. η is a fixed parameter,
but can be arbitrary determined within the range of
η < Tz, where T
z
is the height of the camera above the
floor. SSA: ˆs(x,y) gives a quantitative measure of the
extension of each pixel, in the real world, and plays
an important role in solving the problem of position
variation, as mentioned in the following section.
In the prior article(Arai et al., 2009), ˆs(x,y) is
defined in another way, that is, the average surface
area of the projection of pixel(x,y) from (Z = 0) to
(Z = H), here H is known height of the target object.
Details are not shown here, but the height that yields
the average surface area is the same at any pixel in an
image. Therefore, the former definition can be con-
sidered as a special case of the new definition.
Figure 3: Geometrical configuration of SSA (case η = 0).
2.4 Invariance of Sum of SSA (Case of
Upright Rectangle Model)
Here, let us consider the sum of ˆs
x,y
along with
the foreground pixels for one person similar to
equation(1). To simplify the problem, we consider the
case of η = 0 and approximate the silhouette of the
target object as a rectangle with height H and width
D, see Figure 3. Assumption (c) in 2.1 indicates that
pixel size is very small(image resolution is very high),
so the sum of ˆs(x,y) can be approximated as the fol-
lowing integration formula
∑
(x,y)∈ f
1
ˆs(x,y) =
Z Z
F
1
ˆs(x,y)dxdy. (4)
Here, the range of this integration, F
1
, is the contin-
uous region that corresponds to discrete region f
1
on
the image plane. As shown in Figure 3, considering
a rectangle standing front-on to the camera, with ver-
tical and horizontal edges (u,v), the following equa-
tion,
dudv
dxdy
= s(x,y,X,Y) (5)
is derived from the definition of s(x,y,X,Y) as a trans-
formation coefficient from image area to surface area
in the real world. By using equation(5), equation(4)
can be rewritten as follows,
∑
(x,y)∈ f
1
ˆs(x,y) =
Z Z
F
′
1
ˆs(x,y)
s(x,y, X,Y)
dudv. (6)
Here, the range of this integration F
′
1
is the entire sur-
face of the rectangle. The integrand of equation(6)
can be easily derived from the proportionality of the
cross section and height of cone, as follows,
ˆs(x,y)
s(x,y, X,Y)
=
Tz
Tz− u
2
. (7)
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
88

Therefore, equation(6) can be rewritten as follows,
∑
(x,y)∈ f
1
ˆs(x,y) =
Z Z
F
′
1
Tz
2
(T
z
− u)
2
dudv
=
Z
D
0
Z
H
0
Tz
2
(T
z
− u)
2
dudv
= S
0
(1+
T
z
H
(Tz− H)Tz
)
= S
unit
. (8)
As can be seen in equation(8), the sum of ˆs(x,y)
along with f
1
, the set of the foreground pixels of
each rectangle, does not depend on (x, y,X,Y), only
on Tz:the vertical position of camera, H:the height of
rectangle, and S
0
:the total surface area of the rectan-
gle in the real world. We denote this invariant S
unit
.
By simple analogy to equation(2), the number of
people can be estimated by using following equation,
N =
∑
(x,y)∈F
ˆs(x,y)
S
unit
, (9)
here, F is the set of foreground pixels for all people
in the image. This enables people number to be esti-
mated without knowing the position of each person.
While there are several ways to calculate ˆs(x, y)
in practice(Arai et al., 2009), we show here a simple
approach. Considering reverse projection of 4 points,
({x± 1/2},{y±1/2}),onto floor plane, s
FL
(x,y); the
cross section on floor plane can be calculated (see Fig-
ure 3). The angle between pixel (x,y) and floor plane,
α(x,y), can be easily calculated. Using these values,
the ˆs(x, y) for each pixel can be calculated as follows,
ˆs(x,y) = s
FL
(x,y) · tan[α(x,y)]. (10)
2.5 Problems of Upright Rectangle
Model
The former method, which is based on the upright
rectangle model, has two problems. One is that it can
not be applied to areas directly below the camera. On
viewing an upright rectangle directly from above, the
silhouette becomes a thin line or disappears. In such
cases, ˆs(x,y) goes to a significantly large value or to
infinity. Therefore, number estimation fails for areas
directly below the camera. The other is that the sil-
houette of target object is limited to a simple rectan-
gle. These problems reduce the measurement accu-
racy, and also narrow the application, as mentioned in
section 2.
3 SLANT SILHOUETTE
ANALYSIS
In this section, we extend the original theory and tech-
nique to be able to deal with the directly downward
case. We introduce the slant silhouette model to solve
this problem.
3.1 Basic Idea of Slant Rectangle Model
The fundamental problem of the upright rectangle
model mentioned above is that the silhouette almost
disappears with downward facing cameras(pixels).
Therefore, the geometrical model should be changed
to have non-zero area in the case of downward obser-
vation. Considering that the target is people, a cuboid
or ellipsoid body might be the first choice. How-
ever, analytical calculation of the silhouette of an el-
lipsoid body is significantly difficult with perspective
projection. Cuboids raise another problem; because a
cuboid has more than one plane, analytical calculation
will be almost impossible.
We introduce the slant rectangle model to solve
this problem. Slant rectangles, for example in Figure
4, can well approximate cuboids, in the sense of sil-
houette approximation. They have non-zero silhou-
ettes in plan and because they have only one plane,
analytical calculation is not so difficult.
Figure 4: Slant rectangle model (approximation of cuboid).
3.2 SSA of Slant Rectangle Model
Figure 5 shows the geometrical configuration of the
slant rectangle model. The rectangle is inclined back-
ward at a specific angle β. The top of the rectangle is
at height H, so the long edge has length of H/cosβ.
β should be determined to yield an area of the same
order as the target object in the case of downward ob-
servation.
In this model, SSA: ˆs(x,y) is defined as the cross
section of pixel (x,y) on the β-slant plane at floor
level(see Figure 5). Considering the ratio of s
FL
(x,y)
and ˆs(x, y) , and applying sine theorem, yields
ˆs(x,y) =
sin[α(x,y)]
cos[α(x,y) − β]
s
FL
(x,y). (11)
SurfaceAreaAnalysisforPeopleNumberEstimation
89

Figure 5: SSA for slant rectangle case.
Next, let us consider the property of SSA in this
model. The s(x,y,X,Y) is cross section of pixel (x,y)
on the slant rectangle which stands at (X,Y) on floor
plane. Suppose that this cross section is at the height
of u. A consideration of the coordinate system on the
slant rectangle (u
′
,v) , as in Figure 5, yields
ˆs(x,y)
s(x,y, X,Y)
=
Tz
T
z
− u
2
, (12)
s(x,y, X,Y) =
du
′
dv
dxdy
, (13)
u = u
′
cos(β). (14)
Considering the sum of ˆs
x,y
along with foreground
pixels of one object(person) yields
∑
(x,y)∈ f
1
ˆs(x,y) =
1
cos(β)
Z
D
0
Z
H
0
T
z
Tz− u
2
dudv
=
1
cos(β)
S
unit
. (15)
Here, S
unit
is the same as in equation(8). Therefore, in
the case of the slant rectangle model, SSA, ˆs(x,y), is
calculated by equation(11), and the estimated number
is calculated by
N =
∑
(x,y)∈F
ˆs(x,y)
S
unit
cos(β). (16)
By using the slant rectangle model, the silhouette
has a non-negligiblearea evendirectly below the cam-
era. As you can see in equation(11), SSA: ˆs(x,y) does
not diverge, because (α− β) can not reach π/2. This
model thus solves the problem of observation directly
under the camera.
In addition, if the slant angle β is 0, all equations
of the slant model devolve into those of the upright
model mentioned before.
4 EXTENSION TO ARBITRARY
SILHOUETTE SHAPES
The second problem, mentioned in Section 2, is that
the silhouette of the target object is limited to a simple
rectangle. In this section we extend the former theory
to deal with arbitrary silhouettes.
4.1 Decomposition of Silhouette
As the shape of the silhouette changes, value S
unit
, the
sum of SSA: ˆs(x,y), diverges from rectangle case. In
the first equation of equations(8),
S
unit
=
Z Z
F
′
1
Tz
2
(T
z
− u)
2
dudv, (17)
the range of integration F
′
1
can be a arbitrary silhou-
ette. However, calculating this integral in an analyti-
cal way, as in the rectangle case, is not assured for all
cases, and in many cases it is impractical. To allow ar-
bitrary silhouettes to be handled in a practical way, let
us consider a partial rectangle that floats on the floor,
see Figure 6. The integration of equation(17) can be
carried out in a way similar to that mentioned in Sec-
tion2. Thus the value of the integration for the small
rectangle j : ∆S
j
unit
becomes
∆S
j
unit
= d · Tz
2
(
1
Tz− h
2
−
1
Tz− h
1
). (18)
Assuming that the whole silhouette in the real world
is divided into J partial rectangles, the S
unit
value of
the entire silhouette can be calculated as follows,
S
unit
=
J
∑
j=1
∆S
j
unit
(19)
Using equations(18)and (19) makes it practical to cal-
culate the S
unit
of an arbitrary silhouette.
Figure 6: Partial rectangle.
4.2 Occlusion Model for Arbitrary
Silhouette
The influence of occlusion strengthens with the num-
ber of people. When occlusion occurs, the foreground
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
90

pixels become smaller than when occlusion does not
occur. This section explains how to add the influence
of occlusion into the estimation algorithm mentioned
above. The former paper(Arai et al., 2009) introduced
an occlusion model for the simple rectangle case. In
this paper the occlusion model is expanded to cover
arbitrary silhouettes.
Figure 7 is used in the explanation of occlusion.
Imagine triangle objects standing on the floor. To
model the influence of occlusion, the density of ob-
jects ρ, i.e. number of objects per unit square on the
floor plane, is considered. When pixel (x,y) is de-
tected as foreground, it indicates that ”at least one and
ρ Ω(x,y) persons are present”; here Ω(x, y) is the area
that corresponds to the set of possible positions, see
reversed shadow region in Figure 7. Let R(x,y) de-
note the redundancy of pixel(x,y) as follows,
R(x,y) = 1+ ρΩ(x,y). (20)
From assumptions (b) and (c) given in 2.1, Ω(x,y)
can be approximated as
Ω(x,y) = S
0
tanθ, (21)
here S
0
is the whole surface area of the silhouette in
the real world, and θ is the angle of pixel(x,y), see
Figure 7. If density ρ is given, and from the assump-
tion of (d): positions of objects on the floor are ran-
dom, the expectation value of observed surface area
for one object,
¯
S, becomes
¯
S ∼
S
0
¯
R
=
S
0
1+ ρ ¯qS
0
. (22)
¯
R is the expectation values of R(x,y), and ¯q is the
average value of tanθ in the region of interest(ROI).
When the ROI on the floor is given beforehand and
its area is A, the number of people can be expressed
using ρ as follows,
N = ρA. (23)
We note that the observed surface area and expec-
tation value of surface area for one person
¯
S have the
Figure 7: Geometric model of occlusion.
following relationship,
∑
(x,y)∈F
ˆs(x,y)
S
unit
=
¯
S
S
0
N. (24)
From equations (22)(23)(24),
N ∼
ν
(1−
ν ¯qS
0
A
)
ν =
∑
(x,y)∈F
ˆs(x,y)
S
unit
(25)
is derived.
The use of equation (25) permits number estima-
tion with consideration of the influence of occlusion.
5 EXPERIMENTS AND RESULTS
To confirm the validity of the proposed method, two
experiments were carried out. The first was to eval-
uate the validity of the slant rectangle model. The
second was to confirm the method of silhouette de-
composition. Both experiments used CG images gen-
erated by our simulation program.
5.1 Evaluation of Slant Rectangle
Model
To confirm the validity and effectiveness of the slant
rectangle model, an experiment was carried out us-
ing artificially generated binary images. To compare
the slant model against the upright model, SSA was
calculated for each model. Figure 8 shows examples
of SSA calculated according to the upright rectangle
model, and Figure 9 covers the slant rectangle model.
The SSA of the upright rectangle model takes huge
values at areas below the camera. On the other hand,
the SSAs of the slant rectangle model do not signifi-
cantly differ.
Cuboid images were generated to test the valid-
ity of the proposed method. In this experiment, only
one cuboid is generated, and the distance from camera
was changed incrementally changed(see Figure 10).
Figure 11 shows the result of object number estima-
tion. The horizontal axis corresponds to the lateral
offset of the camera to the object, and vertical axis in-
dicates the estimated number. The thick-dotted line
indicates the result generated by the SSA value of the
upright rectangle model as applied to the cuboid im-
ages. The thick-solid line indicates the result gener-
ated by the SSA value of the slant rectangle model.
SurfaceAreaAnalysisforPeopleNumberEstimation
91

Figure 8: Example of SSA and CG-image (upright rect.).
Figure 9: Example of SSA and CG-image (slant rect.).
Figure 10: Examples of cuboid images.
Figure 11: Estimation result (1-object case).
As can be seen, the upright model changes rapidly
as the object approaches the camera. The slant model,
on the other hand, changes little. This shows that the
slant rectangle model can be applied to the directly
downward case.
5.2 Evaluation of Silhouette
Decomposition
To confirm the validity of the silhouette decompo-
sition method, we conducted several experiments.
Three types of silhouette images were generated, see
Figure 12.
Figure 12: Examples of generated silhouettes.
Figure 13: Invariance of sum of SSA: comparison of both
theory and image processing.
Figure 13 shows the results of this experi-
ment. The horizontal axis indicates the positions
of the target objects, and vertical axis indicates
S
unit
/S
0
as given by the theoretical calculation, and
∑
(x,y)∈F
ˆs(x,y)/S
0
by summing SSA values along
with foreground pixels in generated image. As can
be seen in Figure 13, each derived value is close to its
theoretical value. The invariance of summed SSA, in
the case of arbitrary silhouette, was confirmed by this
experiment.
The second experiment was carried out to confirm
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
92
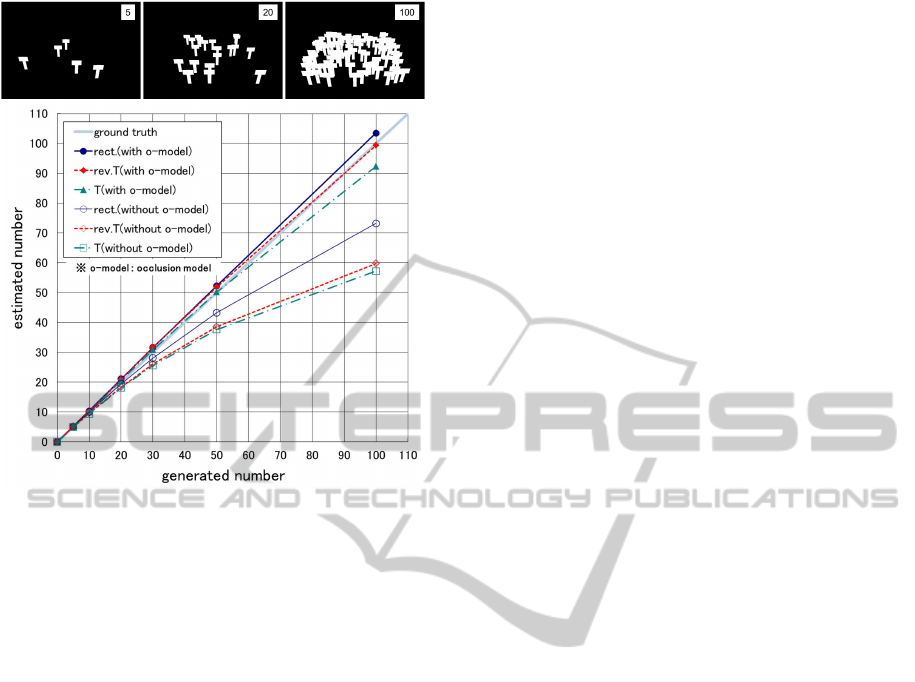
Figure 14: Estimation result in crowded situations.
the effectiveness of the proposed number estimation
algorithm for arbitrary silhouettes. Three types of sil-
houette shapes with various numbers of silhouettes
were generated, see examples in Figure 14. The hori-
zontal axis plots the actual number of silhouettes gen-
erated, and the vertical axis indicates the estimated
numbers. As can be seen, when the number of silhou-
ettes is below 20 or 30, the estimated numbers with-
out occlusion model are very close to the generated
number, the ground-truth. On the other hand, with
more than 30, the lines of estimated numbers without
occlusion model deviate from the ground-truth. Ap-
plying the occlusion model mentioned in 4.2 makes
the estimated numbers approach the ground-truth.
6 CONCLUSIONS
In this paper, we extended the basic theory of surface
area analysis by introducing two improved techniques
to better estimate the number of objects in images.
We extended the basic theory to be able to deal with
the directly downward capture case and with arbitrary
silhouettes. The slant silhouette analysis realizes re-
liable estimation even if the object is directly under a
camera. The silhouette decomposition technique ex-
tends object shape from a simple rectangle to arbitrary
silhouettes. Experiments showed the validity of the
proposed theory and the effectiveness of our crowd
estimation technique.
REFERENCES
Antonini, G. and Thiran, J. (2006). Counting pedestrians
in video sequences using trajectory clustering. IEEE
Transactions on Circuits and Systems for Video Tech-
nology, 16(issue 8):1008–1020.
Arai, H., Miyagawa, I., Koike, H., and Haseyama, M.
(2009). Estimating number of people using calibrated
monocular camera based on geometrical analysis of
surface area. IEICE Transactions, 92-A(8):1932–
1938.
Cho, S.-Y., Chow, T., and Leung, C.-T. (1999). A neural-
based crowd estimation by hybrid global learning al-
gorithm. IEEE Transactions on Systems, Man, and
Cybernetics, 29(PartB)(issue 4):535–541.
Kong, D., Gray, D., and Tao, H. (2006). A viewpoint in-
variant approach for crowd counting. Proceedings of
the 18th International Conference on Pattern Recog-
nition, 03:1187–1190.
Marana, A., Costa, L., Lotufo, R., and Velastin, S. (1998).
On the efficacy of texture analysis for crowd monitor-
ing. Proceedings of the International Symposium on
Computer Graphics, Image Processing, 6:3521–3524.
Min, L., Zhaoxiang, Z., Kaiqi, H., and Tieniu, T. (2008).
Estimating the number of people in crowded scenes
by mid based foreground segmentation and head-
shoulder detection. International Conference on Pat-
tern Recognition(ICPR 2008), pages 1–4.
Rabaud, V. and Belongie, S. (2006). Counting crowded
moving objects. Proceedings of the 2006 IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition, 1:705–711.
Sheng-Fuu Lin, J.-Y. C. and Chao, H.-X. (2001). Estima-
tion of number of people in crowded scenes using per-
spective transformation. IEEE Transactions on Man
and Cybernetics, 31(PartA)(Issue 6):645–654.
Sidla, O., Lypetskyy, Y., Brandle, N., and Seer, S. (2006).
Pedestrian detection and tracking for counting appli-
cations in crowded situations. Proceedings of the
IEEE International Conference on Video and Signal
Based Surveillance(AVSS06), pages 70–.
Wen, Q., JIA, C., Yu, Y., Chen, G., Yu, Z., and Zhou, C.
(2011). People number estimation in the crowded
scenes using texture analysis based on gabor fil-
ter. Journal of Computational Information Systems,
7:11:3754–3763.
Zhao, T., Nevatia, R., and Wu, B. (2007). Segmentation
and tracking of multiple humans in crowded environ-
ments. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 30(7):1198–1211.
SurfaceAreaAnalysisforPeopleNumberEstimation
93
