CoSMo: Intent-based Composition of Shader Modules

Georg Haaser, Harald Steinlechner, Michael May

Michael Schw

arzler, Stefan Maierhofer and Robert Tobler

VRVis Research Center, Donau-City-Strasse 1, Vienna, Austria

Keywords:

Shader, Composition, Rendering, Language, Embedded.

Abstract:

We propose a novel shader programming model which operates on intent-oriented shader modules instead

of speciﬁc programs for dedicated GPU rasterization pipeline stages. In constrast to existing pipeline shader

frameworks, our system exposes a radically simpliﬁed pipeline, which we purposefully aligned with our basic

intuition of shaders as per-primitive and per-pixel operations and compositions thereof. This simplicity lends

itself to structure modules purely based on their intent, instead of dealing with structure enforced by speciﬁc

versions of graphics APIs. Consequently, this offers great ﬂexibility when it comes to reusing and combining

modules with completely different semantics, or when targeting different graphics APIs. The simplicity and

uniformity of our system also motivates automatic parameterization and simpliﬁcation of shader programs as

well as interesting interactive shader development and management techniques.

1 INTRODUCTION

Programming shaders for hardware-accelerated ras-

terization frameworks like DirectX or OpenGL has

attained an important role in the development pro-

cess of rendering applications. Even though the

ﬂexibility and possibilities in graphics development

have drastically improved with the introduction of

these shaders over the last few years, recent advances

in “CPU-based” programming languages and soft-

ware engineering are often not reﬂected in shader-

programming. Especially the limitations in terms of

shader management in larger software projects cause

the tasks of combining shader effects, targeting dif-

ferent hardware, supporting older API versions or

optimizing these shader permutations to become ex-

tremely time-consuming, tiresome, and error-prone.

The C-style deﬁnition of a single shader stage pro-

gram is only simple during the primary creation pro-

cess: As soon as such an effect has to be combined

with other shaders to generate the desired ﬁnal surface

illumination, or has to be used on another API version

or target platform, programmers either tend to build

large, complex

Uber-Shader constructs with computa-

tionally expensive dynamic branching techniques, or

manage hundreds of shader combinations and permu-

tations manually. Object-oriented approaches (Mc-

Cool et al., 2002; Kuck and Wesche, 2009; Foley

and Hanrahan, 2011) and novel Shader Model 5 func-

tionality (e.g. interfaces (Microsoft, 2010)) ex-

tend procedural languages with abstractions like in-

terfaces and limit code duplication via inheritance. In-

heritance as mechanism for composition however has

shortcomings in terms of ad hoc compositions and re-

usability, as each composition has to be stated explic-

itly (see sections 2.1 and 2.2) and in terms of exten-

sibility, as extension points have to be anticipated by

providing abstract or virtual methods.

Based on these observations, we propose a novel

shader programming model that emphasizes the intent

of a shader, based on the following ideas:

• abstract shader stages: by freeing the shader

modules from concrete pipeline stages, we let

the programmer specify what he wants his

shader modules to do in an abstract, backend-

independent manner

• composition via semantic input/output types: with

the introduction of semantically annotated input

and output types, these types encode the intent

of what is computed by each shader module, and

thus composition operators can be built, that com-

bine the modules according to this intent

• ﬁne-tuning of semantics: by providing more de-

tailed information for the semantic types such as

computation rates, the programmer can exactly

specify the intent of his shader

Using these ideas to provide a system that au-

189

Haaser G., Steinlechner H., May M., Schwärzler M., Maierhofer S. and Tobler R..

CoSMo: Intent-based Composition of Shader Modules.

DOI: 10.5220/0004687201890199

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 189-199

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Example built with composed shader modules (from left to right): transformation and per-pixel lighting, transfor-

mation and texturing, transformation/normal mapping/texturing and lighting, transformation/normal mapping/texturing/point

sprite generation and lighting, transformation/normal mapping/texturing/point sprites/thick line generation and lighting.

tomatically combines modules based on their intent,

we overcome the combinatorial explosion of typical

shader systems where each and every combination

has to be speciﬁed explicitly: Modules are typically

expressed only in their most general form, and can

be composed either statically as hard-coded expres-

sions, or programmatically, which is useful to gener-

ate shaders based on runtime information or whole

families of related shaders. Our high-level shader-

code requires a speciﬁc functionality to be deﬁned

only once—no matter how often it is combined with

other shaders and on how many target platforms it

is deployed—while unneeded calculations are auto-

matically eliminated. We leave the error-prone task

of ﬁnding the optimal shader stage for each com-

putation to the machine, which automatically maps

shaders onto speciﬁc pipeline architectures (e.g. Di-

rectX), performs global and local optimizations and

code generation for distinct shader permutations, and

ﬁnally emits a low-level shader program (e.g. HLSL)

comparable to hand-crafted code.

2 BACKGROUND

The ancestors of today’s shading languages are

Cook’s shade trees (Cook, 1984) and Perlin’s image

synthesizer (Perlin, 1985). Cook’s shade trees clas-

sify independent aspects like lighting, surface and

volume into separate modules called shading pro-

cesses. As a mechanism for composition each process

is represented as an expression tree which supports

grafting of commonly used expressions into other

processes. However, the underlying model of compu-

tation which is purely declarative allows for no con-

ditional control ﬂow like loops as well as no mutable

state. Perlin’s image synthesizer is based on impera-

tive procedures and therefore dissolves these limita-

tions, but abandons the idea of logically independent

shading processes. Procedures work on streams of

fragments, and describe shading computations after

hidden surface removal.

The most prevalent shader languages for real-time

rendering (Cg (Mark et al., 2003), HLSL (Microsoft,

2012), and GLSL (Kessenich et al., 2012)) follow

the shader-per-stage approach. Similarly to Perlin’s

image synthesizer each stage works on streams of

objects like vertices, primitives or fragments. As a

consequence they directly reﬂect the various pipeline

stages of the hardware in the language itself. Al-

though there are little restrictions in terms of algo-

rithms that can be formulated, a corresponding shader

function must be provided for each of the stages.

2.1 Towards Composability

Shader languages like HLSL provide procedures as

their main structuring mechanism.

Uber-Shaders usu-

ally implement the sum of all desired features and use

ad-hoc mechanisms like macros and plain text pro-

cessing for specialization and feature selection.

Metaprogramming frameworks (McCool et al.,

2002; McCool and Toit, 2004; McGuire, 2005; Kuck

and Wesche, 2009) overcome the lack of language

level abstractions by utilizing meta-programming and

macros. LibSh (McCool et al., 2002) provides an em-

bedded language in C++, utilizing its features like ob-

jects and templates for combining shaders. McCool et

al. (McCool et al., 2004) extends LibSh with algebraic

combinators connection and combination which pro-

vides an expressive basis for combining shader func-

tions.

Elliot (Elliott, 2004) proposes Vertigo, an em-

bedded domain speciﬁc language written in Haskell

that provides combinators in a very natural way.

Based on these combinators, an implementation of

a sophisticated shading infrastructure comparable to

RenderMan Shading Language (RSL) (Hanrahan and

Lawson, 1990) is demonstrated, including a subse-

quent compilation process which creates vertex- and

fragment-shader programs.

Abstract shade trees (McGuire et al., 2006) are

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

190

based on a visual programming approach for shaders,

and also provide automatic linkage of shader param-

eters as well as semantic operations like vector ba-

sis conversion. Although different shader components

compose well, geometry shaders and tessellation are

not treated at all. Trapp et al. (Trapp and D

ollner,

2007) structures GLSL shader code into code frag-

ments, each typed with predeﬁned semantics. Code

fragments may be composed at run-time and com-

piled to

Uber-Shaders. Of course

Uber-Shaders suffer

from bad performance. Like other metaprogramming

approaches the system cannot provide proper seman-

tic analysis and cross-fragment optimization.

2.2 Towards Pipeline Shaders

The RenderMan Shading Language by Hanrahan and

Lawson (Hanrahan and Lawson, 1990) combines the

expressiveness of Perlin’s image synthesizer with in-

dependent shader processes introduced by Cook. The

concept resembles object-oriented classes, whereby

each virtual method corresponds to an entry point

called by the render system. Subclasses like surface,

light and volume may be attached to surfaces. Fur-

thermore RSL extends the concept with computation

rates, i.e. the notion of inputs varying two different

rates: uniform and varying. Specialized control-

ﬂow constructs provide mechanisms for communica-

tion between shaders.

A further reﬁnement for computation rates was

introduced by Proudfoot et al. (Proudfoot et al.,

2001) in their Stanford Real-Time Shading Language

(RTSL): constant, primitive group, vertex and

fragment, where the last two rates directly corre-

sponded to the stages of early programmable GPUs.

Like Cook’s shade trees (Cook, 1984), RTSL pro-

grams are purely declarative and can therefore be rep-

resented as DAGs, which affects expressiveness (e.g.

limited data dependent control ﬂow).

Renaissance (Austin, 2005) takes a more gen-

eral approach and represents different shader pipeline

stages as single functional shader programs. Parame-

ters implicitly correspond to different computations

rates. Compilation automatically lifts expressions

into the earliest possible pipeline stage while main-

taining semantics. However, Renaissance lacks sup-

port for structuring monolithic shader programs into

well deﬁned reusable modules, and no semantics for

lifting expressions to groupwise shader stages (e.g.

geometry shaders) are presented.

Foley and Hanrahan introduce Spark (Foley and

Hanrahan, 2011), a pipeline shader approach based

on RTSL (Proudfoot et al., 2001). Its two-layer ap-

proach uses declarative shader graphs on top of pro-

cedural subroutines and therefore combines the ap-

proaches of Cook (Cook, 1984) and Perlin (Perlin,

1985). Spark expands RSL’s idea of treating a shader

in an object-oriented way by using extending, virtual-,

and abstract identiﬁers for compositing and customiz-

ing shaders. Rate-qualiﬁers and conversions between

different rates are extensible and thus deﬁned individ-

ually by each supported pipeline. Different modules

may be composed by using mixin inheritance. Like

other

Uber-Shader approaches before, Spark does not

solve the combinatorial explosion problem because

each composition must be stated explicitly.

3 DESIGN

3.1 A Shader as a Pixel-valued Function

Shader programming targets a highly parallel execu-

tion environment, where shading can be performed

independently for each surface point, therefore func-

tional programming is a natural match for specifying

shaders (Cook, 1984). Although parts of a shader can

be programmed in procedural style using local vari-

ables and loops, a complete shader program only has

a single output value—the target pixel—and can thus

be viewed as a single function. By using tail recur-

sion instead of loops, and higher-order functions for

control-ﬂow it is even possible to map any procedural

shader program to a purely functional representation.

Rennaissance (Austin, 2005) is an example of such a

functional approach to shader programming.

Since the output value of a shader expression for

a single pixel can be an aggregate of multiple simple

values (e.g. it can contain a colour, a depth value,

etc.), we use the term shader module to denote a

shader function with multiple input and output values.

Multiple output values are programmatically handled

by returning a single structure containing the individ-

ual output values.

Although our approach is based on the compo-

sition of such shader modules, and thus retains the

expressiveness and extensibility of a functional de-

sign (which goes beyond what is possible with the

specialised control ﬂow elements introduced in RSL

(Hanrahan and Lawson, 1990)), we have included

control ﬂow functions that are modelled on impera-

tive languages in order to cater to shader programmers

that are used to imperative shader languages. Details

on these control ﬂow functions are given in Section 4.

CoSMo:Intent-basedCompositionofShaderModules

191

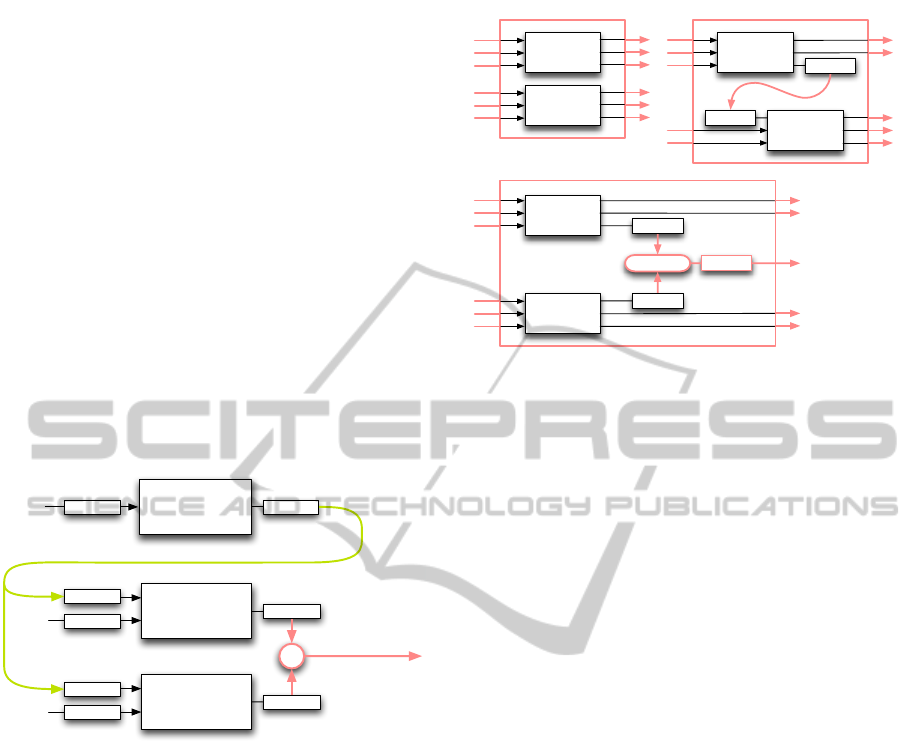
3.2 Semantic Composition of Shader

Modules

Combining shaders modules that are formulated as

expressions can be done in a pipeline approach, by

routing the output of one component into the input of

another component. In order to derive the necessary

composition functions for combining shader mod-

ules we will look at a simple example that combines

three shader modules with two composition operators,

namely Sequence and Combine(operator) that are ap-

plied to the individual output ﬁelds (see Figure 2).

Note, that the different composition operators need to

be applied to different types of input and output (Nor-

mal, Color, LightPos). We use the term semantic for

these types, as they go beyond the typical notion of

data types in a language: both Normal and LightPos

are represented as ﬂoat vectors, but this does not cap-

ture their intent.

Diﬀuse

Illumina,on

Shader2Module

Bump6Map

Shader2Module

Specular

Illumina,on

Shader2Module

Normal

LightPos

Normal

Color

Normal

LightPos

Color

Sequence

Combine

Figure 2: The output values of three simple shaders can be

combined with two composition operators: Sequence and

Combine(operator +).

Generalizing from this example, we deﬁne the fol-

lowing three basic composition operators for semantic

shader composition, that operate on arbitrary shader

modules each with one or more semantic input types

and one or more semantic output types (see Figure 3):

Compose(module

, module

) composes the output

of the two shader modules. All output semantics

of the two input shader modules must be different.

Sequence(module

, module

, {semantic

, ..., semantic

})

combines the speciﬁed semantics of the supplied

shader modules in sequence. The remaining

output semantics of the two input shaders must

be different.

Combine(module

, module

, semantic, operator)

applies the supplied binary operator to the output

of the two input shaders with the given semantic

to return a value of the same semantic. The

shader

module

₂

seman-c

shader

module

₁

seman-c

shader

module

₂

seman-c

operator

Compose

Combine

Sequence

seman-c

shader

module

₁

seman-c

shader

module

₁

shader

module

₂

Figure 3: The three semantic-aware basic composition op-

erators for shader composition. For illustration purposes,

the Sequence function is depicted with only one semantic

routed between its shader module arguments.

remaining output semantics of the two input

shader modules must be different.

For all composition operators, the input semantics

of the two input shader modules are allowed to be ei-

ther partially or completely equal. In this case, the

same value is supplied to both shaders. These basic

composition operators add the concept of semantic-

speciﬁc operations to the usual composition functions

used in functional languages. On top of these basic

composition operators we can now deﬁne a more gen-

eral composition function that sequences, combines,

and composes multiple shader modules based on their

semantic:

Composition(module

, module

, . . . module

semantic

: composition

semantic

: composition

de f ault : composition

de f ault

)

where a separate composition operator (either

Sequence or Combine(operator)) is speciﬁed to com-

bine each semantic and Compose is wrapped around

the result.

We provide a number of convenience composi-

tions in our approach, that are specializations of this

general composition function with various predeﬁned

function and operator arguments. For convenience we

also predeﬁne simple shaders for changing semantics

(e.g. Position → Color). An example composition

can be found in Section 5.

Our approach of automatically combining shaders

based on their semantically tagged inputs and out-

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

192

puts is inherently more ﬂexible than a static object-

oriented approach as implemented by Spark (Foley

and Hanrahan, 2011):

• The object-oriented way of extending functional-

ity by overriding virtual functions requires, that

each possible extension point needs to be foreseen

by the implementer of the base shaders. Since

only a limited number of possible ways of extend-

ing functionality can be provided in a typical de-

sign of such base shaders, the extensibility of such

an object-oriented approach is necessarily limited.

• Due to the static way of combining and extending

shaders, each and every new combination of sim-

ple shader functions must be explicitly and man-

ually implemented. Since the number of com-

binations of simple shaders is exponential in the

number of shaders, this leads to a combinatorial

explosion that cannot be handled by a static ap-

proach. The use of a composition function as

shown above, makes it possible to automatically

combine simple shaders based on the geometry

that needs to be rendered: the rendering frame-

work can analyse the properties of the geometry,

and combine only the simple shaders that are ac-

tually needed for rendering the combination of

properties encountered.

All composition possibilities offered by a static

object-oriented approach can be easily built using a

sub-set of the available functionality in our meta-

function approach:

• Each virtual method corresponds to a semantic

tag: different simple shaders can perform differ-

ent operations on the input with the same seman-

tic tag. Changing the implementation of one vir-

tual method thus corresponds to replacing one of

the simple shaders in a composition of multiple

shaders.

• The effect inheritance in the object-oriented ap-

proach can be realised using the combine com-

position operator on two simple shaders that cor-

respond to the base-class implementation and the

overriding implementation. By using a function

that ignores the result of the simple shader corre-

sponding to the base-class the result of the combi-

nation corresponds to the result of the overriding

simple shader.

Thus our approach provides a superset of the func-

tionality provided by the object-oriented approach,

and the additional functionality eliminates the large

number of shader combinations that have to be man-

ually speciﬁed.

3.3 Abstract Stages

The various stages in the shader pipeline can be

viewed as optimizations on the single pixel-value

function, in order to reduce the number of evaluations

of various expressions (for an example see Figure 4).

per$pixel$opera*ons

ViewTrafo

LightPos Posi1on

Normalize

(ViewTrafo88)

Normal

Normalize

DotProductDiﬀuseColor

–

Interpola*on

-1

per$primi*ve$opera*ons

Figure 4: Optimizing the evaluation of a shader expression

by evaluating the parts at different stages. The indicated in-

terpolation functionality is provided by the hardware stages.

Although in principle, every shader could be for-

mulated as a single function that returns a pixel value,

this would require the implicit interpolation that is

performed between the vertex and fragment stages

of the shader pipeline (see Figure 4) to be explic-

itly speciﬁed in this function. In order to overcome

this inconvenience, we propose to retain the notion

of shader stages, but as opposed to the multiple hard-

ware stages we only specify two abstract stages, that

turn out to be sufﬁcient in practice :

per-pixel operations :

also called per-fragment operations, these are all

the operations that need to be performed for each

pixel or fragment. Typically this includes all tra-

ditional shading operations that affect the material

of an object. In functional notation, these opera-

tions perform the mapping: per pixel parameters

→ per pixel output.

per-primitive operations :

all operations performed for each primitive (e.g.

triangle or line). This typically encompasses ge-

ometric transformations. In functional notation,

these operations perform the following mapping:

per primitive parameters → per primitive output.

Thus all the simple shaders that can be composed

in our framework consist of explicitly speciﬁed per-

pixel and/or per-primitive operations, and thus each

of our simple shaders can be viewed as either a partial

CoSMo:Intent-basedCompositionofShaderModules

193

or a fully speciﬁed, but still abstract pipeline of oper-

ations (see Figure 5). Since we do not explicitly spec-

ify operations for a speciﬁc hardware pipeline, all our

shaders are still speciﬁed in an abstract manner, and

need to be explicitly mapped onto the hardware stages

of a concrete pipeline.

This has some consequences for the composition

operators deﬁned in the previous section: speciﬁcally,

a per-pixel output of a shader module cannot serve

as an input for a per-primitive shader module. If

each shader module that consisted of a per-geometry

stage and a per-pixel stage was viewed as a monolithic

block with no allowed change in the routing of data

between the per-geometry and the per-pixel stage, this

would lead to signiﬁcant limitations on which shader-

modules could be combined.

In order to avoid that, we combine the stages of

our shader modules individually, i.e. the composition

works independently on the per-primitive stage and

on the per-pixel stage. This makes it possible to com-

bine shader modules as simply as if they were single

stage modules, and retain the intended functionality

programmed in the different stages. The semantically

tagged inputs and output of the individual stages are

available for automatic composition with other shader

modules (see Figure 5).

Thus we extend our concept of shader modules

to encompass whole shader pipelines, on which our

composition operators work, retaining the semantic

input and output types between the abstract stages,

which is beyond the functionality of the algebraic

combinators of McCool et al. (McCool et al., 2004).

3.4 Optimization

ıvely mapping such high-level shaders onto the

hardware stages of a concrete pipeline such as the Di-

rectX 11 pipeline results in a lot of overhead due to

a number of possible inefﬁciencies. In order to pro-

vide comparable performance in our system, we per-

form several optimisations highlighted in the follow-

ing section.

Dead code elimination. Since our modules are pro-

grammed to be maximally reusable, they are imple-

mented to cover the most general case, and thus pro-

vide a large number of semantic outputs which can be

used by other modules that are placed later in a com-

position. Thus it is of vital importance for the overall

performance to identify all unused outputs, and elim-

inate these from the composition result: this is done

by starting with all used pixel outputs and tracking all

necessary inputs back through the pipeline. All un-

used inputs and outputs are removed, essentially per-

forming a dead code elimination step.

Backend stage mapping. A typical hardware shader

pipeline has a number of stages that can be used

to perform the operations in our pipelined shaders.

Based on the abstract stage, the following optimisa-

tion steps are performed:

per-primitive operations :

Since the current (DirectX 11) backend basi-

cally offers three stages for geometry processing

(vertex shader, tesselation shader, and geometry

shader) with different capabilities and associated

computation rates our composed modules need to

be mapped onto these efﬁciently. Since the com-

putation rates for these hardware-stages are gen-

erally unknown (we don’t know what our inputs

will look like) we decided to move all operations

to the earliest stage possible, with the underlying

assumption, that each operation is thus performed

at the lowest rate. It is, for example, possible

to move geometry shader operations, which are

equally performed for all vertices, to the vertex

shader. Similar rules can be derived for the other

hardware-stages, an overview of these rules can

be found in Section 4. A number of additional

limitations (due to hardware capabilities) are in-

troduced, e.g, the tessellation-shader needs to be

done prior to a geometry-shader, etc.

per-pixel operations :

pixel or fragment-shaders are divided into two

parts: the ﬁrst part represents calculations invari-

ant respective to rasterizer-interpolation, which

can therefore be performed per primitive (in gen-

eral the faster solution). The second part con-

sists of all operations that can only be performed

in a pixel shader. This splitting may cause addi-

tional trafﬁc for the rasterizer-interpolation since

this may need e.g. the interpolation of a vector

instead of a scalar. Since these costs are hard to

estimate we move only operations where the in-

terpolated type does not exceed the result type in

size.

Shader module specialization. Since a single gener-

ated shader module might still cover a number of dif-

ferent input-setups (textured vs. non-textured, etc.)

using shader-control-ﬂow we provide methods for

simply specialising a shader module using contextual

information (e.g. there are no textures available, etc.)

The shader modules are then partially evaluated using

this information and recompiled for the backend. If,

for example, a geometry does not contain normals the

corresponding shader modules are optimised to elim-

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

194

ViewTrafo

LightPos

GlobalPrimi4veNormal

GlobalPrimi4vePosi4on

DiﬀusePixelColor

LocalPixelLightDir

LocalPixelNormal

PixelColor

LocalPrimi4ve

LightDir

LocalPrimi4ve

Normal

per$primi've

opera'ons

per$pixel

opera'ons

Inter&

pola+on

Inter&

pola+on

Figure 5: A simple shader module consists of explicitly speciﬁed per-primitive and per-pixel operations each with their

semantic inputs and outputs. This shows the example from ﬁgure 4 tagged with semantic inputs and outputs.

inate any code that accesses normals of the geometry,

thereby improving rendering performance.

Shader module uniﬁcation. Since shaders are compo-

sitions of abstract modules it’s relatively easy to ﬁnd

common operations for them using the high level in-

formation provided by the composition operators. If

the rendering performance can be improved by reduc-

ing switches between shaders, two shader modules

can be uniﬁed using simple control ﬂow, adding a pa-

rameter to select the shader module as an additional

input to the combined shader module.

Common subexpression elimination. Although com-

mon subexpression elimination results in optimal

code respective to the number of operations, ad-

ditional temporary variables stressing the HLSL-

compiler need to be introduced. In optimizing

compilers, sophisticated analysis carefully choose

subexpressions to be considered for code motion

(e.g. (Knoop et al., 1992)) in order to limit tempo-

raries. Our system in contrast heuristically elimi-

nates expressions exceeding a syntactic complexity

threshold. These complexities are based on estimated

complexities for all intrinsic functions which are sim-

ply summed for each expression. With this simple

scheme the HLSL-compiler does a good job in opti-

mizing shaders while maintaining good compile-time

performance.

Constant/Uniform-calculations. All computations re-

sulting in a constant value (for each draw call) can

be pre-calculated by the rendering system. Since a

brute force approach would result in a large number

of uniform-parameters only calculations exceeding a

certain complexity (as mentioned above) are consid-

ered.

Arithmetic optimizations. Since there are only very

few restrictions on how to compose shaders (i.e. out-

puts and inputs must match), it is possible to in-

troduce unnecessary calculations through these com-

positions (e.g. normalize(normalize(vector)),

(a − a), etc.). Similarly to tree parsers (Fraser

et al., 1992), used for instruction selection in code

generators our optimizer maintains a set of expres-

sion patterns with associated rewrite rules and some

estimated cost. Notably, our system also consid-

ers domain-speciﬁc knowledge as a variables vector-

basis for further optimization. As an example,

ViewMatrix*ModelMatrix is transformed to use the

uniform ModelViewMatrix in order to eliminate ex-

pensive matrix multiplications.

User guided simpliﬁcation. Additional contextual in-

formation can be speciﬁed for shader inputs values.

As an example, the user may annotate the vertex col-

ors to be constant or the normals to be constant per

face.

Using these annotations the backend stage map-

ping can perform further optimisations by moving op-

erations to earlier stages. Together with redundancy

removal, dead code elimination, and constant/uniform

calculations this can lead to signiﬁcantly simpliﬁed

shaders. As an example, it is unnecessary to interpo-

late face normals in a shader, when the normals are

known to be constant per primitive.

Further optimization possibilities. Our abstract

pipeline representation is general enough to support

completely different approaches like perceptual sim-

pliﬁcation methods (Sitthi-Amorn et al., 2011), or

automatic approaches exploiting temporal coherence

(Sitthi-Amorn et al., 2008), which we will pursue in

the future.

4 IMPLEMENTATION

Our shading language is implemented as an extension

of an existing in-house rendering framework written

in C#. Of course it is possible to implement our ex-

pression tree based approach with any language that

provides abstract data types, the use of anonymous

functions signiﬁcantly reduces the syntactic overhead.

A C++ 11 implementation would be equivalent to

our approach, while a Java implementation would use

anonymous classes instead of anonymous functions.

The expression trees in our approach are created

and combined using so called shader types, which

represent predeﬁned data types available to shaders

(e.g. vectors, matrices, textures, aso.). Each shader

CoSMo:Intent-basedCompositionofShaderModules

195

Figure 6: Shader effects composed with our approach. From left to right: raytraced reﬂections with simple texturing, a

composition of an illumination and shadow mapping shader, and a subsivision shader (all from section 5), as well as a screen-

shot from our lighting design application (see Section 6.1) demonstrating texturing and reﬂective materials with environment

mapping.

type provides methods (e.g. the operators + and – or

the dot product) that do not actually perform opera-

tions, but build an expression tree for the correspond-

ing operations. Thus each expression that speciﬁes a

shader module, returns the complete expression tree

for that shader module upon execution.

Due to the ﬂexibility of our functional-style imple-

mentation we are not limited to predeﬁned control

ﬂow statements such as the RenderMan Shading Lan-

guage (RSL) (Hanrahan and Lawson, 1990) : we pro-

vide higher-order functions that encapsulate condi-

tional evaluation and loops. This makes it possible to

integrate conditions and loops into expression trees in

typical implementation languages of rendering frame-

works, even if it is not possible to overload intrinsic

language constructs such as the conditional evaluation

operator condition ? value

: value

and the for loop

for shader types:

var floatVal = Fun.IfThenElse<Float>(c < 1.0f, c, 1.0f);

var initial = new { Index = Int.Zero, Val = Float.Zero };

var diffuse = Fun.Loop(initial, i => i.Index < lightCount,

i => {

var dir = light[i.Index] - worldPosition.XYZ;

return new { Index = i.Index + 1,

Val = i.Val + normal.Dot(dir.Normalized) };

});

Figure 7: Example usage of higher-order functions for

loops and conditional execution.

As mentioned in Section 3.4, the evaluation of each

expression is moved to the earliest possible stage in

any given hardware pipeline. In the following list

we give the conditions for performing the indicated

optimizations:

PixelShader → GeometryShader : An expression

can be moved, if it comprises a linear function.

Note that functions can be linear under speciﬁc

circumstances, e.g. if one function argument is a

constant.

GeometryShader → DomainShader/VertexShader

: If the same function is applied to all vertex-

dependent inputs (i.e. it appears for each of

the vertices), the function-expression with its

arguments can be moved.

DomainShader → HullShader : If an expression

does not contain the tessellation coordinate (i.e.

the domain location) it can be moved.

DomainShader → HullShaderConstantFunction

Similar to DomainShader → HullShader.

HullShader → VertexShader : Identical pre-

conditions to GeometryShader → VertexShader

stage.

Although we focussed on the Rules for DirectX 11

and OpenGL 4 we also implemented an experimen-

tal backend for our OpenCL based raytracer, which

only supports one shader-stage computing the color

for a primitive at a certain coordinate. Due to our ab-

stract stage interpretation the modules could easily be

mapped onto this stage when possible (features like

tessellation are currently not supported by the ray-

tracer)

The ﬁrst step of the compilation process is the cre-

ation of a single pipeline for the completely combined

shader modules. This abstract pipeline is then pro-

cessed using the optimisation stages shown in Section

3.4. The output of the optimisation process is a com-

plete hardware shader in the shading language of the

backend: in our case a complete HLSL shader for the

DirectX 11 backend.

5 EXAMPLES

In order to demonstrate the applicability of our ap-

proach to common techniques, we provide code ex-

cerpts for per-pixel lighting, shadow mapping and

subdivision (see Figure 6). Furthermore, we demon-

strate the interactive capabilities of our system in the

accompanying video.

The following example shows the full implemen-

tation of a basic transformation pipeline with per-

pixel lighting. Note that user-deﬁned parameters are

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

196

communicated by name (e.g. "LightPosition"),

and vertices of primitives supplied to the primi-

tive shader can be accessed using iterators (e.g.

.DoByVertex). We also provide swizzle operators

(e.g. .XYZ) including constants (letter O is zero, letter

I is one) for all vector types.

public class PerPixelLighting : Module {

public class Vertex {

public Float4 Position = Varying.Position;

public Float3 Normal = Varying.Normal;

public Float4 WorldPosition = Varying.WorldPosition;

public Float4 Color = Varying.Color;

}

public class Pixel {

public Float4 Color = Varying.Color;

public Pixel(Float3 color, Float alpha = 1) {

Color = new Float4(color, alpha);

}

public Fragment<Pixel> Shader(AnyPrimitive<Vertex> input) {

var transformed = input.DoByVertex(v => {

v.Position = Uniform.ModelViewProjTrafo * v.Position;

v.Normal = Uniform.NormalTrafo * v.Normal;

v.WorldPosition = Uniform.ModelTrafo * v.Position;

return v;

});

return transformed.Rasterize(f => {

var dir = (Uniform.LightPositions[0]

- f.WorldPosition).XYZ.Normalized;

return new Pixel(dir.Dot(f.Normal.Normalized) * f.Color.XYZ,

f.Color.W);

});

}

Figure 8: Vertex transformation and per pixel lighting ex-

ample.

Geometry vertex colors are automatically bound

to the Varying.Color input if needed.

Here we demonstrate the composability of mod-

ules by combining per-pixel lighting from Figure 8

with a simple shadow mapping module.

public class ShadowMapping : Module {

public Float4x4 ShadowMapTrafo;

public Texture2D ShadowMap;

private Float3 GetShadowTexCoord(Float4 worldPos) {

var p = ShadowMapTrafo * worldPos; var pp = p.XYZ / p.W;

var tc = new Float3((Float2.II + pp.XY) * 0.5f, pp.Z);

tc.Y = 1 - tc.Y; return tc;

}

public Fragment<Pixel> Shader(AnyPrimitive<Vertex> input) {

return input.Rasterize(f => {

var mytc = GetShadowTexCoord(f.WorldPosition);

var smValue = ShadowMap.SampleCmp(mytc.XY, mytc.Z);

return new Pixel(f.Color.XYZ * smValue, f.Color.W);

});

}}

Figure 9: Shadow-mapping example.

Both modules can be simply composed in the fol-

lowing way:

...

var sg = ... // some scene graph node

var shadowMapping = new ShadowMapping();

var surface = Composition.Sequence.Compose(new PerPixelLighting(),

shadowMapping);

shadowSurface.ShadowMap = renderTarget.DepthTexture;

shadowSurface.ShadowMapTrafo = ... // the transformation value

sg = sg.Surface(surface);

...

Figure 10: Composition of lighting and shadow mapping.

The code shown in Figure 10 assigns values to

module inputs by implicitly creating uniform inputs

in the backend code and setting their values using

the renderer infrastructure. These values can thus be

changed at runtime.

public Float GetFactor(Float4 p0, Float4 p1) {

var len = (p1.XYZ - p0.XYZ).Length;

return Float.Clamp(len / MaxLineLength, 1, 64);

}

public Triangle<Vertex> Shader(Triangle<Vertex> input) {

return input.DoByPrimitive( tri => {

var f0 = GetFactor(tri.P1.Position, tri.P2.Position);

var f1 = GetFactor(tri.P2.Position, tri.P0.Position);

var f2 = GetFactor(tri.P0.Position, tri.P1.Position);

var factors = new TessellationFactors();

// tessellation is defined as in OpenGL 4/DirectX 11

factors.EdgeFactors = new[] { f0, f1, f2 };

factors.InnerFactors[0] = (f0 + f1 + f2) / 3.0f;

return factors;

(tri, constant, crd) => return new Vertex() {

Position = Float4.Lerp(

tri.P0.Position, tri.P1.Position, tri.P2.Position,

crd)

});

}

Figure 11: Simple tessellation example.

Figure 11 shows a simple subdivision operation

mapped to the DirectX 11 tessellation stages. The ﬁrst

anonymous function which calculates the tessellation

factors can return any custom type inheriting from

TessellationFactors. The constant argument in

the interpolation function then refers to that type. Al-

though it would theoretically be possible to create ar-

bitrary output triangles for a given input patch using

the DirectX/OpenGl tessellation stages we decided

to expose the functionality as provided by our main

backend. The ﬁrst lambda function basically corre-

sponds to the Hull-/TessellationControl-Shader and

the second to the Domain-/TessellationEvaluation-

Shader.

6 ANALYSIS

6.1 A Real-world Comparison

We evaluated our concept by re-implementing all

shaders used in a production-quality real-world appli-

cation for lighting design: it uses shaders for comput-

ing global illumination, for drawing lines and points

CoSMo:Intent-basedCompositionofShaderModules

197

in debugging and editing views, and for rendering a

number of different materials with diffuse, and spec-

ular components and environment maps for realistic

looking reﬂections. The complexity of shaders ranges

from simple ﬂat-shading all the way to a global-

illumination shader that needs to perform polygon

clipping for each rendered pixel (see Figure 6 as well

as the demonstration in the accompanying video).

The following table gives an overview of the number

of shader modules and the lines of code for the same

functionality using standard HLSL and our composed

shader modules (CoSMo).

Table 1: Code metrics for a real-world lighting design ap-

plication.

lines # modules compile time

HLSL 2324 37 7.5s

CoSMo 1148 20 11.8s

We were able to roughly halve the number of

code-lines as well as the number of modules, while

maintaining comparable shader-compile-times and

shader performance. Due to the high level of reuse

enabled by our shader modules, the shader modules

implemented for this application are a lot less speciﬁc,

and can therefore be reused in a number of future ap-

plications.

6.2 Performance

We evaluated CoSMo performance using three sam-

ple shaders:

skinning: renders two animated simple meshes repli-

cated 50 times without hardware instancing with

standard skinning and diffuse lighting, where

skinning is performed with a maximum of four

bone inﬂuences per vertex.

tesselation: subdivides all 871414 triangles of the

Stanford dragon to 1-pixel-sized triangles using

simple interpolation of positions, normals and

light direction, and applies diffuse lighting.

shadow mapping: renders a shadow mapped Stan-

dard dragon using a pre-calculated shadow map.

A 9x9 Gaussian ﬁlter implemented in the pixel

shader is used to blur the shadow.

All our tests were performed on an Intel(R)

Core(TM) i7 CPU 930 @ 2.80 GHz system with 12

GB of RAM and a GeForce GTX 480 graphics card.

In our ﬁrst evaluation (see Table 2) we compared

the ﬁnal rendering speed of manually coded shaders

with CoSMo-generated shaders. We found that in

most cases CoSMo produced equally fast or faster

shader code. We rely on the aggressive optimizations

in the compiler backend (HLSL or GLSL) to over-

come some of the deﬁciencies in our code genera-

tor. The tessellation example was slightly faster since

some calculations performed in the DomainShader

were automatically moved to the vertex shader.

Table 2: Performance results in frames per second (fps)

comparing CoSMo generated shaders with manually coded

shaders.

shader manual CoSMo factor

skinning 35 fps 35 fps 1.00

tesselation 178 fps 189 fps 1.06

shadow-mapping 209 fps 209 fps 1.00

Our second evaluation (see Table 3) shows the

compile times for manually coded shaders compared

to the sum of code generation and compile times for

CoSMo shaders. The additional generation of HLSL

from CoSMo code results in compile-times that are

less than 2 times longer for the given examples, an ac-

ceptable overhead given the increased ﬂexibility and

reusability.

Table 3: Compile times in milliseconds (ms) of manually

written HLSL code and CoSMo code. The CoSMo com-

pile times are given as the sum of generation of HLSL from

CoSMo and the HLSL compile time.

shader manual CoSMo factor

skinning 140 ms 217 ms (78+139) 1.54

tessellation 46 ms 81 ms (33+48) 1.77

shadow-map 85 ms 110 ms (24+86) 1.30

7 CONCLUSIONS AND FUTURE

WORK

We have demonstrated a powerful framework for

combining simple shader modules into complex

shaders, by providing semantic composition of mod-

ules, an abstract model of two shader stages and a

powerful optimizing backend for mapping this pro-

gramming model onto existing hardware pipelines.

With only moderate increase in shader compilation

time, this results in a signiﬁcant reduction of code

while retaining the execution performance of hand-

coded shaders. Shader composition is performed fast

enough for interactively combining shaders, allowing

rapid shader development in an explorative manner.

Due to the high reusability of the shader modules of

our new approach, we have already started to build a

comprehensive library of modules that can be freely

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

198

combined and provide a framework for rapid devel-

opment of rendering applications that minimises the

necessity of writing shader modules.

However, our current treatment of tessellation

modules does not cover all possible composition sce-

narios and only provides for a single tessellation

stage. Thus we cannot handle the sequential com-

position of tessellation modules. We are currently

working on more ﬂexible techniques for specifying

and composing tessellation modules, in order to lift

this restriction on our semantically speciﬁed shaders.

In a number of use cases such as volume rendering

and global illumination, we found that using a pure

expression based language—although possible—can

be somewhat inconvenient, since it requires a com-

plete reformulation of some algorithms that can be

easily expressed in procedural languages. We there-

fore plan to add support for imperative shader frag-

ments while maintaining composability.

ACKNOWLEDGEMENTS

We would like to thank Manuel Wieser for providing

3D models, especially Eigi, The Dinosaur. The com-

petence center VRVis is funded by BMVIT, BMWFJ,

and City of Vienna (ZIT) within the scope of COMET

Competence Centers for Excellent Technologies. The

program COMET is managed by FFG.

REFERENCES

Austin, C. A. (2005). Renaissance: A Functional Shad-

ing Language. Master’s thesis, Iowa State University,

Ames, Iowa, USA.

Cook, R. L. (1984). Shade Trees. SIGGRAPH Comp.

Graph., 18(3):223–231.

Elliott, C. (2004). Programming Graphics Processors Func-

tionally. In Proc. of the 2004 ACM SIGPLAN work-

shop on Haskell, Haskell ’04, pages 45–56, New York,

NY, USA. ACM.

Foley, T. and Hanrahan, P. (2011). Spark: Modular, Com-

posable Shaders for Graphics Hardware. ACM Trans-

actions on Graphics, 30(4):107:1–107:12.

Fraser, C. W., Henry, R. R., and Proebsting, T. A. (1992).

BURG: fast optimal instruction selection and tree

parsing. SIGPLAN Not., 27(4):68–76.

Hanrahan, P. and Lawson, J. (1990). A Language for Shad-

ing and Lighting Calculations. SIGGRAPH Comput.

Graph., 24(4):289–298.

Kessenich, J., Baldwin, D., and Rost, R. (2012). OpenGL

Shading Language, version 4.3. Available from:

http://www.opengl.org/documentation/glsl/ (accessed

23 October 2012).

Knoop, J., R

uthing, O., and Steffen, B. (1992). Lazy code

motion. SIGPLAN Not., 27(7):224–234.

Kuck, R. and Wesche, G. (2009). A Framework for Object-

Oriented Shader Design. In Proc. of the 5th Interna-

tional Symposium on Advances in Visual Computing:

Part I, ISVC ’09, pages 1019–1030, Berlin, Heidel-

berg. Springer-Verlag.

Mark, W. R., Glanville, R. S., Akeley, K., and Kilgard,

M. J. (2003). Cg: a system for programming graphics

hardware in a C-like language. ACM Trans. Graph.,

22(3):896–907.

McCool, M., Du Toit, S., Popa, T., Chan, B., and Moule, K.

(2004). Shader Algebra. In ACM SIGGRAPH 2004

Papers, SIGGRAPH ’04, pages 787–795, New York,

NY, USA. ACM.

McCool, M. D., Qin, Z., and Popa, T. S. (2002). Shader

Metaprogramming. In Proc. of the ACM SIG-

GRAPH/EUROGRAPHICS conf. on Graph. Hard-

ware, HWWS ’02, pages 57–68, Aire-la-Ville,

Switzerland. Eurograph. Assoc.

McCool, M. D. and Toit, S. D. (2004). Metaprogramming

GPUs with Sh. A K Peters.

McGuire, M. (2005). The SuperShader. Shader X4: Ad-

vanced Rendering Techniques, chapter 8.1, pages

485–498. Cengage Learning Emea.

McGuire, M., Stathis, G., Pﬁster, H., and Krishnamurthi, S.

(2006). Abstract Shade Trees. In Proc. of the 2006

symposium on Interactive 3D graphics and games,

I3D ’06, pages 79–86, New York, NY, USA. ACM.

Microsoft (2010). Shader model 5 DirectX HLSL.

from: http://msdn. microsoft.com/en-us/library/ win-

dows/desktop/ff471356 %28v=vs.85 %29.aspx (ac-

cessed Oct. 23, 2012).

Microsoft (2012). Programming Guide for HLSL.

from: http://msdn. microsoft. com/en-us/library

/bb509635(v=VS.85).aspx (accessed Oct. 23, 2012).

Perlin, K. (1985). An Image Synthesizer. In Proc. of the

12th annual conference on Comp. graph. and inter-

active techniques, SIGGRAPH ’85, pages 287–296,

New York, USA. ACM.

Proudfoot, K., Mark, W. R., Tzvetkov, S., and Hanrahan,

P. (2001). A Real-time Procedural Shading System

for Programmable Graphics Hardware. In Proc. of

the 28th annual conf. on Comp. graph. and inter-

active techniques, SIGGRAPH ’01, pages 159–170,

New York, NY, USA. ACM.

Sitthi-Amorn, P., Lawrence, J., Yang, L., Sander, P. V., Ne-

hab, D., and Xi, J. (2008). Automated Reprojection-

Based Pixel Shader Optimization. ACM Trans.

Graph., 27(5):127:1–127:11.

Sitthi-Amorn, P., Modly, N., Weimer, W., and Lawrence, J.

(2011). Genetic Programming for Shader Simpliﬁca-

tion. ACM Trans. Graph., 30(6):152:1–152:12.

Trapp, M. and D

ollner, J. (2007). Automated Combina-

tion of Real-Time Shader Programs. In Cignoni, P.

and Sochor, J., editors, Eurographics 2007 Shortpa-

per, pages 53–56. Eurograph. Assoc.

CoSMo:Intent-basedCompositionofShaderModules

199