Efficient Inference of Spatial Hierarchical Models
∗
Jan Maˇc´ak and Ondˇrej Drbohlav
Department of Cybernetics, Czech Technical University in Prague,
Technick´a 2, 166 27 Prague, Czech Republic
Keywords:
Hierarchical Probabilistic Models, Graphical Models, Pattern Recognition.
Abstract:
The long term goal of artificial intelligence and computer vision is to be able to build models of the world
automatically and to use them for interpretation of new situations. It is natural that such models are efficiently
organized in a hierarchical manner; a model is build by sub-models, these sub-models are again build of
another models, and so on. These building blocks are usually shareable; different objects may consist of
the same components. In this paper, we describe a hierarchical probabilistic model for visual domain and
propose a method for its efficient inference based on data partitioning and dynamic programming. We show
the behaviour of the model, which is in this case made manually, and inference method on a controlled yet
challenging dataset consisting of rotated, scaled and occluded letters. The experiments show that the proposed
model is robust to all above-mentioned aspects.
1 INTRODUCTION
Efficient inference of complex hierarchical proba-
bilistic models is an important milestone on the way
to automatic, unsupervised learning of such struc-
tures. These structures are important because they
represent a simple and efficient way of modelling
real world objects, scenes and situations which al-
most always exhibit certain level of compositional-
ity and hierarchical structure (Tsotsos, 1990; Bienen-
stock et al., 1996).
Hierarchical models are also very efficient in pre-
cisely describing very complex objects with com-
pletely natural ordering of semantic information on
the given object. They model very local properties
on lower layers and general ones on higher layers
and they are also capable of describing very com-
plex mutual relations, e.g. non-rigid shape defor-
mations caused by rotations and stretching of certain
model components. These advantages are unfortu-
nately counterweighted by the fact that these models
are computationally very demanding when classify-
ing with them.
Although these models can work with any type
of information like variously described image re-
gions (Ommer and Buhmann, 2010; Ullman, 2007),
the models describing shapes are of special interest
∗
The authors were supported by the Czech Science
Foundation under the Project P103/12/1578 (SeMoA).
for us. The most common approaches to instantiating
such shape models in unknown data are based on dy-
namic programming
(Zhu and Mumford, 2006; Zhu
et al., 2010; Zhu et al., 2011) with pruning, coarse-to-
fine
schemes (Kokkinos and Yuille, 2011) or Bottom-
up
building of instances and their sparsification
2
(Fi-
dler and Leonardis, 2007). These works alsodeal with
learning such models, either their complete structure
or their parameters, which is also our long-term goal,
but is outside the focus of this paper.
2 CONTRIBUTION
In this paper, a new simple yet effective probabilistic
model is proposed. It is philosophically inspired by
the Bottom-up/Top-Down system (Fidler et al., 2006;
Fidler and Leonardis, 2007), but there are significant
differences. Particularly novel is
• the compositional model itself, which is fully cast
in probabilistic framework and can easily cope
with missing or redundant data, though it is still
reasonably simple and easily computable analyti-
cally (cf. (Kokkinos and Yuille, 2011)).
2
Preferably globally optimal reduction of generated hy-
potheses as to avoid combinatorial explosion on higher
layers. This basically means at least approximately solv-
ing a Set-Covering problem, known and proven to be NP-
complete (Karp, 1972).
500
Ma
ˇ
cák J. and Drbohlav O..
Efficient Inference of Spatial Hierarchical Models.
DOI: 10.5220/0004687705000506
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 500-506
ISBN: 978-989-758-003-1
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

• The inference system generates lower number of
Bottom-up hypotheses, which means that sparsi-
fication is not necessary. This results in more effi-
cient utilization of computational resources.
• The object structure is acyclic allowing for exact
computing of model probability using simple
Be-
lief propagation
3
.
• As a side effect, the
Bottom-Up process can be
easily implemented and run in parallel, achieving
another computational time savings.
3 CONCEPTS
The key concepts in this framework are an
instance
(of a composition)
and an area which serves as a con-
tainer for
instances .
The notation is the following: the individual com-
positional models on the layer a are distinguished by
subscript (a
1
, a
2
, etc.) and individual instances of a
composition a
k
are indexed by a superscript (a
1
k
, a
2
k
).
An instance – always associated with a certain
layer – is a hypothesis on presence of a realization
of a composition from the library conditioned on the
observed data D
i
∈ D. This hypothesis is assigned
probability, e.g. P(D
1
, D
2
, ...D
n
|a
k
j
) at the layer a or
P(D
1
, D
2
, ...D
n
|σ
k
j
) at the root layer, etc.
At the beginning of processing, the initial set of
areas to start with is the set of pixels. At each layer,
an image gets partitioned into areas.
Having a partition set at the layer l, the parti-
tion set at the higher layer l + 1 is obtained simply
by merging spatially close sets from layer l together.
That way, each area at the higher layer is composed of
several areas in the lower layer. Optimally, we would
like each area at the higher layer to have similar size
and to contain similar number, N, of lower layer ar-
eas.
It is not possible to satisfy both constraints, so we
use an algorithm which is only sub-optimal with this
respect, however is simple and fast: It selects an area
at the lower layer randomly, then merges it with k
nearby areas (k approaches N, and the closer the bet-
ter).
As a consequence, the collection of area sets over
all layer forms a tree. Having formed the areas, in-
stances are formed based on underlying children and
every single instance has to contain all area children.
That way each child is used exactly once within one
3
To avoid the need of using the general loopy version
which takes more computational time as well as has still
some unsolved issues (Weiss, 2000; Mooij and Kappen,
2007).
instance and the tree structure (acyclicity) of instance
is guaranteed.
Problems occur when there is a piece of data (an
instance) in the area which is not modelled by a cer-
tain composition which on the other hand models the
rest of the local data well. This is overcome by the
choice that the compositions are represented by gen-
erative models, so they can be equipped by an abil-
ity of generating random patterns according to some
probability distribution.
Another mechanism related to area is its so called
empty hypothesis (σ
e
). This hypothesis states that
the data within the area was created randomly with-
out any known (explicit) model.
This
empty hypothesis is necessary for correct
inference of the model’s presence. This necessity
is justified by the fact that the library can not con-
tain descriptions of all possible objects in the do-
main (world), because there is an infinite number of
them, and therefore a mechanism for detecting un-
known patterns (previously unseen) is required. The
empty hypothesis does the job - if the probability
P(σ
e
|D
1
, D
2
, ...D
n
) is higher than the probabilities of
the other models, the underlying data are either part
of a poorly-modelled object or real random noise and
the learning algorithm can focus on this area.
3.1 Example
An illustration of an area and a composition is shown
in the Figure 1. The area contains three instances (b
1
1
,
b
1
2
and b
1
3
) at the layer b and for the layer a, there is
one composition a
1
consisting of two components b
1
and b
2
. Because of the restriction that there can only
be one instance in one area at a time, there are two
hypotheses for such area possible. It can be either the
hypothesis that the composition a
1
generated the data
within the area or that this data has been generated by
the background process a
e
.
The probability of the data conditioned on the
presence of an instance of the composition a
1
1
is given
by
P(D
1
, D
2
, D
3
|a
1
1
) = P(D
1
|a
1
1
)P(D
2
|a
1
1
)P(D
3
|a
1
1
) =
=
Z
b
1
1
P(D
1
|b
1
1
)P(b
1
1
|a
1
1
)db
1
1
×
×
Z
b
1
2
P(D
2
|b
1
2
)P(b
1
2
|a
1
1
)db
1
2
×
×
Z
Ω
P(D
3
|b
e
)P(b
e
|a
1
1
)db
e
(1)
and P(D
3
|a
1
1
) in this case represents the probability
EfficientInferenceofSpatialHierarchicalModels
501

+
b
1
1
∼ N (µ
b
1
1
, Σ
b
1
1
)
+
b
1
3
∼ N (µ
b
1
3
, Σ
b
1
3
)
+
b
1
2
∼ N (µ
b
1
2
, Σ
b
1
2
)
(a)
+
P(b
1
|a
1
) ∼ N (µ
b
1
, Σ
b
1
)
+
a
1
+
P(b
2
|a
1
) ∼ N (µ
b
2
, Σ
b
2
)
(b)
Figure 1: (a) An example of an area containing three in-
stances b
1
1
, b
1
2
and b
1
3
on the layer b. (b) The model of the
composition from the layer a consisting of two components
whose configurations are specified by the conditional prob-
abilities P(b
1
|a
1
) and P(b
2
|a
1
) respectively. The composi-
tion a
1
models the area in the (a) with high probability and
in that case the instance b
1
3
is considered as a random noise.
that the D
3
has been generated by the background pro-
cess. Ω represents the area size (the area of circle with
radius of predefined constant related to the actual po-
sition in the hierarchy).
The probability that the whole of the content of the
area has been generated accidentally (the probability
of the
empty hypothesis) is given by the formula
P(D
1
, D
2
, D
3
|a
e
) =
3
∏
i=1


Z
Ω
P(D
i
|b
e
)P(b
e
|a
e
)db
e


,
(2)
where b
e
and a
e
stand for labels of
empty hypotheses.
Having known prior probabilities P(a
1
) and
P(a
e
), the probability of presence of the object a
1
can
be easily computed using Bayes formula
P(a
1
|D
1
, D
2
, D
3
) =
P(D
1
,D
2
,D
3
|a
1
1
)P(a
1
)
P(D
1
,D
2
,D
3
|a
1
1
)P(a
1
)+P(D
1
,D
2
,D
3
|a
e
)P(a
e
)
(3)
and similarly for the probability of the
empty hypoth-
esis.
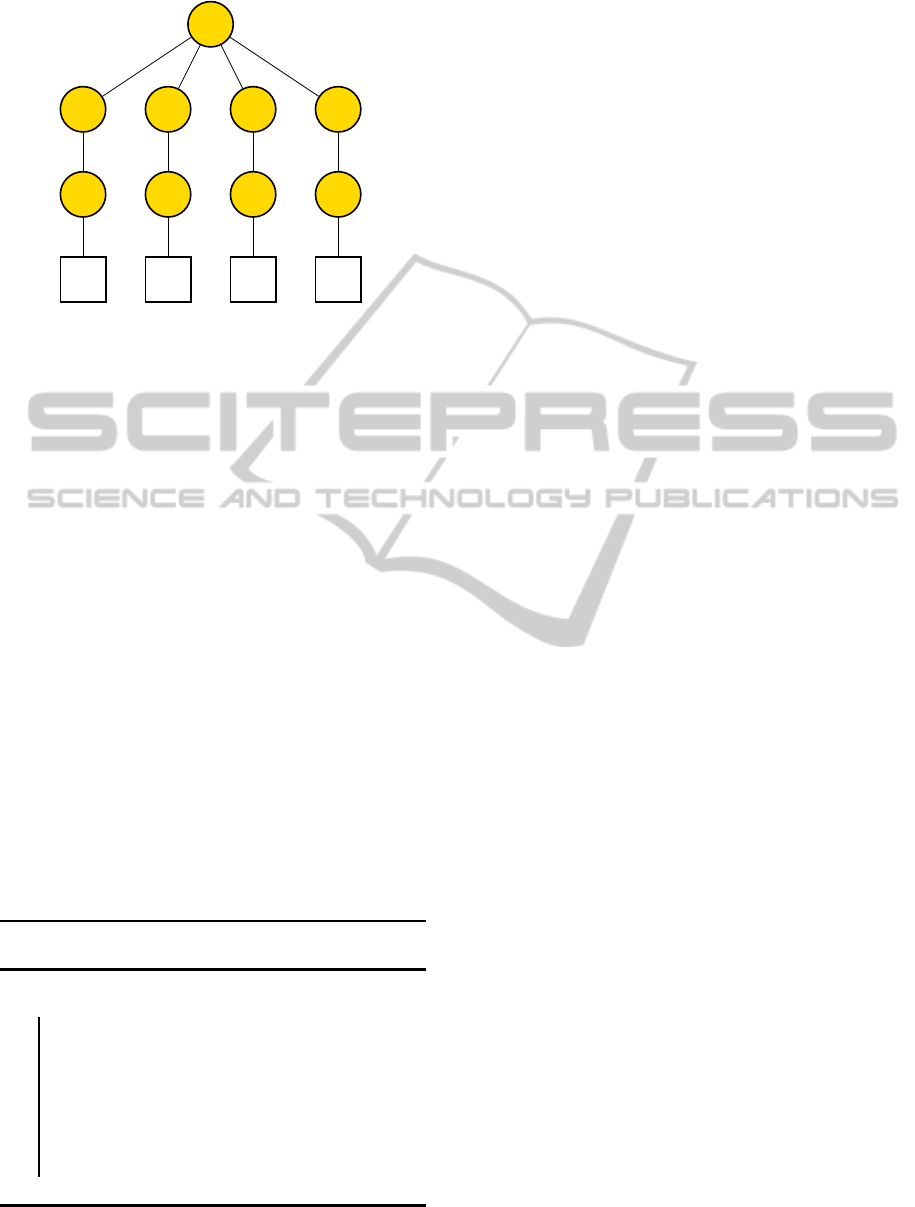
4 PROBABILISTIC MODEL
A detailed scheme of the probabilistic model of a
composition is shown in the Figure 2. Nodes a, b rep-
resent the basic compositional model as shown e.g.
in the Figure 1(b). Apart from these compositional
nodes, there is a hidden layer of nodes in this model.
These nodes, named as m
1
, m
2
etc., are two-state and
indicate if the correspondingdata (or sub-component)
is present or missing. The right-most node named
e is a discrete-state node stating the number of un-
assigned (unexplainable) data. The individual condi-
tional probabilities are
P(b
11
|m
1
= 1) ∝ N (µ, σ), (4)
P({}|m
1
= 0) = 1, (5)
P(m
1
|a) =

p
1
if m
1
= 1
1− p
1
if m
1
= 0
, (6)
P(e|a) =
λ
k
k!
e
−λ
(7)
and
P(b
e
|e) = N (b
e
;µ
AREA
, Σ
AREA
) (8)
with p
1
and λ as new parameters. The symbol {}
stands for a missing part.
The advantage of this model is that it can explic-
itly model every possible data configuration, regard-
less of the fact that the data can be completely alien
to the structural model included. In that case, all data
is assigned to the e-branch and all m nodes are set to
the state
missing . Naturally, the probability of this
model would be in that case lower than the probabil-
ity of the
empty model, because besides the e-branch
in the compositional model, there are also unassigned
compositional branches which serve as a penalty term
in such scenarios.
Even though the model is more complex than the
schematically introduced one, it is still quite easy to
evaluate (marginalize the hidden nodes) because all
hidden nodes (m and e) are constructed such that they
have only one non-zero state at a time. An item D
i
is always either present or missing, and the number
of non-assigned items is also always known – it de-
pends on the actual assignment of data to individual
leaf nodes which is fixed – from all possible assign-
ments, the one resulting in the maximal probability of
instance is selected. This indeed implies that the prob-
abilities are not precise but approximated, but simple
experiments show that other assignments give signif-
icantly (in terms of magnitudes) lower probabilities
and therefore even in the sum are negligible. More-
over, this choice keeps the resulting probability pro-
portional to a normal distribution.
5 INFERENCE SCHEME
The inference works gradually from the bottom layer
to higher layers exploiting principles of
Belief Propa-
gation
(Bishop, 2006; Pearl, 1988) which means that
first the compositions of the lowest model layer are
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
502

a
1
m
1
b
11
D
11
m
2
b
12
D
11
m
3
b
13
D
13
e
b
e
D
Figure 2: The structure of the probabilistic model of a com-
position, the rectangular nodes denoted with letter D are in-
put data, the round nodes m, e and b are internal nodes,
Nodes b model spatial relations of children and parent, m
model the decision if the child is present. Such composi-
tions are organized hierarchically to model whole objects.
instantiated using a method similar to (Felzenszwalb
and Huttenlocher, 2000) and all internal model nodes
are marginalized (in the case of the example in the
Section 3.1 nodes b, m and e) and instances are then
taken as new ’input’ data. This is done in each area
and after the layer inference is done, new area parti-
tioning on higher layer is made. This process goes
iteratively until the top (root) layer is achieved.
What makes this inference scheme robust is a si-
multaneously running
Top-Down adjustment process
which takes non-optimally found instances and tries
to improve them – either by focused search of missing
underlying instance which might have been missed
due to non-optimal area division, or by search of new
underlying instances in order to improve instances’
probability (when a sub-instance is e.g. too far from
its expected position).
The inference can be summarized by the Algo-
rithm 1.
Algorithm 1: The sketch of inference algorithm with
its steps.
1) get layer 1 instances from an image for i ← 1
to 5 do
2) find random partitioning of instances of
previous layer;
3) infer instances of current layer
(
bottom-up process);
4) merge the partitioning in previous layer;
5) improve the instances - find missing
parts (
top-down process);
end
In the step 3 of the Algorithm 1, the efficiency is
achieved by creating not all possible but only at most
five most probable hypotheses. The step 4 discards
the lower layer partitioning which allows to collect
and complete the instances that have been split into
multiple areas which affects their probabilities. This
step is actually very simple, because these split in-
stances have similar locations and therefore it is suffi-
cient to track multiple compositions from different ar-
eas appearing close each other and fuse them together.
This process cancels possible over-fitting of areas par-
titioning in favour of the highest-probable instance.
The step 5 is also quite lightweight – again only a lim-
ited number of instances are subject to updating. The
update itself works in the following scheme. The in-
stance tree is analysed and missing and non-optimally
detected sub-instances are detected. These candidates
for updating are sorted according to their importance,
which in this case means the highest layer has prior-
ity, because changes on this layer embodies the most
significant changes of instance’s probability. Further-
more, it does not make much sense to improve the
model on a lower layer and then replace this branch
completely. This
top-down update of an instance ends
when there are no defects detected or the maximal
number of attempts is reached.
6 EXPERIMENTS
The aim of the experiment was to show that the prob-
abilistic model and inference scheme are suitable for
character recognition with possible rejection of deci-
sion when the model fails to model the data.
6.1 Character Recognition
The model (its structure) for two letters –
a and b
(see the Figure 3) has been built manually and con-
sists of five layers of compositions. The whole library
of compositions is shown in the Figure 4. The mod-
els are set in to represent the individual shapes with
the goal to create share-able models and make the li-
brary as compact as possible. Nevertheless, the cor-
respondence of the model to the dataset images is not
perfect, especially the sub-models locations on higher
layers were chosen by hand and no optimization with
respect to the locations of individual composing com-
ponents was done in order to come closer to the real-
world situation when the unknown data always differ
from learned models and to see if the model is not too
sensitive to the choice of its parameters.
Probabilities p
1
in the Eq. 6 were set equally for
all library compositions as 0.9. Parameters λ for Pois-
son distribution used in the Eq. 7 were also set equally
EfficientInferenceofSpatialHierarchicalModels
503

−20 0 20
−20
−10
0
10
20
2
2
2
L=2 T=1
−20 0 20
−20
−10
0
10
20
5
5
5
L=2 T=2
−20 0 20
−20
−10
0
10
20
1
1
1
L=2 T=3
−20 0 20
−20
−10
0
10
20
7
7
7
L=2 T=4
−20 0 20
−20
−10
0
10
20
3
3
3
L=2 T=5
−20 0 20
−20
−10
0
10
20
6
6
6
L=2 T=6
−20 0 20
−20
−10
0
10
20
4
4
4
L=2 T=7
−20 0 20
−20
−10
0
10
20
8
8
8
L=2 T=8
−50 0 50
−50
0
50
3
3
2
2
L=3 T=1
−50 0 50
−50
0
50
4
5
4
5
L=3 T=2
−50 0 50
−50
0
50
6
1
6
1
L=3 T=3
−50 0 50
−50
0
50
8
7
8
7
L=3 T=4
−100
0
100
3
1
4
2
L=4 T=1
−100
0
100
4
1
3
2
L=4 T=2
−100
0
100
2
1
4
1
2
L=4 T=3
−100
0
100
2
2
2
2
2
L=4 T=4
−200
−100
0
100
200
1
2
3
L=5 T=1
−200
−100
0
100
200
1
4
2
L=5 T=2
(a)
Figure 4: Complete model library. Letter
L depicts the layer within the hierarchy, letter T its type (id) within the layer and
numbers in the pictures encode the underlying component type (can be matched with
T in preceding layer). The model library
can be seen as a recursive structure, one would obtain the structures shown in the Figure 3 by taking the model from 5th layer
and placing the appropriate models from the 4th layer at marked positions and repeating that until the second layer.
−100 0 100
−300
−200
−100
0
100
200
−100 0 100
−300
−200
−100
0
100
200
(a)
−100
0
100
−300
−200
−100
0
100
200
0
5
−100
0
100
−300
−200
−100
0
100
200
0
5
(b)
Figure 3: The complete structure models of
a , resp. b in
the (a) from top, in the (b). The
z axis shows the depth of
the models, layers are also emphasized by the thickness of
the line.
for all compositions to the value 1 and for the case of
empty hypothesis the value was set to be the max-
imum likelihood
estimate over corresponding layer.
This parameter reflects the average number of data
points within an area on certain layer.
The dataset consists of images of letters a , b , c
and d which were randomly rescaled by a factor rang-
ing from 0.95 to 1.05 and also randomly rotated by a
small angle, up to 5 degrees
4
.
These images were processed by a pair of orthog-
onal Gaussian filters to find edges and their orienta-
tion. The edges have been sorted according to their
orientations into eight groups. The set of these edges
represents the lowest (first) layer. To make the data
more challenging and to show that the method is natu-
rally insensitive to occlusions, a random square region
covering 25% of that particular image was cut out in
the first version of the experiment and converted into
random noise in the second version of the experiment.
6.1.1 Results
The inference scheme was tested on 61 images from
the described dataset, the numbers of each letter were
set equally to 15 instances and the 61st image was
generated randomly but with the same statistics of
4
Within this range are e.g. the usual residual errors after
preprocessing steps like rectification or rotation and scale
compensation.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
504

bottom layer instances
5
. This additional random
pattern was intended to show the behaviour of the
method on completely unknown data.
The selected letters exhibit a high level of similar-
ity – especially in the case when a random 25% of an
image is cut out. It can happen that the piece which
has been cut out was the most discriminative feature
between the letters. Consider the appearance of letter
a with its right part cut and its similarity to letter c as
an illustrative example. There is definitely a differ-
ence in the scale in this particular example, but this
difference is cancelled (compensated) by scale invari-
ance built in the model. Therefore, the success rate
might not be as high as one would expect, especially
on the second half of the dataset when poorly mod-
elled but still compositional data is being dealt with.
In the first version of the experiment, the overall
success rate on the first half of the data was 100%
which means that all data that was explicitly repre-
sented in the model library were recognized properly,
some examples are shown in the Figure 5(a), Fig-
ure 5(b) and Figure 5(c). However, in few images the
models were not located precisely, as can be seen in
the Figure 5(d), resulting in the overall location preci-
sion of 90% – 80% for the
a category, 100% for the b
category – correctly located models. These misplace-
ments are caused mainly by the fact that both models
are built of similar components – in the case of let-
ter
a the middle part and top part models differ only
in two sub-models (see the Figure 4, models denoted
L=4 T=2 and L=4 T=3 ) and when some of impor-
tant sub-model is not found – due to occlusion or due
to unfavourable partitioning – the winning hypothesis
might be wrong. Nevertheless, this is a problem only
on the top layer, lower layers get updated using the
information from the top.
The results on the other half of the data show how
the method behaves on a not-so-well modelled data.
In the cases of letters
c and d , it tends to instanti-
ate any of the library models, because there is almost
always a part of letter which can be interpreted us-
ing a model from library, especially on the lower lay-
ers. In the case of the last image – the random pat-
tern – it shows the desired property that unknown pat-
tern is quickly labelled as unknown (
empty hypothe-
sis wins).
The complete confusion matrix for the labelling is
shown in the Table 1, the empty hypothesis is denoted
as
/
0.
In the second version of the experiment, when the
occluded part of the image data was covered by ran-
5
This random pattern was constructed by taking an im-
age, processing it and then randomly permuting instances
locations.
100 200 300
−100
0
100
200
300
400
(a)
100 200 300
−100
0
100
200
300
400
(b)
100 200 300
−100
0
100
200
300
400
(c)
100 200 300
−100
0
100
200
300
400
(d)
Figure 5: A fewselected examples of winning model instan-
tiation in the first version of the experiment (missing data),
blue dots are unexplained edge segments. (d) shows a mis-
placed model (the only example in the results), (a), (b) and
(c) show completely correct instantiations. It is also visible
which parts of image were cut off.
Table 1: Confusion matrix for the letters dataset labelling
for missing data, rows show the correct label and columns
assigned label.
a b
/
0
a 1.00 0.00 0.00
b 0.00 1.00 0.00
/
0
0.52 0.32 0.16
Table 2: Confusion matrix for the letters dataset labelling
(occlusion by random noise), rows show the correct label
and columns assigned label.
a b
/
0
a 0.73 0.20 0.07
b 0.00 1.00 0.00
/
0
0.45 0.52 0.03
dom noise, the results are slightly worse, achieving
86.7% labelling accuracy on the a and b categories.
On the rest of the data, the method behaved similarly
as in the previous case and the completely random
pattern – the image 61 – was again labelled correctly
as unknown. Regarding the correctness of location, in
EfficientInferenceofSpatialHierarchicalModels
505

100 200 300
−100
0
100
200
300
400
(a)
100 200 300
0
100
200
300
400
500
(b)
Figure 6: Two selected examples of winning model instan-
tiation for the second version of the experiment (occlusion
by random noise), the colour interpretation is the same as in
the Figure 5.
all images that were correctly labelled were also the
models correctly located, achieving 86.7% accuracy
without any fine-tuning of the parameters. The com-
plete confusion matrix can be found in the Table 2 and
two illustrative results are shown in the Figure 6.
7 CONCLUSIONS
In this paper, a new hierarchical probabilistic model
for modelling object appearance is introduced and an
efficient method for its inference is described. Main
and novel features of this approach are the follow-
ing: first, the model is acyclic by definition, which
allows for precise computation of probabilities using
a very simple version of
Belief propagation . Second,
thanks to the partitioning of layers it is easy to com-
pute the probabilities of the model conditioned on the
observed data, which is very useful for
Maximum-
likelihood
learning of parameters. This partitioning
also prevents us from the combinatorial explosion in
the
Bottom-up generation of hypotheses and allows
for parallel processing. The model and the method is
also robust to occlusions.
The experiments on a controlled dataset of images
of letters with a hand-made hierarchical model show
that the proposed approach is generally usable for vi-
sual data. The dataset is characterized by small ro-
tations and scale changes as well as occlusions (non-
presence or replacing by random noise) of 25% of the
image, none of which causes significant difficulties to
the inference algorithm.
To briefly outline the future directions, the frame-
work is planned to be used in a completely unsuper-
vised structural learning method and is going to be
compared to the state-of-the-art methods in structural
learning and recognition.
REFERENCES
Bienenstock, E., Geman, S., and Potter, D. (1996). Com-
positionality, MDL priors, and object recognition. In
Mozer, M., Jordan, M. I., and Petsche, T., editors,
NIPS, pages 838–844. MIT Press.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer Science+Bussiness Media, New
York, NY.
Felzenszwalb, P. and Huttenlocher, D. (2000). Efficient
matching of pictorial structures. In Computer Vision
and Pattern Recognition, 2000. Proceedings. IEEE
Conference on, volume 2, pages 66 –73 vol.2.
Fidler, S., Berginc, G., and Leonardis, A. (2006). Hier-
archical statistical learning of generic parts of object
structure. In Proc. CVPR, pages 182–189.
Fidler, S. and Leonardis, A. (2007). Towards scalable repre-
sentations of object categories: Learning a hierarchy
of parts. In Proc. CVPR.
Karp, R. M. (1972). Reducibility among combinatorial
problems. In Miller, R. E. and Thatcher, J. W., editors,
Complexity of Computer Computations, The IBM Re-
search Symposia Series, pages 85–103. Plenum Press,
New York.
Kokkinos, I. and Yuille, A. (2011). Inference and learning
with hierarchical shape models. International Journal
of Computer Vision, 93:201–225. 10.1007/s11263-
010-0398-7.
Mooij, J. and Kappen, H. (2007). Sufficient conditions
for convergence of the sum-product algorithm. Infor-
mation Theory, IEEE Transactions on, 53(12):4422–
4437.
Ommer, B. and Buhmann, J. (2010). Learning the compo-
sitional nature of visual object categories for recog-
nition. IEEE Trans. Pattern Anal. Mach. Intell.,
32(3):501 –516.
Pearl, J. (1988). Probabilistic reasoning in intelligent sys-
tems: networks of plausible inference. Morgan Kauf-
mann Publishers Inc., San Francisco, CA, USA.
Tsotsos, J. K. (1990). Analyzing vision at the complex-
ity level. Behavioral and Brain Sciences, 13(03):423–
445.
Ullman, S. (2007). Object recognition and segmentation
by a fragment-based hierarchy. Trends in Cognitive
Sciences, 11(2):58 – 64.
Weiss, Y. (2000). Correctness of Local Probability Propaga-
tion in Graphical Models with Loops. Neural Comp.,
12(1):1–41.
Zhu, L., Chen, Y., and Yuille, A. L. (2010). Learning a hi-
erarchical deformable template for rapid deformable
object parsing. IEEE Trans. Pattern Anal. Mach. In-
tell., 32(6):1029–1043.
Zhu, L. L., Chen, Y., and Yuille, A. (2011). Recursive com-
positional models for vision: Description and review
of recent work. J. Math. Imaging Vis., 41(1-2):122–
146.
Zhu, S.-C. and Mumford, D. (2006). A stochastic gram-
mar of images. Found. Trends. Comput. Graph. Vis.,
2:259–362.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
506