Shape Segmentation using Medial Point Clouds with Applications to

Dental Cast Analysis

Jacek Kustra

1,3

, Andrei Jalba

and Alexandru Telea

Philips Research, Eindhoven, The Netherlands

Eindhoven University of Technology, Eindhoven, The Netherlands

University of Groningen, Groningen, The Netherlands

Keywords:

Dental Cast Analysis, Surface Segmentation, Medial Axes.

Abstract:

We present an automatic surface segmentation method for dental cast scans based on the point density proper-

ties of the surface skeleton of such shapes. We produce quasi-ﬂat segments separated by soft ridges, in contrast

to classical surface segmentation methods that require sharp ridges. We compute the surface skeleton by a fast

3D skeletonization technique followed by its regularization using surface geodesics. We segment the resulting

skeleton by a mean-shift approach and transfer the segmentation results back to the surface. We demonstrate

our results on an industrial dental-cast segmentation application and several generic 3D shape models.

1 INTRODUCTION

Segmenting 3D surfaces into their natural compo-

nents has many applications in shape analysis, com-

puter vision, shape compression, and medical imag-

ing. Segmentation requirements strongly depend on

the target application, so many segmentation meth-

ods exist. One can distinguish between patch-type

and part-type segmentation methods (Shamir, 2004).

Patch-type methods use local shape information such

as surface curvature to produce quasi-ﬂat segments

separated by high-curvature creases or ridges. Part-

type methods are more semantically-oriented, i.e., try

to ﬁnd segments that a human user would intuitively

see as distinct logical shape parts. Such segments are

not always separated by high-curvature ridges.

For some shapes, both patch-type and patch-type

methods do not yield the desired result. Consider for

example the dental cast model in Fig. 2 a, where we

want to ﬁnd the separate teeth as individual segments,

and also separate them from the gums. Part-based

methods fail here, since the teeth are not clear pro-

trusions from the shape’s rump, as would be, e.g.,

the limbs sticking out of an articulated body model.

Patch-based methods also fail, since ridges separat-

ing teeth from each other and from the gums are quite

shallow. Detecting a compact, closed, and thin sep-

aration region between the segments based on curva-

ture is quite hard. Fig. 2 b illustrates this by showing

the surface’s curvature (concave=blue, convex=red).

The main motivation of this work is the need to

segment dental casts, which are tools used to cre-

ate orthodontic treatment plans for dental patients.

Advances in range imaging and 3D scanning allow

capturing dental scans directly from a patient (Atron,

Inc., 2013), and next to digitize such shapes into 3D

surface meshes of the teeth-and-gum structure. Dig-

ital casts allow the automatic assessment of several

orthodontic metrics, such as the arch length discrep-

ancy, and new opportunities towards teeth alignment

treatment planning and simulation. However, all such

analyses require a prior segmentation of the scan into

individual teeth and the gums. Typical dental scans

do not exhibit sharp creases between individual teeth

(due to scanning resolution limitations or actual teeth

touching), nor between teeth and gums. Hence, exist-

ing patch-based segmentation cannot be directly used.

For the motivating use-case of segmenting den-

tal casts, we present here a new method to compute

patch-based segmentations of 3D shapes which do not

exhibit strong creases between segments. Instead of

using local information such as curvature, we take a

global approach, based on the shape’s surface skele-

ton. Key to our method is the observation that surface

skeletons capture all input shape creases, regardless

of their sharpness. To compute a high-resolution sur-

face skeleton, we use a GPU-based method which de-

livers point-cloud skeletons for models of hundreds

of thousands of polygons in a few seconds. Next,

we regularize the surface skeleton, to eliminate small

162

Kustra J., Jalba A. and Telea A..

Shape Segmentation using Medial Point Clouds with Applications to Dental Cast Analysis.

DOI: 10.5220/0004688301620170

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 162-170

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Algorithm workﬂow: A shape is transformed into

the medial domain. Its skeleton is next segmented by a

mean-shift approach. The segmentation is transferred back

to the original shape.

manifolds that do not correspond to segments large

enough to be of interest. Next, rather than segment-

ing the surface (as virtually all patch-based method

do), we segment its regularized surface skeleton, by

a mean-shift approach. Finally, we project back the

found skeletal segments onto the input surface, and

use a nearest-neighbor approach to yield a segmenta-

tion that entirely covers the input shape (Figure 1).

The structure of this paper is as follows. Section 2

reviews related work on skeletonization and dental

cast segmentation. Section 3 details our method. Sec-

tion 4 presents our results. Section 5 discusses our

method. Section 6 concludes the paper.

2 RELATED WORK

Related work can be organized into three areas:

Surface Segmentation. Patch-based segmentation

subdivides a 3D shape into non-overlapping, com-

pact, segments or patches which (a) respect desir-

able properties such as minimal size and bound-

ary smoothness, and (b) are separated by local sur-

face features, typically sharp creases. By construc-

tion, segments are much ﬂatter than creases between

them. Many methods exist in this area. (Garland

et al., 2001) hierarchically clusters the input mesh

faces to yield a segmentation consisting of planar

segments. (Clarenz et al., 2004) propose a fuzzy

multiscale segmentation based on surface curvature.

This method often creates noisy segment boundaries

in low-curvature regions. (Borgefors et al., 2009)

compute local thickness in combination with a mul-

tiresolution structure to hierarchically segment 3D

voxel shapes. (Mangan and Whitaker, 1999) seg-

ment surfaces into similar-curvature patches by a wa-

tershed technique with curvature as the height func-

tion. (Zuckerberger et al., 2002) improved the wa-

tershed method and give many applications. (Provot

and Debled-Rennesson, 2008) segment voxel shapes

by detecting discrete planes with variable width.

Dental Segmentation. Dental cast segmentation has

been widely explored recently due to the increasing

availability of digital models. Manual segmentation

is prohibitively slow for current orthodontic practice.

Several methods have been proposed instead, ranging

from fully automated methods (Kondo et al., 2004) to

methods needing minimal user interaction (Kronfeld

et al., 2010; Zhao et al., 2005; Hirogaki et al., 2001).

(Kondo et al., 2004) avoids the 3D mesh processing

complexity by ﬁrst transforming the 3D data into

a plan-view range image which is next segmented.

Recently, a snake-based approach for teeth segmenta-

tion has been proposed (Kronfeld et al., 2010). Here,

a snake is iteratively ﬁt to the surface curvature until

it reaches local minima. However, such methods have

problems in low curvature regions, i.e., where creases

separating teeth are shallow. Also, such methods

assume a way to ﬁnd the positions and amount of

teeth prior to segmentation, e.g. using the dental arch

metric. In our proposal, we do not rely on such priors.

Skeletonization. Skeletons, or medial axes, contain

the loci of maximally inscribed circles (in 2D) or

spheres (in 3D) (Blum, 1967). 2D medial axes are

collections of curves. 3D shapes admit two skeletons:

Surface skeletons are sets of curved manifolds con-

taining the loci of maximally inscribed spheres. They

fully describe the shape, i.e., the shape can be recon-

structed from the skeleton. Curve skeletons are sets

of 1D curves locally centered in the shape, accord-

ing to various heuristics. They cannot fully capture

the geometry of the input shape, and are most useful

for tubular objects (Cornea et al., 2007). Given these,

we next focus on surface skeletons. Several meth-

ods compute surface skeletons either from a meshed

surface or a volumetric (voxel) model. Volumetric

methods have signiﬁcantly higher memory and speed

costs and lower accuracy. Skeletonization methods

can be divided into thinning (Pudney, 1998; Palagyi

and Kuba, 1999), geometric (Amenta et al., 2001;

Stolpner et al., 2009; Stolpner et al., 2011), and ﬁeld-

based (Siddiqi et al., 2002; Pizer et al., 2003; Bouix

et al., 2005; Bouix et al., 2006; Reniers et al., 2008b).

For a survey, we refer to (Siddiqi and Pizer, 2009).

Only few 3D segmentation methods use skeletons.

(Reniers and Telea, 2008a) uses curve skeletons for

part-type segmentations of tubular shapes. (Reniers

and Telea, 2008b) use surface skeletons for part-type

segmentation of shapes with sharp edges. The latter is

of interest to us: Given a voxel shape, we compute its

surface skeleton by (Reniers and Telea, 2008a), and

next simplify it to remove small-scale details. Next,

we detect the skeleton boundary and back-project it

on the surface via the inverse feature transform (Re-

ShapeSegmentationusingMedialPointCloudswithApplicationstoDentalCastAnalysis

163

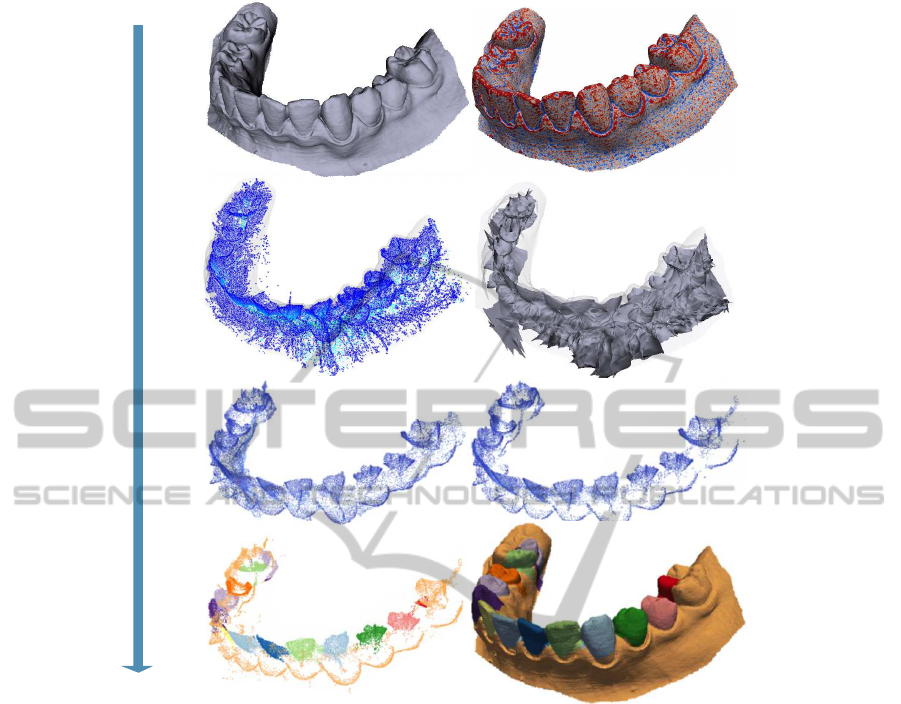
Skeletonization InitializationRegularizationSegmentation

a) input mesh

c) surface skeleton

e) thresholded importance f) seed points

g) segmented skeleton h) segmented mesh

d) reconstructed skeleton

b) surface curvature

Figure 2: Algorithm steps: Input shape (top row). Surface skeletonization (second row). Medial cloud regularization (third

row). Medial cloud segmentation and segments’ transfer to the input surface (bottom row).

niers and Telea, 2007). This robustly detects creases

between quasi-ﬂat patches, as skeleton boundaries

correspond to the surface’s curvature maxima (Pizer

et al., 2003). Finally, we ﬁll surface areas between

these creases to compute segments. (Reniers et al.,

2008a) use a similar relation between the skeleton and

surface to robustly ﬁnd ridges of anatomical surfaces.

However, they do not actually segment the surface.

A main blocker in using surface skeletons for seg-

mentation is the difﬁculty to efﬁciently compute accu-

rate skeletons of complex models. Recently, this has

been overcome by (Ma et al., 2012) and (Jalba et al.,

2013) who compute point-cloud skeletons for meshes

of millions of polygons in seconds on the GPU. How-

ever, these methods produce an unstructured cloud

rather than a compact voxel model (as in e.g. (Reniers

and Telea, 2008a)), so they cannot be used to segment

surfaces along (Reniers and Telea, 2008b). We next

propose a shape segmentation method combining the

skeleton description power with its local point density

properties when extracted from a uniformly sampled

surface. This enables a meaningful shape segmenta-

tion based on both global and local properties.

3 METHOD

Our proposal ﬁrst transforms the surface into its me-

dial domain (see Fig. 2). We next exploit skeletal

point density properties to do the segmentation in this

domain. Finally, we project the medial segmentation

back to the surface. We detail these steps next.

3.1 Skeletonization Preliminaries

Given a shape Ω ⊂ R

with boundary ∂Ω, we ﬁrst

deﬁne its distance transform DT

∂Ω

: R

→ R

∂Ω

(x ∈Ω) = argmin

y∈∂Ω

kx−yk. (1)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

164

The skeleton of Ω is next deﬁned as

Ω

= {x ∈Ω|∃f

, f

∈ ∂Ω, f

6= f

kx−f

k = kx−f

k = DT

∂Ω

(x)}, (2)

where f

and f

are two of the contact points with ∂Ω

of the maximally inscribed ball in Ω centered at x,

also called feature transform (FT) points (Strzodka

and Telea, 2004; Reniers and Telea, 2007). The vec-

tors f

−x and f

−x linking the skeleton points x with

their feature points are called feature vectors or spoke

vectors (Stolpner et al., 2009). In some cases, a skele-

ton point can havemore than two such feature points –

consider e.g. the center of a ball whose feature points

are the entire ball surface. For our purposes, we how-

ever need only two of these points, which are faster to

compute and store than the full feature transform.

Given a densely sampled mesh surface ∂Ω, we ex-

tract its densely sampled surface skeleton following

(Jalba et al., 2013; Ma et al., 2012). In detail, for each

point p ∈ ∂Ω having the surface normal n, we create

a ball B(s, r) of center s = −rn+ p and initial radius r

larger than the diameter of ∂Ω. The ball is iteratively

shrunk by searching the closest surface point to s until

it touches ∂Ω in exactly two points f

= p and f

. At

this moment, the center s is a newly found skeleton

point with feature points f

and f

. To remove small-

scale skeleton details created by equally small-scale

convexities (bumps) on ∂Ω, we next regularize the

skeleton. For this, we compute an importance met-

ric ρ : S → R

for each skeleton point. ρ(s ∈S equals

the shortest-path distance on ∂Ω between the feature

points f

and f

of s. As shown in (Reniers and Telea,

2008a; Jalba et al., 2013), ρ monotonically increases

from the skeleton boundary inwards. Thresholding it

with a small value τ yields a simpliﬁed skeleton

= {s ∈S

Ω

|ρ(s) > τ} (3)

which captures all salient branches of S

Ω

but removes

those for surface details shorter than τ. Figure 2

shows this: From a dental cast (a), we compute the

skeleton cloud. Image (c) shows the simpliﬁed skele-

ton S

for a value τ = 3% of the shape’s diameter,

colored by ρ (blue=low, red=high). We see how sim-

pliﬁcation removedmany spurious skeletal points cre-

ated by small surface wiggles. Image (d) shows, for

comparison, the surface skeleton reconstructed from

the skeletal cloud following (Telea and Jalba, 2012).

Given the high resolution of the skeletal cloud, the

reconstructed skeleton also has a very complex man-

ifold structure. Robustly ﬁnding the boundaries of

these manifolds, to further apply the patch-based seg-

mentation of (Reniers and Telea, 2008b), is very chal-

lenging, as already noted in Sec. 2.

sampled convex surface

sampled skeleton

sampled concave surface

sampled skeleton

high-density medial

point clusters

Figure 3: Relationship between local surface curvature and

medial cloud density. Top: Concept sketched in 2D. Bot-

tom: High-density point clusters are formed inside positive-

curvature 3D surface areas (front teeth).

3.2 Surface Curvature vs Skeleton

Density

To further segment our skeleton cloud, we use the fol-

lowing observations linking the curvature of ∂Ω and

point density on S

Ω

. Consider a densely sampled ∂Ω.

For a positive-curvature region of ∂Ω (bump, or con-

vexity), the ball-shrinking directions rn, identical to

the feature vector directions, point inwards in a con-

verging fashion. Hence, the density of the skeletal

points for this region will be higher than the surface

density. Conversely, for a region with negative curva-

ture (a crease, or concave, region), the ball-shrinking

directions will point inwards in a diverging fashion,

so the density of the skeletal points for this region

will be lower than the surface density. Figure 3 (top)

illustrates this in 2D. Figure 3 (bottom) shows an ac-

tual example for a 3D skeletal cloud computed from

a dental cast. We observe that skeletal parts enclosed

in the front teeth present a high point density, since

these teeth are indeed convex shape parts.

3.3 Mean Shift Clustering

We now show how to use the density-related observa-

tions in Sec. 3.2 to segment the skeleton cloud.

Since the skeletal cloud exhibits strong density

variations, it should be possible to segment it into

point clusters representing the dense regions based on

a method which exploits such density variations. An

ideal such method is mean shift clustering (Comani-

ciu and Meer, 2002), which we extend to our seg-

mentation needs, as follows. We start by selecting

a set of seed points P ⊂ S

from the simpliﬁed skele-

ton. The seed point selection is discussed separately

ShapeSegmentationusingMedialPointCloudswithApplicationstoDentalCastAnalysis

165

seed point

convergence

point

convergence points

a) b) c)

Figure 4: Mean shift clustering: (a) A seed point (black dot) is shifted to the centroid of its skeleton-cloud neighborhood

density until convergence (red dot). (b) Final convergence points for dental cast. (c) Segment IDs assigned to skeleton points.

in Sec. 3.4. Each seed point x ∈P is assigned a unique

‘segment id’. For each seed point x ∈ P, we aim to

ﬁnd its so-called convergence point c(x) ∈ R

. For

this, we ﬁrst ﬁnd all neighbors N

⊂ S

of x within a

small ﬁxed radius ε and determine the centroid of N

m(x) =

∑

y∈N

K(kx−yk)y

∑

x∈N

K(kx−yk)

(4)

where K is a Gaussian kernel

K(x) =

√

2π

2σ

(5)

following the kernel density estimation idea in (Co-

maniciu and Meer, 2002). ε is set to a small frac-

tion (about 5%) of the model size. We next iteratively

shift the seed points x to their centroids m(x) follow-

ing Eqn. 4 (see also Fig. 4 a) until these stabilize,

i.e., move at one iteration less than a small threshold

λ = km(x)−xk, set in practice to 10

−4

. Also, for each

non-seed point (which is not shifted), we deﬁne a vot-

ing weight v(y), initialized to zero at the beginning of

the algorithm. At every mean-shift iteration, we add a

value K(k y −m(x)k) to v(y) for each non-seed point

y ∈ N

, and also add a pointer from y to m(x), to in-

dicate that y was int he neighborhood of m(x). When

m(x) has converged, we search its neighborhood for

other existing convergence points c

′

than itself. If one

exists, we merge the ids of m(x) and c

′

. Otherwise,

we create a new convergence point c = m(x).

At the end of the mean shift, all seed points have

thus converged to a set C of convergence points (see

Fig. 4 b). The ids of the points c ∈ C give us the ﬁ-

nal segments. Finally, to assign each non-seed point

y ∈ S

to a segment, is done by assigning to y the id

of the convergence point that it is linked to and which

has the highest amount of votes within the k last iter-

ations (Fig. 4 c). Different segmentation levels can be

achieved by considering the voting of only the last k

iterations of the mean shift process. This way, only

the areas around the skeleton-cloud density peaks are

considered. This is illustrated by the dental cast mod-

els, where the gum areas remain mostly unsegmented

(Fig. 5 a-e), for which we used a value k = 20. In con-

trast, for the other shapes in Fig. 5 f-k, the full mean-

shift path has been considered for the voting, leading

to the full surface being segmented into patches.

3.4 Seed Point Detection

We ﬁnd the initial seed points P used in mean shift

clustering by using the speciﬁc geometry of our den-

tal casts. We want at least one seed point in each rel-

evant segment (that is, inside each high-density clus-

ter such as the ones in Fig. 3; we do not want seed

points outside such segments. We allow more seed

points in a segment, so that ﬁnding seed points is not

parameter-critical. The deﬁnition of segment rele-

vance is application-dependent: For our dental cast

use-case, we only want the teeth segments and the

gum, i.e., we don’t want to over-segment the gum. To

achieve this, we use as seed points all skeleton points

which (a) have a low distance DT

∂Ω

(s) to the original

surface ∂Ω and (b) have a high curvature, computed

as the angle between the feature vectors f

−s, f

−s.

3.5 Segmentation Transfer to Surface

In the last step, we transfer the skeleton segmenta-

tion to the input surface, as follows. For each point

s ∈S

, we copy the segment ID of s to its two feature

points f

and f

. However, this does not assign a seg-

ment ID to all points on ∂Ω, since we segmented the

simpliﬁed skeleton S

rather than the full skeleton S

Ω

For all points p ∈ ∂Ω which are not assigned a seg-

ment ID, we search the closest surface point p

′

∈ ∂Ω

which has an ID ID(p

′

) assigned, and mark p with the

same ID(p

′

). This ﬁlls the gaps between segments on

∂Ω in distance order, yielding a full, non-overlapping,

surface segmentation.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

166

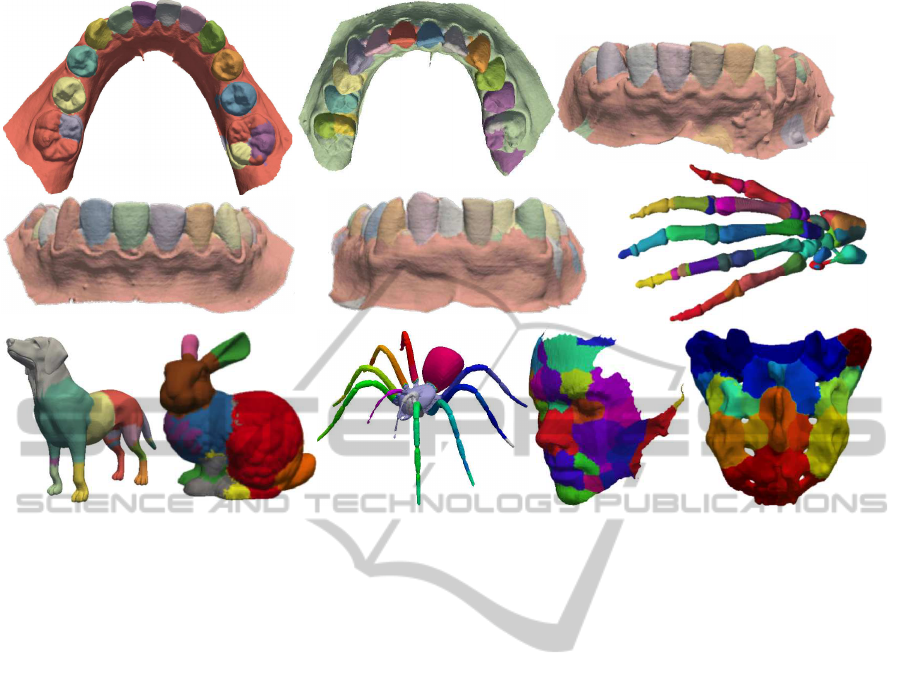
a) b) c)

d) e)

g) h) i) j)

Figure 5: Segmentation results for different dental casts (a-e) and other shapes (f-k).

4 RESULTS

Figure 5 shows several results. Surface segments are

colored differently, for illustration. For images (a-e),

which show dental cast scans, we see that the method

separates very well the incisives, canines, molars and

pre-molars, both from each other, and also from the

gums. We also see several problems. The molars

are over-segmented (Fig. 5 a,b), and occasionally the

gums are also oversegmented (Fig. 5 c,e). The gums

oversegmentation is not problematic for the consid-

ered orthodontic application, since users are only in-

terested to analyze the teeth, and not the gums. The

molars oversegmentation is be explained by the fact

that they (a) have a more complex geometry than the

other teeth (more internal creases) and also that, in

our models, the input surface has less points here.

Hence, the skeletal manifolds for to these detail-rich

areas are too poorly sampled to fully capture their

features. We also segmented other shapes than den-

tal casts, to get more insight in the method’s behav-

ior (Figs. 5 f-k). Several observations can be made.

For models having convex surface areas separated by

well-delimited concave ridges, such as the hand or

spider, we get the expected segmentation, just as for

the dental casts. For the other models, segments are

created around the most salient convex bumps of the

shape. These segments meet along the model concav-

ities, or creases – see e.g. the nose, eyes, and chin

of the face model (Fig. 5 j); bunny years, tail, head,

rump, and front paw (Fig. 5 h); and the convex bone

components of the sacrum model (Fig. 5 k).

5 DISCUSSION

Several aspects are relevant for our method.

Simplicity and Novelty. A key asset of our method

is its algorithmic simplicity. We use algorithms

with proven accuracy, convergence, and complexity

properties (Comaniciu and Meer, 2002; Reniers and

Telea, 2008a; Jalba et al., 2013). Our method is

the ﬁrst we are aware of to use surface skeletons

computed on mesh models to segment surfaces.

Its only competitor, using more expensive and

lower-resolution voxel models, is (Reniers and Telea,

2008b). This is also the ﬁrst use of mean shift to

cluster skeletons.

Robustness. The method is robust to different

surface point-sampling densities, as the segmentation

is performed based on the medial surface density

properties. We tested our method on several dental

cast models with the same parameter settings, and

ShapeSegmentationusingMedialPointCloudswithApplicationstoDentalCastAnalysis

167

Table 1: Segmentation timings.

Model dental 1 dental 2 dental 3 dog bunny bone hand spider face

# points (surface) 119594 127578 82887 18114 34834 41035 327323 29741 35437

# points (skeleton S

)

6136 24339 11214 16823 10706 8271 128839 8389 8450

# seed points

339 487 373 336 535 827 644 829 1041

CPU skeletonization (sec) 51.3 48.53 22.87 34.89 10.96 10.26 151.68 5.85 12.8

GPU skeletonization (sec)

11.7 11.0 5.78 3.24 3.6 1.82 31.2 0.95 2.11

CPU segmentation (sec)

1.95 1.92 1.3 43.07 2.71 40.12 152.02 167.53 11.35

CPU total (sec) 53.25 50.45 24.17 77.96 13.67 50.38 303.7 173.38 24.15

GPU total (sec)

13.65 12.92 7.08 46.31 6.31 41.94 183.22 168.48 13.46

obtained identical results (cf. Figs. 2, 5).

Applicability. Our method is, by construction,

geared towards the segmentation of convex surface

patches separated by shallow creases. In this sense,

we stress that the skeleton simpliﬁcation (Eqn. 3)

only eliminates skeleton points corresponding to

small-scale surface bumps (convexities), but no

skeleton point corresponding to a concavity (crease).

This makes our method principially more robust than

many other curvature-based segmentation methods.

Also, our method can handle non-watertight surfaces

(such as our teeth scans, which are not closed at the

base, or the face model in Fig. 5 j) with no problems.

Performance. We implemented our method in C++

using ANN (Mount and Arya, 2011) to ﬁnd nearest

neighbors and the GPU skeletonization in (Jalba

et al., 2013). The latter also provides the needed

distance transform, feature points, and importance

metric (Sec. 3.1). For 3D surface supersampling, we

used Yams (Frey, 2001). Tab. 1 shows timings on a

Windows PC at 2.66 GHz with an Nvidia 690 GTX

for several shapes. Skeletonization times include

regularization (Eqn. 3); we show timings for (Jalba

et al., 2013) on both GPU and GPU. Segmentation

timings include mean shift, segment ID assignment,

and transfer on the original surface, all done on the

CPU. As expected, GPU skeletonization is much

faster than its CPU counterpart. The segmentation

cost varies in function of the actual model. For the

dental casts, this cost is quite low. Indeed, for these

models, we use only the last k iterations (Sec. 3.3),

whereas for the other models we use the full mean

shift path. The segmentation (not optimized, unlike

skeletonization) is dominated by the nearest neighbor

searches. Such searches can be massively accelerated

using GPUs, as shown in (Jalba et al., 2013), so a

GPU mean shift implementation should massively

accelerate this step.

Dental Use-case. For teeth segmentation, our method

can segment all teeth whose medial surfaces converge

to a point density maximum. Given the geometry

of the incisives, canines, molars and pre-molars,

we saw that these present the expected properties,

so are robustly segmented. Molars have a slightly

more complex geometry, including too shallow

separation creases from gums. This creates some

challenges (over-segmentation) when using the exact

same mean-shift parameters as for the other teeth

(see e.g. Fig. 2 a,b). Possible ways to overcome

this are supersampling the input mesh, leading to

a surface skeleton with better separated manifolds.

However, we stress that, even with such limitations,

our method is superior to existing alternatives in the

orthodontic industry (see references in Sec. 2), as all

such methods require a non-trivial amount of user

input to produce their segmentations.

Limitations. As seen in Fig. 5, our method cannot

be directly applied to any 3D shape. The method

is geared towards segmenting shapes whose skele-

tal manifolds exhibit clearly separated high-density

branches, each branch corresponding to one surface

segment. These are surfaces with convexpatches sep-

arated by concave ridges. As such, one should not

attempt to compare our current method with other

general-purpose surface segmentation methods. Still,

the main added value of our technique for segmenting

general shapes (apart from the segmentation of den-

tal casts) is the proof that point-cloud skeletons can

be used for segmenting complex 3D surfaces. To our

knowledge, this result has not been shown so far in

current literature. Future work is needed to study how

this result can be extended to more general surfaces.

6 CONCLUSIONS

We have presented a method for segmenting compact

convex patches of 3D polygonal surfaces from den-

tal cast scans which are separated by shallow creases.

For this, we use the properties of surface skeletons,

in particular the sampling relationship between the

skeleton and its original surface, and the correspon-

dence relationship between the two surfaces given by

the feature transform. To our knowledge, our method

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

168

is the second existing technique able to use surface

skeletons to segment 3D surfaces. In contrast to the

ﬁrst published technique in this area (Reniers and

Telea, 2008b), we can directly handle meshed mod-

els without a costly voxelization step; we do not re-

quire the complex and sensitive detection of skeletal

boundaries; and we can treat signiﬁcantly more com-

plex shapes than the earlier cited method in this class.

Our research is motivated by the need to create

robust and fast segmentations of dental cast models,

driven by a concrete industrial application at Philips

Research, Eindhoven, the Netherlands. We foresee

several possible extensions of our method towards

a more general-purpose surface segmentation tech-

nique. Examples are the incorporation of surface dif-

ferential properties, captured by the feature transform,

in the analysis and segmentation of the surface skele-

ton, and application-adaptive skeleton simpliﬁcation

metrics that preserve or eliminate speciﬁc surface de-

tails for the purpose of more versatile segmentation.

REFERENCES

Amenta, N., Choi, S., and Kolluri, R. (2001). The power

crust. In Proc. SMA, pages 65–73. ACM.

Atron, Inc. (2013). 3D intraoral scanner. www.a-

tron3d.com/en/products/id-3d-intraoral-scanner.html.

Blum, H. (1967). A Transformation for Extracting New

Descriptors of Shape. In Wathen-Dunn, W., editor,

Models for the Perception of Speech and Visual Form,

pages 362–380. MIT Press, Cambridge.

Borgefors, G., di Baja, G., and Svensson, S. (2009). De-

composing digital 3D shapes using a multiresolution

structure. In Proc. DGCI, pages 19–28. Springer.

Bouix, S., Siddiqi, K., and Tannenbaum, A. (2005). Flux

driven automatic centerline extraction. Medical Image

Analysis, 9(3):209–221.

Bouix, S., Siddiqi, K., Tannenbaum, A., and Zucker, S.

(2006). Medial axis computation and evolution. In

Statistics and analysis of shape, chapter 1, pages 1–

28. Springer LNCS.

Clarenz, U., Griebel, M., Schewitzer, M., and Telea, A.

(2004). Feature sensitive multiscale editing on sur-

faces. Visual Computer, 20(5):329–343.

Comaniciu, D. and Meer, P. (2002). Mean shift: A robust

approach toward feature space analysis. IEEE TPAMI,

24(5):603–619.

Cornea, N., Silver, D., and Min, P. (2007). Curve-skeleton

properties, applications, and algorithms. IEEE TVCG,

13(3):87–95.

Frey, P. (2001). YAMS: a fully automatic adaptive isotropic

surface remeshing procedure. tech. rep. 0252, INRIA.

http://www.ann.jussieu.fr/ frey.

Garland, M., Willmott, A., and Heckbert, P. (2001). Hierar-

chical face clustering on polygonal surfaces. In Proc.

ACM Symp. I3D, pages 49–58.

Hirogaki, Y., Sohmura, T., Satoh, H., Takahashi, J., and

Takada, K. (2001). Complete 3-d reconstruction of

dental cast shape using perceptual grouping. Medical

Imaging, IEEE Transactions on, 20(10):1093–1101.

Jalba, A., Kustra, J., and Telea, A. (2013). Surface and

curve skeletonization of large 3D models on the GPU.

IEEE TPAMI, 35(6):1495–1508.

Kondo, T., Ong, S., and Foong, K. W. C. (2004). Tooth seg-

mentation of dental study models using range images.

IEEE Trans Med Imag, 23(3):350–362.

Kronfeld, T., Brunner, D., and Brunnett, G. (2010). Snake-

based segmentation of teeth from virtual dental casts.

CAGD, 7(2):221–233.

Ma, J., Bae, S., and Choi, S. (2012). 3D medial axis point

approximation using nearest neighbors and the normal

ﬁeld. Vis. Comput., 28(1):7–19.

Mangan, A. and Whitaker, R. (1999). Partitioning 3D sur-

face meshes using watershed segmentation. IEEE

TVCG, 5(4):308–321.

Mount, D. and Arya, S. (2011). Approximate nearest neigh-

bor search software. www.cs.umd.edu/ mount/ANN.

Palagyi, K. and Kuba, A. (1999). Directional 3D thinning

using 8 subiterations. In Proc. DGCI, volume 1568,

pages 325–336. Springer LNCS.

Pizer, S., Siddiqi, K., Szekely, G., Damon, J., and Zucker,

S. (2003). Multiscale medial loci and their properties.

IJCV, 55(2-3):155–179.

Provot, L. and Debled-Rennesson, I. (2008). Segmentation

of noisy discrete surfaces. In Proc. IWCIA, volume

4958, pages 160–171. Springer LNCS.

Pudney, C. (1998). Distance-ordered homotopic thinning:

A skeletonization algorithm for 3D digital images.

CVIU, 72(3):404–413.

Reniers, D., Jalba, A., and Telea, A. (2008a). Robust classi-

ﬁcation and analysis of anatomical surfaces using 3D

skeletons. In Proc. VCBM, pages 61–68. EG Press.

Reniers, D. and Telea, A. (2007). Tolerance-based fea-

ture transforms. In Advances in Comp. Graphics and

Comp. Vision, pages 187–200. Springer.

Reniers, D. and Telea, A. (2008a). Part-type segmentation

of articulated voxel-shapes using the junction rule.

CGF, 27(7):1837–1844.

Reniers, D. and Telea, A. (2008b). Patch-type segmenta-

tion of voxel shapes using simpliﬁed surface skele-

tons. CGF, 27(7):1954–1962.

Reniers, D., van Wijk, J. J., and Telea, A. (2008b). Com-

puting multiscale skeletons of genus 0 objects using a

global importance measure. IEEE TVCG, 14(2):355–

368.

Shamir, A. (2004). A formulation of boundary mesh seg-

mentation. In Proc.3DPVT, pages 378–386.

Siddiqi, K., Bouix, S., Tannenbaum, A., and Zucker, S.

(2002). Hamilton-Jacobi skeletons. IJCV, 48(3):215–

231.

Siddiqi, K. and Pizer, S. (2009). Medial Representations:

Mathematics, Algorithms and Applications. Springer.

Stolpner, S., Whitesides, S., and Siddiqi, K. (2009). Sam-

pled medial loci and boundary differential geometry.

In Proc. IEEE 3DIM, pages 87–95.

ShapeSegmentationusingMedialPointCloudswithApplicationstoDentalCastAnalysis

169

Stolpner, S., Whitesides, S., and Siddiqi, K. (2011). Sam-

pled medial loci for 3D shape representation. CVIU,

115(5):695–706.

Strzodka, R. and Telea, A. (2004). Generalized distance

transforms and skeletons in graphics hardware. In

Proc. VisSym, pages 221–230.

Telea, A. and Jalba, A. (2012). Computing curve skeletons

from medial surfaces of 3D shapes. In Proc. TPCG

(Eurographics UK), pages 273–280.

Zhao, M., Ma, L., Tan, W., and Nie, D. (2005). Interactive

tooth segmentation of dental models. In Proc. EMBS,

pages 654–657.

Zuckerberger, E., Tal, A., and Shlafman, S. (2002). Poly-

hedral surface decomposition with applications. Com-

puters & Graphics, 26(5):733–743.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

170