Joint Learning for Multi-class Object Detection

Hamidreza Odabai Fard

1,2

, Mohamed Chaouch

, Quoc-cuong Pham

, Antoine Vacavant

and Thierry Chateau

CEA, LIST, Vision and Content Engineering Laboratory, Point Courrier 94, F-91191, Gif-sur-Yvette, France

Institut Pascal, UMR6602, CNRS, Blaise Pascal University, Clermont-Ferrand, France

Image Science for Interventional Techniques, UMR6284, CNRS, University of Auvergne, Auvergne, France

Keywords:

Multi-class Object Detection, Structured Support Vector Machines, Joint Learning.

Abstract:

In practice, multiple objects in images are located by consecutively applying one detector for each class and

taking the best conﬁdent score. In this work, we propose to show the advantage of grouping similar object

classes into a hierarchical structure. While this approach has found interest in image classiﬁcation, it is not

analyzed for the object detection task. Each node in the hierarchy represents one decision line. All the decision

lines are learned jointly using a novel problem formulation.

Based on experiments using PASCAL VOC 2007 dataset, we show that our approach improves detection

performance compared to a baseline approach.

1 INTRODUCTION

Recent years have seen a steady progress in the

domain of object detection in still images. Focus

has been on developing robust features (e.g. (Dalal

and Triggs, 2005a)), capturing object variation (e.g.

(Felzenszwalb et al., 2010)) or incoorporating contex-

tual information (e.g. (Desai et al., 2011; Choi et al.,

2012)) to just name a few.

In this paper, we focus on showing that combin-

ing classes into a hierarchical structure further im-

proves object detection performance. In image clas-

siﬁcation, tree-like hierarchies have gained in popu-

larity (e.g. (Bengio et al., 2010; Grifﬁn and Perona,

2008)) as they allow to improve performance and de-

tection time compared to a classical one-versus-all

(OvA) technique. Improved performance using bi-

nary trees have been shown also in text categorization

in e.g. (Tsochantaridis et al., 2004). At this point, it is

essential to distinguish between the object detection

and the categorization (classiﬁcation) task. In the for-

mer case, the goal is to correctly localize k possible

object classes in an image. In the latter case, the task

is to distinguish between k given categories. The main

difference lies in the classes that the classiﬁer needs

to distinguish : In object detection, one is further con-

fronted with the background label which is usually

not modelled given us k + 1 classes. This background

class needs special attention and how to successfully

manage this issue is one of the contributions of the

underlying paper.

One difﬁculty in object detection is the ability to

generalize well from the training data. Most state-of-

the-art approaches assume a ﬂat separation between

the object categories and concentrate on improving

the performance of a generic detector. However,

from childhood on, humans tend to organize different

classes into a set of clusters (Joshua B. Tenenbaum1,

2011) giving them the ability to generalize from only

few seen (training) samples. This kind of represen-

tation assumes that nearby object classes share com-

mon properties. The importance of sharing between

different classes was among others also point out in

(Torralba et al., 2004; Salakhutdinov et al., 2011; Ott

and Everingham, 2011). Traditional techniques such

as OvA SVM detectors are unable to capture common

properties between classes.

We propose to group automatically similar classes

into a tree structure. The k leaf nodes of the tree rep-

resent the individual classes. The background class

is not modelled. The predecessors of the leaf nodes

are called super-classes as they group several classes

together. Each vertex in the tree represents a linear

classiﬁer. There are two intuitions why our tree im-

proves performance. First, similar classes share com-

mon features increasing the discriminative power of

104

Odabai Fard H., Chaouch M., Pham Q., Vacavant A. and Chateau T..

Joint Learning for Multi-class Object Detection.

DOI: 10.5220/0004692401040112

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 104-112

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

super-classes. Second, the increased number of lin-

ear classiﬁers allows to be non-linear during detec-

tion. This is due to the approximation of the non-

linear decision line between classes by a piece-wise

linear classiﬁcation function.

We call the linear SVMs for each vertex a ﬁlter.

There are as many ﬁlters as nodes in the tree. Ev-

ery ﬁlter is represented by a weight vector. These

weight vectors are learned in a novel joint framework.

During detection, we extract features in the image on

different scales. Every location is then scored by all

the ﬁlters in the tree. The scores of individual paths

are added together producing k ﬁnal scores. These

scores are ranked and the highest score determines the

foreground class. In case of a background region, the

score is negative. This allows us to implicitely clas-

sify background regions without modelling it in the

tree. Our algorithm combines ranking and classiﬁca-

tion constraints. We rank between the k classes and

are able to between foreground and background la-

bel. This is very different from the classiﬁcation task

where all the possible classes are directly modelled

and one needs to rank among the known classes.

In summary, we make the following contributions:

(i) We show that hierarchical learning improves ob-

ject detection performance. (ii) We combine ranking

and classiﬁcation constraints into one hybrid learn-

ing framework. All the weight vectors in the tree are

learned jointly. (iii) Our approach is independent of

the underlying feature descriptor and many descrip-

tors can be exploited (e.g. (Dalal and Triggs, 2005b;

Felzenszwalb et al., 2010; Zhang et al., 2011)).

In Sec. 2 we give an overview of the previous

works. In Sec. 3, we describe our detector and show

in Sec, 4 how it is trained, We show the evaluations in

Sec, 5 and conclude in Sec. 6.

2 RELATED WORK

Multi-class detection is a challenging task and an im-

portant subject of research. We show an approach that

is generic in the choice of features. This is an impor-

tant constraint on our formulation as feature descrip-

tors change over time. Traditional techniques such as

OvO (Kressel, 1999) or DAGSVM (Platt et al., 2000)

cannot be exploited as they are only able to distin-

guish between k known categories thus not handling

background.

Tree structures are widely used in image classiﬁ-

cation not handling a negative class. Here, we further

have to discriminate background regions. To our best

knowledge, Salakhutdinov et al. (Salakhutdinov et al.,

2011) were the ﬁrst to present a tree structure for ob-

ject detection where the weight vectors are learned it-

eratively one after another. We jointly optimize over

the tree. Their objective was to show that equilibrat-

ing the number of samples between classes helps to

improve object detection. We show that grouping

classes based on their feature similarity improves per-

formance.

In the domain of object detection, the idea of fea-

ture sharing using boosting was proposed by Torralba

et al. (Torralba et al., 2007). The decisions among the

classes are shared using combined weak classiﬁers.

Opelt et al. (Opelt et al., 2008) enhanced the previous

system by further incorporating geometric part infor-

mation.

Others take a more global approach by sharing

parts instead of features. Razavi et al. (Razavi et al.,

2011) apply a voting scheme where different parts

shared among classes use multi-class hough trans-

form to determine the object label. A similar tech-

nique (Ott and Everingham, 2011) applies a modi-

ﬁed version of the DPM (Felzenszwalb et al., 2010)

where common parts are found and grouped together.

Other approaches include sharing part locations and

deformations across the classes such as in (Fidler and

Leonardis, 2007; Fidler et al., 2010; Zhu et al., 2010).

These approaches in object detection lack to use

a generic feature descriptor as they are a multi-class

extension of their single-class formulation.

As mentioned earlier, hierarchical classiﬁcation

using SVM has been a subject of research in classiﬁ-

cation. (Grifﬁn and Perona, 2008) exploit binary trees

where each node in the tree is learned in a top-down

manner. Structured SVM was used in (Tsochantaridis

et al., 2004; Cai and Hofmann, 2004) to learn the ﬁl-

ters of a tree jointly. Zhou et al. (Xiao et al., 2011)

enforce orthogonality between parent and child in a

tree. Dekel et al. (Dekel et al., 2004) speed up the

training process by updating the vectors in the tree

using an online approach. In (Gao and Koller, 2011;

Marszalek and Schmid, 2008) the strict separation be-

tween categories is relaxed and each class can be fur-

ther split into sub-classes.

Again, these approaches are not suited for multi-

class object detection with a dominant background

label. We show an elegant algorithmic approach to

overcome the previously mentioned limitations.

3 SYSTEM OVERVIEW

In this section, we introduce our notation of the hier-

archical classiﬁcation module. We present our multi-

class detection procedure and describe how our model

attributes a score to different locations in an image.

JointLearningforMulti-classObjectDetection

105

(a)

car:9x5

bus:11x7

person:5x9

sheep:7x7

11x7

7x9

11x9

(b)

\boldmath{$x$}

descriptor

Figure 1: (a) We annotate the root ﬁlter by n

and the leaf ﬁlters by n

where y is its position from the left and corresponds

to a class. We also show the ﬁlter dimensions. The sizes for the leaf nodes are learned in as in (Felzenszwalb et al., ). The

parents’ nodes choose between the maximum height and width among their children’s dimensions. The attribute vector and

the ﬁnal score for the ’car’ class is also depicted for an example. In (b), the example from (a) is used to show how the nodes

extract features around a center position x. The white bounding box indicates the ground truth annotation.

Let |T | be an arbitrary tree with k leaf nodes. Each

path to a leaf node models a class. n

.i ∈ {1, . . . , |T |}

designates any node in the tree and |T | is the total

number of leaf nodes. Further, n

and n

, i ∈ {1, . . . , k}

shall represent the root node and the i-th leaf node

as annotated in Fig. 1. anc(n

) is the set of the an-

cestors of node n

including itself and desc(n

) the

set of the descendants excluding n

. Each path to

node n

is determined by its attribute vector Λ

(λ

, . . . , λ

|T |

) ∈ R

|T |

with



1 , if n

∈ anc(n

)

0 , otherwise

(1)

In other words, the entries λ

in the attribute vec-

tor are 1 for nodes lying on the path up to the node

and 0 otherwise (see Fig. 1). In addition, let x

be a position in an image. The feature vector φ

(x)

the features for node n

at the location x. As can be

seen in Fig. 1, every node extracts features around

a region centered by x. We refer to the concate-

nated vector of all the feature vectors from top-to-

bottom and left-to-right by Φ(x). The class labels

∈ Y ≡ {y

, . . . , y

, y

} ≡ Y

∪ {y

} are positive

for the target classes and negative y

= −1 for the

background regions.

Every node represents a parameter vector w

de-

termined during training. They are ﬁlters attribut-

ing a partial score w

· φ

(x) to a location x. Finally,

let w = {w

, w

, . . . , w

|T |

} be the stacked vector of all

w(n

3.1 Our Object Detection Model

Given an input image, our objective is to locate ob-

jects belonging to the k target classes. We assign to

ever possible location in the image a label y

∈ Y

the object is an target object or y

= y

if the region

is background.

Our object detection process follows the follow-

ing pipeline as shown in Fig. 2. The input image is

scaled with different scaling factors to allow detecting

objects of various sizes. Next, features are extracted

for every scale. The grouping of all these features

across all levels is called a feature pyramid. We do

not limit our choice to a speciﬁc feature descriptor.

Here, we report our experiments on a variant of the

histogram of orientated gradients (HOG) (Dalal and

Triggs, 2005b) as proposed in (Felzenszwalb et al.,

2010) for its popularity and simplicity. Our hierar-

chical classiﬁer attributes a score and label to every

location in the feature pyramid. For a positive re-

gion, there maybe several positive responding posi-

tions around that region. We merge all the overlap-

ping responses using a non-maxima suppression step

(see Sec. 3.2). The result is a set of possible instances

of the target objects.

Our detection module uniﬁes classiﬁcation and

ranking tasks. The objects in the feature pyramid are

ranked among the k target class. The class label is de-

termined by the highest scoring class. The object is

classiﬁed as background if the highest score is nega-

tive.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

106

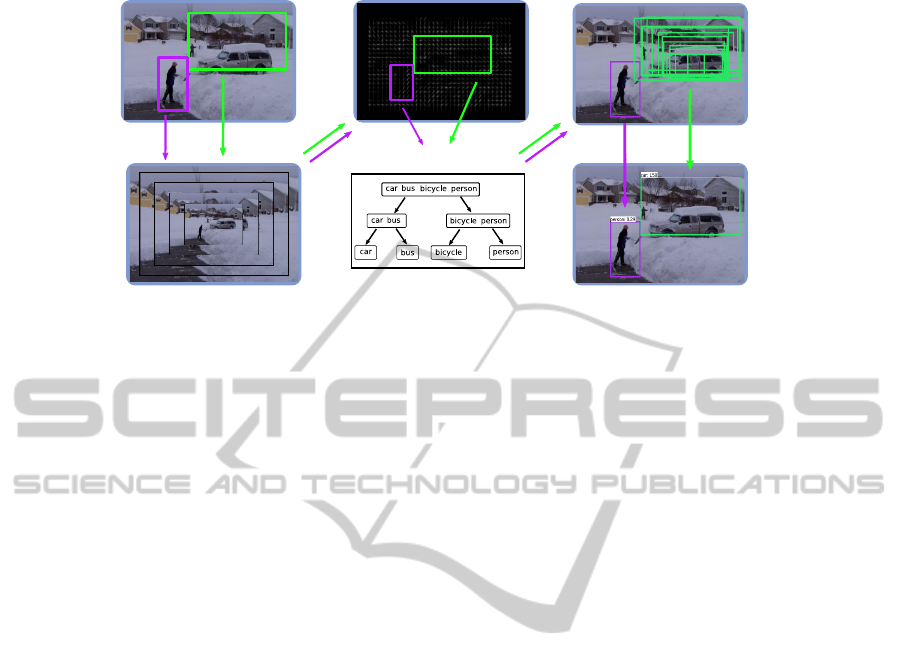
Input image

Feature extraction at one scale

NMS

Scaled images

Multi-class classiﬁer

Output image

Figure 2: We use a sliding window approach to detect objects of different categories in still images. Our hierarchical detector

ranks and classiﬁes between object categories and background.

3.2 Inference

For a given location x in the feature pyramid, we cal-

culate a score score(x) which is the best score pro-

duced by all the single classes:

score(x) = max

y∈{1,...,k}

score

(x) (2)

The object label ˆy is determined by :

ˆy =



−1 , if score(x) ≤ 0

argmax score(x) , otherwise

(3)

Next, let Φ

(x) deﬁne the concatenated feature vec-

tors of all the features φ

(x) extracted by each node

lying on the path to node n

. The features extracted

by nodes not being an ancestor of n

are zeroed. More

formally:

(x) = Λ

⊗ Φ(x) =







· φ

(x)

· φ

(x)

···

|T |

· φ

(x)







(4)

This kind of representation allows to deﬁne classes

by local to global parameters as individual classes are

grouped together into global super-classes. Then, the

scoring function of a class y is given by:

score

(x) = w

· Φ

(x) (5)

The Eq. 5 is used in Eq. 3 and Eq. 2 to determine the

ﬁnal class score and label of a position x in the feature

pyramid.

3.3 Non-maxima Suppression

We assume that object instances of the same class

cannot share the same location in an image. We sup-

press multiple instances using our non-maxima sup-

pression scheme (NMS). We treat every class sepa-

rately. For a given class, we sort all the scores in

decreasing order and reject the remaining detections

having a sufﬁcient overlap (e.g. 0.5%) with the higher

scoring detections. Thus, we assure that same in-

stances do not share the same positions. Different ob-

ject categories can share nearby locations e.g. a per-

son and bicycle.

4 LEARNING THE

HIERARCHICAL TREE

MODEL

In this section, we describe our learning algorithm

which automatically learns the tree structure, the di-

mensions of the ﬁlters and the weight vectors of each

node in the tree in a joint hybrid framework.

4.1 Learning the Hierarchy

The tree T is built in an automatic way. The goal is

to hierarchically group similar classes. We say two

classes are similar if they are likely to be confused.

Grouping classes together allows to better general-

ize to future unseen examples as the super-classes

are trained using all the samples of its descendant

classes. For example a ’bicycle’ and a ’motorbike’

share many features and training a super-class node

{’bicycle’,’motorbike’} increases their discriminative

power.

We build a class similarity matrix S : k × k where

each element s

i j

measures the similarity between

class i and j. To this end, a detector is trained for

each class. The k detectors classify the objects of

all the other classes. The similarity s

i j

is the median

value given by classifying examples of class i with the

JointLearningforMulti-classObjectDetection

107

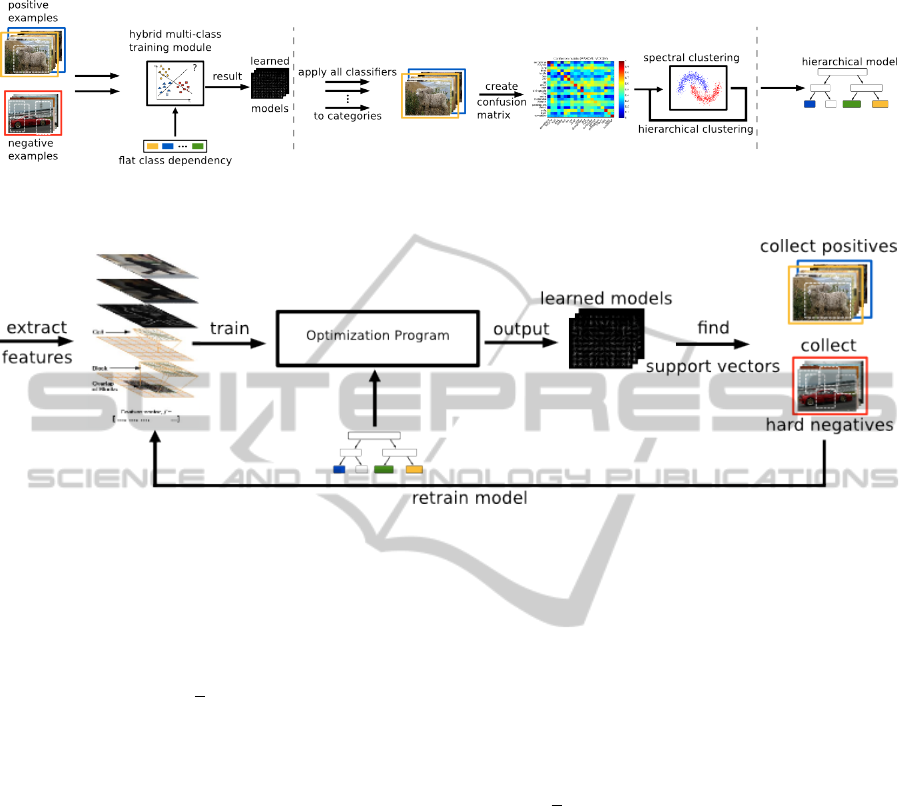
(a)

(b)

Figure 3: Illustating the different steps during the training process. (a) shows the creation of the hierarchy. The hybrid multi-

class training module is shown in (b). Given some training data, it extracts the features, trains the ﬁlters of the tree and if

necessary applies boostrapping to collect support vectors.

detection model of class j. To obtain a symmetrical

matrix, we average with its transposed:

S ←

(S + S

) (6)

Spectral clustering (Luxburg, 2007) is a clustering

technique which uses the spectrum of a similarity ma-

trix to partition the data. The objective is to build

(two) groups having a high intra-class but low inter-

class similarity. We apply spectral clustering hierar-

chically to S . At each iteration, the data is split into

two groups until the leaf nodes are reached. We en-

force balanced binary trees in the k-means step of the

spectral clustering algorithm. The result is the struc-

ture of our tree T . The tree building process is de-

picted in Fig. 3.

4.2 Problem Formulation

As described in Sec. 3, our hierarchical framework

ranks and classiﬁes object regions. We use support

vector machines (SVM) to learn the weight vectors,

of each node in the tree. Traditional SVM solvers

as (Joachims, 1999; Chang and Lin, 2011) minimize

a max margin problem subject to classiﬁcation con-

straints. Other solvers such as RankSVM (Joachims,

2002) or PRSVM (Chapelle and Keerthi, 2010) train

on ranking constraints where the goal is to rank the

correct class label higher than all the other classes.

We suggest a novel optimization problem consist-

ing of a mixture of classiﬁcation and ranking con-

straints. Given n

positive and n

−

negative samples,

the problem is formulated as following:

min

w,ξ

( j)≥0

kwk

∑

i=1

(ξ

∑

j=1

i j

) +

−

×n

∑

i, j

i j

(7a)

s.t. ∀y

∈ Y

, ∀y

∈ Y

: w

· δΦ

) ≥ 1 − ξ

i j

(7b)

: w

· Φ

) ≥ 1 − ξ

(7c)

∀y

∈ {y

}, ∀y

∈ Y

: −w

· Φ

) ≥ 1 − ξ

i j

(7d)

where δΦ

(y) = Φ

) − Φ

) and w a concatena-

tion of the ﬁlter weights in the tree T. The objective

function 7a minimizes two kinds of errors:

∑

i=1

−

∑

i, j

i j

is the error of classifying target

regions as negative or classifying a background

sample as one of the k classes.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

108

Algorithm 1: Learn weight vectors of each node in T .

1: Input: Tree T

2: Samples: {(x

, y

), . . . , (x

, y

)} ∈ X × Y

3: Output: w = {w

, . . . , w

|T |

}

4: W =

5: repeat

6: for all i = 1 . . . n do

7: ¯y

= argmax

y∈Y

1 + w

· Φ

)

8: end for

9: W ←

{

∑

i=1

· Φ

)−

max(w

·Φ

¯y

), 0) −

∑

−

i=1

·Φ

¯y

)} ≥ 1 −

10: W → SVM

light

11: until stopping criteria is reached

∑

j=1

i j

is the error of classifying an object of class

as y

7d and 7c represent the (n

+ n

−

) classiﬁcation con-

straints where as 7b are the (n

× n

−

) ranking con-

straints. This makes a total of (n

× n

−

+ n

−

)

constraints which need to be optimized (Sec. 4.3).

4.3 Cutting-plane Optimization

The optimization problem in Eq. 7 is a convex op-

timization problem. We apply the cutting plane algo-

rithm (Joachims et al., 2009) to considerable speed-up

detection time. First, the n-slack formulation in Eq.

7 is rewritten as a 1-slack formulation, All the con-

straints share the same slack variable ξ thus giving us

the following learning task:

min

w,ξ≥0

kwk

+Cξ (8a)

s.t. ∀( ¯y

, · · · , ¯y

) ∈ Y

{

∑

i=1

· δΦ

( ¯y) + w

· Φ

))

−

∑

i=1

· Φ

¯y

)} ≥ 1 − ξ.

(8b)

At the ﬁrst sight, the formulation suffers from the

huge amount of constraints Y

namely one constraint

for each possible combination of labels (¯y

, · · · , ¯y

) ∈

. The cutting plane algorithm only uses a small

subset of all possible constraints by iteratively build-

ing a working set W of constraints. At each iteration,

one constraint at a time is added to W . The cutting

plane optimization is summarized in Algorithm 1.

The algorithm starts with an empty working set

and a starting weight vector w. In line 7, the most

discriminative class label is calculated for each train-

ing sample. The label ¯y

is the class which confuses

most with the ground truth class. Line 9 adds the

new constraint into the working set. This constraint is

the sum of individual constraints producing only one

single new constraint per iteration. We use SVM

light

(Joachims, 1999) to solve the constraints in the work-

ing set.

4.4 Implementation Details

We changed the publicly available SVMStruct pack-

age (Joachims et al., 2009) to include our deﬁnition

of the joint feature vector and the combined con-

straints. The object descriptors are histogram of ori-

entated gradients (Felzenszwalb et al., 2010).

During training, we ﬁrst learn the hierarchy. Us-

ing the tree, we train a model based on all posi-

tive samples and randomly collected negatives. This

model is iteratively used to collect high scoring neg-

ative samples called hard negatives. This bootstrap-

ping procedure strongly improves object detection

systems.

The nodes are characterized by a pair (v

, dim

is a vector specifying the location of the ﬁlter rel-

ative to the root position. dim

designates the dimen-

sions of node n

. These dimensions for every class are

built in a bottom-to-up fashion. First the dimensions

of the leaf ﬁlters are determined as in (Felzenszwalb

et al., ). The aspect ratio is chosen to be the most

common mode in the annotated bounding boxes. The

size is picked up not to be larger than 80% of the data.

Given the width and height of each node, the dimen-

sions of the remaining nodes are the maximum width

respectively height H

over its children dimensions

(refer to Fig. 1 for an example):

= max

∈desc(n

)

= max

∈desc(n

)

(9)

5 EXPERIMENTAL RESULTS

The following section shows the evaluations of our

approach on the PASCAL VOC’07 (Everingham

et al., ) dataset and protocol. The dataset has a to-

tal of 20 classes represented by 12608 annotated ob-

jects. It is equally divided into a training and valida-

tion set. We study and illustrate (1) the importance

of hierarchy to increase multi-class object detection

performance which is the main contribution of this

work and (2) the ability to generalize fast when using

our tree. We use simple HOG features to show our

contribution. As such, our results are relative to the

performance of HOG and should not be compared to

JointLearningforMulti-classObjectDetection

109

state-of-the-art object detectors. More powerful fea-

tures could have been used. We opted for HOG for its

popularity and widespread usage.

Detection Models. Our method is tested on ﬁve de-

signed detection algorithms which allow to validate

the different aspects of our method : (1) One-vs-

All (OvA) treats every class separately. It trains an

SVM for each class. The ﬁnal decision functions are

transformed into a probabilistic output using (Platt

et al., 2000). (2) The second model called ’ours ﬂat’

learns all the weight vectors jointly using the hybrid

learning algorithm but no hierarchical structure. The

last model ’ours tree’ trains a complete hierarchical

model using the combination of ranking and classiﬁ-

cation constraints.

Detection Performance. The goal is to show how

the hierarchical structure optimized using the hybrid

training algorithm improves detection performance.

We evaluate on 5 different settings by varying the

number of classes k = {2, 4, 6, 8, 10} and show that

the improvement is true independent of k. The 10

selected classes are: {’bus’, ’bicycle’, ’motorbike’,

’car’, ’aeroplane’, ’person’, ’cow’, ’horse’, ’dog’,

’cat’}. Among the classes are certain ones where

we would expect a strong degree of feature sharing

(e.g.’car’ and ’bus’) and other categories with less

common properties (e.g.’person’ and ’aeroplane’).

Table 1 illustrates the detection performance of the

detection models for the different settings (k) in terms

of the mean average precision (mAP) used in PAS-

CAL VOC’07 evaluation protocol. The tree structure

for k = 10 classes with the corresponding similarity

matrix used to deduce the tree is depicted in Fig. 5.

’ours ﬂat’ achieves slightly better results compared to

OvA. A joint learning of all ﬁlters and mixing clas-

siﬁcation and ranking constraints achieve at least as

good results as OvA. Using our complete algorithm

’ours tree’ which uses a tree yields the best results.

This is due to an increase of the number of linear ﬁl-

ters used for the ﬁnal classiﬁcation and the feature

sharing between neighboring nodes.

The individual scores for k = 10 are depicted in

table 2. 8 out of 10 classes improve in performance

compared to OvA using our joint learning framework.

Only 2 classes {’bus’,’dog’} degrade in performance.

The classes ’car’ (+3.1) and bicycle (+5.9) have the

best increase in performance.

Fast Generalizing Ability. We learn a model rep-

resenting the classes {’bicycle’,’motorbike’} using

OvA and our hierarchical detector. We investigate

how quickly the average precision (AP) of class ’mo-

torbike’ achieves its maximum score when we vary

the number of its training examples. The intuition be-

Table 1: Mean average precision (mAP) of the 4 detection

models. Our hierarchical approach always improves over

OvA.

k 2 4 6 8 10

OvA 24.1 23.4 20.6 18.3 15.2

ours ﬂat 24.4 23.9 20.7 18.8 15.5

ours tree 25.5 25.7 23.6 20.6 16.4

hind this setup is to understand how the knowledge

of class ’bicycle’ helps to quickly learn the similar

class ’motorbike’. This comes close to transfer learn-

ing techniques (e.g. (Aytar and Zisserman, 2011; Lim

et al., 2011)) aiming at learning a new class with as

few examples as possible. Here, the class ’bicycle’

using all of its examples helps the class ’motorbike’

having fewer examples but highly similar features and

examples.

In Fig. 4, we illustrate the relative average preci-

sion of class ’bicycle’ using these two techniques in

function of the relative percentage of examples used.

We normalize all the AP to the AP when full examples

are available for both classes. We note that for OvA,

having very few training examples only 40% of the

ﬁnal score is reached. However, using the hierarchi-

cal classiﬁer, even with very few training examples,

nearly the full AP is attained. Our approach is able to

generalize fast when a small amount of samples are

available. This is due to the fact that these two classes

have may features and examples in common.

6 CONCLUSIONS

We presented a novel hierarchical multi-class detec-

tion system. Our approach is not limited to the

choice of the object descriptors. We combined rank-

ing and classiﬁcation constraints giving a new op-

timization problem. Foreground objects are ranked

among each other while being able to classify fore-

ground/background regions. We learn the model in

a joint framework where we ﬁrst learn the hierarchy

between objects and the train all the weight vectors

jointly.

The experimental results clearly showed an in-

crease of detection performance for different set-

tings in the number of classes. This is due to the

increased number of discriminative weight vectors

learned. Moreover, similar classes share features and

examples which help to generalize faster. This was

further illustrated in our experiments where having

few samples for one class still allowed to achieve the

score when the full training set is available.

In the future, we would like to enhance our hierar-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

110

Table 2: Mean average precision for each class after learning k = 10 classes.

class aero bike bus car cat cow dog horse mbike person

#samples 306 353 229 1250 376 259 510 362 339 4690

OvA 17.6 20.3 24.0 29.2 2.3 8.4 3.1 14.4 15.3 17.5

ours ﬂat 17.9 24.6 21.8 26.2 6.0 8.2 4.5 12.1 15.6 18.1

ours tree 20.3 26.2 21.5 32.3 2.3 11.4 1.2 15.4 15.5 18.2

0.2

0.4

0.6

0.8

1.2

0.2 0.4 0.6 0.8 1

Percentange of used samples

Learning with Few Samples

OvA

Hierarchy

Relative AP

Figure 4: The generalization ability of our approach. We

train a model for two classes {’motorbike’,’bicycle’} with

OvA and with our algorithm. We vary the number of ex-

amples and analyze the inﬂuence on the AP compared to

the AP when all the examples are available. OvA slowly

increases in performance as the number of examples in-

creases. Our approach achieves much faster its ﬁnal AP

score. We noted a slightly better AP when using 80% of the

dataset. We believe that using all the samples introduces

more noise in the training process shifting the separating

decision line.

(a) (b)

Figure 5: (a) The similarity matrix S obtained for k = 10

classes when building the taxonomy. (b) The resulting tree

structure derived by the similarity matrix S .

chy with the deformable part model of (Felzenszwalb

et al., ). This new hierarchical deformable part model

allows us to automatically ﬁnd parts between object

classes and understand its role to improve object de-

tection performance.

REFERENCES

Aytar, Y. and Zisserman, A. (2011). Tabula rasa: Model

transfer for object category detection. In IEEE Inter-

national Conference on Computer Vision.

Bengio, S., Weston, J., and Grangier, D. (2010). Label em-

bedding trees for large multi-class tasks. In NIPS.

Cai, L. and Hofmann, T. (2004). Hierarchical document

categorization with support vector machines. CIKM.

Chang, C.-C. and Lin, C.-J. (2011). LIBSVM: A library for

support vector machines. ACM Transactions on Intel-

ligent Systems and Technology. Software available at

http://www.csie.ntu.edu.tw/∼cjlin/libsvm.

Chapelle, O. and Keerthi, S. S. (2010). Efﬁcient algorithms

for ranking with svms. Inf. Retr.

Choi, M. J., Torralba, A., and Willsky, A. S. (2012). Context

models and out-of-context objects. Pattern Recogni-

tion Letters.

Dalal, N. and Triggs, B. (2005a). Histograms of oriented

gradients for human detection. In CVPR.

Dalal, N. and Triggs, B. (2005b). Histograms of oriented

gradients for human detection. In International Con-

ference on Computer Vision & Pattern Recognition.

Dekel, O., Keshet, J., and Singer, Y. (2004). Large margin

hierarchical classiﬁcation. In ICML.

Desai, C., Ramanan, D., and Fowlkes, C. (2011). Discrimi-

native models for multi-class object layout. IJCV.

Everingham, M., Van Gool, L., Williams, C. K. I., Winn,

J., and Zisserman, A. The PASCAL Visual Object

Classes Challenge 2007 (VOC2007) Results. http://

www.pascal-network.org/ challenges/ VOC/ voc2007/

workshop/index.html.

Felzenszwalb, P. F., Girshick, R. B., McAllester, D., and

Ramanan, D. Object detection with discriminatively

trained part based models. PAMI.

Felzenszwalb, P. F., Girshick, R. B., McAllester, D. A., and

Ramanan, D. (2010). Discriminative latent variable

models for object detection. In ICML.

Fidler, S., Boben, M., and Leonardis, A. (2010). A coarse-

to-ﬁne taxonomy of constellations for fast multi-class

object detection. In ECCV.

Fidler, S. and Leonardis, A. (2007). Towards scalable repre-

sentations of object categories: Learning a hierarchy

of parts. In CVPR.

Gao, T. and Koller, D. (2011). Discriminative learning of

relaxed hierarchy for large-scale visual recognition. In

ICCV.

Grifﬁn, G. and Perona, P. (2008). Learning and using tax-

onomies for fast visual categorization.

JointLearningforMulti-classObjectDetection

111

Joachims, T. (1999). Advances in kernel methods. chapter

Making large-scale support vector machine learning

practical.

Joachims, T. (2002). Optimizing search engines using click-

through data. In KDD.

Joachims, T., Finley, T., and Yu, C.-N. (2009). Cutting-

plane training of structural svms. Machine Learning.

Joshua B. Tenenbaum1, Charles Kemp, T. L. G. N. D. G.

(2011). How to grow a mind: Statistics, structure, and

abstraction. Science.

Kressel, U. H.-G. (1999). Advances in kernel methods.

chapter Pairwise classiﬁcation and support vector ma-

chines.

Lim, J. J., Salakhutdinov, R., and Torralba, A. (2011).

Transfer learning by borrowing examples for multi-

class object detection. In Neural Information Process-

ing Systems (NIPS).

Luxburg, U. (2007). A tutorial on spectral clustering. Statis-

tics and Computing.

Marszalek, M. and Schmid, C. (2008). Constructing cate-

gory hierarchies for visual recognition. In ECCV.

Opelt, A., Pinz, A., and Zisserman, A. (2008). Learning

an alphabet of shape and appearance for multi-class

object detection. IJCV.

Ott, P. and Everingham, M. (2011). Shared parts for de-

formable part-based models. In CVPR.

Platt, J. C., Cristianini, N., and Shawe-taylor, J. (2000).

Large margin dags for multiclass classiﬁcation.

Razavi, N., Gall, J., and Gool, L. J. V. (2011). Scalable

multi-class object detection. In CVPR.

Salakhutdinov, R., Torralba, A., and Tenenbaum, J. B.

(2011). Learning to share visual appearance for mul-

ticlass object detection. In CVPR.

Torralba, A., Murphy, K. P., and Freeman, W. T. (2004).

Sharing features: efﬁcient boosting procedures for

multiclass object detection. In CVPR.

Torralba, A., Murphy, K. P., and Freeman, W. T. (2007).

Sharing visual features for multiclass and multiview

object detection. PAMI.

Tsochantaridis, I., Hofmann, T., Joachims, T., and Altun, Y.

(2004). Support vector machine learning for interde-

pendent and structured output spaces. In ICML.

Xiao, L., Zhou, D., and Wu, M. (2011). Hierarchical clas-

siﬁcation via orthogonal transfer. In ICML.

Zhang, J., Huang, K., Yu, Y., and Tan, T. (2011). Boosted

local structured hog-lbp for object localization. In

CVPR.

Zhu, L., Chen, Y., Torralba, A., Freeman, W. T., and Yuille,

A. L. (2010). Part and appearance sharing: Recursive

compositional models for multi-view. In CVPR.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

112