Pose Recognition in Indoor Environments using a Fisheye Camera

and a Parametric Human Model

K. K. Delibasis

, V. P. Plagianakos

and I. Maglogiannis

University of Central Greece, Department of Computer Science and Biomedical Informatics, Lamia, Greece

University of Piraeus, Dept. of Digital Systems, Piraeus, Greece

Keywords: Human Activity Detection, Computer Vision, Fisheye Camera Modeling, 3D Human Modeling, Posture

Recognition.

Abstract: In this paper we present a system that uses computer vision techniques and a deformable 3D human model,

in order to recognize the posture of a monitored person, given the segmented human silhouette from the

background. The video data are acquired indoors from a fixed fish-eye camera placed in the living

environment. The implemented 3D human model collaborates with a fish-eye camera model, allowing the

calculation of the real human position in the 3D-space and consequently recognizing the posture of the

monitored person. The paper discusses the details of the human model and fish-eye camera model, as well

as the posture recognition methodology. Initial results are also presented for a small number of video

sequences, of walking or standing humans.

1 INTRODUCTION AND

RELATED WORK

The field of automated human activity recognition

utilizing fixed cameras in indoor environments has

gained significant interest during the last years. It

finds a wide variety of applications in diverse areas,

such as assistive environments, supporting the

elderly or the chronic ill, surveillance and security,

traffic control, industrial processes etc. This work

focuses in pose estimation of walking or standing

human from fisheye video: therefore human

silhouette segmentation of the video sequence is a

prerequisite. The proposed algorithm is based on a

parametric three-dimensional (3D) human model

that can move its legs and arms, as well as on a

model of the fisheye camera that allows the

rendering of the parametric model. An evolutionary

optimization algorithm is used to recover the

parameters of the 3D human model.

The first step in applications dealing with human

activity recognition from video is foreground

segmentation. Most of the video segmentation

algorithms are based on background subtraction. The

background has to be modelled, since it may change

due to a number of reasons, including: motion of

background objects, differences in light conditions,

or video compression artefacts. Therefore, a number

of techniques have been proposed for constructing a

model of the background that is being gradually

updated using the values of the current video frame.

In (Willems 2009) the background model is defined

as the previous frame. Background can be modelled

by median filtering (Cucchiara 2003) of a predefined

number of last frames that are hold in a buffer. The

background value of each pixel in the model is

independently computed as the temporal median of

the pixel values along the buffer. This approach

however may become slow for large frame sizes.

Other approaches (eg. McFarlane and Schofield

1995, or the running average Willems 2009) use an

incremental update of the background, without the

need of a buffer to store previous frames. An

extension of the aforementioned methods is the

running Gaussian average which was proposed in

(Wren 1997). A more complex but popular

segmentation algorithm is the Mixture of Gaussians

(MoG), initially described for video sequences by

Stauffer and Grimson (1999).

In this work we have performed video

segmentation using the illumination sensitive

method (Cheng 2011), as implemented in

(Christodoulidis 2012). This technique is based on

the entropy calculation of each frame and it solves

the problem of sudden illumination changes, which

470

Delibasis K., Plagianakos V. and Maglogiannis I..

Pose Recognition in Indoor Environments using a Fisheye Camera and a Parametric Human Model.

DOI: 10.5220/0004693704700477

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 470-477

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

affect significantly the background modelling.

Therefore it is considered appropriate for the

proposed system.

Regarding the human silhouette modelling,

articulated stick human models are quite popular for

pose estimation. Volumetric human models use

geometric primitives such as are spheres, cylinders

or tapered super-quadrics (Delamarre 2001), (Kehl

2006). Surface-based models of the human body

typically consist of a mesh of polygons that may be

deformed (Barron 2001).

Pose estimation is achieved by recovering the

values of the human model parameters. A number of

reported works use the “top-down estimation”, by

comparing the rendered 3D human model with the

actual frame, using local search methods (Bregler

2004).

A small number of approaches use information

about the camera model and setting, to assist pose

recovery. In (Taylor 2000) the perspective

information of a mono-occular camera is used. In

(Liebowitz 2003) reconstruction of 3D poses from

2D point correspondences is reported, using multiple

views and known body segment lengths. Detailed

description of these approaches can be found in the

survey of (Poppe 2007).

In the proposed system video is captured using

360 degrees field of view (FoV) hemispheric

cameras, also known as fisheye cameras. The

utilization of fisheye cameras is increasing both in

robotic applications and in video surveillance

(Kemmotsu 2006), (Zhou 2008). In (Saito 2010) a

probabilistic model of pedestrians imaged by a

fisheye camera is utilized. As fisheye cameras with

megapixel sensors are now available, research in

calibration of such cameras becomes increasingly

useful. Thus, the topic of fish-eye camera calibration

has attracted significant attention, on its own. In (Li

2006) and (Basu 1993) the calibration of fisheye

camera is reported using high degree polynomials to

emulate the strong deformation effects introduced by

the fisheye lens. In (Shah 1996) a detailed model is

presented for fisheye camera calibration, which

estimates the radial and tangential deformation,

using a polynomial mapping between the radial

distance from the optical axis of a real world point

and its imaged point on the image plane. In this

work, we employ the forward and inverse camera

model that was proposed in (Delibasis 2013).

Regarding human modeling we employ a simple

triangulated 3D parametric model with a number of

degrees of freedom and follow a “top-down”

approach by matching the model rendered through

the calibrated fisheye camera, with the segmented

frame of the video. Evolutionary optimization is

used to recover the model parameters and determine

human motion and pose. The range of the

parameters of the model is narrowed, using the

segmentation refinement algorithm that we proposed

in (Delibasis 2013). The rest of the paper is

structured as follows: Section 2 discuss the technical

details of the proposed algorithms and techniques,

Section 3 presents some initial results and finally

Section 4 concludes the paper.

2 MATERIALS AND METHODS

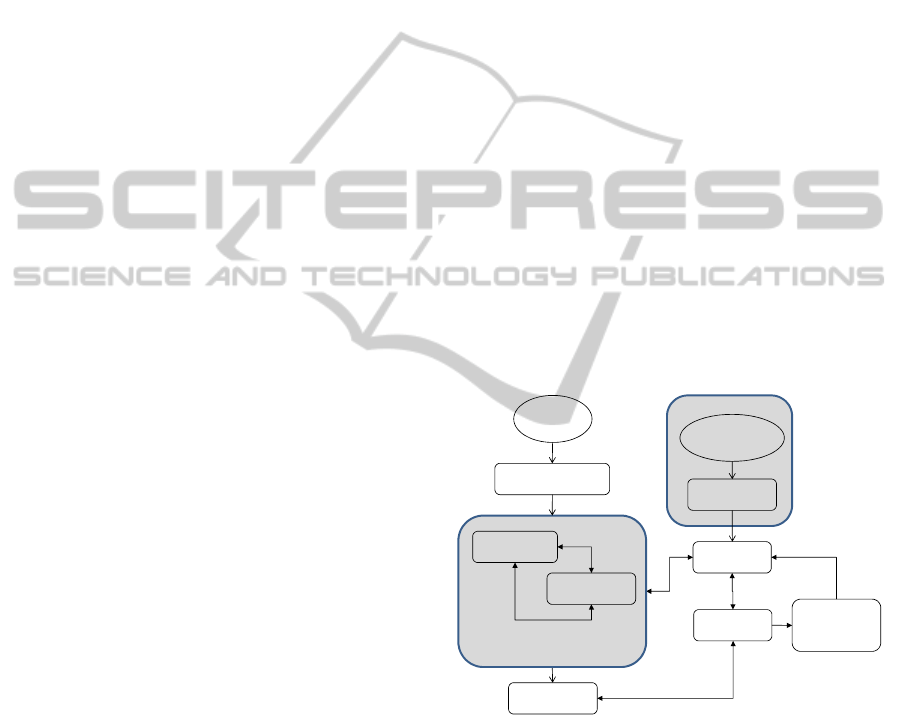
2.1 Overall Architecture

The overall architecture of the proposed system is

illustrated in Fig. 1. It comprises of a) a model of the

fisheye camera that enables the extraction of the

direction of view of each pixel of the video frame

(originally proposed in Delibasis 2013), b) a 3D

parametric model of a human and c) an evolutionary

algorithm that recovers the parameters of the 3D

human model, based on an objective function that

compares the rendering of the 3D model through the

camera model to the segmented human.

Figure 1: The overall system architecture.

2.2 Fisheye Camera Model

The main characteristic of the fisheye camera is that

it can cover a field of view of 180 degrees. We use a

model to simulate the image formation using the

fisheye camera, so that given the real-world position

of an object (x,y,z), we may calculate the image

coordinates (j,i) of its pixels. The action of the

fisheye model M can be written in the general form









,,,ji M x yz



(1)

Calibration of

Fisheye model

Background

segmen tation

Human posture

recognition

Parametric model

of 3D Human

Fisheye

simulation

Video

input

Video Single

frame, User

measurements

Evolutionary

optimization

Performed once

Iteratedpart

Reject binary

objects

Merge binary

objects

Refinement of segmentation

of Human

PoseRecognitioninIndoorEnvironmentsusingaFisheyeCameraandaParametricHumanModel

471

We adopted a model for the fisheye camera that is

based on the physics of image formation, as

described in (Max 1983), (Greene 1986) and

demonstrated in (http://paulbourke.net/ dome/

fisheye/) and (Delibasis 2013). We consider a

spherical element of arbitrary radius R

with its

center at K(0,0,z

sph

) (as it will become clear soon, the

radius R

is not a parameter of the model). For any

point P with real world coordinates (x,y,z), we

determine the intersection Q of the line KP with the

spherical optical element of the fisheye lens. The

point P is imaged at the central projection





im im

of Q on the image plane with equation z=z

plane

, using

the O(0,0,0) as center of projection, assuming that

the installation of the camera is such that the

imaging plane (i.e. the image sensor) is horizontal

and the axis of the spherical lens is not misaligned.

Thus, it becomes obvious that all real world points

that lie on the KP line are imaged at the same point



im im

y of the image plane. The KP line is

uniquely defined by its azimuth and elevation

angles, θ, φ respectively. The concept of the fisheye

geometric model is shown in Fig. 2.

The fisheye camera has no moving parts.

Therefore, the ratio

ph plane

pz z is the primary

parameter of the fisheye model.

plane

is set to an

arbitrary value less than

, thus

ph plane

zpz . It is

possible that small internal lens misalignments may

introduce unanticipated imaging deformations (Shah

1996). Thus, we introduce two extra model

parameters, the

X and Y position of the center of

spherical lens

ph sph

y with respect to the optical

axis of the camera. Now the center of the spherical

element becomes K(x

sph

, y

sph

, z

sph

). Fig. 2 shows the

case for

0, 0

sph sph

xy

for simplicity. The

position of any point of the line segment KP, thus Q

as well, is given by

 

,, , ,

y z sph sph sph

QQQ x x y y z z



  

(2)

where λ is a parameter in range [0,1].

If we insert this into the equation of the spherical

optical element, we derive an equation whose

solution defines λ and the position of Q:









sph sph sph sph

sph sph

xx x yy y

zz z R





  

 

(3)

Figure 2: The geometry of the fisheye model.

The final step is the calculation of the central

projection





im im

of Q on the image plane:



plane

im im x y

sph

yQQ



(4)

For any point P with real world coordinate

z>z

sph

, its projection onto the image plane



im im

is bounded by the radius of the virtual spherical

optical element R

00im sph

Rx x R



 . When



then





0im sph

xR . The same holds for

the y coordinate. The image pixel (i,j) that

corresponds to





im im

y is calculated by a simple

linear transform:

 



,, ,

FoV

im im x y

ixy CoDCoD



(5)

where (CoD

, CoD

) is the center of distortion pixel

that corresponds to elevation φ=π/2 and R

FoV

is the

radius of the circular field of view (FoV). For the

fish-eye camera, (Micusik 2006) suggests that the

CoD is located as the center of the circular field-of-

view (see Fig. 3 for a typical video frame). We

therefore apply the canny edge detector, using a

standard deviation equal to 2 in order to detect the

stronger edges in the image, which are the edges of

the circular field of view. Then, we employ a simple

least squares optimization to obtain the CoD and the

radius of the FoV. This is done only once, during the

calibration of the camera model.

The calibration process of the camera model

recovers the values of the unknown , ,

ph sph

px y

P(x,y,z)

O(0,0,0)

)

K(0,0,z

sph

)

Imageplane

z=z

plane

Q(Q

)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

472

parameters. The user provided the position of N

=18

landmark points





, , 1, 2,...,

im im p

XY i N on one

video frame. The real world coordinates of these

landmark points





iii

real real real

xyz were also

measured. The expected position of the landmark

points on the video frame, according to the model

parameters are (superscripts are not powers):

 

,,,;,,

ii i i i

im im real real real sph sph

xy Mx y z px y

(6)

The values of the model parameters are obtained by

minimizing the error between the expected and the

observed frame coordinates of the landmark points:









arg min

sph sph

ii ii

sph sph im im im im

px y

px y X x Y y













(7)

Figure 3: Visualization of the resulting fisheye model

calibration.

This minimization is performed by exhaustive

search in just few minutes using the Matlab

programming environment in an average personal

computer. Since the fisheye camera was

permanently installed on the roof of the university

laboratory, the calibration of the model is performed

only once. The resulting calibration of the fisheye

model is shown in Fig. 4, where a virtual grid, laid

on the floor and on the two walls of the imaged

room, is rendered on the captured frame, using the

fisheye model. The user-defined landmark points

are shown as ‘o’, whereas their projected location on

the video frame, using the calibrated model are

shown as ‘*’.

2.3 Human Model

In this work, we utilized a free triangulated model of

a standing human, of 27.000 vertices

(http://www.3dmodelfree.com/models/20966-

0.htm), approximately. Since we are interested in

simulating the rendering of the human model

through the fisheye camera in real time, we discard

the triangle information of the model and we treat it

as a cloud of points. We also applied a vertex

decimation process to reduce the number of vertices

by a factor of 8.

The vertices of the model were labelled using

logical spatial relations, into 5 classes: right and left

arm, right and left leg and the rest of the body (torso

and head). The pose of the human is modified by

changing the position of the hands and legs

independently, using the following controlling

parameters. Legs are allowed to rotate round the Y

axis with respect to the hips (thus they remain on the

sagital - YZ plane). Arms are allowed to rotate round

the shoulders. Fig. 4 shows an example of the

parametric human model along the coronal and the

sagital plane.

(a) (b)

Figure 4: The model of the human (anterior view and right

view), with labels as color. The axis of the limbs and their

angles with the vertical human axis, that define the

parameters of the 3D human model, are also shown.

The rotation of the hands involves all three Euler

angles. In order to avoid dependence on the order of

rotation and possible gimbal lock, we utilized the

following matrix, that transforms, a unit vector

v=(a,b,c) on the Z axis.

00 01

ab ac

vvv

ab c

vv v

























(8)

Assuming that

v coincides with the axis of the

hand, matrix

A is applied to the vertices of the two

hands separately, using homogeneous coordinates.

PoseRecognitioninIndoorEnvironmentsusingaFisheyeCameraandaParametricHumanModel

473

In addition to the 6 parameters that control the arms

and legs of the model, global parameters are also

introduced that control: the model’s location (x and y

translation), size (x, y and z scaling) and global

rotation round the Z axis. In order to narrow the

range of these global parameters, we utilized the

geometric reasoning-based segmentation refinement

that we reported in (Delibasis 2013, section 2.4).

More specifically we utilize the calibrated fisheye

camera model to obtain an estimation of the real

real

, y

real

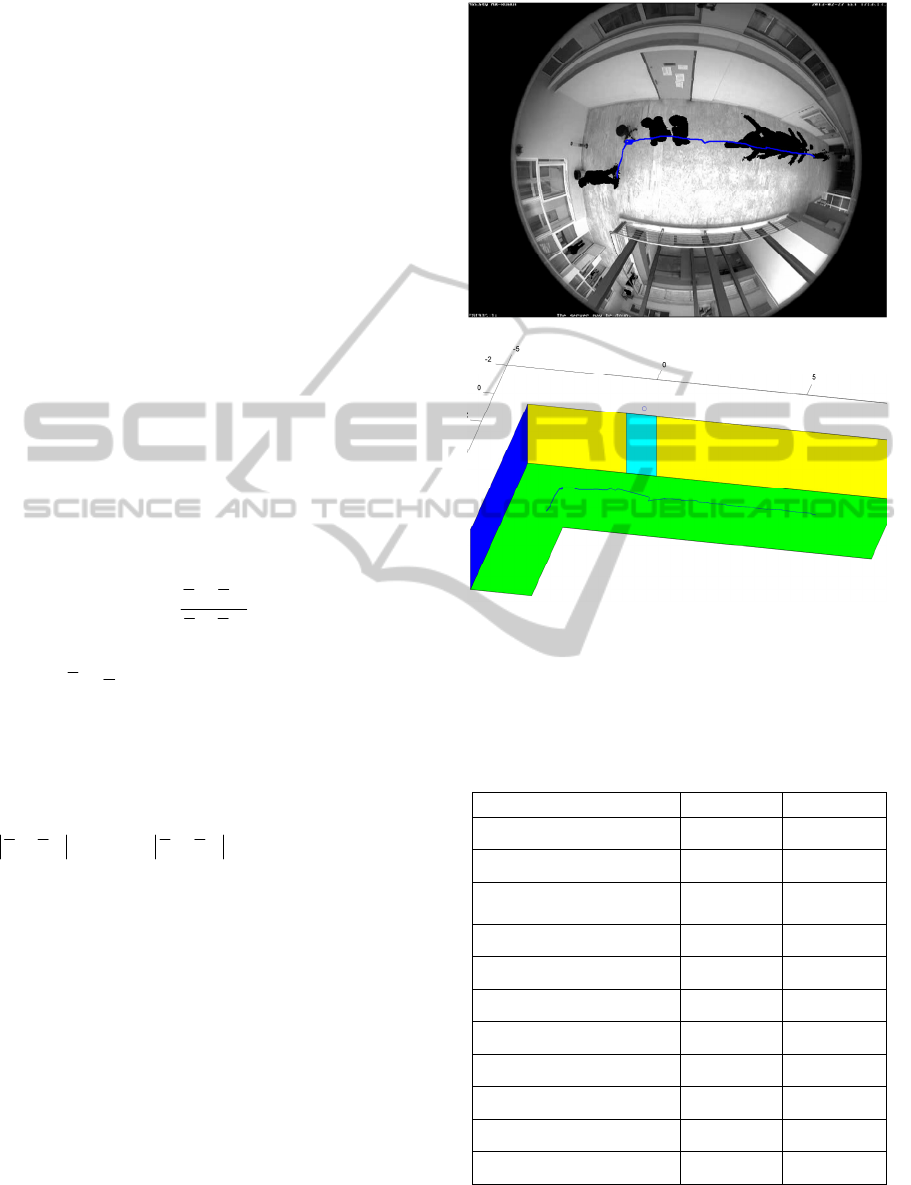
) positions of the segmented human. Some

instances of the segmented human from a typical

video are shown in Fig. 5(a), whereas the path of the

walking human in the real world frame of reference

is plotted in Fig. 5(b), as estimated using the

segmentation refinement (Delibasis 2013, section

2.4). The path is overlaid back on the composite

video frame (Fig. 5a) using the forward fisheye

model (Delibasis 2013, section 2.2).

The estimated (x

real

, y

real

) coordinates are used to

initialize the model’s location (x and y translation).

The global rotation round the Z axis, is calculated

using the direction θ

of the velocity vector

(assuming that the human is facing towards the

direction that he/she is walking), as following:

tan

















(9)

where



ttt

t real real real

x xxx





is the running

average of the last estimated real world coordinates

(same hold for y

real

coordinate), which prevents

amplification of the noise, induced by errors in

position estimation.

If the human is stationary (

10 10tt t t

xdANDyyd



  , d

=0.1) then the

angle θ

is not utilized for narrowing the range of z-

rotation angle, which is then set to [0,2π]. The range

of the model parameters are shown in Table 1.

The human model is used to produce a simulated

(rendered) segmented video frame that is compared

to the actually segmented one. A model of a

standing man is shown in Figure 6(a), scaled to

height=1.8 m and it is placed at several locations in

the imaged room, touching the floor. The rendered

frame using the fisheye model is shown in Fig.6(b).

The human pose can be extracted by recovering

the values of the parameters of the human model in

vector

. Let us denote by I

the binary image of

the parametric model generated by the fisheye model

and by I

the segmented image of the corresponding

video frame.

(a)

(b)

Figure 5: The resulting segmentation for a number of

frames (a) and the estimated path of the walking person in

real world coordinates, using the geometric reasoning-

based refinement of segmentation proposed in (Delibasis

2013) (b).

Table 1: The parameters of the 3D human model.

Parameter Min. value Max. value

X translation

real

-0.4 x

real

+0.4

Y translation

real

-0.4 y

real

+0.4

Scaling (independently in

3 axis)

0.8 1.2

Z-rotation

-π/8 θ

+π/8

Right, Left Leg angle

-π/6 π/6

Right arm coordinate a

-0.9 0

Right arm coordinate b

-0.4 +0.4

Right arm coordinate c

-1 0

Left arm coordinate a

0 0.9

Left arm coordinate b

-0.4 +0.4

Left arm coordinate c

0 +1

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

474

(a)

(b)

Figure 6: (a) scaling the model to height=1.8 m, touching

the floor and reproducing the model at several locations of

the imaged room and (b) rendering the 3D human models

through the calibrated fisheye lens.

The objective function is defined as following:





MS MS MS

image

domain

f IIIIII 



(10)

where,

I denotes the boolean negative of I, 

denotes the boolean AND operator and the

summation is done over the whole image domain.

The objective function is defined as the number of

non-zero pixels of I

on non-zero pixels of I

minus

the number of non-zero pixels of I

on zero pixels of

, minus the number of zero pixels of I

on non-

zero pixels of I

. Thus, the objective function should

be maximized.

Due to the large number of parameters and the

complexity of the objective function, which cannot

be written in closed form and its derivatives cannot

be analytically computed, we employed a simple

Genetic Algorithm as an optimizer. The simple GA

is a generational one, as described in (Goldberg

1999), it uses real encoding, one-point crossover, a

population of 80 chromosomes and it is allowed to

converge for a maximum number of 1000 function

evaluations. The probability of crossover and

mutation was set to 0.8 and 0.01 respectively. For

these initial results, the step of evolutionary

optimization is not performed in real time. In the

Discussion section, we provide details about

execution times as well as future work towards the

direction of near real time execution.

3 EXPERIMENTAL RESULTS

The video sequences used in this work were

acquired using the Mobotix Q24 hemispheric

camera, which was installed on the ceiling of the

imaged room. The pixilation of each frame is

480x640.

(a) (b) (c) (d)

Figure 7: (a) An original video frame showing a human,

(b) the 3D model with its parameters fitted to the

segmented original frame, (c) the fisheye-rendered 3D

model in a simulated frame and (d) the matching (yellow)

between the segmented human (green) and the fisheye-

rendered model (red).

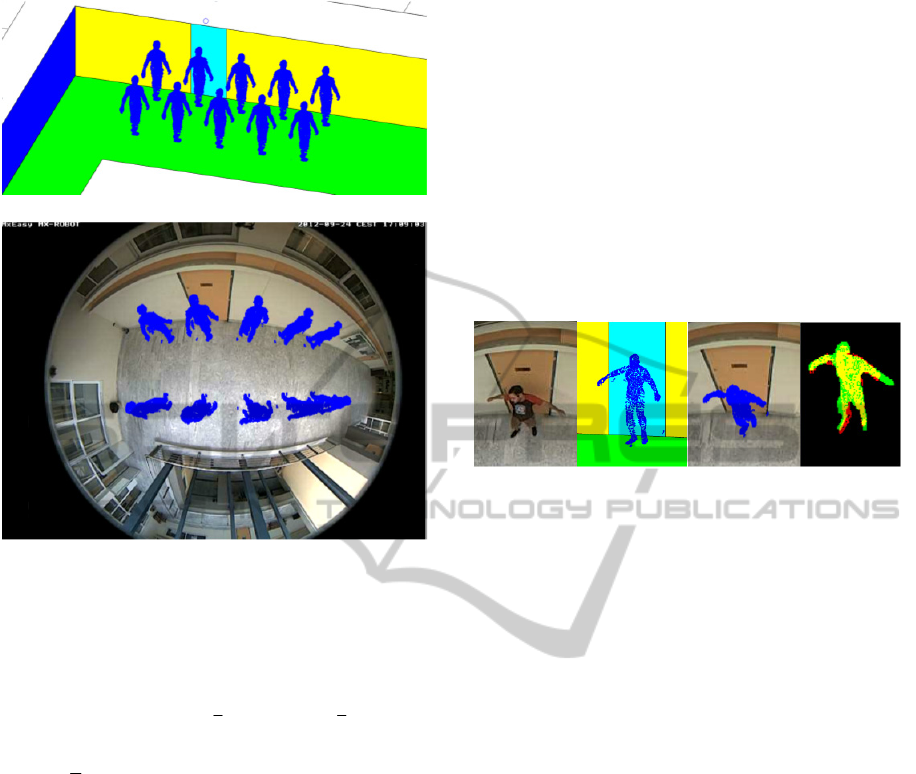
Figure 7 shows results from a typical frame (a). The

recovered 3D human model is shown in (b) and the

rendered 3D human model using the fisheye model

is shown in (c). The fitting of the fisheye-rendered

parametric 3D human model to the segmented frame

is shown in Fig. 7(d), as following: segmented frame

in green, the fisheye rendered 3D human in red and

their intersection in yellow. It can be observed that

the proposed algorithm was able to detect the

specific human pose. Initial results were obtained by

testing the proposed algorithm in 5 video sequences

of 1500 – 2000 frames, of a walking or standing

human. In Fig. 8a, the resulting segmentation from a

number of frames is shown in a single composite

frame. The results of fitting the fisheye-rendered 3D

human model to the actual segmented human

silhouette using GAs-based optimization is shown in

(8b) (same colours as in Fig.(7)). In (8c) the

recovered 3D human models are shown in the real

world space. These experiments show that it is

feasible to extract the human pose from a significant

percentage the fisheye video frames, even imperfect

segmentation.

PoseRecognitioninIndoorEnvironmentsusingaFisheyeCameraandaParametricHumanModel

475

(a)

(b)

(c)

Figure 8: (a) a single composite frame the resulting

segmentation from a number of frames. (b) The fisheye-

rendered parametric 3D human models fitted to the

segmented frames (see text). (c) the recovered 3D human

models in the Cartesian space.

4 CONCLUSIONS

A methodology for human pose recognition has been

presented in this paper. The proposed algorithms are

based on a deformable 3D human model, a

parametric model of the specific fisheye camera and

a top-down approach using GAs-based optimization.

Given the video foreground segmentation refinement

and its geometry-based refinement, the algorithm

estimates the human’s position and pose,

considering the orientation of its limbs. Initial results

have been presented that show the feasibility of the

proposed methodology.

The generation of the 3D parametric human

model is performed in approximately 1 msec. The

rendering of a 3D human model with 2.500 vertices

through the modelled fisheye camera is also

performed in 1.5 msec. The calculation of the

objective function (Eq. 10) requires approx. 8 msec

for a 3D model with 2.500 vertices and a frame of

480x640 pixels. All timing was performed using an

Intel(R) Core i5-2430 CPU @ 2.40 GHz Laptop

with 4 GB Ram, under Windows 7 Home Premium.

The code was developed using the Matlab

programming environment. No special code

optimization or any kind of parallelization was

performed. It becomes clear that the optimization of

the objective function in order to extract the human

pose has not been performed in real time. At this

stage, these initial results serve as proof of concept

that the proposed algorithm is feasible. Further work

will include, the adoption of a more robust statistical

3D model for the human and the refinement of the

fisheye model, using more parameters to increase its

accuracy. Finally more efficient implementation of

the genetic algorithm based optimization will be

explored for the determination of the 3D model

parameters. These approaches include exploiting the

converged population from the previous frames to

initialize the search for the current frame and/or

restricting the parameter range according to their

optimal values from the previous frames.

ACKNOWLEDGEMENTS

The authors would like to thank the European Union

(European Social Fund ESF) and Greek national

funds through the Operational Program "Education

and Lifelong Learning" of the National Strategic

Reference Framework (NSRF) - Research

Funding

Program: \Thalis \ Interdisciplinary Research in

Affective Computing for Biological Activity

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

476

Recognition in Assistive Environments for

financially supporting this work.

REFERENCES

Willems J., Debard G., Bonroy B., Vanrumste B. and

Goedemé T., “How to detect human fall in video? An

overview”, In Proceedings of the positioning and

contex-awareness international conference (Antwerp,

Belgium, 28 May, 2009), POCA '09.

Cucchiara, R., Grana, C., Piccardi, M., and Prati A. 2003.

Detecting moving objects, ghosts, and shadows in

video streams. IEEE Transactions on Pattern Analysis

and Machine Intelligence 25, 10, (2003), 1337-1442.

McFarlane, N. and Schofield C., “Segmentation and

tracking of piglets in images”, MACH VISION APPL.

8, 3, (May. 1995), 187-193.

Wren, C., Azarhayejani, A., Darrell, T., and Pentland, A.

P. 1997. Pfinder: real-time tracking of the human

body, IEEE Transactions on Pattern Analysis and

Machine Intelligence 19, 7, (October. 1997), 780-785.

Stauffer C., and Grimson W., “Adaptive background

mixture models for real-time tracking”. In

Proceedings of the conference on computer vision and

pattern recognition (Ft. Collins, USA, June 23-25,

1999), CVPR '99. IEEE Computer Society, New York,

NY, pp. 246-252.

Cheng F. C., Huang S. C. and Ruan S. J. 2011,

Implementation of Illumination-Sensitive Background

Modeling Approach for Accurate Moving Object

Detection, IEEE Trans. on Boardcasting, vol. 57, no.

4, pp.794-801, 2011.

Christodoulidis A., Delibasis K., Maglogiannis I., “Near

real-time human silhouette and movement detection in

indoor environments using fixed cameras”, in The 5th

ACM International Conference on PErvasive

Technologies Related to Assistive Environments,

Heraklion, Crete, Greece, 2012.

Delamarre, Q., Faugeras, O., “3D articulated models

andmultiview tracking with physical forces”,

Computer Vision and ImageUnderstanding (CVIU) 81

(3) (2001) 328–357.

Kehl, R., Van Gool, L., “Markerless tracking of complex

human motions from multiple views”, Computer

Vision and Image Understanding (CVIU) 104 (2–3)

(2006) 190–209.

Barron, C., Kakadiaris, I., “Estimating anthropometryand

pose from a single uncalibrated image”, Computer

Vision andImage Understanding (CVIU) 81 (3) (2001)

269–284.

Bregler, C., Malik, J., Pullen, K., “Twist basedacquisition

and tracking of animal and human kinematics”,

International Journal of Computer Vision 56 (3)

(2004) 179–194.

Taylor, C., Reconstruction of articulated objects from

point correspondences in a single uncalibrated image,

Computer Vision and Image Understanding (CVIU)

80 (3) (2000) 349–363.

Liebowitz, D., Carlsson, S., “Uncalibrated motion

captureexploiting articulated structure constraints”,

International Journal of Computer Vision 51 (3)

(2003) 171–187.

Poppe, R., “Vision-based human motion analysis: An

overview”, Computer Vision and Image

Understanding, 108 (2007) 4–18.

Kemmotsu, K., Tomonaka, T., Shiotani, S., Koketsu, Y.,

and Iehara, M., "Recognizing human behaviors with

vision sensors in a Network Robot System," IEEE Int.

Conf on Robotics and Automation, pp.l274-1279,

2006.

Zhou, Z., Chen, X., Chung, Y., He, Z., Han, T. X. and

Keller, J., "Activity Analysis, Summarization and

Visualization for Indoor Human Activity Monitoring,"

IEEE Trans. on Circuit and systems for Video

Technology, Vol. 18, No. II, pp. 1489-1498,2008.

M. Saito and K. Kitaguchi, G. Kimura and M.

Hashimoto,“Human Detection from Fish-eye Image by

Bayesian Combination of Probabilistic Appearance

Models”, IEEE International Conference on Systems

Man and Cybernetics (SMC), 2010, pp243-248.

Li H. and Hartley R., “Plane-Based Calibration and Auto-

calibration of a Fish-Eye” Camera, P.J. Narayanan et

al. (Eds.): ACCV 2006, LNCS 3851, pp. 21–30, 2006,

c Springer-Verlag Berlin Heidelberg 2006.

Basu A., Licardie S., “Modeling fish-eye lenses”,

Proceedings of the 1993 IEEWSJ International

Conference on Intelligent Robots and Systems

Yokohama, Japan July 2630,1993.

Shah S. and Aggarwal J., “Intrinsic parameter calibration

procedure for a high distortion fish-eye lens camera

with distortion model and accuracy estimation”,

Pattern Recognition 29(11), 1775- 1788, 1996.

Delibasis K. K., Goudas T., Plagianakos V. P. and

Maglogiannis I., Fisheye Camera Modeling for

Human Segmentation Refinement in Indoor Videos, in

The 6th ACM International Conference on PErvasive

Technologies Related to Assistive Environments,

PETRA 2013.

Max, N., “Computer Graphics Distortion for IMAX and

OMNIMAX Projection”, Proc Nicograph 83, Dec

1983 pp 137.

Greene, N., “Environment Mapping and Other

Applications of World Projections”, IEEE Computer

Graphics and Applications, November 1986, vol.

6(11), pp 21.

http://paulbourke.net/dome/fisheye/

Micusik, B. and Pajdla, T., “Structure from Motion with

Wide Circular Field of View Cameras”, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, PAMI 28(7), 2006, pp. 1-15.

http://www.3dmodelfree.com/models/20966-0.htm.

Goldberg D., “Genetic Algorithms in Search,

Optimization, and Machine Learning”, Addison

Wesley, 1989.

PoseRecognitioninIndoorEnvironmentsusingaFisheyeCameraandaParametricHumanModel

477