Interactive Visualizer for the Extended Perspective System

as Support for Architectural Design

Robin Burgess

, Teresa Chambel

, Ana Paula Cláudio

, Maria Beatriz Carmo

, Carlos Albuquerque

José Vitor Correia

, Luís Romão

, Susana Rosado Ganhão

, Manuel Couceiro da Costa

Ana Santos Guerreiro

and Sara Garcia

Faculty of Science, University of Lisbon, Lisbon, Portugal

Faculty of Architecture, University of Lisbon, Lisbon, Portugal

Keywords: Non-linear Projection, Curvilinear Perspective, Drawing, Visualization, Architectural Design.

Abstract: The flexibility of free-hand drawing perspectives denotes the dynamic nature of human sight and no single

perspective system, linear or curvilinear, can translate human vision with such agility. For instance, linear

perspective cannot deal with large fields of view, and curvilinear perspectives introduce curvature in lines.

But together, complementing each other, they can overcome many of their limitations. This paper describes

an interactive computational tool for architectural visualization – a digital perspectograph that implements a

new theoretical and operative hybrid solution to perspective, the Extended Perspective System (EPS) – and

presents a user evaluation carried out to determine its usability, perceived usefulness, satisfaction and ease

of use, as an interactive tool to support the design process in architecture. It also aimed to learn about the

most effective and appreciated features and interface design options to support the EPS perspective, and

identify potential directions for improvement. The user study involved participants with different

backgrounds – students and experts, in the target audience of architects and informatics engineers with

experience in using and developing interactive tools, HCI and computer graphics. The visualizer was highly

appreciated, in terms of layout, available features, produced images and flexibility, and the most effective

design options were identified, mainly for their simplicity, visibility, and familiarity. It was considered

advantageous compared to conventional perspective visualizers, and users would like to see it integrated

into 3D modelling tools.

1 INTRODUCTION

The complexity and dynamics of human visual

perception can be observed, symptomatically, in the

structural

diversity of free hand perspective drawings.

No single rigorous geometric perspective system can

produce such a holistic graphical interpretation of

vision. For instance, linear perspective cannot deal

with

large fields of view without the known peripheral

distortions, while curvilinear perspectives alter the

geometric nature of lines.

Throughout the history of perspective, classical

linear perspective was counterpointed by several

authorial

propositions defining alternative curvilinear

perspective systems. These systems never gained a

broad

use, probably because of the intrinsic difficulty

of their graphical procedures. In fact, such

complexity renders its teaching and practice

complicated. But their sheer existence emphasizes

that linear perspective is just a particular intellectual

construct for pictorial purposes, and other ways of

translating visual data into depictions may be

considered. So, the notion of perspective may be

more inclusive, by addressing not just the result of a

static gaze, but also the overall result of dynamic

visual perception and visually based cognition.

The starting point for this research project was

previous work by members of the team: a systematic

approach to the issue of perspective that resulted in

the general formulation of a new representational

method called Extended Perspective System (EPS)

(Correia & Romão, 2007). This concept congregates

current perspective systems in a unified theoretical

build, turning them into just boundary states of a

broader dynamic system that contains an unlimited

set of new in-between states. The outcome is a

453

Burgess R., Chambel T., Cláudio A., Carmo M., Albuquerque C., Vitor Correia J., Romão L., Ganhão S., Couceiro da Costa M., Santos Guerreiro A. and

Garcia S..

Interactive Visualizer for the Extended Perspective System as Support for Architectural Design.

DOI: 10.5220/0004694604530463

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 453-463

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

significant increase in the variety of graphical

perspective states that fosters new applications,

useful in architectural drawing and design projects,

as well as virtual exploration of spatial and visual

immersiveness.

With the EPS, it is possible to generate

perspective images that convey larger fields of view

with less distortion for enhanced descriptive

capabilities. In addition, a computational tool that

implements the EPS concept has several advantages:

it supports complex calculations inherent to

curvilinear perspectives; allows users to quickly

explore different graphical perspective states in real

time by manipulating perspective parameters; is

compatible with digital formats widely used by

CAAD software.

Our multidisciplinary research team conceived

and implemented a novel digital perspectograph: a

tool, the EPS Visualizer, for producing vectorial

drawings from 3D architectural models, using new

alternative projection procedures.

This interactive application was designed and

implemented as a proof of concept of the EPS

conceptual model. By controlling a single camera

and a set of parameters, the user can visualize 3D

scenes and gain a better understanding of the spatial

characteristics of the model.

The challenge posed in the design of the

interface was to provide adequate support for the

distinctive EPS concepts. The interface has to

provide intuitive and effective interaction when

manipulating camera position, viewport control, and

projection surface parameters like radius and

eccentricity.

A user evaluation was carried out to determine

the EPS Visualizer usability, its perceived

usefulness, satisfaction and ease of use, to learn

about the most effective and appreciated features

and interface design options to support the EPS

perspective, receiving comments and suggestions,

and identify potential directions for inprovement.

This user study involved users with different

backgrounds - students and experts in architecture

and informatics.

This paper is organized as follows: section 2

describes some of the more relevant related work;

section 3 presents the ideas behind the formulation

of the EPS and addresses its definition; section 4

describes the EPS Visualizer; section 5 presents the

user evaluation; section 6 draws conclusions and

presents future work.

2 RELATED WORK

A common characteristic of the main historical

approaches to curvilinear perspective is that they

configure static concepts of perspectograph, by

electing a single kind of projection surface and

stipulating unique graphical procedures.

Hansen (1973) developed a hyperbolic linear

perspective, trying to respond graphically to the

historically alleged curvatures sensed in vision.

Casas (1983) and Moose (1986) developed graphical

methods to obtain 360º degrees spherical perspective

depictions of space. Barre and Flocon's (1968) La

perspective curviligne establishes the use of a sphere

surrounding the viewer as the ideal depiction

surface, where equal visual magnitudes would have

corresponding equal projected magnitudes.

However, for pragmatic purposes, the depiction is

then transferred to a picture plane with the

cartographic procedure that less distorts those

magnitudes. A very similar method, Perspective

Spherique, was also proposed by BonBon (1985).

Another curvilinear system, with a diffuse origin, is

the cylindrical perspective, where projections are set

upon a cylindrical surface. This surface is then

unrolled in order to obtain a final depiction on a

picture plane. This kind of perspective has recently

gained a broader visibility through digital panoramic

photography.

Our approach, as will be described, proposes a

more versatile concept, based on different principles:

the curved projection surface becomes mutable,

within specific constraints, and graphical results are

consequence of mapping that surface onto a planar

surface, using one of multiple alternative methods.

In computational drawing, linear perspective is

the prevalent system regarding the production of

depictions that intend to simulate the direct visual

appearance of things. But, despite its effectiveness,

it cannot deal with large fields of view, where raised

distortions will, at the limit, compromise the

recognition of the represented objects. Alternative

curvilinear systems, cylindrical and spherical

perspectives, much less known and hardly used, can

overcome this difficulty. These systems can translate

graphically the result of a viewer’s sight in motion,

conveying a sense of dynamic vision, although at the

cost of bending the represented straight lines. The

three systems: linear, cylindrical and spherical

perspectives, despite being separate theoretical

builds, can have complementary roles, in terms of

representational capabilities.

Several computational tools have been

implemented for curvilinear perspective, using a

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

454

number of different techniques. Some are based on

raytracing, such as in works like (Wyvill and

McNaughton, 1990; Glassner, 2000; Gröller, 1995;

Weiskopf, 2000). Though ray tracing solutions are

powerful, they are also computationally quite heavy.

Other approaches have used multiple cameras to

produce single images, such as (Rademacher and

Bishop, 1998; Agrawala et al., 2000; Singh, 2002;

Yu and McMillan, 2004). These approaches are

often artistic in nature and are not suitable to

reproduce the rigorous single-camera projections

that architects require.

Trapp and Döllner (2008), used cube mapping,

as described by (Gröller, 1995), to capture the

environment efficiently using established techniques

and maximizing the use of the capabilities of

graphics cards. They then applied transformations on

to those images in order to achieve the desired

curvilinear projections.

Brosz et al. (2007) described a projection

framework based on a flexible viewing volume. This

parametrically defined volume functions as a single

camera and as a projection surface and can take on

an almost inexhaustible number of different shapes.

This allows the framework to simulate a variety of

linear, non-linear and custom artistic projections.

The main purpose that led the team was the

design of a tool that implements a single unified

perspective system with which a much wider range

of possible perspective representations of an object

or a scene can be generated.

3 CONCEPTUAL MODEL

In the formulation of the EPS, linear (or planar),

spherical

and cylindrical perspectives were considered

fundamental landmarks to take into account. Next, we

present the conceptual model of EPS and show its

application in an architectural scene.

3.1 The Extended Perspective System

Three fundamental principles characterize the

framework of the EPS: first, the separation of the

projection

surface (PS) from the representation

surface (RS); second, the mutability of the projection

surface; and third, the selection of the methods for

transferring the projections from the PS to the RS.

The PS is the surface upon which the scene is

initially projected. The RS is the surface on to where

the projected information is then transferred, thus

producing the final result or perspective depiction.

These guidelines led to the following particular

specifications of the EPS: (a) the RS is a plane; (b)

the PS is a spheroid (an ellipsoid with a vertical axis

of revolution), initially having its center on the

viewer position, and tangent to the RS at a point on

its equator, which is also the viewer's target point;

transformations, controlled by two parameters:

radius (Rad) and eccentricity (Ecc).

Figure 1: The three referential perspective systems: planar,

cylindrical, spherical – separated (top), and gathered by

the EPS concept (bottom).

The Rad parameter defines the distance between the

target point and the centre of the PS. By

incrementing Rad, the center of the PS detaches

from the viewer and moves backwards along the

visual axis, so the PS is progressively up-scaled.

With an infinite Rad, the PS becomes a plane,

coinciding with the planar RS. Along variation of

the parameter Rad, in both directions, an infinite

number of intermediate states of PS is found. This

parameter determines the overall curvature of

depicted lines and attainable field of view.

InteractiveVisualizerfortheExtendedPerspectiveSystemasSupportforArchitecturalDesign

455

The Ecc parameter defines the ratio between the

vertical axis and the equatorial diameter of the

spheroidal PS. By incrementing Ecc, the spheroid

becomes progressively elongated. With Ecc at its

lower limit (1:1), the surface is a perfect sphere, and

at infinity the surface is cylindrical. Again, an

infinite number of intermediate ellipsoidal states can

be found. This parameter determines the curvature

of the vertical lines in the final depiction.

So, with the combined effect of the two

parameters, the PS can assume diverse forms, going

from spherical, to cylindrical or planar and through

an infinite number of intermediate states. This

relationship is seen in Figure 1.

Therefore, the EPS is able to reproduce planar,

cylindrical or spherical perspectives and, moreover,

infinite number of in-between hybrid perspectives.

When implementing and testing the EPS algorithm,

it proved necessary to separate the calculations of

cylindrical

projection, planar projection and

spherical/ellipsoidal projection. While in initial

conception cylindrical projection corresponded to

ellipsoidal projection with an infinite eccentricity

value, they turned out not to be entirely identical and

required different methods of mapping onto the

representation surface.

3.2 EPS in an Architectural Scene

The use of the new parameters Rad and Ecc in

addition to the already established variables, like

'distance' or 'zoom', turns perspective depiction of an

object into a choice made from a much wider range

of possibilities. Nonetheless, the number of variables

to control can be reduced by making some of them

dependent on others, for meaningful combinations.

In Figure 2, a set of 16 images, resulting from

variations of Rad, Ecc and Field of View (zooming

effect), exemplifies that diversity.

On the lower left corner, the EPS depiction turns

into current spherical perspective. On the upper left

corner, the EPS depiction nearly turns into current

cylindrical perspective. On the upper right corner,

the EPS depiction resembles current linear

perspective, with a narrow field of view. In the

middle, we find EPS hybrid depictions.

It is noticeable that a full range (0-360º) of field

of view is attainable, despite the eventual

anamorphic character of the image or some of its

parts. We believe it shall depend on the EPS user to

evaluate and decide on the appropriateness of the

depiction, regarding the specific representation

purposes or intents of visual analysis.

Figure 2: A table of diverse EPS depictions of an architectural scene - Mãe d’Água reservoir in Lisbon.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

456

4 EPS VISUALIZER

The EPS Visualizer is an interactive application

designed and implemented as a proof of concept of

the EPS conceptual model. By controlling a single

camera and the parameters (Rad, Ecc, FoV), the user

can visualize 3D scenes and gain a better

understanding of the spatial

characteristics of the

model. To test alternative interface options, two

versions of the EPS Visualizer were conceived –

version A (VA) and version B (VB). The main

features and the evaluation of

the Visualizer are

presented in the next subsections.

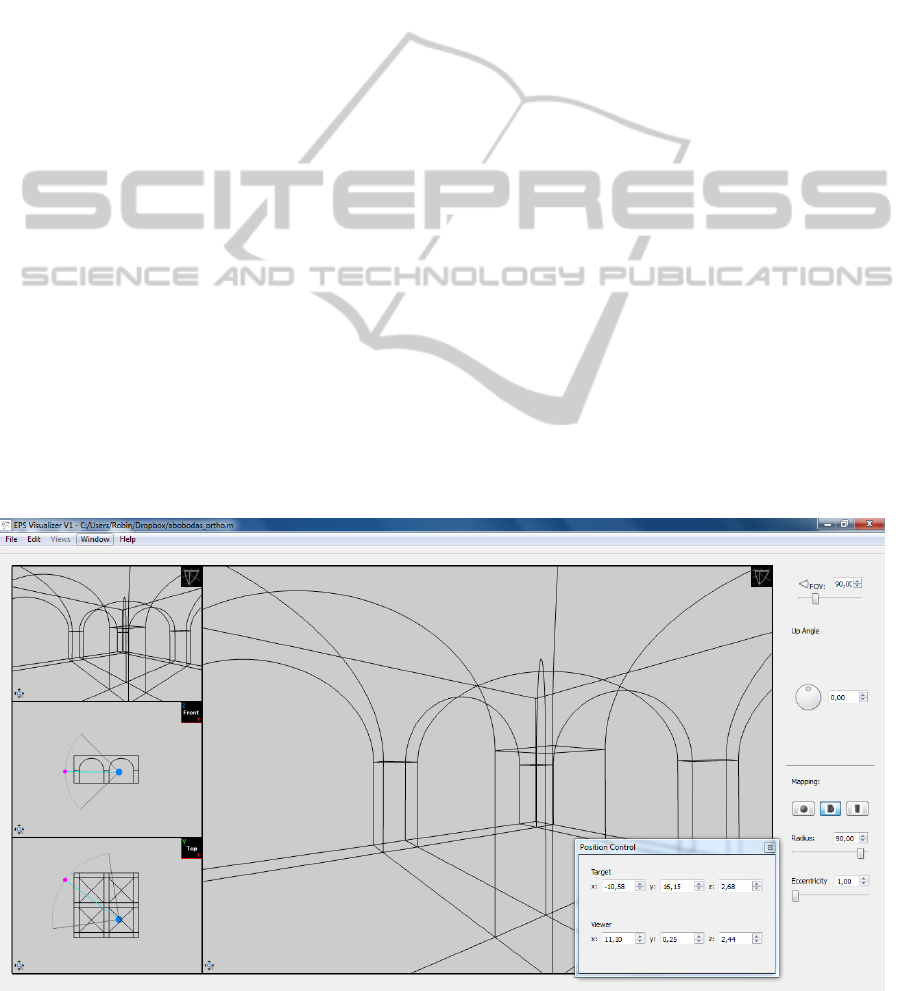
4.1 Layout

The layout of the main window is a simple one that

does not stray far from familiar ground (Figure 3).

There are four viewports, one larger and the other

three organized vertically on the left side of the

screen. Apart from these four viewports the main

window has only a small menu on the top left with

the File, Edit, Views, Windows and Help menus.

Each viewport can show one of eight different

views. Two views show the point of view of a

camera, one using EPS projection and the other

using classical perspective. The other six views

show orthogonal side-views of the model, one for

each of the six axis-aligned views: front, back, top,

bottom, left and right. By default, the large viewport

displays the EPS View.

An icon on the top right corner of each viewport

indicates which view is currently active on that

viewport, and a small button on the lower left corner

corresponds to the extend view option.

4.2 Camera and Cursor

The camera on which the EPS and classical

perspective views are based is defined by two points

and an up angle. The viewer point indicates where

the camera is located and the target point indicates

what direction the camera is looking at. The up

angle then gives the vertical orientation of the

camera's image, which would correspond to a

rotation of the camera along the viewer-target axis.

The camera's viewer and target points are

displayed on each of the six orthogonal views as a

part of the camera cursor. The camera cursor is

composed of a blue sphere that represents the viewer

point, a magenta sphere that represents the target

point and a circle sector (the circle is centred in the

Viewer and the Target is a point on the circle) of

which the internal angle corresponds to the field of

view of the camera. A thin circle sector represents a

narrow field of view, while a complete circle

represents the full 360º field of view. (The cursor

can be visualized in Figure 4, in each of the four

bottom viewports.)

It is possible to control the position and direction

of the camera in two ways. First, it is possible to

input the coordinates of the viewer and target points

directly in the position control window (Figure 3,

Figure 3: The EPS Visualizer Layout.

InteractiveVisualizerfortheExtendedPerspectiveSystemasSupportforArchitecturalDesign

457

bottom right). Second, it is possible to drag these

two points on the orthogonal views where the

camera cursor is displayed (Figure 4).

Two modes of dragging the points were

conceived. One mode, in VB, involves holding the

mouse over the viewer or target cursor sphere so that

it is highlighted. Then the left mouse button is

pressed and the corresponding point is dragged. It is

possible to drag both points together by pressing on

the line that connects the two points. This is a fairly

familiar point, click and drag method.

Figure 4: Camera and Cursor: Movement of the camera

and its effects (initial position in left column and final

position in right column). Viewports in: EPS view (top);

front view (middle); and top view (bottom).

The other mode, in VA, does not require the mouse

to be held over the point. Instead any point in the

viewport is acceptable. If the left mouse button is

pressed and the mouse dragged, the viewer point

will be highlighted and dragged along with it. If the

right mouse button is pressed, then the target point

will be highlighted and dragged instead. To move

both points in parallel, the user needs only to press

both buttons. While this method is less intuitive than

the other, it is potentially more efficient once the

user has grown accustomed to it.

Two possible colour schemes were chosen for

the cursor (Figure 5). One colours only the viewer

and target sphere, aiming to highlight only that

which can be dragged by the mouse (VA). The other

also colours the circle sector (red), highlighting the

selected controls in yellow, and displaying the three

icons (red circle sector, blue sphere, magenta sphere)

in their corresponding input boxes and sliders in the

control windows (VB).

Figure 5: The two cursor colour schemes (VA: minimal

colour; VB: colourful), in normal (top) and highlighted

viewer (bottom) modes.).

4.3 Viewport Control

By default, the four viewports display the EPS

camera view in the main viewport and the classical

perspective camera, front view and top view in the

other three viewports. However, three different

methods of changing the view of a viewport were

devised. Method 1 (Figure 6, top) requires the user

Figure 6: Changing the view: method 1, 2 and 3 (from top

to bottom).

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

458

to select the viewport by clicking on it, activating

the Views menu and picking the view they want

from that menu. Method 2 (Figure 6, middle)

requires the user to open a settings window from the

menu. The settings window has four dropdown

menus, one per viewport, and changes the views by

selecting them in the corresponding dropdown

menu. Method 3 (Figure 6, bottom) is the simplest,

requiring the user to click on the symbol at the top

right corner of the viewport and selecting the view

from the menu that pops up under the mouse.

Each viewport can also be panned by dragging

with the middle mouse button. While holding the

mouse over one of the orthogonal views, the mouse

wheel will zoom in and out. Over the two camera

views, the mouse wheel will control the FoV. The

zoom extends button, found in the lower left corner

of the viewport will re-centre the image. For the

orthogonal views it will also set the zoom so that the

whole model fits in the viewport; it will not change

the FoV for the two camera views.

4.4 Projection Control

Apart from the main window, the most important

window is the projection control window (Figure 3,

right). This window contains input boxes, sliders and

buttons, for the field of view, up angle, mapping

mode, radius and eccentricity parameters. The FoV,

up angle, radius and eccentricity parameters are each

controlled by an input box and a slider, the input box

doubling as a display for the current value. The up

angle slider is in the form of a dial. The mapping

mode is controlled by either a single button or one

per mode. The single button displays the current

active mode and clicking on it cycles through the

various modes. The alternative method has a smaller

button per mode, which remains pressed while the

corresponding mode is active. Each button has a

symbol representing the mapping mode but will

display the name of the mode in a tool tip.

5 USER EVALUATION

A user evaluation was carried out to determine the

EPS Visualizer usability, its perceived usefulness,

satisfaction and ease of use, as a tool to support the

design process in architecture. It was also aimed at

making decisions in regards to the various

alternative methods

designed, receiving comments

and suggestions, and identifying aspects to refine.

For a more comprehensive evaluation, this user

study involved users with different backgrounds -

students and experts, in the target audience of

architecture and informatics with experience in

using and developing interactive tools, HCI and

computer graphics.

5.1 Method

The evaluation followed a task-oriented approach

based mainly on Observation, and one-on-one semi-

structured Interviews, followed by a final

Questionnaire aiming at a global opinion on

usefulness of and user experience with the EPS

Visualizer.

Each interview would take place between one

interviewer and one subject, in front of a computer

with two screens, each screen displaying one of the

variant visualizers (VA and VB). After explaining

the purpose of the evaluation and a brief

introduction about the concept behind the Visualizer,

demographic questions were asked, followed by the

presentation of a short video demo (3 min) about the

Visualizer, around 7 min of free exploration, and a

set of 4 main tasks with the two versions of the

software, each version implementing different

options in regard to the alternative interfaces.

The fisrt three tasks, and their subtasks, took the

user through each feature and variant of the

interface. If a particular feature had a variant, then

the user would be prompted to try both versions and

indicate their preference. The order in which the

variants were tried was defined at the beginning of

the interview, being chosen alternately so as not to

favour one of them over the other. The fourth task

was more complex and free-form, requiring the

users to use the interface to reach a goal, in the form

of an image that they were to reproduce with the

visualizer. By this point, they would already be quite

familiar with the basic features of the interface.

During the tasks, the interviewer observed and

registered whether each sub-task was successful,

ocurring errors, hesitations, performance, comments,

and the resulting image of the fourth task (exported

from the Visualizer). At the end of each of the main

sub-tasks, users provided a 1-5 (very bad – very

good) rating based on the USE questionnaire (Lund,

2001), for Usefulness, Satisfaction and Ease of use.

Finally, users filled in a questionnaire about their

experience with the software, focusing on their

global opinions and including the well known SUS:

System Usability Scale (Brooke, 1996) usability

questions, due to its simplicity and robustness,

allowing some standardized usability measures that

are considered reliable. The answers were mostly in

the form of a 1-5 scale (‘never’ to ‘always’; or ‘very

InteractiveVisualizerfortheExtendedPerspectiveSystemasSupportforArchitecturalDesign

459

weak’ to ‘very good’ and NA for 'not applicable’),

with some open ones, allowing the students to

express their opinions more freely.

Each evaluation session (tasks + interview +

questionnaire) took a rough average of one hour.

5.2 Population

The evaluation process had the participation of 50

subjects. Most of the population could be separated

into three groups: ASG – Architecture Students

Group – with 24 first and second year subjects, aged

18-20; APG – Architecture Professionals Group –

with 14 subjects, 13 from architecture and 1 in the

related fields of mathematics, geometry and

painting, aged 27-62; all of them working

professionally in these areas, 5 BSc, 3MSc, 6 PhD;

all but 2 have experience in architectural projects,

for 13 years on average; and IEG – Informatics

Engineering Group - with 12 subjects, 9 MSc and 3

PhD students of computer engineering who took

courses on computer graphics and HCI, aged 23-32.

Almost all the participants had prior experience

with 3D modelling software, and most reported

using perspective views in these software tools. Half

of the APG users resported knowing the concept of

curvilinear perspective; also half reported already

knowing of the EPS perspective concept. They also

reported drawing by hand in perspective fairly

frequently (Mean (in 1-5 scale): 3.5; Standard

Deviation: 1.0), and playing 3D videogames rarely

(1.6;1.0). 63% of ASG users knew the curvilinear

perspective concept, but none knew about the EPS

concept. They draw by hand in perspective more

frequently than other groups (3.9;0.9), but seldom

play 3D videogames (1.9;1.0); whereas the IEG

users knew of neither curvilinear or EPS perspective

concepts, and rarely draw by hand in perspective

(1.7;0.9), but they play 3D video games quite often

(3.8;1.2).

5.3 Results

The analysis of the collected data allowed finding a

tendency in perceived usefulness, ease of use and

satisfaction with the Visualizer, comparing design

alternatives, assessing main usability aspects, and

obtaining feedback from target users. The main

results are presented next; some aspects are

highlighted by graphics, and reflected in the most

proeminent comments that are presented.

5.3.1 Initial Observations

During their initial exploration of the software, users

noticed the absence of the orbit viewer, and a real-

time update in the EPS View. Some users suggested

the zoom command be made uniform, as different

zooming types are activated in the same way -

graphical zoom in orthogonal views and FoV in

camera views.

5.3.2 Camera and Cursor

In task one, users began by importing a given model,

which they easily accomplished. They then

introduced numerical values for the camera position,

radius and eccentricity and FoV, which they found

to be easy to use (4.8;0.4) and satisfactory (4.5;0.8).

Notably, the APG user group had greater ease and

satisfaction with this subtask. Afterward, users were

given two orthogonal projections of the model, seen

from the top and front views, where points were

marked for the viewer and target. They were asked

to place the two points near the marked positions by

dragging the cursor in both variants of the software

(dragging by using each mouse button for each

element - viewer or target (VA) vs. by clicking on

the element (VB)). When asked which version they

preferred, users overwhelmingly chose VB (84%)

over VA (16%). They indicated that it was easier to

use (VA:3.8;1.0;VB:4.5;0.6) and were more satisfied

(VA:4.2;0.7;VB:4.6;0.6), and reported finding VB

more intuitive. Indeed the alternative is not

commonly found and is thus less familiar. Some of

the users who preferred VA promptly identified it as

a shortcut with the potential to be appreciated more

by more experienced users in the long term.

Users also preferred the colour scheme where the

circle sector and the highlighted control were

coloured (VB:83%) over the one that only coloured

the viewer, target and connecting line (VA:17%), as

they found it to be more easily distinguished from

the background and the 3D model itself.

5.3.3 Viewport Control

In task two, users were first asked to change one of

the viewports to a given view, being given no

indication of how or even that there were three

alternate methods to arrive at this result.

Of the three methods (M1, M2, M3), the users

most often first found method 3 which required the

users to click on the symbol at the top right corner of

the viewport (M1:28%;M2:8%;M3:64%). They were

then shown all three methods and were asked which

they preferred. The most popular was 3 (94%), due

to being faster and more direct. In a distant second

place was method 1 (6%) that required the selection

of the viewport and use of the Views menu. Indeed,

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

460

method 1 was most often indicated as being an

alternative method to method 3. Despite being the

least preferred option (0%), method 2 was

sometimes indicated by users as being a good option

for setting the default views for each viewport, as

opposed to when spontaneously changing a viewport

while working. The ASG and APG groups were the

ones who found this subtask the easiest.

For the next subtask, users were required to use

the zoom and pan features of the viewports so as to

focus a viewport on a given detail of the model.

Here too, they were given two variants to try, where

the mapping between the mouse wheel and the zoom

function was inverted. The majority of users

expressed a preference for the choice where a

forward movement of the mouse wheel results in

zooming in and a backwards movement results in

the opposite effect (73%). APG was the group that

found manipulating the viewport the easiest.

The last subtask of task two required users to

turn on the grid (U(sefulness):3.1;1.3; S(atisfaction):

3.2;1.2; E(ase of Use):3.7;1.1).

5.3.4 Projection Control

Task three began by requiring the subject to switch

the mapping mode. The two variant button schemes

were used. Between the two, users preferred having

multiple buttons (73%) as opposed to a single one,

as it made all the possible options immediately

visible to the user and was more efficient. However;

users also indicated some confusion about the

meanings of the icons used.

Again, the APG and ASG groups found this task

the easiest and most satisfactory.

Task three then requires the users to rotate the

image by 95°, render the image, save the projection

as an epsv file and export an SVG image of the EPS

view. The Up Angle was considered more easy to

use (4.6;0.6), than satisfactory (3.7;1.2) or useful

(3.4;1.1).

5.3.5 Final Task: Reproduce an Image

in EPS

The fourth task required the use of EPS Visualizer,

and its specific features to recreate a given image. It

was more complex and free-form than the previous

tasks. Users seemed to have some difficulty with the

task due to their initial unfamiliarity dealing with a

different way of perceiving space and interpreting

the image perspective, and yet they evaluated the

Visualizer’s ease of use during the task as (3.4;0.8).

Almost all users found the use of the mouse

consistent (Yes:92%; No:8%; S:4.2;0.9;E:4.1;0.8)

and found the radius and eccentricity parameters

very useful (Radius:4.2;0.7;Eccentricity:3.8;1.0).

The eccentricity parameter was found less useful by

the IEG than by the architecture groups (ASG and

APG), which is understandable due to the less

familiarity with the use of different perspectives.

5.3.6 Global Opinion

Users stated that they would use the EPS Visualizer

as a support for the design process, during the stage

of prior study and development quite often (3.9;0.9),

and during the final stage of presentation just as

often (3.8;1.1). They often found the EPS Visualizer

to be a complement to free-hand drawing (3.8;0.9)

(Figure 7), and an aid in learning and drawing in

free-hand style (3.5;1.1). When compared with other

conventional perspective visualizers, users found the

EPS Visualizer advantageous (4.0:0.9). They also

found the Grid useful to guide free-hand drawing in

perspective (3.4;1.0). As suggestions for additional

graphical elements, four users mentioned XYZ axis,

two suggested the inclusion of a horizon line

reference, and also two suggested the grid should be

more flexible to allow free positioning and 3D.

The answers to the SUS usability questions were

processed in the standard way by converting the

answered values so that they would fit a 0-4 scale

(less-more positive), and then adding them up and

multiplying the total by 2.5, reaching a 0-100 value

– the SUS score for each user answers. The average

SUS score in our case was 76 (std:12), which is a

very positive result, reflecting the appreciation of the

system. Most salient results refer to not finding the

application cumbersome (3.5), much too inconsistent

(3.2), unnecessarily complex (3.2), found the various

functions

well-integrated (3.2) and would imagine that

most people would learn to use it very quickly (3.1).

Figure 7: EPS Visualizer vs. other perspective visualizers

and free-hand drawing.

When asked about some global EPS Visualizer

features (Figure 8), in general the users showed no

particular preference (nor were there visible trends

InteractiveVisualizerfortheExtendedPerspectiveSystemasSupportforArchitecturalDesign

461

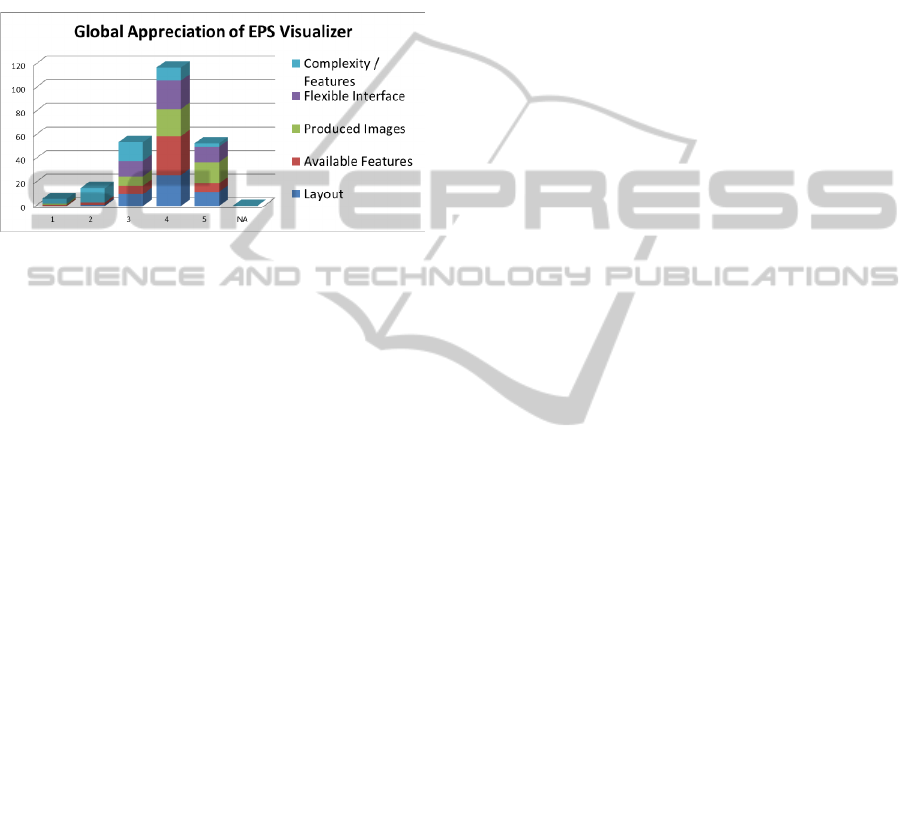
in the different user groups), between layout,

available features, produced images, and flexible

interface. Most of them did not find the system too

complex for the available features, hence the higher

frequency of lower values in this dimension.

Although the differences between user groups are

small: for ASG and APG users, the EPS resulting

images were the most important, whereas for IEG

users, it was the available features that were most

important.

Figure 8: Global Appreciation of EPS Visualizer.

As for future versions: most users would like to see

the EPS features integrated into 3D modeling tools

(4.3,0.9), although more by APG (4.5;1.1), then by

the ASG (4.3;0.08), and IEG (4.0;0.6); and

suggested other applications for the EPS Visualizer,

such as product design, video games, education (e.g.

concept illustration in analytical geometry classes),

and photography. As for what to add to the EPS

Visualizer, four mentioned 3D modeling, more

advanced graphics rendering, among others, mainly

concerned with additional flexibility. They found the

presented demo useful (4.5;0.9). The most

appreciated features included: the new perspective

possibilities; the ease of use; increased field of view;

easier perspective of space; viewer and target

manipulation; and the simplicity of the interface.

Least

appreciated features included: the floating

windows overlapping the main window, although the

possibility

to integrate them at the borders of the main

window

was already implemented but not yet visible;

inability to move the camera via the EPS and linear

views;

confusing viewer and target control (in contrast

with being considered a favourite by other users).

6 CONCLUSIONS AND FUTURE

WORK

This paper described the EPS Visualizer, aimed at

supporting the design process in architecture and

presented a user evaluation of its interface and

usefulness.

This interactive tool implements the EPS

representational system, with flexibility in the

parametrization of the perspectives. It allows users

to interactivelly control the radius and eccentricity of

the projection surface, while navigating in the 3D

scene, by controlling the camera and the viewport,

as a way to explore and learn about perspective,

make drawings in diverse new types of perspectives

and support free-hand drawing, e.g. through the use

of grids. In the evaluation carried out to determine

its usability as a tool to support the design process in

architecture, the visualizer was very appreciated, in

terms of layout, available features, produced images

and flexibility, and the most effective design options

were identified, mainly for their simplicity,

visibility, and familiarity. SUS usability scores also

confirm this general satisfaction with the use and

adoption of this tool.

Overall, the results validate interface design and

encourage future work highlighting directions for

improvements and new developments.

These directions include: improving camera

control features; rendering capabilities; integration

with existing 3D modeling software, this way the

EPS depictions could be used together with editing

and throughout all the design process; development

of the EPS system itself, adding new parameters and

projection surfaces and thus increasing the variety of

projections available to the user; and expansion

beyond the domain of architectural design into other

realms such as product design, videogames,

education, art and culture, through new ways to

communicate and depict the world.

ACKNOWLEDGEMENTS

This work was financially supported by the

Portuguese Foundation for Science and Technology

(FCT) through the NAADIR project (PTDC/AUR-

AQI/098388/2008) and by the R&D units LaSIGE

and LabMAg. We are grateful for the assistance of

Vera Sanchez Osório and Diogo Pereira Henriques

in the user evaluation task and Christian Marques in

the initial prototype implementation.

REFERENCES

Agrawala, M., Zorin, D., Munzner, T., 2000. Artistic

multiprojection rendering. In Proceedings. of the

Eurographics Workshop on Rendering Techniques, pp.

125-136, London, UK. Springer-Verlag.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

462

Bonbon, B. S., 1985. La Geometrie Spherique

Tridimensionnelle. Éditions Eyrolles, Paris.

Brooke, J., 1996. "SUS: a "quick and dirty" usability

scale". In P. W. Jordan, B. Thomas, B. A.

Weerdmeester, & A. L. McClelland. Usability

Evaluation in Industry. London: Taylor and Francis.

Brosz, J., Samavati, F. F., Carpendale, S. M. T., Sousa, M.

C. 2007. Single camera flexible projection. In

Proceedings of the 5th International Symposium on

Non-Photorealistic Animation and Rendering

(NPAR’07), pages 33–42. ACM.

Casas, F. R., 1983. Flat-Sphere Perspective, Leonardo,

Vol.16, No. 1 (Winter) pp. 1-9, The MIT Press.

Coleman, P., Singh, K. R., 2004. Rendering your

animation nonlinearly projected. In Proceedings of the

3rd international symposium on Non-photorealistic

animation and rendering, NPAR ’04, pp. 129–156,

New York, NY, USA, ACM.

Correia V., Romão, L., 2007. Extended perspective

System. In Proceedings of the 25th eCAADe

International Conference, pp. 185-192.

Flocon, A., Barre, A., 1968. La Perspective Curviligne,

Flammarion Éditeur, Paris.

Glassner, A. S., 2000. Cubism and cameras: Free-form

optics for computer graphics. Technical Report MSR-

TR-2000-05, Microsoft, California.

Gröller, E., 1995. Nonlinear ray tracing: Visualizing

strange worlds. Visual Computer, 11(5): pp. 263-274.

Hansen, R., 1973. This Curving World: Hyperbolic Linear

Perspective, The Journal of Aesthetics and Art

Criticism, Vol. 32, No. 2 (Winter) pp. 147-161, Wiley.

Lund, A. M., 2001. Measuring Usability with the USE

Questionnaire. STC Usability SIG Newsletter, 8:2.

Moose, M., 1986. Guidelines for Constructing a Fisheye

Perspective, Leonardo, Vol. 19, No. 1, pp. 61-64, The

MIT Press.

Rademacher, P., Bishop, G., 1998. Multiple-center-of-

projection images. In Proceedings of the 25th annual

conference on Computer graphics and interactive

techniques, SIGGRAPH ’98, pp. 199–206, New York,

NY, USA, ACM.

Singh, K., 2002. A fresh perspective. Graphics Interface

(GI'02), pp. 17-24, May (2002).

Trapp, M., Döllner, J., 2008. A generalization approach

for 3d viewing deformations of singlecenter

projections. In GRAPP International Conference on

Computer Graphics Theory and Applications, pp.

163-170, January.

Weiskopf, D., 2000. Four-dimensional non-linear ray

tracing as a visualization tool for gravitational physics.

In Proceedings of the conference on Visualization ’00,

VIS ’00, pp. 445–448, Los Alamitos, CA, USA, IEEE

Computer Society Press. (2000).

Wyvill, G., McNaughton, C., 1990. Optical Models. In

Proc. of the 8th international conference of the Comp.

Graphics Society on CG International: comp.

Graphics around the world, pp. 83-93. Springer

Verlag, November.

Yu, J., McMillan, L., 2004a. A framework for

multiperspective rendering. In Rendering Techniques,

pp. 61–68.

Yu, J. and McMillan, L., 2004b. General linear cameras.

In ECCV (2), pp. 14–27.

InteractiveVisualizerfortheExtendedPerspectiveSystemasSupportforArchitecturalDesign

463