
Model Matching for Model Transformation
A Meta-heuristic Approach
Hajer Saada
1
, Marianne Huchard
1
, Cl
´
ementine Nebut
1
and Houari Sahraoui
2
1
LIRMM, Universit
´
e Montpellier 2, CNRS, Montpellier, France
2
Universit
´
e de Montr
´
eal, Montr
´
eal, Canada
Keywords:
Model Driven Engineering, Model Matching, Model Transformation, Meta-heuristic, Multi-Objective
Optimization, NSGA-II.
Abstract:
Model Transformation By Example (MTBE) is a recent approach that derives model transformation rules from
a source model, a target model, and matching between models. Building a match between models may be a
complex task especially when models have been created or edited manually. In this paper, we propose an
automated approach to generate mappings between source and target models. The novetly of our approach
consists in the production of many-to-many mappings between the elements of the two models.
1 INTRODUCTION
MTBE aims at defining a model transformation ac-
cording to a set of examples of this transformation.
Examples are given in the form of a source model, a
target model and a matching between the two mod-
els. A matching between two models is a set of
correspondences between their elements. Retriev-
ing those correspondences is a complex and time-
consuming task, especially when models are created
or edited manually. Hence, the transformed elements
may be different from the ones of the source model
or may use different naming conventions. This task is
well-known in different application domains such as
schema and ontology integration, e-commerce, data
warehouse and semantic web (Rahm and Bernstein,
2001; Shvaiko and Euzenat, 2005). It takes as input
two schemas to generate relations between the input
schemas entities.
In (Saada et al., 2013), we proposed an approach
to recover transformation traces from transformation
examples. In this paper, we propose an extension of
this approach to deal with the model matching prob-
lem. The novelty of this work, compared to other
proposals (Lopes et al., 2006; Falleri et al., 2008;
Dolques et al., 2011), is to find many-to many match-
ing links between the source and target models by as-
sociating a set of m source elements to a set of n target
elements. The source model is fragmented using the
minimal cardinalities of its meta-model and some de-
fined OCL constraints. Then we search for each frag-
ment in the source model the list of candidate corre-
sponding fragments in the target model. A solution to
our problem is a set of pairs of source and target frag-
ments, that maximize the lexical and structural simi-
larities between them, and cover the target model to
ensure its completeness. Due to the huge number of
possible solutions, NSGA-II, a metaheuristic method,
is used to solve this problem.
This paper is organized in the following way. Sec-
tion 2 is dedicated to the problem statement and the
overview of our approach. Section 3 introduces the
used method and its adaptation to the matching prob-
lem. Section 4 presents the experimental evaluation
and the obtained results. Section 5 presents the re-
lated work. Finally, Section 6 concludes our work and
draws some perspectives.
2 OVERVIEW
In this paper, we aim at generating a matching from
an input model M
source
, conforming to a metamodel
MM
source
, and a target model M
target
conforming to
a metamodel MM
target
. Our approach is based on a
fragmentation of M
source
and M
target
.
Definition 1. A fragment F is a set of connected con-
structs of a model M. A construct e ∈ M is an instance
of a meta-class C ∈ MM (e : C).
We denote by RhC
1
: R, R : C
2
i, an e-reference of
C
1
, which has C
2
as a type, and such that R (resp.
174
Saada H., Huchard M., Nebut C. and Sahraoui H..
Model Matching for Model Transformation - A Meta-heuristic Approach.
DOI: 10.5220/0004695601740181
In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 174-181
ISBN: 978-989-758-007-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
R) is the minimal (resp. maximal) cardinality of R.
For RhC
1
: R, R : C
2
i, eRe
0
means that we have e : C
1
,
e
0
: C
2
and e is connected to e
0
by R.
Definition 2. A meaningful fragment M f F of a model
M is a fragment that respects the minimum cardinal-
ities of the references defined on the metamodel and
its OCL constraints.
Consequently, a fragment F of a model M which
conforms to a metamodel MM (which is provided
with a set of OCL constraints) is a M f F iff:
∀e : C
1
∈ F, (∃C
2
|RhC
1
: R, R : C
2
i ∈ MM) ⇒
|{e
0
: C
2
∈ F|eRe
0
}|≥ R.
11
1
0..1
specific
association
0..1
<<invariant>>
self.association --> notEmpty()
implies
self.type --> notEmpty()
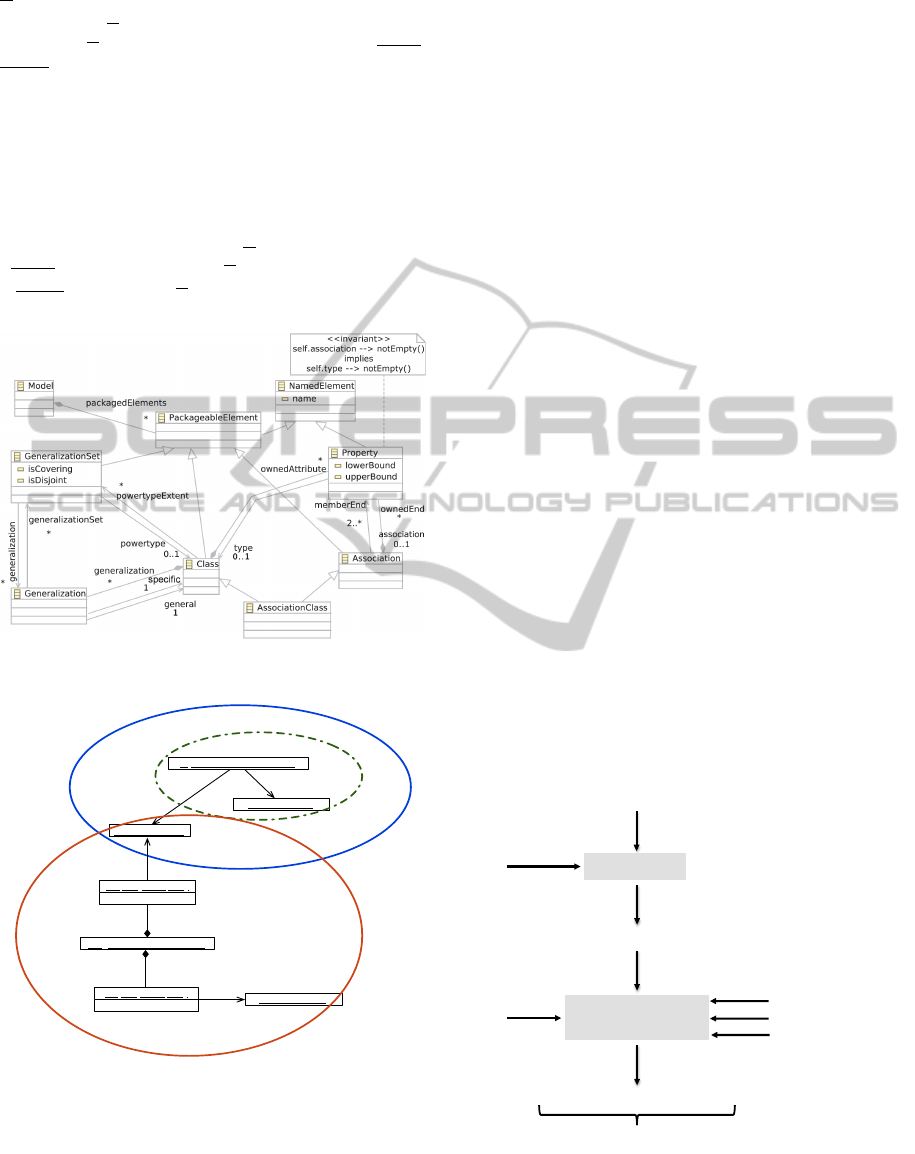
Figure 1: A simplified metamodel for UML class diagrams.
Person: Class
F3
F2
Gperson: Generalization
Teacher: Class
F1
Registration: Association
name = "teacher"
property: Property
Module: Class
name = "module"
property: Property
type
type
specific
general
Figure 2: An instance diagram of the class diagram meta-
model of Figure 1.
Let us consider the instance diagram of Figure 2
that conforms to the simplified UML class diagram
metamodel MM of Figure 1. It contains three cir-
cled fragments, F
1
, F
2
, and F
3
. F
2
is a meaningful
fragment because it respects the minimal cardinalities
defined on the generalization meta-class in MM. A
generalization consists of a relation between a gen-
eral class and a specific class. Thus, the generaliza-
tion between Class Person and Class Teacher consti-
tutes a meaningful fragment. F
3
is also a meaningful
fragment because it satisfies the minimal cardinalities
defined on the association meta-class in MM. An as-
sociation must have two properties, each one having a
type class (according to the OCL constraint shown in
MM). So, Association Registration, Property teacher
of type Teacher and Property module of type Module
form a meaningful fragment.
F
1
is composed of two connected constructs in the in-
stance diagram (the generalization Gperson and its
general class named Person). But in MM, a gen-
eralization must have a general class and a specific
class. Thus, although F
1
conforms with the definition
of fragment, it is not a meaningful fragment, because
it violates the cardinality in MM.
Definition 3. A matching between M
s
and M
t
is a set
of pairs that match a source meaningful fragment in
M
s
to a target fragment in M
t
.
We denote by F(M) (resp. MfF(M)) the set of all frag-
ments (resp. meaningful fragments) that can be built
from a model M.
A specific matching of n pairs takes the following form
{(M f F
s
i
, F
t
i
) | i ∈ {1..n}} ⊆ M f F(M
S
) × F(M
T
).
The problem is to search a mapping between M
S
and M
T
. This search needs to find all the matching
possibilities (2
M f F(M
s
)×F(M
t
)
). To find the best match
between each MfF in M
S
and F in M
T
, using a meta-
heuristic search may help.
Meta-heuristic Search
{MfF
1
, MfF
2
, …, MfF
n
}
M
S
{(MfF
1
,F
1
), (MfF
2
,F
2
), …, (MfF
n
,F
n
)}
Matching
Meta-model cardinalities
OCL constraints
Fragmentation
M
T
Lexical similarity
Structural similarity
Target model coverage
Figure 3: Approach overview.
Figure 3 shows an overview of our approach:
• The first step consists in the fragmentation of the
ModelMatchingforModelTransformation-AMeta-heuristicApproach
175
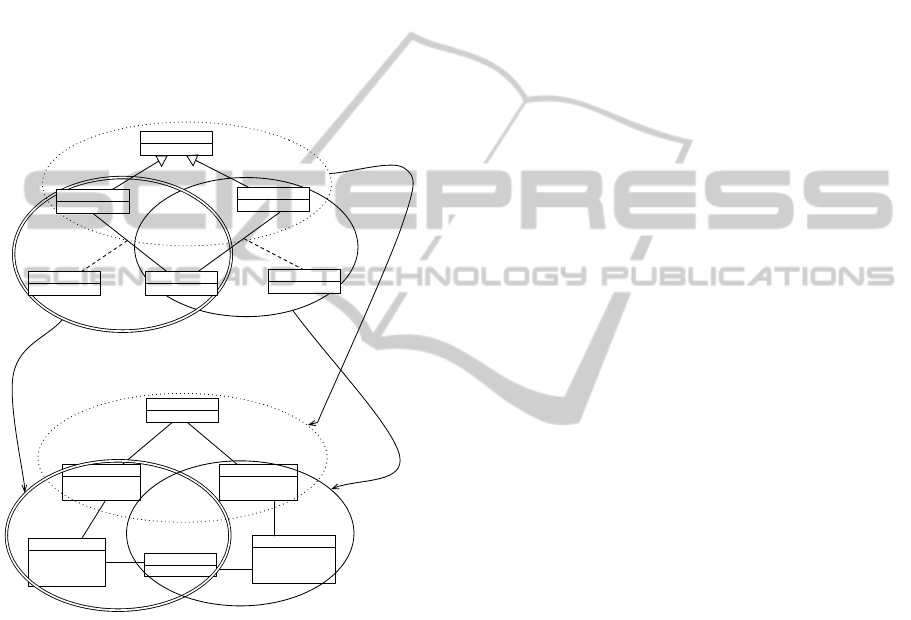
source model into meaningful fragments accord-
ing to the minimal cardinalities and the OCL con-
straints of its meta-model.
• In the next step, a metaheuristic method is used to
search for each source meaningful fragment, the
corresponding target fragment. This search takes
on consideration three factors: 1) Lexical similar-
ity between the fragments in each pair; 2) Struc-
tural similarity of the fragments matched by sim-
ilar meaningful fragments (similar source frag-
ments should be matched to similar target frag-
ments) and 3) Completeness of the target model
by the produced mapping.
IdPerson
Person
Name
Student
Name
Teacher
IdModule
Module
Date
Registration
Date
Intervention
IdPerson (PK)
Person
IdPerson (PFK)
Name
Student
IdPerson (PFK)
Name
Teacher
IdModule (PK)
Module
IdPerson (PFK)
IdModule (PFK)
Date
Registration
IdPerson (PFK)
IdModule (PFK)
Date
Intervention
MfF1
MfF2MfF3
F1
F2
F3
Figure 4: An example of matching between a class diagram
and relational schema model.
Figure 5 shows an example of matching between
an UML class diagram and a relational schema model.
The choice of this example is only motivated by clar-
ity considerations. Our approach does not depend
on any specific source and target metamodels. The
class diagram is decomposed into three meaningful
fragments according to the minimal cardinalities and
the OCL constraints of the metamodel of Figure 1.
In terms of lexical similarity, we note that M f F1
matches well F1. They contain the same identifiers
(Person, Student and Teacher). We observe also a
comparable similarity between M f F2 and F2, and
between M f F3 and F3. In terms of structural sim-
ilarity, the meaningful fragments M f F2 and M f F3
which have the same type (an association class be-
tween two classes) are matched to the fragments F2
and F3, which have also the same type (three con-
nected tables).
Lexical similarity, structural similarity and the tar-
get model coverage are used in this work to find the
best match between two models. Thus, the matching
problem can be seen as a multi-objective optimization
problem. Hence, we choose NSGA-II algorithm (in-
troduced in the next section) to solve our problem.
3 APPROACH
3.1 The NSGA-II Algorithm
Search-based software engineering (SBSE) is a do-
main with a growing interest. It aims at solving a va-
riety of software engineering optimization problems
using meta-heuristic approaches, including evolution-
ary algorithms (EAs) (Harman, 2011). Evolutionary
algorithms (EAs) develop the metaphor of the biolog-
ical evolution of a population. They implement dif-
ferent variations on operators that act on the popula-
tion by selecting individuals, and crossing or mutating
them to obtain new individuals.
Specific EAs have been proposed to solve prob-
lems with multiple (possibly conflicting) objectives,
where it is even more difficult to find a single optimal
solution. These algorithms are searching for multi-
ple solutions, non comparable when all objectives are
considered in combination, although each one is op-
timal for an objective, known as Pareto-optimal solu-
tions (Deb et al., 2002). Most famous multi-objective
EAs are described in (Horn et al., 1994; Zitzler and
Thiele, 1999; Knowles and Corne, 1999; Deb et al.,
2002). The non-dominated sorting genetic algorithm
(NSGA-II) has been proved to have a better perfor-
mance than its predecessors in (Deb et al., 2002) and
it has been successfully used in the SBSE commu-
nity (Harman et al., 2012).
NSGA-II Procedure. The evolution of the popu-
lation during an iteration of the NSGA-II procedure is
presented in Figure 5 which is taken from the original
paper. First, an initial population P
0
of N solutions
is created. The individuals of P
0
are sorted based
on the non-domination. Non-dominated individuals,
corresponding to the best known solutions (with re-
gard to at least one objective) at the current step,
are grouped in the first non-dominated front (rank 1).
Discarding the individuals of the first front, the cur-
rent non-dominated individuals form the second non-
dominated front (rank 2), and so on. Diversity is pre-
served thanks to a crowding distance which is calcu-
lated for each solution (Laumanns et al., 2002). Fi-
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
176

nally, a binary tournament selection operator, which
is based on the crowding distance, selects the best
solutions. At step t, an offspring population Q
t
of
size N is created using selection, crossover and mu-
tation operators. Populations P
t
and Q
t
are combined
to form the population R
t
. From R
t
, the best individu-
als in terms of non-dominance and diversity are kept
to form P
t+1
. Then those steps are repeated till some
termination criteria are satisfied.
P
t
Q
t
F
1
F
2
F
3
Non-dominated sorting
Crowding distance sorting
Rejected
R
t
P
t+1
Figure 5: NSGA-II main (Deb et Al, 2002).
Fast Non-dominated Sorting Principle. A solu-
tion s
1
dominates another solution s
2
if: (i) s
1
is no
worse than s
2
in all objectives, and (ii) s
1
is strictly
better than s
2
in at least one objective. The first non-
dominated front in a population of size N is thus com-
puted as follows. The algorithm calculates first, for
each solution p: 1) the domination count n
p
, i.e. the
number of solutions which dominate the solution p
and 2) S
p
, the set of solutions that the solution p dom-
inates. The solutions p such that n
p
= 0 are found in
the first non-dominated front. Now, to obtain the sec-
ond non-dominated front, for each p of the first front,
each solution q ∈ S
p
is visited, and its domination
count is reduced by one. When the domination count
of a solution q becomes zero, q is put in a separate list
Q which represents the second non-dominated front.
Then, the procedure is continued with the members of
Q to identify the third front, and so on. If N
ob j
is the
number of objectives and N is the size of the popula-
tion, this algorithm has a time complexity evaluated
in O(N
ob j
N
2
), which is better than the complexity of
the previous algorithms, which require O(N
ob j
N
3
).
Diversity Preservation. From the parent and off-
spring populations (each of size N), N best solutions
are selected to form the next population. As many
non-dominated fronts as possible are included in the
next population, by increasing rank, keeping the num-
ber of individuals less than N. Let denote k the
number of these included fronts. Including the non-
dominated front of rank k + 1 would result in exceed-
ing N. The solutions of the front of rank k + 1 are
thus sorted, and only a part of them is selected to fill
the next population and obtain N solutions. This is
done by selecting the solutions the less crowded, that
is, that are maximally apart from their neighbors ac-
cording to the crowding distance. For a given solu-
tion s, this is measured as the average distance of two
nearest solutions (neighbors of s) along each of the
objectives (in the same non-dominating front). The
resulting crowded-Comparison operator helps select-
ing scattered solutions.
3.2 Adapting NSGA-II to the Model
Matching
In this section, we describe the adaptation of NSGA-II
to the matching problem. To apply this type of algo-
rithm to a specific problem, we must have a pair of
source and target models. We must also define the so-
lution encoding. We also need to specify the fitness
functions, one per objective, to evaluate the results,
and guide the search process, and the operators to se-
lect, crossover and mutate the solutions.
Encoding a mapping between source and target
models is an essential element in our approach. In our
case, a solution is a set of fragment pairs, s = { f p
i
, i ∈
{1, 2, ...n
s
}}. Each fragment pair f p
i
is, in turn, en-
coded as a pair f p
i
= (M f F
i
, F
i
) where M f F
i
is a
source meaningful fragment in the source model and
F
i
is its corresponding fragment in the target model.
As stated before, our approach is based on the
fragmentation of source and target models. The
source model is divided into three criteria: respecting
the minimum cardinalities in the source metamodel,
respecting the OCL constraints defined on the source
metamodel and ensuring the source model coverage
(each construct in the source model must belong to at
least one meaningful fragment). The target model is
randomly fragmented to match a fragment with each
meaningful fragment. We suppose that:
• The corresponding constructs of a source mean-
ingful fragment in the target model need not nec-
essarily to form a meaningful fragment
• The target model may contain constructs which
are independent from the ones of source model.
Thus, they can have different sizes.
After the fragmentation of the source model into
n
s
meaningful fragments, the target model is divided
randomly into n
s
+ x fragments such that −y < x < y.
y is a parameter of our algorithm which is the maxi-
mum variation of the number of target fragments with
respect to the source ones. We have a maximum of
4 constructs in a target fragment. The size is chosen
ModelMatchingforModelTransformation-AMeta-heuristicApproach
177

randomly for each fragment (1 < size < 4). if size = 4,
we select randomly a construct, call it c, from the tar-
get model. Then, if c is connected to other constructs,
we extend the fragment by randomly selecting three
of them. If c is connected only to two constructs c
1
and c
2
, we can extend the fragment by one of the
constructs connected to c
1
or c
2
. Then, c is removed
from the set of constructs for the next fragments. If c
has connections with others constructs, it may still be
included in others fragments.
Once the source and target fragments sets are cre-
ated, we associate each source meaningful fragment
MfF, with a target fragment F. A solution is then a
vector whose dimensions are the M f F
s
and values
are the F
s
.
s = {(M f F
1
, F
1
), (M f F
2
, F
2
), (M f F
3
, F
3
)} corre-
sponds to the matching solution proposed in Figure
5.
For the initial population, we build a set of N solu-
tions (N is a parameter of our approach). Each one
represents a matching possibility between the source
and target models.
During the evolution process, the fitness functions
evaluate the matching solutions. In our case, we have
three fitness functions corresponding to three objec-
tives: 1) Lexical similarity in a pair composed of a
MfF and a F, 2) Structure similarity: in a solution
s, the set of MfF which have the same type must be
matched to a set of F in the target model which have
the same type and 3) In a solution s, the obtained frag-
ments must cover the target model. The three objec-
tives should be maximized.
• Lexical Similarity: to compute the lexical sim-
ilarity in a solution s, we use: 1) information
retrieval methods, which sort documents accord-
ing to queries by extracting information about the
terms’ occurrences within document and 2) natu-
ral language processing techniques which identify
the original forms of the words.
First, we extract the property value lemmas
of M f F
i
and F
i
in each f p
i
using TreeTagger
(Schmid, 1994; Schmid, 1995), a tool for annotat-
ing text with part-of-speech and lemma informa-
tion. It is used to tag various languages including
English, French German, etc. Then, all the dis-
tinct lemmas in s are extracted in a list li. li repre-
sents the dimensions of vectors associated to each
source or target fragment in s. For each fragment
and each term, the corresponding dimension is set
to 1 if the term exists in the fragment or to 0 oth-
erwise. Then, the similarity is calculated between
each pair M f F
i
and F
i
using the cosine similarity
between the two concerned vectors. The resulting
lexical similarity ranges from −1, meaning that
M f F
i
and F
i
do not share any term, to 1, meaning
that M f F
i
and F
i
use exactly the same terms. The
lexical similarity LexSim(s) of a solution s equals
the average of the contained pairs’ lexical similar-
ities.
• Structural Similarity: to compute structural simi-
larity in a solution s, we proceed in three steps:
1. We classify the solutions per type of their re-
spective meaningful fragments M f F
i
.
2. We measure for each two pairs of fragments,
which have the same type of MfF, the structural
similarity of the matched target models. To this
end, we use also the cosine similarity, but be-
tween vectors whose dimensions are the con-
struct types in the metamodel. Indeed, for each
construct type instantiated in the target model,
a term is created. Then for each target model
fragment, the dimension is set to 1 if it contains
a construct of the corresponding type, and to 0
otherwise.
3. The structural similarity StrSim(s) of a solution
s is the average of the target-fragment similari-
ties of the pairs having the same MfF type.
• Target model coverage: the completeness of the
target model is very important because it ensures
that the obtained matching covers all the target
model constructs. It is measured by the number
of distinct constructs in the matched target frag-
ments divided by the number of constructs in the
target model.
In a metaheuristic method, a population of match-
ing solutions is improved by applying genetic oper-
ators (mutation and crossover). Before applying the
operators, the solution are selected according to their
fitness values. The selection strategy used is the Bi-
nary Tournament Selection. It favors the fittest so-
lution for reproduction. The selection criteria are the
rank of the containing front and the crowding distance
for solutions within the same front.
The crossover operation consists of producing
new solutions by crossing the existing ones. It is ap-
plied to each pair of selected solutions. After select-
ing two parent solutions for crossing, two new solu-
tions are created by exchanging parts of the parents.
The cut point is decided randomly.
After applying the crossover operation, the ob-
tained solutions may be mutated with a given prob-
ability. At each iteration, a solution is selected for
mutation. A mutation strategy is also randomly se-
lected. We define two mutations strategies: extending
a target fragment with a new construct or deleting a
construct from a target fragment.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
178

4 EVALUATION
To illustrate the ability of our approach to derive map-
pings from source and target models, we conducted
an experiment on six source and target models com-
ing from several sources on the Internet. The size of
models varies between 20 and 40 constructs.
• UML class diagram to Relational Schema model
(cl2rs).
• EMF metamodel to Kermeta metamodel
(em2ker).
• Kermeta metamodel to EMF metamodel
(ker2em).
• UML class diagram to Java code model (cl2jc).
• Ecore metamodel to Jess (Jess, 1997) metamodel
(ec2je).
• Book model to publication model (bo2pu).
Source and target models are not obtained by a trans-
formation program and they are not written by the
same person. Thus they may have different vocabu-
laries.
As mentioned before, our algorithm uses a set of
parameters. For these examples, there are set as fol-
lows:
• Crossover probability is set to 0.8.
• Mutation probability is set to 0.35
• The initial population is set to 400 solutions for
each example.
• We ran the algorithm with a number of iterations
equal to twice the size of the population.
• The maximum variation y of the number of target
fragments with respect to the source ones is set
to 1. This means that in a solution, we can have
a MfF without a corresponding fragment, or an F
without an assigned MfF.
• With a metaheuristic method, we can obtain, for
the same example, with the same parameters, dif-
ferent results on different executions. Thus, we
took the best result from four executions.
Testing the examples consists in generating the
mapping from each source and target models and
comparing the obtained mapping with those provided
by an expert. This comparison allows calculating the
precision and the recall for each pair f p
i
= (M f F
i
, F
i
)
in the obtained solutions.
The precision of a pair is defined as the number of
correctly assigned constructs (C
correct
) among the
total number of constructs (C
totalNbr
) (equation1).
The recall of a pair is defined as the number of
correctly assigned constructs among the number of
expected constructs (C
expert
) (equation2).
Precision( f p
i
) =
C
correct
C
totalNbr
(1)
Recall( f p
i
) =
C
correct
C
expert
(2)
The precision (resp. the recall) of a solution is defined
as the average precision (resp. recall) of its fragment
pairs.
Results and Discussion
0
0.2
0.4
0.6
0.8
1
cl2rs em2ker ker2em cl2jc ec2je bo2Pu
Precision Average
Figure 6: Precision average measured on the six examples
0
0.2
0.4
0.6
0.8
1
cl2rs em2ker ker2em cl2jc ec2je bo2Pu
Recall Average
Figure 7: Recall average measured on the six examples
During our experiments, we obtained good results
confirmed by the precision and recall averages shown
in Figures 6 and 7. The precision scores are all be-
tween 0.87 and 0.92 and the recall scores are higher
than 0.76 in all cases. The scores of UML class dia-
gram to relational schema model are interesting (0.92
precision and 0.86 recall). This is very encouraging
since we used different type of examples.
ModelMatchingforModelTransformation-AMeta-heuristicApproach
179

Results and Discussion
The execution time is very important since we use a
metaheuristic method. In our experiments, we used
a simple macBook (2.4 GHz CPU and 2G of RAM).
The execution time for generating a mapping between
source and target models with a number of iterations
up to 800, is less than 90 seconds. We note also that
the execution time increases quasi linearly with the
models’ size.
Threats to validity
The experiment is here conducted on six source and
target models. Those models have different size, vo-
cabulary and structure. To help us improving the
model matching algorithm, additional experiments
have to be conducted, especially to study the two fol-
lowing issues:
• The relatively fixed size of the used examples.
Larger models and more examples have to be con-
sidered in the future.
• The correctness of the obtained mapping is mea-
sured manually by an expert and this is may be a
hard task especially when using larger models. An
automatic measure may be defined in the future.
5 RELATED WORK
In the following, we give an overview on related
work, dealing with model matching.
In database and ontologies domains, this task is
called schema matching (Rahm and Bernstein, 2001;
Shvaiko and Euzenat, 2005). The basic idea of the
main approaches (Do and Rahm, 2002; Madhavan
et al., 2001; Ehrig and Staab, 2004; Euzenat et al.,
2004; Melnik et al., 2002) is to find semantic corre-
spondences between elements of two schemas. They
make the assumption that the relations between the
two models being compared are identical. They com-
pute a similarity between the elements using their
names. They compute also a structural similarity be-
tween the elements. For this, they assume that there
is the same kind of relations between the elements in
the two compared models.
For model transformation, Fabro and Valduriez
(Fabro and Valduriez, 2009) create links between
source and target metamodels by using the similarity
flooding technique (Melnik et al., 2002) to construct
propagation models which capture the semantics of
the relationships between the two models. Then, links
are designed by an expert and are used to produce
transformation. In (Dolques et al., 2011) a semi-
automatic matching approach for discovering links
between source and target model is proposed.They
assume that the target model results from a trans-
formation from the source model. They extend the
Anchor-Prompt approach to discover the pairs of el-
ements for which there is a strong assumption of
matching. In (Lopes et al., 2006; Lopes et al., 2009),
the authors define an algorithm (SAMT4MDE) that
assumes that source and target metamodels are sim-
ilar in their structure. It finds correspondences using
string values of attributes and structure similarity. The
contribution of (Falleri et al., 2008) consists to evalu-
ate different parameterizations of the similarity flood-
ing algorithm to compute the mappings.
The approach that we propose does not have any
constraint on the used models or metamodels. Target
models do not result from an automatic transforma-
tion from the source model and they are not written
by the same person. Thus, they can have different
vocabularies and structures. Furthermore a many-to-
many matching is obtained from two models.
A mid-term objective of our work is to gener-
ate transformation rules from examples. Several ap-
proaches (Wimmer et al., 2007; Balogh and Varr
´
o,
2009; Kessentini et al., 2008; Saada et al., 2012) use
examples to produce rules. Examples consist of a
source model, a target model and links between el-
ements or fragments of the models.
6 CONCLUSIONS
Model Transformation By Example is a novel ap-
proach to ease the development of model transforma-
tion using examples of source and target models. In
this context, model matching is a crucial element to
extract links between models elements, or model frag-
ments and learn transformation rules.
The main contribution of this work is a model
matching approach, which adapts the NSGA-II algo-
rithm to explore the space of matching possibilities
between the source and target model elements. We
used TreeTagger, a lexical tool to solve the problem
of vocabulary between models.
In order to validate the proposed approach, we
performed experiments on six source and targets
models and compared, using retrieval information
metrics, the obtained matchings to the expected ones.
The results are promising. For all the examples, pre-
cision average is higher than 0.8 and recall average is
higher than 0.76.
To confirm these encouraging results, we plan to
improve our work by conducting more experiments
to test our approach on other type of examples. We
plan also to compare our matching tool to some ex-
isting ones. Other techniques can be also explored to
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
180

improve the lexical similarity between models.
REFERENCES
Balogh, Z. and Varr
´
o, D. (2009). Model transformation by
example using inductive logic programming. Software
and System Modeling, 8(3):347–364.
Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T.
(2002). A fast and elist multiobjective genetic algo-
rithm: Nsga-II. IEEE Trans, Evolutionary Computa-
tion, 6(2):182–197.
Do, H.-H. and Rahm, E. (2002). Coma: a system for flex-
ible combination of schema matching approaches. In
Proceedings of the 28th international conference on
Very Large Data Bases, VLDB ’02, pages 610–621.
Dolques, X., Dogui, A., Falleri, J.-R., Huchard, M., Nebut,
C., and Pfister, F. (2011). Easing model transforma-
tion learning with automatically aligned examples. In
7th European Conference, ECMFA 2011, pages 189–
204.
Ehrig, M. and Staab, S. (2004). Qom quick ontology map-
ping. In In Proc. 3rd International Semantic Web Con-
ference (ISWC04, pages 683–697. Springer.
Euzenat, J., Loup, D., Touzani, M., and Valtchev, P. (2004).
Ontology alignment with ola. In In Proceedings of the
3rd EON Workshop, 3rd International Semantic Web
Conference, pages 59–68. CEUR-WS.
Fabro, M. D. D. and Valduriez, P. (2009). Towards the ef-
ficient development of model transformations using
model weaving and matching transformations. Soft-
ware and System Modeling, 8(3):305–324.
Falleri, J.-R., Huchard, M., Lafourcade, M., and Nebut, C.
(2008). Metamodel matching for automatic model
transformation generation. In Proceedings of the 11th
international conference on Model Driven Engineer-
ing Languages and Systems, MoDELS ’08, pages
326–340.
Harman, M. (2011). Software engineering meets evolution-
ary computation. IEEE Computer, 44(10):31–39.
Harman, M., Mansouri, S. A., and Zhang, Y. (2012).
Search-based software engineering: Trends, tech-
niques and applications. ACM Comput. Surv.,
45(1):11:1–11:61.
Horn, J., Nafpliotis, N., and Goldberg, D. (1994). A niched
pareto genetic algorithm for multiobjective optimiza-
tion. In Proceedings of the First IEEE Conference on
Evolutionary Computation, pages 82–87. IEEE.
Jess (1997). Jess rule engine,
http://herzberg.ca.sandia.gov/jess.
Kessentini, M., Sahraoui, H., and Boukadoum, M. (2008).
Model transformation as an optimization problem. In
Proceedings of the 11th international conference on
Model Driven Engineering Languages and Systems,
MoDELS ’08, pages 159–173. Springer-Verlag.
Knowles, J. and Corne, D. (1999). The pareto archived evo-
lution strategy: A new baseline algorithm for pareto
multiobjective optimisation. In Proceedings of the
Congress on Evolutionary Computation, volume 1,
pages 98–105. IEEE.
Laumanns, M., Thiele, L., Deb, K., and Zitzler, E. (2002).
Combining convergence and diversity in evolutionary
multiobjective optimization. Evolutionary computa-
tion, 10(3):263–282.
Lopes, D., Hammoudi, S., and Abdelouahab, Z. (2006).
Schema matching in the context of model driven en-
gineering: From theory to practice. In Advances in
Systems, Computing Sciences and Software Engineer-
ing, pages 219–227. Springer.
Lopes, D., Hammoudi, S., and Abdelouahab, Z. (2009). A
step forward in semi-automatic metamodel matching:
Algorithms and tool. In Filipe, J. and Cordeiro, J.,
editors, Proceeding of ICEIS 2009, pages 137–148.
Springer.
Madhavan, J., Bernstein, P. A., and Rahm, E. (2001).
Generic schema matching with cupid. In Proceedings
of the 27th International Conference on Very Large
Data Bases, VLDB ’01, pages 49–58.
Melnik, S., Garcia-Molina, H., and Rahm, E. (2002). Sim-
ilarity flooding: A versatile graph matching algorithm
and its application to schema matching. In Proceed-
ings of the 18th International Conference on Data En-
gineering, ICDE ’02, pages 117–. IEEE Computer So-
ciety.
Rahm, E. and Bernstein, P. A. (2001). A survey of ap-
proaches to automatic schema matching. The VLDB
Journal, 10(4):334–350.
Saada, H., Dolques, X., Huchard, M., Nebut, C., and
Sahraoui, H. A. (2012). Generation of operational
transformation rules from examples of model trans-
formations. In MoDELS 2012, pages 546–561.
Saada, H., Huchard, M., Nebut, C., and Sahraoui, H. A.
(2013). Recovering model transformation traces using
multi-objective optimization. In ASE, pages 688–693.
Schmid, H. (1994). Probabilistic part-of-speech tagging us-
ing decision trees.
Schmid, H. (1995). Improvements in part-of-speech tagging
with an application to german. In In Proceedings of
the ACL SIGDAT-Workshop, pages 47–50.
Shvaiko, P. and Euzenat, J. (2005). A survey of schema-
based matching approaches. Journal on Data Seman-
tics, 4:146–171.
Wimmer, M., Strommer, M., Kargl, H., and Kramler, G.
(2007). Towards model transformation generation by-
example. In Proceedings of the 40th Annual Hawaii
International Conference on System Sciences, HICSS
’07, pages 285b–.
Zitzler, E. and Thiele, L. (1999). Multiobjective evolu-
tionary algorithms: a comparative case study and the
strength pareto approach. IEEE Trans. Evolutionary
Computation, 3(4):257–271.
ModelMatchingforModelTransformation-AMeta-heuristicApproach
181
