
Femtosecond Pulse Propagation in Gas-filled Hollow-Core Photonic
Crystal Fibers
Sílvia Rodrigues
1
, Margarida Facão
2
, Sofia Latas
3
and Mário Ferreira
4
I3N-Institute of Nanostructures, Nanomodelling and Nanofabrication, Department of Physics,
University of Aveiro, 3810-193 Aveiro, Portugal
Keywords: Hollow-Core Photonic Crystal Fibers, Nonlinear Optics, Optical Solitons, Pulse Compression,
Supercontinuum Generation.
Abstract: We investigate the ultrafast dynamics of femtosecond pulse propagation in a gas-filled kagome hollow-core
photonic crystal fiber (HC-PCF). We show that, by varying the gas pressure, the zero dispersion wavelength
of such fiber can be tuned across the ultraviolet (UV), visible and near-infrared spectral regions. The soliton
effect compression, deep-UV light and supercontinumm generation are investigated using a generalized
nonlinear Schrödinger equation.
1 INTRODUCTION
Hollow–core photonic crystal fibers (HC-PCF)
(Russel, 2003; Russel, 2006) with a hexagonal
arrangement of holes in the cladding guide light by
the photonic bandgap mechanism which offer low-
loss transmission. These fibers offer an effective
environment for nonlinear optics in gases, providing
long interaction lengths while avoiding beam
diffraction (Russel, 2006). The main drawback of
these fibers is their intrinsically narrow transmission
bandwidth determined by the bandgaps, which
excludes its implementation in a large number of
applications in ultrafast nonlinear optics requiring
broadband guidance or guidance in the visible and
UV.
An alternative HC-PCF design replaces the
hexagonal lattice cladding with a kagome lattice
(Couny et al., 2006; Pearce et al., 2007). In kagome-
type HC-PCFs the field overlap with the surrounding
silica structure is particularly low (Couny et al.
2007). In contrast to the photonic bandgap-type
fibers, the guiding mechanism is based on the
inhibited coupling between the core and cladding
modes (Couny et al., 2007) and not the bandgap-
effect.
Kagome HC-PCF offers in addition broadband
transmission and weak anomalous dispersion from
the UV to the near-IR. These properties not only
help support ultrafast soliton dynamics, but also
allow the guidance of any UV light that is
subsequently generated at a relatively low loss of ~3
dB/m (Joly et al., 2011). The possibility of adjusting
the gas species and gas pressure inside the fiber core
also offers a new degree of freedom over
conventional fibers, providing a perfect environment
for demonstrating many different nonlinear effects
(Mak et al., 2013).
In this paper we investigate the ultrafast
dynamics of femtosecond pulse propagation in a
gas-filled kagome HC-PCF. In Section 2 we show
that by varying the gas pressure, the normal group-
velocity dispersion (GVD) of the filling gas can be
balanced against the anomalous GVD of the kagome
PCF allowing the zero dispersion wavelength
(ZDW) to be tuned across the ultraviolet (UV),
visible and near-infrared spectral regions. A
generalized nonlinear Schrödinger equation
(GNLSE) is used in Section 3 to describe ultrashort
pulse propagation in a gas-filled kagome PCF. The
soliton self-compression effect and the generation of
dispersive wave radiation in the UV region are
described.
2 DISPERSION PROPERTIES
In kagome-type HC-PCFs the field overlap with the
surrounding silica structure is particularly low
(Couny et al., 2007), since a good confinement of
51
Rodrigues S., Facão M., Latas S. and Ferreira M..
Femtosecond Pulse Propagation in Gas-filled Hollow-Core Photonic Crystal Fibers.
DOI: 10.5220/0004696000510055
In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 51-55
ISBN: 978-989-758-008-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

the optical field in the core can be generally
achieved. Fig. 1 shows the mode field profile of a
kagome HC-PCF with a core diameter of 40 m
filled with 10 bar of Xe.
Figure 1: Mode field profile of a kagome PCF with a core
diameter of 40 m filled with 10 bar of Xe.
The effective modal refractive index of the
11
HE
mode in a kagome HC-PCF is accurately
approximated by that of a glass capillary and is
given by
22
2
01
2
0
0
8
2
)(1),,(
a
u
T
T
p
p
Tpn
eff
(1)
where
is the vacuum wavelength,
)(
the
Sellmeier expansion for the dielectric susceptibility
of the filling gas,
p
the gas pressure,
0
p
the
atmospheric pressure,
T
the temperature,
0
T
=
273.15 K,
a
the core radius and
01
u
is the first zero
of the Bessel function
0
J
. Finite element
simulations and numerous experiments have
confirmed the reliability of this expression (Nold et
al., 2010; Chang et al., 2011).
The propagation constant
)(
is given by
c
n
eff
)(
(2)
Mathematically, the effects of fiber dispersion are
accounted for by expanding )(
in a Taylor series
about the carrier frequency
0
at which the pulse
spectrum is centred:
...)(
2
1
)()(
2
02010
(3)
where
0
k
k
k
d
d
(
k
= 0, 1, 2, …)
(4)
For pulse propagation purposes, one are specially
interested on the group velocity dispersion (GVD)
that is characterized by the parameter
2
.
The kagome HC-PCF provides ultrabroadband
guidance at low loss levels and it presents, when
evacuated, weak anomalous GVD over the entire
transmission window. However, when filled with a
noble gas, the normal GVD of the gas can be
balanced against the anomalous GVD of the fiber,
allowing the ZDW to be tuned across the ultraviolet
(UV), visible and near-infrared spectral regions.
This can be observed in Fig. 2, which shows the
group velocity dispersion of a kagome HC-PCF with
a 30
m core diameter, filled with 0 to 20 bar Ar.
Figure 2: Dispersion curves of a kagome PCF with a 30
m core diameter, filled with 0 to 20 bar Ar (2 bar steps).
We can compare the above results with those of a
solid core PCF, where the shortest ZDW that can be
achieved is about 500 nm. Moreover, the dispersion
magnitude is significantly smaller in a kagome PCF,
which means that ultrafast pulses broaden much less
quickly in this case.
3 ULTRAFAST NONLINEAR
DYNAMICS
The propagation of ultrashort pulses in gas-filled
PCF can be described by the following generalized
nonlinear Schrödinger equation (GNLSE):
2
2
1
k
k
k
k
k
Uz,t
i i Uz,t=iUz,t Uz,t
zk!
τ
(5)
where,
U
is the normalized amplitude of the optical
field,
k
are the coefficients given by Eq. (4) , and
is the fiber nonlinear parameter, defined as
(Ferreira, 2011):
eff
A
n
c
)(
020
(6)
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
52

where
2
n the Kerr parameter of the gas and
dxdyyxF
dxdyyxF
A
o
eff
4
0
2
2
),,(
),,(
(7)
is the effective mode area,
),,(
0
yxF representing
the spatial distribution of the transverse electric field
mode in the fiber’s cross section.
3.1 Soliton-effect Compression
The If the input pulse propagates in the anomalous-
GVD regime of the fiber, it becomes compressed
through an interplay between SPM and GVD. This
compression mechanism is related to a fundamental
property of the higher-order solitons., which follow
a periodic evolution pattern such that they go
through an initial narrowing phase at the beginning
of each period. If the fiber length is suitably chosen,
the input pulses can be compressed by a factor that
depends on the soliton order, N, given by
2
2
00
2
tP
N
(8)
where
0
P and
0
t are the soliton peak power and
width, respectively.
The optimum pulse compression factor,
opt
F
, of a
soliton-effect compressor can be estimated from the
following empirical relations (Ferreira, 2011):
NF
opt
1.4
(9)
In practice, extreme pulse compression is limited
by higher order effects, namely by higher order
dispersion. However, this limitation becomes less
significant in the case of a kagome PCF, since it
presents a relatively smaller dispersion slope.
Compressed pulses with a duration of some few fs
can be achieved. This is illustrated in Fig. 3, which
shows the spectral and temporal evolution of a 30 fs
pulse through a kagome PCF with a 30 m diameter
core filled with Ar, presenting a ZDW at 500 nm.
The pumping is realized at 800nm, situated in the
anomalous dispersion region, and the corresponding
soliton order is N = 3.5. As a consequence of the
soliton self-compression effect, the pulse temporal
profile is dramatically sharpen, producing a ~2 fs
pulse. For higher values of N the self-compressed
pulses can achieve subcycle durations, but the
corresponding quality factor is reduced.
(a)
(b)
Figure 3: (a) Spectral and temporal evolution of self-
compression of a 30 fs input pulse at 800 nm through a
kagome PCF with a 30 m diameter core filled with Ar
(ZDW at 500 nm). (b) Initial (red) and final (green) pulse
profiles in spectral and time domains.
2.1 Dispersive-wave Generation
Extreme soliton-effect pulse compression of the
input pulse results in a spectral expansion that
overlaps with resonant dispersive-wave frequencies,
which are consequently excited in the UV region.
Fig. 4 shows this effect in the case of kagome PCF
with a 30m diameter core filled with 9.8 bar Ar,
presenting a ZDW at 600 nm, pumped at 800 nm
with pulses of duration
FWHM
=15 and 60 fs. The
same normalized soliton order
FWHM
NS
/ = 0.26
is assumed in both cases.
The temporal evolution in Fig. 4 shows clearly
the soliton fission phenomenon, which occurs
approximately at a characteristic length
N
L
L
D
fiss
(10)
where
2
2
0
/
tL
D
is the dispersion length. We
observe also from the spectral evolution in Fig. 4
that the UV band is generated approximately at the
soliton fission length. The quality of the UV
FemtosecondPulsePropagationinGas-filledHollow-CorePhotonicCrystalFibers
53
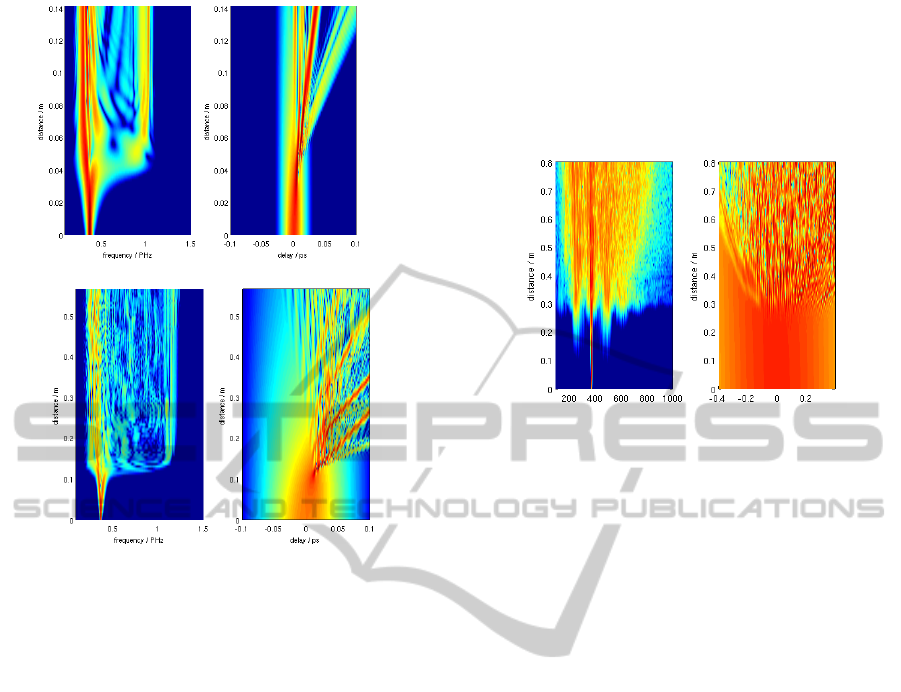
(a)
(b)
Figure 4: Spectral and temporal evolution of 15 fs (a) and
60 fs (b) input pulses at 800 nm through a kagome PCF
with a 30m diameter core filled with 9.8 bar Ar, (ZDW at
600 nm).
emission can be evaluated by the ratio between the
spectral power within the FWHM of the strongest
UV peak and the total spectral power in the UV
region. Fig. 4 shows that such quality is relatively
high for the 15 fs pulse, but it degrades significantly
at 60 fs. Such degradation is due to the reduced
quality factor of the pulse self-compression for high
values of N.
The above results suggest that an ultrafast and
coherent UV light source could be constructed using
a kagome HC-PCF, that is tunable by varying the
gas pressure or the pulse characteristics. Such
tunable UV source could find numerous potential
applications in spectroscopy and metrology or even
in the seeding of a free-electron laser.
When the soliton order N assumes sufficiently
high values, the UV band develops a considerably
fine structure and evidence of modulation instability
(MI) can be observed. This is illustrated in Fig. 5,
which shows the spectral and temporal evolution of
a 600 fs pulse with an energy of 10 J (N ~245) at
800 nm in a kagome PCF with a 30m diameter core
filled with 25 bar Ar (ZDW at 750 nm). Quantum
noise has been included in the simulation. The
fission of the input pulse into a large number of
ultrashort solitons, that subsequently undergo
multiple collisions, can be clearly observed in the
temporal domain. In the spectral domain, this
produces a smooth and flat supercontinuun
extending from 0.2 to 0.8 PHz.
Figure 5: Spectral and temporal evolution of a 600 fs pulse
with an energy of 10 J (N ~245) at 800 nm in a kagome
PCF with a 30m diameter core filled with 25 bar Ar
(ZDW at 750 nm).
4 CONCLUSIONS
In this paper we investigated the ultrafast dynamics
of femtosecond pulse propagation in a gas-filled
kagome HC-PCF. We have shown that by varying
the gas pressure, the normal group-velocity
dispersion (GVD) of the filling gas can be balanced
against the anomalous GVD of the kagomé PCF
allowing the zero dispersion wavelength to be tuned
across the ultraviolet (UV), visible and near-infrared
spectral regions. A generalized Schrödinger
equation has been used to describe ultrashort pulse
propagation in a gas-filled kagome PCF. The soliton
self-compression effect has been observed,
providing pulses with some few fs. We
demonstrated that such extreme self-compression
can lead to a highly efficient deep-UV dispersive
wave generation. Input pulse durations shorter than
~60fs are necessary for obtaining high-quality UV
spectra.
ACKNOWLEDGEMENTS
This work was supported by FCT (Fundação para a
Ciência e Tecnologia) through the Projects PEst-
C/CTM/LA0025/2011 and PTDC/FIS/112624/2009.
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
54

REFERENCES
Chang, L., Nazarkin, A., Travers, J., Nold, J., Hölzer, P.,
Joly, N., and Russell, P., Opt. Express 19(21), 21018–
21027 (2011).
Couny, F., Benabid, F. and Light, P. Opt. Lett. 31(24),
3574–3576 (2006).
Couny, F., Benabid, F., Roberts, P., Light, P., and Raymer,
M., Science 318(5853), 1118–1121 (2007).
Joly, N., Nold, J., Chang, W., Hölzer, P., Nazarkin, A.,
Wong, G., Biancalana, F., and Russell, P., Phys. Rev.
Lett. 106(20), 203901 (2011).
Ferreira, M., Nonlinear Effects in Optical Fibers (John
Wiley & Sons, Hoboken, New Jersey, 2011).
Mak, K., Travers, J., Hölzer, P., Joly, N., and Russell, P.,
Opt. Express, 21 (9), 10942-10953 (2013).
Nold, J., Hölzer, P., Joly, N., Wong, G., Nazarkin, A.,
Podlipensky, A., Scharrer, M., and Russell, P., “Opt.
Lett. 35(17), 2922–2924 (2010).
Pearce, G., Wiederhecker, G., Poulton, C., S. Burger, and
Russell, P., Opt. Express 15(20), 12680–12685 (2007).
Russel, P., J. Light. Technol. 24 (12) 4729-4749 (2006) .
Russell, P. Science 299(5605), 358–362 (2003).
FemtosecondPulsePropagationinGas-filledHollow-CorePhotonicCrystalFibers
55
