
Adaptive GP-based Algorithm for Hardware/Software Co-design
of Distributed Embedded Systems
Adam Górski
1
and Maciej Ogorzałek
2
1
Department of Information Technologies, Jagiellonian University in Cracow, Reymonta 4, Cracow, Poland
2
Department of Information Technologies, Jagiellonian University in Cracow, Cracow, Poland
Keywords: Embedded Systems, Genetic Programming, Genetic Algorithm, Architecture, Hardware/Software
Co-design, Adaptive Systems.
Abstract: In this work, a novel adaptive approach to co-design of embedded systems is presented. The approach is
based on developmental genetic programming. Unlike most of existing algorithms, presented methodology
involves evolving co-synthesis process, not the system architecture directly. Genotype is a tree which nodes
include system construction options. The system can adapt to the environment by increasing chromosomes
which give better results in each situations. Half of the next populations is created using genetic operators
(crossover, mutation, reproduction). Second half is obtained by generating additional solutions but with
different probability of the options.
1 INTRODUCTION
Nowadays we are surrounded by many embedded
systems: SoC systems, modern cars, mobile phones,
digital cameras, etc. Thus it is necessary to find
effective design methodologies. Co-design (De
Micheli and Gupta, 1997) is a process which
automatically gives an architecture of embedded
system. The goal of the process is to optimize
parameters such time, cost or power consumption.
Most of existing solutions (eg. Jiang, Eles and Peng,
2012) assume distributed target architecture
consisting of many processing elements (PE), which
can be divided into two groups: programmable
processors (PP) and hardware cores (HC).
Co- design process consists of: 1. allocation – choice
of number and types of resources and
communication channels;2. assignment – choice of
PE for each task and transmission between
resources; 3. task scheduling – determining when
each task should begin its execution.
Most of existing methods are iterative
improvement algorithms (Yen and Wolf 1995;
Deniziak, 2004) which start from sub-optimal
solution and, by local changes, try to improve the
system quality. Usually, as the initial solution, the
fastest architecture (where each task is executed on
different PE) is selected, but the results are still sub-
optimal. Constructive algorithms (Bharat,
Lakshminarayana and Jha, 1997) build system step
by step by choosing PE for each task separately.
Those methods tend to stop in local minima of
optimizing parameters.
Probabilistic algorithms, especially genetic
algorithms (Chehida and Auguin, 2002; Purnaprajna,
Reformat and Pedrycz, 2007), can escape from local
minima. This group of algorithms is represented for
example by simulated annealing (Eles, Peng,
Kuchciński and Doboli, 1997). Good results were
obtained using developmental genetic programming
(Deniziak and Górski, 2008). This algorithm builds
initial population and generates next populations
using genetic operators.
The most important weakness of this methodology is
that probability of choosing each option is constant.
In some cases obtaining better solutions is possible
only after changing the probabilities. Therefore in
computer system design adaptive algorithms are
more and more popular (Shankaran, Roy, Schmidt,
Koutsoukos, Chen and Lu, 2008).
Genetic programming (Koza, Bennett III, Lohn,
Dunlap, Keane and Andre, 1997) is an extension of
genetic algorithms (Holland, 1992). The main idea
of genetic programming is the evolution of computer
programs. The most important difference between
genetic algorithm and genetic programming is the
difference between genotype (the tree) and
phenotype (the final solution). Each node in
125
Górski A. and Ogorzalek M..
Adaptive GP-based Algorithm for Hardware/Software Co-design of Distributed Embedded Systems.
DOI: 10.5220/0004696601250130
In Proceedings of the 4th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2014), pages
125-130
ISBN: 978-989-758-000-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
genotype represents parts of computer programs.
In this article a new self-adaptive approach based
on developmental genetic programming (Koza,
2010) is presented. The main advantage of proposed
solution is the possibility of making changes of
probabilities when the algorithm is running. Thus
the algorithm can adjust to the behaviour without
manual modification of initial conditions.
Probability of stopping in local minimum is
decreasing. Algorithm is described in section 3.
Sections 4 and 5 present experimental results and
conclusions.
2 PRELIMINARIES
Embedded system is specified by an acyclic directed
graph called the task graph. Each node v
i
V
represents task, and edge e
i
E presents
dependence between tasks. Every edge has a label
d
ij
which describes the amount of data that has to be
sent between two connected tasks. Example of a task
graph is presented on fig. 1. The graph includes
7 tasks.
T2
T0
T1
T3 T4
114 114
20
20
20
T5
20
T6
20
Figure 1: Example of task graph.
Table 1 presents an example of a resource database
for the graph on figure 1. Here we proposed to use
two programmable processors (PP1 and PP2), two
Hardware cores (HC1 and HC2) and two
communication links (CL1 and CL2). Every task is
defined by time of execution (t) and an area
occupied by this task. Areas occupied by the tasks
mean the size of memory needed to execute these
task. Each communication link is defined by
a bandwidth (b) and an area (s) occupied by the link
connected to PE. HC can only execute one task.
Table 1 also includes the area (S) occupied by each
PE. The area of the tasks implemented in HC
includes the area occupied by the core. Task T2 is
not compatible with PP1, and task T5 can’t be
implemented in HC2. Communication link CL2 is
not compatible with PP1.
Table 1: Resource database.
Task
PP1
S=200
PP2
S=300
HC1 HC2
t s t s t s t s
T0 150 4 120 6 50 180 30 250
T1 40 3 35 2 14 100 10 140
T2 - - 320 17 250 200 150 650
T3 235 10 220 15 140 160 90 200
T4 165 8 150 10 65 100 40 140
T5 70 4 40 5 25 100 - -
T6 23 2 20 1 5 40 2 80
CL1,
b=6
s=2 s=2 s=10
CL2,
b=15
- s=2 s=15
Target architecture of the system described by
the above graph consists of n processes,
m programmable processors and p communication
links (CLs) selected from available resources as
specified in table 1. Overall area (S
o
) of the
constructed system is described by the following
formula:
p
k
P
l
PCCL
n
j
j
m
i
PEo
k
iki
ssSS
11
,
11
(1)
T is the time when execution of the last task is
finished. Parameters u and q are set manually.
The fitness function (F) is described below:
T*q + S*u = F
(2)
The goal of co-design is to find an architecture
with the lowest F value.
3 THE ALGORITHM
In accordance with genetic programming rules the
genotype is evolving. It is based on task graph, each
node in the tree corresponds to equal system
constructing function. The embryo is
an implementation of the first task on randomly
chosen PE. At the beginning initial population is
created containing randomly generated genotypes.
П is the size of initial population:
p*n* =
(3)
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
126

where: n – number of tasks in task graph,
p – number of possible PEs, α – parameter which
controls the number of individuals in populations; it
is set manually.
Table 2: Options for constructing system.
Step Option
PE a.min (s*t) between used PEs
b. PE with the lowest time of
execution of all allocated tasks
c. the fastest
d. min (s*t)
e. the lowest cost
f. not used from kind of the rarest
used
CL a. the lowest cost
b. the highest b
c. last used
Task scheduling list scheduling
The system is constructed by executing functions
in order corresponding to the level of the node in the
genotype tree. Then solutions are sorted by the
lowest fitness function. Algorithm counts how many
times each function appears in first rank list, the
percentage result is a new value of the probability of
a chosen option. New populations are obtained
using genetic operators: crossover, mutation and
selection (half of the population) and by generating
new individuals using options in table 2 but with
modified probability. The number of individuals
obtained by using genetic operators is given:
Φ = β*П/2 –individuals obtained by selection;
Ψ = γ*П/2 –individuals obtained by crossover;
Ω = δ*П/2 –individuals obtained by mutation;
β + γ + δ = 1 – this condition should be
satisfied to have the same number of
individuals in each population.
The values of parameters β, γ, δ are set manually.
They control the evolution process.
Selection copies the Φ solution from the current
population. Individuals are chosen randomly but
with different probability dependent on the position
in rank list:
r
P
(4)
Crossover chooses randomly the Ψ solutions. To
prevent the algorithm from stopping in local
minima, the best of chosen individuals are crossed
over with the worst. The crossing point is selected
randomly - the same for both genotypes and then
substitutes the sub-trees.
Mutation randomly selects one individual and one
node, afterwards changes option in this node to a
different one from the option list, but with
probability currently selected in the population.
The process is stopped when solution with lower
function F wasn’t found in next ε steps (last
ε generations). Parameter ε is set manually.
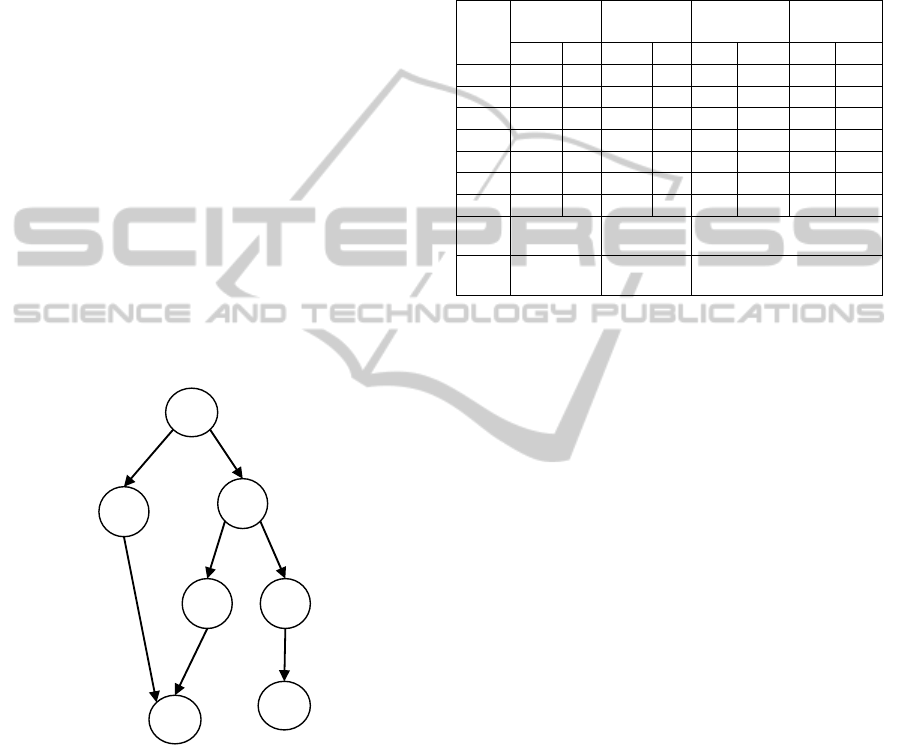
Figure 2 shows an example of genotype for the
task graph of figure 1.
d/b
PP1
c/a
b/b e/c
a/c
c/b
Figure 2: Example of genotype.
Implementation of the first task (the embryo) is
chosen randomly on PP1. Second task is executed on
HC2 as the fastest. For the transmission between T0
and T1 CL1 is chosen. Third task can be
implemented on PP2 choosing option min (s*t) and
CL1 is used for the transmission. Fourth task can be
assigned to HC2 (PE with the lowest time of
execution of all allocated tasks), CL2 is chosen for
the transmission (the highest b). Next task can be
executed on PP1 using option the lowest cost. Sixth
task can be assigned on PP2 (min (s*t) between used
PEs). For the last task the fastest implementation
(HC2) was chosen, and CL2 was used for the
transmission (the highest b).
4 EXPERIMENTAL RESULTS
Because of very large computational complexity of
the co-design problem, the only way to check
effectiveness of the proposed methodology is to
compare the performance with other existing
methods. All experiments were carried out on
randomly generated graphs with 10 and 30 nodes.
In table 3 the results are compared with DGP
AdaptiveGP-basedAlgorithmforHardware/SoftwareCo-designofDistributedEmbeddedSystems
127
algorithm (Deniziak and Górski, 2008) and
Yen-Wolf (Yen and Wolf, 1995) for co-design.
Algorithm DGP was compared with algorithm
Ewa (Deniziak, 2004). Part of the results were also
obtained using the task graphs presented in the
present work. Algorithm Ewa was proved to be more
effective than MOGAC (Dick and Jha, 1998).
In every experiment the parameters were set to: u=8,
q=1, ε=5, β = 0,1, γ = 0,3, δ = 0,6.
Table 3: Experimental results.
graph
Yen
Wolf
DGP
ADGP
min F Average F
min F Average F
10 12899 9017 9247
8179 8538
30 28301 18835 19067
16439 21402
For the graph with 10 nodes, the min. function
F value obtained by ADGP was 8179, while for
DGP it was 9017, and for Yen-Wolf it was 12899.
The average value of function F, for probabilistic
algorithms, was also obtained by ADGP – 8538
while for DGP it was 9247. For bigger graph (with
30 nodes) the best average function (18835) was for
the DGP algorithm (21402 for ADGP). However
comparing the best results the ADGP gives better
results for both presented graphs (8179 for graph
with 10 nodes, and 16439 for graph with 30 nodes)
when compared with DGP (9017 for graph with 10
nodes, and 18835 graph with 30 nodes) and
Yen-Wolf (12899 for graph with 10 nodes, and
28301 for graph with 30 nodes).
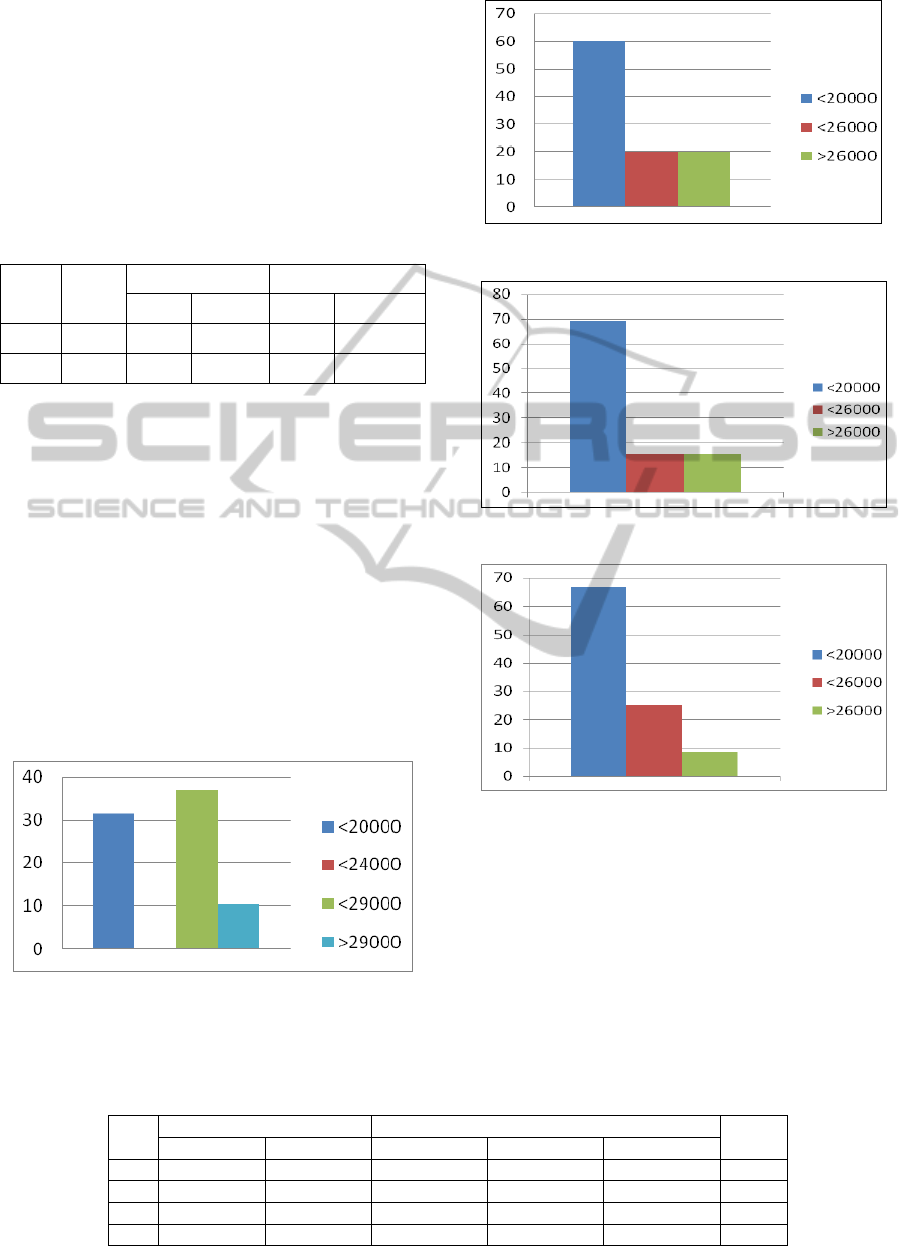
Figure 3: Percentage range of results for α=10.
Figure 4: Percentage range of results for α=20.
Figure 5: Percentage range of results for α=30.
Figure 6: Percentage range of results for α=50.
Comparison of obtained results for a graph with
30 nodes with different value of parameter
α is
presented in table 4. The last column presents
percentage difference between average values of
DGP and ADGP.
The average results, as presented in table 4,
indicate that the algorithm DGP gives solutions with
lower F function value but the best individuals are
obtained by the methodology presented in this work.
Table 4: Comparison of the results for different size of population.
α
DGP
ADGP
Δ[%]
min F average F
min F average F max F
10 19131 19249
16884 23549 30030 22
20 18835 19105
17278 24101 40514 26
30 18835 19008
16673 19953 28046 5
50 18835 18915
16439 19977 28857 6
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
128

Figures 3, 4, 5 and 6 indicate that the algorithm is
not random. When parameter α was 10 most of the
best results in each trial had the F value between
24000 and 29000 but a large group of best
individuals had the value of function F lower than
20000. So it was not accidental that best system was
found by using our presented algorithm. Analysis of
other figures with bigger value of parameter
α allows to notice more dependencies. In almost
every situation most of the best results (60-70% of
obtained individuals) are in first (the lowest) area
and number of best results in last area (the highest
value of F function) is decreasing. When parameter
α was 10 the average value of function F was 23549
for ADGP, while the function value for DGP was
19249. Similar results were obtained for α=20
(24101 for ADGP and 19105 for DGP). For α=30
the average function F was 19953 for ADGP and
19008 for DGP. The bigger parameter α the smaller
the difference between average values of DGP and
ADGP (parameter
Δ). When value of α was at least
30 that difference was only about a 5%. However
the best solutions (with the smallest function
F value), in every cases, were obtained using ADGP
(16884, 17278, 16673 and 16439 for adequate
values of α). What is more the percentage difference
of the best solutions obtained with presented
methodology and DGP is much bigger than average
values of function F. This indicates that ADGP can
be more effective than DGP. With increasing α the
maximum value of function F is also reduced.
5 CONCLUSIONS
In this work a new approach based on
developmental genetic programming for co-
synthesis of distributed embedded systems specified
by task graphs has been presented. The main
innovation of the approach is that the algorithm is
based on statistics adaptive to the environment. This
is achieved by changing the probability of selection
of options constructing the system. First
experimental results show that results obtained by
the presented methodology are better than those
obtained using other known approaches. It should be
noted however that in some relatively rare cases
results can be worse because of the probabilistic
nature of the algorithm.
To compare DGP and ADGP some test like
t-test, Mann-Whittey test or Wilcoxon test (Ruxton,
2006) can be made, but we were afraid that they may
underestimate the true significance of results.
The future work will concentrate on examining
another chromosomes, genetic operators. We will
also test different representations of genotype tree.
ACKNOWLEDGEMENTS
This work is supported by the Foundation for Polish
Science, under grant “Mistrz 2012” No. 9/2012:
“New methodologies for designing next-generation
micro-electronic circuits”.
REFERENCES
De Micheli, G., Gupta, R., 1997. Hardware/software
co-design. In Proceedings IEEE 95.3 (Mar). IEEE.
Jiang, K., Eles, P., Peng, Z., 2012. Co-design techniques
for distributed real-time embedded systems with
communication security constrains. Design
Automation and Test in Europe (DATE 2012).
Deniziak, S., 2004. Cost-efficient synthesis of
multiprocessor heterogeneous systems. In Control and
Cybernetics, vol. 33, No. 2.
Yen, T., Wolf, W., 1995. Sensivity-Driven Co-Synthesis
of Distributed Embedded Systems. In Proceedings of
the International Symposium on System Synthesis.
Dave, B., Lakshminarayana, G., Jha, N., 1997. COSYN:
Hardware/software Co-synthesis of Embedded
Systems. In Proceedings of the34th annual Design
Automation Conference (DAC’97).
Deniziak, S., Górski, A., 2008. Hardware/Software Co-
Synthesis of Distributed Embedded Systems Using
Genetic programming. In Proceedings of the 8th
International Conference Evolvable Systems: From
Biology to Hardware, ICES 2008. Lecture Notes in
Computer Science, Vol. 5216. SPRINGER-VERLAG.
Shankaran, N., Roy, N., Schmidt, D. C.,
Koutsoukos, X. D. C., Chen, Y., Lu, C., 2008. Design
and performance evaluation of an adaptive resource
management framework for distributed real-time and
embedded systems. EURASIP Journal on Embedded
Systems.
Koza, J., R., Bennett III, F., H., Lohn, j., Dunlap, F.,
Keane, M., A., Andre, D., 1997. Automated synthesis
of computational circuits using genetic programming.
In Proceedings of the IEEE Conference on
Evolutionary Computation. IEEE.
Eles, P., Peng, Z., Kuchciński, K., Doboli, A., 1997.
System Level Hardware/Software Partitioning Based
on Simulated Annealing and Tabu Search. In Design
Automation for Embedded Systems, vol. 2, No 1.
Chehida, K., B., Auguin, M., 2002. HW/SW Partitioning
Approach for Reconfigurable System Design. In
Proceedings of the International Conference on
Compilers, Architectures and Synthesis for Embedded
Systems, CASES 2002.
Purnaprajna, M., Reformat, M., Pedrycz, W., 2007.
Genetic algorithms for hardware-software partitioning
AdaptiveGP-basedAlgorithmforHardware/SoftwareCo-designofDistributedEmbeddedSystems
129

and optimal resource allocation. In Journal of Systems
Architecture, 53(7).
Holland., J., H., 1992. An Introductory Analysis with
Applications to Biology, Control, and Artificial
Intelligence. MIT Press, Cambridge, MA.
John R. Koza. 2010. Human-competitive results produced
by genetic programming. In Genetic programming and
evolvable machines, vol. 11, issue 3-4. SPRINGER-
VERLAG.
Dick, R., P., Jha, N., K., 1998. MOGAC: a multiobjective
Genetic algorithm for the Co-Synthesis of
Hardware-Software Embedded Systems. In IEEE
Trans. on Computer Aided Design of Integrated
Circiuts and systems, vol. 17, No. 10.
Ruxton., G., D., 2006. The unequal variance t-test is an
underused alternative to Student’s t-test and the
Mann–Whitney U test. In Behavioral Ecology, 17(4).
doi:http:// dx.doi.org/10.1093/beheco/ark016.
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
130
