Directionality Control of Light-emitting Devices through Sub-micron

Dielectric Structures

Yoshikuni Hirano, Katsu Tanaka, Yasushi Motoyama, Nobuo Saito

and Hiroshi Kikuchiand Naoki Shimidzu

Science & Technology Research Laboratories, NHK (Japan Broadcasting Corporation),

1-10-11 Kinuta, Setagaya-ku, Tokyo, Japan

Keywords: Light-emitting Diodes, Directionality Control, Direct-view-Type Display.

Abstract: We have been investigating directional light control methods of light-emitting diodes (LEDs). We propose a

method that makes it possible to control a principal axis in field intensity through fine-structures on the

LEDs. We also describe the concept of this method and essential points for obtaining a sharply defined

principal axis. The effectiveness of the method was verified through differences in angular distributions by

using the finite-different time-domain method.

1 INTRODUCTION

Light emitting diodes (LEDs) are expected to be a

next generation light source and have been applied

to many lighting applications, such as general

lighting (Krames, 2007), visible-light

communication (McKendry, 2012), and displays

(Day, 2011) due to advances in high-brightness

technology. Because of the Lambertian pattern in the

spatial intensity distribution of an LED, the direct-

view-type display, which consists of as many fine

LED chips as the number of pixels, has wider

viewing angles (Sony corp., 2012).

The Lambertian pattern is not suitable for certain

applications, and the directionality control of LEDs

has been studied for mainly narrowing the angular

distribution. In an automotive lighting area, for

example, the sharper angular distribution will enable

the lighting of a restricted region and reduce

blinding glare from oncoming vehicles (Krames,

2007). In projection display systems, light use

efficiency is improved by increasing the incident

light flux from a light source to projection optics

(Fournier, 2008). In addition to the modifying

angular distribution of LEDs, new applications will

be possible if off-axis directionality control becomes

possible.

Projection optics for modifying the far-field

pattern of an LED is also important to downsize

projection display systems (Tu, 2009). Recently,

several directional light control methods have been

proposed for LEDs with photonic crystals

(McGroddy, 2008). For instance, the angular

distribution of the directional light at half intensity

near 66º from a 5-m aperture was demonstrated in

an experiment with a prototype of GaN-based LEDs

with photonic crystals (Lai, 2012). This result

indicates that increasing light emission in useful

directions eliminates the need for some optical

elements to concentrate the emission light from an

LED into projection optics. The directional light

control method enables a projector to be small, light

weight, and exhibit high definition. In addition, the

off-axis directionality control reduces the projection

optics and allows more compact projection systems.

However, more complex designed crystal lattice and

excessive lattice points are necessary to achieve

sharply defined off-axis directional light beam.

Off-axis directionality control allows high

picture quality technology for auto-stereoscopic

three-dimensional (3D) multi-view displays (Son,

2010). Several types of 3D displays produce 3D

images by using many directional lights using a

multi-projector, parallax barrier, and lens array. The

ideal 3D display requires a number of directional

lights across the entire viewing space. Therefore, a

high-density array of an off-axis directionality-

controlled light emitting device is useful for such 3D

displays. More recently, multi-directional backlight

technology has been proposed to provide high-

163

Hirano Y., Tanaka K., Motoyama Y., Saito N., Kikuchi H. and Shimidzu N..

Directionality Control of Light-emitting Devices through Sub-micron Dielectric Structures.

DOI: 10.5220/0004698701630169

In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 163-169

ISBN: 978-989-758-008-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

resolution, full-parallax 3D images by using an

optical grating (Fattal, 2013). Fattal et al. introduced

the directional control method for an LED using a

number of 10-m optical gratings having various

directions. They then fabricated a 64-view backlight

and produced 3D images with a spatial resolution of

88 pixels per inch and full-motion parallax.

However, because of the reduction of undesirable

lights, the device size is un-diminishable and this

method is not suitable for high-density array

devices.

In this study, we propose a method for

controlling the off-axis directionality control of

LEDs, which is suitable for high-density array

devices. In the method, a control unit, which consists

of several sub-micron dielectric structures, is placed

on the light emitting surface and the tops of these

structures function as apertures. The control unit

provides a directional light, called a principal axis,

by the diffraction of light from the apertures. The

principal axis direction depends on the phase

difference at the apertures and is controlled by the

difference in the height of the sub-micron dielectric

structures h.

We also describe the design rules of the sub-

micron dielectric structures’ dimensions and

arrangements for controlling directional light. We

also describe the essential points for obtaining a

sharply defined principal axis. The effects of the

proposed method were verified through

directionality control characteristics in one control

unit by using the finite-different time-domain

(FDTD) method.

2 BASIC STRUCTURE

2.1 Directionality Control Method

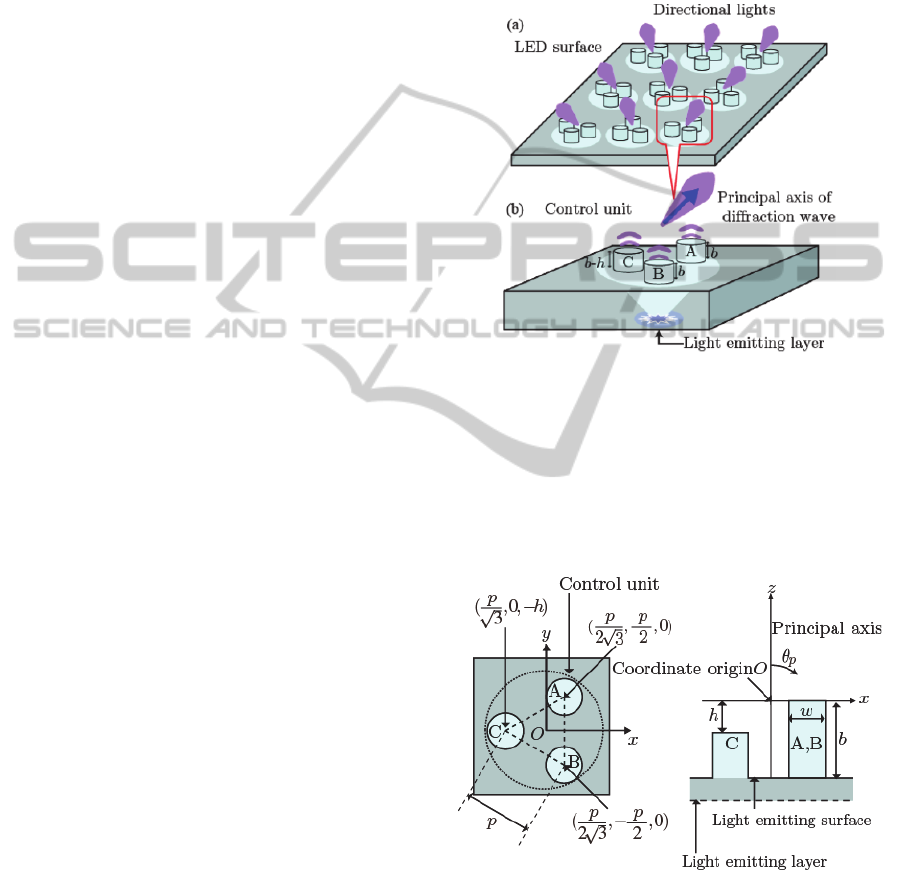
Multiple control units on an LED surface are shown

in Figure 1(a). A control unit manipulates a principal

axis toward a different direction. A single control

unit (Figure 1(b)) consists of cylinders of w in

diameter, where w is the length divided by the center

wavelength



of the LED. In this section, we

describe the dimensions in units of



, unless

otherwise stated. The cylindrical structures A, B,

and C on an LED surface and the LED are of the

same material of a refractive index n (n > 1). Heights

of structures A and B are denoted as b and that of

structure C is b - h in height. The structures are

placed on a vertex of a regular triangle p on a side,

which means their gaps are p - w. We use a system

of coordinates with their origin at the center of the

control units on the plane containing the tops of

structures A and B. The z-axis is perpendicular to

the LED surface, then the principal axis contains the

z-axis when h = 0. The x-axis is parallel to the line

from the origin to the midpoint of the center points

of structures A and B. In addition,



and



are the

horizontal and zenithal angle, as shown in Figure 2.

Figure 1: Schematics of (a) device with proposed method

and (b) directionality control unit in device array. Control

unit consists of three cylindrical structures A, B and C.

Lights from light emitting layer enter from bottom of each

structure and exits from their tops. Optical path lengths via

each structure depend on height of structures. Principal

axis, defined as direction of optical path differences via all

structures equal to zero, is controlled by difference in

height of structures h.

Figure 2: Top view and cross-sectional diagram on vertical

plane including x-axis of control unit. Cartesian coordinate

system is used with their origin at center of tops of

structures at h = 0. Z-axis is perpendicular to light emitting

surface and x-axis is parallel to line from origin to

midpoint of center points of structures A and B.

Multiple lights, which are emitted from the tops

of the structures in phase, form a diffraction pattern,

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

164

like hexagonally arranged spots in an image plane.

For simplicity, we assume that incident light is in

phase at the bottoms of the structures. The center

spot in the diffraction pattern corresponds to a

principal axis, whose direction is determined as that

where all of the optical path lengths from the

bottoms of the structures to the image plane are

equal.

If h is not equal to 0, the optical path length from

the bottom to the top of structure C is nh shorter than

those of structures A and B. The distance from the

top of structure C to the image plane is longer than

those from the tops of structures A and B. Because

the structures’ arrangements are in symmetry with

the xz-plane, the principal axis direction is denoted



. We define a plane S, which is perpendicular to

the xz-plane and at a distance of l from the original

point, as the image plane, as shown in Figure 3.

Optical paths l

, l

, and l

from the bottoms of

structures A, B, and C to S by way of the tops of the

structures are expressed as

(1)

(2)

Then the difference in optical path lengths between

, l

, and l

are expressed as

(3)

Here, m is the optical path difference between the

lengths of l

, l

, and l

. The



of an m-th order

diffraction wave on the vertical plane including the

x-axis can be obtained by solving Equation (3).

(4)

Here,

(5)

When we assume that the principal axis direction is

given by Equation (1) at m = 0,



depends on

parameter q, and monotonically increases within the

following range.

(6)

However, the maximum angle of the principal axis



is given by Equation (7), which depends only on

the index.

(7)

Figure 3: Principal axis direction on vertical plane

including x-axis. Image plane S is l in shortest distance

from origin point and



in angle formed by l and z-axis.

Therefore the maximum value of



is constrained

by the structures’ dimensions. A principal axis

should be made within the airly patterns of the

structures. The



is restricted to the following range.

(8)

Too small of structure gaps p - w confine the

working range of



. The gap and h should satisfy

the following equation to prevent an obstruction in

the line of sight along the x-axis from the top of

structure C by another structure.

(9)

Regarding the y-direction, we use the following

condition to prevent light scattering by another

structure.

(10)

Figure 4: Principal axis angles as function h. Suffixes t

and c correspond to analytically and numerically

calculated results.

DirectionalityControlofLight-emittingDevicesthroughSub-micronDielectricStructures

165

Equation (10) suggests that the orthogonally

projected profile of a structure on the xz-plane

prevents the overlap with other structures that have

different x-coordinate values of the central axis.

These are additional conditions of structure

dimensions.

2.2 Simulation Results

In this section, we describe the basic characteristics

for the proposed method by using numerical

analysis. With the proposed method, the distance

between a light emitting surface to a light emitting

layer is several wavelengths. The wave-optics

should be used instead of the geometric optics for

analysis in the LED medium. We applied the 3D

FDTD method with a perfectly matched layer (PML)

boundary condition to verify the control function of

the proposed method.

We used InGaN-GaN LEDs as an example. The

center wave-length and full width at half maximum

(FWHM) of the spectrum were assumed to be 465

and 20 nm, and we ignored the absorption of emitted

light in the LEDs. The spectral envelop of emitted

light from the LEDs is a Gaussian shape. Therefore,

the multiple-dipole sources polarized in the xy-plane

is arranged in the light emitting layer and excited

with a Gaussian profile in time. For simplicity, the

light emitting layer is at 465 nm from the bottom of

the structures. The LED and the structures on the

light emitting surface were of the same material with

index of 2.47 (http://refractiveindex.info/).

The coordinate origin shown in Figure 2

corresponds to the position at the center of the

calculation space. The calculation space was 6 m

and accordingly discretized using 15-nm grids. The

light emitting layer was distributed inside a circle

930 nm in diameter. The dimensions of the structure

were w = 750 nm, p = 930 nm, and b = 750 nm.

First, we discuss the calculated results of the

principal axis direction angle



depending on h.

Figure 4 shows the direction angles



. In Figure 4,



, indicated with a solid line, was calculated from

Equation (4);



, indicated with a dashed line, was

obtained from the simulation results. The calculated

direction angle



shows the same tendency as



Below 90nm in h, they are quantitatively the same;

above 90nm in h, the increasing tendency of



falls

into a sluggish pace compared with



. This is partly

because Equation (4) is derived without

consideration of aperture shapes. As viewed from



the shapes of the structure tops are ellipses in wcos



which is a minor axis parallel to the x-axis, and the

apparent position of structure C moves hsin



to the

coordinate origin. In this result, a spot of the

principal axis is expanded toward -



, and it limits



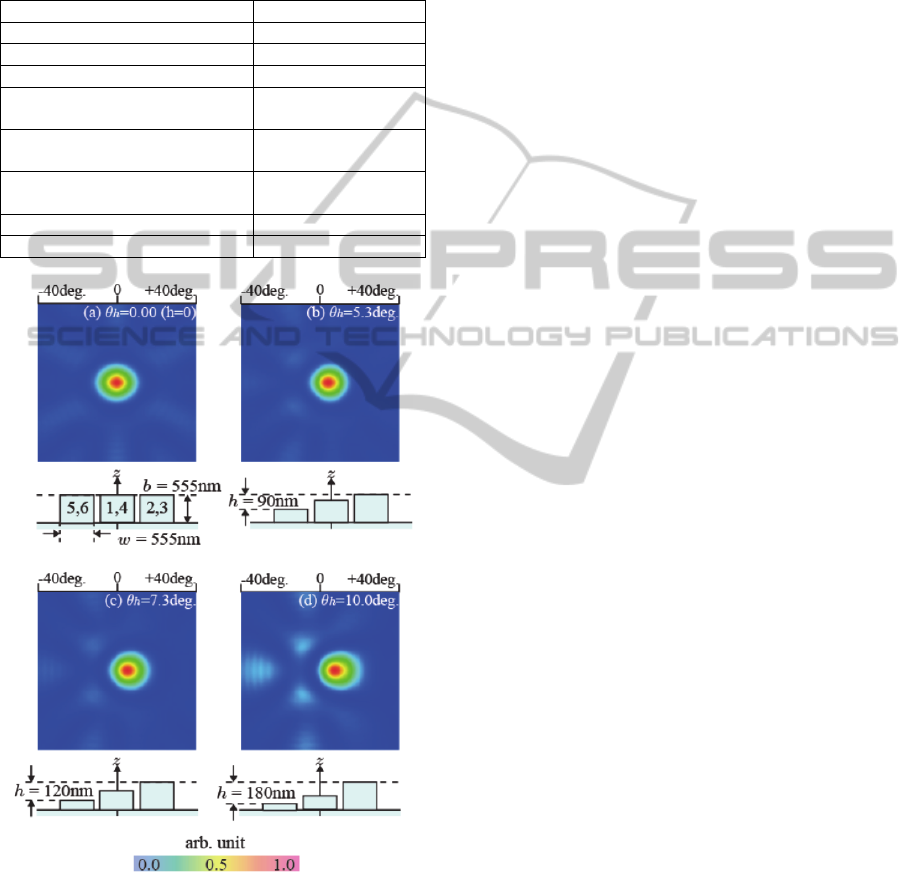
Figure 5: Field intensity distribution corresponding to h =

(a) 0, (b) 90 and (c) 180 nm, and cross-section diagram of

control unit. Images (a), (b) and (c) were calculated by

temporal integration of Poynting vector at 3000 nm from

tops of structures. Red and blue regions represent high-

and low-intensity parts of field intensity distribution.

Figure 6: Top view and cross-sectional diagram on vertical

plane including x-axis of control unit at N=6.

Next, we discuss the clarity of the principal axis

for the proposed method. Figure 5 shows field

intensity distribution corresponding to



= 0, 90 and

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

166

180 nm. Each image is constructed by temporal

integration of a Poynting vector at 3000 nm from the

top of the structures. In Figure 5, the high- and low-

intensity parts are represented by red and blue

regions, respectively. We also show the cross-

sectional diagram in a vertical plane. The principal

axis direction increases in step with h in Figure 5.

The principal axis becomes less clear as h increases.

This is because diffraction wave without some kind

of stray light affects the field intensity distribution.

This is an undesirable characteristic in beaming

devices. We discuss a method for obtaining a

sharply defined principal axis.

3 IMPROVED STRUCTURE

3.1 Design Rules

In this section, we describe the design rules to

improve the clarity of the principal axis based on

light use efficiency.

The principal axis consists of lights from the

light emitting layer to S via the top of the structures.

Other lights, which directly come from the light

emitting surface to S, are not involved in forming

the principal axis. Thus, a ring-shaped distribution is

acceptable as a light emitting layer distribution

profile. The inside and outside diameters of the light

emitting layer distribution should be equal to those

of the inscribed and circumscribed circles of the

structures on the light emitting surface.

The light use efficiency of the proposed method

is also affected by the number of structures. We

estimate the ratio



of light intensity via the tops of

N structures to the total amount of light intensity

from the light emitting surface. Here, N structures

are w in diameter and equally spaced on a circle

with a radius r and pitch p. This ratio is expressed as

(11)

To calculate



according to Equation (11), we

should modify Equation (10) as follows.

(12)

(13)

(14)

(15)

We then obtain



= 0.325 (N=3), 0.707 (N=4), 0.866

(N=6), and 0.541 (N=8). By comparing these values,

we obtain the maximum



at N=6. We can then

diminish excess light by using the ring-shaped

distribution profile of the light emitting layer and

use six structures.

We now describe a modification of Equation (4)

for six structures. In this case, r and p are equal. We

use p instead of r. Figure 6 shows a single control

unit of six structures. For simplicity, structures that

have the same x-coordinate value of the central axis

are the same height. Then the principal axis direction

is described as



. The height of structures 1, 2, 3, 4,

5 and 6 are shown in Figure 6. In this case, optical

paths l

(k = 1 – 6) from the bottoms of structures k

to S by way of the tops of the structure are expressed

by the following equations.

(16)

(17)

(18)

From Equations (16), (17), and (18), the differences

in optical path lengths are of three types. First, an

optical path length from a pair of structures that are

symmetric about the xz-plane is zero in the entire

area on the xz-plane. Next, if the x-coordinate value

of one of the structures is zero, the optical path

length is expressed by the following equation.

(19)

If the signs of the x-coordinate values of structures

are opposite, the optical path length is expressed by

the following equation

(20)

Equations (19) and (20) are equivalent at m=0. We

then obtain



by the following equation.

(21)

3.2 Simulation Results

We now explain the simulation results to diminish

excess light with the proposed method. To calculate

field intensity distribution, we used the 3D FDTD

method mentioned in Section 3. The differences

with that mentioned in Section 3 are the calculation

space size and device structure. The calculation

space was 9 m. The light emitting surface was

DirectionalityControlofLight-emittingDevicesthroughSub-micronDielectricStructures

167

covered with a metal mask to obscure light other

than from the control unit. The light emitting surface

had a hole and the control unit was arranged at the

bottom of the hole. Other calculation conditions are

listed in Table 1.

Table 1: Calculation conditions.

Diameter of structure (w) 555 nm

Pitch of structures (p) 630 nm

Height of structure (b) 555 nm

Difference in height (h) 0, 90, 180 nm

Outside diameter of

light emitting layer

1815 nm

Inside diameter of

light emitting layer

705 nm

Depth of light emitting layer

from bottoms of structures

465nm

Hole diameter 2325 nm

Metal mask thickness 135 nm

Figure 7: Field intensity distribution of control unit at N=6

corresponding to h = (a) 0, (b) 90, and (c) 180 nm. Images

(a), (b), and (c) were calculated by temporal integration of

Poynting vector at 5400 nm from tops of structures.

The field intensity distribution corresponded to h

= 0 90 and 180 nm. Each image was constructed in

the same manner as in Figure 5. However, these

images were constructed by the temporal integration

of a Poynting vector at 5400 nm from the tops of the

structures. Excess light was greatly reduced, as

shown in Figure 7. We then obtained a sharply

defined principal axis by using the improved

proposed method.

4 CONCLUSIONS

We proposed a method for controlling the principal

axis direction of LEDs and to obtain a sharply

defined principal axis through fine-structures on the

light emitting surface. We also verified the

effectiveness of the method by using the FDTD

method. In this result, a sharply defined principal

axis from a 2.3-m aperture is obtained by using the

proposed method.

The proposed method is suitable for high-density

array devices because it uses several sub-micron

dielectric structures as a means for directional

control. By applying the proposed method, high-

density beaming array devices are possible. The

method is also suitable for ray-based displays or

other applications.

We are planning to fabricate a new device with

the proposed structure by means of focused ion

beam (FIB) technique, which is promising for the

fabrication of fine structures with precise control of

height as well as in-plane dimension. For the FIB

fabrication, the structure and dimension will be

designed with FIB's characteristics taking into

account. Then, the directional control properties of

the new device will be evaluated to verify the

effectiveness of the proposed method.

REFERENCES

Krames, M. R., Shchekin, O. B. Mueller-Mach, R.,

Mueller, G. O., Zhou, L., Harbers, G., and Craford, M.,

G., 2007, “Status and Futre of High-Power Light-

Emitting Diodes for Solild-State Lighting”, IEEE

Journal of Display Technology, 3 (2), 160 - 175.

doi:10.1109/JDT.2007.895339.

McKendy, J. J. D., Massoubre, D., Zhang, S., Rae, B. R.,

Gree, R. P., Gu, E., Henderson, R. K., Kelly, A. E.,

and Dawson, M. D., 2012, “Visible-Light

Communications Using a CMOS-Controlled Micro-

Light-Emitting-Diode Array”, IEEE Journal of

Lightwave Technology, 30 (1), 61 - 67.

doi:10.1109/JLT.2011.2175090.

Sony Corp., 2012, Sony Develops Next-generation

Display, “Crystal LED Display”, Ideal for High

Picture Quality on Large screens. Full HD 55-inch

Prototype model Exhibited At 2012 International CES,

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

168

News releases of Jan. 10, 2012, Retrieved from:

http://www.sony.net/SonyInfo/News/Press/201201/12-

005E/

Fournier, F., Rolland, J., 2008, “Design Methodology for

High Brightness Projectors”, IEEE Journal of Display

Technology, 4 (1), 86 - 91.

doi:10.1109/JDT.2007.907110.

Tu, S. -H., Pan, J. -W., Wang, C. -M., Lee, Y. -C., and

Chang, J. -Y., 2009, “New Collection Systems for

Multi LED Light Engines”, Optical Review, 16 (3),

318 - 322.

McGroddy, K., David, A., Matioli, E., Iza, M., Nakamura,

S., DenBaars, S., Speck, J., S., Weisbuch, C., and Hu,

E., L., 2008, "Directional emission control and

increased light extraction in GaN photonic crystal light

emitting diodes", Appl. Phys. Lett., 93 (10), 103502.

Doi:10.1063/1.2978068.

Lai, C. -F., 2012, Emission aperture size limited the

guided mode extraction characteristics of GaN-based

ultrathin-film photonic crystal micro-light-emitting

diodes, Appl. Phys. Lett., 101, 023109. doi:

10.1063/1.4734509.

Son, J. -Y., Javidi, B., Yano, S., and Choi, K. -H., 2010,

“Recent Developments in 3-D Imaging Technologies”,

IEEE Journal of Display Technology, 6 (10), 394 -

403. doi:10.1109/JDT.2010.2045636.

Fattal, D., Pheng, Z., Tran, T., Vo, S., Fiorentino, M.,

Brug, J., Beausoleil, R. G., 2013, A multi-directional

backlight for a wide-angle, glasses-free three-

dimentional display, Nature, 495, 348-351.

Doi:10.1038/nature11972.

Handbook of Optics, 3rd edition, Vol. 4. McGraw-Hill

2009. Retrieved July 30, 2013, from

http://refractiveindex.info

DirectionalityControlofLight-emittingDevicesthroughSub-micronDielectricStructures

169