
Model Composition for Biological Mathematical Systems
Mandeep Gill
1
, Steve McKeever
2
and David Gavaghan
1
1
Department of Computer Science, University of Oxford, Parks Road, Oxford, U.K.
2
Department of Informatics and Media Studies, Uppsala University, Uppsala, Sweden
Keywords:
Modules, Collaborative Modelling, Biological Mathematical Systems, Heart Models, Generics.
Abstract:
Mathematical models are frequently used to model biological process, such as cardiac electrophysiological
systems. In order to separate the models from the implementations, and to facilitate curation, domain specific
languages (DSLs) have become a popular and effective means of specifying models (Lloyd et al., 2004; Hucka
et al., 2004). In previous papers (Gill et al., 2012a; Gill et al., 2012b; McKeever et al., 2013) we have argued for
including parameterised modules as part of such DSLs. We presented our prototype Ode language and showed
how models could be created in a generic fashion. In this paper we extend our work with concrete examples
and simulation results. We show how complex heart models can be constructed by aggregation, encapsulation
and subtyping. Our use-case retraces the steps taken by (Niederer et al., 2009), which investigated the common
history between cardiac models, and shows how they can be cast in our language to be reused and extended.
Our DSL enables ‘physiological model engineering’ through the development of generic modules exploiting
high cohesion and low coupling.
1 INTRODUCTION
We are investigating the application of system engi-
neering methods to mathematical continuous models
of biological systems, where the complexity of such
models prohibits the use of discrete modelling and
simulation methods. The mathematics within a model
lends itself to a textual representation, traditionally this
has been accomplished in an operational manner using
numerical languages such as MATLAB and Python.
Research has also resulted in the development of the
Systems Biology Markup Language (SBML) (Hucka
et al., 2004) and CellML (Lloyd et al., 2004) domain
specific formats for common interchange and archiv-
ing. This modelling approach has a successful his-
tory (Noble and Rudy, 2001) that can be seen through
the large number of individual models curated within
the CellML model repository (Lloyd et al., 2004).
Such modelling is collaborative. With the advent of
domain specific languages for describing models we
are looking at incorporating features from program-
ming language theory to improve collaborative design
of physiological models. Modular programming in-
volves describing a system in terms of encapsulated
modules and the interactions between them through
well-defined interfaces. Such modular program de-
sign is commonly used in software engineering when
designing large-scale reusable systems, with the key
tenets including encapsulation, abstraction, reuse and
extensibility (Booch, 2006).
We have been developing our own prototype
modelling language, Ode, to investigate modularity
and structured software engineering concepts (Som-
merville, 2010) that may facilitate collaborative design
within this domain. Ode is influenced by the men-
tioned biological DSLs and functional programming
languages rooted in the lambda calculus (Barendregt,
1985). Figure 1 presents the Ode grammar.
odeStmt ← componentDe f | valueDe f | odeDe f
componentDe f ← component f (id
1
,...,id
n
)
{exprStmt
1
,...,exprStmt
j
, return (E
1
,...,E
n
)}
valueDe f ← val id
1
,...,id
n
= E
E ← t
1
∗t
2
|t
1
/t
2
|t
1
>t
2
|...|t
1
&& t
2
|t
t ← (E) | number | boolean | piecewise
| f (E
1
,...,E
n
) | time | id
piecewise ← piecewise {E
C1
: E
T 1
,...,E
Cn
: E
T n
,
default : E
de f
}
odeDe f ← ode {init : id
v
, [ deltaVal : id
delta
] } = E
Figure 1: Abbreviated syntax of the core Ode language using
a simplified variant of EBNF that assumes common rules.
The semantics of this core language have been
217
Gill M., McKeever S. and Gavaghan D..
Model Composition for Biological Mathematical Systems.
DOI: 10.5220/0004699202170224
In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 217-224
ISBN: 978-989-758-007-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

described in a previous paper (Gill et al., 2012a). Con-
stant values may be defined as the result of mathe-
matical expressions; the syntax for such expressions
is similar to most programming languages. Compo-
nents are a means to group, abstract and parameterise
repeated computations. However they are inlined at
compile-time in a manner similar to C++ templates.
Piecewise terms enable conditional control-flow sim-
ilar to a switch statement. A deliberate limitation is
the lack of looping control-flow constructs that, when
coupled with a recursive restriction on components,
ensures termination during model simulation.
The basic expression language is extended with
several constructs to support the mathematical mod-
elling of (biological) systems over time, including or-
dinary differential equations (ODEs). ODEs require
an initial value y(0), and a derivative expression y
0
.
The focus of this research has been to apply soft-
ware engineering techniques that allow models de-
veloped in Ode to be highly reusable and extensible,
facilitating rapid composition to investigate certain pa-
rameters of interest. To the best of our knowledge,
these characteristics have eluded the majority of bio-
logical modelling software frameworks to date.
Our paper in outlined as follows. Section 2 mo-
tivates modular model design. In Section 3 we pro-
vide a precise description of our module system and
motivating example. In Section 4 we present re-
sults from simulating composite models derived from
experimentally-related model modules. Finally in Sec-
tion 5 we conclude our work and discuss current re-
search. We demonstrate the utility of the module
system using examples from a modular form of the
Hodgkin-Huxley (HH52) electrophysiological model
of the squid giant-axon (Hodgkin and Huxley, 1952).
2 MODULAR MODEL DESIGN
AND DEVELOPMENT
Modelling biological systems is an integrative, interdis-
ciplinary process, drawing on work from researchers
in a global environment from a variety of fields, in-
cluding physiologists, mathematicians, and computer
scientists. Models themselves are comprised from data
collected through various studies and are developed it-
eratively, with newer, generally more realistic, models
derived from existing ones (Niederer et al., 2009).
As such a need exists to efficiently facilitate the
collaborative development and reuse of models. This
would allow for the safe construction of models, guar-
anteeing the validity of models developed collabora-
tively and derived from multiple sources, and ensuring
that they may be composed successfully. We believe
Figure 2: Cell and stimulus parameters for the HH52 model
grouped and encapsulated into a single parameters module.
our research provides features that facilitate such col-
laborative modelling in a structured and safe manner.
We present a summation of the methodologies
used to structure and develop large-scale reusable bi-
ological mathematical models using Ode, inspired
by many techniques utilised in software engineer-
ing (Sommerville, 2010; Booch, 2006).
Encapsulation is the wrapping up of operations
and attributes into a module, so that those attributes
may only be manipulated through or accessed via the
operations provided by the module.
We can view modules as similar to objects, repre-
senting a convenient data-centric manner to decom-
pose systems into understandable and manageable
units/building blocks. Good encapsulation hides the
details of a module’s internal attributes and operations
from its users. These techniques are known as infor-
mation hiding and implementation hiding, and their
use is essential for promoting the understandability
of code within a reusable domain-specific modelling
framework. It allows abstracting away the low-level
details and providing a high-level interface to the mod-
ule functionality. Explicit export definitions within
module declarations facilitate implementation hiding
and help to achieve this goal. Figure 2 provides an
example encapsulating several HH52 cell-level param-
eters into a module.
Generic modules allow modellers to operate on en-
capsulated objects in an abstracted manner, enabling
polymorphic reuse and substitutability, similar to C++
templates. It is a style of programming in which al-
gorithms are written in terms of to-be-specified-later
constructs that are then instantiated when needed by
replacing the generic variables with appropriate con-
crete parameters. In the context of heart modelling,
we show that this technique enables module reuse, the
creation of alternative implementations, and the mixed
usage of ion channel models from a variety of sources.
Structural subtyping is implemented at the module
level, where we say that module
B
is a subtype of
module
A
, the supertype. This occurs when module
B
has the same (or a superset of the) interface as
A
,
yet may contain a different implementation. In this
case modules of type
A
can be substituted by modules
of type
B
. This occurs because methods written to
operate on elements of the supertype can also operate
on elements of the subtype; in a manner similar to
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
218

Figure 4: Diagram indicates use of containment and aggregation to provide code structure and reuse. We compose the parameters
module with the main model, whilst specifying that it is a subtype of
HH52Parameters
. The
HH52DefaultParameters
module
implements this interface via the aggregation and reuse of two sub-modules containing the required code.
Figure 3: Application of a parameterised module, the bind-
ing relationship indicates the assignment of a module as an
argument, generating a new module. The applied module
must implement the parameters interface.
inheritance in object-orientated programming (OOP).
However it is implemented at compile-time with-
out any performance penalty and does not require a
direct, nominative relation between the supertype and
subtype. Any modules that have a similar ‘shape’ can
be considered a subtype, providing low-coupling be-
tween modules and allowing rapid development and
substitution of alternate implementations. If used prop-
erly, subtyping, coupled with generics, can improve
the understandability of model code by reducing the
conceptual distance between code and the real-world
system which the code models. For instance, Figure 3
presents a use of both generics and subtyping to pro-
duce a parameterised module of a given supertype.
In software development, code reuse provides
many benefits — the code has already been developed,
tested and potentially deployed. A similar effect is
observed with model code, where equations and defini-
tions are often similar and should be reused if possible.
However in both domains, code often requires modi-
fications specific to each particular instance of reuse.
Containment-based relationships, such as composition
and aggregation, can be implemented by modules to
enable lightweight and flexible code reuse.
Modules may be imported and wrapped within con-
taining modules to re-implement and augment existing
functionality, delegating to existing code as needed.
This provides code-reuse through composition and ag-
gregation rather than OO inheritance.
This technique works hand-in-hand with the substi-
tutability property of modules and structural subtyping
mechanism to allow modellers to create model imple-
mentations which are both malleable and extensible.
It enables type-safe substitution whilst avoiding deep
inheritance hierarchies often seen in systems imple-
mented using traditional OO-languages (Booch, 2006).
When parameterised modules are utilised with ag-
gregation they allow generic code reuse, abstracting
the particular instances until simulation time. This
provides compile-time substitutability and a powerful
mechanism for rapid model construction and modifi-
cation. Figure 4 demonstrates aggregation to structure
and reuse code with the HH52 parameters module.
3 MODULE SYSTEM – SYNTAX
AND SEMANTICS
In this section we describe the Ode module system
used to structure models into modules consisting of
collections of related value and component definitions
that form some logical (and potentially biological)
grouping. We describe the syntax and semantics; the
grammar for the module language is provided in Fig-
ure 5.
moduleStmt ← moduleDe f | importStmt | applyModule
moduleDe f ← module id moduleBody |
module id (id
1
,. .., id
n
) moduleBody
moduleBody ← { odeStmt
1
,. .., odeStmt
n
}
importStmt ← import id
1
[as id
2
]
exportStmt ← export [id
1
,. .., id
n
]
applyModule ← id = f (id
1
,. .., id
n
) | id
Figure 5: Module extensions to Ode DSL.
ModelCompositionforBiologicalMathematicalSystems
219

We discuss parameterised modules, enabling
compile-time substitution of components and generic,
interface-driven development that provides further op-
portunities for abstraction and model reuse.
The module system was inspired by OCaml,
where it is effectively a higher-level language that en-
ables the programmable creation of independent mod-
ules (Leroy, 2000). The Ode module system operates
similarly; providing variable definitions, references,
function abstraction and application (i.e. parametrised
modules), and limited computation, all at the typed
module level. This provides extensive power to recon-
figure models for particular tasks.
3.1 Module Definition
module Parameters {
val E_R = -75 { unit : mV }
val Cm = 1 { unit : mF.cmˆ-2 }
val period = 60 { unit : ms }
val i_Stim = piecewise {
time >= 10 and time <= 10.5:
20 { unit : mA.cmˆ-2 },
default: 0 { unit : mA.cmˆ-2 }
} }
A standard module in Ode consists of a collection of
expressions, i.e. value and component definitions, that
form a grouping. This may be a logical or biological
grouping, e.g. an ion channel within a cardiac model.
The code fragment above presents the syntax for cre-
ating a module encapsulating several HH52 cell-level
parameters, as was illustrated in Figure 2.
Several modules may be defined within a single
file, where the directory path in which the files are
placed creates a module hierarchy. Modules may be
referenced using a dot-notation that corresponds to
lookup within the module hierarchy. This structure
enables the creation of multiple repositories of mod-
elling components, each with their own hierarchy, that
can be shared, reused and uniquely identified.
3.2 Importing & Using Modules
module HH52Model {
import Cardiac.HH52.Parameters as Pa
// leakage current
val E_L = Pa.E_R + 10.613 { unit : mV }
val i_L = 0.3 { unit : mS.cmˆ-2 } * (V - E_L)
// ... channels i_Na & i_K ...
init V = -75 { unit : mV }
ode { init : V } =
-(-Pa.i_Stim + i_Na + i_K + i_L) / Pa.Cm
}
A module may reference another module’s expressions
through an
import
declaration. This is demonstrated
in the above code sample, illustrating the composi-
tion of the HH52 parameters module with the HH52
base model, as in Figure 2. The declaration uses a
dot-notation to reference a filepath within the module
hierarchy and a module within the specified file. Thus,
in the above example the HH52 base model imports
a module
Parameters
from a file
HH52
within the
Cardiac
directory of an available module repository.
When processing the import, the module is retrieved
and loaded into the global module environment.
The visible definitions of an imported module are
again accessed using a dot-notation on the qualified
module name, demonstrated by references to
Pa
above.
3.3 Module Interface
Modules expose an interface, or signature, comprised
from the collection of identifiers and their types vis-
ible from outside the module. The uses of a module
within a model also leads to the implicit creation of
a required interface that any imported modules must
implement. When importing a module, interfaces are
matched and checked by the module type-system to
ensure successful composition.
A modeller may configure the visibility of cer-
tain definitions to modify the interface. This may
be achieved by structuring the model code such that
only exportable definitions are visible, or by explicitly
declaring the definitions to export (similar to the pub-
lic/private access modifiers in OO languages) through
the use of an export command.
In this manner only the vital information is ex-
ported in the interface, mimicking biological mecha-
nisms of compartmentalisation and containment.
3.4 Parametrised Modules
Grouping related definitions into modules enables
modularity and code reuse, however the modules and
the abstractions within them are fixed rather than
generic. When creating reusable components it is desir-
able to configure them according to a specific use-case,
for instance altering the parameters of a reusable ion
channel or creating protocols to compare simulations
against experimental data.
In several languages parameterised modules
present a flexible and powerful means for accomplish-
ing this. They are implemented as compile-time con-
struct used to create generic components in a similar
manner to ML functors (Leroy, 2000) and C++ tem-
plates, allowing type-safe substitutability of compo-
nents with differing implementation details.
Modules may be parameterised by other modules
leading to the creation of complex, specialised mod-
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
220

ules via a form of aggregation. This flexibility and
abstraction enables rapid investigations into parameter
variations, including parameter sweeps and sensitivity
analysis from a single code-base (O’Hara et al., 2011).
3.5 Parameterised Module Definition
module HH52ModelBase(Pa) {
// leakage channel
val E_L = Pa.E_R + 10.613 { unit : mV }
val i_L = 0.3 { unit : mS.cmˆ-2 } * (V - E_L)
// ... channels i_Na & i_K ...
init V = -75 { unit : mV }
ode { init : V } =
-(-Pa.i_Stim + i_Na + i_K + i_L) / Pa.Cm
}
The above example demonstrates parameterised mod-
ules within Ode, where the specific parameters mod-
ule utilised by the HH52 base model is parameterised
and made generic. The syntax extends module defini-
tions to include a list of module parameters, these are
generic module arguments that are determined during
application. Parameterised modules can be considered
analogous to functions over modules, they take a set
of input module arguments and return a new module.
Parameterised modules enable a form of interface-
based model construction that allows for the special-
isation of reusable module components. They facil-
itate several component based modelling techniques
through the modification of parameters and equations
used within a module, for instance the creation of mul-
tiple model subcomponents ranging in complexity and
accuracy to minimise computational demands.
3.6 Parameterised Module Application
module HH52Model = HH52ModelBase(Parameters)
The above code fragment demonstrates applying a
concrete version of the HH52 parameters module to
the base module, resulting in a complete version of the
HH52 model, as was illustrated in Figure 3.
Applying a functor is the process of replacing the
generic module parameters with real modules, the ef-
fect of which is to instantiate a new module derived
from applying the parameters to the functor body. This
new, concrete module can then be used elsewhere.
We can dynamically apply functors, enabling the
run-time configuration of models that exhibit certain
behaviours and investigation of effects using particular
parameters. This provides a flexible means for rapidly
constructing families of specialised models that can be
controlled by an external process at run-time.
4 MODULAR CARDIAC
SIMULATIONS
In this section we utilise the module system and
DSL abstractions previously described to design a
component-based modular modelling framework. We
hope this will eventually enable the agile develop-
ment, reuse and investigation/experimentation of car-
diac electrophysiological models in a collaborative
fashion (Noble and Rudy, 2001).
Our use case is influenced by research in (Niederer
et al., 2009) that investigated the common history be-
tween cardiac and ion channel models, but we conduct
similar simulations through programmable modular
composition rather than manual model construction.
Our sample framework is used to conduct several sim-
ulations, generating action potential (AP) membrane
voltage curves for cardiac models created from the
dynamic substitution of ion channel modules. This is
intended to show the ease at which a well-designed
framework lends itself to reuse, extensibility and flexi-
bility for modellers to investigate particular phenom-
ena. Furthermore it demonstrates the use of the type
system to ensure subsequent model validity.
4.1 Methodology
We investigate and construct a modelling architecture
suitable for creating models in a flexible and extensi-
ble manner comprised from individual modules. This
framework is used to develop a repository of cardiac
models to help qualitatively determine the DSL’s effec-
tiveness in the large-scale structure and rapid, collab-
orative development, modification and reuse of mod-
els. Several cardiac models are safely composed in a
scripted manner from modules in the repository.
4.1.1 Cardiac Models
The cardiac models are listed in Table 1, and are cho-
sen to demonstrate the iterative development process
and reuse of parameters and equations.
4.1.2 Model Structure & Development
We separate the cell models into reusable and substi-
tutable ion channel objects that each model the flow
of a particular charged ion across the cell membrane,
resulting in the generation of an AP. We abstract and
modularise at this point as most cardiac cell exper-
iments, and subsequent research data, occurs at the
ion channel level. As more information is derived
regarding their function we hope that their differing
representations within cell models may be used inter-
changeably and gradually unify into single canonical
ModelCompositionforBiologicalMathematicalSystems
221

Table 1: Cardiac ventricular electrophysiological models used within study, where the base model is denoted with a *.
Model Year Species Ion Channels State Variables
BR77 * (Beeler and Reuter, 1977) 1977 Mammalian 4 8
LR91 (Luo and Rudy, 1991) 1991 Guinea Pig 6 8
LRd94 (Luo and Rudy, 1994) 1994 Guinea Pig 11 12
Figure 6: Interface for reusable ion channel models, con-
sists of component,
getCurrent
, that computes I
Ion
for
calculating the membrane voltage. All ion channel models
implement this interface, as NaChannel and KChannel do.
form. This abstraction can be expressed neatly within
our module system; multiple modules representing the
same ion channel may be created, coexist and be sub-
stituted within existing and ever more complex newer
models. In this way, appropriate relationships, which
mimic real-world relationships, are defined between
modules in our modelling domain.
A standardised interface for ion channels mod-
els was determined that enables their use and re-
placement within cell models. This interface is illus-
trated in Figure 6, and consists of a single component,
getCurrent
. The input parameters represent the mem-
brane potential and equilibrium potential respectively,
and the output is the current generated by ionic flow.
A cardiac model structurally depends upon and
contains the ion channel modules, requiring that they
expose the
IonChannel
signature to be compatible.
This signature is checked at compile-time by the type
system to ensure that only valid ion channel objects are
used. The structure used to associate a cardiac model
and its related ion channels is illustrated in Figure 7.
We have used encapsulation to separate definitions
for ion channels into modules that expose a specified
interface. We now demonstrate how aggregation, en-
capsulation and subtyping may be used to abstract out
common functionality and enable code reuse. From a
cardiac modelling perspective, we can define common
functionality for ion channels. These are then encap-
sulated and extended in later, more complex channel
model subtypes through aggregation (mirroring the
real life development of such models), as was demon-
strated in Figure 2. We can thus delegate to existing
code, and override and specialise as needed within the
newer encapsulated module, whilst ensuring it exposes
the same interface to enable substitutability.
We use generics to specify the input ion channels
to each model via parameterised modules, allowing
simulation-time configuration and instantiation of con-
crete modules. Generics provide a standardised man-
ner to alter models and parameters, providing substi-
tutability without incurring a performance penalty. For
example, in Figure 8 the model,
BR77Model
, contains
the generic module reference
NaChannel
that exposes
the
IonChannel
interface. We do not need to specify
during model development which specific
NaChannel
implementation we are referring to.
We utilise encapsulation, aggregation, subtyping
and generics to abstract behaviour and provide substi-
tutability of reusable model components. This benefits
modellers by enabling model reuse, component-driven
development, and type-checked model composition.
These techniques orthogonally help model develop-
ment by increasing cohesion and decreasing coupling.
4.2 Results
module BR77NaChannel {
export (getCurrent)
component getCurrent(V, E_R) {
// ... channel constants & computations ...
// calculate current
val i_Na = (g_Na*pow(m, 3.0)*h*j+g_Nac)
* (V - E_Na)
return (i_Na)
} }
The above listing contains a segment from the BR77
I
Na
model (Beeler and Reuter, 1977), this segment
includes the top-level component that comprises the
module interface and implements the type-signature
required for reusable channels within our framework.
module BR77Model(NaChannel) {
// membrane voltage
init V = -84.624 { unit : mV }
// ... model constants and computations ...
val i_Na = NaChannel.getCurrent(V, E_R)
// Membrane Voltage ODE
ode { initVal : V, deltaVal : dV } =
(i_Stim - (i_Na+i_s+i_x1+i_K1))/C
}
Similarly, the listing above contains a segment from a
cardiac model within the framework. It shows a BR77
cell model parametrised by a module representing I
Na
,
this may be provided by any ion channel model that
implements the correct module signature.
We ran a series of simulations that demonstrate the
substitution and impact of the NaChannel within the
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
222
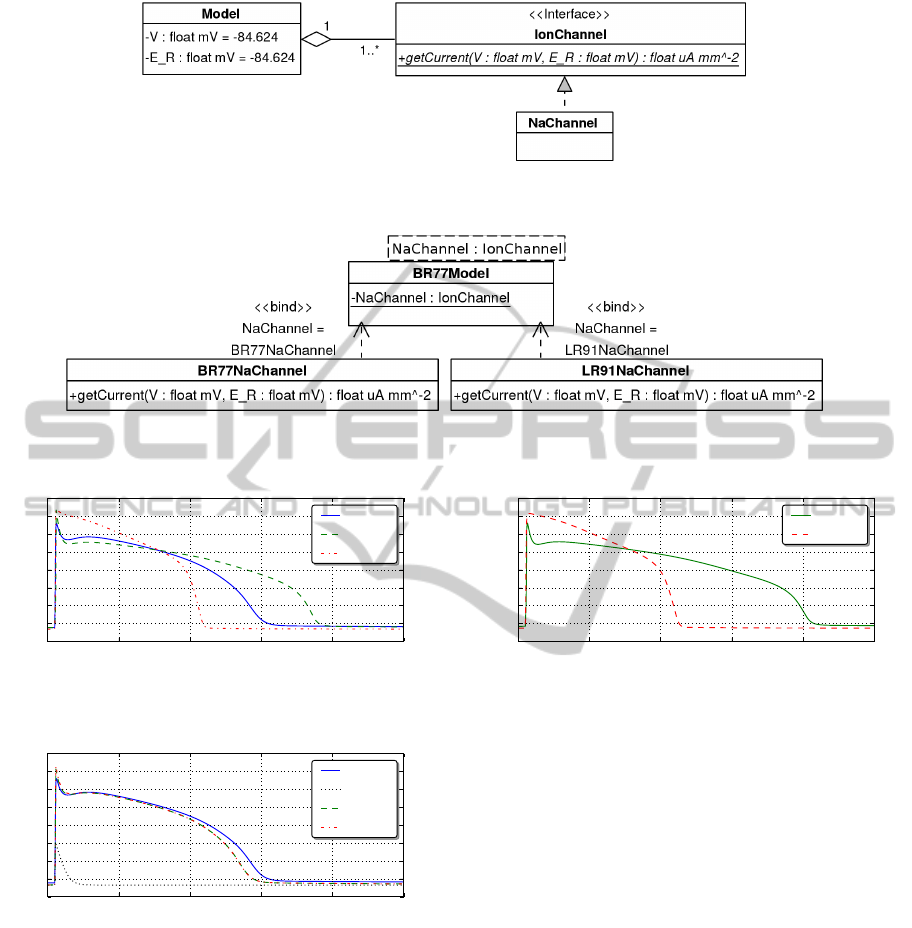
Figure 7: Modular structure of a cardiac model in the repository. The base model represents the cell membrane and calculates
the membrane voltage through references to many ionic channels that implement the IonChannel interface.
Figure 8: Using generics within the model framework — either
BR77NaChannel
or
LR91NaChannel
can be applied as module
argument to the base BR77Model cardiac model to represent the generic NaChannel.
1000 1100 1200 1300 1400
1500
Time (ms)
−100
−80
−60
−40
−20
0
20
40
60
Voltage (mV)
BR77
LR91
LRd94
Figure 9: AP curves from applying original I
Na
channels
into models using modules.
1000 1100 1200 1300 1400
1500
Time (ms)
−100
−80
−60
−40
−20
0
20
40
60
Voltage (mV)
BR77
`Zero'
LR91
LRd94
Figure 10: AP curves from applying alternate I
Na
channels
into BR77 cardiac cell model using modules.
models in a fully scripted manner. This was inspired
by the work in (Niederer et al., 2009) and the modular
framework was structured to safely enable such rapid-
modifications and experimentation. We initially com-
posed each cardiac base model with its corresponding
sodium channel and simulated the resulting complete
model to generate the reference AP curves depicted
in Figure 9. The sodium channels from the alternate
models were then applied to the BR77 cell model to
generate a new family of models whose AP curves
are presented in Figure 10. This plot shows that the
1000 1100 1200 1300 1400
1500
Time (ms)
−100
−80
−60
−40
−20
0
20
40
60
Voltage (mV)
LR91
LRd94
Figure 11: AP curves from applying BR77 I
Na
channel into
alternate models using modules.
LR91 and LRd94 I
Na
models slightly shortens the AP
duration of the BR77 cell model. I
Zero
, implementing
the same module signature but returning a zero current,
fails to trigger an AP. This is expected as sodium ions
are responsible for AP initialisation.
We performed the inverse operation, applying the
I
Na
BR77 model into the remaining cellular models
to investigate its influence. The AP curves from simu-
lating these models are presented in Figure 11, where
replacing the I
Na
from the LR91 and LRd94 models
increases the AP duration and alters the peak AP. We
do not consider these results particularly important in
terms of their biological meaning, instead they serve
to demonstrate the application and benefits of modular
programming and architecture to developing reusable,
extensible and dynamic models. The results were ob-
tained from a high-performance DSL implementation
that we intend to discuss in future publications.
ModelCompositionforBiologicalMathematicalSystems
223

5 CONCLUSIONS
Our use-case driven design process has yielded a mod-
ular framework which allows a family of cardiac elec-
trophysiological models to be extended both intuitively
and easily. This extensibility was achieved by utilis-
ing features such as generics and subtyping which
exploit the substitutability property of module hierar-
chies along with encapsulation for code structure and
aggregation for reuse. This is a common approach
used to structure large-scale software projects. New
cardiac models may utilise existing ion channel mod-
els, enabling the DSL to naturally capture the reuse
of models and experimental data. Thereby increasing
robustness which is important if these models are ever
used in a predictive pharmaceutical or clinical setting.
We can create hybrid models that include ion chan-
nel representations from several models. This can
be undertaken automatically simply by utilising ion
channel modules from different models when instanti-
ating a generic cell model. Generic modules may be
used to perform sensitivity analysis of the model to
parameter fluctuations. They can be used to alter equa-
tions, for example to model ion channel changes and
resulting effect on the AP caused by mutation or drug
block (O’Hara et al., 2011) in an abstracted manner.
Models created in the fashion that we have illus-
trated do not depend on each other explicitly. They do
not communicate with one another either. Parameteri-
sation only requires the type signature of the parameter
object to be known. Consequently they demonstrate
low coupling and high cohesion, an aspect of model
design that we feel is important for reusability and
extensibility (McKeever et al., 2013).
We are currently developing a repository to repro-
duce existing models. Our notation is textual but as
we have shown the modularity constructs trialled in
Ode have equivalent UML-style graphical representa-
tions. Therefore visual physiological modelling envi-
ronments could also be developed to support collabo-
rative efforts to construct future models.
REFERENCES
Barendregt, H. (1985). The lambda calculus: Its syntax and
semantics, volume 103. Access Online via Elsevier.
Beeler, G. and Reuter, H. (1977). Reconstruction of the
action potential of ventricular myocardial fibres. The
Journal of physiology, 268(1):177.
Booch, G. (2006). Object Oriented Analysis and Design
with Applications. Pearson.
Gill, M., McKeever, S., and Gavaghan, D. (2012a). Modular
Mathematical Modelling of Biological Systems. In
Symposium on Theory of Modeling and Simulation
(TMS’12).
Gill, M., McKeever, S., and Gavaghan, D. (2012b). Modules
for Reusable and Collaborative Modelling of Biologi-
cal Mathematical Systems. In 21ST IEEE International
WETICE Conference (WETICE-2012).
Hodgkin, A. and Huxley, A. (1952). A quantitative de-
scription of membrane current and its application to
conduction and excitation in nerve. The Journal of
physiology, 117(4):500.
Hucka, M., Finney, A., Bornstein, B., Keating, S., and
Shapiro, B. (2004). Evolving a lingua franca and as-
sociated software infrastructure for computational sys-
tems biology: the Systems Biology Markup Language
(SBML) project. Systems Biology.
Leroy, X. (2000). A modular module system. Journal of
Functional Programming, 10(3):269–303.
Lloyd, C., Halstead, M., and Nielsen, P. (2004). CellML: its
future, present and past. Progress in Biophysics and
Molecular Biology, 85:433–450.
Luo, C. and Rudy, Y. (1991). A model of the ventricular
cardiac action potential. Depolarization, repolarization,
and their interaction. Circulation research, 68(6):1501.
Luo, C. and Rudy, Y. (1994). A dynamic model of the
cardiac ventricular action potential. II. Afterdepolariza-
tions, triggered activity, and potentiation. Circulation
research, 74(6):1097–113.
McKeever, S., Gill, M., Connor, A., and Johnson, D. (2013).
Abstraction in physiological modelling languages. In
Symposium on Theory of Modeling & Simulation
(TMS’13).
Niederer, S., Fink, M., Noble, D., and Smith, N. (2009). A
meta-analysis of cardiac electrophysiology computa-
tional models. Experimental physiology, 94(5):486–95.
Noble, D. and Rudy, Y. (2001). Models of cardiac ven-
tricular action potentials: iterative interaction between
experiment and simulation. Philosophical Transac-
tions of the Royal Society A: Mathematical, Physical
and Engineering Sciences, 359(1783):1127–1142.
O’Hara, T., Vir
´
ag, L., Varr
´
o, A., and Rudy, Y. (2011). Simula-
tion of the undiseased human cardiac ventricular action
potential: model formulation and experimental valida-
tion. PLoS computational biology, 7(5):e1002061.
Sommerville, I. (2010). Software Engineering. Addison
Wesley.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
224
