Efﬁcient Multi-kernel Ray Tracing for GPUs

Thomas Schiffer

and Dieter W. Fellner

1,2,3

Institut f

ur ComputerGraphik & Wissensvisualisierung, Technische Universit

at Graz, Graz, Austria

Graphisch-Interaktive Systeme, Technische Universit

at Darmstadt, Darmstadt, Germany

Fraunhofer Institut f

ur Graphische Datenverarbeitung, Fraunhofer Gesellschaft, Darmstadt, Germany

Keywords:

Ray Tracing, SIMT, Parallelism, GPU.

Abstract:

Images with high visual quality are often generated by a ray tracing algorithm. Despite its conceptual simplic-

ity, designing an efﬁcient mapping of ray tracing computations to massively parallel hardware architectures

is a challenging task.In this paper we investigate the performance of state-of-the-art ray traversal algorithms

for bounding volume hierarchies on GPUs and discuss their potentials and limitations. Based on this analysis,

a novel ray traversal scheme called batch tracing is proposed. It decomposes the task into multiple kernels,

each of which is designed for efﬁcient parallel execution. Our algorithm achieves comparable performance to

currently prevailing approaches and represents a promising avenue for future research.

1 INTRODUCTION

Ray tracing is a widely used algorithm to compute

highly realistic renderings of complex scenes. Due to

its huge computational requirements massively paral-

lel hardware architectures like modern graphics pro-

cessing units (GPUs) have become attractive target

platforms for implementations. We investigate high

performance ray tracing on NVidia GPUs, but many

of our contributions and analysis may also apply

to other wide-SIMD hardware systems with similar

characteristics. In this paper, we use bounding vol-

ume hierarchies (BVHs) as acceleration structure for

ray traversal and we solely focus on the task of inter-

secting a ray with a scene containing geometric prim-

itives only and do not include shading and other oper-

ations into our discussion.

In general, we evaluate our algorithms on ray

loads generated by a path tracer with a ﬁxed maxi-

mum path length of 3. Our test scenes contain only

purely diffuse materials, from which rays bounce off

to a completely random direction of the hemisphere.

So, the generated ray data covers a broad spectrum

of coherency ranging from coherent primary rays to

highly incoherent ones after two diffuse bounces.

For a diligent performance assessment, we use a di-

verse set of NVidia GeForce GPUs consisting of a

low-end Fermi chip (GT 540M), a high-end Fermi

chip (GTX 590) and a high-end Kepler-based prod-

uct (GTX 680).

Our paper has the following structure: First, we

provide an analysis of the state-of-the-art ray tracing

algorithms and their characteristics that seem to leave

signiﬁcant room for improvement. We subsequently

discuss our novel algorithmic approach called batch

tracing that addresses the current problems. Finally,

we analyze the practical implementation as well as

some optimizations and point out possible directions

for future research.

2 PREVIOUS WORK

This paper targets massively parallel hardware archi-

tectures like NVidia’s Compute Uniﬁed Device Ar-

chitecture (CUDA) that was initially presented by

Lindholm et al. (Lindholm et al., 2008). CUDA hard-

ware is based on a single-instruction, multiple-thread

(SIMT) model, which extends the commonly known

single-instruction, multiple-data (SIMD) paradigm.

On SIMT hardware, threads are divided into small,

equally-sized groups of elements called warps (cur-

rent NVidia GPUs batch 32 threads in one warp).

Contrary to SIMD, execution divergence of threads

in the same warp is handled in hardware and thus

transparent to the programmer. To avoid starvation

of the numerous powerful computing cores of GPUs,

L1 and L2 caches were introduced with the advent

of the more recent generation of hardware called

Fermi (NVIDIA, 2009). The latest architecture of

209

Schiffer T. and Fellner D..

Efﬁcient Multi-kernel Ray Tracing for GPUs.

DOI: 10.5220/0004703502090217

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 209-217

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

GPU hardware termed Kepler (NVidia, 2012) con-

tains several performance improvements concerning

atomic operations, kernel execution and scheduling.

In 2009, Aila et al. (Aila and Laine, 2009) pre-

sented efﬁcient depth-ﬁrst BVH traversal methods,

which still constitute the state-of-the-art approach for

GPU ray tracing. Their implementation uses a sin-

gle kernel containing traversal and intersection, that is

run for each input ray in parallel. More recently they

presented some improvements, algorithmic variants

to increase the SIMT efﬁciency and updated results

for NVidia’s Kepler architecture in (Aila et al., 2012).

They also reported that ray tracing potentially gen-

erates irregular workloads, especially for incoherent

rays. To handle these uneven distributions of work,

compaction and reordering have been employed in

the context of shading computations (Hoberock et al.,

2009), ray-primitive intersection tasks (Pantaleoni

et al., 2010) and GPU path tracing (Wald, 2011).

Garanzha et al. propose a breadth-ﬁrst BVH traver-

sal approach in (Garanzha and Loop, 2010), which is

implemented using a pipeline of multiple GPU ker-

nels. While coherent rays can be handled very ef-

ﬁciently using frustra-based traversal optimizations,

the performance for incoherent ray loads signiﬁcantly

falls below the depth-ﬁrst ray tracing algorithms as

reported in (Garanzha, 2010).

3 THE QUEST FOR EFFICIENCY

While the SIMT model is comfortable for the pro-

grammer (e.g. no tedious masking operations have

to be implemented), the hardware still has to sched-

ule the current instruction for all threads of the warp.

Diverging code paths within a warp have to be se-

rialized and lead to redundant instruction issues for

non-participating threads. If code executed on SIMT

hardware exhibits much intra-warp divergence, a con-

siderable amount of computational bandwidth will be

wasted. In accordance with Section 1 of (Aila and

Laine, 2009), we use the term SIMT efﬁciency, which

denotes the percentage of actually useful operations

performed by the active threads related to the total

amount of issued operations per warp to quantify this

wastage in our experiments. As computational band-

width continues to increase faster than memory band-

width, SIMT efﬁciency is one of the key factors for

high performance on current and most probably also

future GPU hardware platforms.

Beside computational power, memory accesses

and their efﬁciency are a crucial issue too. Threads

of a warp should access memory in a coherent fash-

ion, in order to get optimal performance by coalescing

their requests. However, traditional ray tracing algo-

rithms (as well as many others) are known to gener-

ate incoherent access patterns that potentially waste

a substantial amount of memory bandwidth as dis-

cussed in (Aila and Karras, 2010). The caches of

GPUs can help to improve the situation considerably

as discussed by Aila et al. in (Aila and Laine, 2009)

and (Aila et al., 2012), where they describe how re-

cent improvements of the GPU cache hierarchy affect

the overall ray tracing performance.

In general, GPUs are optimized for workloads that

distribute the efforts evenly among the active threads.

As reported in (Aila and Laine, 2009), ray tracing al-

gorithms generate potentially unbalanced workloads,

especially for incoherent rays. This fact poses sub-

stantial challenges to the hardware schedulers and can

still be a major source for inefﬁciency as noted by

Tzeng et al. (Tzeng et al., 2010). To support the

scheduling hardware and achieve a more favorable

distribution of work, compaction and task reorder-

ing steps are explicitly included in algorithms. This

paradigm has been successfully applied to shading

computations of scenes with strongly differing shader

complexity (Hoberock et al., 2009), where shaders of

the same type are grouped together to allow more co-

herent warp execution. In the context of GPU path

tracing, Wald applied a compaction step to the rays

after the construction of each path segment in order

to remove inactive rays from the subsequent compu-

tations (Wald, 2011).

3.1 Depth-ﬁrst Traversals

The most commonly used approach for GPU ray trac-

ing is based on a depth-ﬁrst traversal of a BVH as dis-

cussed in (Aila and Laine, 2009). Their approach is

based on a monolithic design, which combines BVH

traversal and intersection of geometric primitives into

a single kernel. This kernel is executed for each ray

of an input array in massively parallel fashion. Given

two different rays contained in the same warp, poten-

tial inefﬁciencies now stem from the fact that either

they require different operations (e.g. one ray needs

to execute a traversal step, while the other ray needs

to perform primitive intersection) or the sequences of

required operations have a different length (e.g. one

ray misses the root node of the BVH, while the other

ray does not). These two fundamental problems have

a negative impact on SIMT efﬁciency and lead to an

uneven distribution of work, especially for incoherent

ray loads.

To mitigate the effects of irregular work dis-

tribution, Aila et al. investigated the concept of

dynamic work fetching. Given a large number of

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

210

Figure 1: Ray tracing-based renderings of our test scenes approximating diffuse illumination. From left to right: Sibenik (80K

triangles), Conference (282K triangles) and Museumhall (1470K triangles).

Table 1: SIMT efﬁciency percentages for traversal (T) and intersection (I) as well as kernel’s warp execution efﬁciency

(K) of the two best performing ray tracing kernels f ermi speculative while while (from (Aila and Laine, 2009)) and

kepler dynamic f etch (from (Aila et al., 2012)) using different thresholds of active rays for dynamic fetching of work. The

numbers are averages of multiple views taken of the Sibenik and the Museum scene for different generations of rays.

Scene Rays

while-while dyn-fetch 25% dyn-fetch 50% dyn-fetch 75%

T I K T I K T I K T I K

Sibenik

1. gen 87.0 61.3 80.1 86.4 59.9 79.2 86.4 60.0 79.4 86.3 60.0 79.1

2. gen 46.7 27.7 40.5 49.2 30.1 43.0 49.7 30.5 43.3 50.4 31.4 43.9

3. gen 38.4 23.6 33.8 41.0 26.2 36.2 42.1 27.6 37.2 42.5 28.2 37.6

Museum

1. gen 65.4 45.8 59.0 66.2 46.2 59.4 66.8 47.1 60.3 65.9 47.7 59.8

2. gen 32.6 19.8 28.8 37.9 28.7 34.8 39.7 31.7 36.6 40.3 33.2 37.2

3. gen 27.8 16.6 24.5 33.6 25.8 31.2 35.3 28.7 32.9 36.3 30.3 33.9

input tasks, the idea is to process them using an

(usually signiﬁcantly smaller) amount of worker

threads that fetch new input items until all input

elements have been processed. In this paradigm, the

fetching of a new task can happen immediately after

the current one has been ﬁnished or depending on a

more general condition (e.g. all threads of a warp

have completed their tasks). This dynamic software

scheduling was introduced in Section 3.3 of (Aila

and Laine, 2009) called persistent threads, where

they used dynamic fetching on a per-warp basis to

balance the shortcomings of the hardware scheduler

on Tesla generation hardware. In (Aila et al., 2012)

they suggest fetching new rays on Kepler hardware, if

more than 40% of the threads of a warp have ﬁnished

their work. It is important to note that dynamic

fetching of work attempts to increase warp utilization

and thus potentially SIMT efﬁciency at the expense

of memory bandwidth, because it tends to generate

incoherent access patterns when fetching single or

only a few new work items.

To have a baseline for our further exper-

iments, we evaluated the SIMT efﬁciency of

the two best performing ray tracing kernels

f ermi speculative while while (from (Aila and

Laine, 2009)) and kepler dynamic f etch (from

(Aila et al., 2012)) using different thresholds for

the dynamic fetching paradigm. We directly used

large parts of Aila et al.’s kernels with minor adap-

tations for our evaluation framework. Table 1 shows

SIMT efﬁciency percentages of the traversal and

the intersection code parts and the kernel’s overall

warp execution efﬁciency as reported by the CUDA

proﬁler obtained by averaging over multiple views

of the test scenes. The SIMT efﬁciency for traversal

and intersection have been computed by inserting

additional code into the kernel, which counts the

number of operations that are executed by the kernel

and that are actually issued on the hardware using

atomic instructions. However, the percentages in

Table 1 vary from what Aila et al. reported in Table 1

of (Aila and Laine, 2009), since we use different view

points and a different BVH builder. In (Aila et al.,

2012), Aila et al. note that ﬁne-grained dynamic

work fetching on Kepler improves the performance

by around ten percent, especially for incoherent rays.

This fact can be well explained by looking at the

corresponding efﬁciency percentages in Table 1. For

coherent primary rays the percentages are already

quite high and hardly change, so there is no notable

overall performance gain. Incoherent ray loads,

however, deﬁnitely beneﬁt from this optimization.

A newly fetched ray can either require the same se-

quence of operations as the others and thus increases,

or require a different sequence of operations and thus

decreases the SIMT efﬁciency of a warp. Assuming

EfficientMulti-kernelRayTracingforGPUs

211

equal probabilities for traversal and intersection, it is

therefore probable that low percentages of incoherent

rays are increased as indicated by the measurements.

We also experimented with speculative traversal

as proposed in Section 4 of (Aila and Laine, 2009)

using a postpone buffer of small size of up to three el-

ements. Comparing ordinary and speculative traver-

sals, we observed an increase in traversal efﬁciency

of up to 10% for coherent and up to 50% for inco-

herent rays, which becomes smaller for larger buffer

sizes. Please note that the kernels shown in Table 1

already use a ﬁxed size postpone buffer of one ele-

ment. So, enlarging the speculative buffer yields just a

slight increase of up to 10% in traversal efﬁciency for

incoherent rays, but no overall performance improve-

ment in our experiments. Also, we noted a slight de-

crease in intersection efﬁciency for buffer sizes larger

than one for ray tracing kernels based on the while-

while paradigm, which is in accordance with the re-

sults in Table 1 of (Aila and Laine, 2009). These re-

sults hint that in a monolithic design, SIMT efﬁciency

of traversal and intersection are correlated and cannot

be increased arbitrarily without adversely impacting

the other. Pantaleoni et al. (in Section 4.4 of (Pan-

taleoni et al., 2010)) address this problem by redis-

tributing intersection tasks of the active rays among

all rays of the warp. After the intersection they per-

form a reduction step to obtain the closest intersec-

tion for each ray. This structural modiﬁcations of the

monolithic approach result in a signiﬁcantly increased

SIMT efﬁciency of intersection (50%-60% instead of

about 25%), but is used only for specialized spherical

sampling rays in an out-of-core ray tracing system.

3.2 Breadth-ﬁrst Traversals

A radically different approach to GPU-based ray trac-

ing was presented by Garanzha et al. in (Garanzha

and Loop, 2010). They implemented a ray tracing al-

gorithm that traverses their specialized BVH structure

in a breadth-ﬁrst manner including some key modi-

ﬁcations. In a ﬁrst step before the actual traversal,

the input rays are sorted and partitioned into coherent

groups bounded by frusta. Then, traversal starts at the

root node. At the currently processed tree level, all

active frustra (active means intersecting a part of the

BVH) are intersected with the inner nodes and these

results are propagated to the next lower level. Traver-

sal stops at the leaf nodes and yields lists of inter-

sected leaves for each frustum. Subsequently, all rays

of each active frustum are tested for intersection with

the primitives contained in each leaf to obtain the ﬁ-

nal results. As described in (Garanzha, 2010), each of

these steps is implemented using multiple kernels re-

sulting in a rather long pipeline. Although we did not

provide an actual implementation of their algorithm,

we still want to note several important characteristics

of their approach.

First of all, we argue that large parts of their imple-

mentation can be assumed to exhibit high SIMT efﬁ-

ciency. Each kernel is carefully designed to perform

a single task (e.g. frustum intersection) and com-

plex operations are broken down into smaller compo-

nents (e.g. ray sorting exploiting existing coherency),

which can again be efﬁciently implemented. Sec-

ondly, this approach also tends to generate workloads

that are signiﬁcantly more coherent and regular than

the ones of depth-ﬁrst traversal. There appear to be no

sources for such major inefﬁciencies in the traversal

phase and persistent threads are used to balance the

workloads in the intersection stage, since the length

of the corresponding list of leaf nodes may vary sig-

niﬁcantly. We believe that the performance wins over

monolithic traversals reported on rather coherent rays

are not only due to potentially efﬁcient multi-kernel

implementation, but also largely due to their clever

frusta-traversal based optimization.

Despite these favorable properties, the approach

also possesses a major algorithmic inefﬁciency. In the

traversal stage, a complete traversal of the accelera-

tion structure is performed for each frustum regard-

less of the number of the actually necessary opera-

tions. Thus, a lot of likely redundant work per ray is

carried out, since the ray may intersect a primitive that

is referenced by the ﬁrst leaf that is encountered in

traversal. This node over-fetching potentially leads to

a lot of redundant instructions and memory accesses.

For coherent rays, this drawback apparently does not

outweigh the beneﬁts from the efﬁcient traversal and

intersection stages. For incoherent rays, however, the

set of the traversed nodes grows considerably and the

node over-fetching dominates the all aforementioned

beneﬁts resulting in a signiﬁcantly reduced overall

performance.

4 MULTI-KERNEL BATCH

TRAVERSAL

Based on the room for improvement that is left by

current state-of-the-art ray tracing algorithms, we pro-

pose a novel approach called batch traversal. It is de-

signed to achieve the following objectives:

• Given the low percentages for incoherent rays of

depth-ﬁrst traversals shown in Table 1, our algo-

rithm should notably increase SIMT efﬁciency.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

212

Traversal &

Intersection

Compaction &

Reordering

Leaf Collection

Intersection

Frustum

Traversal

Intersection

Figure 2: High-level system designs for monolithic depth-ﬁrst (left), breadth-ﬁrst (middle) and our batch tracing approach

(right). Batch tracing consists of multiple phases, which are repeatedly executed until all rays have terminated. Blocks denote

logical parts of the algorithms, black arrows denote the control ﬂow.

• Unlike breadth-ﬁrst traversal, the algorithm

should not exhibit substantial inefﬁciencies in

handling ray loads of varying coherency.

The components of our algorithm and their interplay

are shown in Figure 2 (right) together with depth-ﬁrst

(left) and breadth-ﬁrst (middle) traversals. Like in

breadth-ﬁrst traversal, our approach splits the ray trac-

ing task into several algorithmic stages implemented

in multiple kernels to increase SIMT efﬁciency of the

single code parts. During leaf collection stage, the ray

traverses the BVH similar to depth-ﬁrst traversal and

collects a number of intersected leaf nodes called in-

tersection candidates. In the subsequent phase, the

collected intersection candidates are reorganized to

achieve efﬁcient execution of the intersection stage

and the active rays are compacted for the next exe-

cution of the traversal stage. In the intersection phase

the primitives contained in the intersection candidates

are tested for intersection with the ray and the results

are used to update the rays. These stages are executed

in a loop until all input rays have terminated. Con-

trary to breadth-ﬁrst traversal, our approach performs

partial BVH traversals and intersection testing alter-

nately in order to avoid collecting a large number of

redundant intersection candidates.

4.1 Leaf Collection

As mentioned before, the leaf collection stage per-

forms a partial depth-ﬁrst traversal of the BVH similar

to the monolithic ray tracing algorithms and is imple-

mented in a single kernel. If a leaf is encountered dur-

ing traversal, it is stored into the buffer of the corre-

sponding ray and traversal continues immediately as

shown in Algorithm 1. A ray terminates this stage if

the whole BVH has been traversed or a certain maxi-

mum number of collected leaves has been found. The

efﬁciency of this stage depends on the number of in-

tersection candidates that have to be expected for a

given ray. The second crucial question is how the col-

lection of these leaves should be distributed optimally

among the various iterations.

Algorithm 1 Leaf Collection Stage

while ray not terminated do

while node is inner node do

traverse to the next node

end while

store leaf into buffer

if maximum number of leaves collected then

return

end if

end while

As the overall number of collected leaves for a ray

is inﬂuenced by many factors (e.g. input ray distri-

bution and scene geometry), we provide probabilis-

tic bounds backed up by experiments. To estimate

the size of the intersection candidate set, we assume

a uniformly distributed ray load and that our input

scene consists of N objects O

. Each O

is enclosed

by a bounding box B

and all objects are enclosed by

a scene bounding box W . Furthermore, let B = ∪B

the union of all bounding boxes and p(n) be the prob-

ability for a random line to intersect n objects, given

it intersects W . Using Proposition 5 from (Cazals

and Sbert, 1997), a tight upper bound for p(n) is then

given by Equation 1 (SA denotes surface area).

p(n) ≤

SA(B)

nSA(W )

(1)

EfficientMulti-kernelRayTracingforGPUs

213

This probabilistic bound shows that the size of a

set of intersection candidates for a random ray can be

expected to be reasonably small. In practice, we can

hope for an even smaller candidate set, because we

are only interested in intersections occurring before

the ﬁrst hit of the ray.

To assess the quality of these theoretical consider-

ations in practice, we have evaluated the size of the in-

tersection candidate set for multiple views of our test

scenes. The obtained results prove our probabilistic

assumption that for a large number of rays the size

of the candidate is small (< 4 for 70% and < 8 for

90% of the rays) regardless of their distribution. Fig-

ure 3 shows a histogram of the size of the intersection

candidate set for different ray generations for a view

of the Sibenik and a view of the Museumhall scenes.

Firstly, the histogram varies signiﬁcantly for small set

sizes (e.g. up to 8 for Figure 3) depending on the

distribution of the input rays (e.g. viewpoint). How-

ever, the distribution of the larger candidate set sizes

exhibits no dependence on the input ray distribution

approaching zero for all scenes and viewpoints. Ad-

ditionally, the overall shape of the histogram curves is

also similar for all tested ray loads and input scenes.

Although speciﬁc ray-geometry conﬁgurations might

cause exceptionally large intersection candidate lists,

these cases can still be handled by our implementation

in a reasonably efﬁcient manner.

50000

100000

150000

200000

250000

0 5 10

Mus 1

Mus 2

Mus 3

Sib 1

Sib 2

Sib 3

Ray Set

Figure 3: Histogram of size of the intersection candidate

set for rays of different generations (1-3) for a view of the

Sibenik (Sib) and a view of the Museumhall (Mus) scene.

The intersection candidate set of a ray consists of all leaves

that are pierced by this ray from its origin to its ﬁrst hit

point. The X axis shows the size of the intersection candi-

date set, the Y axis displays the corresponding number of

rays. The graphs for larger candidate set sizes all are very

close to the X axis, thus only set sizes up to 10 are shown.

The second important open issue that remains is,

how the collection of the leaves should be distributed

among the various passes. It is challenging to provide

a short and optimal solution, since choosing the num-

ber of intersection candidates per iteration is a trade-

off. Collecting a large number of leaves per iteration

reduces the total number of required passes and thus

potentially increases overall performance. However,

a lot of potentially redundant traversal and intersec-

tion operations might be introduced, since most of the

rays have only got a small candidate set. To counter

this effect, a small number of intersection candidates

per pass can be chosen to minimize the overhead, po-

tentially increasing the total number of iterations re-

quired. We ﬁnally came up with the following heuris-

tic, which is backed up by numerous experiments: We

start with a small number (e.g. 2 for GT 540M) in the

ﬁrst pass and increase the size of the intersection can-

didate set gradually over the next few passes. This

avoids much redundant work in the ﬁrst passes and

also keeps the number of total passes in an acceptable

range.

4.2 Compaction and Reordering

The compaction and reordering stage performs vari-

ous housekeeping tasks in a single kernel. Firstly, we

perform a compaction of the rays that remain active

after the execution of the leaf collection stage. We

simply map the active rays to consecutive slots us-

ing parallel reduction based on atomic instructions for

shared and global memory. This removes already ter-

minated rays and helps to maintain a high efﬁciency

during the leaf collection stage. Additionally, this

stage is responsible for managing the leaf collection

buffer. At the start of our batch tracing algorithm, this

buffer is allocated once with a size that is a ﬁxed mul-

tiple of the number of input rays (e.g. number of rays

times eight elements).

In each leaf collection pass we partition this buffer

in equal parts among the remaining active rays. This

layout can ﬂexibly accommodate a wide range of

thresholds for the number of collected leaves with-

out the need to perform costly memory reallocations.

Secondly, a parallel grid-wide reduction is made to

compute the total number of intersection tasks and to

assign these tasks to threads for the subsequent in-

tersection stage. Again, rays, which have collected

leaves during the previous stage, are mapped to con-

secutive slots for efﬁciency reasons. For storing the

different mappings generated by work compaction,

index arrays are allocated at the start of the algorithm.

They keep track of the original indices for all active

rays and intersection tasks and help to save costly

movements of larger data structures (e.g. input ray

data or traversal stacks).

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

214

4.3 Intersection

Our implementation of the intersection stage maps the

intersection tasks of one ray to one thread, which it-

eratively processes its array of collected leaves. For

each leaf, all contained primitives are intersected with

the ray and the results are stored for use in the subse-

quent phases of the algorithm.

5 RESULTS AND DISCUSSION

In this section, we evaluate the previously discussed

batch tracing algorithm and discuss some optimiza-

tions. To see how the total running time is distributed

we proﬁled our implementation for different scenes

and ray loads. Around 70% of the time is spent in the

leaf collection, which makes this stage the primary

target for optimizations. Intersection computations

constitute 25% of total time and compaction and re-

ordering 5%, while negligible overhead is caused by

memory allocations and CPU-GPU communication.

5.1 Optimized Leaf Collection

In order to assess the efﬁciency of the leaf collection

stage, we analyzed the resulting distribution of work-

loads. As the number of operations for different rays

may vary considerably, we implemented an optimized

version that uses dynamic fetching of work to counter

the effects of this imbalance. If the SIMT efﬁciency of

a warp drops below a certain threshold, already termi-

nated rays get replaced with new input rays. We ex-

perimented with different threshold percentages and

empirically determined an optimal threshold of 25%

for the GTX 590. For the GT 540M dynamic fetch-

ing is only beneﬁcial if performed on a per-warp ba-

sis, i.e. when the last active ray of a warp termi-

nates, a whole group of new 32 work items is fetched.

For a detailed comparison with monolithic traver-

sal approaches we implemented an extended ker-

nel based on f ermi speculative while while that uses

dynamic fetching of rays in the sense of (Aila et al.,

2012). Table 2 shows the ray tracing performance for

the Museum scene of our monolithic dynamic fetch

kernel (DF), the batch tracing baseline implementa-

tion (Batch) and its improved variant using dynamic

fetching (Batch+DF) relative to the performance of

the f ermi speculative while while kernel. Our opti-

mized batch tracing algorithm (Batch+DF) achieves

comparable performance on the 540 GT, but is con-

sistently outperformed on the 590 GTX by our mono-

lithic dynamic fetch kernel. The low-end card with

few compute cores seems to beneﬁt from our batch

Table 2: Ray tracing performance for our monolithic

dynamic fetch kernel (DF), the batch tracing base-

line implementation (Batch) and its improved variant

using dynamic fetching again (Bt+DF). Numbers are

relative to the performance of our implementation of

f ermi speculative while while and were averaged over

multiple views of the Museum scene. The largest speed-ups

are shown in bold numbers.

GPU Ray Type DF Batch Bt+DF

GT 540M

1. gen 1.13 0.97 1.04

2. gen 1.46 1.42 1.54

3. gen 1.55 1.42 1.55

GTX 590

1. gen 1.09 0.78 0.79

2. gen 1.42 1.10 1.17

3. gen 1.51 1.12 1.21

tracing approach especially in combination with per-

warp dynamic fetching, because irregular workloads

can be hardly balanced out by the hardware. On Ke-

pler hardware batch traversal is around 70% slower

than our fastest monolithic kernel regardless of the

coherency of the input rays.

While dynamic fetching increases the perfor-

mance of the monolithic ray traversal notably,

only small speedups (up to 10%) are achieved

for the leaf collection stage. Contrary to the

obtained results, we expected larger beneﬁts (at

least in a range similar to the difference between

f ermi speculative while while and its dynamic work

fetching variant) from this optimization: Since the

leaf collection kernel contains no intersection code,

dynamic fetching should deliver large increases in

SIMT efﬁciency and also improve overall perfor-

mance. In order to ﬁnd a plausible cause for this

discrepancy, we measured the warp execution efﬁ-

ciency of the leaf collection stage. Table 3 shows the

percentages obtained by batch tracing using different

variants of dynamic fetching (per-warp and using dif-

ferent thresholds) in comparison to the highest SIMT

efﬁciency values for traversal achieved by state-of-

the-art monolithic kernels in the Museum scene. As

we expected, the efﬁciency of the BVH traversal is

slightly increased for primary rays (up to 10%) and

substantially enhanced for high order rays (up to al-

most 60%).

Since these improvements do not result in an over-

all performance win, we decided to proﬁle our im-

plementation comprehensively. The analysis revealed

that using dynamic fetching for our leaf collection

kernels results in an increased number of instruction

issues due to memory replays. This fact strongly hints

that the performance of this stage is limited by the

caches of the GPU. As the available DRAM band-

width is not entirely used up, we believe that the unex-

pected results are caused by the unfavorable memory

EfficientMulti-kernelRayTracingforGPUs

215

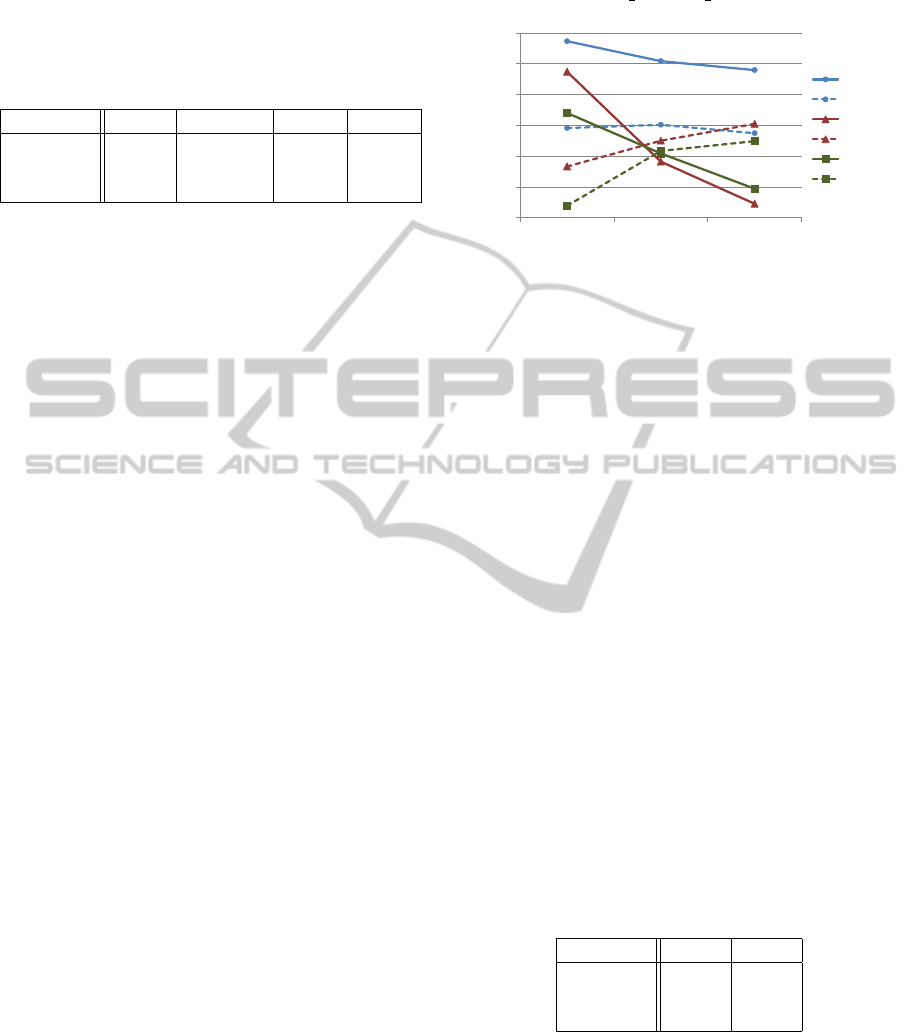
Table 3: SIMT efﬁciency percentages for traversal of mono-

lithic kernels (Mono) and for the leaf collection stage of

batch tracing using dynamic fetching per-warp (Warp DF)

and with different thresholds (DF 25% and DF 50%) in the

Museum scene. For the ﬁrst column, we use the highest

percentages achieved by any monolithic kernels, including

all variants of dynamic fetching (see also Table 1).

Ray Type Mono Warp DF DF 25 DF 50

1. gen 66.8 66.5 72.1 69.3

2. gen 40.3 36.7 52.3 56.8

3. gen 36.3 32.6 50.3 54.6

access pattern resulting from traversal of incoherent

rays. This leads to an exhausted cache subsystem that

cannot service all the memory requests on time result-

ing in severe latency that nulliﬁes most of the beneﬁts

of the increased SIMT efﬁciency.

To verify the aforementioned assumptions exper-

imentally and to identify primary performance lim-

iters we use selective over-clocking of the process-

ing cores and the memory subsystem (e.g. the perfor-

mance of memory-bounded kernels will beneﬁt from

an increased memory clock rate). In fact, our leaf col-

lection kernels hit the memory wall much earlier than

we expected, given the fact that they perform no inter-

section computations and thus have a smaller memory

working set compared to monolithic traversal. While

we obtained an optimal threshold of 25% for dynamic

fetching on the GTX 590, it only decreases perfor-

mance on the Kepler hardware. In our opinion, this

shows a drawback of separating traversal and inter-

section: Leaf collection kernels cannot hide the oc-

curring memory latencies as well as a monolithic ker-

nel, which can potentially schedule additional opera-

tions while waiting for memory fetches (e.g. execute

primitive intersection while waiting for a BVH node

memory access). These observations raise the ques-

tion for alternative memory layouts and acceleration

structures, which better suit this kind of traversal al-

gorithm.

5.2 Traversal Performance Limiters

However, the analysis of our monolithic ray tracing

kernels revealed that memory performance becomes

a major challenge for this kind of algorithms, too. As

discussed by Aila et al. (Aila and Laine, 2009), tra-

ditional depth-ﬁrst traversal are commonly believed

to be compute-bound. This is conﬁrmed by our re-

sults and and holds for Fermi hardware regardless of

whether dynamic fetching is used or not. The Kepler-

based GTX 680, however, provides a signiﬁcantly in-

creased amount of computational power, while mem-

ory bandwidth has grown only moderately in com-

parison. Our speculative depth-ﬁrst traversal kernel

is apparently still compute-bound as shown in Fig-

ure 4. The kepler dynamic f etch kernel similarly

100,00%

105,00%

110,00%

115,00%

120,00%

125,00%

130,00%

1. gen 2. gen 3. gen

WW-inst

WW-mem

DF25-inst

DF25-mem

DF50-inst

DF50-mem

Figure 4: Kernel performance limiter analysis for mono-

lithic ray traversals on Kepler-based 680 GTX. We evaluate

our fastest monolithic kernel (WW) using different thresh-

olds for dynamic fetching (DF25 and DF50). Series suf-

ﬁxed with ”-instr” denote that processor clock has been in-

creased by 20%, ”-mem” means that the memory clock has

been over-clocked by 20%. The graphs show obtained per-

formance relative to the default settings of the device.

exhibits compute-bound behavior for coherent ray

loads. With diminishing coherence of the input rays,

dynamic fetching overcharges the cache subsystem

with incoherent memory requests, which in turn be-

comes the dominating factor. Contrary to the spec-

ulations in (Aila et al., 2012), this shows that mono-

lithic state-of-the-art traversal already tends to be lim-

ited by cache and memory performance, at least for

incoherent rays. Since a signiﬁcant decrease in the

instruction-to-byte ratio in future GPUs cannot be ex-

pected, memory bandwidth and cache throughput will

become the primary limiter for traditional algorithms.

5.3 Intersection Stage

Table 4 shows the SIMT efﬁciency of our implemen-

tation of the intersection stage in comparison to the

highest numbers that have been achieved by mono-

lithic traversals. Our approach improves the efﬁ-

Table 4: SIMT efﬁciency percentages of primitive intersec-

tion for monolithic kernels (Mono) and our batch tracing

implementation (Batch) for the Museum scene.

Ray Type Mono Batch

1. gen 47.7 58.3

2. gen 33.2 47.1

3. gen 30.3 45.4

ciency of primitive intersection notably which is now

in the range of what has been achieved by intersection

task reordering (Pantaleoni et al., 2010). As the leaf

collection pass usually submits an amount of redun-

dantly collected leaves to the traversal stage, we tried

to avoid all unnecessary primitive tests by storing the

entry distance of a ray along with every intersection

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

216

candidate. The ray always examines this value before

any contained primitives are tested. However, this

optimization yielded no noticeable performance im-

provements and might pay off only for more complex

geometric primitives. Our basic mapping which lets

one ray work on one intersection candidate set gener-

ates potentially uneven workloads, since the number

of primitives contained in a single leaf may vary as

well as the size of the intersection candidate set. Mea-

surements hint that our intersection implementation is

memory-bounded and we suppose that it would ben-

eﬁt signiﬁcantly from a more elaborate reordering of

the intersection tasks.

6 CONCLUSIONS AND FUTURE

WORK

Given our comprehensive analysis of current ray

traversal algorithms, we believe that state-of-the-art

approaches leave a lot of room for future algorithmic

improvements. A prominent example is the SIMT

efﬁciency of depth-ﬁrst traversal algorithms, which

waste a considerable amount of computational band-

width when dealing with incoherent rays. However,

also the limits of traditional paradigms become ob-

vious, which puts the research focus on alternative

traversal methods like the batch tracing algorithm pro-

posed in this paper.

Although the provided implementation cannot

quite compete with mature and heavily optimized

monolithic traversal, our multi-kernel method pos-

sesses appealing characteristics, which makes it an at-

tractive direction for further research. A central point

is to ﬁnd an acceleration structure that permits in-

creased traversal performance to make our approach

more beneﬁcial. Furthermore, we would like to op-

timize the intersection stage of our algorithm and in-

vestigate efﬁcient handling of multiple types of geo-

metric primitives.

ACKNOWLEDGEMENTS

We thank Marko Dabrovic for providing the Sibenik

cathedral model and the University of Utah for the

Fairy Scene. Many thanks also go to Timo Aila for

making his testing and benchmarking framework pub-

licly available. We also want to thank the anonymous

reviewers for their valuable comments.

REFERENCES

Aila, T. and Karras, T. (2010). Architecture considerations

for tracing incoherent rays. In Proceedings of the

Conference on High Performance Graphics, HPG ’10,

pages 113–122, Saarbr

ucken, Germany. Eurographics

Association.

Aila, T. and Laine, S. (2009). Understanding the efﬁciency

of ray traversal on gpus. In Proceedings of the Confer-

ence on High Performance Graphics 2009, HPG ’09,

pages 145–149, New York, NY, USA. ACM.

Aila, T., Laine, S., and Karras, T. (2012). Understanding the

efﬁciency of ray traversal on gpus – kepler and fermi

addendum. NVIDIA Technical Report NVR-2012-02,

NVIDIA Corporation.

Cazals, F. and Sbert, M. (1997). Some integral geom-

etry tools to estimate the complexity of 3d scenes.

Technical report, iMAGIS/GRAVIR-IMAG, Greno-

ble, France, Departament dInformtica i Matemtica

Aplicada, Universitat de Girona, Spain.

Garanzha, K. (2010). Fast ray sorting and breadth-ﬁrst

packet traversal for gpu ray tracing. Oral presentation

at EG2010.

Garanzha, K. and Loop, C. (2010). Fast ray sorting and

breadth-ﬁrst packet traversal for gpu ray tracing. In

Proceedings of the Eurographics, EG ’10, pages 289–

298. Eurographics Association.

Hoberock, J., Lu, V., Jia, Y., and Hart, J. C. (2009).

Stream compaction for deferred shading. In Proceed-

ings of the Conference on High Performance Graphics

2009, HPG ’09, pages 173–180, New York, NY, USA.

ACM.

Lindholm, E., Nickolls, J., Oberman, S., and Montrym, J.

(2008). Nvidia tesla: A uniﬁed graphics and comput-

ing architecture. Micro, IEEE, 28(2):39 –55.

NVIDIA (2009). Nvidia’s next generation cuda compute

architecture: Fermi.

NVidia (2012). Nvidia gk110 architecture whitepaper.

Pantaleoni, J., Fascione, L., Hill, M., and Aila, T. (2010).

Pantaray: fast ray-traced occlusion caching of mas-

sive scenes. In ACM SIGGRAPH 2010 papers, SIG-

GRAPH ’10, pages 37:1–37:10, New York, NY, USA.

ACM.

Tzeng, S., Patney, A., and Owens, J. D. (2010). Task

management for irregular-parallel workloads on the

gpu. In Doggett, M., Laine, S., and Hunt, W., edi-

tors, High Performance Graphics, pages 29–37. Euro-

graphics Association.

Wald, I. (2011). Active thread compaction for gpu path trac-

ing. In Proceedings of the ACM SIGGRAPH Sympo-

sium on High Performance Graphics, HPG ’11, pages

51–58, New York, NY, USA. ACM.

EfficientMulti-kernelRayTracingforGPUs

217