Combinatorial Approach for Geographic Routing
with Delivery Guarantees
Kasun Samarasinghe and Pierre Leone
Department of Computer Science, University of Geneva, Geneva, Switzerland
Keywords:
Geographic Routing, Anchor Coordinates, Delivery Guarantees.
Abstract:
In this paper we present a novel combinatorial approach for geographic routing with delivery guarantees.
Proposed algorithm can be seen as a variant of GFG (Greedy Face Greedy of Bose et.al) algorithm, but based
on the defined combinatorial properties of the graph. We utilize a distributed planarization algorithm of a
geometric graph, which is based on the Schnyder’s characterization of planar graphs. The new approach is
combinatorial in the sense that the nodes are ordered with respect to three distinct order relations satisfying
the suitable properties. The coordinate system motivated the development of this routing algorithm is VRAC
(Virtual Raw Anchor Coordinates), which localizes nodes based on the raw distances from three fixed anchors.
Since the positions of the anchors need not to be known, the nodes localized by the VRAC coordinate system
does not correspond to the exact geographic location of nodes, yet leaving sufficient information to define
necessary combinatorial constructs.
1 INTRODUCTION
Geographic routing is a routing paradigm proposed
for wireless ad-hoc networks, which are capable
of geographically locating nodes in the network
(Bose et al., 1999), (Karp and Kung, 2000). This
approach is promising due to its scalability and
efficiency in the face of network dynamics, compared
to the on-demand routing schemes proposed for
wireless ad-hoc networks. Even though its seminal
work on geographic routing focused on unicast
routing, subsequent proposals build higher level
communication abstractions like geographic hash
tables, following a data centric approach (Ratnasamy
et al., 2003).
Geographic routing relies on geographic
information of nodes in the network. Therefore it
should be supported by an auxiliary localization
service. Localization is an independent problem,
which was extensively studied, especially for the
networks where expensive localization methods are
not feasible. Thus most of the localization schemes
assume that, only a small number of nodes (referred
as beacons or anchors) know their exact geographic
location information and the rest of the nodes can
determine the distance between anchor nodes and them
selves. With these two pieces of information a node
can perform a geometric computation technique like
trilateration to derive their geographic information.
In order to make sure that all the nodes get localized,
newly localized nodes have to collaboratively act as
anchors and propagate their geographic locations.
This class of algorithms are practically attractive since
they are distributed and computationally efficient
specially for resource constraint devices.
One drawback of anchor based localization
protocols is the problem of bootstrapping the system
by placing the anchors and providing them geographic
locations. This is not trivial specially in an
environment like wireless sensor networks due to
the ad-hoc nature of node deployment. Anchor free
localization is proposed as a solution to overcome
difficulties associated with anchors, where it only
based on the distances between nodes. Main aim
of this class of algorithms is to find an euclidean
embedding of the network graph, such that it preserves
the inter-distances of nodes. Such coordinate systems
are termed as virtual coordinate systems, since they
do not hold any correspondence with the physical
coordinates of nodes.
Alternatively we explore a new avenue of virtual
coordinate systems, where it uses the raw distance
measurements from anchors as the coordinates. Fang
et.al (Fang et al., 2005) and Fonseca et.al (Fonseca
et al., 2005) independently proposed geographic
routing schemes on top of virtual raw coordinate
195
Samarasinghe K. and Leone P..
Combinatorial Approach for Geographic Routing with Delivery Guarantees.
DOI: 10.5220/0004712501950204
In Proceedings of the 3rd International Conference on Sensor Networks (SENSORNETS-2014), pages 195-204
ISBN: 978-989-758-001-7
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

systems. But none of the two performed geographic
face routing as the fall-back mechanism when greedy
routing hits a local-minima. In this paper we construct
basic combinatorial properties to perform geographic
face routing with delivery guarantees using only the
raw distance measurements as the coordinates.
The remainder of the paper initially develops the
combinatorial constructs in the form of order relations
to be used in geographic face routing. This will
be followed by the face routing algorithm based on
the defined basic constructs. Finally we provide the
simulation results of our algorithm comparing with
standard geographic routing algorithms.
2 BACKGROUND
2.1 Virtual Coordinate Systems
A different direction of localization research is to
localize nodes with a virtual coordinate system
(VCS), which is different from the Euclidean system.
VCS, as opposed to real coordinates are desirable
in some applications, which only need to preserve
topological structure rather than their exact geographic
locations. Geographic routing is one such application
of this nature. Rao et.al proposed a mechanism to
assign synthetic coordinates to perform geographic
routing, commonly referred to as NoGeo (Rao
et al., 2003). NoGeo computes an embedding
of the network on the Euclidean space, starting
from an initial coordinate assignment at each node.
It models the coordinate assignment problem as
a mass-spring model and performs an iterative
relaxation algorithm to achieve on an approximation
of the optimum coordinate assignment. Shang et.al
have incorporated inter distances between nodes
into the coordinate construction problem, hence to
compute an embedding of the network preserving the
topological structure of the network (Shang et al.,
2003). The problem formulation was based on a
technique borrowed from psychometrics called multi
dimensional scaling and based on an iterative approach.
These virtual coordinate systems does not to bare any
correspondence with their geographic coordinates in
the Euclidean space. Therefore on these coordinate
systems, it is not possible to perform operations which
resemble geometric relationships with the physical
topology. Specifically when considering geographic
routing, face routing as a local-minima recovery
scheme is not a candidate, thus failing to provide
delivery guarantees.
2.2 Virtual Raw Anchor Coordinates
Even though virtual coordinate systems offer sound
grounding to the localization problem, in a more
realistic setting their applicability is questionable.
This is mainly due to most of these mechanisms
being iterative in nature, making them impractical
for large networks. Additionally individual nodes
would be computationally burdened with the numerical
calculations involved in such algorithms. Identifying
these discrepancies, (Fonseca et al., 2005) and (Fang
et al., 2005) have independently proposed a virtual
coordinate scheme relying only on the raw measures
from anchor nodes. Both these mechanisms assign
nodes their coordinates, simply as a hop-count vector
from the anchors. Therefore this mechanism does
not demand any further computational manipulations
as in other virtual coordinate construction schemes.
It is similar to VCS, as it does not physically
related to the geographic locations. Huc et.al have
proposed a similar virtual coordinate system which
assigns raw distances from anchors as the coordinates;
VRAC (Huc et al., 2010). A local routing strategy
was proposed for VRAC in (Samarasinghe and Leone,
2012), where geographic primitives were identified
(which can be performed locally) to perform classical
algorithms like GFG and GPSR over VRAC. This
proposal was based on a variant of original VRAC,
where it assumed inter distances between anchors.
In this work, we propose a combinatorial
constructs (based on order relations) to perform
geographic face routing. We emphasis that
these combinatorial constructs are very efficient to
implement in practice, since they have to perform only
basic comparison operations. Further more, we prove
the delivery guarantees of face routing based on our
approach.
3 COMMUNICATION GRAPH
PLANARIZATION IN VRAC
The local planarization of the communication graph
in the VRAC coordinate system is presented in (Huc
et al., 2012) where we adapt the planarity criterion
introduced in (Schnyder, 1989) to Unit Disk Graph
(UDG), i.e. the nodes are positioned in a region of the
plane and two nodes are connected if and only if the
distance among them is less that a constant r called
the range of communications. In our setting, the nodes
are localized in the VRAC coordinate system and this
associates to each node u the coordinates

u
1
, u
2
, u
3

=

d(u, A
1
), d(u, A
2
), d(u, A
3
)

, see Figure 1. Moreover,
we assume that all the nodes are inside the triangular
SENSORNETS2014-InternationalConferenceonSensorNetworks
196

region,
\
A
1
A
2
A
3
, with suits the anchors A
1
, A
2
, A
3
, see
(Huc et al., 2012) for the explanation of why this is
necessary and the description of possible further works
to remove this assumption.
We can define three order relations on the set of
nodes V .
Definition 1. The three order relations <
i
, i = 1, 2, 3
on V ×V are defined by
∀u, v ∈V u <
i
v ⇐⇒ d(u, A
i
) < d(v, A
i
) ⇐⇒ u
1
< v
i
.
The three order relations are total and it makes
sense to associate the minimum of a set with respect
to one of the three order. We will denote this by min
i
for i = 1, 2, 3.
These three order make possible the definition of
sectors associated to a node u.
Definition 2. We define the following sectors
associated to a node u ∈ V , see Figure 1. Note that the
reference node u does not belong to the sectors.
s
u
1
= {v | u <
1
v, u >
2
v, u >
3
v} ∩
\
A
1
A
2
A
3
.
s
u
2
= {v | u <
1
v, u <
2
v, u >
3
v} ∩
\
A
1
A
2
A
3
.
s
u
3
= {v | u >
1
v, u <
2
v, u >
3
v} ∩
\
A
1
A
2
A
3
.
s
u
4
= {v | u >
1
v, u <
2
v, u <
3
v} ∩
\
A
1
A
2
A
3
.
s
u
5
= {v | u >
1
v, u >
2
v, u <
3
v} ∩
\
A
1
A
2
A
3
.
s
u
6
= {v | u <
1
v, u >
2
v, u <
3
v} ∩
\
A
1
A
2
A
3
.
In the text, we refer to these sectors as sector
number 1, 2, . . . , 6 respectively, i.e. for instance, s
u
4
is sector number 4 of u.
Definition 3. Given a node D , we also use the
convenient notation s
u
D
to denote the sector j of u such
that D ∈ s
u
j
, i.e. D ∈ s
u
D
.
Given a UDG G with vertex set V and edge set E
we define the graph
e
G = (
e
V ,
e
E) by
Definition 4. The vertex set
e
V = V and
1
e
E =

(u, v)



v ∈ s
u
2k−1
and v = min
k
(s
u
2k−1
) k = 1, 2, 3}
2
We emphasize that the graph
e
G is undirected (as
the UDG G ). There is an edge (u, v) ∈
e
E if v is in
sector s
u
1
, s
u
3
, or s
u
5
and is the closest with respect to
the order relation <
1
, <
2
, <
3
respectively or, if the
same conditions apply with u and v interchanged. The
important property is that:
1
In the following, we use alternatively (u, v) ∈ E or v ∈
N
u
to indicate that the nodes u, v are neighboring nodes.
2
The notation min
k
(s
u
i
means that we consider the node
in the sector s
u
i
and connected to u that is the minimal with
respect to the order <
i
.
v
u
d(u, A
2
)
d(u, A
1
)
d(u, A
3
)
Figure 1: The Virtual Raw Anchor Coordinate (VRAC). On
the right, given that there is an edge (u, v) the hatched region
must not contain any nodes to ensure planarity.
Property 1. A node u has at most one neighboring
node in each of s
u
1
, s
u
3
, s
u
5
(the closer with respect to the
corresponding order relation). Indeed, if v ∈ s
u
1
, v ∈ s
u
3
,
or v ∈ s
u
5
then u ∈ s
v
4
, u ∈ s
v
6
, or u ∈ s
v
2
respectively and
then, the only possibility for an edge (u, v) ∈
e
E is that
v is minimal with respect to <
1
, <
3
or, <
5
respectively.
The next proposition proves to be useful for
implementing face routing, see Proposition 4.
Proposition 1. We consider nodes u and v such that
(u, v) ∈
e
E. Then,
s
u
v
∩ s
v
u
=
/
0.
Proof. With loss of generality we can assume that
u >
1
v, u >
2
v, u <
3
v (the proof is the same if we
permute the indices). Because u and v are connected it
must be that v = min
3
{z | u >
1
z, u >
2
z, u <
3
z} . Then
sector s
v
u
is defined by {z | z >
1
v, z >
2
v, z <
3
v} and,
the intersection is s
u
v
∩ s
v
u
= {z | u >
1
z >
1
v, u >
2
z >
2
v, u >
3
z <
3
v} the last inequality shows that if it were
a node in the intersection u should be connected to that
node instead of v.
However, a node u can have many neighboring
nodes in the sectors v ∈ s
u
2
, s
u
4
or v ∈ s
u
6
. In (Huc et al.,
2012) we call the edges (u, v) with v in s
u
1
, s
u
3
, or s
u
5
outgoing edges. With this terminology, a node has at
most three outgoing edges and possibly many ingoing
edges (and edge (u, v) such that v ∈ s
u
2
, s
u
4
or v ∈ s
u
6
).
We emphasize that this is a useful denomination but
the graph
e
G is not oriented.
We proved in (Huc et al., 2012) that under some
conditions on the length of the edges the resulting
graph
e
G is planar and we discuss the stretch factor
compared to the original graph G . Our aim in the
following is to present a geographic routing algorithm
on top of this planar graph that guarantee the delivery
of the data. In the paper (Huc et al., 2012) we
investigate some geometrical properties that imply
that the graph
e
G = (
e
V ,
e
E) is planar. Actually, the aim
of these geometrical properties is to ensure that the
following property is satisfied.
CombinatorialApproachforGeographicRoutingwithDeliveryGuarantees
197

Property 2. Given that there is an edge between node
u and v and, says, v ∈ s
u
i
for i ∈ {1, 3, 5} = {2 j − 1 |
j = 1, 2, 3} then, there are no other nodes in the region
defined by the intersection of s
u
i
and {z | d(A
j
, z) <
d(A
j
, v)} with j = 1, 2, 3 with i = 2 j − 1 , see the right
of Figure 1.
This property is crucial to ensure that if there is
an edge (u, v) in
e
E then there are no nodes w such
that w <
k
v and (u, w) 6∈ E i.e., the node w should be
connected to u to ensure planarity but, unfortunately,
is out of the range of u. Notice that the property must
be true because the node v is the minimal node in
s
u
2 j−i
, j ∈ {1, 2, 3} with respect to the order relation
<
j
(defined by d(A
j
, z)) to ensure the planarity of
e
G.
In this work, we focus on the delivery guarantee of
the routing algorithm and we assume that the graph
e
G
is planar. This graph can result from the planarization
process applied to a UDG graph, as in (Huc et al.,
2012), or any other way.
4 IMPLEMENTATION OF THE
ROUTING PRIMITIVES
Our routing algorithm is a variant of the combined
greedy-face routing algorithm. However, the
major difference is that in our restricted coordinate
system it is not possible to implement face routing
independently of greedy routing, see Proposition 3.
In the classical setting, the routing primitives are
the implementation of the left or right hand traversal
rule to explore a face of the planar graph and, the
detection of the intersection of an edge of the path
with the source destination line. Unfortunately, in
our setting it is not always possible to detect such
an intersection. This is why we consider a region that
contains the source and destination nodes, see equation
(1) , and we detect when we cross this region. Also, we
switch to greedy routing when data are transmitted to
a node belonging to this region because face routing is
no longer implementable in this case, see Proposition
3.
Notice that our version of greedy routing does not
use an explicit distance function in a closed form.
Anyway, our solution can be called greedy routing
since it satisfies the axioms characterizing greedy paths
provided in (Li et al., 2010), i.e.(transitivity) if node
y is greedy for x and z is greedy for y then z is greedy
for x as well and (odd symmetry) if y is greedy for x
then x is not for y.
Input: Node source u and destination D
Output: Node x ∈ N
u
∩ s
u
D
∩ s
D
u
or error
Determine the sector s
u
D
;
Determine the sector s
D
u
by reversing the signs of
the inequalities;
if N
u
∩ s
u
D
∩ s
D
u
6=
/
0 then
select arbitrarily x in the set;
return x;
else
return error;
end if
Figure 2: Implementation of the routine greedy(u,D).
4.1 Greedy Routing Primitives
Definition 5. Given a destination node D , a path
{u
i
}
i=1,...,k
is a greedy path if (u
i
, u
i+1
) ∈ G , i =
1, . . . , k − 1 and
u
i+1
∈ s
u
i
D
\
s
D
u
i
. (1)
In this case, we will say that a node u
i
makes a greedy
routing decision.
Figure 2 contains a pseudo-code of the
implementation of the primitive for greedy routing.
Proposition 2. If u
i+1
∈ s
u
i
D
T
s
D
u
i
and u
i+2
∈
s
u
i+1
D
T
s
D
u
i+1
then u
i+2
∈ s
u
i
D
T
s
D
u
i
.
Proof. For concreteness, we consider s
u
i
D
= s
u
i
5
=
{z | z <
1
u
i
, z <
2
u
i
, z >
3
u
i
} and, then s
u
i
D
=
{z | z <
1
D, z <
2
D, z <
3
D} (we reverse the
signs of the inequalities). The assumption u
i+1
∈
s
u
i
D
T
s
D
u
i
leads to D <
1
u
i+1
<
1
u
i
, D <
2
u
i+1
<
2
u
i
,
D >
3
u
i+1
>
3
u
i
. We then conclude that s
u
i+1
D
= {z |
z <
1
u
i+1
, z <
2
u
i+1
, z >
3
u
i+1
} ⊂ s
u
i
D
and that
s
D
u
i
= s
D
u
i+1
. This proves the proposition.
Corollary 1. Given a destination node D , a greedy
path {u
i
} eventually reaches the destination D.
Proof. Using Proposition 2 by induction proves that
s
D
u
i
= s
D
u
j
for all nodes in the greedy path and that D ∈
∩
i=1...k
s
u
i
D
. Because the area of this last intersection
decreases, it must eventually hold that the destination
D is reached (there cannot be an infinite number of
nodes in an infinitesimally small surface).
Notice that this result follows directly from the
results in (Li et al., 2010) since the paths satisfy the
required axioms. However, we provide a direct simple
and independent proof of the delivery of data.
SENSORNETS2014-InternationalConferenceonSensorNetworks
198

4.2 Face Routing Primitives
In the following we describe the implementation of
the face routing primitives. Basically if u is the source
and D the destination of data the routing algorithm
at u switches to face routing if N
u
∩ s
u
D
∩ s
D
u
=
/
0 .
The algorithm selects to start the face traversal the
node v such that v ∈ N
u
and the edge (u, v) is the
first edge encountered when the line uD is rotated
counterclockwise. The face traversal stops if the path
goes through a node belonging to N
u
∩s
u
D
∩s
D
u
or, if an
edge (v, w) intersects this region the algorithm decides
whether the face traversal algorithm must follow or
switch the face. Because we implement only the
primitives for the left hand traversal rule, keeping or
switching the face is done by choosing if the path
traverses the region (by selecting w as the next node)
or if the path does not traverse the region by inverting
the order of the nodes (v, w) , i.e. the node v continues
the execution of the left hand traversal algorithm by
assuming that the data is received from node w.
Notice that our implementation is not an
implementation of a classical algorithm like GFG
or GPSR since it cannot be executed independently
of greedy routing for the reasons mentioned in the
introduction and substantiated below. However, our
implementation follows the rule of GFG for face
switching. To easier the comparison with GFG, we
also keep the same terminology when needed. Indeed,
in the following we say that an edge (u, v) is on the
left of an edge (u, w) or a line uD if the angle between
the two measured counterclockwise is smaller that π.
Given an edge (u, v) , a first primitive to implement
the face traversal is to rotate the edge around u
counterclockwise and to determine the next edge (u, w)
that we encounter. Actually, this amounts to find the
edge (u, w) that makes the smaller angle with (u, v)
where the angle is measured counterclockwise. In
our coordinate system, we cannot compute the angles
since we only know the order relations defined by the
three anchors. In the following we say that an edge
is the next edge to an edge (u, v) or a line to indicate
that we rotate the edge counterclockwise around u and
stop to the next edge that we encounter.
4.3 The Implementation Barrier,
Impossibility Result
There is a particular configuration where it is not
possible to determine which of two edges (u, v) and
(u, w) are next to a line uD .We emphasize that this
is due do the fact that the nodes u and D are not
connected. However, this configuration is frequent
when u is the source of data and D is the destination.
d(A
3
, u)
d(A
2
, u)
d(A
1
, u)
u
D
v
d(A
3
, u)
d(A
2
, u)
d(A
1
, u)
u
D
v
w
w
Figure 3: An illustration of the proof of Proposition 3. Given
the order relations it is not possible to decide whether we are
on the configuration depicted on the left or on the right of
this Figure.
Proposition 3. If the nodes v, w ∈ s
u
D
∩s
D
u
and, D 6∈ N
u
while v, w ∈ N
u
it is not possible in our coordinate
system to determine which of the edge (u, v) or (u, w)
is the next edge of the line uD.
Proof. Figure 3 shows two configurations where
v, w, D ∈ s
u
4
and, where the same order relations exist
between the nodes, i.e. D <
1
v <
1
w <
1
u , D >
2
v >
2
w >
2
u and, D >
3
w >
3
v >
3
u . On the left side of the
figure the edge (u, w) is next to the line uD while on
the right (u, v) is.
This proposition implies that face routing cannot
be implemented as soon as the path reaches a node,
says u , that is in the same sector than the destination D .
Indeed, Proposition 3 shows that it is not possible the
determine the face that must be traversed among the
one supported by (u, v) and the one by (u, w) . In that
case, our routing algorithm switches to greedy routing
mode.
4.4 The Edges are not in the Same
Sector of the Data Destination
If the destination D is not in the same sector as the
nodes v, w it is possible to select the edge next to the
line uD . To make this possible, we number the sectors
of a node u depending on the destination D in the
following manner. The sector s
u
D
(see Definition 3)
gets the number 0 and, the others sectors of u are
increasingly numbered counterclockwise. We denote
by num(s
u
j
, D) this number. Given a node v , we
denote num(s
u
v
, D) the number of the sector to which
v belongs.
The implementation of this function is done by
first determining the number k of the sector s
u
v
defined
in Definition 2 by inspection. Then, computing
num(s
u
v
, D) = k + 6 − j mod 6 where D ∈ s
u
j
(or
equivalently j is the number of s
u
D
), see Figure 6 .
With these conventions, it is possible to determine
which of the edges (u, v) and (u, w) is next to the line
uD.
CombinatorialApproachforGeographicRoutingwithDeliveryGuarantees
199

s
u
4
v
w
u
s
u
3
D
s
u
4
v
w
u
s
u
3
D
d(A
3
, v)
Figure 4: On the left a configuration where the algorithm
of Proposition 4 would fail, on the right an illustration that
the by comparing d(A
3
, v) and d(A
3
, w) it is possible to
determine the edge that is on the right of the other.
Proposition 4. Given that two nodes v, w 6∈ s
u
D
the
edge (u, v) is next to the line uD if
1. num(s
u
v
, D) < num(s
u
w
, D),
2. num(s
u
v
, D) = num(s
u
w
, D) , v, w ∈ s
u
2
and
d(A
2
, v) < d(A
2
, w) or equivalently v <
2
w,
3. num(s
u
v
, D) = num(s
u
w
, D) , v, w ∈ s
u
4
and
d(A
3
, v) < d(A
3
, w) or equivalently v <
3
w,
4. num(s
u
v
, D) = num(s
u
w
, D) , v, w ∈ s
u
6
and
d(A
1
, v) < d(A
1
, w) or equivalently v <
1
w,
Proof. The first case is clear if u and w are separated
by a sector. However, because the sectors are not
convex it is not clear that it is true if u and w belong
to two adjacent sectors. In the left of Figure 4,
we represent the case where w ∈ s
u
3
, v ∈ s
u
4
and the
algorithm of the Proposition return the edge (u, w) but,
the edge (u, v) is next to the destination D . In the
following, we prove that this case is not possible. We
remind that because there is an edge (u, v) there must
exist i ∈ {1, 2, 3} such that u, v <
i
w . Because v ∈ s
u
4
is equivalent to u >
1
v, u <
2
v, u <
3
v and w ∈ s
u
3
to
u >
1
w, u <
2
w, u >
3
w i must be 2 , i.e. u, v <
2
w , the
node w must belong to the hatched region in left of
Figure 4. We then conclude that the edge (u, w) as
depicted on Figure 4 is not possible. The cases where
v belongs to s
u
2
or s
u
6
are proved similarly.
Next, we assume that v, w ∈ s
u
4
. Notice that it is
not possible that u and v belong to s
u
1
, s
u
3
or s
u
5
because
there can be only one edge in these sectors by Property
1. Because there is an edge (u, v) the node w cannot
be in the region s
v
1
and satisfying u >
1
w >
1
v , see
Proposition 1. Then, if the edges (u, v) is next to (u, D)
then the node w must satisfy d(A
3
, w) > d(A
3
, v) and
reciprocally, see the right of Figure 4. Notice that the
hatched region on the right of Figure 4 is forbidden
to w . Indeed, if w were in this region then v ∈ s
w
1
,
like u . But, because u >
1
v >
1
w then w would
be connected to v instead of u , a contradiction. The
proofs of others cases are similar.
For convenience we implement a subroutine
right(u,v,w) that returns which of the edges (u, v) or
(u, w) is the closest to right border when v and w are
Input: Nodes u, v, w such that v, w ∈ N
u
and v, w
belong to the same sector of u
Output: Node x ∈ {v, w} that is the closer to the right
border of the sector the nodes belong to
if w ∈ s
u
2
then
else if d(A
2
, w) < d(A
2
, v) then
return w;
else
return v;
end if
if w ∈ s
u
4
then
else if d(A
3
, w) < d(A
3
, v) then
return w;
else
return v;
end if
Figure 5: Implementation of the routine right(u,v,w).
in the same sector, see Figure 5. This corresponds to
the implementation of the points 2, 3, 4 of Proposition
4. The complete implementation of Proposition 4 is
included in the implementation of the face traversal
algorithm, see Algorithms 11 and 9.
4.5 Starting Face Routing, Extension of
the Function num(s
u
v
, D), num(s
u
w
, D)
when v, w ∈ s
u
D
In Proposition 3, we proved that if v, w ∈ s
u
D
∩ s
D
u
it is
not possible to determines which of the edge (u, v) or
(u, w) is next to the line uD . Actually, if v or w belong
to s
u
D
∩ s
D
v
the algorithm selects this node and switches
to greedy routing. However, we need to extend the
function num(s
u
v
, D) to the case where v, w ∈ s
u
D
\ s
D
u
.
Let us assume that D ∈ s
u
4
. Because the algorithm
described in Proposition 4 selects the nodes that belong
to the sector with the smaller number, the solution
consists in keeping the number 0 for the sector defined
by s
u
D
∩ {v | d(v, A
3
) > d(D, A
3
)} , see Figure 6 and
assign the number 6 to the complement of this sector
in s
u
4
.
By inspection, we extend the function num(s
u
v
, D)
by assigning the number 6 to the sector
s
u
D
∩ {v | d(v, A
2
) < d(D, A
2
)} if D ∈ s
u
2
s
u
D
∩ {v | d(v, A
3
) < d(D, A
3
)} if D ∈ s
u
4
s
u
D
∩ {v | d(v, A
1
) < d(D, A
1
)} if D ∈ s
u
6
Next, if two or more nodes belong to the sector number
0 we choose the one that is next to the line uD by
using the function right (u, v, w) presented in Figure
SENSORNETS2014-InternationalConferenceonSensorNetworks
200

u
D
$
0
1
2
3
4
5
d(A
3
, D)
0
6
Figure 6: An illustration of the function num(s
u
D
, D) where
s
u
D
= s
u
4
. The sectors labeled 0, . . . , 5 are described in Section
4.4. The sectorl 6 is a refinement of the sector 0 and contains
the nodes v ∈ s
u
D
\

s
D
u
∪ (s
D
u
− 1) ∪ (s
D
u
− 2)

such that (u, v)
is on the right of the line uD.
Input: Nodes u, v, w, D such that v, w ∈ N
u
, v, w 6∈ s
u
D
and D 6∈ N
u
Output: Node x ∈ {v, w} such that ux is next to uD
if num(s
u
v
, D) < num(s
u
w
, D) then
return v;
end if
if num(s
u
v
, D) > num(s
u
w
, D) then
return w;
end if
if v ∈ s
u
1
∪ s
u
3
∪ s
u
5
then
return error;
end if
return right(u,v,w)
Figure 7: Implementation of the routine nextto(u,D,v,w).
5. The entire algorithm is presented in Figure 9. The
resulting routing primitive nextto(u,D,v,w) uses the
extended definition of the function num discussed in
this section. Provided that no neighbouring nodes of u
belong to s
u
D
∩ s
D
u
it is used to start face routing.
We emphasize that this is not contradictory with
Proposition 3. Indeed, this procedure returns the edge
next to the line uD provided that the region s
u
D
∩s
D
u
=
/
0 .
The impossibility result holds when this intersection
is not empty.
4.6 Selecting the Next Edge in Face
Routing
To implement face routing, we face the problem that
given that node u receives the data from node v we
must determine which edge is next to (u, v) by rotating
the edge around u counterclockwise. The function
nextto, Figure 7 discussed in Section 4.5 cannot be
used in this form. Indeed, if we consider that two
nodes x, y ∈ N
u
∩ s
u
v
the function nextto does not every
v
u
v
v
x
y
Figure 8: When the two nodes x and z belong to the same
sector as v we must pay attention to decide which one of
(u, x) or (u, y) is next to (u, v) . The three nodes labeled v
show the different case we must consider.
time return the right nodes. The problem is again
that the function nextto assumes that x, y 6∈ s
u
D
∩ s
D
u
.
However, because in our case there is an edge between
u and v the function right can be used.
To determine the the next edge to (u, v) is similar
than in the function nextto if x, y not ∈ s
u
v
. On the other
case, we must distinguish the three configurations
illustrated in Figure 8 using the function right. The
resulting function, FaceNextEdge is presented in
Figure 11.
4.7 Face Switching
According to the proof that GFG delivers data with
certainty for any planar graph given in (Bose et al.,
1999), when an edge (v, w) of face routing cuts the
source destination line uD , face traversal must change
the traversed face if the line wD is on the right of the
edge (w, v) . That means that the angle between (w, v)
and the line wD measured counterclockwise is larger
than π , i.e. we need to rotate the line (w, v) for an angle
larger than π to match the line uD.
In our case, we cannot detect the intersection of
the line uD . What we detect is that the edge (v, w)
crosses the region s
u
D
∩ s
D
u
. This is equivalent to detect
that (v, w) ∩uD 6=
/
0 because we know that s
u
D
∩s
D
u
=
/
0 .
By direct inspection and using the Property 2, we
conclude that a crossing that triggers a face switching
occurs if and only if (the arrow → indicates the
direction of the data, and the number of the sectors are
all mod 6, i.e.s
u
D
+ 1 means s
u
D
+ 1(mod 6))
CombinatorialApproachforGeographicRoutingwithDeliveryGuarantees
201

Input: Nodes u, v, w, z such that v, w, z ∈ N
u
Output: Node x ∈ {w, z} such that (u, x) is first
encountered when (u, v) rotates counterclockwise
around u
if num(s
u
w
, v) > num(s
u
z
, v) then
return z;
end if
if num(s
u
z
, v) > num(s
u
w
, v) then
return w;
end if
x =right(u,w,z);
if (s
u
v
6= s
u
w
) then
return x;
else if (x == w) then then
y = z;
else
y = w;
end if
if (v == right(u, x, v)) then
return x;
end if
if (v == right(u, y, v)) then
return y;
end if
return x;
Figure 9: Implementation of the routine
FaceNextEdge(u,v,w,z).
v
v
v
s
D
u
∩ s
u
D
w
w
w
D/u
u/D
Figure 10: Different node placements to cross the region
s
u
D
∩ s
D
u
.
s
u
D
+ 1 → s
u
D
− 1, or s
D
u
+ 1, or s
D
u
+ 2
s
D
u
− 1 → s
u
D
− 1
s
D
u
− 2 → s
u
D
− 1
s
u
D
+ 2 → s
D
u
+ 1 (2)
s
u
D
+ 1 → s
D
u
+ 1
s
D
u
− 1 → s
D
u
+ 1, or s
u
D
− 1, or s
u
D
− 2
We represent on Figure 10 the edges that cross the
region s
u
D
∩ s
D
u
.
5 THE ROUTING ALGORITHM
The guaranteed delivery routing algorithm that we
present in this section combine two different algorithm
in the spirit of classical greedy-face routing algorithm
(Bose et al., 1999; Karp and Kung, 2000). Our routing
algorithm combine two routing modes that we call
sector routing and face routing.
6 SIMULATIONS
In this section we present a comparative analysis
of our geographic routing algorithm with GPSR.
Evaluation is done in a simulation environment, which
purely focuses on routing algorithms, while ideal
radio characteristics and link layer complexities are
abstracted. As mentioned earlier, schnyder’s criteria
should be applied to planarize the graph. Therefore
in the simulations, we compare our algorithm over
schnyder planarization along with our algorithm
against the GPSR over Gabrial Graphs and Relative
Neighborhood Graphs. We analyze the classical metric
namely the stretch f actor which is commonly used in
performance analysis of geographic routing. Stretch
factor represents the ratio between the number of hops
required by the geographic routing over the shortest
path from the source to the destination node.
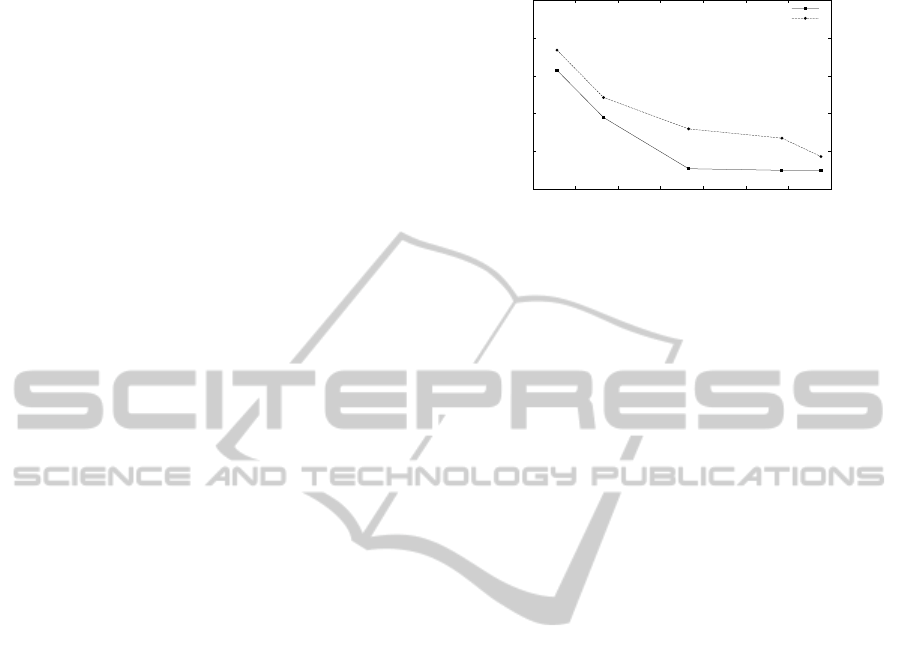
6.1 Stretch Factor
We perform simulations varying the node density
within an area of 400 x 400. Radio ranges of nodes
are set to be 50 units and nodes are spread uniformly
throughout the area. Shortest path is found between
two randomly selected source and destination nodes in
the randomly deployed topology using the Dijkstra’s
algorithm in a centralized manner. Note that we do
not perform better compared to GFG on a euclidean
plane. But we emphasis the trade-off between cheap
localization schemes like VRAC and relatively low
stretch factor performance.
7 CONCLUSION
Geographic routing over virtual coordinate systems
has studied extensively as an alternative to real
localization systems. Despite of the numerous
proposals mostly in theoretical perspectives, their
practical realisable is questionable due to unfavorable
computations required. Use of raw distance measures
from a set of anchors as the coordinate like in VRAC,
SENSORNETS2014-InternationalConferenceonSensorNetworks
202

Input: A tuple (i, u, v, D, modeGreedy, modeFace),
s = node that initiate the current face routing, u =
past node, v = current node, D = destination node,
the mode indicators are boolean.
Initialization: u = nil, v = current node,
modeGreedy= true, modeFace= false.
Output: Select the next node w and set the mode
indicators modeGreedy, modeFace.
if N
v
=
/
0 then return error // disconnected node
if modeGreedy then select w ∈ s
v
D
∩ s
D
v
∩ N
v
//
selection mechanism is free
if w 6= nil then return
(i, v, w, D, modeGreedy, modeFace)
else modeFace = true
if modeFace then
if modeGreedy then // here we start Face
routing
modeGreedy=false
select w ∈ N
v
for x ∈ N
v
do
w =nextto(v, D, w, x)
return (v, v, w, D, modeGreedy, modeFace)
else // here we continue face routing
if s
i
D
∩ s
D
i
∩ N
v
6=
/
0 then // we switch to
Greedy routing
select any node w in the intersection
modeGreedy = true, modeFace = false
return
(nil, nil,w,D, modeGreedy, modeFace)
else
if w ∈ N
v
and | N
v
|= 1 then return
(i, v, w, D, modeGreedy, modeFace)
else select w ∈ N
v
for x ∈ N
v
\ {w}
w =FaceNextEdge(v, u, w, x)
if v → w
satisfy one of the conditions (2) then //switch the
face
return
(i, w, v, D, modeGreedy, modeFace) // v routes data
else
return
(i, v, w, D, modeGreedy, modeFace)// continues
Figure 11: Implementation of the routine
FaceNextEdge(u,v,w,z).
posed to be promising mainly due to its simplicity
offered in wireless sensor network environments.
Even though, partial nature of geographic information
carried by VRAC coordinates make geographic
routing not so trivial. Especially in the absence
of fundamental geometric concepts like angle and
distance, raw coordinate systems require a different
approach to perform geographic routing algorithms.
0
2
4
6
8
10
2 3 4 5 6 7 8 9
Stretch Factor
Average Node Degree
Stretch Factor
GFG + Gabrial
VRAC Routing + Schnyder
Figure 12: Stretch factor vs node density for VRAC and
Euclidean coordinate systems.
In this paper we take a combinatorial approach to
construct basic properties needed to perform both
greedy and face routing phases. Further more we
prove that, based on those constructs it can perform
delivery guaranteed face routing in arbitrary graphs.
We evaluate our approach with standard geographic
routing algorithm GPSR comparing the stretch factor.
As the first attempt in this line of research towards
geographic face routing, we further believe that the
combinatorial constructs could demonstrate resilience
towards erroneous distance measures. Further more
we believe that, with future contributions our approach
would be a candidate with real wireless sensor network
characteristics.
REFERENCES
Bose, P., Morin, P., Stojmenovi
´
c, I., and Urrutia, J. (1999).
Routing with guaranteed delivery in ad hoc wireless
networks. In Proceedings of the 3rd international
workshop on Discrete algorithms and methods for
mobile computing and communications, DIALM ’99.
Fang, Q., Gao, J., Guibas, L. J., Silva, V., and Zhang, L.
(2005). Glider: Gradient landmark-based distributed
routing for sensor networks. In Proceedings of the
24th Conference of the IEEE Communication Society
INFOCOM.
Fonseca, R., Ratnasamy, S., Zhao, J., Ee, C. T., Culler, D.,
Shenker, S., and Stoica, I. (2005). Beacon vector
routing: scalable point-to-point routing in wireless
sensornets. In Proceedings of the 2nd conference
on Symposium on Networked Systems Design &
Implementation - Volume 2, NSDI’05.
Huc, F., Jarry, A., Leone, P., and Rolim, J. (2010).
Virtual raw anchor coordinates: a new localization
paradigm. In Proceedings of the 6th international
conference on Algorithms for sensor systems, wireless
adhoc networks, and autonomous mobile entities,
ALGOSENSORS’10.
Huc, F., Jarry, A., Leone, P., and Rolim, J. D. P. (2012).
CombinatorialApproachforGeographicRoutingwithDeliveryGuarantees
203

Efficient graph planarization in sensor networks and
local routing algorithm. In DCOSS ’12.
Karp, B. and Kung, H. T. (2000). Gpsr: greedy perimeter
stateless routing for wireless networks. In Proceedings
of the 6th annual international conference on Mobile
computing and networking, MOBICOM ’00.
Li, Y., Yang, Y., and Lu, X. (2010). Rules of designing
routing metrics for greedy, face, and combined
greedy-face routing. IEEE Trans. Mob. Comput., 9(4).
Rao, A., Ratnasamy, S., Papadimitriou, C., Shenker, S.,
and Stoica, I. (2003). Geographic routing without
location information. In Proceedings of the 9th annual
international conference on Mobile computing and
networking, MOBICOM ’03.
Ratnasamy, S., Karp, B., Shenker, S., Estrin, D., Govindan,
R., Yin, L., and Yu, F. (2003). Data-centric storage in
sensornets with ght, a geographic hash table. MONET.
Samarasinghe, K. and Leone, P. (2012). Geographic routing
with minimal local geometry. In ICPADS ’12.
Schnyder, W. (1989). Planar graphs and poset dimension.
Order, 5(4):323–343.
Shang, Y., Ruml, W., Zhang, Y., and Fromherz, M.
P. J. (2003). Localization from mere connectivity.
In Proceedings of the 4th ACM international
symposium on Mobile ad hoc networking & computing,
MOBIHOC ’03.
SENSORNETS2014-InternationalConferenceonSensorNetworks
204