A New Flexible Method for Advising Metamodel Matching

Lamine Lafi

, Jamel Feki

and Slimane Hammoudi

University of Gabès, Laboratory Miracl, Gabès, Tunisia

University of Sfax, Laboratory Miracl, Sfax, Tunisia

ESEO, Ecole Supérieure de l’Ouest, Angers, France

Keywords: Metamodel Matching, Metamodel Benchmarking, Decision Tree, Expert Assistance, Score Measure.

Abstract: One relevant issue in metamodel matching is how to select the most suitable matching technique to execute

for a given couple of metamodels, and how to adjust parameters (e.g., threshold, F-measure, quality). In this

paper, we present a flexible method for selecting the most appropriate metamodel matching technique for a

given couple of metamodels. The proposed method assists the user to choose the most suitable matching

technique that provides good quality of matches. This method relies on a new quality metric called Score

and, on using a decision tree. In order to validate our method, we conduct experimental results on ten real-

world metamodels and four recent matching techniques.

1 INTRODUCTION

Matching different data sources (Schema matching,

ontology, and recently metamodel matching) has

become a critical issue to enable the generation of

transformation rules in the Model Driven

Engineering (MDE) technology. However, some

processes needed for these matching and

transformation cannot be entirely automated due to

their complexity. Among these processes, one

relevant is mapping which became, since more than

a decade, a main topic of research in order to its

automation (Kappel, 2007), (Falleri, 2008-1), (De

souza, 2009), (Garces, 2009). It tackles the problem

of finding correspondences between elements of two

metamodels (Lopes, 2006). In the literature, several

issues around MDE have been studied and subjected

to intensive research, e.g. modeling languages

(Bézivin, 2004), (Blanc, 2005), model

transformation languages (OMG, 2005), mapping

between metamodels (Hammoudi, 2005).

Many efforts have been invested over the past

two decades to develop software tools for mapping

metamodels; the proposed tools aim to automatically

discover mappings between metamodel elements.

However, they perform matching based on specific

criteria, such as large-scale scenario (i.e., size of

metamodels, metamodels type, user preferences ....)

or complex mapping discovery (i.e., inequivalence

size of metamodels, metamodels from different

area).

Unlike research on alignment patterns (Rahm,

2001), (Do, 2007) or ontologies (Shvaiko, 2005),

(Feiyu, 2007), (Rosoiu, 2011), and to the best of our

knowledge, there is lack of platforms for evaluating

these tools in order to compare their results and

identify those best suited for a given scenario (i.e.,

couple of metamodels to be matched). This situation

does not facilitate, for a given scenario, the choice of

an appropriate matching technique that finds the

maximum of good correspondences between

metamodel elements. In a previous work (Lafi,

2013-1), we have proposed a software tool for the

assessment of metamodel matching techniques.

However, this tool lacks a feature to recommend

to the expert-user a matching technique that finds

the best matches for a given matching scenario. To

overcome this shortcoming, we define a new quality

measure called Score which aims to assist the

expert-user to select one among several available

matching techniques; i.e., the technique that

produces good results.

This new Score quality measure is calculated

based on conventional similarity measures (i.e.,

Precision, Recall, F-measure and Overall). Then, in

order to exploit the different values of the Score

metric by several combinations of scenarios with

matching techniques, we elect the concept of

decision tree. The use of decision tree will help

deciding what technique of matching is more

376

Laﬁ L., Feki J. and Hammoudi S..

A New Flexible Method for Advising Metamodel Matching.

DOI: 10.5220/0004714903760383

In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 376-383

ISBN: 978-989-758-007-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

suitable, and then recommended it, for a metamodel

matching scenario.

This paper is organized as follows: Section 2

positions our work and motivates our contribution

for metamodel matching techniques planner. Section

3 overviews the proposed method to assist expert-

users to select a suitable matching technique for a

given scenario. It focuses on the definition of the

new Score measure and decision tree, in addition to

highlighting their usefulness. The experimental

results showing the effectiveness of our method are

presented in Section 4. Finally, Section 5

summarizes our contribution and suggests some

immediate perspectives.

2 RELATED WORK

AND MOTIVATIONS

The problem of finding mappings between database

schemas (Rahm, 2001), (Shvaiko, 2005), (Do,

2007), ontology alignment (Feiyu, 2007), (Rosoiu,

2011), XML schemas or documents and more

recently between metamodels (Kappel, 2007),

(Falleri, 2008-1), (De souza, 2009), (Chukmol,

2005) has been widely addressed during the last

decade. However, there are few works that

addressed the evaluation of metamodel matching

techniques as (Lafi, 2013-1), (Lafi, 2011). In

(Kappel, 2007), the authors propose an approach

called “lifting”, allowing transforming the source

and target metamodels into equivalent ontologies.

This approach proposes a framework for metamodel

matching thanks to a transition of ModelWare into

OntoWare. Once the matching task is over, the

transition of the ontology mapping into a weaving

model is performed. In the same work (Kappel,

2007), the authors concentrate on evaluating

schema-based matching tools. Indeed, they are using

the data provided by metamodels (Element-level)

but not data issued from models (instance-level) to

find equivalences between metamodels elements.

In (Falleri, 2008-1), before applying the

Similarity Flooding (SF) alignment algorithm, a

transformation phase is required; it transforms the

source and target metamodels into directed labeled

graphs called graph source (Gsource) and graph

target (Gtarget) respectively. Along this

transformation phase a set of six strategies to encode

the metamodel into such a graph has been suggested.

In this paper, we restrict ourselves to only three

among these six strategies namely: Standard,

Saturated, and Flattened. We have elected these

strategies since they give the best quality measures

according to (Falleri, 2008-1). SF is a generic

alignment algorithm that allows calculating the

correspondences between the nodes of two labeled

graphs (Melnik, 2002). It is based on the following

intuition: If two nodes stemming from two graphs

have been determined as similar, therefore there

would be strong opportunities for the neighboring

nodes to be similar too. SF applies five successive

phases on the input labeled graphs and then

generates an alignment between a source metamodel

and a target metamodel.

The contribution of (De souza, 2009) to this field

of metamodel matching is an algorithm that uses

structural comparison between a class and its

neighboring classes in order to select equal or

similar classes from the source and target

metamodels. This algorithm is an extension and

enhancement of the algorithm presented in

(Chukmol, 2005); it is implemented in the Semi-

Automatic Matching Tool for Model Driven

Engineering (SAMT4MDE) which is capable of

semi-automatically creating mapping specifications

and making matching suggestions that can be

evaluated by expert-users. This provides more

reliability to the matching process which becomes

less error-prone. The Extended Semi-Automatic

Matching Tool for Model Driven Engineering

(SAMT4MDE+) can identify structural similarities

between metamodels elements. However, elements

are matched based on their structure without sharing

the same meaning; this may leads to semantic

mismatches. This lack about element meaning leads

the tool to find false positives, i.e., derived

unrealistic correspondences.

AtlanMod Matching Language (AML) is a

model adaptation technique that adapts models in

three steps (Garces, 2009). In the first step, AML

computes equivalences and changes between two

input metamodels MM1 and MM2. The second step

translates the output of the previous step into an

adaptation transformation using HOT model

transformations (High Order Transformations).

Finally, the adaptation transformation is executed to

produce a mapping model.

To conclude with this state of the art, we notice

despite most of these approaches use techniques that

improve the measures of quality and the reliability

of the matching process, no attempts have been

made so far towards a comparative study of these

techniques. This had motivated us to propose an

approach for the evaluation of metamodel matching

techniques and benchmarking (Lafi, 2013-1) where

the first step was the design of the whole

ANewFlexibleMethodforAdvisingMetamodelMatching

377

architecture for this approach. This architecture has

two main components: i) Metamodel matching

evaluation and benchmarking, and ii) Generation of

transformation rules. In particular, we discussed

various aspects that contribute to the match quality

obtained as the result of an evaluation. Recently, we

have compared four recent metamodels matching

techniques to build the prototype M

BenchMatch

(MetaModel Benchmark Matching tool) of our

benchmark presented in (Lafi, 2013-2). However,

BenchMatch software tool has a main drawback:

it does not assist the expert-user to select a matching

technique that guarantees good results for a given

matching scenario. In this paper, we continue to

enrich our benchmark with adding a new feature that

addresses the user-expert assistance. In addition, we

can incrementally build a complete repository of

metamodel matching techniques and news

metamodels.

In this paper we are particularly interested in

studying how to assist the expert-user in selecting

the process of metamodels matching. In short, we

aim to advise a well-founded decision for the

following question: What technique should be

adopted for a given pair of input metamodels to be

matched?

For this assistance we propose a generic method

which has the merit to be extensible to new

evaluation criteria, new metamodel matching

techniques, new quality metrics. It is based on a new

measure called Score and the usage of decision trees

(c.f., Section 3.1). The necessity of defining the

Score measure was dictated by the conclusions

drawn from our previous works (Lafi, 2013-1),

(Lafi, 2013-2).

3 OVERVIEW

OF THE PROPOSED METHOD

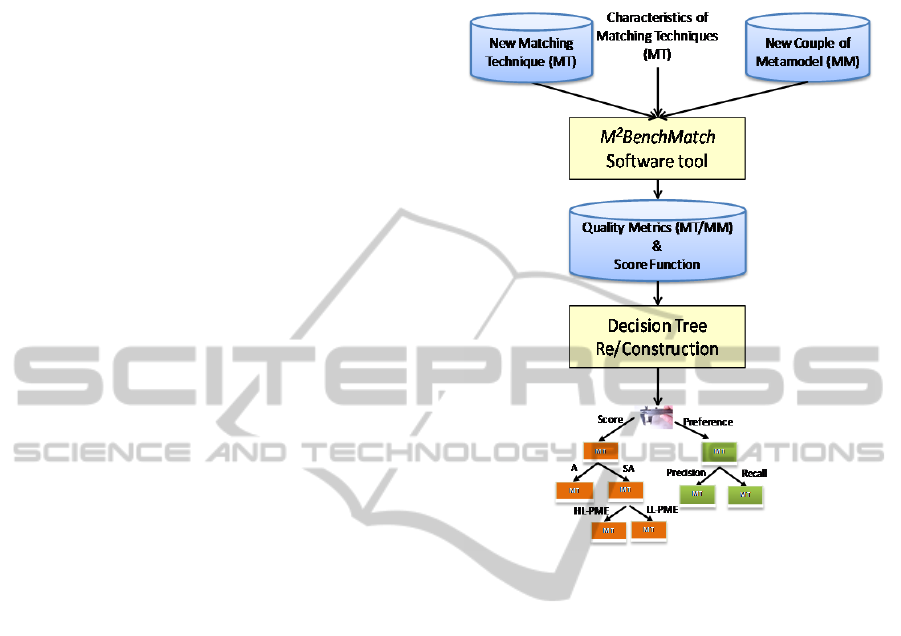
Figure 1 depicts the proposed method for assisting

the user to choose a suitable matching technique for

a given scenario. This method is built on the

BenchMatch tool (Lafi, 2013-2), (Lafi, 2013-3)

for the assessment of metamodel matching

techniques.

BenchMatch accepts as input a set of one or

several couples of metamodels noted MM (c.f.,

Figure 1), a set of one or several matching

techniques MT (c.f., Figure 1), and all their

characteristics. As output, it returns a set of quality

metrics for each combination MM-MT (Lafi, 2013-

1), (Lafi, 2013-3), even when one or both of the

couple of metamodels or the matching technique are

newly inserted into the tool.

Figure 1: Decision Tree Construction.

These quality measures are very useful for

Re/construction of the decision tree which will be

used to assist the expert-user to choose the most

appropriate matching technique for a given scenario

(i.e., available couple of metamodel, new couple of

metamodel). Initially in our M

BenchMatch tool we

have studied four techniques ModelCVS, SF,

SAMT4MDE+ and AML applied on ten well known

couples of metamodels. For the first two techniques

the Ecore Alignment model is obtained immediately

after the execution of the matching process, whereas

for SAMT4MDE+ and AML the matching process

produces a first mapping model which will be

updated, adapted and validated by the expert-user.

We can advise that mapping model allows the expert

to accept, discard or modify the obtained mappings,

along with specifying correspondences which the

matcher was unable to find. It produces the Ecore

Alignment model ready for the generation of a

complete evaluation. The Evaluation enables the

expert to compare the results of several matching

techniques applied on the same pair of input

metamodels. It is based on quality metrics

(Precision, Recall and F-measure) (Do, 2002) in

order to identify the appropriate matching technique

MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

378

that guarantees the generation of good results. The

Comparison with a reference is useful when the

expert assesses a new metamodel matching

technique or a new couple of metamodel in order to

incorporate and add it into the repository of

BenchMatch. So when the expert-user would like

to add and evaluate a new couple of metamodel, the

matching process will be executed on the four

techniques available on M

BenchMatch tool, in

order to produce all quality metrics with all

techniques, this latter helps to the Re-construction of

the decision tree. In the same way, when new

matching technique should be added by the expert-

user to our tool, then this new technique will be

executed on all pairs of metamodels. The news

quality measures obtained are very required to the

Re-construction of the decision tree. In our case, the

decision tree is deduced from quality metrics values

obtained after the execution of matching algorithms

in previous evaluation. It can be also built according

to a new measure that we have called Score (c.f.,

Section 3.2).

3.1 Advantages of using Decision Tree

Several advantages of decision trees have been

pointed out in the literature (Quinlan, 1987),

(

Rokach, 2010); mainly, they

 Are often used in context of identifying a strategy

most likely to reach a goal, by modeling decisions

and probable outcomes. In addition, they are easy

to understand and interpret,

 Are self explanatory and when compacted (i.e.,

having a reasonable number of leaves) they

become easy to follow,

 Can handle both nominal and numeric input

attributes,

 Furthermore decision trees can be converted into a

set of rules.

Now, if we want to illustrate the construction of

decision tree based on quality metrics, then two

alternatives are offered: i) Score-Measure based

construction (c.f., Section 3.2 and Section 4.1), and

ii) preference based construction where the expert-

user favors a measure among Precision, Recall and

F-Measure (α) (c.f., Section 4.2).

3.2 Score Measure

In order to assist the expert-user to choose one of the

metamodel matching techniques, we develop a new

measure called Score (c.f., formula (5)) that

estimates the effectiveness of each metamodel

matching technique. The calculation of this Score is

based on the four well-known measures (Do, 2002):

Precision, Recall, F-Measure and Overall. We

remember each of them hereafter:

Precision 

||



||







It reflects the share of real correspondences among

all found ones.

Recall 

|B|

|B|

(2)

It specifies the share of real correspondences that are

found.

FMeasure

2∗|B|











|C|



2∗

Precision∗Recall

Precision Recall

(3)

Overall  Recall∗ 2

Precision



(4)

To define the Score measure we have elected the

Precision, Recall and Overall; we have intentionally

excluded the F-Measure since it is non basic, i.e.,

derivable from Precision and Recall (c.f., formula

(3)). In the calculation of the Score, the three

measures are weighted. By default, the component

measures of the Score are equally weighted (1/3).

However, in practice, this default weight could

be changed by the skilled user to raise the role of

one among these measures (c.f., Figure 3). In such a

case, the Score will be reevaluated on all couples of

metamodels available in the benchmark in order to

find out one candidate technique.

Scorei,

|Vm



|∗W









(5)

With:

n is the number of conventional measures used

in the calculation of Score.

Wj represents the weight for measure j, with Wj

 [0, 1].

W



1.





Its default value is 1/n.





is the value of measure j obtained for a

couple k of metamodels and a matching technique i.

This value comes from the benchmark (Lafi, 2013-

2), (Lafi, 2013-3). For some techniques applied on

certain pairs of metamodels the Overall measure is

negative (mainly when precision value is < 0.5); this

can affect the Score values and then decreases the

assistance of the expert. The absolute value |Vm



alleviates this problem.

For a given couple of metamodels, thanks to the

Score, we are able to advise an appropriate matching

ANewFlexibleMethodforAdvisingMetamodelMatching

379

technique (i.e., that provides ‘good’ satisfaction) to

the expert-user according to their settings for

weights.

If a pair of metamodels has the maximum value

of Score throughout several matching techniques,

BenchMatch interacts with the expert-user

advising him which technique is preferable; to do so,

(s)he should enter their preferences (e.g., automatic

or semi-automatic matching technique, high or low

level of post-matching effort).

In addition to the Score, we use a second

measure called F-Measure (α) introduced in (Van

Rijsbergen, 1979); it is useful to recommend

metamodels matching techniques relying the

decision on the Precision and Recall.

3.3 F-Measure (α)

F-Measure (α) is an α-weighted generic combination

of the Precision and Recall; it is adopted from the

information retrieval domain (Van Rijsbergen, 1979)

and defined by formula (6).

FMeasure







Precision∗Recall



1α



∗ Precisionα∗Recall

(6)

Where α  [0, 1] and indicates the importance we

wish to grant to Precision and Recall. The more the

value of α is high the more the Recall is considered

important than the Precision, and inversely. In

particular if α = 0 then F-Measure (α) = Recall,

whereas when α = 1 then F-Measure (α) = Precision.

Note that F-Measure (α)  [0, 1].

In (Falleri, 2008-1) , and in order to select the

most appropriate configuration among the six

configurations of the SF metamodel matching

technique, the authors have set the value of α to 0.5;

thus granting the same importance for Precision and

Recall.

In the remaining of this paper, we will use the

Score and F-Measure (α) in order to assist the

expert-user to select a metamodel matching

technique for a given scenario. This assistance will

use decision tree.

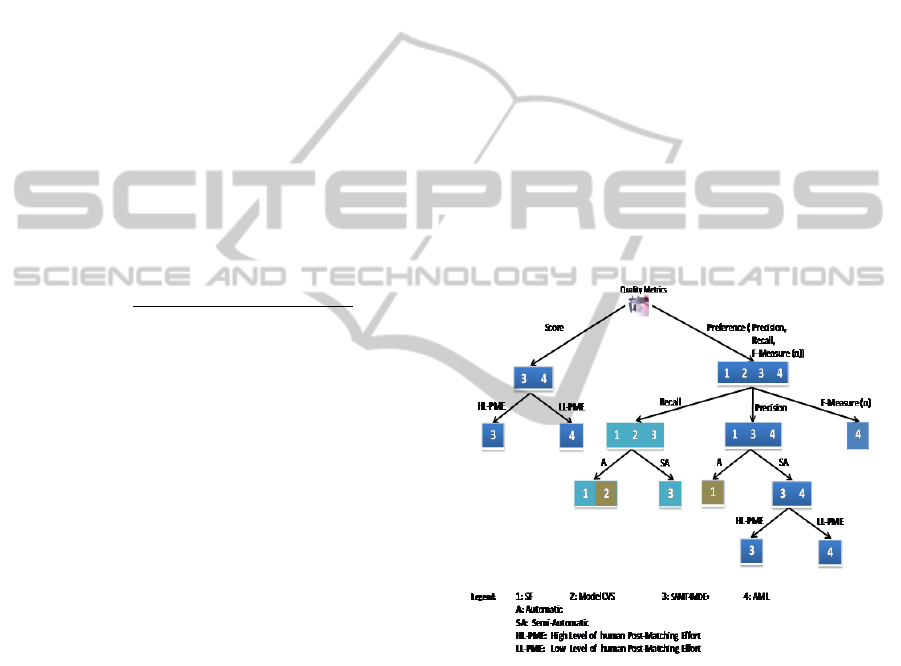
3.4 Decision Tree for Matching

Technique Selection

To decide which metamodel matching technique is

suitable for a given pair of metamodels to be

matched, we elaborate one decision tree on the basis

of the quality measures (c.f., Figure 2).

In this decision tree, each internal node

represents a name of a MM matching technique, and

an edge between two nodes from n

to n

stands for a

condition to move from n

to n

As depicted in Figure 2, two branches are

allowed: Score branch (left) of the tree (i.e., where

the Score is calculated using a default value of

weight Wj=1/3; c.f., Formula (5)) and Preference

branch (right) of the tree (i.e., where the expert-user

can be assisted based on Precision, Recall or F-

Measure (α) according to his choices). Following

the left branch, techniques numbered 3 and 4 (resp.

SAMT4MDE+ and AML) are always recommended

according to the level (high or low) of human Post-

Matching effort desired by the expert-user.

On the other hand, for the Preference branch,

four techniques numbered 1, 2, 3 and 4 are

recommended (resp. SF, ModelCVS, SAMT4MDE+

and AML). Follow this right branch; three decisions

can be made according to whether the expert-user

favors the Recall, the Precision or F-Measure (α).

For instance, favoring the Recall then three

techniques are advised: SF (1), ModelCVS (2) and

SAMT4MDE+ (3).

Figure 2: Decision Tree based on Quality metrics.

Note that both techniques SF and ModelCVS

produce good results for certain scenarios (with

some couples of metamodels and/or for certain

configurations of SF). Nevertheless they sometimes

produce poor results, even very low with

ModelCVS.

For instance, if the expert-user gives more

importance to Precision for example

Precision=50%, Recall= Overall=25%, then this

preferences will be represented in the right branch of

the following decision tree (c.f., Figure 3).

MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

380

Figure 3: Score and Default Score Decision Tree.

3.5 Assisting the Matching

of Metamodels via Decision Trees

The kernel of traditional matching tools is the

aggregation measure, which combines the similarity

values computed by different matching techniques.

As this aggregation measure suffers from several

drawbacks (c.f., section 2), our idea consists in using

a decision tree instead.

Given a new couple of metamodels to be

matched, our objective is to select and then apply the

most appropriate matching technique for this couple;

i.e., the matching techniques that gives good

matching result. To do so, we appeal to decision

tree. Decision trees are used in similar contexts in

(OMG, 2005), they assist the expert-user during the

selection of the best matching technique.

The decision and selection of the suitable

matching technique are based on the quality metrics

which are also influenced by the input metamodel

size and the characteristics of each technique. This

decision satisfies the condition and criteria on the

edges that aims to access a next node when other

criteria or preferences need to be considered when

matching two metamodels using decision tree.

According to this tree, the edge for which its

condition is satisfied leads to the next tree node.

This process will iterate until a leaf node is reached,

indicating whether the matching technique should be

recommended or not.

4 DEMONSTRATION

AND EXPERIMENTS

In order to assist the expert-user for a given scenario

or comparison of metamodel matching techniques,

we conduct an experimental evaluation based on the

decision tree of figure 2. More accurately, we

experiment the four techniques ModelCVS, SF,

AML and SAMT4MDE+ on the ten couples of

metamodels below, described in (Walderhaug,

2006), (Kappel, 2006), (Falleri, 2008-2), (Budinsky,

2003), (OMG, 2003) and (Fleurey, 2009):

Table 1: Ten couples of Metamodels.

Couples of Metamodels Size*

Ecore2Minjava2.0 Large

Ecore2UML Large

Webml2ODM Small

traceabilityToolMM2traceRepository Medium

etrace2traceabilityToolMM Medium

Ecore2UML2.0 Large

BibTeXA2BibTeXB Small

Ecore2Minjava Large

Ecore2Kermata Large

Minjava2Kermata Large

(*) The size of a metamodel is the number of its elements

(Classes, data type…). Small: size <80; Medium: 80≤size<150;

Large: size≥150.

We are interested in these four techniques since they

are recent and accessible through their software

tools.

Note that both AML and SAMT4MDE+ enable

the expert to intervene and improve the matching

automatically obtained. Therefore, in order to insure

that the evaluation is conducted in the same

conditions for the four matching techniques we

exclude expert interventions during these two

techniques. This implies that matching results are

not influenced by the expert skills. To conduct this

evaluation, we provide two alternative measures for

assisting the expert-user: i) Score-based (c.f.,

section 4.1), and ii) F-Measure (α)-based (c.f.,

section 4.2).

4.1 Score-based Measure for Assisting

the Expert-user

Note that in our experiment we have chosen a

default weight Wj = 1/3 for the three measures

precision, recall, and overall in calculating the

Score. If an expert-user wishes to privilege one of

these three measures (e.g, accuracy, indicating that

the correct number of mappings is more important to

him) in Score calculation then he can set different

weights. This is done through Score calculation

using different weight.

Figure 4 shows the values of Score obtained for the

four metamodel matching techniques. We note that

ANewFlexibleMethodforAdvisingMetamodelMatching

381

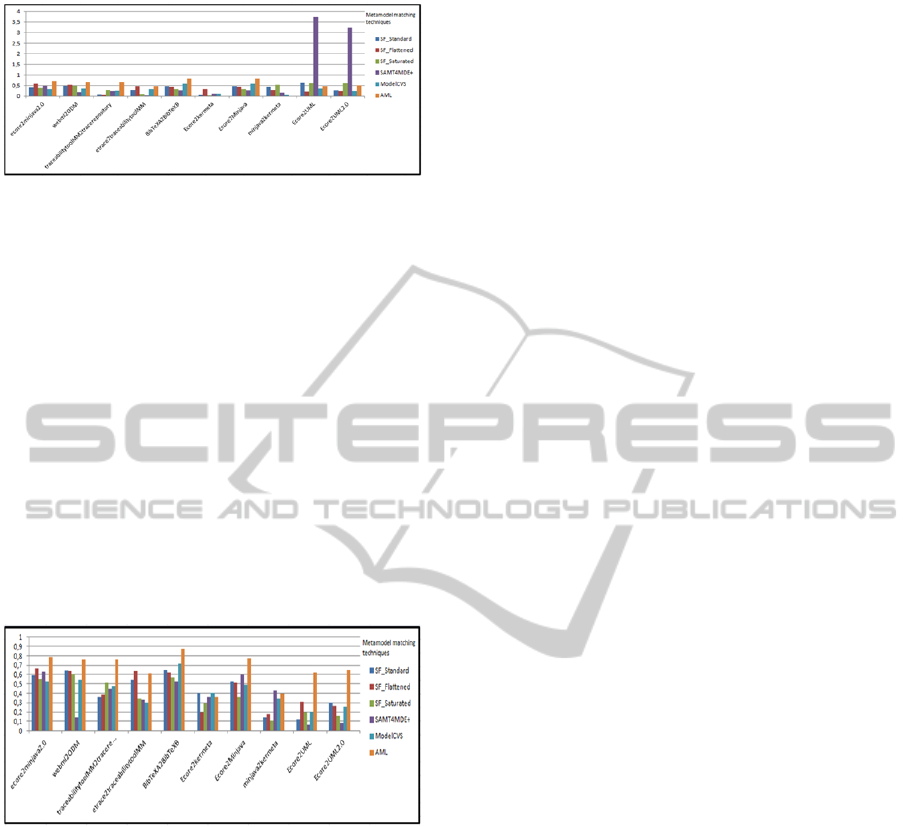
Figure 4: Score values produced with four techniques on

ten couples of metamodels.

the SAMT4MDE + technique gives the highest

Score for the two couples of metamodels

Ecore2UML and Ecore2UML2.0. For the other

couples, the AML technique has best Score values.

4.2 F-Measure (α) for Assisting

the Expert-user

The F-Measure (α) measurement (cf., formulas (6))

is presented on the right branch of the decision tree

(c.f., Figure 2) by the label preferences (Precision,

Recall, F-Measure (α)). In this section we restrict

ourselves only to the curve F-Measure (α), since

Precision, Recall have been presented in (Lafi, 2013-

1) and then used during the construction of tree.

Figure 5: F-Measure (0.5) values produced with four

techniques on ten couples of metamodels.

After testing we found that AML gives the best

value of F-Measure (α) with most pairs of

metamodels. Comprehensive results obtained by this

technique are listed in Figure 5. At the end of these

experiments, we recommend the technique AML,

because that the results of the various measures are

good in the most part case (F-Measure (α) close to 1;

Score greater than 0.5).

Note that these results appear to be more

important than those obtained through the alignment

of XML schemas or ontologies. This is due to the

intervention of the expert-user to correct, adapt and

validate the suggestions of mapping produced by the

technique SAMT4MDE+.

5 CONCLUSIONS

Metamodel matching stands for the keystone of the

semi-automatic transformation process. In this

paper, we have tackled one problematic closely

related to this issue; indeed our objective was to

assist expert users to select an appropriate matching

technique for a given couple of metamodels to be

matched. In order to reach this objective, we have

presented a novel and flexible methodology for

metamodel matching assistance; it relies on i) the

definition of two new measures called Score, F-

Measure (α), and ii) the use of decision tree. The

Score measure reuses the standard quality metrics

(Recall, Precision…); it is returns a bonded value (in

the range [0.1]) evaluating the efficiency of applying

a given matching technique on a pair of metamodels.

Whereas the decision tree concept is adopted to

determine the most appropriate technique among all

matching techniques available within our

BenchMatch software tool (Lafi, 2013-2). Based

on these two elements, the proposed flexible method

improves matching quality. The flexibility comes

from the flexibility of the Score function. Actually,

two strategies are offered for the calculation of the

Score according to whether the expert wants to

privilege the standard Recall measure or not.

REFERENCES

Bézivin, J., Hammoudi, S., Lopes, D., Jouault, F.:

Applying MDA Approach for Web Service Platform.

8th IEEE International Conference on EDOC.

Monterrey California, USA. pp. 58--70 (2004).

Blanc, X (Ed.1): MDA en action, Ingénierie logicielle

guidée par les modèles. Paris, France: EYROLLES

(2005).

Budinsky, F., Brodsky, S. A., Merks, Ed.: Eclipse

modeling framework. Pearson Education (2003).

Chukmol, U., Rifaiem, R., Benharkat, N.: EXSMAL:

EDI/XML Semi-Automatic Schema Matching

Algorithm, Proceedings of the Seventh IEEE

International Conference on ECommerce Technology,

IEEE Computer Society, 422--425 (2005).

De Sousa, J., Lopes, D., Barreiro, C. D., and Abdelouahab,

Z.: A Step Forward in Semi-automatic Metamodel

Matching: Algorithms and Tool. In: Filipe, J.,

Cordeiro, J. (eds.) Enterprise Information Systems.

LNBIP, vol. 24, pp. 137--148. Springer, Heidelberg

(2009).

Do, H. H., Erhard R.: Matching large schemas:

Approaches and evaluation. Inf. Syst. 32 (6): 857--885

(2007).

Do, H. H., Melnik, S., Rahm, E.: Comparison of schema

matching evaluations. In: Web, Web-Services, and

MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

382

Database Systems. LNCS Vol. 2593, pp. 221--237.

Springer (2002).

Falleri, J. R., Huchard, M., Lafourcade, M., C. Nebut.:

Metamodel matching for automatic model

transformation generation. In: Proceedings of

MoDELS’08, pp. 326--340 (2008-1).

Falleri, J. R.: Minjava, http://code.google.com/p/minjava/

(2008-2).

Feiyu L.: State of the Art: Automatic Ontology Matching,

Research Report, School Of Engineering, Jonkoping,

Sweden (2007).

Fleurey, F., Drey, Z., Vojtisek, D., Faucher, C., Mahé, V.

Kermeta Language, Reference Manual. http://

www.kermeta.org/ (2009).

Garces, K., Jouault, F., Cointe, P., Bezivin, J.: Managing

Model Adaptation by Precise Detection of Metamodel

Changes. In: In Proc. of ECMDA 2009, Enschede, The

Netherlands, Springer (2009).

Hammoudi, S., Lopes, D.: From Mapping Specification to

Model Transformation in MDA: Conceptualization

and Prototyping. In MDEIS’2005, First International

Workshop On Model Driven Development, Miami,

USA. pp. 15--23 (2005).

Kappel, G., Kargl, H., Kramler, G., Schauerhuber, A.,

Seidel, M., Strommer, M., Wimmer, M.: Matching

Metamodels with Semantic Systems – An Experience

Report. In BTW 2007, Datenbank systeme in Business,

Technologie und Web, pp. 38--52 (2007).

Kappel, G., Kapsammer, E., Kargl, H., Kramler, G.,

Reiter, T., Retschitzegger, W., Wieland, S., Wimmer,

M.: Lifting metamodels to ontologies: A step to the

semantic integration of modeling languages. In

Nierstrasz et al., pp. 528--542 (2006).

Lafi, L., Feki, J., Hammoudi, S.: Metamodel Matching

Techniques Evaluation and Benchmarking. In

International Conference on Computer Applications

Technology (ICCAT’2013), Sousse, Tunisia. ISBN

978-1-4673-5284-0 (2013).

Lafi, L., Hammoudi, S, Feki, J.: Metamodel matching

techniques in MDA: Challenge, issues and

comparison, in 1st International Conference on Model

& Data Engineering (MEDI’2011), LNCS volume

6918, pp. 278--286, September (2011), Obidos-

Portugal.

Lafi, L., Feki, J., Hammoudi, S.: M

BenchMatch: An

Assisting Tool for MetaModel Matching. In

International Conference on Control, Decision and

Information Technologies (CoDIT'13), Hammamet,

Tunisia (2013-2).

Lafi L., Feki, J., Hammoudi S.,: Metamodel Matching

Techniques: Review, Comparison and Evaluation,

International Journal of Information System Modeling

and Design (IJISMD 2013-3).

Lopes, D., Hammoudi, S., De Souza, J., Bontempo, A.:

Metamodel matching: Experiments and comparison. In

Proceedings of the International Conference on

Software Engineering Advances (ICSEA'06), Tahiti,

French Polynesia (2006).

Melnik, S., Garcia-Molina, Jr. H., Rahm, E.: Similarity

Flooding: A Versatile Graph Matching Algorithm and

Its Application to Schema Matching. In Proceedings

of the 18th international Conference on Data

Engineering (February 26-2002). ICDE. IEEE

Computer Society, Washington, pp. 117--128 (2002).

OMG UML. 2.0 superstructure final adopted specification.

OMG Document reference ptc/03--08, 2 (2003).

OMG. (2005).: MOF QVT Final Adopted Specification,

OMG/2005-11-01.

Quinlan, J. R.: Induction of decision trees. Mach. Learn.,

1(1):81--106 (1987).

Rahm, E., and Bernstein, P.: A survey of approaches to

automatic schema matching. VLDB Journal 10(4): pp.

334--350 (2001).

Rokach, L., Maimon, O.: Decision Trees. A book chapter

of data mining and knowledge discovery handbook

(2010).

Rosoiu, M., Trojahn, C., Euzenat, J.: Ontology matching

benchmarks: generation and evaluation. OM (2011).

Shvaiko, P., Euzenat J.: A Survey of Schema-Based

Matching Approaches. J. Data Semantics IV: pp. 146--

171 (2005).

Van Rijsbergen, C.J.: Information Retrieval. 2nd edition,

1979, London, Butterworths.

Walderhaug, S., Johansen, U., Stav, E., Aagedal, J.:

Towards a generic solution for traceability in MDD.

In ECMDA Traceability Workshop (2006).

ANewFlexibleMethodforAdvisingMetamodelMatching

383