
A Constraint Programming Approach for Managing End-to-end
Requirements in Sensor Network Macroprogramming
Farshid Hassani Bijarbooneh
1
, Animesh Pathak
2
, Justin Pearson
1
,
Valerie Issarny
2
and Bengt Jonsson
1
1
Uppsala University, Department of Information Technology, Box 337, SE-75105, Uppsala, Sweden
2
INRIA Paris, Rocquencourt, France
Keywords:
Sensor Networks, Macroprogramming, Constraint Programming, Non-functional Requirements, Task Map-
ping.
Abstract:
Though several high-level application development (macroprogramming) approaches have been proposed in
literature for wireless sensor networks (WSN), there is a need to enable support for expressing and support-
ing end-to-end non-functional constraints such as latency in WSN macroprograms. We augment an existing
macroprogramming language and its compilation process to enable the specification of end-to-end require-
ments, and propose task mapping algorithms to satisfy those requirements through a constraint programming
approach. Through evaluations on realistic application task graphs, we show that our constraint programming
model can effectively capture the end-to-end requirements and efficiently solves the combinatorial problem
introduced.
1 INTRODUCTION
Sensor network macroprogramming refers to the de-
velopment of Wireless Sensor Network (WSN) appli-
cations at the system level (as opposed to at the node
level), and holds the promise of enabling not just sys-
tems programmers (as is the case today) but also do-
main experts (e.g., architects, biologists, city planners
etc.) to develop WSN applications. A sizeable body
of work exists in this area (Mottola and Picco, 2011),
with programming styles ranging from Haskell-like
functional languages (Newton et al., 2007) to Python-
like imperative ones (Gummadi et al., 2005).
To complement the above, algorithms have been
developed to convert the high level descriptions to
node-level code by solving problems such as optimal
task-mapping in order to satisfy non-functional prop-
erties. While existing approaches focus on system-
wide or node-level goals, such as minimising total
energy consumption or minimising the maximum en-
ergy consumed by any node, work on managing end-
to-end requirements (e.g., minimising the latency be-
tween the sensing of a phenomenon and the resulting
action) in WSN macroprogramming is largely miss-
ing.
The focus of this paper is precisely the above kind
of scenarios, where the developer is interested in min-
imising an end-to-end property while mapping tasks
on the nodes in a particular sensor network deploy-
ment. A classic case would be a highway traffic man-
agement application (e.g., the one used in (Mottola
et al., 2007)), where local regulations might need a
particular deployment to provide guarantees between,
say, the sensing of a traffic jam (speed = 0) and the
actuation of the ramp signals to red in order to stop
more cars from coming in. Similar latency restrictions
apply in the case of, for example, traffic lights con-
trolling access to a railroad crossing (US Department
of Transportation, Federal Highway Administration,
2012).
We base our work on the Abstract Task Graph
(ATaG) macroprogramming language (Bakshi et al.,
2005b), based on the data-driven macroprogramming
paradigm, where the developer breaks up the func-
tionality of their application into tasks that interact
with each other only using the data items that they
produce and consume, and do not share any state oth-
erwise. This technique is shown to be especially use-
ful in specifying a wide range of sense-and-respond
applications (Pathak et al., 2007). ATaG includes an
extensible, high-level programming model to specify
the application behaviour, and a corresponding node-
level run-time support, the data-driven ATaG runtime
(DART) (Bakshi et al., 2005a). The compilation of
28
Hassani Bijarbooneh F., Pathak A., Pearson J., Issarny V. and Jonsson B..
A Constraint Programming Approach for Managing End-to-end Requirements in Sensor Network Macroprogramming.
DOI: 10.5220/0004715200280040
In Proceedings of the 3rd International Conference on Sensor Networks (SENSORNETS-2014), pages 28-40
ISBN: 978-989-758-001-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ATaG programs consists of mapping the high-level
ATaG abstractions to the functionality provided by
DART, thus involving a task-mapping process. While
the ATaG compiler currently supports task-mapping
while optimising node-level energy properties, it does
not have support for end-to-end properties such as la-
tency.
The main related work to ours is (Pathak and
Prasanna, 2010), where the authors optimised task-
mapping for energy-related metrics using an MIP,
and (Hassani Bijarbooneh et al., 2011), which used
constraint programming (CP) (Rossi et al., 2006)
to solve this. In (Tian et al., 2005), the authors
only investigate single-hop homogeneous WSNs. We
consider multi-hop heterogeneous networks including
routing costs. To the best of our knowledge, there has
been no work addressing a CP approach for a general
case of task mapping in a multi-hop WSN achieving
end-to-end latency optimisation under routing costs.
Works such as the one by Wu et. al., in (Wu et al.,
2010) are complementary to this, since they perform
runtime evaluation of the WSN, while we focus on
providing feedback to the developer before deploy-
ment. Note that the task mapping problem with end-
to-end requirements is different from those encoun-
tered in traditional distributed systems such as clus-
ters, since in our work, there is a strong relationship
between the physical regions and the sensor nodes, as
well as the constraints enforced by the end-to-end re-
quirements between the tasks and the sensor nodes.
The main contributions of this paper are i) The
formulation of the task-mapping problem arising
out of the need to satisfy end-to-end constraints in
WSN macroprogramming; ii) Constraint program-
ming techniques to solve the latency problem; and
iii) Extension of the approach to address situations
where replication of tasks is allowed to improve la-
tency performance.
We provide background on the macroprogram-
ming language used in Section 2, followed by the
problem definition in Section 3 and the mathemati-
cal formulation of the optimisation goal in Section 4.
Section 5 presents our CP-based approach, and Sec-
tion 6 discusses the results of our evaluation on a re-
alistic traffic-management application. Section 7 con-
cludes.
2 BACKGROUND
For completeness, in this section we provide some
background on the programming model and compi-
lation process of ATaG programs, as well as the mod-
ifications we have made to the language. For more
TemperatureSampler
AverageTemperature
Calculator
Temperature
every(attachedSensors,
TempSensor)
periodic: 10
oncein(Floor)
anydata
(1,Floor)
Figure 1: ATaG program for data-gathering.
complete details of ATaG, we refer the readers to the
work in (Pathak and Prasanna, 2011).
2.1 Programming Model
ATaG provides a data driven programming model
and a mixed imperative-declarative program specifi-
cation. Developers use a data driven model for spec-
ifying reactive behaviours, and declarative specifica-
tions to express the placement of processing locations
and the patterns of interactions.
The overall structure of computation in an ATaG
program is expressed as a task graph (see Figure 1 for
an example), which consists of the following:
• Abstract Data Items: These represent the in-
formation in the various stages of its processing
through the deployed application.
• Abstract Tasks: These are software entities that
consume and produce instances of abstract data
items. To specify their location and invocation
patterns, they are annotated with instantiation
rules and firing rules respectively.
• Abstract Channels: Abstract tasks and data
items are connected through abstract chan-
nels, which are further annotated with logical
scopes (Mottola et al., 2007), expressing the inter-
est of tasks in only certain instances of data items.
In addition to the above, the developer speci-
fies the internal functionality of each abstract task
in an ATaG program using an imperative lan-
guage such as Java. To interact with the under-
lying runtime system, each task must implement a
handleDataItemReceived() method for each
type of data item that it is supposed to process. The
task can output its data by calling the putData()
method implemented by the underlying runtime sys-
tem.
Figure 1 illustrates an example ATaG program
specifying a data gathering application (Choi et al.,
2004) for building environment monitoring. Sen-
sors within a cluster take periodic temperature read-
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
29

ings, which are then collected by the correspond-
ing cluster-head. The TemperatureSampler task rep-
resents the sensing in this application, while the
AverageTemperatureCalculator task takes care of
the collection and computing the average. The
tasks communicate through the Temperature data
item. The TemperatureSampler is triggered ev-
ery 10 seconds according to the periodic firing
rule. The any-data rule requires AverageTemper-
atureCalculator to run when a data item is ready
to be consumed on any of its incoming channels.
The every(<property>,<value>) instantia-
tion rule requires the task to be instantiated on
each node where the particular property has that
value. E.g., the TemperatureSampler task in the ex-
ample will be instantiated on every node equipped
with a temperature device. Since the programmer
requires a single AverageTemperatureCalculator to
be instantiated on every floor in the building, the
oncein(Floor) instantiation rule is used for this
task. Its semantics is to derive a system partition-
ing based on the values of the node attribute provided
(Floor).
The (1,Floor) annotation on the channel spec-
ifies a number of hops counted in terms of how many
system partitions can be crossed, independent of the
physical connectivity. Since Temperature data items
are to be used within one partition (floor) from where
they generated, they will be delivered to AverageTem-
peratureCalculator instances running on the same
floor as the task that produced them, as well as ad-
jacent floors.
2.2 Compilation Process
In the previous section, we described the ATaG data-
driven macroprogramming paradigm. In this section,
we provide a formal definition of the process of com-
piling data-driven macroprograms to node-level code
using the application given in Figure 1 as an example.
TS ATC
T
TS ATC
Floor 3
Floor 2
Floor 1
Channel
Composition
Task
Instantiation
Figure 2: An example illustrating the compilation process
of our sample program. Task names have been abbreviated.
2.2.1 Input
The input to the compilation process consists of the
following three components.
Abstract Task Graph (Declarative Part): Formally,
an abstract task graph A(AT, AD, AC) consists of a
set AT of abstract tasks and a set AD of abstract data
items. The set of abstract channels AC can be divided
into two subsets – the set of output channels AOC ⊆
AT × AD and a set of input channels AIC ⊆ AD × AT .
Imperative Code for Each Task: As mentioned ear-
lier, each abstract task is accompanied by code that
details the actions taken when data is received by in-
stances of that task.
Network Description: For every node n in the
target network N, the compiler is also given the
list of sensors and actuators attached to the sensor
node n, as well as, a set of (RegionLabel, RegionID)
attribute-value pairs to denote the membership of the
sensor node n in the regions of the network (e.g.,
{(Floor, 5), (Room, 2)}).
Runtime Library Files: These files contain the code
for the basic modules of the runtime system that are
not changed during compilation, including routing
protocols etc.
2.2.2 Output
The compilation process generates a distributed appli-
cation for the target network description commiserate
with what the developer specified in the ATaG pro-
gram. The output consists of the following parts:
Task Assignments: This is a mapping between the
instances of the members of AT onto the nodes in N,
in accordance with their instantiation rules.
The compiler must decide on the mapping to al-
locate the instantiated copies of the abstract tasks in
AT to the nodes in N so as to satisfy all placement
constraints specified by the developer.
Customised Runtime Modules: The compiler must
customise the DataPool of each node to contain a list
of the data items produced or consumed by the tasks
hosted by it. It also needs to configure the ATaGMan-
ager module with a list of composed channel annota-
tions, so when a data item is produced, the runtime
can compute the constraints imposed on the nodes
which are hosting the recipient tasks for it.
Cost Estimates: The compiler also reports on the
non-functional aspects of the final deployed applica-
tion, informing the developer of the cost of executing
application A on a network N. Note that the actual na-
ture of the cost estimates returned can vary depending
on the developer’s needs. This is the place where this
paper builds upon the existing work, by bringing end-
to-end cost estimates also in the compiler’s purview.
SENSORNETS2014-InternationalConferenceonSensorNetworks
30

2.2.3 Process Overview
The overall process takes place in the following steps:
Composition of Abstract Channels: In this step,
each path AT
i
→ AD
k
→ AT
j
in the abstract task graph
is converted to an edge AT
i
→ AT
j
, resulting in a graph
with only task-task edges, keeping the annotation of
the channel AD
k
→ AT
j
.
Instantiating Abstract Tasks: The instantiated task
graph (ITaG) consists of instances of the tasks de-
fined in AT, connected to each other according to the
channel annotations in A. e.g., due to the (1,Floor)
channel annotation, instances of TemperatureSampler
for floor i are connected only to instances of Aver-
ageTemperatureCalculator destined for floors i − 1, i,
and i + 1.
Formally, the ITaG I(T, IC) is a graph whose ver-
tices are in a set T of instantiated tasks and whose
edges are from the set IC of instantiated channels. For
each task AT
i
in the abstract task graph from which I is
instantiated, there are f (AT
i
, N) elements in T , where
f maps the abstract task to the number of times it is in-
stantiated in N. IC ⊆ T × T connects the instantiated
version of the tasks. The ITaG I can also be repre-
sented as a graph G(V, A), where V = T and A = IC.
Additionally, each T
j
in the ITaG has a label indicat-
ing the subset of nodes in N it is to be deployed on.
This overlay of communicating tasks over the target
deployment enables the use of modified versions of
classical techniques meant for analysing task graphs.
For example, for the application in Figure 2,
since there are seven nodes with attached tem-
perature sensors, f (AT
1
, N) = 7, following the
every(AttachedSensors,TemperatureSensor
instantiation rule of the TemperatureSampler task.
Similarly, f (AT
2
, N) = 3, since the AverageTem-
peratureCalculator task is to be instantiated once
on each of the three floors. The figure shows one
allocation of the tasks in T , with arrows representing
the instantiated channels in IC (it shows channels
leading to only one instance of AT
2
for clarity).
Note that the although the ITaG notation captures
the information stored in the abstract task graph
(including the instantiation rules of the tasks and
the scopes of the connecting channels) it does not
capture the firing rules associated with each task. The
compiler’s task involves incorporating the firing rule
information while making decisions about allocating
the tasks on the nodes.
Task Mapping: This task graph with composed
channels is then instantiated on the given target net-
work. Figure 2 illustrates an example of a target net-
work. The nodes are on three different floors, and
those marked with a thermometer have temperature
sensors attached to them. In this stage, the compiler
computes the mapping M : T → N, while satisfying
the placement constraints on the tasks.
Customisation of Runtime Modules: Based on the
final mapping of tasks to nodes, and the composed
channels, the Datapool and ATaGManager modules
are configured for each node to handle the tasks and
data items associated with it.
2.3 Changes to ATaG
For our work, we augment the above in two ways:
1. The abstract task graph now includes end-to-end
non functional requirements. We use latency in
this paper as an example, but our approach is ap-
plicable to other requirements as well.
2. The network description contains probability esti-
mates of the time it takes for messages to be routes
between nodes in same and neighbouring regions.
Using the above, we can reason about applications
such as the Highway Traffic management application
from (Mottola et al., 2007) (shown in Figure 3), and
answer questions such as “Is it possible to deploy this
application in a given city so that whenever the av-
erage speed of a highway sector goes to 0, the ramp
signal for that sector turns red within 1 second with
98% probability?”. The details of the above are dis-
cussed next.
3 PROBLEM DEFINITION
The task mapping problem with end-to-end require-
ments is solved in several steps. In Figure 4 we show
a high-level description of each component involved
in the process of mapping the tasks to the nodes, and
the input and output of our constraint programming
(CP) approach. As explained in programming model
Section 2.1, the developer specifies an abstract task
graph and the rules required to instantiate the tasks.
We preprocess the abstract task graph and instan-
tiate tasks according to the rules specified in the task
graph, which results in instantiated task graph and
placement constraints, as shown in Figure 4, where
the placement constraints enforce a task to be mapped
only to a subset of sensor nodes.
The probability model, provided by the developer,
specifies the delay distribution for sending a message
between nodes in different and the same regions, as
well as rules on how to combine probability distribu-
tions when messages travel more than one hop. This
allows both independent and dependent message de-
lays to be modelled. In our experiments, for simplic-
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
31
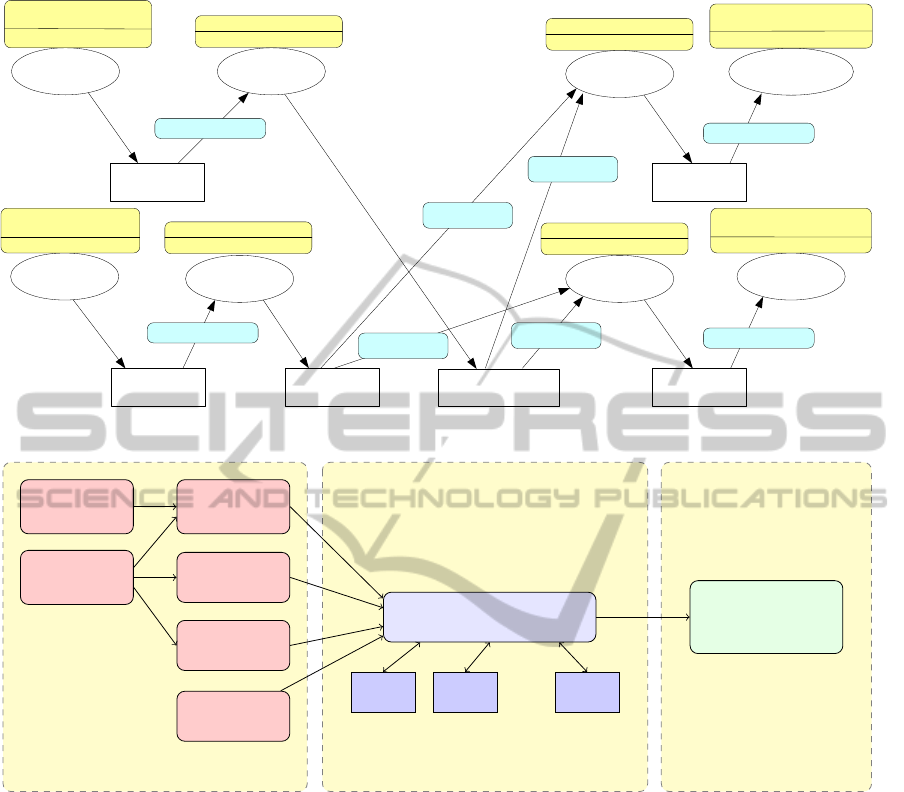
AvgQueueLength
RampSignal
Calculator
RampSignal
RampSignal
Displayer
[every(attachedActuators,
rampSignalActuator)]
[anydata]
AvgSpeed
SpeedLimit
Calculator
SpeedLimit
SpeedLimit
Displayer
[every(attachedActuators,
speedLimitActuator)]
[anydata]
(1, HighwaySector)
RampSampler
VehiclePresence
AvgQueueLength
Calculator
SpeedSampler
RawSpeed
AvgSpeed
Calculator
[every(attachedSensors,
presenceSensor)]
[periodic:10]
[every(attachedSensors,
speedSennsor)]
[periodic:10]
(0,HighwaySector)
[oncein(HighwaySector)]
[anydata]
(1, HighwaySector)
(0,HighwaySector)
(0,HighwaySector)
(0,HighwaySector)
(1, HighwaySector)
(1, HighwaySector)
[oncein(HighwaySector)]
[anydata]
[oncein(HighwaySector)]
[anydata]
[oncein(HighwaySector)]
[anydata]
Figure 3: ATaG Program for the traffic app in (Mottola et al., 2007).
CSP
main
CSP
sub
on path 1
CSP
sub
on path 2
CSP
sub
on path p
·· ·
Network
Description
Abstract
Task Graph
Instantiated
Task Graph
Placement
Constraints
Path Delay
Constraints
Probability
Model
Input
Constraint Programming Model
An Optimal
Mapping of
Tasks to Nodes
Output
Figure 4: Block diagram representing the main components of the task mapping problem with end-to-end requirements.
ity, we have assumed that all distributions are inde-
pendent and normally distributed. In the mathemati-
cal formulation in Section 4, we formulate the aggre-
gation of the delay requirements over the channels.
In our approach, we use a constraint program-
ming model called CSP
main
to perform the compila-
tion process (see Section 2.2). The constraint pro-
gramming model CSP
main
takes the input (instantiated
task graph, placement constraints, and the probability
model), and outputs the optimal mapping from tasks
to nodes. The end-to-end requirements are expressed
in terms of maximum allowed delay between two task
types. For example, we require that the delay for
sending one unit of data between the operational tasks
and the actuating tasks be within a certain threshold.
We first convert the end-to-end requirements into a
set of paths (namely path delay constraints), where
each path includes all the tasks (subset of the instanti-
ated tasks) between the two end-points. The probabil-
ity model should specify how the probability distribu-
tion of the delay is computed along each path, given
a mapping from task to nodes, also it should specify
how the probability distribution of delay is computed
if we replicate the tasks along each path.
In our CSP
main
model, we create one CSP
sub
model per path delay constraint, where the CSP
sub
model solves and returns all the valid solutions (map-
ping of tasks to nodes) for one path delay constraint.
The rules provided in the probability model are used
in the CSP
sub
model to check (in polynomial time)
whether a mapping from the tasks to the nodes along
one path is valid. If the requirements on a path can-
not be satisfied, then we allow the CSP
sub
model to
replicate the operational tasks on the path to improve
SENSORNETS2014-InternationalConferenceonSensorNetworks
32

the probability of receiving the data at the end-point.
The valid solutions returned by CSP
sub
for each path
delay constraints are then composed in the CSP
main
model to find an optimal mapping of the tasks to the
nodes, minimising the number of replicated tasks. In
the next section, we show how CSP
main
and CSP
sub
are modelled, the probability is computed as we repli-
cate tasks, and how the overall problem is solved to
optimality.
4 MATHEMATICAL
FORMULATION
We first instantiate the abstract task on the target net-
work, this process creates several copies of tasks per
region. We then have the following constants in our
model:
• Let N be the set of WSN nodes.
• Let T be the set of instantiated tasks.
• Let A be the set of arcs/edges in the directed
acyclic task graph G = (T, A), with edge (t
i
, t
j
) in-
dicating that instantiated task t
i
is sending data to
task t
j
.
• Let D[t
i
, t
j
] be the random variable representing
the delay for sending one unit of data from the
task t
i
to t
j
, where (t
i
, t
j
) ∈ A (the tasks are on the
same edge of the task graph G).
• Let F
D
[t
i
, t
j
] be the cumulative distribution func-
tion (c.d.f) of the random variable D[t
i
, t
j
].
• Let S ⊆ T be the set of (start) tasks where a trig-
gering event is produced.
• Let E ⊆ T be the set of (end) tasks where pro-
ducing an output within a given latency time is
required.
For each task t let node[t] be the decision variable
denoting the node that task t is mapped to, with t ∈ T
and node[t] ∈ N.
As explained in Section 3, the task mapping prob-
lem with end-to-end requirements consists of place-
ment and path delay constraints. The placement con-
straints enforce that a task may be restricted to a suit-
able subset of the sensor nodes, and therefore it can-
not be mapped to any other node. Such placement
constraints are modelled as follows:
node[t] 6= n for every task t that
cannot be mapped to node n
(1)
The path delay constraints ensure that for every path
in the task graph G starting from the tasks in S and
t
1
t
2
t
3
L[t
1
, t
3
]L[t
1
, t
2
]
D[1, 2] ∼ N(0.5, 1) D[2, 3] ∼ N(0.5, 1)
Figure 5: A path from the task t
1
to t
3
via task t
2
in the task
graph, and the delay random variable D[1, 2] and D[2, 3] for
the edges.
ending with the tasks in E the delay requirements are
satisfied:
∀ t
i
∈ S, t
j
∈ E,
P(L[t
i
, t
j
] ≤ maxDelay) ≥ minProbability
(2)
where L[t
i
, t
j
] is a random variable representing the
latency for producing an output data by the task
t
i
∈ S in response to a triggering event produced
by the task t
j
∈ E, and the constants maxDelay
and minProbability are the requirements of the task
graph expressed by the developer. The allowed
maximum delay is represented with maxDelay, and
minProbability is the minimum probability threshold
for the delay requirement probability to hold, where
delay is at most maxDelay. The path delay con-
straints (2) are equivalent to:
∀ t
i
∈ S, t
j
∈ E,
F
L
[t
i
, t
j
](maxDelay) ≥ minProbability
(3)
where F
L
[t
i
, t
j
] is the cumulative distribution function
(c.d.f) of the latency random variable L[t
i
, t
j
]. In our
formulation, we consider F
L
[t
i
, t
j
] as an auxiliary vari-
able, that should specify the c.d.f of the delay in the
mapping of the tasks to the nodes on the path from
t
i
to t
j
, and depends on F
D
[u, v] for each edge (u, v)
in the path from t
i
to t
j
, and the rules specified by the
probability model on how to combine the distributions
over a path.
Typically, the tasks in the set S are operational
tasks, e.g. AverageSpeedCalculator, and the tasks in
the set E are the end-points of the data flow in the
task graph, e.g. RampSignalDisplayer. For exam-
ple, Figure 5 shows a path from the task t
1
∈ S of
the type AverageSpeedCalculator to the task t
3
∈ E
of the type RampSignalDisplayer, with the delay ran-
dom variables D[1, 2] and D[2, 3] for the two edges on
the path. In this example, as we consider the delay
random variables D[1, 2] and D[2, 3] independent, it is
trivial to see that the latency L[t
1
, t
3
] is equal to the
sum of the delay random variables on each edge:
L[t
1
, t
3
] = D[1, 2] + D[2, 3] (4)
We observe that according to the path delay con-
straints (2) the probability P(L[t
1
, t
3
] ≤ 3.0) ≥ 0.98
states that for every event triggered by the Average-
SpeedCalculator task t
1
, we require that in 98% of
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
33

t
i
···
t
k
t
j
L[t
i
, t
k
]
L[t
i
, t
j
]
D[t
k
, t
j
]
Figure 6: Path from the task t
i
to t
j
via task t
k
in the task
graph, and the delay random variable D[t
k
, t
j
] for sending a
unit of data from task t
k
to t
j
.
the time the RampSignalDisplayer task t
3
responds
within 3.0 seconds (this corresponds to the require-
ment that in the event of a traffic jam, no more cars
should be allowed onto the highway). If we assume
the delay random variables D[1, 2] and D[2, 3] are
normally distributed with mean 0.5 and variance 1
(N(0.5, 1)), then the c.d.f of L[t
1
, t
3
] is also a nor-
mal distribution with mean 1 and variance 2 (sum of
the means and variances). Therefore, the probabil-
ity P(L[t
1
, t
3
] ≤ 3.0) ≥ 0.98 becomes F
L
[t
1
, t
3
](3.0) =
0.92135 0.98, which is not satisfiable. This im-
plies that given the requirements maxDelay = 3 and
minProbability = 0.98 and in the presence of delay
on both of the channels D[1, 2] and D[2, 3], it is not
possible to receive a message at the end-point task t
3
,
within 3 seconds in at least 98% of the times.
Figure 6 shows an arbitrary path in the task graph
starting from the task t
i
∈ S and ends at t
j
∈ E. The
latency L[t
i
, t
j
] at the task t
j
is the sum of the delay for
all edges in the path originated from the task t
i
:
L[t
i
, t
j
] = L[t
i
, t
k
] ⊕ D[t
k
, t
j
] (5)
where L[t
i
, t
k
] is the latency of the direct predecessor
of the task t
j
namely t
k
in Figure 6, and ⊕ is the rule
provided by the probability model (see Section 3) for
combining the delay distribution over channels. We
consider that there is only one path from t
i
to t
j
in the
task graph, and from here throughout the paper, we
assume that the delay distribution on all channels are
independent, hence the operator ⊕ can be simplified
the sum operator +.
Computing the distribution of the random variable
latency L[t
i
, t
j
] based on the task mapping variables
node[t] is not trivial. In order to simplify the process,
we first show the connection between the mapping
variables node[t] to the delay distribution of each edge
of the task graph G.
We consider that the delay for transmitting a mes-
sage between two tasks placed on the same sensor
node is 0. Therefore, the random variable D[t
i
, t
j
]
becomes 0 if node[t
i
] = node[t
j
] (tasks t
i
and t
j
are
mapped to the same node), and the c.d.f F
D
[t
i
, t
j
]
becomes the degenerate distribution F(D; 0) (Karr,
1993):
F
D
[t
i
, t
j
] =
(
F(D; 0) if node[t
i
] = node[t
j
]
Φ
µ
i, j
,σ
i, j
if node[t
i
] 6= node[t
j
]
(6)
where Φ
µ
i, j
,σ
i, j
is the c.d.f of the normal distribution
with the mean µ
i, j
and the standard deviation σ
i, j
.
The c.d.f F
D
[t
i
, t
j
] of the delay for all tasks in the
same region is the same, e.g. normal distribution.
However, F
D
[t
i
, t
j
] can be a different distribution for
tasks transmitting data between different regions. In
this work, to simplify the presentation, we consider
F
D
[t
i
, t
j
] = Φ
µ,σ
for all tasks, but the parameters µ and
σ might differ from region to region. Given the de-
lay distribution on the edges (6) and the operator ⊕
in (5), we can compute the c.d.f of L. For example, let
the delay distribution for the edges in the path shown
in Figure 5 be the same as in (6). The c.d.f of the de-
lay on the path from the task t
1
to t
3
shown in Figure 5
is:
F
L
[t
1
, t
3
] =
F(D; 0) if node[t
1
] = node[t
2
] ∧
node[t
2
] = node[t
3
]
Φ
µ
1,2
,σ
1,2
if node[t
1
] 6= node[t
2
] ∧
node[t
2
] = node[t
3
]
Φ
µ
2,3
,σ
2,3
if node[t
1
] = node[t
2
] ∧
node[t
2
] 6= node[t
3
]
Φ
µ
1,2
+µ
2,3
,σ
1,2
+σ
2,3
if node[t
1
] 6= node[t
2
] ∧
node[t
2
] 6= node[t
3
]
(7)
If all the tasks are placed on the same sensor node (the
first case in (7)) the c.d.f of two degenerate distribu-
tion with parameter 0 is also a degenerate distribution
with parameter 0. In the second and the third case
in (7), one pair of the nodes are placed on the same
sensor node and the other pair are not, and the c.d.f of
the sum of a degenerate distribution with parameter 0
and a normal distribution is still a normal distribution
maintaining the same parameters. Finally, in the last
case of (7), if all the tasks are placed on different sen-
sor nodes, then the c.d.f of the sum of the two random
variables D[t
1
, t
2
] and D[t
2
, t
3
] with normal distribu-
tion is also normal distribution with its mean being
the sum of the two means, and its variance being the
sum of the two variances (Φ
µ
1,2
+µ
2,3
,σ
1,2
+σ
2,3
), as we
assume the delays are independent.
As shown in equation (7), for three adjacent
pairs of tasks on the path from t
1
to t
3
, choosing
(node[t
i
] = node[t
j
]) or (node[t
i
] 6= node[t
j
]), where
t
i
, t
j
∈ {t
1
, t
2
, t
3
}, creates 2
3−1
= 4 possible combina-
tions, and as a result F
L
[t
1
, t
3
] is a piecewise function
with four sub-function. In the general case, for k ad-
jacent pairs of tasks on the path from t
i
to t
j
, choosing
(node[t
i
] = node[t
j
]) or (node[t
i
] 6= node[t
j
]) creates
2
k−1
possible combinations, hence, the c.d.f of the
delay random variable L[t
i
, t
j
] is a piecewise function
with 2
k−1
sub-functions.
SENSORNETS2014-InternationalConferenceonSensorNetworks
34

t
1
t
2
t
0
1
t
0
2
t
3
t
00
1
t
00
2
p
1
: (t
1
→ t
2
→ t
3
)
p
2
: (t
0
1
→ t
0
2
→ t
3
)
p
3
: (t
0
1
→ t
0
2
→ t
3
)
=
D[t
1
, t
2
]
D[t
2
, t
3
]
D[t
0
1
, t
0
2
] D[t
0
2
, t
3
]
D[t
00
1
, t
00
2
]
D[t
00
2
, t
3
]
Figure 7: A path from the task t
1
to t
3
via task t
2
in the
task graph, the two copies of the tasks t
1
and t
2
denoted by
t
0
1
, t
00
1
and t
0
2
, t
00
2
respectively, and the delay random variable
D[t
i
, t
j
] for an edge (t
i
, t
j
) ∈ A.
4.1 Task Replication
The path delay constraints (3) depends on the con-
stants maxDelay and minProbability, which is pro-
vided by the developer as part of the task graph.
Therefore, it is possible that these constraints are not
satisfiable. To tackle this issue, we replicate certain
tasks more than once in a region, for the express pur-
pose of reducing the possible delay values of the ran-
dom variables L[t
i
, t
j
] (since t
j
can fire as soon as one
of the clones’ data is available). This will incur a
cost in terms of communication overhead. However,
we formulate the problem to minimise the number of
replicated tasks and hence minimise the communica-
tion overhead.
In Figure 7, we show an example of task replica-
tion on the path p
1
from the task t
1
to t
3
, with the
tasks t
0
1
, t
00
1
replicated from the task t
1
, and the tasks
t
0
2
, t
00
2
replicated from the task t
2
. A replicated task also
replicates the incoming and outgoing edges from the
direct predecessor and to the direct successor tasks in
the task graph. We only replicate the operational tasks
(namely t
1
and t
2
in Figure 7), and as a result the two
new paths p
2
and p
3
share the actuator task t
3
.
The latency for the delay at an end-point t
3
on the
path p
1
is equal to the minimum of the delay random
variable L of all paths p
1
, p
2
and p
3
:
L[t
1
, t
3
] = min
L[t
1
, t
3
], L[t
0
1
, t
3
], L[t
00
1
, t
3
]
In the general case, the delay random variable L[t
i
, t
j
]
along a path with the tasks replication is computed by
an additional operator = (operator min in our work,
which is provided by the probability model) to com-
pose the properties of the channels over the (parallel)
fan-in at the end-point task t
j
:
L[t
i
, t
j
] = =
(t
k
,t
j
) ∈ A
0
j
(L[t
i
, t
k
] ⊕ D[t
i
, t
j
]) (8)
where A
0
j
is the set of all replicated edges for the direct
predecessor of the task t
j
including the non-replicated
edge on the path from t
i
to t
j
.
Based on order statistics (Arnold et al., 2008;
David and Nagaraja, 2003), the c.d.f of L[t
i
, t
j
] in (8)
with the operator = being the minimum of indepen-
dent random variables becomes:
∀ t
i
∈ S, t
j
∈ E,
F
L
[t
1
, t
3
] =
1 − (1 − F
L
[t
1
i
, t
j
])· (1 − F
L
[t
2
i
, t
j
])···(1 − F
L
[t
r
i
, t
j
])
(9)
where t
r
i
represents the r
th
copy of the task t
i
.
For example, in Figure 7, we can use the equa-
tion (9) to compute the latency at the task t
3
. As-
sume on the path p
1
the tasks can only be placed on
different nodes (node[t
1
] 6= node[t
2
] 6= node[t
3
]), also
let maxDelay = 2, minProbability = 0.98, and the de-
lay distribution be normal distribution N(0.5, 1) for
all edges. From (7), before replicating the tasks, the
c.d.f F
L
[t
1
, t
3
] of the delay random variable on path p
1
becomes:
node[t
1
] 6= node[t
2
] ∧ node[t
2
] 6= node[t
3
] =⇒
F
L
[t
1
, t
3
] = Φ
0.5+0.5,1+1
= Φ
1,2
and the probability of the latency on the path p
1
being
at most 2.0 seconds is F
L
[t
1
, t
3
](2) = 0.76025. How-
ever, 0.76025 0.98 and the constraint (3) is not sat-
isfiable. In order to satisfy constraint (3), we create
two copies of the tasks t
1
and t
2
as shown in Figure 7.
The replicated tasks maintain the same properties and
the originated tasks. Hence, the probability of latency
being at most 2 seconds on path p
2
and p
3
is also
0.76025. Using equation (9) we have:
F
L
[t
1
, t
3
] =
1−(1−0.76025)·(1−0.76025)·(1−0.76025) = 0.9862
and the constraint (3) is satisfied (0.9862 ≥ 0.98).
The task mapping optimisation problem with tasks
replication becomes:
minimise |T
0
|
subject to:
node[t] 6= n for every task t that
cannot be mapped to node n
(10)
∀ t
i
∈ S, t
j
∈ E,
F
L
[t
i
, t
j
](maxDelay) ≥ minProbability
(11)
where T
0
is the set of all replicated tasks, and F
L
[t
i
, t
j
]
is computed from (9).
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
35

4.2 Task Replication Lower bound
For any given path p from the task t
i
to the task t
j
,
the mapping of all tasks to different nodes incurs the
maximum latency at the end-point task t
j
. Let MF be
the maximum latency incurred by assigning all tasks
to different nodes (MF = max (F
L
[t
i
, t
j
])), and r be the
number of replicated tasks. The lower bound on the
number of tasks replicated is:
F
L
[t
i
, t
j
] = 1 − (1 − MF)
r
≥ minProbability =⇒
(1 − MF)
r
≤ 1 − minProbability =⇒
r · log(1 − MF) ≤ log(1 − minProbability) =⇒
r ≥
log(1 − minProbability)
log(1 − MF)
(12)
For example, as we have shown in Figure 7 with
minProbability = 0.98 and MF = 0.76025, we require
to replicate the tasks on the path p
1
at least two times,
which can also be derived using the lower bound (12):
r ≥
log(1 − 0.98)
log(1 − 0.76025)
= 2.74121
In our implementation, we use the floor of the lower
bound in (12) to compute the minimum number of
replicated tasks required.
5 CONSTRAINT
PROGRAMMING APPROACH
FOR END-TO-END
REQUIREMENTS
As we have seen in Section 4, the abstract nature
of the path delay constraints (3) and the c.d.f of la-
tency (7) at an end-point being a piecewise function
of the decision variables node[t], make it very difficult
to implement and solve the task mapping optimisation
problem with end-to-end requirements using conven-
tional approaches and optimisation solvers. In this
section, we use constraint programming (CP) to im-
plement the mathematical model stated in Section 4.
Algorithm 1 lists our CP approach in solving the
task mapping problem with delay requirements. In
our main CP model (CSP
main
in line 2), each path de-
lay constraint (3) is modelled as a sub constraint sat-
isfaction problem (CSP
sub
in line 8), and the whole
solution to each sub-CSP is expressed as an exten-
sional constraint (also known as user-defined or ad-
hoc constraint). Extensional constraints provide a
way to specify all valid solutions to the constraint, us-
ing either a deterministic finite automaton or a tuple
set (table constraint). In this work, we use a tuple set
Algorithm 1: The task mapping with end-to-end
delay requirements algorithm.
input : N, T, S, E, minProbability
output: node
1 solved ← false
2 add placement constraints to CSP
main
3 while not solved do
4 taskCopiesRequired ← false
5 forall t
i
∈ S, t
j
∈ E do
6 tupleSet[t
i
, t
j
] ←
/
0
7 taskCopies ← 0
8 forall solutions s in CSP
sub
hp[t
i
, t
j
]i do
9 if checker(s, MF) then
10 tupleSet[t
i
, t
j
] =
tupleSet[t
i
, t
j
] ∪ s
11 if tupleSet[t
i
, t
j
] 6=
/
0 then
12 add extentsional constraints to
CSP
main
13 else
14 taskCopies ←
log(1−minProbability)
log(1−MF)
15 replicate(p[t
i
, t
j
], taskCopies)
16 taskCopiesRequired ← true
17 if not taskCopiesRequired then
18 solve(CSP
main
)
19 if CSP
main
has a solution then
20 solved ← true
21 return node
22 else
23 replicate (1)
to express all the valid solutions to the path delay con-
straints (3) and enforce these constraints in our main
CP model.
Our CSP
main
model enforces the placement con-
straints (1) and the following extensional constraint
representing the valid solutions to the path delay con-
straints (3):
∀ t
i
∈ S, t
j
∈ E
extensional(p[t
i
, t
j
], tupleSet[t
i
, t
j
])
(13)
where p[t
i
, t
j
] is the set of all tasks on the path from
the task t
i
to the task t
j
including t
i
and t
j
, and
tupleSet[t
i
, t
j
] is the set of tuples, where each tuple
is a valid solution to the path delay constraint (3),
given by solving the CSP
sub
(line 8). The extensional
constraints (13) are then constraining the valid solu-
tions of the path delay constraints to the correspond-
ing variables node[t], t ∈ p[t
i
, t
j
] (line 12), on which
domain consistency (all values not participating in a
SENSORNETS2014-InternationalConferenceonSensorNetworks
36

solution are pruned) is achieved.
For example, in Figure 5, let the delay random
variable D be a normal distribution N(0.5, 1), and the
domain of the tasks be as follows:
node[t
1
] = {1, 2}, node[t
2
] = {1, 2}, node[t
3
] = {2}
also let maxDelay = 3, minProbability = 0.98. The
path delay constraints according to (7) become:
F
L
[t
1
, t
3
] =
F(D; 0) if node[t
1
, t
2
, t
3
] = [3, 3, 3]
Φ
0.5,1
if node[t
1
, t
2
, t
3
] = [2, 3, 3]
Φ
0.5,1
if node[t
1
, t
2
, t
3
] = [2, 2, 3]
Φ
1,2
if node[t
1
, t
2
, t
3
] = [3, 2, 3]
(14)
where node[t
1
, t
2
, t
3
] = [3, 3, 3] is a vector notation for
the assignment node[t
1
] = 3, node[t
2
] = 3, node[t
3
] =
3. The path delay constraints (3) for all the possible
assignments in (14) become:
node[t
1
, t
2
, t
3
] = [3, 3, 3] =⇒
F
L
[t
1
, t
3
](3) = F(D; 0) = 1 ≥ 0.98 (15)
node[t
1
, t
2
, t
3
] = [2, 3, 3] =⇒
F
L
[t
1
, t
3
](3) = Φ
0.5,1
(3) = 0.99379 ≥ 0.98 (16)
node[t
1
, t
2
, t
3
] = [2, 2, 3] =⇒
F
L
[t
1
, t
3
](3) = Φ
0.5,1
(3) = 0.99379 ≥ 0.98 (17)
node[t
1
, t
2
, t
3
] = [3, 2, 3] =⇒
F
L
[t
1
, t
3
](3) = Φ
1,2
(3) = 0.92135 0.98 (18)
The possible assignments (15), (16), and (17) sat-
isfy the path delay constraint, except the assign-
ment node[t
1
, t
2
, t
3
] = [3, 2, 3] (18). Note that the
tupleSet[t
1
, t
3
] only includes valid assignments:
tupleSet[t
1
, t
3
] = {[3, 3, 3], [2, 3, 3], [2, 2, 3]}
and therefore in this example the extensional con-
straint (13) is:
extensional({t
1
, t
2
, t
3
}, {[3, 3, 3], [2, 3, 3], [2, 2, 3]})
(19)
The extensional constraint (19) constrains the deci-
sion variables node[t
1
], node[t
2
], and node[t
3
] to the
given valid assignments by the tupleSet. In the pres-
ence of many extensional constraints for several path
delay constraints, our CSP
main
model can effectively
prune the values that do not participate in a solution,
using the produced valid assignments tupleSet given
by the CSP
sub
model.
The CSP
sub
model produces solutions to the
ground instance of the task mapping problem with
only decision variables limited to one path on the
task graph, and only includes placement constraints.
Therefore, it is efficient to produce all solutions and
check the validity of each solution using a checker
function (line 9). The checker function computes
the c.d.f of the delay according to (9) and incremen-
tally maintains the maximum value of the c.d.f (MF)
to be used in computing the lower bound taskCopies
on the tasks replication (line 14). The checker func-
tion returns true if in the assignment s the c.d.f of the
delay is at least minProbability satisfying the path de-
lay constant (3), and false otherwise. If the checker
function returns true, the valid solution s is added to
the tupleSet[t
i
, t
j
] (line 10), and if there is at least one
valid solution (tupleSet[t
i
, t
j
] 6=
/
0, line 11), then the
extensional constraint (13) is added to the CSP
main
model (line 12). Note that the initial domain reduc-
tion is performed by the extensional constraints at this
point (all values not participating in a solution to the
CSP
main
are pruned from the domains of the decision
variables), which reduces the number of solutions for
the consecutive CSP
sub
models.
If there is no valid solution to CSP
sub
(tupleSet[t
i
, t
j
] =
/
0, line 13), then at least one of
the path delay constraints can not be satisfied, hence
CSP
main
is also not satisfiable, and we required to
replicate the tasks. We replicate the tasks such that
the path delay constraints over the path p are satisfied,
and we start from the mathematical lower bound on
the number of task copies taskCopies (line 14). The
replicate function (line 15) takes the path p[t
i
, t
j
]
and creates taskCopies replicates of the operational
tasks along the path maintaining the same incoming
and outgoing edges in the path p[t
i
, t
j
] from the task
graph.
We solve CSP
main
(line 20) only if all path
delay constraints are individually satisfiable
(no task replicate per path basis is required,
taskCopiesRequired = false, line 17). If CSP
main
has
a solution, the node decision variables are returned
(line 21) and the algorithm ends, otherwise CSP
main
became unsatisfiable due to the composition of all
path delay constraints, therefore we add one more
copy of each operational tasks in the task graph G
(line 23).
We further optimise the CSP
sub
model by adding
symmetry breaking constraints (Rossi et al., 2006).
Let p
k
[t
i
, t
j
] be the k
th
set of replicated tasks on the
path from t
i
to t
j
, where p
0
[t
i
, t
j
] represents the initial
tasks from t
i
to t
j
. We refer to p
k
[t
i
, t
j
] as the k
th
repli-
cated path. Let v
k
[t
i
, t
j
] be the vector of the decision
variables node[t] on the k
th
replicated path in the or-
der of the directed edges. We enforce lexicographic
ordering to remove the equivalent permutation of val-
ues in a solution to CSP
sub
between replicated paths,
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
37

where there is at least one replicated path required:
∀p
k
[t
i
, t
j
], 0 ≤ k ≤ NR[t
i
, t
j
]
v
k
[t
i
, t
j
]
lex
v
k+1
[t
i
, t
j
]
(20)
where NR[t
i
, t
j
] is the number of replicated paths from
task t
i
to t
j
and
lex
is the lexicographic ordering
constraint between the vectors of decision variables
v
k
[t
i
, t
j
] and v
k+1
[t
i
, t
j
].
6 EVALUATION
6.1 Experimental Setup
In our experiments, we use the realistic road traffic
application and its latency requirements in (US De-
partment of Transportation, Federal Highway Admin-
istration, 2012). We start from the smallest highway
traffic size of h|N|, |T|i = h7, 9i and increase the in-
stance size by one region per instance (each region is
a sector in a highway with at least 6 sensor nodes)
up to the largest instance of highway traffic with 25
regions (highway traffic h150, 216i). We assume that
the delay distribution for sending a message between
any two regions is a normal distribution N(0.5, 1)
with mean 0.5 and variance 1. For each instance, we
enforce the end-to-end delay constraints between the
AverageSpeedCalculator tasks and the RampSignalD-
isplayer tasks with the message delay probability of
0.98 within 1, 2, or 3 seconds.
Our CP model is implemented in Gecode (Gecode
Team, 2006) (revision 4.2.0)
1
and runs under
Mac OS X 10.8.4 64 bit on an Intel Core i5 2.6 GHz
with 3MB L2 cache and 8GB RAM. We separately
solve each instance for the maximum delay value
(maxDelay) of 1, 2, or 3 seconds. We set a timeout
of 60 seconds for each instance, recording the time to
solve optimally and the number of replicated tasks.
6.2 Analysis of Results
In Figure 8, we present the average runtime results (in
seconds) of 10 runs for solving the highway traffic in-
stances with our CP model. Each instance is solved
upon varying the delay requirement (maxDelay) on
the values 1, 2, and 3 seconds. The lower values
of maxDelay makes the instances more difficult to
solve, as the delay requirement becomes harder to
satisfy and more task replicates are required. All in-
stances were solved optimally, minimising the num-
ber of replicated tasks.
1
available from http://www.gecode.org/
0.0001
0.001
0.01
0.1
1
10
h7, 9i
h13, 18i
h19, 27i
h25, 36i
h32, 45i
h38, 54i
h44, 63i
h50, 72i
h57, 81i
h63, 90i
h69, 99i
h75, 108i
h82, 117i
h88, 126i
h94, 135i
h100, 144i
h107, 153i
h113, 162i
h119, 171i
h125, 180i
h132, 189i
h138, 198i
h144, 207i
h150, 216i
Runtime (seconds)
Highway traffic instances
maxDelay = 1
maxDelay = 2
maxDelay = 3
Figure 8: Average runtime in seconds of 10 runs and in log-
arithmic scale for solving optimally the task mapping prob-
lem with end-to-end requirements on the highway traffic ap-
plication with a maximum allowed delay of 1, 2, or 3 sec-
onds. The instances are represented with h|N|, |T|i, where
|N| is the number of sensor nodes and |T| is the number of
instantiated tasks.
0
50
100
150
200
250
300
350
h7, 9i
h13, 18i
h19, 27i
h25, 36i
h32, 45i
h38, 54i
h44, 63i
h50, 72i
h57, 81i
h63, 90i
h69, 99i
h75, 108i
h82, 117i
h88, 126i
h94, 135i
h100, 144i
h107, 153i
h113, 162i
h119, 171i
h125, 180i
h132, 189i
h138, 198i
h144, 207i
h150, 216i
Replicated tasks
Highway traffic instances
maxDelay = 1
maxDelay = 2
maxDelay = 3
Figure 9: Number of replicated tasks required to satisfy the
end-to-end requirements on the highway traffic application
with a maximum allowed delay of 1, 2, or 3 seconds. The
instances are represented with h|N|, |T|i, where |N| is the
number of sensor nodes and |T| is the number of instantiated
tasks.
The runtimes for instances with maxDelay = 2 and
3 seconds are very short, therefore we take the aver-
age runtime of 10 runs. In Figure 8, we present the
runtimes with logarithmic scale to further distinguish
the difference of runtime between the instances with
maxDelay = 2 and instances with maxDelay = 3 sec-
onds. The runtime includes the preprocessing time to
create and solve the CSP
sub
models, and the runtime
to solve the CSP
main
model. The runtime increases
linearly as the size of the problem increases and the
maximum allowed delay (maxDelay) decreases. For
the first instance h7, 9i, the runtime is significantly
shorter than larger instances, because this instance in-
volves only one region with one path delay constraint,
and requires only 2 task replicates to satisfy the de-
SENSORNETS2014-InternationalConferenceonSensorNetworks
38

0.001
0.01
0.1
1
10
100
1000
0.7 0.8 0.9 1.0 1.2 1.4 1.6 1.8 2 4 8 16 32
Runtime (seconds)
maxDelay
Highway traffic instance h132, 189i
Figure 10: The average runtime in seconds and logarithmic
scale for solving highway traffic instance h132, 189i with
10 runs, varying maxDelay.
lay requirement when maxDelay = 1 or 2 seconds.
The runtime drastically increases as the maximum al-
lowed delay drops below the average delay on a path
between two end-points with delay requirements. In
our instances, the paths between the two end-points
includes three edges (path length is 3), where the
average delay on each edge is 0.5 second, therefore
the average delay between the two end-points on the
path is 1.5 seconds, and choosing maxDelay = 1 sec-
ond requires several iterations of creating task repli-
cates, hence the longer runtimes. The standard de-
viation of the runtimes for all instances is on average
0.05 seconds, and at most 1.69 seconds, while varying
maxDelay between 1 and 3 seconds with 10 runs.
In Figure 9 we present the number of replicated
tasks in order to satisfy the end-to-end requirements
expressed by the path delay constraints in our CP
model. As we expected, a tighter requirement on the
allowed maximum delay (maxDelay) requires more
replicated tasks to improve the chance of a message
delivery at an end-point and to satisfy the path de-
lay constraints. As the delay requirement maxDelay
drops from 2 seconds to 1 second, the replicated tasks
are not exactly doubled, as some path delay con-
straints are satisfied with fewer replicated tasks. How-
ever, increasing the instance size by one region in-
creases the number of task replicates equally between
two consecutive instances, which is due to the equal
delay distribution between all regions.
In Figure 10, we present the average runtime re-
sults (in seconds) of 10 runs for solving a reason-
ably large instance of the highway traffic application
(namely instance h132, 189i), varying the values of
maxDelay from 0.7 to 32 seconds. In Figure 11, we
show the results for the number of replicated tasks
with the same setup as in Figure 10. The result shows
that the runtime and the number of replicated tasks
follow the same trend, while varying the maximum al-
0
50
100
150
200
250
300
350
400
450
0.7 0.8 0.9 1.0 1.2 1.4 1.6 1.8 2 4 8 16 32
Replicated tasks
maxDelay
Highway traffic instance h132, 189i
Figure 11: Number of replicated tasks required to satisfy
the end-to-end requirements on the highway traffic instance
h132, 189i, varying maxDelay.
lowed delay maxDelay. The runtime tightly depends
on the number of replicated tasks, and there is an in-
terval on the values of maxDelay, where the average
runtime and the number of replicated tasks does not
change significantly.
These results show that constraint programming
can efficiently solve the combinatorial problem with
end-to-end requirements introduced in task mapping
for WSNs.
7 CONCLUSIONS
In this paper, we formulated the problem as a con-
straint program of task-mapping while honouring
end-to-end requirements encountered during sensor
network macroprogramming, and presented efficient
algorithms to solve it. We also addressed the case
when copies of certain tasks are permitted in or-
der to increase performance guarantees. Our evalu-
ations, performed on a realistic highway traffic ap-
plication task graph for the special case of manag-
ing end-to-end latency, show that this problem can
indeed be solved efficiently using our approach, al-
though increased computation time is needed for
tighter bounds. We investigated the specific case of
latency requirement in this paper. However the end-
to-end requirements are only given as an example. It
is possible to address other end-to-end requirements
by changing the rules of the probability model for
combining the probability distributions along the path
between the two end points. For example, if instead of
latency we consider link quality as a random variable
over the channels, then the probability model must
state the distribution of the random variable link qual-
ity and how it is combined over channels (path be-
tween two end-points). We then replace the operator
AConstraintProgrammingApproachforManagingEnd-to-endRequirementsinSensorNetworkMacroprogramming
39

⊕ and = (8) in the the probability model with the op-
erator product and the operator min, respectively, and
our formulation (see Section 4) is still valid for main-
taining the link quality requirements. Our immediate
future work is in two parallel directions: i) integra-
tion of our approach into the publicly available Srijan
toolkit
2
for ATaG, and ii) further exploring the over-
head induced by creating copies of tasks and devel-
oping more accurate CP models to minimise it while
achieving the desired non-functional guarantees. We
also envision the application of our work in cloud
computing and related technologies, where guaran-
teeing certain requirements on the services running in
the cloud is essential, and latencies among co-located
nodes are similar to those in different data centres.
ACKNOWLEDGEMENTS
This research is partially sypported by the Swedish
Foundation for Strategic Research (SSF) under re-
search grant RIT08-0065 for the project ProFuN,
and the French ANR-BLAN-SIMI10-LS-100618-6-
01 MURPHY project. Special thanks to the reviewers
for their comments.
REFERENCES
Arnold, B. C., Balakrishnan, N., and Nagaraja, H. N.
(2008). A first course in order statistics, volume 54 of
Classics in Applied Mathematics. Society for Indus-
trial and Applied Mathematics (SIAM), Philadelphia,
PA. Unabridged republication of the 1992 original.
Bakshi, A., Pathak, A., and Prasanna, V. K. (2005a).
System-level support for macroprogramming of net-
worked sensing applications. In Intl. Conf. on Perva-
sive Systems and Computing (PSC).
Bakshi, A., Prasanna, V. K., Reich, J., and Larner, D.
(2005b). The Abstract Task Graph: A methodol-
ogy for architecture-independent programming of net-
worked sensor systems. In Workshop on End-to-end
Sense-and-respond Systems (EESR).
Choi, W., Shah, P., and Das, S. (2004). A framework for
energy-saving data gathering using two-phase cluster-
ing in wireless sensor networks. In Proc. of the 1
st
Int.
Conf. on Mobile and Ubiquitous Systems: Networking
and Services (MOBIQUITOUS).
David, H. A. and Nagaraja, H. N. (2003). Order statis-
tics. Wiley Series in Probability and Statistics. Wiley-
Interscience [JohnWiley & Sons], Hoboken, NJ, third
edition.
Gecode Team (2006). Gecode: A generic constraint devel-
opment environment. http://www.gecode.org/.
2
http://code.google.com/p/srijan-toolkit/
Gummadi, R., Gnawali, O., and Govindan, R. (2005).
Macro-programming wireless sensor networks using
Kairos. In Proc. of the 1
st
Int. Conf. on Distributed
Computing in Sensor Systems (DCOSS).
Hassani Bijarbooneh, F., Flener, P., Ngai, E., and Pearson, J.
(2011). Energy-efficient task mapping for data-driven
sensor network macroprogramming using constraint
programming. In Operations Research, Computing,
and Homeland Defense, pages 199–209. Institute for
Operations Research and the Management Sciences.
Karr, A. (1993). Probability. Springer Texts in Statistics
Series. Springer-Verlag.
Mottola, L., Pathak, A., Bakshi, A., Prasanna, V. K., and
Picco, G. P. (2007). Enabling scope-based interactions
in sensor network macroprogramming. In Proc. of the
4th Int. Conf. on Mobile Ad-Hoc and Sensor Systems.
Mottola, L. and Picco, G. (2011). Programming wireless
sensor networks: Fundamental concepts and state of
the art. ACM Computing Surveys (CSUR), 43(3):19.
Newton, R., Morrisett, G., and Welsh, M. (2007). The reg-
iment macroprogramming system. In Proceedings of
the 6th international conference on Information pro-
cessing in sensor networks, pages 489–498. ACM.
Pathak, A., Mottola, L., Bakshi, A., Prasanna, V. K., and
Picco, G. P. (2007). Expressing sensor network inter-
action patterns using data-driven macroprogramming.
In Third IEEE International Workshop on Sensor Net-
works and Systems for Pervasive Computing (PerSeNS
2007).
Pathak, A. and Prasanna, V. K. (2010). Energy-efficient
task mapping for data-driven sensor network macro-
programming. IEEE Transactions on Computers,
59(7):955–968.
Pathak, A. and Prasanna, V. K. (2011). High-Level Applica-
tion Development for Sensor Networks: Data-Driven
Approach. In Nikoletseas, S. and Rolim, J. D., editors,
Theoretical Aspects of Distributed Computing in Sen-
sor Networks, Monographs in Theoretical Computer
Science. An EATCS Series, pages 865–891. Springer
Berlin Heidelberg.
Rossi, F., van Beek, P., and Walsh, T., editors (2006). Hand-
book of Constraint Programming. Elsevier.
Tian, Y., Ekici, E., and
¨
Ozg
¨
uner, F. (2005). Energy-
constrained task mapping and scheduling in wireless
sensor networks. In IEEE International Conference
on Mobile Ad hoc and Sensor Systems, pages 8–218.
IEEE Computer Society Press.
US Department of Transportation, Federal Highway Ad-
ministration (2012). Manual on uniform traffic con-
trol devices: Preemption and priority control of
traffic control signals. http://mutcd.fhwa.dot.gov/
pdfs/2009r1r2/part4.pdf. Section 4D.27.
Wu, Y., Kapitanova, K., Li, J., Stankovic, J. A., Son, S. H.,
and Whitehouse, K. (2010). Run time assurance of
application-level requirements in wireless sensor net-
works. In Proceedings of the 9th ACM/IEEE Interna-
tional Conference on Information Processing in Sen-
sor Networks, IPSN ’10.
SENSORNETS2014-InternationalConferenceonSensorNetworks
40
