
Exploiting Material Properties to Select a Suitable Wavelet Basis
for Efficient Rendering
Jeroen Put, Nick Michiels and Philippe Bekaert
Hasselt University - tUL - iMinds, Expertise Centre for Digital Media, Wetenschapspark 2, 3590 Diepenbeek, Belgium
Keywords:
Rendering, Wavelets, Parameterisation, Materials.
Abstract:
Nearly-orthogonal spherical wavelet bases can be used to perform rendering at higher quality and with signif-
icantly less coefficients for certain spherical functions, e.g. BRDF data. This basis avoids parameterisation
artifacts from previous 2D methods, while at the same time retaining high-frequency details in the light-
ing. This paper demonstrates the efficiency of this representation for rendering purposes. Regular 2D Haar
wavelets can still occasionally perform better, however. This is due to their property of being fully orthogonal.
An important novelty of this paper lies in the introduction of a technique to select an appropriate wavelet basis
on-the-fly, by utilising prior knowledge of materials in the scene. To show the influence of different bases on
rendering quality, we perform a comparison of their parameterisation error and the compression performance.
1 INTRODUCTION
Research in computer graphics has led to mathemat-
ical models and algorithms to render photorealistic
images (Dutr
´
e et al., 2006). A challenging aspect
of rendering algorithms is how to parameterise the
functions that are used in the rendering equation (Ka-
jiya, 1986). For instance, in an all-frequency relight-
ing framework, it is particularly important to repre-
sent all the details in the visibility, BRDF and lighting
functions. Previous approaches use harmonic anal-
ysis to approximate the lighting, but fail to capture
sharp details like shadows and specular highlights. To
provide these, representations based on 2D wavelets
have been introduced. These representations suffer
from distortion artifacts, because a completely uni-
form one-to-one mapping of the spherical to the pla-
nar domain is not available. Their inherent compact-
ness is particulary important for inverse rendering ap-
plications, since the estimation of geometry, lighting
and material from a set of uncalibrated images is a
challenging problem and requires a lot of processing
power and storage.
Earlier work focused either on improving the effi-
ciency of the underlying representation or enhancing
the performance of triple product calculations. Our
contribution in this paper is the combination of these
ideas. The nearly-orthogonal basis avoids parame-
terisation artifacts, while at the same time retaining
high-frequency details in the lighting. On the other
hand, Ng.’s triple product (Ng et al., 2004) provides
an efficient manner to simulate complex lighting in-
teraction from precalculated datasets. It is through
the combination of precisely these ideas that we are
able to perform rendering with more complex spa-
tially varying BRDFs and more intricate lighting. An-
other contribution of this paper is the exploitation of
prior knowledge of scene materials to choose an ap-
propriate wavelet basis. We have observed during our
experiments that specular and diffuse BRDFs require
different bases for optimal approximation.
2 PREVIOUS WORK
Rendering requires the processing of vast quantities
of data. Often such data consists of visibility, BRDF
and lighting information. An efficient representation
is required for rendering with high quality and per-
formance. We focus on inverse rendering as an ap-
plication in this paper, as the problem of large vol-
umes of data is even more pronounced for this cate-
gory of techniques. Earlier techniques used spherical
harmonics, extending Fourier decomposition to the
spherical domain (Okabe et al., 2004; Yu et al., 2006).
Spherical harmonics have the disadvantage that they
can only represent low frequencies. For high frequen-
cies, the number of coefficients required grows expo-
nentially. This makes solving the triple product (Ng
et al., 2004) integral inefficient. Okabe et al. (Ok-
218
Put J., Michiels N. and Bekaert P..
Exploiting Material Properties to Select a Suitable Wavelet Basis for Efficient Rendering.
DOI: 10.5220/0004717202180224
In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 218-224
ISBN: 978-989-758-002-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Quality comparison for two different datasets. Leftmost column: environment map and meshes. Two central
columns: Rendering with optimal choice of basis (green) versus 2D parameterisation (red). Rightmost column: Zoomed
images to compare quality. Our method reduces parameterisation errors. See also the video accompanying this paper.
abe et al., 2004) showed an alternative representation
based on 2D Haar wavelets. Haber et al. (Haber et al.,
2009) use a 2D Haar wavelet basis to represent the
BRDF and visibility functions for every vertex in the
scene and to approximate the illumination environ-
ment map for every viewpoint. The main advantage
is that 2D Haar wavelets are able to capture high fre-
quency detail. However, they also suffer the disad-
vantage that there is no one-to-one mapping from the
planar domain to the spherical domain, resulting in
distortion when using 2D wavelets to represent spher-
ical functions. To minimise the distortion, octahedral
parametrisation (Praun and Hoppe, 2003a) is often
used.
Sweldens et al. (Schr
¨
oder and Sweldens, 1995)
proposed the construction of various wavelet basis
functions on the surface of the sphere. This construc-
tion is based on his earlier work on the lifting scheme.
He concluded that lifted spherical wavelets are par-
ticulary performant for the representation of BRDF
functions. This paper draws from these ideas, but con-
tributes by combining the triple product integration
from Ng. (Ng et al., 2004) with a nearly-orthogonal
wavelet basis.
A large body of work has been dedicated to the
analysis and representation of BRDFs (Ruiters and
Klein, 2010; Bilgili et al., 2011). However, these
representations are not particularly suitable for other
spherical functions, such as the illumination. Tsai et
al (Tsai et al., 2008) developed an importance sam-
pling strategy to sample products from illumination
and BRDF with spherical radial basis functions. This
technique is limited in its application, due to the
costly process of fitting their basis functions. Their
method also focuses on double products, where we
require triple product integral calculations in our for-
ward rendering.
The remainder of this paper is organized as fol-
lows. Section 3 shows how a Haar wavelet basis can
be constructed on a sphere and explains which sub-
division scheme is required. Section 4 presents the
results, where a comparison is made between the new
spherical Haar wavelet basis and the original 2D Haar
wavelet basis. Finally we complete this paper by pre-
senting our conclusions and future work in Section 5.
ExploitingMaterialPropertiestoSelectaSuitableWaveletBasisforEfficientRendering
219

3 SPHERICAL HAAR WAVELETS
Many functions in graphics are naturally expressed in
the spherical domain. Like previous methods, in our
rendering application the light at every surface point
x is expressed as a triple product integral:
B(x,ω
0
) =
Z
Ω
L(x, ω
i
)V (x,ω
i
)ρ(x,ω
i
,ω
o
)(ω
i
·n(x))dω
i
(1)
In this equation, B is the radiance as a function of
position x and outgoing direction ω
o
. L and V are the
lighting and visibility functions respectively, ρ is the
BRDF and n is the surface normal. To avoid the need
for separate environment maps per vertex, we assume
furthermore that L is a distant illumination function
and incorporate the term (ω
i
·n(x)) into V, so equation
1 becomes:
B(x,ω
0
) =
Z
Ω
˜
L(ω
i
)V (x,ω
i
)ρ(x,ω
i
,ω
o
)dω
i
(2)
L, V and ρ are all functions on the spherical domain
Ω.
˜
L is the globally defined environment map, rotated
into the local frame of V and ρ.
Current techniques use 2D Haar wavelets and are
able to represent details with relatively few coeffi-
cients. On the other hand, they introduce distortion
artifacts due to the parameterisation step of the spher-
ical domain to the planar domain. Often, the hemi-
octahedral parameterisation by Praun and Hoppe is
used to perform this mapping (Praun and Hoppe,
2003b):
V (ω) =
∑
i
V
i
Ψ
i
(ω),
˜
L(ω) =
∑
j
˜
L
j
Ψ
j
(ω),
ρ(~x,ω) =
∑
k
ρ
k
(~x)Ψ
k
(ω)
(3)
where Ψ is an appropriate basis on the octahedron.
In this paper, V , ρ and L are projected into a spherical
wavelet basis Ψ. This way, we can write equation 2
in terms of these basis functions:
B(x,ω
0
) =
∑
i
∑
j
∑
k
L
i
V
j
ρ
k
Z
Ω
Ψ
i
(ω)Ψ
j
(ω)Ψ
k
(ω)dω
(4)
Ψ
i
(ω), Ψ
j
(ω) and Ψ
k
(ω) are the tripling coefficients,
as defined by Ren et al. (Ng et al., 2004). More re-
cent work pointed out the existence of a generalized
wavelet product integral (Sun and Mukherjee, 2006).
3.1 Wavelet Basis and Subdivision
Scheme
To avoid artifacts, sampling of the spherical function
domain should happen as uniform as possible. In this
paper, an octahedral subdivision structure was cho-
sen, because of its favourable sampling characteristics
and because of symmetric sampling of hemispheric
functions.
The wavelet basis is defined over the triangles of
the subdivision scheme. Each of the octahedron oc-
tants is represented by a quadtree of wavelet coef-
ficients. In each subdivision step, every triangle is
split into four children, using the geodesic bisector
criterium as defined by Sweldens et al. (Schr
¨
oder and
Sweldens, 1995).
Let T
k
be such a triangle at depth k (k=0 for the
lowest level). T
k+1
0
, T
k+1
1
, T
k+1
2
and T
k+1
0
are the four
children of T
k
. Figure 2 shows an example of such a
triangle.
Figure 2: Decomposition of four pixel values into one
scaling coefficient and three wavelet coefficients (Bonneau,
1999).
Here, Φ
k
represents a scaling function. It is a con-
stant function with value 1 on T
k
and zero otherwise.
Ψ
k
1
, Ψ
k
2
and Ψ
k
3
are the three wavelet functions, with
T
k
as their support.
A fundamental property of the above triangular
Haar wavelets, is that every piecewise constant func-
tion over the four subtriangles (T
K+i
,i = 0, 1, 2, 3)
can be expressed as a linear combination of the con-
stant scaling function and the three wavelet func-
tions. From this, a local reconstruction can be de-
rived, which converts this combination of functions
to colour values again. The conversion of a scaling
function and three wavelet functions into colour val-
ues is called synthesis:
x
k+1
0
x
k+1
1
x
k+1
2
x
k+1
3
=
1 r
k
01
r
k
02
r
k
03
1 r
k
11
r
k
12
r
k
13
1 r
k
21
r
k
22
r
k
23
1 r
k
31
r
k
32
r
k
33
x
k
y
k
1
y
k
2
y
k
3
(5)
Here, r
k
i j
is the value of ψ
k
j
for the subtriangle T
k+1
i
.
Analysis can be performed by inverting the foregoing
synthesis matrix.
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
220
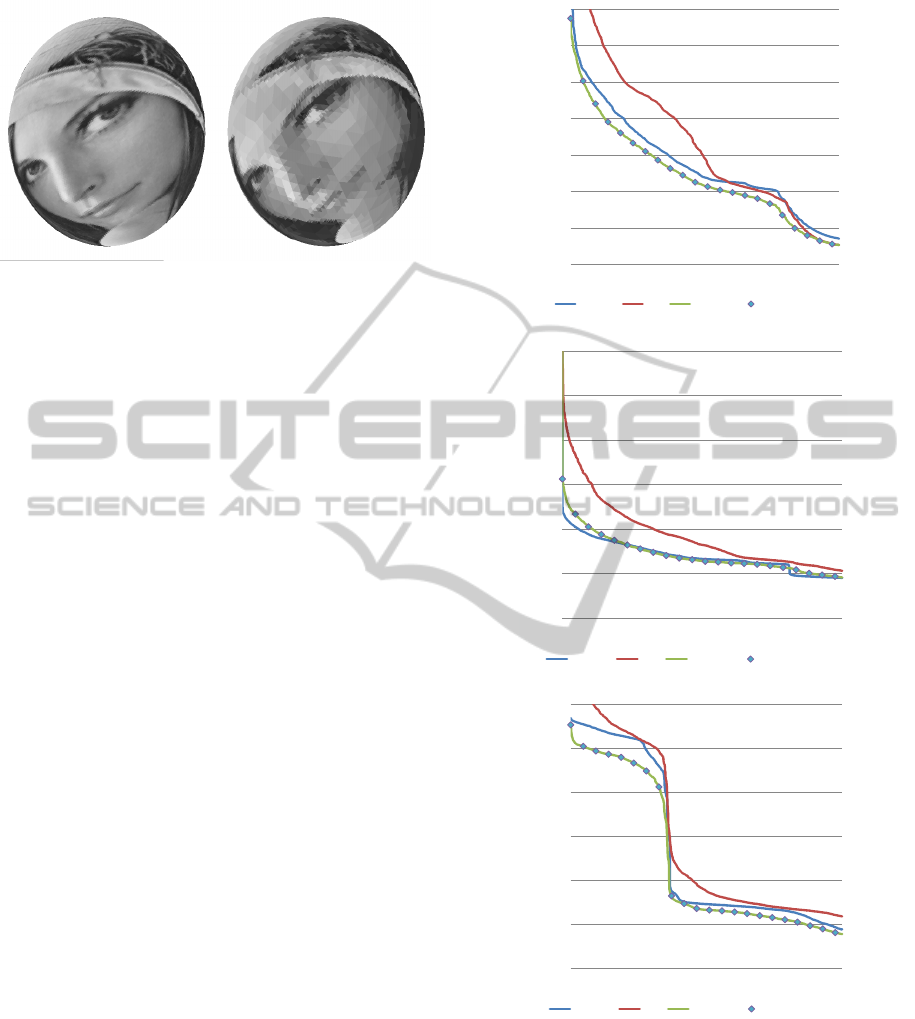
Figure 3: Compression with Bonneau spherical wavelets.
Left: original; Right: reconstruction with 5% of the coeffi-
cients.
3.2 Choosing a Suitable Basis
During our evaluation, we experimented with var-
ious Haar wavelet bases. The first representation
were the Bio-Haar wavelets introduced by Sweldens
et al. (Schr
¨
oder and Sweldens, 1995). This basis has
the property of being semi-orthogonal:
Z
ψ
k
1
φ
k
=
Z
ψ
k
2
φ
k
=
Z
ψ
k
3
φ
k
= 0 (6)
Semi-orthogonality is a necessary condition for the
existence of a wavelet basis over a certain domain.
This paper has opted for the nearly-orthogonal Bon-
neau wavelet basis (Bonneau, 1999). This basis is,
in the limit of its subdivision, guaranteed to provide
good compression performance when truncating the
least significant coefficients. At the same time it is
a convenient basis for a triple product integral imple-
mentation. Figure 3 demonstrates the compression on
a spherical image.
More interesting bases, like SOHO
wavelets (Lessig, 2007), also provide orthogo-
nality:
Z
ψ
k
1
ψ
k
2
=
Z
ψ
k
1
ψ
k
3
=
Z
ψ
k
2
ψ
k
3
= 0 (7)
Orthogonality guarantees that the best approximation
of the L
2
-norm can be achieved when removing the
least significant coefficients. They also have the ad-
vantage of a fast matrix inversion for the analysis
stage. SOHO wavelets provide orthogonality, but do
so at the cost of increased computation for their subdi-
vision scheme to create triangles of equal area, while
not providing upper bounds on the distortion of image
quality of this scheme.
0
50
100
150
200
250
300
350
L1-norm
6500 BRDF slices; sorted worst to best approximated
2D Haar
Bio
Bonneau
Pseudo Haar
(a)
0
100
200
300
400
500
600
L1-norm
6500 BRDF slices; sorted worst to best approximated
2D Haar
Bio
Bonneau
Pseudo Haar
(b)
0
200
400
600
800
1000
1200
L1-norm
6500 BRDF slices; sorted worst to best approximated
2D Haar
Bio
Bonneau
Pseudo Haar
(c)
Figure 4: Comparison of compression performance in the
L
1
-norm of four wavelet bases on a database with (a) a
representative mixture of BRDF slices, (b) more specular
BRDF slices and (c) more diffuse BRDF slices. 5% of co-
efficients were retained. A smaller norm is better. Our ap-
plication chooses the best basis on-the-fly, by taking the ma-
terial properties into account. As a consequence we always
get the best possible representation.
ExploitingMaterialPropertiestoSelectaSuitableWaveletBasisforEfficientRendering
221

(a) (b) (c)
Figure 5: Comparison of a diffuse BRDF approximation.
2% of coefficients retained. Smaller L
2
-norm is better. (a)
original; (b) spherical wavelets (L
2
-norm: 2,2739); (c) 2D
Haar-wavelets (L
2
-norm: 2,5831).
(a) (b) (c)
Figure 6: Comparison of specular BRDF approximation.
2% of coefficients retained. Smaller L
2
-norm is better. (a)
original; (b) spherical wavelets (L
2
-norm: 0,9323); (c) 2D
Haar-wavelets (L
2
-norm: 0,8895).
4 RESULTS
This section will compare the performance and qual-
ity of the nearly-orthogonal spherical wavelet repre-
sentation in a rendering context. Good compression
performance guarantees the need for less coefficients.
Therefore, this shall be the main focus in this section.
Figure 4 shows a comparison of compression per-
formance of five wavelet bases in the L
1
-norm on a
database of BRDF functions. In literature, it is argued
that the L
1
-norm often corresponds better to the vi-
sual perception by humans observers (Antonini et al.,
1992). The five wavelet bases are the lifted Bio-Haar
basis introduced by Sweldens et al. (Schr
¨
oder and
Sweldens, 1995), the regular 2D Haar wavelets used
by Haber et al. (Haber et al., 2009), the pseudo Haar
spherical wavelet basis suggested by Ma et al. (Ma
et al., 2006) and the two nearly-orthogonal Bonneau
spherical wavelets (Bonneau, 1999). We do not in-
clude a comparison with a spherical harmonics basis,
as its unsuitability for representing high frequencies
has already been proved in earlier literature (Ng et al.,
2004). Every representation performed compression
with a fixed budget of coefficients, where the least
significant coefficients were truncated. We used the
MERL BRDF database (Matusik et al., 2003; Ngan
et al., 2005) for rendering since it contains a repre-
sentative mixture of Lambertian, Cook-Torrance and
Lafortune BRDF slices. The chart sorts the BRDF
functions from worst to best approximated. It can be
observed that the Bio-Haar basis is significantly out-
performed in nearly all cases by the other bases. Both
Bonneau and pseudo Haar bases have better compres-
sion performance than the 2D Haar basis. The pseudo
Haar basis performs identical to the Bonneau basis.
To confirm our observation that spherical wavelets
compress diffuse BRDF slices better than very specu-
lar BRDF slices, we customised the content of the in-
ternal BRDF database. This results in two additional
graphs. The first graph is displayed in Figure 4(b)
and shows a scenario with significantly more specu-
lar BRDF slices. The graph shows that the spheri-
cal wavelets perform slightly worse than the 2D Haar
wavelets. The second graph is shown in Figure 4(c)
and demonstrates a scenario with predominantly dif-
fuse BRDF slices. The graph clearly demonstrates
that there are two groups of BRDF approximations.
The approximation yields large norms for specular
BRDFs and lower norms for more diffuse BRDFs.
The contents of the database has an influence on how
the two groups are distributed on the graph. This indi-
cates that the choice of wavelet basis can significantly
enhance the compression performance if prior knowl-
ege of material properties in the scene is available.
Therefore the selection of an appropriate basis can be
guided by the location of the cut-off that separates the
two groups.
For the next part of our evaluation, we select some
noteworthy BRDF slices out of the BRDF databse. A
BRDF slice is defined as a 2D subfunction of a 6D
BRDF defined over the hemisphere of all incomming
directions In Figure 5, a comparison of diffuse BRDF
slice approximation is shown between the Bonneau
spherical wavelet basis and the 2D Haar wavelet ba-
sis. It can be seen that the spherical wavelets provide
13,59% better compression performance in this case.
Figure 6 shows another comparison, with a
strongly specular BRDF. This time, 2D Haar wavelets
outperform spherical wavelets, albeit marginally.
This is a trend that was observed during our exper-
iments. We believe this is due to three main fac-
tors. First, spherical wavelets approximate the origi-
nal signal with the triangles of the underlying octahe-
dral subdivision scheme, while 2D Haar wavelets use
rectangular areas (pixels). A large portion of specular
BRDFs tend to have a circular shape, due to the dis-
tribution of light around the specular lobe. It was ob-
served in our implementation that the circular shape
can be approximated by fewer coefficients with rect-
angular areas.
Second, specular BRDFs with a large specular ex-
ponent subtend only a small solid angle on the hemi-
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
222
sphere. It is therefore less likely that the specular lobe
will cross areas of non-uniform sampling due to the
parameterisation method. In the cases such specular
BRDFs do overlap such areas, they are expected to
undergo severe distortion.
Finally, in the aforementioned case where very
specular BRDFs avoid parameterisation artifacts, the
2D Haar wavelets are expected to slightly outperform
the spherical wavelets. This can be attributed to the
fact that the 2D Haar basis is a fully orthogonal basis,
while the nearly-orthogonal wavelet bases are only or-
thogonal in the limit of the subdivision. As demon-
strated by Sweldens et al. (Schr
¨
oder and Sweldens,
1995), BRDF functions can be represented with very
few coefficients and the approximation therefore of-
ten takes place on a low number of subdivisions of
the underlying octahedral structure.
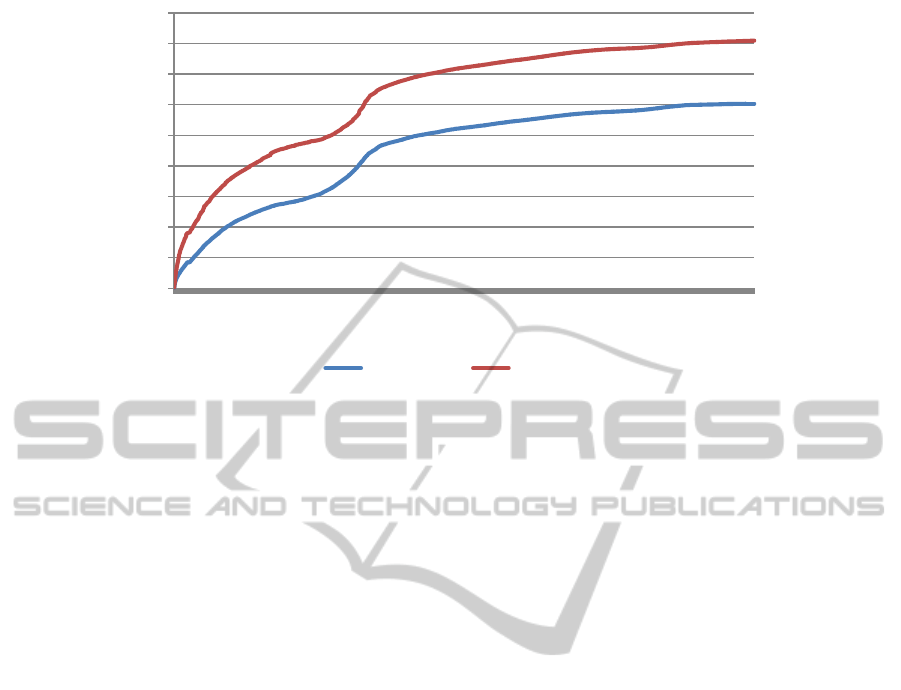
To have a more clear measure of the parameterisa-
tion error, independent from different wavelet repre-
sentations, we performed another experiment shown
in Figure 8. Here, we first sampled the BRDF
slices uniformly on the unit sphere with a statistical
method (Dutr
´
e et al., 2006) as a ground truth. We
then sampled the same slices with the octahedron as
well as with the 2D parameterisation method. Fig-
ure 8 shows the accumulated error for both parame-
terisations in comparison with the ground truth. We
can conclude that avoiding parameterisation artifacts
yields better quality approximation.
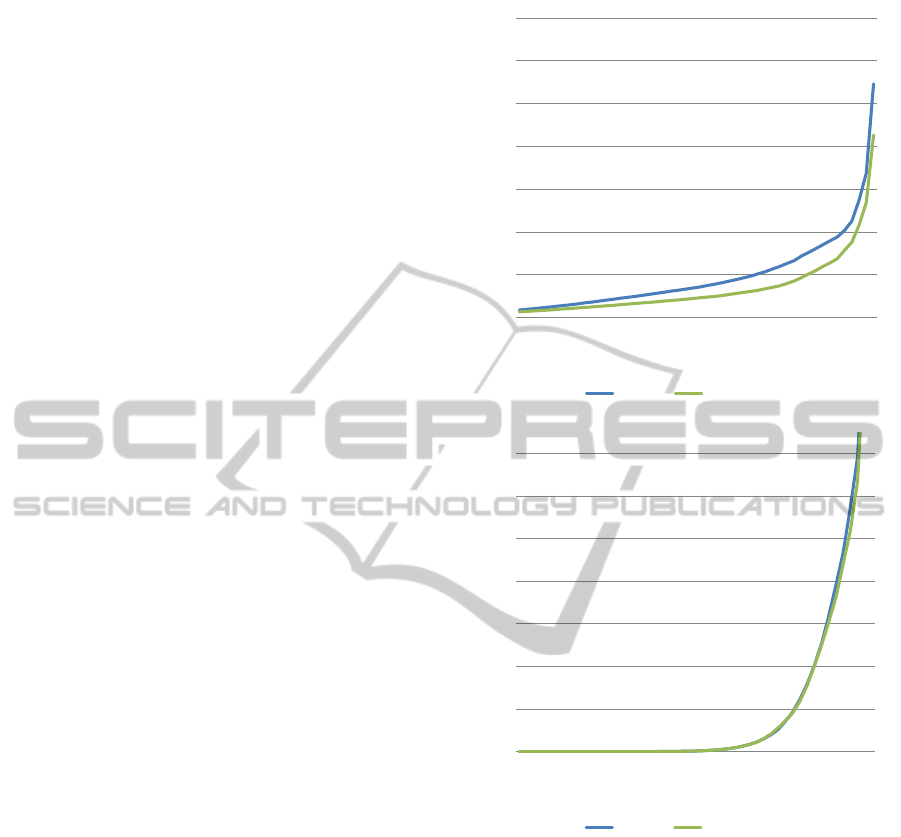
Figure 7 demonstrates the effectiveness of the
spherical wavelets for different compression ratios.
This graph can be used to read the reduction in coeffi-
cients for a certain norm. For example in Figure 7(a),
to reach an L
1
-norm of 20, the sperical wavelets use
9% less coefficients. A first observation is that for a
relatively diffuse BRDF, as shown in (a), the spher-
ical wavelet outperforms the 2D Haar wavelet over
all compression ratios. Second, for a more specu-
lar BRDF, as shown in (b), both wavelets perform
equally well. If we perform this experiment on the
entire BRDF database, spherical wavelets require on
average 20% less coefficients. In the best case we ob-
served 40% reduction in coefficients. A comparison
between our basis selection algorithm and regular 2D
parameterisation is shown in Figure 1.
5 CONCLUSIONS
This paper has introduced the use of nearly-
orthogonal spherical wavelets to perform rendering
at higher quality and lower computational cost. Our
evaluation shows that spherical wavelets often outper-
form 2D Haar wavelets, because they avoid inherent
0
20
40
60
80
100
120
140
50
45
40
35
30
25
20
15
10
5
L1-norm
% of coefficients retained
2D Haar
Bonneau
(a)
0
20
40
60
80
100
120
140
50
45
40
35
30
25
20
15
10
5
L1-norm
% of coefficients retained
2D Haar
Bonneau
(b)
Figure 7: Wavelet performance for different compression
ratios: (a) almost diffuse BRDF; (b) specular BRDF. It is
shown that material properties are a good indicator for an
on-the-fly choice of compression ration.
parameterisation errors. By utilising prior knowledge
of scene materials, we can adaptively choose an ap-
propriate wavelet based on a specularity criterium.
Separation of materials in diffuse and specular pro-
vides only a rough categorisation, but in practise we
observed that compression performance of spherical
versus 2D Haar wavelets is strongly linked with these
properties.
ExploitingMaterialPropertiestoSelectaSuitableWaveletBasisforEfficientRendering
223
0
20
40
60
80
100
120
140
160
180
cumulative error
6500 BRDF slices
Octahedron
2D
Figure 8: Cumulative parameterisation error compared to the ground truth. Octahedron (spherical) parameterisation outper-
forms regular 2D parameterisation.
ACKNOWLEDGEMENTS
This work has been made possible with the help of
a PhD specialization bursary from the IWT. The au-
thors acknowledge financial support from the Euro-
pean Commission (FP7 IP SCENE).
REFERENCES
Antonini, M., Barlaud, M., Mathieu, P., and Daubechies, I.
(1992). Image coding using wavelet transform. IEEE
Transactions on Image Processing, 1(2):205–220.
Bilgili, A.,
¨
Ozt
¨
urk, A., and Kurt, M. (2011). A general brdf
representation based on tensor decomposition. Com-
put. Graph. Forum, 30(8):2427–2439.
Bonneau, G.-P. (1999). Optimal triangular haar bases for
spherical data. LMC - CRNS.
Dutr
´
e, P., Bala, K., and Bekaert, P. (2006). Ad-
vanced global illumination, 2nd edition. A K Peters
(http://www.akpeters.com/).
Haber, T., Fuchs, C., Bekaert, P., Seidel, H.-P., Goesele, M.,
and Lensch, H. P. A. (2009). Relighting objects from
image collections.
Kajiya, J. T. (1986). The rendering equation. In Pro-
ceedings of the 13th annual conference on Computer
graphics and interactive techniques, SIGGRAPH ’86,
pages 143–150, New York, NY, USA. ACM.
Lessig, C. (2007). Orthogonal and symmetric haar wavelets
on the sphere. Master thesis - University of Toronto.
Ma, W.-C., Hsiao, C.-T., Lee, K.-Y., Chuang, Y.-Y., and
Chen, B.-Y. (2006). Real-time triple product relight-
ing using spherical local-frame parameterization. Vis.
Comput., 22(9):682–692.
Matusik, W., Pfister, H., Brand, M., and McMillan, L.
(2003). A data-driven reflectance model. ACM Trans-
actions on Graphics, 22(3):759–769.
Ng, R., Ramamoorthi, R., and Hanrahan, P. (2004). Triple
product wavelet integrals for all-frequency relighting.
ACM Trans. Graph., 23(3):477–487.
Ngan, A., Durand, F., and Matusik, W. (2005). Experi-
mental analysis of brdf models. In Proceedings of
the Sixteenth Eurographics conference on Rendering
Techniques, EGSR’05, pages 117–126, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Okabe, T., Sato, I., and Sato, Y. (2004). Spherical harmon-
ics vs. haar wavelets: Basis for recovering illumina-
tion from cast shadows. In Shadows, Proc. Conf. Com-
puter Vision and Pattern Recognition, pages 50–57.
Praun, E. and Hoppe, H. (2003a). Spherical parametrization
and remeshing. ACM Trans. Graph., 22(3):340–349.
Praun, E. and Hoppe, H. (2003b). Spherical parametrization
and remeshing. ACM TOG, 22(3):340–349.
Ruiters, R. and Klein, R. (2010). A compact and editable
representation for measured brdfs. Technical Report
CG-2010-1, University of Bonn.
Schr
¨
oder, P. and Sweldens, W. (1995). Spherical wavelets:
Efficiently representing functions on the sphere. Uni-
versity of South Carolina.
Sun, W. and Mukherjee, A. (2006). Generalized wavelet
product integral for rendering dynamic glossy objects.
In ACM SIGGRAPH 2006 Papers, SIGGRAPH ’06,
pages 955–966, New York, NY, USA. ACM.
Tsai, Y.-T., Chang, C.-C., Jiang, Q.-Z., and Weng, S.-C.
(2008). Importance sampling of products from illumi-
nation and brdf using spherical radial basis functions.
The Visual Computer, 24(7-9):817–826.
Yu, T., Wang, H., Ahuja, N., and Chen, W.-C. (2006).
Sparse lumigraph relighting by illumination and re-
flectance estimation from multi-view images. In ACM
SIGGRAPH 2006 Sketches, SIGGRAPH ’06, New
York, NY, USA. ACM.
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
224
