
Permutation Entropy of the Electroencephalogram Background
Activity in Alzheimer’s Disease
Investigation into the Incidence of Repeated Values
Samantha Simons and Daniel Abásolo
Centre for Biomedical Engineering, Department of Mechanical Engineering Sciences, Faculty of Engineering and Physical
Sciences, University of Surrey, Guildford, U.K.
Keywords: Alzheimer’s Disease, Electroencephalogram, Non-Linear Analysis, Permutation Entropy.
Abstract: This pilot study applied Permutation Entropy (PE), a non-linear symbolic measure, and a novel modification
(modPE), to investigate the regularity of electroencephalogram (EEG) signals from 11 Alzheimer’s disease
(AD) patients and 11 age-matched controls given input parameters n (embedding vector), τ (coarse graining)
and slide (difference between the start of two concurrent embedding vectors). PE discriminated better than
modPE with controls showing reduced regularity over AD patients. Increasing τ identified the greatest
differences between EEG signals. Longer embedding vectors were also more able to identify differences.
The greatest difference between groups was at Fp1 with n,τ,slide = 3,10,1 (p=0.0112 Kruskal Wallis with
Bonferroni). Subject and epoch based leave-one-out cross validation was carried out with thresholding from
Receiver Operating Characteristic Curves. The greatest ability to correctly identify AD patients and
controls were 81.82% (Fp2 n,τ,slide = 7,4,4, PE and modPE, F7 n,τ,slide = 3,10,1, PE and modPE) and
90.91% (Fp1 n,τ,slide = 3,10,1, PE and modPE), respectively. The maximum accuracy (both groups
correctly identified) was 81.82% seen at many electrode and input combinations. All are with subject based
analysis. This suggests that PE can identify changes in EEG signals in AD, given appropriate variables.
However, modPE makes little improvement over PE.
1 INTRODUCTION
Alzheimer’s Disease (AD) is a neurological
condition of complex aetiology producing
progressive symptoms of memory and function loss
caused by modification of amyloid β and
hyperphosphorated tau in neurons, modifying
information transition in the brain (Pieyani et al,
2011). The ‘preclinical’ phase of the disease, where
the AD patient is undiagnosed, can be as long as 20
years (Reiman et al, 2012) due to the slow symptom
onset and possible misdiagnosis, caused by the range
of symptoms which can be presented (McKann et al,
2011). With the development of more effective
treatments for AD and the increase in the number of
patients suffering from this disease, the need for
early, accurate diagnosis is imperative to ensure that
treatments can be utilised effectively.
There is evidence that the progress of the disease
can be detected through changes of brain signals
measured with an electroencephalogram (EEG)
(Dauwels, Vialatte and Cichocki, 2010). The
disease must be highly progressed for visual
identification from EEG signals but signal
processing techniques may improve the ease at
which changes due to AD can be seen in the early
stages of the disease.
Non-linear signal processing has been shown to
reliably identify changes in EEG signals in AD
patients including the slowing of EEG signals and
increased signal regularity and decreased signal
complexity (e.g. Abásolo et al, 2006; Dauwels,
Vialatte and Cichocki, 2010; Escudero et al, 2006).
Permutation Entropy (PE) is a symbolic, non-linear
method that calculates the complexity of a signal by
identifying different patterns in it (Bandt and
Pompe, 2002). However, information is lost about
the magnitude of the patterns (Zanin et al, 2012) and
so a number of modifications have been proposed to
improve results when used with biological signals
(Bian et al, 2012; Xiao-Feng and Yue, 2009).
In this pilot study PE and a novel modification of
PE (modPE) are tested for investigating the
97
Simons S. and Abásolo D..
Permutation Entropy of the Electroencephalogram Background Activity in Alzheimer’s Disease - Investigation into the Incidence of Repeated Values.
DOI: 10.5220/0004721000970103
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 97-103
ISBN: 978-989-758-011-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
regularity of EEG signals of AD patients in
comparison to age-matched controls. It is
hypothesised that the modPE method will show clear
differences between the two groups, while PE will
show reduced differences between the two groups.
Further, it is hypothesised that the AD patients will
show an increased EEG regularity when compared
to the control subjects.
The paper is arranged as follows. Section 2
introduces the test database and the methods used in
this study. Section 3 contains results and a
discussion is held in section 4. Section 5 contains
the conclusion of this study.
2 METHODS
2.1 EEG Signals Database
This database has been described in a number of
different studies (e.g. Escudero et al, 2009). The
pertinent points are repeated here for completeness.
The sample group contained 22 subjects, 11
probable AD patients (6 men and 5 women, 72.5 ±
8.3 years, mean ± standard deviation (SD)), who had
a Mini-Mental State Examination (MMSE) score of
13.1 ± 5.9 (mean ± SD) and 11 age-matched controls
(4 women and 7 men, 72.8 ± 6.1 years, mean ± SD)
with a MMSE score of 30 ± 0 (mean ± SD). The
MMSE is a long established method of measuring
the level of cognitive function of a patient (Folstein,
Folstein and McHugh, 1975). Full ethical approval
was obtained for the collection and use of this
database.
Signals were recorded at 256Hz with a 12-bit
analogue to digital converter using the international
10-20 electrode placement system (electrodes Fp1,
Fp2, F3, F4, C3, C4, P3, P4, O1, O2, F7, F8, T3, T4,
T5, T6, Fz, Cz and Pz) with subjects in an awake but
resting state with closed eyes. In excess of 5
minutes of data were recorded from each subject.
This data was then reviewed by a clinician who
selected 5 second epochs (1280 data points) with
minimal electromyographic activity and no
movement and electrooculographic artefacts. These
epochs were copied for off-line analysis and were
then further filtered using a Hamming window finite
impulse band-pass filter with cut-off frequencies at
0.5 and 40Hz to remove DC components and
residual noise. For each subject, 30.0 ± 12.5 (mean
± SD) epochs were collected. All epochs were
tested with the methods described in this paper.
2.2 Permutation Entropy
PE is a symbolic dynamics non-linear method which
has been shown to be robust to noise and can be
applied to short time series (Bandt and Pompe,
2002). The method is as follows (Bandt and Pompe,
2002):
Take the first embedding vector of the dataset n
data points long, skipping τ data points between
each data point selected to join the embedding
vector. I.e. given time series {x(i), i = 1,2,…},
embedding vector = x(i), x(i+τ), …, x(i+(n-1)τ).
Assign the lowest data point in the embedding
vector 0, the second lowest 1 and on until all data
points in the embedding vector have been replaced
with their ranking order.
Collect a new embedding vector from the original
dataset. The first data point is slid further along
the original dataset from the first data point of the
previous embedding vector. The subsequent data
points of the embedding vector are found using the
same pattern as the first embedding vector from its
first data point. The movement of vectors along
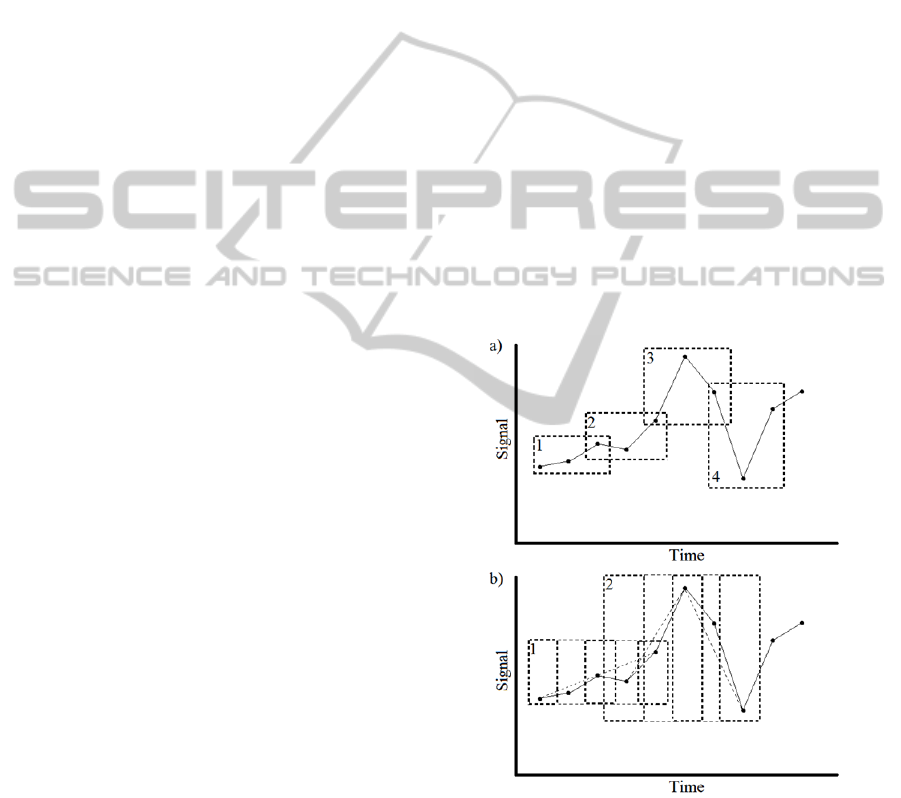
the dataset is shown in Figure 1.
Figure 1: Two graphs showing how different combinations
of n,τ,slide move along the same dataset with a) showing
3,1,2 and b) showing 3,2,4. In figure b) the dashed line
between points indicate the pattern of the embedding
vector created by τ=2.
Again replace this with the ranking of the new
vector as detailed in the previous point.
Continue this until all possible embedding vectors
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
98

have been created and ranked. Then calculate the
PE with equation 1.
k
v
vv
PPslidenPE
1
2
log),,(
(1)
where k is the number of different sub-sequence
ranked vectors and P
v
is the fraction of the sub-
sequence ranked vectors. Equation 1 is similar to
Shannon’s Entropy (Shannon, 1948). A less regular
signal will have a greater range of embedding
vectors and, therefore, a higher PE. Given the
pattern recognition method in PE, where the ranking
of each data point in order of assent is mapped back
to their position in the original vector, {0.2 0.5 0.1
0.4 0.7} would create the ranking {1 3 0 2 4}.
The outcome of PE will be influenced by the
choice of n, τ and slide. A greater value of n, the
embedding dimension, will give a greater possible
range of ranking vectors and, therefore a greater
resolution. Bandt and Pompe (2002) recommended
n=3 to 7 but n! must be less than the length of the
original time series. However, testing with epilepsy
patients showed n=3 and 4 were too small to be of
use (Cao et al, 2004). In this study this range will be
adhered to along with testing of n=10 to identify if
values greater than n=7 may also identify
statistically significant differences between the two
study groups.
Coarse-graining of the recorded EEG signal for
creation of the sub-sequence vectors is carried out
by τ. Initially Bandt and Pompe (2002) used τ=1 but
it was identified that this may not be the optimum
value for signal analysis (Cao et al, 2004). No
studies have been completed to identify the most
reliable range of τ and there is little consensus in the
studies already completed using PE on the value(s)
chosen for τ. The maximum τ seen in biological
studies is 50, used to investigate EEGs of AD
patients (Frantzidis et al, 2012) though this study
produced results showing AD patients with more
irregular EEGs, a finding inconsistent with the large
body of other, already published results from similar
studies. In this study, τ=1 to 4 was chosen with a
further test of τ=10.
There is another variable that has not yet been
investigated by previous work on PE. This is the
movement of the sub-sequence vector along the
original data set and will be denoted by slide in this
paper. All previous papers have used slide=1 but
this may not be the optimal choice of variable and
could have a significant effect on the PE calculation
given its interaction with the other two input
variables. Therefore, this study looked at slide=1 to
4.
The combinations of n,τ,slide tested in this study
are summarised in Table 1, chosen to investigate the
influence of each input variable and variable
combinations and to compare how low and high
input variable combinations interact:
Table 1: Combinations of input variables tested.
n τ slide
3 to 7, 10 1 1
3 2 to 4, 10 1
3 1 2 to 4
7 4 1, 4
The results were normalised to allow for direct
comparison between different variations in n, τ and
slide. Equation 2 shows the normalisation
procedure:
)!ln(
),,(
),,(
n
slidenPE
slidenPE
n
(2)
with ln(n!) the maximum number of ranking
permutations given the length of the ranking vector.
Note that the number of possible permutations is not
dependent on τ or slide as these do not directly affect
the theoretical maximum of possible permutations.
2.3 Modified Permutation Entropy
As previously mentioned, PE loses information
which relates to the relative magnitude of the sub-
sequence vector data points, including ignoring any
repeated values, giving the first repeated value in the
vector (the value to the left of the vector) a lower
integer than subsequent repeats and so on until all
repeats are accounted for (Bandt and Pompe, 2002).
With biological datasets this can cause a significant
loss of information due to the level of sampling
applied in the data collection phase or the
information needed being held in the signal
amplitude (Bian et al, 2012).
A number of methods have been proposed to
improve the PE algorithm when applied to biological
datasets, Fine-grained PE (FGPE) (Xiao-Feng and
Yue, 2009), Weighted permutation entropy (WPE)
(Fadlallah et al, 2013) and index-modified PE
(imPE- identified as mPE in the seminal paper)
(Bian et al, 2012). FGPE adds a further argument to
the sub-sequence ranking vector which relates
mathematically to the specific values contained in
the sub-sequence vector but maintains the PE
method in all other aspects. WPE creates a
multiplication factor of each logarithmic calculation
which are created using amplitude information from
each embedding vector. However, imPE allows for
PermutationEntropyoftheElectroencephalogramBackgroundActivityinAlzheimer'sDisease-Investigationintothe
IncidenceofRepeatedValues
99

repeated values to be given the same ranking value.
The created ranking vector from imPE does not
follow the same method as PE, unlike FGPE. The
ranking of each data point in order of increasing
value is not mapped back to their position in the
original embedding vector, as in PE. Instead the
ranking denotes the position of the data point in the
embedding vector in an order that describes
ascending value of each of those data points. The
vector {0.2 0.5 0.1 0.4 0.7} described before with
PE as pattern {1 3 0 2 4} would now be {2 0 3 1 4}
with imPE. This is because as, when reordered, the
lowest value 0.1 comes from the third position,
denoted as two when starting from zero rather than
one, the next lowest 0.2 is from position one,
denoted zero in the ranking, and so on (Bian et al,
2012).
The method proposed in this paper, modPE,
combines the ability to cope with repeated values
within the embedding vector suggested by Bian et al
(2012) with the ranking mapping used in the original
PE method. The method will be described as PE
though repeated values will retain the same ranking
index, rather than being given differing ranking
indexes. Retention of information pertaining to
repetition of data points in an embedding vector of
two or more instances with one or more values will
be incorporated into the method. For example sub-
sequence vector {0.2 0.5 0.1 0.2 0.7} will create the
ranking {1 3 0 1 4}. Note position 2 is not recorded
in the ranking vector as there are two 1’s.
The variables for n, τ and slide will be the same
as those tested for PE to allow for easy comparison.
Again the results will also be normalised to allow for
direct comparison by the method identified by
equation 2, though the denominator for this method
will be calculated differently due to the increased
numbers of possible permutations. For modPE, this
was calculated by summing the number of different
combinations given different repeated values.
2.4 Statistical Analysis
Results given PE and modPE analysis from all
epochs were averaged for each electrode from each
subject. Normality of these average values was
tested using Lilliefors test. Statistically significant
differences were identified between the 11 AD
patients and the 11 controls using Student’s t test if
the data were found to be normally distributed and
Kruskal Wallis if not. Statistical significance was
indicated with p<0.05 in both cases with a
Bonferroni correction for the 16 electrodes. This
correction leads to an uncorrected statistical
significance of 0.0031.
Statistically significant combinations were
further investigated using Receiver Operating
Characteristic (ROC) curves (Fawcett, 2006) with a
leave-one-out cross-validation procedure.
Sensitivity is defined as the proportion of correctly
identified AD patients and specificity is defined as
the proportion of correctly identified controls, while
accuracy identifies the total number of correctly
identified AD and control subjects combined.
3 RESULTS
Controls have a higher PE and modPE value than
AD patients, suggesting an increase of EEG
regularity due to this form of dementia. At low n, τ
and slide combinations, electrodes F7, T3 and T4 do
not follow this trend. At n = 5 to 7 with τ and slide
= 1 electrodes Fp1, Fp2, F7, F8, C4, T3, T4, T5 do
not follow this trend though all these cases show a
difference between values of less than 2%. At these
values of n, increasing τ reduces the number of
electrodes not following the trend but the modPE is
less able to distinguish between the two groups, with
almost all electrodes showing an increased modPE
for patients as τ increases. With n,τ,slide = 10,1,1
electrodes T3, T4 and T5 show increased irregularity
in AD patients. In total, 75.21% of calculations
showed increased irregularity in controls over AD
patients, but this was not equally distributed; some
input parameters showed increased irregularity in
EEG signals of AD patients in all electrodes and
others increased regularity in EEG signals of AD
patients in all electrodes. Results were found to be
predominately normally distributed except for when
τ=10. All electrodes showing statistically significant
differences between the two groups are presented in
Table 2.
With low values of n with slide and τ both equal
to 1 both methods were unable to distinguish with
statistical significance between the two test groups at
any electrode. The ability to distinguish between the
two groups increased as n increased. The choice of τ
was found to be the most critical in distinguishing
between the two test groups. Slide values had little
effect on distinguishing between the two groups.
However, a greater significance was seen between
the two groups as slide increased though this did not
reach statistical significance.
All statistically significant electrode
combinations were then subjected to leave-one-out
cross-validation analysis with the threshold
identified through ROC plots. The results are also
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
100

Table 2: Statistical results for PE and modPE. Statistical significance calculated with Student’s t Test is identified by S
while statistical significance calculated with Kruskal Wallis is denoted KW. P values in this table have already been
corrected with a Bonferroni correction. As such, statistical significance is denoted as p<0.05. Leave-one-out with subject
based analysis is denoted SB and with epoch based analysis is denoted EB.
Electrode n,τ,slide Method Normalised
control
(mean±SD)
Normalised
AD
(mean±SD)
Statistical
method
P with
Bonferroni
correction
Leave-
one-out
method
Sensitivity
(%)
Specificity
(%)
Accuracy
(%)
Fp1 3,10,1 PE 0.9957
±0.0016
0.9886
±0.0058
KW 0.0112 SB 72.73 90.91 81.82
EB 60.93 69.55 65.04
modPE 0.6588
±0.0011
0.6541
±0.0039
KW 0.0224 SB 72.73 90.91 81.82
EB 61.52 71.47 66.26
Fp2 7,4,1 PE 0.7981
±0.0071
0.7860
±0.0082
S 0.0224 SB 63.64 81.82 72.73
EB 76.61 69.86 73.56
7,4,4 PE 0.6654
±0.0020
0.6609
±0.0033
S 0.0144 SB 63.64 81.82 72.73
EB 67.54 73.05 70.03
F7 3,10,1 PE 0.9964
±0.0023
0.9927
±0.0034
KW 0.0368 SB 81.82 81.82 81.82
EB 58.09 70.68 64.18
modPE 0.6593
±0.0015
0.6568
±0.0023
KW 0.0368 SB 81.82 81.82 81.82
EB 56.36 64.51 60.30
held in Table 2. For subject-based analysis, the
greatest sensitivity of 81.82% was obtained at
electrode F7 with n,τ,slide = 3,10,1 and the greatest
specificity was 90.91% at electrode Fp1 with
n,τ,slide = 3,10,1. In both cases this is the same for
both PE and modPE. The greatest accuracy,
81.82%, was seen at a number of electrode and
calculation combinations with subject based
methods. Epoch based results were less sensitive to
differences between the two groups, with a
maximum sensitivity of 76.61% with Fp2 at n,τ,slide
= 7,4,1, a maximum specificity of 73.05% with Fp2
at n,τ,slide = 7,4,4, and an accuracy of 73.56% with
Fp2 at n,τ,slide = 7,4,1. This shows a significant
ability to distinguish between controls and AD
patients at this electrode.
4 DISCUSSION
In this study we tested PE and a novel version of PE,
denoted modPE, to analyse the EEG signals of 11
AD patients and 11 age-matched controls. PE is a
symbolic non-linear method and other symbolic
non-linear methods, such as Lempel-Ziv
Complexity, have been shown to discriminate
between the EEG signals of AD patients and
controls with statistical significance (Abásolo et al,
2006). While PE is not a new method, little research
has been carried out into its behaviour with EEG
signals from AD patients.
The increased signal irregularity of control
subjects when compared to AD patients EEG signals
supports the hypothesis stated in section 1 that
controls show a less regular signal than AD patients.
Morabito et al (2011; 2012) tested AD and MCI
subjects using PE and multivariate multi-scale PE
with n=3 and τ=1, also finding increased irregularity
in control subject EEGs in comparison to AD
patients. However, modPE did not perform
significantly better than PE as hypothesised, a
hypothesis which was based on the work by Bian et
al (2012) where imPE was used with input
parameters n,τ = 3-7,1 and 3,1-4 on R-R intervals
from ECG signals rather than complete EEG signals.
The inability of small n (n < 5) to identify
changes in signals caused by pathological changes in
the brain was identified by Cao et al (2004) testing
combinations of input parameters which included
n=3-7 and τ=2,3 and 10. This is supported by our
results, with low values of n unable to discriminate
between control subjects and AD patients. Further,
ranges of n outside those suggested by Bandt and
Pompe (2002) can be utilised successfully with this
method, shown by the support of the trend of
reduced regularity in AD EEG signals seen with the
lower values of n. These findings suggest that the
differences in EEG signals between AD patients and
controls only manifest themselves in larger patterns
and similar smaller patterns are seen in both signal
types.
The influence of τ was the greatest of all input
variables on the ability of PE and modPE in
distinguishing between the two groups. This input
variable effectively coarse-grains the signal before
calculating PE or modPE. It has been found that
coarse-graining of signals can provide a greater
understanding of those signals under investigation
and in some cases has increased the ability to
distinguish between differing groups such as AD
PermutationEntropyoftheElectroencephalogramBackgroundActivityinAlzheimer'sDisease-Investigationintothe
IncidenceofRepeatedValues
101

patients and controls (Escudero et al, 2006; Simons,
Abásolo and Escudero, 2012a; 2012b). The ability
of this method to improve understanding and
discrimination and the link between coarse-graining
and τ supports the findings of this study.
It was found in the range of slide variables tested
in this study that this had no influence on the ability
of the methods to distinguish between the two
groups, though a trend was seen in the resulting p
values that suggests that increasing slide may
improve resolution for investigation of EEG signals.
However, significantly increasing slide reduces the
data investigated directly in the calculation of PE.
Given the findings of this pilot study, it is
suggested that n,τ,slide = 3,10,1 is the optimum
selection of parameters for discriminating between
AD patients and controls. However, there may be
another combination with higher n and τ values
which has not been tested in this study which is
more able to discriminate between the two groups.
The novel method of modPE was introduced to
investigate the improvement over PE by retaining
the information contained in the appearance of
repeated values, identified as a key component of the
changing R-R intervals from ECG signals
investigated in the paper by Bian et al (2012) and
vital to distinguish between the data from patients
and healthy controls. This study does not confirm
their findings, both as PE identified statistically
significant differences in the EEG signals of AD
patients and controls and that modPE, while also
identifying statistically significant differences, did
not provide a large increase in the ability of the
methodology to distinguish between signals from
healthy controls and patients.
This change in the abilities of the two methods to
distinguish between the two groups is thought to be
due to significant differences in the signal types
analysed and, therefore, the appearance of repeated
values. An ECG is more prone to repeatability than
signals from other, more complex neuronal systems
such as the EEG from the brain. This means that the
probability of repeated values within a given pattern
from an ECG trace is significantly higher than that
from an EEG signal. Furthermore, the focus of a
particular metric from a signal, such as the R-R
interval, rather than the entirety of a signal further
increases the possibility of repeated values.
While PE is currently undergoing wide ranging
testing (e.g. Fadlallah et al, 2013; Li et al, 2013;
Riedl, Müller and Wessel, 2013), there are few
studies applying this method to AD diagnosis. The
differences in signal regularity found by a majority
of PE and modPE calculations with this dataset are
comparable to those found with Multi Scale Entropy
(Escudero et al, 2006), historically the most accurate
method with this database.
Some limitations of this study should be
mentioned. The small sample size of this dataset
leads the findings of this work to be a pilot study.
Furthermore, a greater range of input variables must
be trialled to understand the optimum combination
of input variables to discriminate between these two
groups and other groups with similar pathologies
such as Mild Cognitive Impairment (Albert et al,
2011). In addition, recent evidence suggests that the
increased regularity observed in AD patients’ EEGs
with non-linear methods might be closely linked
with the slowing found with traditional spectral
techniques (Dauwels et al, 2011). Therefore, further
research looking at possible correlations between
different implementations of PE and spectral
techniques is needed. One possible option might
include synthetic signal analysis (Riedl, Müller and
Wessel, 2013). In spite of these shortcomings, PE
and modPE are able to distinguish changes in the
EEG signal of AD patients with a range of input
parameters.
5 CONCLUSIONS
This work has shown the application of PE and a
novel modified version of PE to the analysis of EEG
in AD patients in comparison to age-matched
controls. The findings with PE corroborate other
studies with this dataset and others with similar
methods, in that control subject’s EEGs were found
to be more irregular than those of AD patients. The
choices of input parameters were found to be a key
component in identifying the changes in the signal.
However, caution must be taken due to the small
size of the dataset studied.
REFERENCES
Abásolo, D., Hornero, R., Gómez, C., García, M., Lopez,
M., 2006 Analysis of EEG background activity in
Alzheimer’s disease patients with Lempel-Ziv
complexity and central tendency measure. Medical
Engineering and Physics, 28, pp. 315-322.
Albert, M. S., DeKosky, S. T., Dickson, D., Dubois, B.,
Feldman, H. H., Fox, N. C., Gamst, A., Holtzman,
D.M., Jagust, W. J., Petersen, R. C., Snyder, P. J.,
Carrillo, M. C., Thies, B., Phelps, C. H., 2011. The
diagnosis of mild cognitive impairment due to
Alzheimer’s disease:Recommendations from the
National Institute on Aging-Alzheimer’s Association
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
102

workgroups on diagnostic guidelines for Alzheimer’s
disease. Alzheimer’s & Dementia, 7, pp. 270-279.
Bandt, C., Pompe, B., 2002. Permutation entropy- a
natural complexity measure for time series. Physical
Review Letters, 88(17), 174102.
Bian, C., Qin, C., Ma, Q. D. Y., Shen, Q., 2012. Modified
permutation-entropy analysis of heartbeat dynamics.
Physical Review E, 85, 021906.
Cao, Y., Tung, W., Gao, J. B., Protopopescu, V. A.,
Hively, L. M., 2004. Detecting dynamical changes in
time series using the permutation entropy. Physical
Review E, 70, 046217.
Dauwels, J., Srinivasan, K., Ramasubba Reddy, M.,
Musha, T., Vialatte, F.-B., Latchoumane, C., Jeong, J.,
Cichocki, A., 2011. Slowing and loss of complexity in
Alzheimer’s EEG: Two sides of the same coin?.
International Journal of Alzheimer’s Disease, 2011,
539621.
Dauwels, J., Vialatte, F., Cicjocki, A., 2010. Diagnosis of
Alzheimer’s disease from EEG signals: Where are we
standing?. Current Alzheimer’s Research, 7, pp. 487-
505.
Escudero, J., Abásolo, D., Hornero, R., Espino, P., López,
M., 2006. Analysis of electroencephalograms in
Alzheimer’s disease patients with multiscale entropy.
Physiological Measurement, 27, pp. 1091-1106.
Fadlallah, B., Chen, B., Keil, A., Príncipe, J., 2013.
Weighted-permutation entropy: A complexity measure
for time series incorporating amplitude information.
Physical Review E, 87, pp. 022911.
Fawcett, T., 2006. An introduction to ROC analysis.
Pattern Recognition Letters, 27, pp. 861-874.
Folstein, M. F., Folstein, S. E., McHugh, P. R., 1975.
Mini-mental state. A practical method for grading the
cognitive state of patients for the clinician. American
Journal of Physiology: Heart and Circulatory
Physiology, 12, pp. 189-198.
Frantzidis, C. A., Ladas, A., Diamantoudi, M. D.,
Semertzidou, A., Grigoriadou, E., Tsolaki, A., Liapi,
D., Papadopoulou, A., Kounti, F., Vivas, A.B.,
Tsolaki, M., Pappas, C., Bamidis, P.D., 2012. What
are the symbols of Alzheimer? A permutation entropy
based symbolic analysis for the detection of early
changes of the electroencephalographic complexity
due to mild Alzheimer. In Proceedings of the 12
th
International Conference on Bioinformatics, IEEE.
Li, D., Liang, Z., Wang, Y., Hagihira, S., Sleigh, J. W., Li,
X., 2013. Parameter selection in permutation entropy
for an electroencephalographic measure of isoflurane
anesthetic drug effect. Journal of Clinical Monitoring
and Computing, 27, pp. 113-123.
McKann, G. M., Knopman, D. S.,. Chertkow, H., Hyman,
B. T., Jack, C. R., Kawas, C. H., Klunk, W. E.,
Koroshetz, W. J., Manly, J. J., Mayeux, R., Mohs, R.
C., Morris, J. C., Rossor, M.N., Scheltens, P., Carrillo,
M. C., Thies, B., Weintraub, S., Phelps, C. H., 2011.
The diagnosis of dementia due to Alzheimer’s disease:
Recommendations from the National Institute on
Aging-Alzheimer’s Association workgroups on
diagnostic guidelines for Alzheimer’s disease.
Alzheimer’s & Dementia, 7, pp. 263-269.
Morabito, G., Bramanti, A., Labate, D., la Foresta, F.,
Morabito, F.C., 2011. Early detection of Alzheimer’s
onset with permutation entropy analysis of EEG.
Natural Intelligence: the INNS Magazine, 1(1), pp. 30-
32.
Morabito, F. C., Labate, D., la Foresta, F., Bramanti, A.,
Morabito, G., Palamara, I., 2012. Multivariate multi-
scale permutation entropy for complexity analysis of
Alzheimer’s disease EEG. Entropy, 14, pp. 1186-
1202.
Pievani, M., de Haan, W., Wu, T., Seeley, W. W., Frisoni,
G. B., 2011. Functional network disruption in the
degenerative dementias. Lancet Neurology, 10, pp.
829-843.
Reiman, E., Quiroz, Y., Fleisher, A., Chen, K., Velez-
Pardo, C., Jimenez-Del-Rio, M., Fagan, A. M., Shah,
A. R., Alvarez, S., Arbelaez, A., Giraldo, M., Acosta-
Baena, N., Sperling, R. A., Dickerson, B., Stern, C E.,
Tirado, V., Munoz, C., Reiman, R. A., Huentelman,
M. J., Alexander, G. E., Langbaum, J. B. S., Kosik, K.
S., Tariot, K. P., Lopera, F., 2012. Brain imaging and
fluid biomarker analysis in young adults at genetic risk
for autosomal dominant Alzheimer’s disease in the
presenilin E280A kindred: a case control study. Lancet
Neurology, 11, pp. 1048-1056.
Riedl, M., Müller, A., Wessel, N., 2013. Practical
considerations of permutation entropy. The European
Physical Journal Special Topics, 222, pp. 249-262.
Shannon, C. E., 1948. A mathematical theory of
communication. The Bell System Technical Journal,
27, pp. 379-423.
Simons, S., Abásolo, D., Escudero, J., 2012a. Quadratic
sample entropy and multiscale quadratic sample
entropy of the electroencephalogram in Alzheimer’s
disease. In Proceedings of the 5
th
International
Conference on Medical Signals and Information
Processing.
Simons, S., Abásolo, D., Escudero, J., 2012b. Fuzzy
entropy and multiscale fuzzy entropy of the
electroencephalogram in Alzheimer’s disease. In
Proceedings of the Young Researchers Futures
Meeting-Neural Engineering, Royal Academy of
Engineering.
Xiao-Feng, L., Yue, W., 2009. Fine-grained permutation
entropy as a measure of natural complexity for time
series. Chinese Physics B, 18(7), pp. 2690-2695.
Zanin, M., Zunino, L., Rosso, O. A., Papo, D., 2012.
Permutation entropy and its main biomedical and
econophysics applications: A review. Entropy, 14, pp.
1553-1577.
PermutationEntropyoftheElectroencephalogramBackgroundActivityinAlzheimer'sDisease-Investigationintothe
IncidenceofRepeatedValues
103
