Solving Single Vehicle Pickup and Delivery Problems with Time

Windows and Capacity Constraints using Nested Monte-Carlo Search

Stefan Edelkamp and Max Gath

Institute for Artiﬁcial Intelligence, TZI - Center for Computing and Communication Technologies, Bremen, Germany

Keywords:

Nested Monte-Carlo Search, Single Vehicle Pickup and Delivery Problem (PDP), Traveling Salesman

Problem (TSP), Routing and Scheduling Problems.

Abstract:

Transporting goods by courier and express services increases the service quality through short transit times

and satisﬁes individual demands of customers. Determining the optimal route for a vehicle to satisfy transport

requests while minimizing the total cost refers to the Single Vehicle Pickup and Delivery Problem. Beside time

and distance objectives, in real world operations it is mandatory to consider further constraints such as time

windows and the capacity of the vehicle. This paper presents a novel approach to solve Single Vehicle Pickup

and Delivery Problems with time windows and capacity constraints by applying Nested Monte-Carlo Search

(NMCS). NMCS is a randomized exploration technique which has successfully solved complex combinatorial

search problems. To evaluate the approach, we apply benchmarks instances with up to 400 cities which have

to be visited. The effects of varying the number of iterations and the search level are investigated. The results

reveal, that the algorithm computes state-of-the-art solutions and is competitive with other approaches.

1 INTRODUCTION

Especially in urban districts, transporting goods by

courier and express services increases the service

quality through short transit times and satisﬁes indi-

vidual demands of customers. However, determin-

ing optimal routes for the planning and control of

transport requests in real-world operations involves a

set of practical complications. For instance, it is of-

ten mandatory to consider time windows at incom-

ing goods departments and the maximum velocity of

vehicles. Moreover, courier, express, and parcel ser-

vices (CEP) provide direct transports from one cus-

tomer to another customer without storing the loads

at a central depot to minimize the transit times. Par-

ticularly in recent years, there is an increasing demand

for CEP services by e-commerce companies to offer

same-day deliveries.

This paper addresses the Single Vehicle Pickup

and Delivery Problem (1VPDP) (Parragh et al., 2008),

which is concerned with determining a least cost

route for a single vehicle to satisfy customer requests

for transporting objects from an origin to a desti-

nation, while considering additional constraints (see

Figure 1). Thus, the particular application area is the

paired pickup and delivery of goods, which is also

known as the Traveling Salesman Problem (TSP) with

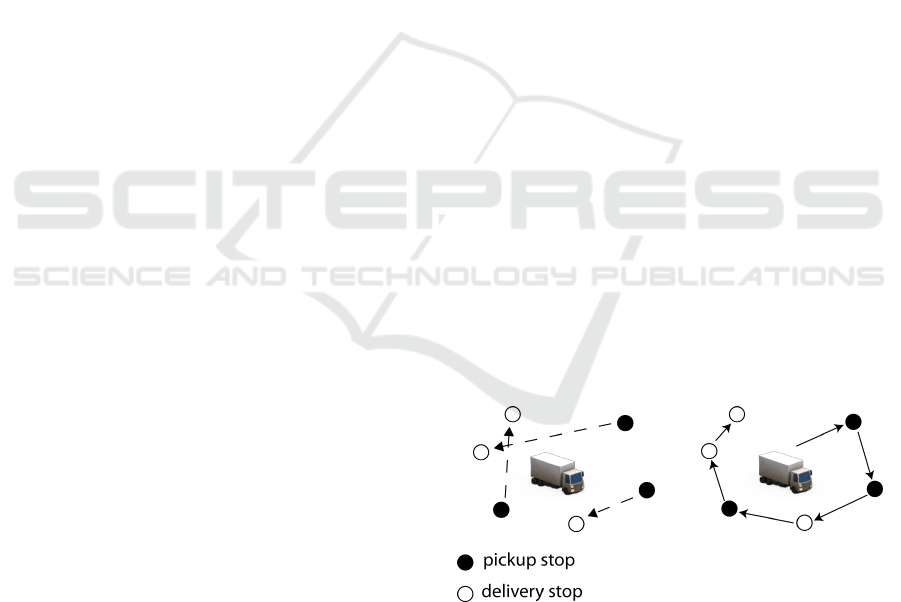
Figure 1: The Single Vehicle Pickup and Delivery Problem

and a solution with three orders (and six stops).

pickups and deliveries (PD) as well as time windows

(TW) and capacity (C) constraints.

Motivated by the success in (very-close-to) opti-

mal solving TSPs with time windows (TSPTWs) with

Nested Monte-Carlo Search (NMCS) (Cazenave and

Teytaud, 2012; Edelkamp et al., 2013) for transporta-

tion requests from and to a designated depot, in this

work we look at advances in combinatorial and ran-

domized search for the 1VPDPTW.

Orders are pairs of locations associated with the

resource and time constraints for the transport. For n

orders we obtain 2n + 1 possible locations of trans-

port actions. In our application, we work on an

underlying transport infrastructure represented by a

weighted graph. The initial distance matrix between

Edelkamp S. and Gath M..

Solving Single Vehicle Pickup and Delivery Problems with Time Windows and Capacity Constraints using Nested Monte-Carlo Search.

DOI: 10.5220/0004722300220033

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 22-33

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

pickup and delivery locations and a designated depot

are determined by shortest-path(s) searches. In sim-

pliﬁed benchmark settings, straight-line distances are

applied to points in the plane.

The paper is structured as follows. Firstly, Sec-

tion 2 speciﬁes the single vehicle PDP formally and

provides an overview of solution methods. Next, we

introduce NMCS and focus on its application to the

TSP. Section 3 presents the developed approach for

solving 1VPDP with NMCS with policy adaptation.

The evaluation including the description of applied

benchmarks, the experimental setup, and the results

are provided in Section 4. Moreover, we investigate

how to conﬁgure the approach to reach the best results

within shortest time. Finally, Section 5 concludes the

paper.

2 RELATED WORK

Section 2.1 gives an overview of the Pickup and De-

livery Problem (PDP) and speciﬁes the problem for-

mally. Next, Section 2.2 introduces Nested Monte-

Carlo Search (NMCS) and focuses on its application

to the Traveling Salesman Problem (TSP).

2.1 The Single Vehicle PDP

There are single- and multiple-vehicle PDP vari-

ants. In the literature single-vehicle problems are

also denoted as TSPs with pickup and deliveries

(TSPPD) (Gendreau et al., 1999; Hern

andez-P

erez

and Salazar-Gonz

alez, 2004). While the classical

PDP considers the multiple-vehicle variant to trans-

port all kinds of goods, the so-called dial-a-ride prob-

lem (DARP) (Cordeau and Laporte, 2003b) or hand-

icapped persons transportation problem (Toth and

Vigo, 1997) deals with passenger transport where ad-

ditional objective functions like minimizing the trans-

port times of the passengers have to be satisﬁed. In

unpaired PDPs transported goods are homogeneous

and exchangeable. Thus, each good can be deliv-

ered to any customer. In paired PDPs every good has

a unique sender and recipient. Most PDP variants

are hard combinatorial optimization problems (Ap-

plegate et al., 2011). The following deﬁnition of PDPs

extends the description provided by (Parragh et al.,

2008).

Deﬁnition 1 (Pickup-and-Delivery Problem). Let V

denote a set of vehicles and S a set of service requests.

Service requests are a super set of a set of pickup re-

quests P ⊂ S and a set of delivery request D ⊂ S \ P.

Thus, each service request is either a pickup request

p ∈ P or a delivery request d ∈ D. Moreover, O de-

notes a set of orders. An order o ∈ O contains exactly

one pickup request p

and one delivery request d

Given the costs c

i, j

for a vehicle v ∈ V for traveling

from i ∈ S to j ∈ S and choosing indicator variables

i, j



1, if (i, j) is part of the vehicle v’s tour

0, otherwise

(1)

the general objective function of PDP is

min

∑

v∈V

∑

j∈S

∑

i∈S

i, j

· x

i, j

(2)

with subject to

∑

v∈V

∑

i∈S

i, j

= 1 for all j ∈ S (3)

∑

v∈V

∑

j∈S

i, j

= 1 for all i ∈ S (4)

∑

v∈V

i, j

{

0,1

}

for all i, j ∈ S (5)

∑

v∈V

∑

j∈S

∑

i∈S

i, j

≤ |Y | − 1 for all Y ⊆ S. (6)

In a paired PDP the pickup and delivery requests

of an order o have to be served by the same vehicle v.

This is guaranteed by

∑

i∈S

i,p

−

∑

i∈S

i,d

= 0 for all i ⊆ S and v ∈ V. (7)

Moreover, time-window constraints as well as

time consumption at the warehouse/customer have to

be considered. If l

denotes the latest pickup/delivery

time, t

the time consumption of the loading or un-

loading process, r

the release time at s ∈ S and time

i, j

vehicle v’s time for driving from i to j

i, j

= 1 ⇒ l

≥ r

+time

i, j

(8)

has to be fulﬁlled. It is obvious that the pickup request

has to be visited before the delivery request d

can

successfully be satisﬁed. Thus, we require

i,p

= 1 ∧ x

i,d

= 1) ⇒ l

≤ r

. (9)

In addition, we have to ensure that the maximum ca-

pacity of a vehicle is not exceeded at any time. Let C

denote the current capacity of vehicle v at stop s ∈ S

and M

the maximum capacity of vehicle v, we re-

quire

≤ M

for all s ∈ S,v ∈ V. (10)

In our case we solve PDPs for one vehicle. Thus

the number of vehicles is restricted to |V | = 1. Note

that the deﬁnition leaves open, if the vehicle have to

return to the depot or not.

In the last decades, numerous efﬁcient heuris-

tics and meta-heuristics have been developed for the

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch

transportation domain and particularly in the area of

PDPs. There are exact solution methods (Ropke et al.,

2007) as well as numerous fast algorithms and meta-

heuristics for solving large problem instances like

tabu-search (Cordeau and Laporte, 2003a), simulated

annealing (Bent and Hentenryck, 2006), genetic algo-

rithms (Pankratz, 2005), and ant systems (Gajpal and

Abad, 2009), just to name a few.

The ﬁrst exact algorithm to optimally solve the

Single Vehicle Pickup and Delivery Problem with dy-

namic programming has been presented by (Psaraftis,

1983). However, the solver was limited to solve only

small problem instances with up to 10 service re-

quests. Thus, also meta-heuristics have been applied

to solve medium- and large-sized problems such as

generic algorithms (Jih and Hsu, 2004), tabu-search

(Landrieu et al., 2001), as well as simulated anneal-

ing and hill climbing methods (Hosny and Mumford,

2010).

2.2 Nested Monte-Carlo Search with

Policy Adaptation

Monte-Carlo Search is a randomized search algorithm

which iteratively performs random searches, so-called

rollouts, within the search space, until the algorithm

ﬁnds a valid solution, a maximum amount of time

is elapsed, or a maximum number of rollouts have

been performed. The search method has particularly

been applied, to solve problems with a huge search

space where no adequate lower and upper bounds are

available. In contrast, nested rollouts perform an ad-

ditional heuristic that determines next moves within

the rollouts, to guide the search (Yan et al., 2004).

In further applications, this heuristic is improved suc-

cessively to apply the algorithm for solving challeng-

ing combinatorial problems such as Klondike Soli-

taire (Bjarnason et al., 2009). Nested Monte-Carlo

Search (NMCS) (Cazenave, 2009) extends this ap-

proach by the concept of levels. At each level l, for

each possible move (decision) at the current node of

the decision tree it performs nested rollouts in level

l − 1. Recursively, level l − 1 investigates all pos-

sible successor moves of the selected move in level

l. If level l = 0, the search executes a random roll-

out. The best result in each level is propagated to

the higher level, to identify and choose the best move

found. Consequently, at each level, the best result has

to be saved, because searches in lower levels may ﬁnd

worse solutions.

NMCS has been further extended by adapting the

policy during the search and introducing the con-

cept of iterations (Rosin, 2011). Thus, if n denotes

the number of iterations, the algorithm performs n

Figure 2: An example of Nested Rollouot Policy Adaptation

(NRPA) with 2 level and 4 iterations.

searches in each level. While the NMCS investi-

gates all possible moves in depth d = l of the deci-

sion tree in level l −1, Nested Rollout Policy Adapta-

tion (NRPA) executes n nested searches in level l − 1,

that all start at the root of the decision tree and fol-

low a policy until they reach a leaf. After a search in

level l − 1 has been performed, the results are eval-

uated at level l and the policy is updated by the best

solution currently found. Beside, a learning rate α ad-

justs the impact of the solution found in level l − 1 to

the policy of level l. The algorithm is successfully ap-

plied for solving Crossword Puzzles as well as Mor-

pion Solitaire (Rosin, 2011). Figure 2 shows an ex-

ample of the NRPA search with 2 level and 4 itera-

tions. In addition, it illustrates the effects of higher-

and lower-level searches to the policy. Thus, the pol-

icy is either progressed, adapted, or copied. A com-

prehensive survey about Monte-Carlo search is pro-

vided by (Browne et al., 2012).

Recently, NRPA search has also been applied to

efﬁciently solve the well-known Traveling Salesman

Problem with Time Windows (TSPTW) optimal or

very close to the optimum for small problem instances

up to 50 cities (Cazenave and Teytaud, 2012). As

described, at level l = 0 of the recursive search a

nested rollout is invoked. The likelihood to chose a

move within a rollout is determined by the policy and

by three additional well-known heuristics for vehicle

routing problems, that are derived from (Solomon,

1987). Therefore, the resulting Bolzmann softmax

policy considers

1. the distance from the last city to the next city,

2. the amount of wasted time, if a city is visited too

early,

3. as well as the remaining time until the latest visit-

ing time of a following city.

Moreover, (Cazenave and Teytaud, 2012) extended

further domain speciﬁc knowledge to solve TSPTWs

with NRPA by restricting the possible successors

within the rollout function. With highest priority, they

force to visit cities, that reached the end of their lat-

est visiting time. The general idea is, to visit these

cities next, because they have to be visited anyway

and this has to be taken into account within further

rollouts. With second highest priority the algorithm

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

only considers cities, that not avoid to visit any other

cities afterwards in time.

If hard constraints such as time windows and

capacity constraints are not satisﬁed within a tour,

the costs increase signiﬁcantly for each violation.

In this case, the result of a rollout is a constraint

violating tour. Consequently, the algorithm mini-

mizes constraint violations with highest priority. De-

tails of the algorithm for solving TSPTWs are pro-

vided by (Cazenave and Teytaud, 2012). Algorith-

mic reﬁnements to accelerate the search are given

by (Edelkamp et al., 2013).

3 NRPA FOR SOLVING

SINGLE-VEHICLE PDPTW

For solving small- and medium-sized single vehicle

PDPs, we extended the NRPA algorithm for TSPTWs

of (Cazenave and Teytaud, 2012). We differ be-

tween problems with a vehicle whose capacity is re-

stricted by exactly one shipment at the moment and

a vehicle whose capacity is restricted by volume or

weight but independent by the number of transported

goods. Concerning both problems, pickup and de-

livery requests imposed by customer orders can be

viewed as cities in a particular TSP. Nevertheless, it

remains possible to have several requests at one loca-

tion. Therefore, each request is modeled as a unique

city which is located at the same location with identi-

cal coordinates.

3.1 Unit Capacities

If the delivery has to be executed immediately after

the pickup, we encounter the Stacker Crane Problem

(SCP) (Srour and van de Velde, 2013). Time window

constraints (TW) may be enforced. In the SCP of n

pickup and delivery orders, each delivery has to be ex-

ecuted immediately after the pickup is made. This can

be a result of imposed unit capacity, as a vehicle can

only serve one order at the same time. The SCP(TW)

is mapped back to an Asymmetric TSP(TW) as fol-

lows: the shortest path length from each delivery lo-

cation d

of an order o, is connected to all pickup loca-

tions j ∈ P. As a result, the input for the ATSP-solver

is a weighted matrix of size (n + 1) × (n + 1).

This mapping allows to apply the TSP(TW) solver

directly to solve SCPs. Including capacity constraints

solving the SCP is simple as the NMCS approach is

based on rollouts, where the capacity constraints can

be incrementally checked while constructing the tour.

3.2 General Capacities

Beside time window and capacity constraints, it is ob-

vious to ensure that the pickup stop of an order has

to be visited before the delivery stop. Due to trans-

porting several goods at the moment, the constraint

that the pickup stop of an order is immediately fol-

lowed by the delivery stop is relaxed. As a result, the

size of the distance matrix for n orders increases to

(2n + 1) × (2n + 1). Thus, the complexity is increas-

ing signiﬁcantly.

Algorithm 1: NRPA search function for 1PVDPTWs.

1: procedure SEARCH(level,iterations )

2: best.score = MAX VALUE

3: if level == 0 then

4: eval = ROLLOUT()

5: best.score = eval

6: best.tour = tour

7: else

8: policyGlobal[level] = polGlobal

9: for i = 0 ; i < iterations ; i + + do

10: r = SEARCH(level − 1, iterations)

11: if score < best.score then

12: best.score = r.score

13: best.tour = r.tour

14: ADAPT(best.tour, level)

15: end if

16: end for

17: polGlobal = policy[level]

18: end if

19: return best

20: end procedure

The recursive search function is shown in Algo-

rithm 1. The level-speciﬁc policy at each level l is up-

dated if a better solution in level l − 1 has been found.

As recently as all iterations have been executed, the

global policy, which is applied by the rollout func-

tion, is updated. If the algorithm reaches level 0, the

search function performs a rollout.

The rollout function is the most important proce-

dure applied in NMCS. It samples one tour from the

root until a complete tour is found at a leaf by fol-

lowing the global policy. The implementation of the

rollout function for the 1VPDPTW is shown in Algo-

rithm 2. Using ﬂags, already visited successors are

eliminated from the set of possible successors, so that

any generated solution is a permutation. The number

of violations to the enforced constraints is included

into the cost function evaluation which is returned by

the NMCS search procedure. Each violation is scaled

with a constant (10

in our case). Further simpliﬁca-

tions to the code have been applied, because in some

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch

benchmarks there is no need to return to the depot

and the makespan ms (the accumulated time at which

the city is visited) can be optimized instead of the

costs (because the objective function is to minimize

the time and not the driven distance).

The procedure shown in Algorithm 2 extends the

rollout function for the TSPTW solver of (Cazenave

and Teytaud, 2012) and (Edelkamp et al., 2013).

Firstly, we deactivate a TSP-related reﬁnement for the

computation of the successor set. In contrast to the

original implementation provided by (Cazenave and

Teytaud, 2012), we do not enforce a successor if a

violation is certain. In small-sized problems choos-

ing the ﬁrst-fail strategy might accelerate the search

because bad moves are identiﬁed early and prevented

by the policy in further runs. However, in medium-

sized problems it is preferable to improve the policy

ﬁrst, because in the exponential growing state space

the ﬁrst fail strategy would consume too much effort

until all failures are included in the policy and there

is less time left to further improve the policy by good

solutions. First test-runs in larger 1VPDPs revealed

a signiﬁcant improvement of the solution quality as

well as of the time performance without the ﬁrst-fail

strategy. Thus, the successors are only determined by

the following remaining heuristic (lines 5-19). All not

visited successors i are checked, if it is possible to sat-

isfy all hard constraints. As hard constraints are not

fulﬁlled, the respective successor is no more consid-

ered. Next, for each remaining successor the proce-

dure checks if there is another not visited successor j

which cannot be visited after i. If the check is pos-

itive, also this i is removed from the set of possible

successors.

If the successor set is empty, a default tour permu-

tation is applied by considering only the precedences

between pickup and delivery stops. Thus, the check(i)

method enforces that every order’s pickup precedes

its delivery (lines 20-26).

As the set of possible successors is ﬁxed, a ran-

dom choice based on the current global policy is ap-

plied (lines 27-36). The biased choice of a successor

refers to (roulette wheel) ﬁtness selection in genetic

algorithms. If the successor has been determined, the

tour is extended by one city (either pickup or deliv-

ery location), all violations are counted, and the while

loop continues for ﬁnding the next city (lines 37-51).

Algorithm 3 depicts the adapt procedure. More

precisely, in a rollout for an existing policy P children

for a state s are chosen wrt. e

P(s,s

)

. Initially, all

policy values are set to 0. As the entire state-to-state

table surely is too big, it is projected to an essential

part to be learned, which is a measurement for going

from one city to the next.

Algorithm 2: NRPA rollout function for 1VPDPTWs.

1: procedure ROLLOUT

2: tourSize = 1

3: while tourSize < N do

4: sum = s = 0

5: for i = 1 ; i < N ; i + + do

6: if vis[i]! = 0∧ CHECK(I) then

7: succ[s + +] = i

8: for j = 1 ; j < N ; j + + do

9: if vis[ j] ∧ i! = j∧

10: CHECK(J) then

11: if l[i] > r[ j]∨

12: ms + d[city][i] > r[ j] then

13: s − −

14: break

15: end if

16: end if

17: end for

18: end if

19: end for

20: if s == 0 then

21: for i = 1 ; i < N ; i + + do

22: if !vis[ j]∧ CHECK(J) then

23: succ[s + +] = i

24: end if

25: end for

26: end if

27: for i = 0 ; i < N ; i + + do

28: value[i] = EXP( policy[city][succ[i]])

29: sum+ = value[i]

30: end for

31: random = rand[0...sum − 1]

32: i = 0

33: sum = value[0]

34: while sum < m do

35: sum+ = value[+ + i]

36: end while

37: prev = city

38: city = succ[i]

39: tour[tourSize + +] = city

40: vis[city] = true

41: cost+ = d[prev][city]

42: ms = MAX(ms + d[prev][city], l[city])

43: cap = weight[city]

44: if cap > maxCap then

45: viol++;

46: end if

47: if ms > r[city] then

48: viol++;

49: end if

50: end while

51: return 10

∗ viol + cost

52: end procedure

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

Algorithm 3: NRPA adapt function.

1: procedure ADAPT(tour, level)

2: for i = 1 ; i < N ; i + + do

3: visited[i] = false;

4: end for

5: node = 0;

6: for p = 1 ; p < N ; p + + do

7: successors = 0;

8: for i = 1 ; i < N ; i + + do

9: if !vis[i] then

10: moves[successors++] = i;

11: end if

12: end for

13: policy[level][node[tour[p]] += 1.0;

14: z = 0.0;

15: for i = 1 ; i < successors ; i + + do

16: z+= EXP(polGlobal[node][moves[i]]);

17: end for

18: for i = 1 ; i < successors ; i + + do

19: policy[level][node][moves[i]] -=

20: EXP(polGlobal[node][moves[i]])/z;

21: end for

22: node = tour[p];

23: visited[node] = true;

24: end for

25: end procedure

Given a solution sequence in form of a tour

that improves the current best one, policy adaption

now performs gradient decent as follows. The se-

quence of successor cities s

= (s

,...,s

) of s =

,...,s

) with s

i+1

= s

has probability Prob(s, s

) =

∏

j=0

P(s

)

∑

i=0

P(s

)

. The gradient of the loga-

rithm at j of this term is 1 − e

P(s

)

∑

i=0

P(s

)

, so

that we add 1 to the selected successor city and sub-

tract e

P(s

)

∑

i=0

P(s

)

from the others. This en-

sures that policy adaptation increases the probability

of the established tour.

To further accelerate the search, we provide an ini-

tial policy which is based on the shortest-path distance

between pickup and delivery locations.

4 EVALUATION

In general, NMCS has two parameters which affect

the solution quality: the number of iterations and the

level. In Section 4.1 we investigate the effects of vary-

ing the level and the number of iterations in a small

and in two medium-sized problems, to determine ad-

equate conﬁgurations for application. For the evalu-

ation of small-sized problems, we applied the bench-

Figure 3: The solution quality for the 1VPDPTW with 20

orders measured by the average number of violated con-

straints of 10 runs for each level and iteration pair.

mark provided by (Jih and Hsu, 2004)

. It includes

problem instances with 10 to 100 orders (20 to 200

pickup and delivery stops) that have to be processed.

In order to evaluate medium-sized problems, we ap-

plied the benchmark given by (Hosny and Mumford,

2007)

which includes problems with 100 up to 200

orders (between 200 and 400 stops). The benchmark

sets include pickup and delivery stops including time

windows and customer demands as well as the initial

location and maximum capacity of the vehicle. Note

that in both benchmarks the objective function is to

minimize the total working time of the vehicle and it

is not required to return to the depot. The distances

between cities are determined by the Euclidian dis-

tance.

Section 4.2 compares the performance of our ap-

proach on small-sized problem instances to the best

solution computed with a genetic algorithm (Jih and

Hsu, 2004). Section 4.3 considers the performance

in medium-sized problem by comparing the results

to the methods provided by (Hosny and Mumford,

2010). Finally, Section 4.4 discusses an iterative

widening strategy for a parameter-fee implementation

of NMCS.

4.1 Parameter Conﬁguration

Firstly, we investigate the effects of varying the num-

ber of iterations and the levels on a small 1VPDPTW

with only 20 orders (40 stops which have to be vis-

ited). In order to determine meaningful results, we

look at the average values of 10 runs for each con-

ﬁguration. As the complete run requires to perform

iterations

level

rollouts, the search is terminated ear-

lier. Due to the fact, that rollouts are the most ex-

The benchmark set is available at http://wrjih.

wordpress.com/2006/12/09/pdptw-test-data/.

The benchmark set is available at http://users.

cs.cf.ac.uk/M.I.Hosny/PDP.zip.

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch

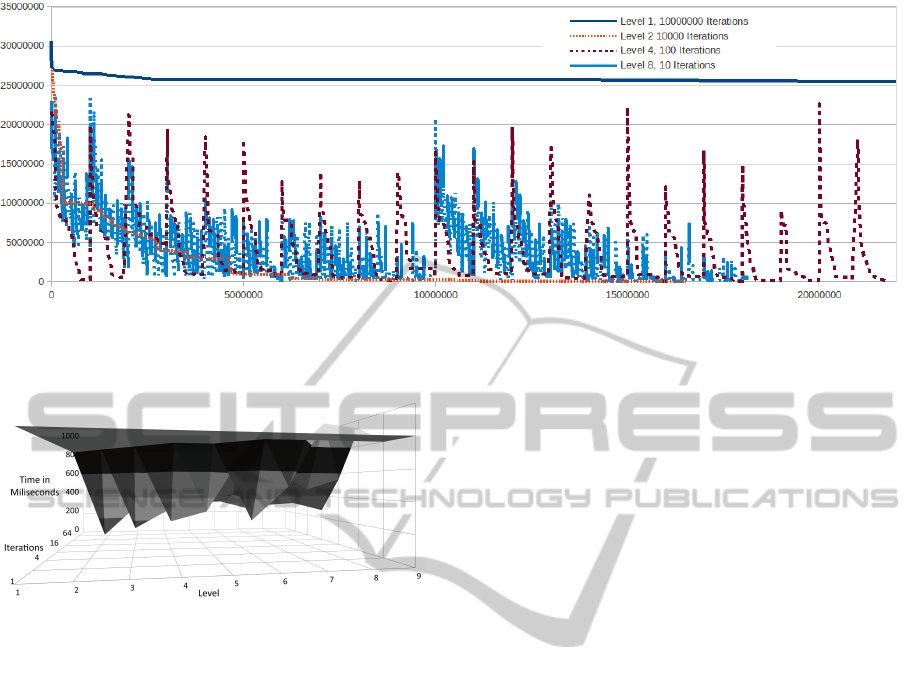
Figure 5: Learning curves for solution quality of the 1VPDPTW 100 benchmark with different NMCS parameters (the x-axis

shows the number of rollouts, while the y-axis the change solution quality for each improvement in a level).

Figure 4: The average computation time of 10 runs for each

level and iteration pair for the results (shown in Figure 3)

for a 1VPDPTW with 20 orders.

pensive operations within the algorithm, it terminates

at the latest after performing 40,000 rollouts. Note

that the algorithm has no knowledge about the best

or optimal solution. Even if it determines the opti-

mal solution quite early, it continuous the search until

all rollouts are performed or a termination is forced.

Figure 3 shows the solution quality measured by the

average number of violated constraints. The results

show that a minimum amount of rollouts have to be

performed to compute adequate results. Thus, feasi-

ble solutions are guaranteed with 4 iterations and at

least 8 levels (max 4

= 65, 536 rollouts) or at least

64 iterations and 2 levels (max 64

= 4, 096 rollouts).

Consequently, Figure 4 investigates the time for de-

termining the ﬁrst found best solution, which refers

to the respective solution in Figure 3.

Figure 4 reveals that a level 2 search with 64

iterations determines feasible solutions in less than

100 milliseconds on average while increasing the

level leads to higher computation times in small-sized

1VPDPTW. In addition, the results proofs that there

is no signiﬁcant difference if the number of levels is

increased and the search is terminated after a ﬁx num-

ber of rollouts. This is obvious, because, e.g., a level

4 search is included in the level 5 search. Thus, if the

algorithm terminates in the level 4 search the level 5

search is never executed and increasing the level has

no impact.

Next, we evaluated several conﬁgurations to solve

the 100 1VPDPTW benchmark provided by (Jih and

Hsu, 2004). Figure 5 displays a cross-comparison be-

tween different parameters for NMCS plotting num-

ber of runs (x-axis) against solution quality (y-axis).

The best result for the 100 1VPDPTW could be ob-

tained with level 2 and 10,000 iterations, while no

solution was computed with level 16 and 3 itera-

tions (even after hours of waiting) and level 1 with

100,000,000 iterations.

The results reveal, that at least 600 iterations are

required to determine feasible solutions. In contrast to

small-sized problems, this is caused by the increased

complexity of the problem. While the number of it-

erations determines the exploitation rate, the level ef-

fects the exploration of the search space. In difﬁcult

problems, more exploitation is required to determine

qualitative solutions. Only qualitative solutions lead

to a qualitative adaption of the global policy. If not

enough iterations are applied, the adaptation of the

global policy is not sufﬁcient goal directed.

As the number of iterations is low, it is obvious

that the level 3 search outperforms the level 2 search,

because level 2 search terminates earlier while the

level 3 search continues looking for better solutions.

If the number of iterations is sufﬁcient large to de-

termine qualitative solutions, Figure 6 indicates that

level 2 is slightly preferred to level 3. As more qual-

itative solutions are determined, a higher level allows

more exploration than a lower level. This prevents to

get stuck in local minima.

Finally, we investigate the effects of increasing

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

the level on medium-sized problems with 200 orders

(400 stops). Figure 6 compares several numbers of

iterations of level 2 and level 3 searches for the 200

PDPTW benchmark provided by (Jih and Hsu, 2004).

The performance ﬁgures contain the average values of

10 runs for each conﬁguration and level respectively.

The second diagram, which describe the score con-

siders only feasible solutions, while the third diagram

depicts the computation time for determine the ﬁrst

best solution. All runs are terminated at the latest af-

ter three hours.

After the investigation of a small (20 orders), a

medium (100 orders), a larger (200 orders) sized

problem, and of two further problem instances with

60 and 80 orders with similar outcome that strengthen

the presented results (not shown in this paper), we

conclude that decreasing the search level and increas-

ing the number of iterations lead to better results for

solving difﬁcult 1VPDPTW with NMCS within short

computational time. Indeed, at both ends of the spec-

trum, i.e., with level 1 and level 16 NMCS in Figure 5,

we could not ﬁnd any solution. The reason is that a

level 1 NMCS is a series of pure rollouts (that is com-

parable to a greedy search), and policy learning is too

weak to direct the search towards ﬁnding feasible so-

lutions, while a level 16 NMCS simply forgets too

much about previous trials. In this case, we observe

the classical extremes of exploration and exploita-

tion. However, in the general case it is more relevant

to determine qualitative solutions to adapt the global

policy qualitatively instead of guiding the search to-

wards new directions and adapting the global policy

by lower quality solutions. The results strengthen this

for 1VPDPTWs.

4.2 Small-sized Problems

The experiments ran on an Intel(R) Core(TM) i7-

2620M CPU at 2.7 GHz. The computer was equipped

with 16 GB RAM. The memory requirements of our

NMCS implementation are insigniﬁcant and domi-

nated by the size of the policy, which is bounded by

O(l · n

) for n locations and a Level l NMCS. The al-

gorithm described in Section 3.2 is implemented in

JAVA.

Table 1 shows the results of running the NMCS al-

gorithm on the benchmark provided by (Jih and Hsu,

2004). Table 2 examines the results achieved with the

best genetic algorithm (MX2(FCGA)) developed by

(Jih and Hsu, 2004) on the same benchmark. The

results pinpoint that the solution quality of both al-

gorithms is nearly identically (only for the 20 PDP a

single score point is not achieved with NMCS). How-

ever, applying NMCS is more reliable. In 37 of 40

runs the NMCS computed feasible solutions, while

the genetic algorithm has an average success rate of

82.92% to ﬁnd feasible solutions (after performing

180 runs in total). Moreover, if the NMCS determines

a feasible solution, this this also the best solution. In

addition, the computation time of NMCS is signiﬁ-

cant lower (but note that the results of the genetic al-

gorithm were computed several years before and no

hardware conﬁguration is presented).

Next, we compared the performance to the al-

gorithm provided by (Hosny and Mumford, 2010).

While the general quality of these results is nearly the

same, in some instances the presented solutions are

better than the optimal solutions determined with dy-

namic programing (Jih and Hsu, 2004). Thus, these

results have to be wrong or at least inconsistent with

the description in the text. We tried different cost

functions to reproduce the error (e.g., by dropping

waiting times at stops) but failed alike. However, if

we compare the solution quality and success rate for

ﬁnding feasible solutions NMCS is still competitive.

In conclusion, we showed that NMCS determines

state-of-the-art solutions in small-sized problems and

has a higher success rate for ﬁnding feasible solutions.

Thus, applying NMCS on this benchmark is more re-

liable than the approaches presented by (Jih and Hsu,

2004) and (Hosny and Mumford, 2010).

4.3 Medium-sized Problems

All experiments ran on an Intel(R) Core(TM) i5-

2520M CPU at 2.5 GHz. The memory requirements

are insigniﬁcant negligible (see Section 4.2).

Table 3 shows that the algorithm solves problems

with up to 200 orders (400 stops) that have to be pro-

cessed. For a sequence of 10 runs, we provide in-

formation on the best and the median solution costs

(because in case of constraint violation the average

value is increasing rapidly). We show the fraction of

valid and best solutions found and provide the aver-

age number of runs required to obtain the best so-

lution. The maximum number of runs is implicitly

given by the limit of the search tree: for the level-

2 NMCS with 2N iterations, the experiment termi-

nates after (2N)

runs. The run-times given are worst-

and average-cases and enforced by either solving the

problem with the best possible solution or by hitting

the limited number of runs - ﬁrst solutions are usually

established much earlier.

As we compare the results with the solutions com-

puted by the most efﬁcient approach (a genetic al-

gorithm) provided by (Hosny and Mumford, 2010),

the NMCS computes solutions with similar quality.

Also the rate of success for ﬁnding optimal and fea-

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch

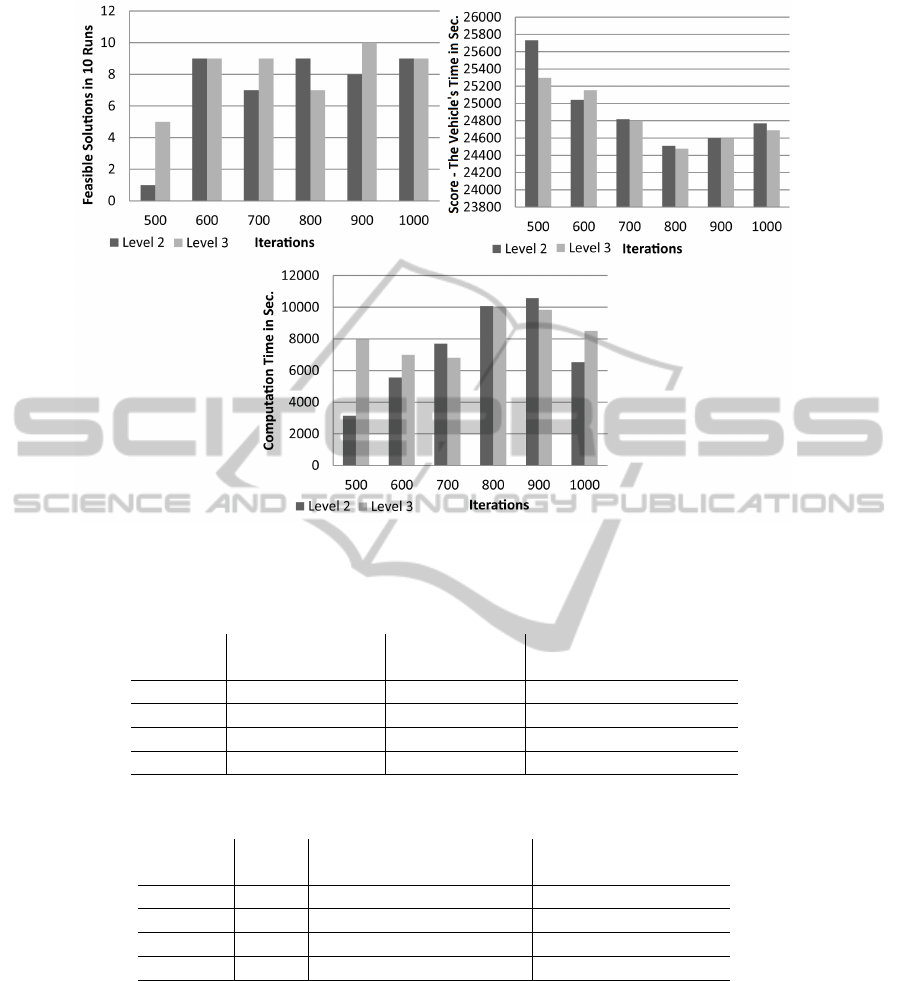
Figure 6: Feasible solutions, the respective average solution quality, and the average time for computing the ﬁrst best solutions

for level 2 and level 3 searches with a varying number of iterations.

Table 1: NMCS (Level-3, 128-Iterations) performed on Jhi’s PDP Benchmark (Jih and Hsu, 2004).

Value Percentage CPU Time

Instance Best Median Valid Best Average Worst-Case

PDP 20 2031 2031 10/10 10/10 0.476s 3.028s

PDP 60 5658 5658 7/10 7/10 100.436s 349.533s

PDP 80 7849 7849 10/10 10/10 101.654s 273.658s

PDP 100 10600 10600 10/10 10/10 495.767s 790.347s

Table 2: The best results achieved with the MX2(FCGA) algorithm on Jhi’s PDP Benchmark (Jih and Hsu, 2004).

Value Percentage CPU Time

Instance Best Valid (180 runs) Best ≈ Average (180 runs)

PDP 20 2030 100 11/30 ≤ 100s

PDP 60 5658 87.22 30/30 300s

PDP 80 7849 80.56 1/30 1400s

PDP 100 10600 63.89 26/30 2300s

sible solutions is approximately equally. However,

also in this benchmark set in some instances Hos-

ney’s genetic algorithm ﬁnds solutions which are bet-

ter than the optimal solution computed with dynamic

programming approaches by (Jih and Hsu, 2004) (see

Section 4.2). Thus, we suppose that small deviations

to the solutions of the generic algorithm may caused

by this.

Finally, the results proof that NMCS computes

valid and state-of-the-art results for medium-sized

1VPDPs. The quality of the results as well as the

rate of success for ﬁnding feasible and best known

solutions reveal, that NMCS is competitive to other

heuristic and meta-heuristic approaches.

4.4 Iterative Widening

Further experiments investigated the performance of

a parameter-free implementation of NMCS that ap-

plies iterative widening. Instead of imposing a ﬁxed

number of iterations for each instance, we gradually

increase it within the search process. The natural op-

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

Table 3: 10 runs of NMCS (Level-2, 2N-Iterations) in Hosny’s PDP Benchmark (Hosny and Mumford, 2007).

Value Percentage Runs CPU Time

Instance N Best Median Valid Best Solution Average Maximum Worst-Case Average

PDP 100 201 9757.00 9757.00 8/10 8/10 102067 161604 6m3s 3m36s

PDP 110 221 11641.03 11641.03 10/10 10/10 144622 195364 8m32s 6m5s

PDP 120 241 12143.00 12143.00 10/10 10/10 96217 232324 7m4s 5m21s

PDP 130 261 14057.00 14057.00 10/10 10/10 146995 272484 17m39s 9m6s

PDP 140 281 15111.00 15160.12 8/10 5/10 271614 315844 25m14s 20m38s

PDP 150 301 16976.00 16976.00 10/10 7/10 190111 362404 23m48s 16m36s

PDP 160 321 18167.00 18167.00 8/10 7/10 316842 412164 45m35s 34m33s

PDP 170 341 19924.00 19924.00 10/10 10/10 246747 465124 55m11s 28m46s

PDP 180 361 22107.29 22107.29 10/10 10/10 244314 521284 42m37s 30m16s

PDP 190 381 23826.00 23826.00 10/10 10/10 270967 580644 61m55s 35m25s

PDP 200 401 24184.00 24198.86 8/10 4/10 587384 643204 128m 111m

tion we chose is to use odd numbers yielding the se-

quence of squares 1, 4, 9, 16, ..., k

for the number

of iterations. The objective is to aim at ﬁrst solutions

propagated bottom-up quickly and to work harder on

ﬁnding better ones later on in the solution process.

Other functions such as Luby sequences (Luby et al.,

1993) (successful in SAT (Een et al., 2007) solving)

are available, but have not been tested.

The experimental results for this approach are in-

deed promising. For instance, in another 10-fold

repeated experiment of Hosny’s 100 PDP problem

(cf. Table 3 ﬁrst row) the optimal solution 9757 of

was found in all cases and obtained even faster with

3m13s (vs. 6m3s) worst-case, and 2m58s (vs. 3m36s)

average-case time.

If we consider only the feasible solutions (8 of

10 computed by the conﬁgured NMCS), the average

number of applied rollouts is decreased from 45,828

to only 16,574 by applying the parameter-free imple-

mentation (in worst case the number of required roll-

outs is reduced from 108,138 to 23,278). Thus, con-

sidering this problem of Table 3, the parameter-free

method is three times faster than the NMCS conﬁg-

ured with level 2 and 401 iterations.

5 CONCLUSIONS

In this paper, we presented a novel approach for solv-

ing Single Vehicle Pickup and Delivery Problems

with time windows and capacity constraints by apply-

ing Nested Monte-Carlo Search (NMCS). In order to

evaluate the approach and determine adequate param-

eter values for the level and the number of iterations,

we solved numerous instances with varying conﬁgu-

rations. Small-sized instances are retrieved from the

benchmark set provided by (Jih and Hsu, 2004), while

the medium-sized instances are gathered from (Hosny

and Mumford, 2007).

While the number of iterations determines the ex-

ploitation rate, the level effects the exploration of the

search space. In difﬁcult problems, more exploitation

is required to determine qualitative solutions. Only

qualitative solutions lead to a qualitative adaption of

the global policy. If not enough iterations are applied,

the adaptation of the global policy is not sufﬁcient

goal directed. The results showed that decreasing the

search level and increasing the number of iterations

lead to better results for solving complex 1VPDPTW

with NMCS within short computational time. Thus, it

is more relevant to determine qualitative solutions to

adapt the global policy qualitatively instead of guid-

ing the search towards new directions and adapting

the global policy by lower quality solutions.

From a machine learning point of view one of the

key observations is the object to be learned in form

of a policy (that generalizes from the state-to-state es-

timates) reﬂects the linkage of cities, i.e., which one

is the best to visit next in a short tour. This grad-

ually improved knowledge starting with some mea-

sure of initial distances is extremely helpful in guiding

the (random) search process to ﬁnd improved tours:

knowing that a particular city is a good successor of

onother one is true not only for one, but for many

other tours. Only a few adaptions to the top level

policy are needed to drive the solver towards better

solutions.

Finally, the results revealed the NMCS is com-

petitive to other heuristics and meta-heuristics such

as genetic algorithms in small- and medium-sized

1VPDPTWs with 20 and 200 orders that have to be

processed. NMCS computes state-of-the-art solutions

and has a high rate of success for ﬁnding feasible

and best known solutions. With a limited amount of

domain-speciﬁc information (only a single heuristic

is applied in the rollout function) the algorithm han-

dles problems sizes with up to 200 orders in adequate

computation time.

Despite of extensive analyses to determine per-

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch

tinent parameter conﬁgurations, initial experiments

showed that applying a Level-2 search and an itera-

tive widening strategy is indeed promising. By the

small memory overhead and the ease of parallelizing

NMCS (either with root or with tree parallelization),

we expect an essential scaling behavior on multiple

cores. Further research will focus on parameter-free

NMCSs.

ACKNOWLEDGEMENTS

The presented research was partially funded by

the German Research Foundation (DFG) within the

project Autonomous Courier and Express Services

(HE 989/14-1) at the University of Bremen, Germany.

REFERENCES

Applegate, D. L., Bixby, R. E., Chvatal, V., and Cook, W. J.

(2011). The traveling salesman problem: a computa-

tional study. Princeton University Press.

Bent, R. and Hentenryck, P. V. (2006). A two-stage hy-

brid algorithm for pickup and delivery vehicle routing

problems with time windows. Computers & Opera-

tions Research, 33(4):875–893.

Bjarnason, R., Fern, A., and Tadepalli, P. (2009). Lower

bounding klondike solitaire with monte-carlo plan-

ning. In ICAPS.

Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,

Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez, D.,

Samothrakis, S., and Colton, S. (2012). A survey of

monte carlo tree search methods. Computational In-

telligence and AI in Games, IEEE Transactions on,

4(1):1–43.

Cazenave, T. (2009). Nested monte-carlo search. In IJCAI,

pages 456–461.

Cazenave, T. and Teytaud, F. (2012). Application of the

nested rollout policy adaptation algorithm to the trav-

eling salesman problem with time windows. In LION,

pages 42–54.

Cordeau, J.-F. and Laporte, G. (2003a). A tabu search

heuristic for the static multi-vehicle dial-a-ride prob-

lem. Transportation Research Part B: Methodologi-

cal, 37(6):579–594.

Cordeau, J.-F. and Laporte, G. (2003b). The Dial-a-Ride

Problem (DARP): Variants, modeling issues and algo-

rithms. Quarterly Journal of the Belgian, French and

Italian Operations Research Societies, 1(2):89–101.

Edelkamp, S., Gath, M., Cazenave, T., and Teytaud, F.

(2013). Algorithm and knowledge engineering for the

TSPTW problem. In IEEE Symposium Series on Com-

putational Intelligence (SSCI).

Een, N., Mishchenko, A., and S

orensson, N. (2007). Apply-

ing logic synthesis for speeding up sat. In Theory and

Applications of Satisﬁability Testing–SAT 2007, pages

272–286. Springer.

Gajpal, Y. and Abad, P. (2009). An ant colony system (acs)

for vehicle routing problem with simultaneous deliv-

ery and pickup. Computers & Operations Research,

36(12):3215–3223.

Gendreau, M., Laporte, G., and Vigo, D. (1999). Heuris-

tics for the traveling salesman problem with pickup

and delivery. Computers & Operations Research,

26(7):699–714.

Hern

andez-P

erez, H. and Salazar-Gonz

alez, J.-J. (2004).

A branch-and-cut algorithm for a traveling salesman

problem with pickup and delivery. Discrete Applied

Mathematics, 145(1):126–139.

Hosny, M. I. and Mumford, C. L. (2007). Single vehi-

cle pickup and delivery with time windows: made to

measure genetic encoding and operators. In Proceed-

ings of the 2007 GECCO conference companion on

Genetic and evolutionary computation, pages 2489–

2496. ACM.

Hosny, M. I. and Mumford, C. L. (2010). The single vehi-

cle pickup and delivery problem with time windows:

Intelligent operators for heuristic and metaheuristic al-

gorithms. Journal of Heuristics, 16(3):417–439.

Jih, W.-r. and Hsu, Y. (2004). A family competition genetic

algorithm for the pickup and delivery problems with

time window. Bulletin of the College of Engineering,

90:121–130.

Landrieu, A., Mati, Y., and Binder, Z. (2001). A tabu search

heuristic for the single vehicle pickup and delivery

problem with time windows. Journal of Intelligent

Manufacturing, 12(5-6):497–508.

Luby, M., Sinclair, A., and Zuckerman, D. (1993). Optimal

speedup of las vegas algorithms. Information Process-

ing Letters, 47(4):173–180.

Pankratz, G. (2005). A grouping genetic algorithm for the

pickup and delivery problem with time windows. OR

spectrum, 27(1):21–41.

Parragh, S. N., Doerner, K. F., and Hartl, R. F. (2008).

A Survey on Pickup and Delivery Problems Part II:

Transportation between Pickup and Delivery Loca-

tions. Journal f

ur Betriebswirtschaft, 58(2):81–117.

Psaraftis, H. N. (1983). An exact algorithm for the single

vehicle many-to-many dial-a-ride problem with time

windows. Transportation Science, 17(3):351–357.

Ropke, S., Cordeau, J.-F., and Laporte, G. (2007). Models

and branch-and-cut algorithms for pickup and delivery

problems with time windows. Networks, 49(4):258–

272.

Rosin, C. D. (2011). Nested rollout policy adaptation for

monte carlo tree search. In IJCAI, pages 649–654.

AAAI Press.

Solomon, M. M. (1987). Algorithms for the vehicle rout-

ing and scheduling problems with time window con-

straints. Operations research, 35(2):254–265.

Srour, F. J. and van de Velde, S. (2013). Are stacker crane

problems easy? A statistical study. Computers & Op-

erations Research, 40(3):674 – 690.

Toth, P. and Vigo, D. (1997). Heuristic algorithms for the

handicapped persons transportation problem. Trans-

portation Science, 31(1):60–71.

Yan, X., Diaconis, P., Rusmevichientong, P., and Roy, B. V.

(2004). Solitaire: Man versus machine. In Saul, L. K.,

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

Weiss, Y., and Bottou, L., editors, Advances in Neu-

ral Information Processing Systems 17, pages 1553–

1560. MIT Press, Cambridge, MA.

SolvingSingleVehiclePickupandDeliveryProblemswithTimeWindowsandCapacityConstraintsusingNested

Monte-CarloSearch