Self-learning Voxel-based Multi-camera Occlusion Maps for 3D

Reconstruction

Maarten Slembrouck, Dimitri Van Cauwelaert, David Van Hamme, Dirk Van Haerenborgh,

Peter Van Hese, Peter Veelaert and Wilfried Philips

Ghent University, TELIN dept. IPI/iMinds, Ghent, Belgium

Keywords:

Multi-camera, Occlusion Detection, Self-learning, Visual Hull.

Abstract:

The quality of a shape-from-silhouettes 3D reconstruction technique strongly depends on the completeness

of the silhouettes from each of the cameras. Static occlusion, due to e.g. furniture, makes reconstruction

difﬁcult, as we assume no prior knowledge concerning shape and size of occluding objects in the scene. In

this paper we present a self-learning algorithm that is able to build an occlusion map for each camera from

a voxel perspective. This information is then used to determine which cameras need to be evaluated when

reconstructing the 3D model at every voxel in the scene. We show promising results in a multi-camera setup

with seven cameras where the object is signiﬁcantly better reconstructed compared to the state of the art

methods, despite the occluding object in the center of the room.

1 INTRODUCTION

Occlusion is undesirable for computer vision appli-

cations such as 3D reconstruction based on shape-

from-silhouettes (Laurentini, 1994; Corazza et al.,

2006; Corazza et al., 2010; Grauman et al., 2003) be-

cause parts of the object disappear in the foreground-

background segmentation. However, in real-world

applications occlusion is unavoidable. In order to

handle occlusion, we propose a self-learning algo-

rithm that determines occlusion for every voxel in the

scene. We focus on occlusion as a result of static ob-

jects between the object and the camera.

Algorithms to detect partial occlusion are pre-

sented in (Guan et al., 2006; Favaro et al., 2003;

Apostoloff and Fitzgibbon, 2005; Brostow and Essa,

1999). However, in these papers occlusion is de-

tected from the camera view itself by keeping an

occlusion map which is a binary decision for each

of its pixels. An OR-operation between the fore-

ground/background mask and the occlusion mask, re-

sults in the input masks for the visual hull algorithm.

The major drawback to this approach is that occlusion

is in fact voxel-related, rather than pixel-related: the

same pixel in an image is occluded when the occlud-

*This research was made possible through iMinds, an

independent research institute founded by the Flemish gov-

ernment.

ing object is located between the object and the cam-

era, but not if the object is placed between the camera

and the occluding object. Pixel-based occlusion de-

tection results in a 3D model which consists of far

more voxels not belonging to the 3D model because

the occluder is also reconstructed and depending on

the position of the person, parts of the occluder are

still left over after subtracting the visual hull of the

occluder (we will show this in Section 5).

Therefore, we propose an occlusion map (one for

each camera) from a voxel perspective, in order to

evaluate each voxel separately. After the occlusion

maps are built, we can use this information and only

evaluate the camera views which are not occluded and

therefore contribute to the 3D model.

We determine occlusion and non-occlusion based

on a fast algorithm of the visual hull concept. In or-

der for the system to work, the occlusion algorithm

requires someone walking in the scene to make oc-

cluded regions appear. Subsets of the different camera

views are used to increase the votes for either occlu-

sion or non-occlusion for each voxel. A majority vote

decides about the ﬁnal classiﬁcation.

We also assign a quality factor to the subset of

chosen cameras because the volume of the visual hull

strongly depends on the camera positions. Instead of

counting integer votes, we increment by the quality

factor which depends both on the combined cameras

and the voxel position.

502

Slembrouck M., Van Cauwelaert D., Van Hamme D., Van Haerenborgh D., Van Hese P., Veelaert P. and Philips W..

Self-learning Voxel-based Multi-camera Occlusion Maps for 3D Reconstruction.

DOI: 10.5220/0004723305020509

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 502-509

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

In Section 2 we explain the fast visual hull algo-

rithm. Section 3 proposes the self-learning occlusion

algorithm. We determine the quality factor for a cam-

era combination which is used for voting in Section 4.

In Section 5 we show the promising results of our test

setup.

2 FAST VISUAL HULL

COMPUTATION

The visual hull of an object is determined by its sil-

houettes as a result of the foreground-background

segmentation (Kim et al., 2006; Zivkovic, 2004) and

the intrinsically and extrinsically camera calibration

parameters. We use a voxel representation for the vi-

sual hull to reduce computation time. It is required

that all cameras face the same area, called the over-

lapping area, because that is the only area where a 3D

model can be built using all cameras with this imple-

mentation.

2.1 Fast Visual Hull Algorithm

Our fast visual hull algorithm loops over all voxels in

a bounded area. For each voxel, the foreground masks

are evaluated at its projected image coordinates for

each camera. A voxel is part of the visual hull, only if

all projections are classiﬁed as foreground. Algorithm

1 shows our fast visual hull implementation.

Algorithm 1: Fast visual hull algorithm.

input: camera calibration, FG/BG-masks, bounded area

output: voxelated visual hull

for all voxel in voxel space do

while voxel occupied and not all camera views evalu-

ated do

lookup the voxel’s projection on next camera view

if projection is foreground then

classify voxel as occupied

else

classify voxel as unoccupied

end if

end while

end for

2.2 Optimization

Within a particular multi-camera setup, the projec-

tions of the voxels are always the same as long as

the cameras do not move. Therefore, we calculate the

image coordinates corresponding to each voxel cen-

ter in the scene in the precomputation phase of our

visual hull algorithm and use a lookup table to deter-

mine the image coordinates. Equation 1 shows how

the voxel center (X,Y, Z) is projected onto the image

sensor, resulting in pixel coordinates (x, y). The pro-

jection matrix P is the product of the intrinsic camera

matrix and the transformation matrix (R|T ).









z }| {





0 c

0 f

0 0 1

























(1)

Note that this does not lead to an exact reconstruc-

tion because only the center of each voxel is evaluated

making it suitable for solid objects but not for objects

with holes. For each camera the traditional implemen-

tation projects eight points (voxel corners) and eval-

uates all pixels within their convex hull whereas we

only project a single point (voxel center) and evaluate

this pixel value. The major advantage of our approach

is that it increases the speed signiﬁcantly (more than

8 times faster).

3 SELF-LEARNING OCCLUSION

ALGORITHM

Visual hull algorithms are inherently sensitive to mis-

classiﬁed pixels in the foreground-background seg-

mentation, the presence of which is to be expected

when camera views are occluded by one or more ob-

jects. Therefore we propose a self-learning algorithm

which determines for every voxel if it is occluded for

any of the cameras. Hence, the number of occlusion

maps equals the number of cameras in the room.

3.1 Deciding if a Voxel is Occluded

Deciding whether a voxel is occluded or not does not

seem to be an easy task. In previous research, occlu-

sion was determined from pixel perspective but this is

not sufﬁcient because of the following reason. Con-

sider a piece of furniture in the middle of the scene

(e.g. a closet). From the perspective of a particular

camera, a person can stand in front of the furniture

or behind it, resulting in occlusion by the closet in

the latter case. But if we look at the occluding pix-

els from the camera view, we see the pixels are only

occluded when the person stands behind the closet.

When the person stands in front of it, those same pix-

els should not be considered as occluded pixels be-

cause they hold relevant information. Since standard

Self-learningVoxel-basedMulti-cameraOcclusionMapsfor3DReconstruction

503

cameras do not have depth information it is not suf-

ﬁcient to keep track of occluded pixels, therefore we

use occluded voxels.

To decide if there is occlusion, we make some as-

sumptions. One of these assumptions is that there

needs to be a consensus about the occupation of a

voxel in the space. This consensus is only possible

if a minimum number of cameras agree that a voxel

at a certain place in space is occupied. If there are

for example three cameras agreeing there is an ob-

ject at a certain position in space, but the fourth cam-

era does not detect anything there, then we can quite

safely assume that those unseen voxels are occluded

for the fourth camera. However, it is not clear how

many cameras need to agree about this visibility. One

could expect as much as possible, but this will fail if

there is a lot of occlusion because the consensus will

be lacking.

Since it is hard to decide whether a voxel is oc-

cluded for a certain camera, we count votes for both

cases: occluded and non-occluded. Every voxel has

a separate count for each camera for both classes.

The only requirement is that a person needs to walk

around in the scene to make occluded regions appear.

Voxels outside the ﬁeld of view of the cameras are

directly classiﬁed as occluded because these voxels

are out of sight. In the following sections we explain

our detection mechanism for both occlusion and non-

occlusion in detail.

3.1.1 Visible

Figure 1 shows a ﬂowchart explaining how we deter-

mine the absence of occlusion for camera C

. Basi-

cally, we randomly pick two other cameras and gen-

erate the visual hull from the masks of camera C

and

these two cameras C

and C

. The voxels deﬁning this

visual hull are the ones who are not occluded for all

these cameras, otherwise they should be carved out of

the visual hull.

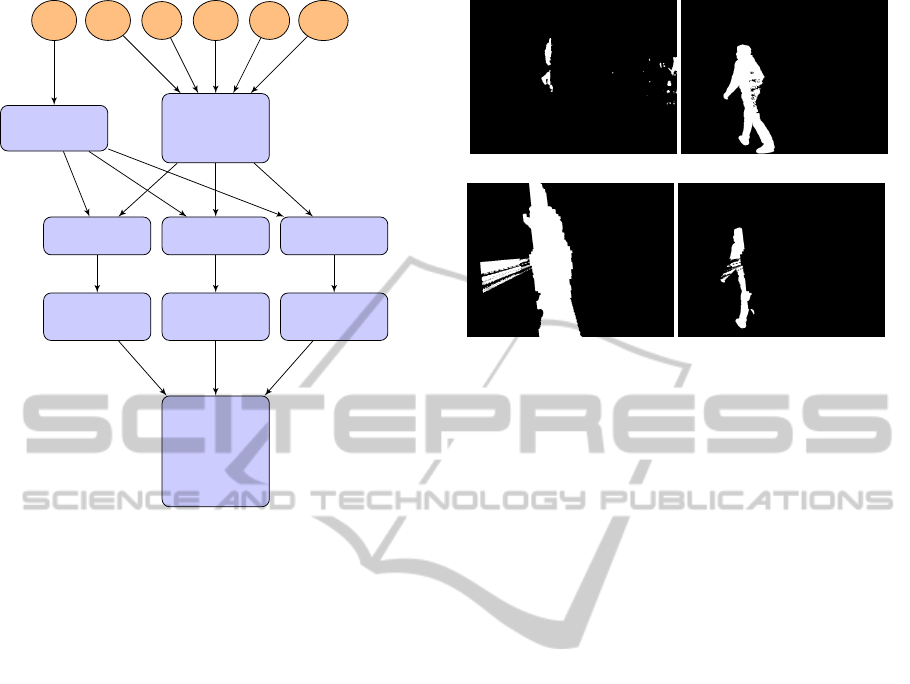
3.1.2 Occluded

One could think that no absence of occlusion means

occlusion but that would be wrong because we can

only determine occlusion in the zone where the per-

son is walking and it strongly depends on the chosen

cameras. Determining occlusion is much more com-

plicated. Figure 2 shows the ﬂowchart to understand

the algorithm. We ﬁrst generate the visual hull with

only the camera of which we want to determine oc-

clusion, camera C

. We randomly pick three cameras

and reproject the generalized cone of C

back on each

of the camera image planes of these cameras: C

, C

pick 2

random

cameras

...

generate

visual hull

Figure 1: Flowchart to determine which voxels are not oc-

cluded for camera C

. Two cameras are randomly picked

from the list and we calculate the visual hull from their

masks together with the mask of camera C

from which we

try to determine the occlusion map. Since camera C

con-

tributes to the visual hull the result is a shape which is not

occluded for these cameras.

and C

. This reprojection results in a different mask

for each camera mask

repr,C

with x = a, b or c.

An example is shown in Figure 3. In Figure 3(a)

we see the mask of camera C

. If we look closely we

see that only half of the person is visible in this mask

which means there is occlusion. Figure 3(b) shows

the mask from another camera (mask

f gbg,C

) which

sees the entire person. We compare mask

f gbg,C

with

mask

repr,C

(Figure 3(c)), which is the reprojected vi-

sual hull from camera C

onto this other camera, ac-

cording to (FG = foreground and BG = background):

mask

occl,C

(x, y) = mask

repr,C

(x, y) = BG

∧ mask

f gbg,C

(x, y) = FG

(2)

The result (mask

occl,C

) is shown in Figure 3(d)

which indicates the invisible parts for camera C

white. The same calculations are made for the two

other randomly chosen cameras. These three masks,

in respect to the correct camera viewpoints, produce

a visual hull which consists mostly of occluded vox-

els for camera C

. Due to the visual hull algorithm,

we cannot guarantee that all of its voxels are really

occluded, hence the voting framework.

Notice that the self-learning occlusion algorithm

also solves another problem. Namely, when the

foreground-background segmentation continuously

fails to classify certain pixels as foreground, the votes

for occlusion will increase and the system will eventu-

ally ignore that camera for those pixels which offers a

great advantage since it would otherwise degrade the

3D model as well.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

504

pick 3

random

cameras

generate

visual hull

...

reproject reproject reproject

determine

occlusion

determine

occlusion

determine

occlusion

generate

visual

hull with

occlusion

masks

mask

occl,C

mask

occl,C

mask

occl,C

mask

repr,C

mask

repr,C

mask

repr,C

Figure 2: Flowchart to determine occlusion for camera C

First we pick three random cameras from the list (C

−C

)

and also calculate the visual hull for C

only (in a bounded

area). Next, we reproject that visual hull on each of the sen-

sors of the chosen cameras. We then compare this repro-

jected mask with the original mask of the respective camera

(using formula 2). This results in occlusion masks for the

three randomly picked cameras. The visual hull generated

by these occlusion masks determines the occluded voxels

for camera C

in that time frame. In case of static occlusion

the complete occlusion map will be built over time.

4 QUALITY FACTOR VOTING

In a multi-camera setup not all cameras are equally

relevant to a certain voxel in space. Not only the dis-

tance to the camera, but also the angles between the

cameras (with the voxel as center) determine the rele-

vance of the information added by each camera. The

self-learning occlusion algorithm takes this into ac-

count: we add this relevance as a quality factor to

the framework. Rather than counting the number of

votes, we count these quality factors Q (0 ≤ Q ≤ 1).

The count for both cases, t

occluded

and t

visible

are kept:

occluded

= t

occluded

+ Q

visible

= t

visible

+ Q

(3)

The visual hull provides a qualitative tool for mea-

suring the relevance of a camera. For every camera we

add to the scene, the resulting 3D model is composed

by the same or less voxels, since every new camera

carves away zero or more voxels. In the next sec-

(a) mask

f gbg,C

(b) mask

f gbg,C

repr,C

(d) mask

occl,C

Figure 3: (3(a)) The mask of the camera C

for which oc-

clusion is checked. (3(b)) The mask of one of the randomly

chosen camera views C

(3(c)). The reprojected image of

the visual hull generated only by mask (3(a)). (3(d)) The

occluded part shown in white, which is combined with two

other cameras to calculate a visual hull and update the oc-

clusion map.

tion we investigate the inﬂuence of angle differences

between given cameras with respect to the resulting

visual hull.

4.1 Quality Factor for Two Cameras

We ﬁrst consider the two-dimensional problem. In

case of two cameras we can visualize the inﬂuence

of the angle variation by keeping both cameras at the

same distance of the object. Because the overlapping

area equals inﬁnity for small angles, we decided to re-

strict the overlapping space in a well deﬁned circular

area. Figure 4 shows three different angles: 20

◦

, 90

◦

and 180

◦

. For an aperture angle of 20

◦

they result in

a visual hull of 2.99%, 0.75% and 4.08% respectively

of the space described by the circle through C1 and

C2, and the voxel as its center. In Figure 5 we see

the overlapping area as a function of the angle (range

from 0

◦

till 180

◦

We distinguish three different zones: 0 − 20

◦

20 − 160

◦

and 160 − 180

◦

. In the ﬁrst part, the over-

lapping area is equal to inﬁnity because the overlap-

ping area is not bounded, both cameras are looking in

the same direction from the same position. In the sec-

ond part, we ﬁnd a more or less symmetrical course

with 90

◦

corresponding to the minimum overlapping

area. The third part results in a constant overlapping

area because both cameras are then facing each other.

The quality factors need to show the same trend.

Self-learningVoxel-basedMulti-cameraOcclusionMapsfor3DReconstruction

505

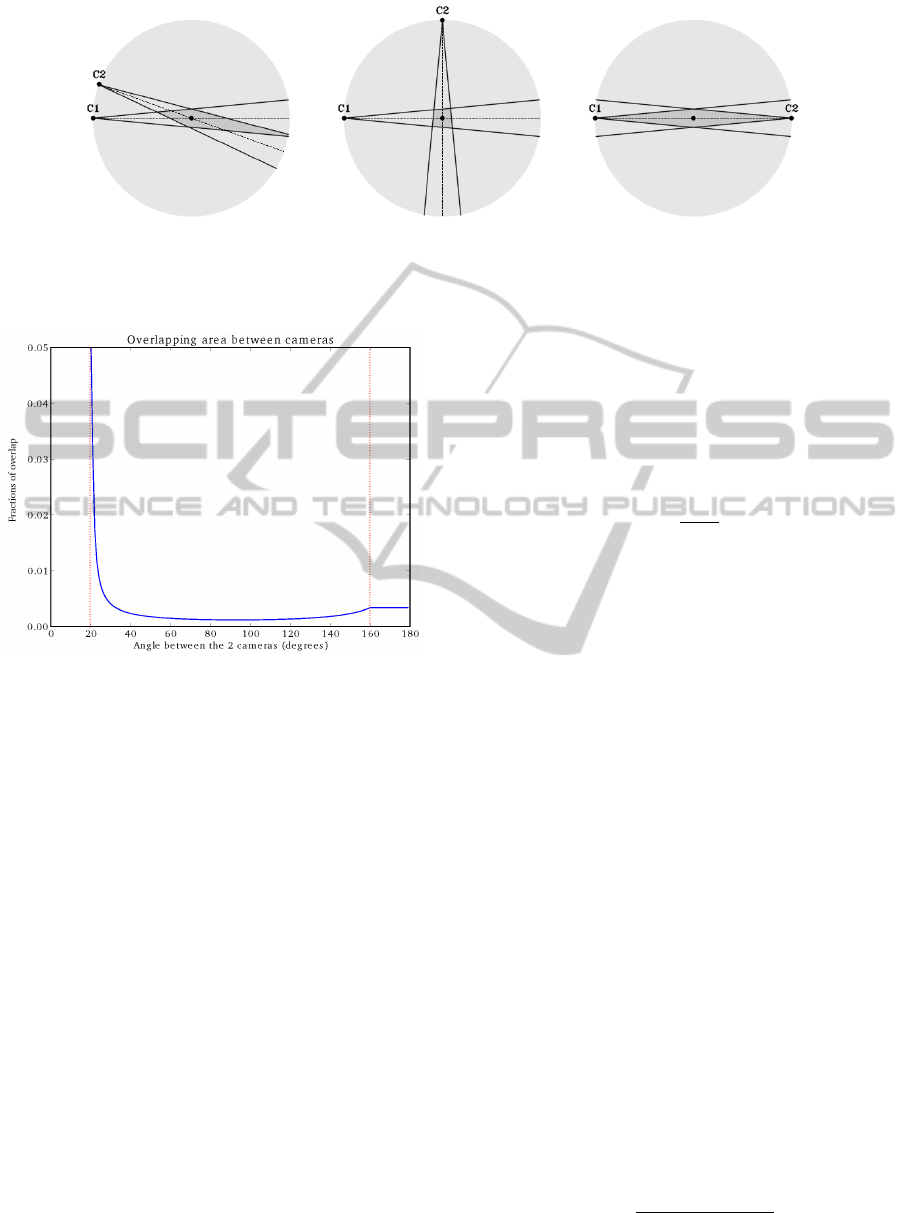
(a) (b) (c)

Figure 4: Overlapping area for an angle of 20

◦

, 90

◦

and 180

◦

between camera C1 and C2 for a certain voxel in space. We

see that the overlapping area (dark gray area) presents respectively 2.99%, 0.75% and 4.08% of the marked space (lightgray

area). We notice an angle of 90

◦

reduces the overlapping area signiﬁcantly.

Figure 5: The fraction of overlap between views of two

cameras equidistant from a certain voxel, both having a

viewing angle of 20

◦

, as a function of the angle between

the cameras. The graph between 180

◦

and 360

◦

is a hori-

zontally mirrored version of this ﬁrst part.

4.2 Proposed Quality Calculation or

Multiple Cameras

In case of more cameras, we determine the quality

factor of the chosen cameras with a practical ap-

proach. Since we have a fully calibrated camera

setup, we are able to determine the visual hull of vir-

tual objects with a number of cameras in this space

and because we know the virtual object, we are able

to compare the volume of the visual hull with the vol-

ume of the original object. Because voxels are cubes,

we opted for this shape. Each cube has the center of

a voxel as its own center. In order to reconstruct the

cube, the corners of the cubes are projected on each

of the image planes (equation 1). The convex hull of

these image coordinates represents the projection of

the virtual cube on the image plane. Consequently,

the visual hull of the cube is build from these projec-

tions.

From the previous section we know that the vol-

ume of the visual hull V

V H

strongly depends on po-

sition of the cameras, hence we use V

V H

to calculate

the quality factor Q. The combination of cameras that

has the smallest visual hull needs to be granted the

highest quality. Therefore we calculate the ratio of

the volume of the original cube V

cube

and the volume

of this visual hull V

V H

and use this as quality factor Q

(equation 4).

Q =

cube

V H

(4)

From the properties of a visual hull, we know that

V H

≥ V

cube

. Therefore Q always satisﬁes 0 ≤ Q ≤ 1.

The most accurate results are obtained by using the

voxels as cubes to calculate the visual hull. However,

in that case, we need subvoxel precision, which would

increase the memory usage signiﬁcantly. Therefore,

we chose to use the same voxel resolution (2 cm

)

as the voxel resolution we use for the visual hull algo-

rithm and we use cubes with edges equal to a multiple

of the voxel resolution (e.g. 20 cm

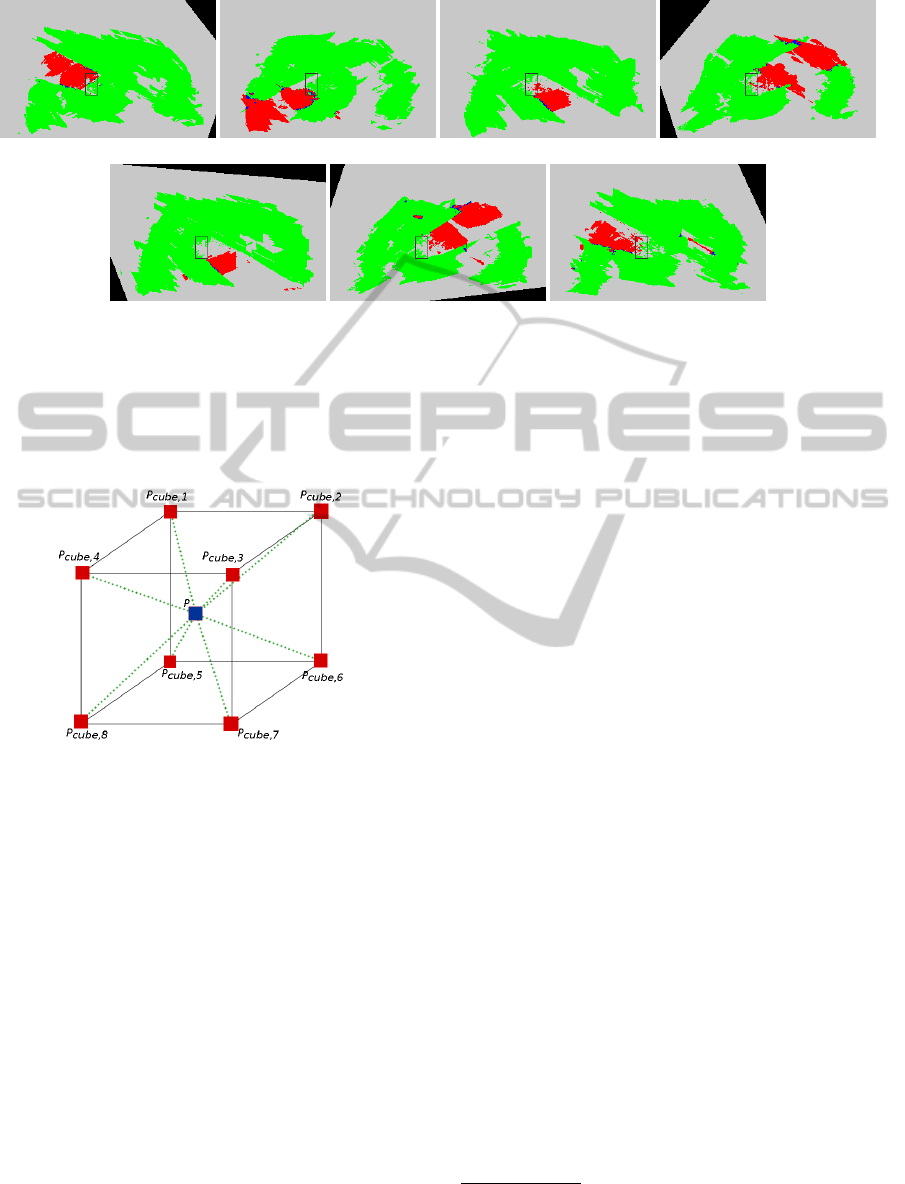
In the pre-computation phase we calculate the

quality factors for all possible combinations of three

cameras. In case of seven cameras, that means





35 unique combinations for every voxel. To reduce

computation time we opt to calculate the aforemen-

tioned quality factors for an oversampled voxel space

(every 10cm in each direction). The quality factors of

the intermediary voxels are calculated from its eight

nearest neighbours in this oversampled voxel space

using weighted averaging (Figure 7). Equation 5 cal-

culates this weighted average. We deﬁne P

cube,i

one of the eight nearest corners from the oversampled

voxel space. The weights are equal to the euclidean

distance between such a corner point P

cube,i

and the

point P we want to calculate the interpolated quality

factor for. Q

represents the quality factor of the voxel

at P

cube,i

∑

i=1

d(P

cube,i

, P)Q

∑

i=1

d(P

cube,i

, P)

(5)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

506

(a) (b) (c) (d)

(e) (f) (g)

Figure 6: One horizontal layer (1.20 m above ground level) of the occlusion maps of all cameras. (6(a)) bottom right corner,

(6(b)) upper right corner, (6(c)) upper left corner, (6(d)) lower left corner, (6(e)) upper left corner, (6(f)) lower left corner and

(6(g)) lower right corner. The top row shows the occlusion maps from cameras at 3.5 m from the ground, the bottom row

from the cameras 1.2 m from the ground. The black rectangle represents the occlusion object. We distinguish ﬁve classes:

occluded (red), non-occluded (green), undecided (blue), unknown (gray) and out of sight (black). Errors in the occlusion map

are due to noise in the foreground-background images.

Figure 7: Interpolation of intermediary voxels. Red ﬁlled

squares represent voxels from the oversampled voxel space

while the blue squares inside the cube represents a voxel

from the normal voxel space. Green dashed lines represent

the distance from the center of the voxel P to one of the

cube corner voxels.

5 RESULTS

5.1 Test Setup

We made a test setup of 8m×4m×3.5m (w × l × h)

with seven cameras, four of them placed in the top

four corners and three others about 1.2 m from the

ground on the vertical edges. In the middle of the

room we placed an occluding object (Figure 8). All

cameras have 780 × 580 px image resolution. We cal-

ibrated all cameras intrinsically and extrinsically. In

the next phase we asked a person to walk through the

room. The aim is to visit each voxel near occluding

objects at least once. However, the more often the per-

son visits a certain voxel, the more certain the system

becomes about occlusion or no-occlusion at that cer-

tain voxel. Because we only take into account static

occlusion for the moment, we can run the occlusion

detection once and use the results later on. In case

of random camera combinations, we need to compute

three visual hulls per camera per frame, hence 21 vi-

sual hulls (with seven cameras). This roughly results

in 0.5 frames per second.

5.2 Classiﬁcation

In Figure 6 we see the results of the algorithm.

The visited voxels have been classiﬁed into ﬁve

classes: occluded (red), non-occluded (green), unde-

cided (blue), unknown (gray) and out of sight (black).

The voxels are classiﬁed by the votes t

occluded

, t

visible

and whether the voxel is visible by the camera:

Class =











occluded if t

occluded

> t

visible

non-occluded if t

occluded

< t

visible

undecided if t

occluded

= t

visible

unknown if t

occluded

= t

visible

= 0

out of sight if voxel not in ﬁeld of view

(6)

Note that in the ﬁnal occlusion map we assume

undecided and out of sight as occluded and un-

known as non-occluded and hence distinguish only

two classes: occluded and non-occluded.

More results of the occlusion maps of these se-

quences can be found at http://telin.ugent.be/∼mslembro/

?q=node/14

Self-learningVoxel-basedMulti-cameraOcclusionMapsfor3DReconstruction

507

(a) (b)

(e) (f)

(g)

(h) Damaged

3D model due to

ignoring occlusion

(i) State of the art (j) Recognizable 3D

model thanks to oc-

clusion maps

Figure 8: 8(a)) - (8(g)) Input images of all camera views. In

(8(h)) we ignore the occlusion information leading to an in-

correct 3D shape. () shows the state of the art method where

we see a lot of extra voxels which should not belong to the

3D model. In (8(j)) on the other hand we still recognise a

person in the 3D model because the cameras responsible for

degrading the 3D shape are ignored.

5.3 Visual Hull Results

Using the generated occlusion maps we are now able

to reconstruct a person, walking trough the room,

without losing occluded parts. The occlusion maps of

all cameras are evaluated to determine for each voxel

separately which cameras are relevant to build the 3D

model. Only cameras classiﬁed as non-occluded for

a voxel are taken into account. In Figure 8 we see

the visual hull constructed with and without occlusion

mapping. The 3D model of the person is signiﬁcantly

more recognizable in Figure 8(j) which takes the oc-

clusion into account.

6 CONCLUSIONS

In this paper we presented a self-learning occlusion

map algorithm derived from the voxel perspective to

improve the 3D reconstruction of an object in a scene

with static occlusion. The method is based on the vi-

sual hull concept and builds a separate occlusion map

for each camera. We designed a voting framework in

order to classify voxels as occluded or non-occluded.

We showed promising results from our test setup with

seven cameras and one occluding object.

7 FUTURE WORK

As a ﬁrst step we chose to only allow purely static

occlusion. It is however also possible to have objects

which are moved around in the scene e.g. chairs. The

occlusion maps could be continuously updated in a

parallel process. We could also estimate the shape of

the occluding objects in the scene. If the camera po-

sitions and orientations are then changed. New occlu-

sion maps could be automatically generated from the

old ones without having to run the occlusion detection

again.

REFERENCES

Apostoloff, N. and Fitzgibbon, A. (2005). Learning spa-

tiotemporal t-junctions for occlusion detection. In

Computer Vision and Pattern Recognition, 2005.

CVPR 2005. IEEE Computer Society Conference on,

volume 2, pages 553–559. IEEE.

Brostow, G. J. and Essa, I. A. (1999). Motion based de-

compositing of video. In Computer Vision, 1999. The

Proceedings of the Seventh IEEE International Con-

ference on, volume 1, pages 8–13. IEEE.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

508

Corazza, S., M

undermann, L., Chaudhari, A., Demattio,

T., Cobelli, C., and Andriacchi, T. (2006). A mark-

erless motion capture system to study musculoskele-

tal biomechanics: Visual hull and simulated anneal-

ing approach. Annals of Biomedical Engineering,

34(6):1019–1029.

Corazza, S., M

undermann, L., Gambaretto, E., Ferrigno,

G., and Andriacchi, T. P. (2010). Markerless motion

capture through visual hull, articulated icp and sub-

ject speciﬁc model generation. International journal

of computer vision, 87(1-2):156–169.

Favaro, P., Duci, A., Ma, Y., and Soatto, S. (2003). On

exploiting occlusions in multiple-view geometry. In

Computer Vision, 2003. Proceedings. Ninth IEEE In-

ternational Conference on, pages 479–486. IEEE.

Grauman, K., Shakhnarovich, G., and Darrell, T. (2003). A

bayesian approach to image-based visual hull recon-

struction. In Computer Vision and Pattern Recogni-

tion, 2003. Proceedings. 2003 IEEE Computer Society

Conference on, volume 1, pages I–187. IEEE.

Guan, L., Sinha, S., Franco, J.-S., and Pollefeys, M. (2006).

Visual hull construction in the presence of partial

occlusion. In 3D Data Processing, Visualization,

and Transmission, Third International Symposium on,

pages 413–420. IEEE.

Kim, H., Sakamoto, R., Kitahara, I., Toriyama, T., and

Kogure, K. (2006). Robust foreground segmentation

from color video sequences using background sub-

traction with multiple thresholds. Proc. KJPR, pages

188–193.

Laurentini, A. (1994). The visual hull concept for

silhouette-based image understanding. Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

16(2):150–162.

Zivkovic, Z. (2004). Improved adaptive gaussian mixture

model for background subtraction. In Pattern Recog-

nition, 2004. ICPR 2004. Proceedings of the 17th In-

ternational Conference on, volume 2, pages 28–31

Vol.2.

Self-learningVoxel-basedMulti-cameraOcclusionMapsfor3DReconstruction

509