
Propagation and Amplification of a Short Subterahertz Pulse in a
Plasma Channel in Air Created by Intense Laser Radiation
A. V. Bogatskaya
1,2,3
, A. M. Popov
1,2,3
and E. A. Volkova
2
1
Department of Physics, Moscow State University, Moscow, 119991, Russia
2
D. V. Skobeltsyn Institute of Nuclear Physics, Moscow State University, Moscow, 119991, Russia
3
P. N. Lebedev Physical Institute, RAS, Moscow, 119991, Russia
Keywords: Multiphoton Ionization, Plasma Channel, Amplification of the Electromagnetic Radiation, Electron Energy
Distribution Function.
Abstract: The evolution of the electron energy distribution function in the plasma channel created in air by the third
harmonic of the Ti:Sa-laser pulse of femtosecond duration is studied. It is shown that such a channel can be
used to amplify few-cycle electromagnetic pulses in subterahertz frequency range at the time of relaxation
of the energy spectrum in air determined by the vibrational excitation of the nitrogen molecules. The
coefficients of the gain as a function of time, electron concentration and frequency of the amplifying
radiation are obtained. The propagation of few-cycle radio-frequency pulses through the amplifying medium
is analyzed.
1 INTRODUCTION
An important feature of the plasma structure
appearing in the field of an ultrashort laser pulse is
its strong nonequilibrium. Such nonequilibrium can
be used for a number of applications, in particular,
for generation of XUV attosecond pulses (Agostini
and Di Mauro, 2004, Krausz and Ivanov, 2009). The
energy spectrum of photoelectrons appearing in
multiphoton ionization of the gas under the
conditions where the pulse duration is compareable
or smaller than the average time interval between the
electron - atomic collisions consists of a number of
peaks corresponding to the absorption of a certain
number of photons. Such an electron energy
distribution function (EEDF) is characterized by the
energy intervals with the inverse population. It is
known, such situation can be used to amplify
electromagnetic radiation in a plasma (Bunkin et al,
1972).
The possibility of using of the plasma channel
created by a high intensity ultrashort pulse of a KrF
excimer laser (
5
eV) in xenon for the
amplification of radio-frequency pulses was
analyzed in the paper (Bogatskaya and Popov,
2013). In this paper time dependences of the gain
factor with various frequencies ω of the amplyfied
radio-frequency radiation in the xenon plasma
channel were obtained. In (Bogatskaya et al, 2013)
the possibilty to amplify the subtrerahertz radiation
in different gases was analyzed. It was demonstrated
that the xenon plasma has some advantages as the
amplifying medium in comparison with other rare
and molecular gases. In this paper we discuss the
possibility of using of the plasma channel created in
the atmospheric air as an amplifying medium for
radio-frequensy radiation. The evolution of the
electron energy spectrum in the relaxing plasma
created by the femtosecond laser pulse is examined
using the Boltzmann kinetic equation and the gain
factor of electromagnetic radiation in the plasma
channel is calculated as a function of time and
electronic concentration in dependence of frequency
in subterahertz band. It is found that for definite
range of the laser frequencies there exists also a
rather short time interval when such a relaxing air
plasma can be also used as an amplifying medium
for radio-frequency ultrashort pulses. The
propagation of such pulses through the amplifiyng
medium is studied in the frames of optical parabolic
approximation.
It should be mentioned that mechanism of the
amplification of electromagnetic radiation in the
plasma channel discussed in this paper is close from
physical point of view to the effect of the negative
199
Bogatskaya A., Popov A. and Volkova E..
Propagation and Amplification of a Short Subterahertz Pulse in a Plasma Channel in Air Created by Intense Laser Radiation.
DOI: 10.5220/0004723501990204
In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 199-204
ISBN: 978-989-758-008-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

absolute conductivity in the gas-discharge plasma
predicted by (Rokhlenko, 1978) and (Shizgal and
McMahon, 1985), experimentally detected by
(Warman et al, 1985), and discussed in detail in
reviews (Aleksandrov and Napartovich, 1993) and
(Dyatko, 2007)
.
2 PHOTOIONIZATION OF AIR
BY THE ULTRASHORT LASER
PULSE
To analyse the properties and evolution of the
plasma channel created by a high intensity
femtosecond laser radiation, it is significant to take
into account that the channel appears only due to the
multiphoton ionization of molecules. In this case, the
avalanche ionization of the gas molecules can be
neglected. Moreover, for pulses with the duration of
100~
p
fs, elastic collisions of electrons with
molecules of the medium during the pulse can also
be neglected. Indeed, the characteristic time of
collisions of electrons with nitrogen or oxygen
molecules in air at atmospheric pressure and room
temperature (
03.0T eV) can be estimated as
vNT
c
1 , where
19
105.2 N cm
–3
is the
density of the particles,
15
10~
cm
2
is the elastic
collision cross section, and
8
10~v cm/s is the
velocity of electrons appearing in photoionization
process. Under these conditions
13
104~
c
T s.
This time exceeds the duration of the laser pulse.
This means that the energy spectrum of
photoelectrons by the end of the laser pulse is
determined only by the photoionization of molecules
of the gas and can be obtained from the solution of
the problem of the ionization of a single atom or
molecule in a strong laser field. The evolution of the
spectrum caused by elastic, inelastic and electron-
electron collisions, which is described by the
Boltzmann kinetic equation, takes place in the
postpulse regime. For this reason, under the
conditions of interest, the problem of the ionization
of the gas by laser radiation can be considered
independently from the problem of the evolution of
the spectrum of photoelectrons. The solution of the
former problem is used as the initial condition for
the latter problem.
For the intensity range
13
10I
W/cm
2
the
ionization probability of O
2
molecules is a cubic
function of the radiation intensity I for the third
harmonic of the Ti:Sa – laser:
3
~ Iw
i
. For the N
2
molecules we have four-photon ionization in this
intensity range:
4
~ Iw
i
. For the moderate fields
with the laser intensity of the third harmonic of the
Ti:Sa laser ~10
11
–10
12
W/cm
2
in accordance with the
perturbation theory the probability of the three-
photon ionization is significantly larger than the
four-photon ionization probability. So plasma
channel is formed mainly by the three-photon
ionization of O
2
molecules. Also in such fields the
AC Stark shift of the continuum boundary can be
neglected and the position of the first peak in the
spectrum of photoelectrons corresponds to the
energy
i
I
3
0
, where 08.12
i
I eV is the
ionization potential of the oxygen molecule, and Ω is
the frequency the laser radiation. For the above
mentioned intensity range the degree of ionization in
air by the end of the laser pulse with the duration
100~
p
fs can be estimated as
67
1010
NN
e
(Delone and Krainov,
2001). Here
e
N is the electron density.
3 BOLTZMANN EQUATION FOR
THE EVOLUTION OF THE
PHOTOELECTRON ENERGY
SPECTRUM
Analyzing the evolution of the energy spectrum, we
assume that the plasma channel with a given degree
of ionization and strongly nonequilibrium electron
energy distribution function is formed at the initial
(zero) instant of time. The electron energy
distribution function (EEDF) is approximated by the
Gaussian
.
)(
)(
exp
1
)0,(
2
2
0
tn
(1)
The width of the peak is determined by the pulse
duration and for
100~
p
fs can be estimated as
2.0
eV. For the above mentioned intensity
range above-threshold ionization peaks can be
neglected.
This electron energy distribution function is
normalized as
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
200

.1)0,(
0
dtn
(2)
The quantity
),( tn
is the probability density
of the existence of the electron with the energy ε.
The temporal evolution of the initial spectrum
(1) was analyzed using the kinetic Boltzmann
equation for the EEDF in the two-term
approximation. We also assumed that the radio-
frequency field amplifying in the plasma was weak
enough and was not taken into account in the
Boltzmann equation. Under above assumptions the
kinetic equation was written in a form (Ginzburg
and Gurevich, 1960), (Raizer, 1977):
.
),(
),()(
2
)()(
),(
23
)(
*
i
i
tr
i
ee
tn
Ttn
M
m
nQnQ
t
tn
(3)
Equation (3) has the form of the diffusion equation
in the energy space. Here,
T
is the gas temperature
(below, we take
03.0T eV), m is the mass of the
electron,
i
M ( 2,1i ) are the masses of the nitrogen
and oxygen molecules respectively, and
mN
i
tri
i
tr
2)(
)()(
is the partial transport
frequency, where
)(
)(
i
tr
is the transport scattering
cross section for N
2
(i=1) and O
2
(i=2) molecules,
NN 79.0
1
and NN 21.0
2
are the
concentrations of N
2
and O
2
molecules in the air,
)(nQ
ee
is the integral of electron-electron collisions,
)(
*
nQ is the integral of inelastic collisions. Equation
(3) with initial condition (1) was solved numerically
using an explicit scheme in the energy range
50
eV. The elastic and necessary inelastic
cross sections for N
2
and O
2
molecules were taken
from (Phelps, 1985) and (Phelps and Pitchford,
1985). The total transport cross section for the
electrons in air is presented at Fig.1.
Among a lot of inelastic collisions of electrons
with nitrogen and oxygen molecules the excitation
of vibrational levels of N
2
(X
1
Σ
+
) is of most
importance. These cross sections are high enough in
the energy range ~ 2–4 eV and contribute
significantly to the temporal evolution of the EEDF
discussed below.
The obtained from Eq. (3) EEDF makes it
possible to calculate the temporal dependence of the
optical properties of the plasma channel created by
laser pulse. For example, the expression for the
012345
0,0
2,0x10
-15
4,0x10
-15
6,0x10
-15
tr
,, cm
2
, eV
Figure 1: Transport cross section for the electrons in air.
complex conductivity )('')(')(
i
at the
frequency
can be written in the form (Ginzburg
and Gurevich, 1960; Bunkin et al, 1972):
),(
)(
))((
3
2
)(
0
22
232
d
tn
i
m
Ne
tr
tre
(4)
The real part of this expression describes the
dissipation of the energy of the electromagnetic
wave in the plasma. So the absorption coefficient at
the frequency ω can be represented in the form:
0
22
232
.
),(
)(
)(
3
8
'4
d
tn
mc
Ne
c
tr
tre
(5)
The electron energy distribution function
typically decreases with the energy, i.e.,
0
n
and, consequently, the integral in Eq. (5) is positive
and, hence,
0
. However, in the process of the
photoionization of atoms by short pulses, energy
ranges with the positive derivative,
0
n ,
appear to exist for the initial instant of time. Such
energy intervals make a negative contribution to the
integral in Eq. (5) and reduce the absorption
coefficient. In (Bunkin et al, 1972) it was
demonstrated that the integral in Eq. (5) can become
even negative in the low-frequency range
tr
in
gases with the pronounced Ramsauer effect for the
EEDF with energy interval with positive derivative,
0
n . In the paper (Bogatskaya et al, 2013) it
was found that for the plasma with the EEDF similar
to (1) the amplification of the electromagnetic
PropagationandAmplificationofaShortSubterahertzPulseinaPlasmaChannelinAirCreatedbyIntenseLaserRadiation
201
radiation with
tr
will be possible, if the
condition
0)(
tr
d
d
(6)
will be fulfilled. Typically, the condition
tr
is
satisfied for the subterahertz frequency range
12
10
s
-1
.
In the paper (Bogatskaya and Popov, 2013) it
was demonstrated that the Ramsauer minimum
presence in the transport cross section of xenon and
as a consequence the rapidly increasing range of the
)(
tr
can be responsible for the appearance of the
amplification of electromagnetic radiation in the
plasma created by multiphoton ionization by short
laser pulse. Both N
2
and O
2
molecules do not
characterized by the Ramsauer minimum.
Nevertheless, the transport cross section for electron
scattering on nitrogen molecule is characterized by
01234
0,0
5,0x10
14
1,0x10
15
1,5x10
15
/
tr
(
)
, eV
Figure 2: The value
)(
tr
for electrons in air.
large positive value of the derivative
dd
tr
in the
energy range of ~1.5–2.3 eV. As a result, the
condition (6) is satisfied in this range (see Fig. 2). It
means that it is also possible to obtain the negative
values of the absorption coefficient.
Results of the numerical calculations for the
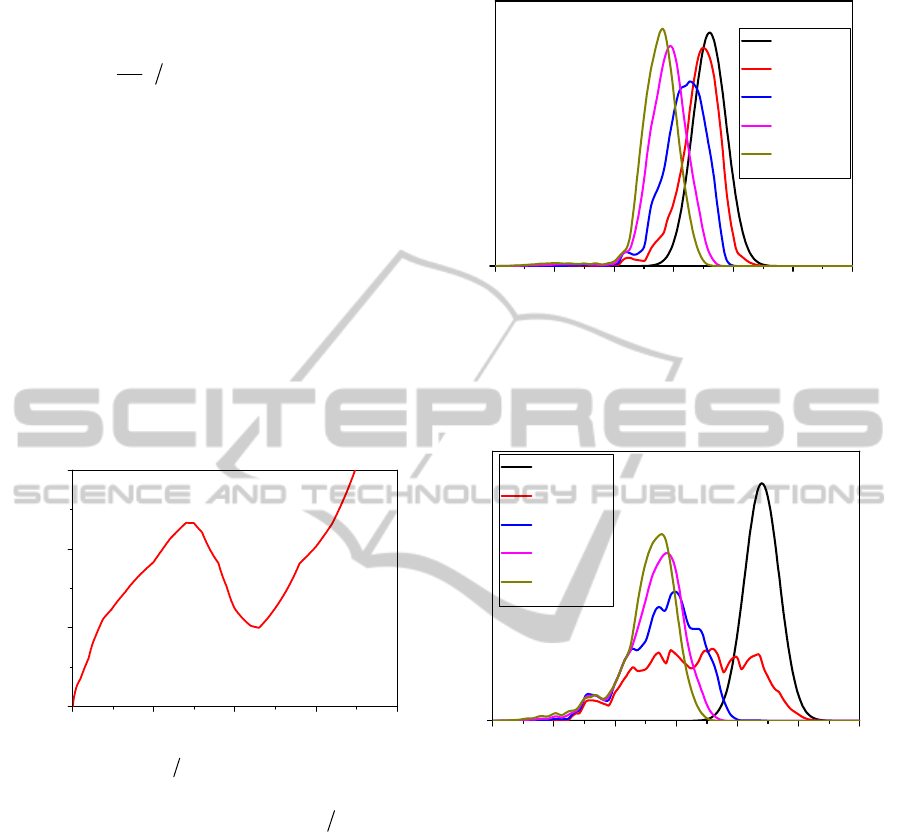
EEDF evolution in time are presented at Fig. 3 and
Fig. 4 for two different energy positions of the initial
photoelectron peak. As can be seen, for the initial
energy of photoelectrons
8.1
0
eV (this energy
value is very close to the ionization of oxygen
molecules by the third harmonic of the Ti:Sa laser)
the electron energy distribution function is
characterized by a pronounced maximum, which is
gradually shifted toward lower energies. While the
average electron energy is more then ~1.5 eV (see
the dependence at Fig.2), it is naturally to expect the
positive value of the gain factor. It should be
0,00,51,01,52,02,53,0
n(
,t)sqrt(
)
, eV
t=0
1*10
-12
s
5*10
-12
s
2*10
-11
s
4*10
-11
s
Figure 3: The EEDF in air at various times after the
creation of the plasma channel. Initial peak of
photoelectrons is characterized by
8.1
0
eV and
electron concentration N
e
= 10
13
cm
–3
.
0,0 0,5 1,0 1,5 2,0 2,5 3,0
n
(
,t
)
sqrt
(
)
, eV
t=0
1*10
-12
s
5*10
-12
s
2*10
-11
s
4*10
-11
s
Figure 4: The EEDF in air at various times after the
creation of the plasma channel. Initial peak of
photoelectrons is characterized by
2.2
0
eV and
electron concentration N
e
= 10
13
cm
–3
.
emphasized that for larger energy of the initial
photoelectrons (
2.2
0
eV) the temporal evolution
of the EEDF is quite different from that was
discussed above (see Fig.4). Due to significant value
of the cross section for the vibrational excitation of
N
2
molecules by electrons with energies above ~2.0
eV the characteristic time of relaxation of the EEDF
for 2.2
0
eV decreases dramatically and
photoelectrons are found to be distributed over the
energy range of
2.20.1
eV even for the t=1 ps.
Later the Gaussian-type EEDF is formed again, but
as the average energy of photoelectrons for these
instants of time is less 1.5 eV, and the positive value
of the gain factor can not be achieved.
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
202
The electron energy distribution functions obtained
in the numerical calculations were used to calculate
the gain factor of electromagnetic radiation
(
k ) in the air plasma for different values of
the initial peak position and the frequency of the
amplified radiation
11
105
s
-1
. These data are
presented at Fig.5. The data presented clearly
demonstrate that the amplification of the radiation is
possible if the energy of photoelectrons is less than
~2.25 eV. On the other hand, the energy of initial
photoelectron peak should not be less than 1.5 eV.
The maximum value of the gain factor can be
obtained for the initial photoelectron peak position
8.1
0
eV. Such energy of photoelectrons appears
to exist for the three-photon ionization by the laser
radiation with
63.4
eV which is very close to
the third harmonics of the Ti:Sa laser. Even for such
value of
0
the gain factor is found to be positive
during approximately 25 ps. It means that the plasma
channel in air can be used for amplification of only
extremely short few-cycled radio-frequency pulses.
For example, for
11
105
s
-1
it is possible to
amplify the pulses of two or three cycle duration.
For higher frequencies of amplified radiation the
gain factor drops dramatically as the condition
tr
is not satisfied already.
4 PROPAGATION OF THE
RADIO-FREQUENCY PULSES
IN THE PLASMA CHANNEL
As it is known, propagation of the electromagnetic
radiation in the medium is described by the wave
equation:
.
41
22
2
2
2
t
j
ct
E
c
E
(7)
Here E is the electric field strength,
Ej
is the
density of the electric current in the plasma and
is
the conductivity determined by expression (4). We
assume that the radio-frequency pulse intensity is
weak enough and do not contribute to the temporal
evolution of the EEDF in the plasma channel.
We use optical parabolic approximation to find
the solution of Eq. 7 (Akhmanov and Nikitin, 1997).
According to this approximation for the pulse
propagation along z-direction E should be
represented as
.exp),,(),(
0
tkzitzEtrE
(8)
Here
0
E is the envelope of the radio-frequency
pulse, and
k is the wave number. As the electronic
density in the plasma channel is low enough, the
permittivity at the frequency
11
105
s
-1
is close
to unity and it is possible to assume that the radio-
frequency pulse propagates in the channel also with
the speed of light. Then
ck
. After some
approximations one can obtain the folowing
equation for the
0
E :
.)(
22
1
1
00
2
00
kEcztk
i
E
t
E
cz
E
ik
(9)
The first term in the right part in Eq. (9) stands for
the diffraction divergence of the electromagnetic
field and the second one represents the absorption
(amplification) process. Actually, the amplification
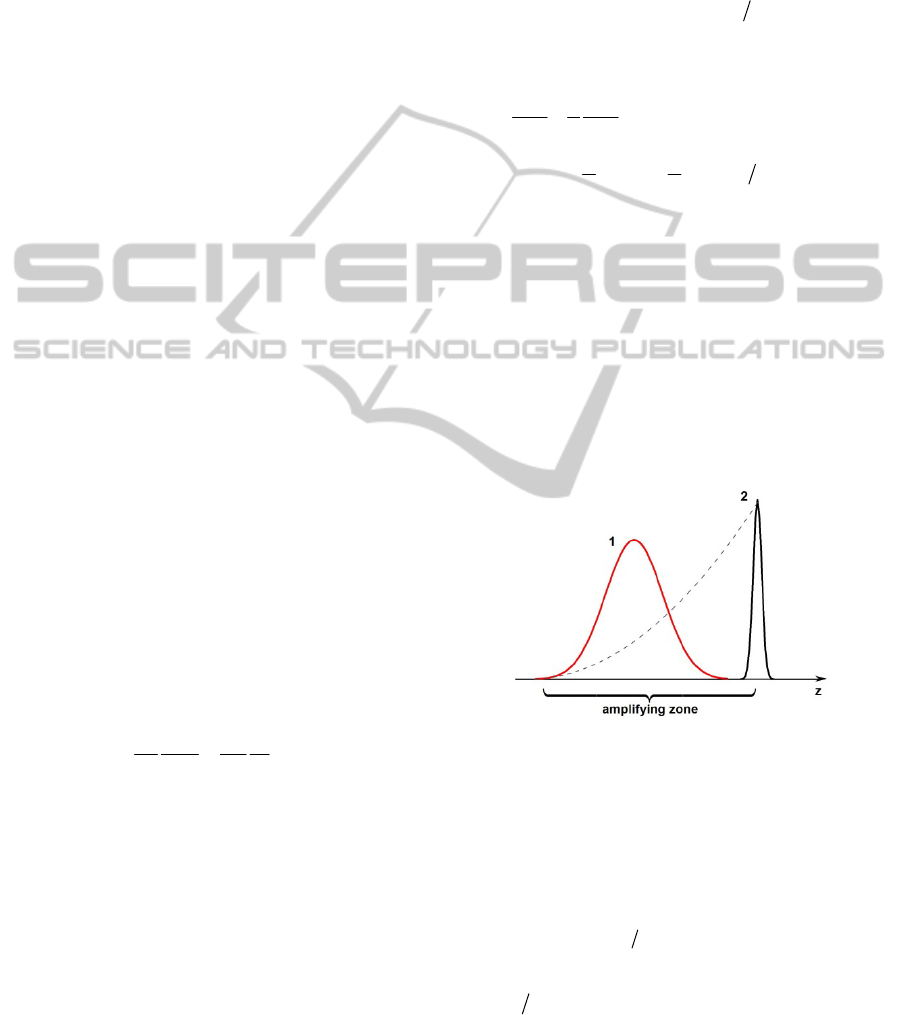
duration
corresponds to the amplification distance
of about
1~
с cm. So the laser pulse creates the
air plasma channel characterized by amplifying
«trail» (see Fig.6). If we launch the laser pulse and
the few-cycled radio-frequency pulse just one after
another simultaneously, the last one will continually
locate in the amplifying zone of the laser pulse.
Figure 6: Spatial structure of radio (1) and laser (2) pulses
for a given instant of time.
To obtain the amplification of the few-cycle
radio-frequency pulse in the plasma channel, the
second term in the right side of Eq. (9) should be
dominant in comparison with the diffraction
divergence. That is possible under the condition:
).2/( RRk
(10)
Here
R
is the plasma channel radius (about 1 cm),
36.02
с cm for frequency
11
105
s
-1
.
So the estimation (10) for the gain factor gives
05.0
k
s
-1
. If one neglects the diffraction of the
electromagnetic pulse the solution of the Eq. (9) for
PropagationandAmplificationofaShortSubterahertzPulseinaPlasmaChannelinAirCreatedbyIntenseLaserRadiation
203
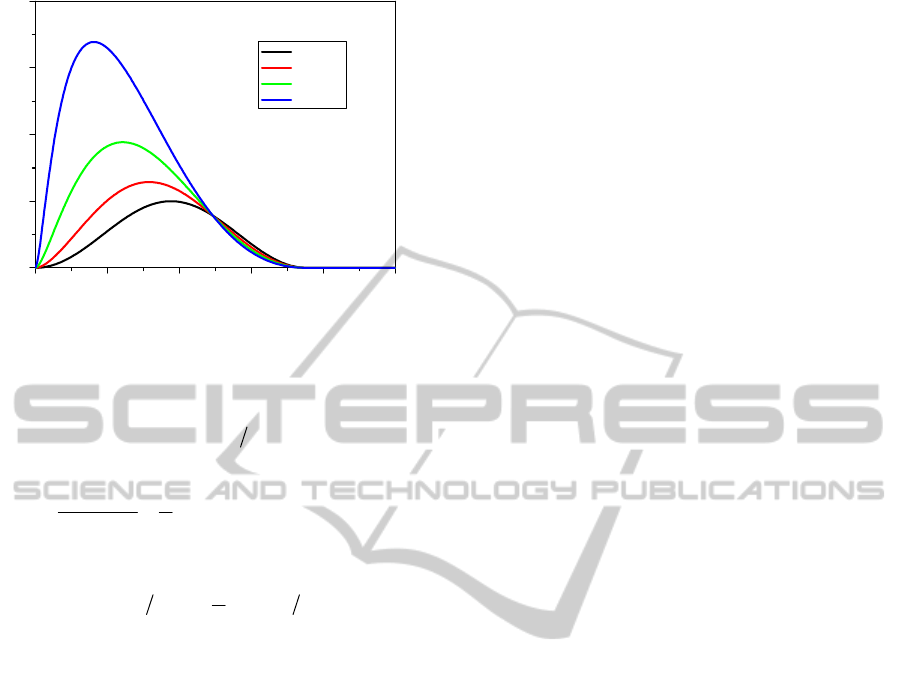
0 1020304050
0
1
2
3
4
Amlitude of electric field, a.u.
t-z/c, ps
z=0
z=10 cm
z=20 cm
z=30 cm
Figure 7: Time dependence of the electric field strength in
the amplifying pulse for different propagation lengths.
weak fields can be found analytically. Introducing
new variables
cztz
, , one obtains from
(9):
).,()(
2
1
),(
0
0
Ek
z
E
(11)
From (11) one obtains:
.)(
2
1
exp)(),(
0
zcztkczttzE
(12)
Here
is the initial envelope of the radio-
frequency pulse. We assume that it has the Gaussian
form with spatial size of
3 . Fig. 7 shows that the
sugnificant increase of the radio-frequency pulse
amplitude can be obtained during its propagation
despite the short time of amplification. It is worth
noting, that the diffraction length of the radio-
frequency pulse can be found:
20
2
kRl
D
cm.
This length determines the applicability limit of the
solution (12).
5 CONCLUSIONS
In this paper it has been shown that a plasma
channel created in the atmospheric air by the third
harmonic of the Ti:Sa laser can be used for
amplification of few-cycle electromagnetic pulses in
subterahertz frequency range. Despite the short time
duration of the positive gain factor there is an
opportunity to reach significant amplification by the
simultaneous launching of the laser and few-cycle
radio-frequency pulses with approximately the same
propagation velocity.
ACKNOWLEDGEMENTS
This work was supported by the Russian Foundation
for Basic Research (projects no. 12-02-00064, 14-
02-31872) and by the “Dynasty” Foundation
(program for support of students). Numerical
modeling was performed on the SKIF-MSU
Chebyshev supercomputer.
REFERENCES
Agostini, P. and Di Mauro, L. F., 2004. Rep. Prog. Phys.,
67, 813.
Akhmanov, S. A. and Nikitin, S. Yu., 1997. Physical
Optics, Oxford.
Aleksandrov, N. L. and Napartovich, A. P., 1993. Phys.
Usp., 36, 107.
Bogatskaya, A. V. and Popov, A. M., 2013. JETP Lett.,
97, 388.
Bogatskaya, A. V., Volkova, E. A. and Popov, A. M.,
2013. Quantum Electronics, 43, №12.
Bunkin, F. V., Kazakov, A. A. and Fedorov, M. V., 1972.
Sov. Phys. Usp., 15, 416.
Delone, N. B. and Krainov, V. P., 2001. Laser-Induced
Nonlinear Ionization of Atoms, Fizmatlit, Moscow.
Dyatko, N.A., 2007. J. of Phys.: Conf. Ser., 71, 012005.
Ginzburg, V. L. and Gurevich, A. V., 1960. Sov. Phys.
Usp. 3, 115.
Krausz, F. and Ivanov, M., 2009. Rev. Mod. Phys., 81,
163.
Phelps, A. V. and Pitchford, L. C., 1985. Phys. Rev. A, 31,
2932.
Phelps, A. V., 1985. JILA Information Center Report No.
26, University of Colorado.
Raizer, Yu. P., 1977. Laser - Induced Discharge
Phenomena, Consultants Bureau, New York.
Rokhlenko, A. V., 1978. Sov. Phys. JETP, 48, 663.
Shizgal, S. and McMahon, D. R. A., 1985. Phys. Rev. A,
32, 3669.
Warman, J. M., Sowada, U. and de Haas, M. P., 1985.
Phys.Rev. A, 31, 1974.
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
204
