
Compiling Graph Transformation Rules
into a Procedural Language for Behavioral Modeling
Sabine Winetzhammer and Bernhard Westfechtel
Applied Computer Science I, University of Bayreuth, Bayreuth, Germany
Keywords:
Graph Transformation Rules, Behavioral Modeling, Code Generation.
Abstract:
Graph transformation rules provide an opportunity to specify model transformations in a declarative way at
a high level of abstraction. So far, compilers have translated graph transformation rules into conventional
programming languages such as Java, C, or C#. In contrast, we have developed a compiler which translates
graph transformation rules into a procedural language for behavioral modeling (Xcore). The generated code is
significantly more concise and readable than programming language code. Furthermore, the code is portable
since it is completely programming language independent.
1 INTRODUCTION
Model transformation languages have been devel-
oped for specifying transformations of models at a
higher level of abstraction than in conventional pro-
gramming languages. Among many features (Czar-
necki and Helsen, 2006), model transformation lan-
guages may be classified according to their underly-
ing paradigm: In procedural languages, the transfor-
mation is described by specifying the order in which
elementary transformation steps are executed. In con-
trast, rule-based languages specify transformations
by a set of rules for matching and replacing pat-
terns. Since the algorithms for pattern matching and
replacement need not be provided by the user, rule-
based languages are located at a higher level of ab-
straction than procedural languages.
A model may be considered as a graph whose
nodes and edges correspond to the model’s objects
and links. Graph transformation rules (Ehrig et al.,
1999) are ideally suited for specifying model trans-
formations in a declarative way. Essentially, a graph
transformation rule consists of a left-hand side and
a right-hand side. The left-hand side describes the
graph pattern to be searched, while the right-hand side
defines the replacing pattern. Quite a number of graph
transformation languages have been proposed, includ-
ing PROGRES (Sch
¨
urr et al., 1999), Fujaba (Norbis-
rath et al., 2013), GReAT (Agrawal et al., 2006), Gr-
Gen.NET (Jakumeit et al., 2010), Henshin (Arendt
et al., 2010), MDELab (Giese et al., 2009), VIA-
TRA2 (Varr
´
o and Balogh, 2007), eMOFLON (An-
jorin et al., 2011), and ModGraph (Buchmann et al.,
2011). Users of these languages specify transforma-
tions with the help of high-level graph transformation
rules. Users are not concerned with the algorithms for
pattern matching and replacement, which are taken
care of by the underlying execution engines.
To support the execution of graph transformation
rules, both interpreters and compilers have been de-
veloped. An interpreter provides excellent support
for debugging, which is slowed down by a compiler.
On the other hand, compiled code is more efficient.
So far, compilers have translated graph transforma-
tion rules into conventional programming languages
such as Java, C, or C#. This approach results in rather
complicated generated code which is difficult to un-
derstand.
In contrast, we have built a compiler which trans-
lates graph transformation rules into a procedural
language for behavioral modeling (Figure 1). The
compiler accepts ModGraph rules and translates them
into Xcore (Eclipse Foundation, 2013), a recently de-
veloped modeling language which is based on Ecore.
Xcore is a textual language which covers both struc-
tural and behavioral modeling. Our compiler trans-
forms ModGraph rules into procedural Xcore opera-
tions, specifically making use of Xcore’s expression
language. The Xcore environment in turn translates
Xcore into Java (and prospectively into other target
languages in the future). Within our work we follow
our goal to provide total model driven software en-
gineering as explained in (Winetzhammer and West-
fechtel, 2013). Xcore interacts with ModGraph in or-
415
Winetzhammer S. and Westfechtel B..
Compiling Graph Transformation Rules into a Procedural Language for Behavioral Modeling.
DOI: 10.5220/0004723604150424
In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 415-424
ISBN: 978-989-758-007-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Xcore
JavaC++ C#
...
...
ModGraph
Figure 1: Staged translation.
der to provide high level control structures for rules.
The translation to Xcore unifies the level of abstrac-
tion between rules and control flow.
This staged translation approach (Figure 1) pro-
vides the following advantages over the traditional ap-
proach of compiling into a conventional programming
language directly, which is followed by all competing
tools:
Conciseness. The generated code is concise (but it
still takes care of the details of pattern matching
and replacement which should be shielded from
the user).
Readability. The generated code is human readable,
which facilitates e.g. code-level debugging.
Simplicity. The task of compiling is simplified sig-
nificantly since Xcore provides more high-level
language constructs than conventional program-
ming languages such as Java.
Portability. With direct compilation into a program-
ming language, one compiler is required for each
target language. In our approach, the compiler
does not depend on the programming language
which is eventually used for execution.
2 OVERVIEW
The Eclipse Modeling Framework (EMF) (Steinberg
et al., 2009) has been designed with the intent to im-
prove the software process by providing lightweight
support for model-driven software engineering. For
this reason, EMF provides a fairly minimalistic meta-
model for structural modeling (Ecore, an implementa-
tion of Essential MOF (EMOF) (OMG, 2011)). Using
the components of the EMF core, software engineers
create Ecore models as instances of the Ecore meta-
model. From an Ecore model, the EMF code gener-
ator creates code for classes, including methods for
creating objects, assigning attribute values, as well as
creating and deleting links which implement the se-
mantics of Ecore. However, for user-defined opera-
tions, the EMF code generator may only create empty
method bodies, which have to be filled in by the user.
ModGraph rules
Structure Behavior
Procedural Rule‐based
call
generate
Javaclasses
MethodsStructure
Xcoremodel
Xbase
operations
Structural
model
implement /
generate
reference
reference
reference
Figure 2: Interplay between ModGraph and Xcore.
Xcore (Eclipse Foundation, 2013) adds behavioral
modeling to EMF. Xcore provides a single language
for both structural and behavioral modeling. To this
end, Xcore introduces a textual syntax for Ecore mod-
els as well as procedural behavioral models. Xcore
is driven by the vision that software engineers need
no longer deal with code in a programming language
such as Java (as current programmers do not inspect
assembly or byte code). In Xcore, the sublanguage
Xbase (Efftinge et al., 2012) is used to model behav-
ior, i.e. the bodies of operations. Xbase is an ex-
pression language that was designed to be reused in
different domain-specific languages. Xbase expres-
sions provide both control structures and program ex-
pressions in a uniform way. Its program expressions
may be used e.g. for navigation in models and check-
ing constraints. Altogether, Xbase programs specify
computations in a procedural way at a higher level of
abstraction than Java.
ModGraph (Buchmann et al., 2011) is an EMF-
based language for specifying graph transformation
rules. With ModGraph, an operation defined in an
Ecore model may be realized as a graph transforma-
tion rule (or rule in short form). A graph pattern
forms the core of a ModGraph rule. The graph pat-
tern describes both the pattern to be searched and the
replacing pattern in a single diagram. If no replace-
ment is specified, the rule describes a test or a query
rather than a transformation. In addition to the core, a
rule may comprise optional components such as tex-
tual pre- and postconditions and graphical negative
application conditions (NACs).
A graph pattern may be composed of several kinds
of nodes and edges. Nodes are distinguished into
a current object, named this, bound nodes, repre-
senting the non-primitive parameters of the operation,
and unbound nodes, representing the objects to be
searched in the model instance. Both may be single-
(simple object and parameter) or multi-valued nodes
(multi-object and multi-parameter). Nodes provide
a status which may be preserved (grey, no marker),
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
416

Listing 1: Definition of annotations.
1 annotation " http :// www . ec lipse . org / e mf /200 2 / Eco r e / OCL / Pi vot " as OCL
2 annotation " ht tp :/ / www . ec l i p s e . org / emf /20 0 2 / Eco r e " as Eco r e
3 annotation " ht tp :/ / www . ec l i p s e . org / emf /20 0 2 / G e nModel " as GenMode l
4
5 @G e n M o d e l ( l o ad I n i t ia l i za t i o n =" t rue " , o pe r a ti o n R ef l e c ti o n =" t rue " ,
6 model D i r e c t o r y = "/[ s o m e P ath ]/ s rc ")
7 @E c ore ( invo c a t i o nD e l e ga t e s =" htt p :// www . eclip s e . org / emf /20 0 2 / Eco re / OCL / Pivo t " ,
8 sett i n g D e l e ga t e s =" h ttp :// www . ec l i pse . org / emf /2 0 0 2/ Ec o re / O CL / Pi v ot ",
9 val i d a t i on D e l eg a t es =" htt p : // www . eclips e . org / emf /200 2 / Eco r e / OCL / Pi vot ")
created (green, ++), or deleted (red, −−). They
can be marked as return parameter (<<out>>) or
as optional (<<optional>>) nodes. Nodes to pre-
serve or to delete may be constrained, nodes to create
or to preserve may be modified, for example by set-
ting an attribute value or calling an operation (opera-
tion calls allow ModGraph rules to interact directly
with each other). All nodes may be connected by
two kinds of edges: links (instances of references)
and paths (derived references). Analogously to nodes,
links provide a status. Creation links instantiating
multi-valued references may be ordered. Paths are
marked with a path expression, written in OCL or
Xbase. Negative application conditions describe pat-
terns which must not occur when the main pattern has
been matched. NACs are specified in a similar way as
graph patterns; however, nodes and edges do not have
a status and nodes may only be single-valued.
The interplay between ModGraph and Xcore is il-
lustrated in Figure 2. The user defines the structural
model in Xcore’s textual notation. With respect to
behavioral modeling, the user may choose between
the procedural and the rule-based paradigm. Simple
operations may be defined directly in Xbase. Com-
plex operations may be specified in ModGraph, tak-
ing advantage of its expressiveness and its easily read-
able graphical notation. If a complex operation may
not be coded as a single rule, the user may resort to
Xbase control structures for controlling the applica-
tion of multiple rules. In general, Xbase operations
may call ModGraph rules and vice versa. For the pur-
pose of execution, ModGraph rules are first compiled
into Xcore operations. The second stage of compi-
lation (currently targeting Java) is performed by the
Xcore compiler. Please note that the user gets in touch
only with Xcore and ModGraph (orange boxes); there
is no need to inspect the generated Java code (yellow
boxes).
In the following sections, we will focus on the
ModGraph2Xcore compilation (see red and bold ar-
row in Figure 2).
3 CODE GENERATION
This section explains from scratch how ModGraph
generates Xcore code and injects it into the Xcore
model.
3.1 Preliminaries for Code Generation
The initial step of integrating a ModGraph rule into an
Xcore model is parsing. We use a recursive, heuristic
greedy algorithm to transform the rule’s graph pattern
into a forest of spanning trees. The forest specifies the
reachability of nodes inside the graph pattern. A node
is reachable if it can be accessed from a non-primitive
parameter of the method or the current object using
links. The forest acts as a search plan and is built in
the following way:
(1) Each bound node in the pattern acts as root of
a tree inside the forest.
(2) Regarding all outgoing edges of the forest’s
nodes, select the instance of the reference with min-
imum multiplicity. Consider paths as multiplicity
many references. If two links instantiating references
of the same multiplicity exist, choose one randomly.
(3) Check if the link’s target node is mandatory and
not contained in any tree yet. If true, add it as a
child into the tree containing the source node. (4) Re-
peat steps (2) and (3) for all mandatory nodes. If any
mandatory node cannot be inserted into a tree it can-
not be bound, is therefore unreachable, and the match-
ing fails. (5) Repeat – without the mandatory check
– steps (2) and (3) for all optional nodes. (This pre-
vents the search of a mandatory object from an op-
tional one.)
For more information on the pattern matching pro-
cess, please refer to (Winetzhammer, 2012).
3.2 Injecting Code into the Xcore Model
Annotating the Xcore Model: Using ModGraph
with Xcore means adding OCL support and some
Genmodel specifications to the original model as
CompilingGraphTransformationRulesintoaProceduralLanguageforBehavioralModeling
417
Listing 2: Xcore Model for Refactoring.
1 class Re f a c t o r i n g {
2 re fers EO p e r a t i o n [] r e f er e n ce T o EO p e ra t i o n
3 re fers EC lass [] r e f e r en c e T oE C l a s s
4 re fers ER e f e r e n c e [] r e f er e n ce T o ER e f er e n c e
5 re fers EP a r a m e t e r [] r e f er e n ce T o EP a r am e t e r
6 re fers ESt r u c t u r al F e a tu r e [] r e fe r en c eT o E St r uc t ur a l Fe a tu r e
7
8 op voi d ch a ng e Un i To B id i re c ti o na l Re f e re n ce (
9 St r i ng c l a s s 1 N a m e , Stri n g cl a s s 2 N a m e )
10 op voi d co l l a ps e H i e ra r c h y ( Cl a ssType c l a s s T y p e ,
11 EC l a ss s u p e r C l a s s , ECla s s su bClass )
12 op voi d r e m o v e S u b ( ECla s s su p e r C l a s s , E C l ass s u bClass )
13 op voi d re m o v e S u p e r ( ECla s s su p e r C l a s s , E C lass su b C l a ss )
14 }
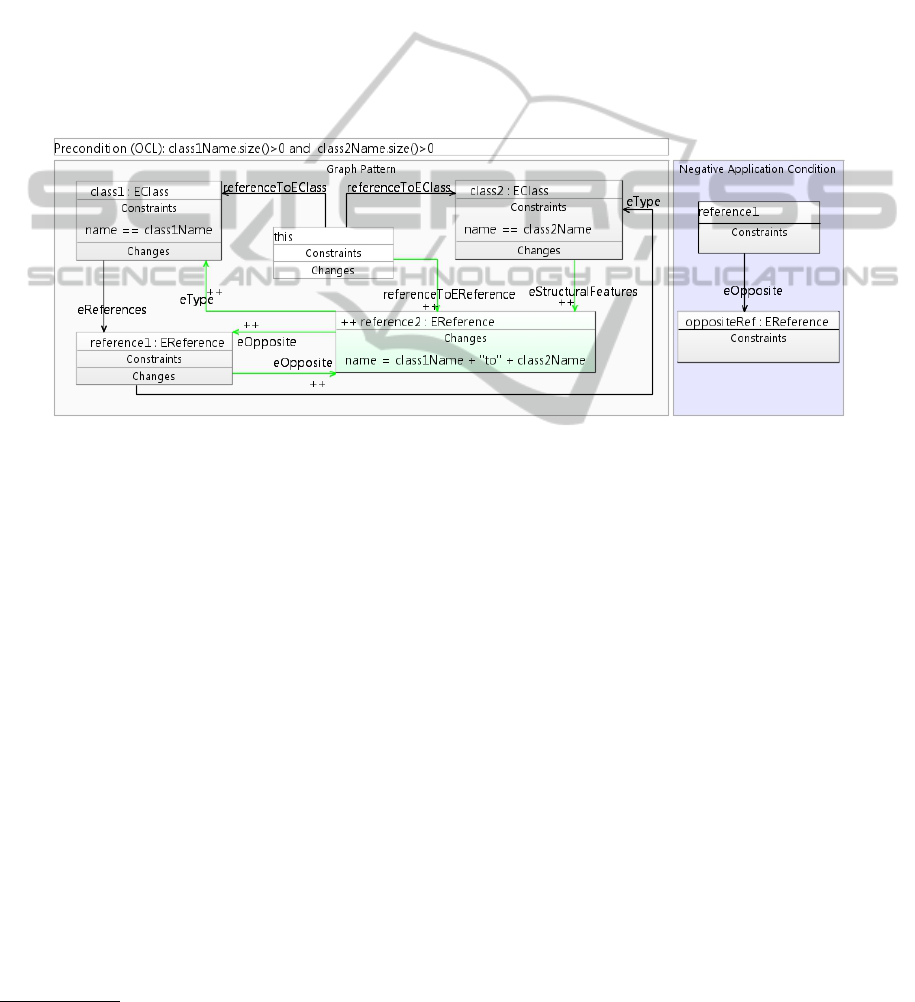
Figure 3: ModGraph rule for changeUniToBidirectionalReference(String class1Name , String class2Name).
shown in Listing 1. Therefore we define annotations
(including Xcore aliases) to ensure that the Xcore
code generator works with correct parameters.
Concerning OCL we add EMF provided invoca-
tion, setting and validation delegates using the Eclipse
OCL Pivot evaluation. The Pivot evaluator is used
here because of its full OMG compliance
1
.
Furthermore we add some Genmodel directives,
e.g. to ensure the operation reflection is set true to
make OCL work or for documentation purposes.
Please note that these changes are applied once for
each Xcore model, no matter how many operations
are implemented within ModGraph.
Annotating the Xcore Operation: In this step we
parse the Xcore model until the rule’s implemented
operation is found. The generator annotates the oper-
ation implemented by the ModGraph rule depending
on it’s content.
In each case it creates an Xcore Genmodel doc-
umentation annotation. This annotation is used
1
See eclipse help: http://help.eclipse.org/kepler/index.jsp
twofold: It contains a note that this Xcore code is
generated by ModGraph as well as the comment on
a ModGraph rule.
Using ModGraph, you may write pre- and post-
conditions in OCL or Xbase. If there are any OCL
pre- or postconditions, they are translated into Xcore
OCL annotations. (Xbase conditions are integrated
into the operation’s body within the subsequent step.)
Implementing the Operation’s Body with Xbase:
Inside the operation’s body, the generated Xbase code
is structured as follows: (1)Check the rule’s precondi-
tions written in Xbase. (2)Define all variables needed
to perform the transformation. (3) Generate code for
pattern matching using nested for-loops. (4)Within
the most inner loop check the negative application
condition using an additional if-condition. (5) If any
object cannot be matched, an exception of type GT-
Failure is thrown. If all objects could be matched, go
on. (6) Calculate all attribute values on the pre-state
of the model. These values are stored in final vari-
ables. (7) Delete or change objects and links between
them and create new ones. (8) If there is any opera-
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
418

tion call inside the rule, call the operation. (9) Check
Xcore postconditions. (10) Return what needs to be
returned.
4 EXAMPLE
This section provides concrete examples on the code
generation mechanism described above. Therefore
we consider two refactoring operations on an Ecore
model: changing an unidirectional reference to a bidi-
rectional one and collapsing the hierarchy between
two classes as defined by Fowler (Fowler, 1999).
These examples have been selected (and slightly
adapted for demonstration purposes) from a bachelor
thesis (D
¨
ummel, 2013) in which a much more com-
prehensive set of refactoring operations has been im-
plemented with ModGraph transformation rules.
The structure of our simple refactoring is de-
scribed textually in Xcore as shown in Listing 2. A
refactoring class references elements of the Ecore
model to be refactored, and defines the refactoring op-
erations to be applied. Each refactoring operation is
applied to model elements fixed by parameters. The
operations are invoked through an interactive user in-
terface. For demonstration purposes, both strings and
objects are used to identify model objects. In the first
example, the use of string parameters implies the in-
sertion of nested loops into the generated code. In the
second example, objects are used instead of strings to
focus on other issues of code generation. In the actual
implementation (D
¨
ummel, 2013), model objects are
identified consistently by strings for implementation-
specific reasons.
To get a clear impression of the pattern matching
in Xcore, we consider the refactoring rule to change
a unidirectional reference into a bidirectional one as
shown in Figure 3. Since only the classes’ names are
given as parameters of the operation, a precondition,
written in OCL ensures them not to be empty or null.
The graph in the graph pattern shows the pattern to be
matched: starting at the current object named this,
two classes with the given names need to be found.
The class we call class1 needs to contain a reference
typed over class2. In that case the negative applica-
tion condition (NAC) ensures that the reference does
not have an opposite set yet. If all these conditions are
fulfilled, an opposite reference is created and embed-
ded into the model by setting the links marked with
++ and colored green.
The Xcore code generated for this rule is shown in
Listing 3. In line 1 a Genmodel annotation is used to
mark the operation as generated by ModGraph. Line
2 checks the OCL precondition (in Figure 3 at the
top), using the EMF OCL Pivot evaluator via an an-
notation. Line 3 & 4 show the Xcore generated oper-
ation head. For each bound object in the rule’s graph
pattern, the generator declares variables as shown in
lines 5-7. Lines 8-19 show the matching, which is
implicitly given in the ModGraph rule. Nested for-
loops are built up according to the spanning forest de-
scribed in 3.1. These for-loops also use the Xbase
λ-expression language to filter the collections they it-
erate by the constraints given to the objects in the rule,
e.g. name == class1Name. The most inner loop con-
tains an if condition, that checks the NAC. If match-
ing succeeds, the variables defined above the loops
are initialized. Unfortunately Xcore does not support
break-commands. Therefore, the variables are initial-
ized with the last match found
2
. Line 19 checks if
matching has succeeded; otherwise, an exception is
raised.
Line 20 shows the calculation of the name for
the new reference depending on the pre-state of the
model. The reference itself is created in line 21 and its
name is set to the calculated one in line 22. Lines 23
to 27 put the new reference into its context executing
the following expressions: The new reference’s oppo-
site is set to the existing one and vice versa. class2
is set as a container for the new reference by adding
it to its structural features. The refactoring class adds
the new reference and the reference’s type is set to
class1.
The second refactoring rule shown here is col-
lapse hierarchy. It shows the interplay of procedu-
ral and rule-based operations. For simplification we
assume that there is only one subclass to a super-
class
3
. Collapsing a hierarchy means eliminating ei-
ther the sub- or the superclass. Both possibilities may
be modeled in separate ModGraph rules implement-
ing the methods removeSub and removeSuper. The
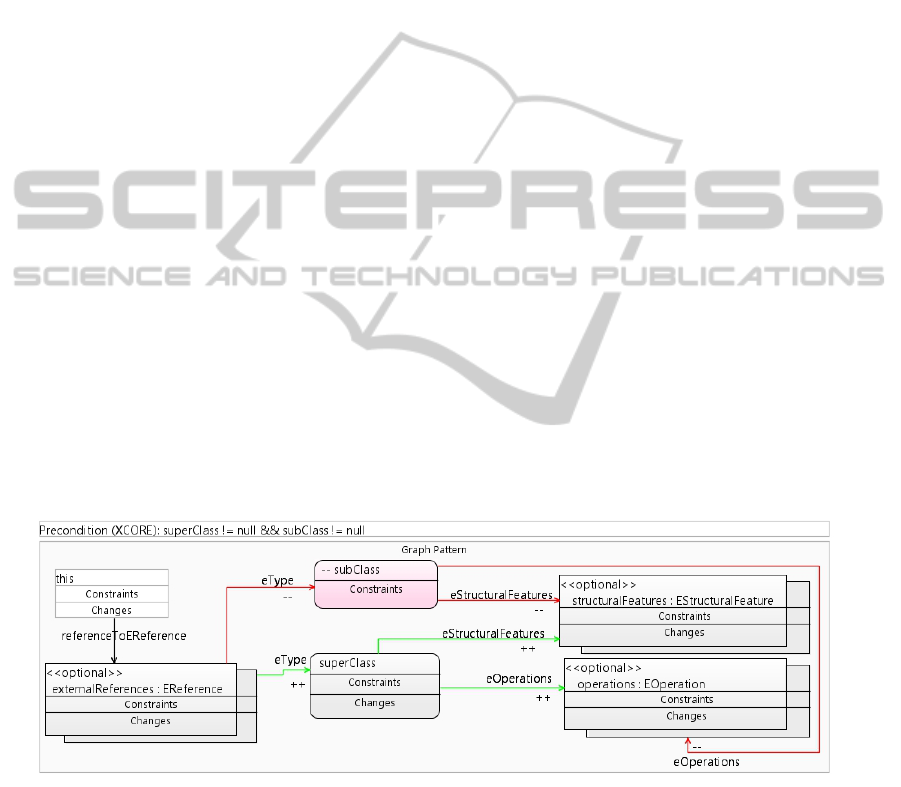
rule to remove the subclass is shown in Figure 4. An
Xcore precondition ensures the parameters not to be
null
4
. The graph pattern shows the superclass and
the subclass as well as all its operations and struc-
tural features, which need to be shifted to the super-
class. Additionally all references typed over the sub-
class need to be retyped by the superclass. All fea-
tures are marked optional because if there is none, the
rule may be executed anyway. The ModGraph rule
for removing the superclass works analogously.
2
Since we expect that break-commands will be added
soon to Xcore, we refrain from rewriting the generated code
with more awkward while-loops returning the first match.
3
The presence of another subclass may be excluded by
a negative application condition in a similar way as already
demonstrated in Figure 3.
4
This precondition is redundant and has been added to
demonstrate that Xcore expressions may be used alterna-
tively to OCL expressions.
CompilingGraphTransformationRulesintoaProceduralLanguageforBehavioralModeling
419
Listing 3: Generated Xcore implementation of method changeUniToBidirectionalReference.
1 @Gen M od e l ( doc u m e n t at i o n =" G en e ra t e d by Mod G ra p h . ")
2 @ OCL ( pre_ p re 1 =" c la s s 1 Na m e . size () >0 a n d cl a ss 2 Na m e . size () > 0 ")
3 op v o id cha ng eU ni To B i d i r e c t i o n a l R e f e r e n c e (
4 Str i ng cla s s1 N am e , Strin g cl a ss 2 N a me ) {
5 var E C la s s cl a s s1 = nu l l
6 var E C la s s cl a s s2 = nu l l
7 var E Re f e r en c e ref e re n ce 1 = null
8 for ( _ c l as s 1 : r ef e r e n c e T oE Cl a s s . fi l ter (e| e . name == c la s s1 N a m e )) {
9 for ( _ c l as s 2 : r ef e r e n c e T oE Cl a s s . fi l ter (e| e . name == c la s s2 N am e )){
10 for ( _ r ef er e nc e 1 : c l as s 1 . E R ef e r e nc e s . filt e r (e |e . E T y pe . equal s ( _c l a ss 2 ))) {
11 if (! ( ref e re n ce 1 . E O pp o si t e != null )) {
12 cla s s1 = _ c la s s 1
13 cla s s2 = _ c la s s 2
14 re f er e n c e1 = _ref e re n c e 1
15 }
16 }
17 }
18 }
19 if( class 1 == null ) th r o w n e w GTF a il u re
20 val r e f e r e n c e 2N am eV a l u e = c l a ss 1 Na m e + " to " + cl a ss 2 N a me
21 var r ef e r e nc e 2 = E co r e F ac t o r y :: e I NS T AN C E . cre at e E R e f er en c e ()
22 r e fe r en c e 2 . name = r ef er en c e 2 N a m e V a lu e
23 r e fe r en c e 2 . EO p p o s i t e = r e f e re n ce 1
24 r e fe r en c e 1 . EO p p o s i t e = r e f e re n ce 2
25 cl a ss2 . ES t r u c t u r a l F e at ur e s . a d d ( ref er e nc e 2 )
26 r ef e r e n c e T o E R e f e r e nc e . a d d ( re f er e n c e2 )
27 r e fe r en c e 2 . ETy p e = class1
28 }
Listing 4: Xcore implementation of method collapseHierarchy.
1 op v o id col l a p se Hi e r a r c h y ( Cl a s s Ty p e classType , EC l ass super C l ass , EC l ass sub C la s s ){
2 if ( cla s sT y pe == Cla s sT y pe :: S UP E R _ CL A SS )
3 re m ov e S u pe r ( su p e rCla s s , subCl a ss )
4 if ( cla s sT y pe == Cla s sT y pe :: S UB _ CL A SS )
5 re m ov e Su b ( sup e r Clas s , s ub C la s s )
6 }
Figure 4: ModGraph rule for removeSub(EClass superClass , EClass subClass).
As we do not want to split up this refactoring, we
use Xcore’s procedural capabilities and write a third
method encapsulating the other two. This method is
called collapseHierarchy. It acts as a control flow
determining which of the two generated methods will
be called. Its Xcore implementation is shown in lines
1-6 in Listing 4.
Listing 5 shows the generated Xcore code for the
ModGraph rule removeSub. Lines 1 and 2 show the
comment complementing the rule. Line 3 contains
the head of the method. Line 4 checks the Xcore
precondition. Lines 5–7 declare variables for stor-
ing matches of multi-objects. In lines 8–11, values
for these variables are retrieved which are assigned in
lines 12–14. Line 15 removes the subclass. Lines 16
and 17 assign the structural features and operations
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
420

Listing 5: Generated Xcore implementation of method removeSub.
1 @G e n M o d e l ( d o c u m en t a t i o n =" Gen e r a t e d by M o d G r a p h : Re moves the
2 su b c l a s s . Par t of the c o l l a p s e hi e rarchy r e f a c t or i n g . ")
3 op v oid re moveSub ( EC l ass s u p e r C l a s s , E C l ass s u b Class ) {
4 if (! ( su p e r C l a s s != nul l && subCla s s != nul l )) th r ow new G T F ailure
5 var EList < ES t r ucturalFeatu r e > s t r u c tu r a l Fe a t u re s = nul l
6 var EList < E O per a tio n > op e r a t i o n s = n ull
7 var EList < E R efe r enc e > ex te r n al R e f e re n c e s = null
8 val _ o p e r a t i o n s = su b C l a ss . EOperat i o n s
9 val _ s tr u c t ur a l Fe a t u re s = su b C l ass . E S t r u c t ur a l Fe a t u re s
10 val _ e xt e r n al R e fe r e n ce s = refe r e n c eT o E R ef e r en c e
11 . fi l ter (e | e . E Typ e . equ a l s ( subC l a s s )) . as E L i s t
12 str u c t u r a lF e a t ur e s = _st r u c t u r al F e at u r e s
13 op e r a t i o n s = _o p e r a t i o n s
14 ext e r n a l R ef e r e nc e s = _ex t e r n a l Re f e re n c e s
15 org :: ec l i p s e :: emf :: ecor e :: ut il :: Ecor e U t i l :: r e move ( su b C l ass )
16 su p e r C l a s s . E St r u ct u r a lF e a t ur e s . a d dAll ( s t ru c t u ra l F e at u r e s )
17 su p e r C l a s s . E O p e r a t i on s . add A l l ( operations )
18 ext e r n a l R ef e r e nc e s . f o r E ach (e | e . E T ype = su p e r C l a s s )
19 }
20
21 op v oid re m o v e S u p e r ( ECla s s su p e r C l a s s , E C lass su b C l a s s ) {
22 /* an a l o g o u s l y to r e m o v e S u b */
23 }
to the superclass, respectively, and line 18 retypes the
references.
5 DISCUSSION
This section discusses the advantages of our staged
transformation approach. To this end, we consider the
three implementations to delete a subclass in an Ecore
model in order to collapse the hierarchy: the Mod-
Graph rule (Figure 4), the generated Xcore implemen-
tation (Listing 5), and the Xcore generated Java code
(Listing 6).
Comparing the ModGraph rule to the Xcore im-
plementation, we observe that a rule is still more intu-
itive than the generated code: its clearly structured
format with the graphical, color-coded, nodes and
edges visualize the pattern to be matched and the ac-
tions to be performed.
The Xcore code is a clearly structured, target lan-
guage independent text which we consider to be still
concise and simple enough to be human readable. Its
high level of abstraction increases the readability es-
pecially when the functional expressions provided by
Xbase come into play.
The generated Xcore code shown in Listing 5
could be written more concisely if written by hand. In
fact, lines 5–14 could be expressed by only three lines
of hand-written code. In contrast, the code generator
creates declarations of variables which are assigned
values only when a complete match has been found.
During the matching, final variables are used to store
partial matches. In this way, it can be checked con-
veniently whether matching has succeeded (if it has
not, the non-final variables will still be null). This
code generation approach supports the most general
case, in which matching has to be performed in (po-
tentially nested) loops (see Listing 3 for the refactor-
ing rule converting a unidirectional to a bidirectional
reference).
This example demonstrates that hand-written code
may be shorter than generated code. This is not sur-
prising and quite common. Nevertheless, the gener-
ated code is still concise and readable. Thus, debug-
ging may be performed quite conveniently on the gen-
erated code.
The result of compiling the Xcore code of List-
ing 5 to Java code is shown in Listing 6. Comparing
them, we note a significant difference in length: The
generated Java code is much longer than the Xcore
code. Furthermore, the Java code is much more dif-
ficult to read. This results from Xcore’s higher level
abstraction. Compare, e.g., the precondition initially
written as one line Xcore expression in the rule in Fig-
ure 4 and the Xcore implementation in Listing 5. The
Java implementation uses lines 6–19 to ensure this
condition. A closer look at the Xcore generated Java
code reveals that internal functions need to be called
or even implemented. The filter function shown in
Listing 5, lines 10–11 to filter the references typed
CompilingGraphTransformationRulesintoaProceduralLanguageforBehavioralModeling
421

Listing 6: Xcore Generated Java Code for method removeSub.
1 / * *
2 * <!- - begin - user - doc - -> <! - - end - user - doc - ->
3 * @ g en e ra t ed
4 */
5 p ubl i c v oid remo v eS u b ( final EClas s super C l ass , fi n al EClass sub C la s s ){
6 try {
7 boo l ea n _and = fal s e ;
8 boo l ea n _n o tE q u a ls = (! Objec t s . equal ( superCl a s s , n ull ));
9 if (! _n o tE q u a ls ) {
10 _and = f a l se ;
11 } e lse {
12 bo o le a n _no t Eq u a l s_ 1 = (! Obj e ct s . equa l ( s u bClass , null ));
13 _and = ( _ n ot E qu a ls && _n o tE qu a ls _ 1 );
14 }
15 boo l ea n _not = (! _an d );
16 if ( _not ) {
17 G T Fa i lu r e _gT F ai l ur e = new GT F ai l ur e ();
18 thr o w _ g TF a il u re ;
19 }
20 EList < ES t ru c tu r al F ea t ur e > str uc tu r a l F e a t ur es = n u ll ;
21 EList < E Oper a t ion > o pe r at i on s = null ;
22 EList < E Refe r e nce > e x t er na l R e f e r e nc es = n u ll ;
23 fina l EList < E O p era t i on > _ o pe r a t io n s = s u bC l as s . g e t E Op er a t i on s ();
24 fina l EList < E St r uc t ur a lF e at u re > _st r u c tu ra lF e a t u r e s =
25 sub C la s s . ge t E S t r u c t u ra lF ea tu r e s ( ) ;
26 Re f a c to r in g _t h i s = this ;
27 EList < E Refe r e nce > _ r e f e r e nc eT oE Re f e r e n c e =
28 _t h i s . ge t R e fe re nc eT oE Re fe r e n c e ( ) ;
29 fina l Functi o n 1 < ERefere n c e , Boolean > _ fu n ct i on =
30 new Fun c t i on1 < E R e fer e n ce , Boolean > ( )
31 {
32 pu b lic Bool e an apply ( final ERe f er e nc e e){
33 E C la s s i fi e r _eTyp e = e . get E Ty p e ();
34 bo o le a n _equa l s = _e T ype . e qua l s ( subC l as s );
35 re t urn Bool e an . val u eOf ( _eq u al s );
36 }
37 };
38 Iterable < E R efer e n ce > _f i lt e r = I te r a b l e E x te ns i o n s .< ER e f ere n c e > filt e r (
39 _ r ef e r e nc e T o ER e fe r e n ce , _func t i o n ) ;
40 fina l EList < E R e fer e n ce > _ e x t e r n a lR ef er e n c e s = ECo l l e ct i o n s . < E R efer e n ce > a s EL i st (
41 (( E R e f er e nc e []) Co n v e rs i on s . u n w r ap A r r ay ( _filter , E Re f er en c e . class )));
42 s t ru ct u r a l F e a t u re s = _ s t ru ct u r a l F e a t u r e s ;
43 op e ra t i o ns = _ o p er a t i on s ;
44 e x te rn a l R e f e r e n ce s = _ e x te rn a l R e f e r e n c e s ;
45 Ec o re U ti l . re m ove ( sub C la s s );
46 EList < ES t ru c tu r al F ea t ur e > _e S tr uc tu r a l F e a t u r e s =
47 su p er C la s s . ge tE S t r u c t u r a l F e a t u r e s ();
48 _ e St ru ct ur a l F e a t u r e s . addA l l ( s t r u c t u r al Fe at u r e s );
49 EList < E Oper a t ion > _ eO p e r at i o n s = s up e rC l as s . g e t E O p er a t i o n s ();
50 _e O p e ra t i o ns . add A ll ( ope r at i o n s ) ;
51 fina l Proce d u re1 < E R efer e n ce > _ f un c t i on _ 1 = new Procedur e 1 < ERefer e n ce > ( )
52 {
53 pu b lic void a p ply ( final ERe f er e nc e e) {
54 e. s e tE T yp e ( s u pe r Cl a ss );
55 }
56 };
57 I t er ab l e E x t e n s i on s . < E R efer e n ce > f o rE a ch ( ext e rn a lR e fe r e n c e s , _fun c t i on _ 1 );
58 } catch ( T hr o wa b le _e ){
59 thro w Ex c ep t io n s . sn e ak y Th r o w ( _e ) ;
60 }
61 }
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
422

Table 1: Graph transformation languages and tools.
language/tool interpreter compiler target language(s) (if compiled)
eMOFLON (Anjorin et al., 2011) x x Java
Fujaba (Norbisrath et al., 2013) x x Java
GReAT (Agrawal et al., 2006) x - -
GrGen.NET (Jakumeit et al., 2010) - x C#
Henshin (Arendt et al., 2010) x - -
MDELab (Giese et al., 2009) x - -
ModGraph (x) x Xcore or Java
PROGRES (Sch
¨
urr et al., 1999) x x C or Java
VIATRA2 (Varr
´
o and Balogh, 2007) - x Java
over the subclass is mapped to lines 38–41 in List-
ing 6. An additional Java filter function is called to
map the procedural expression to Java. The foreach-
expression shown in Listing 5, line 18, even forces
a re-implementation to be mapped to Java, see lines
51–57.
Altogether, these considerations reinforce the
claims stated at the end of Section 1: In fact, the
generated Xcore code is concise, readable, and sim-
ple. In addition, it is also portable since Xcore could
be mapped to other target languages, as well. Thus,
we have clearly demonstrated the advantages of the
staged translation approach (Figure 1).
6 RELATED WORK
In (Winetzhammer and Westfechtel, 2013) we already
gave an overview on how Xcore and ModGraph inter-
act on code level. Here we make Xcore and Mod-
Graph interact on model level.
Code level interaction means that a graph trans-
formation rule is specified which is based on a method
defined in an Xcore model; subsequently, Java code is
generated from the ModGraph rule and injected into
the Xcore generated Java code. That means the Xcore
model is completely independent of the ModGraph
rule and leads to a fully compiled solution: both tools
meet at the generated Java code.
The approach described here goes beyond our pre-
vious work. As before, an operation defined in an
Xcore model is specified by a ModGraph rule. How-
ever, the implemented operation is not compiled di-
rectly to Java code. Instead, we use a staged trans-
lation approach: The rule is compiled into Xcore
code and injected at model level into the textual Xcore
model. Hence we do not leave the model level as we
do in (Winetzhammer and Westfechtel, 2013). In this
way, ModGraph code is independent of the program-
ming language. In our new approach, the code gen-
eration to Java (and possibly other languages) is com-
pletely left to the Xcore generator. Another advan-
tage of compiling into a procedural behavioral mod-
eling language relies on the fact that such a language
resides on a higher level of abstraction than a conven-
tional programming language.
As a side note, we mention that generation of
Xcore code implies partial support of interpretation
of ModGraph rules: Since the generated code is quite
concise and human readable, the Xcore interpreter
may be used conveniently for testing and debugging
ModGraph rules. This is a low-cost alternative to im-
plementing a full-fledged rule-level interpreter.
Concluding, we developed a compiler from graph
transformation rules using a procedural language for
behavioral modeling. The result of compilation is in-
terpretable as well as compilable. A staged transfor-
mation approach is used to make the generated code
independent of the programming language which is
eventually used for execution.
Table 1 provides a short comparison of related
tools / languages. Here we consider only tools related
to EMF and based on the theory of graph transforma-
tion. Some tools provide a direct interpreter. Quite
a number of tools compile graph transformation rules
into widely used programming languages such as C,
C#, or Java. Only ModGraph provides model-level
code generation (into Xcore code). None of the com-
peting tools supports a staged translation approach as
illustrated in Figure 1.
7 CONCLUSIONS
We have presented a new approach of compiling high
level graph transformation rules into a procedural lan-
guage for behavioral modeling (Xcore). Using this
approach, the modeler may resort to graph transfor-
mation rules for complex operations, while simple op-
erations may be directly implemented in Xcore us-
ing Xbase. We described the mechanisms of inject-
ing graph transformation rules into the Xcore model.
CompilingGraphTransformationRulesintoaProceduralLanguageforBehavioralModeling
423

The resulting code may be compiled as well as inter-
preted. It is much more concise, readable, and simple
than programming language code due to the fact that
we do not leave the modeling level. Furthermore, the
Xcore code is portable since it is programming lan-
guage independent. The approach presented here is
unique with respect to these properties: All compet-
ing tools for generating code from graph transforma-
tion rules create code in a conventional programming
language (see Section 6).
REFERENCES
Agrawal, A., Karsai, G., Neema, S., Shi, F., and Vizhanyo,
A. (2006). The design of a language for model trans-
formations. Software and Systems Modeling, 5:261–
288.
Anjorin, A., Lauder, M., Patzina, S., and Sch
¨
urr, A. (2011).
eMoflon: Leveraging EMF and Professional CASE
Tools. In INFORMATIK 2011, volume 192 of Lecture
Notes in Informatics, page 281, Bonn. Gesellschaft f
¨
ur
Informatik, Gesellschaft f
¨
ur Informatik. extended ab-
stract.
Arendt, T., Biermann, E., Jurack, S., Krause, C., and
Taentzer, G. (2010). Henshin: Advanced concepts
and tools for in-place EMF model transformations. In
Petriu, D. C., Rouquette, N., and Haugen, Ø., editors,
Proceedings 13th International Conference on Model
Driven Engineering Languages and Systems (MOD-
ELS 2010), Part I, volume 6394 of Lecture Notes
in Computer Science, pages 121–135, Oslo, Norway.
Springer.
Buchmann, T., Westfechtel, B., and Winetzhammer, S.
(2011). ModGraph — A Transformation Engine
for EMF Model Transformations. In Proceedings
of the 6th International Conference on Software and
Data Technologies (ICSOFT 2011), pages 212 – 219,
Sevilla, Spain.
Czarnecki, K. and Helsen, S. (2006). Feature-based sur-
vey of model transformation approaches. IBM Sys-
tems Journal, 45(3):621–646.
D
¨
ummel, N. (2013). Refactoring mit Graphtransforma-
tionsregeln. Bachelor thesis, University of Bayreuth,
Bayreuth, Germany.
Eclipse Foundation (2013). Xcore.
http://wiki.eclipse.org/Xcore.
Efftinge, S., Eysholdt, M., K
¨
ohnlein, J., Zarnekow, S., Has-
selbring, W., von Massow, R., and Hanus, M. (2012).
Xbase: Implementing domain-specific languages for
java. In GPCE ’12 Proceedings of the 11th Inter-
national Conference on Generative Programming and
Component Engineering, pages 112–121. ACM, New
York, NY, USA.
Ehrig, H., Engels, G., Kreowski, H.-J., and Rozenberg, G.,
editors (1999). Handbook on Graph Grammars and
Computing by Graph Transformation: Applications,
Languages, and Tools, volume 2. World Scientific,
Singapore.
Fowler, M. (1999). Refactoring: Improving the Design of
Existing Code. Addison-Wesley, Boston, MA, USA.
Giese, H., Hildebrandt, S., and Seibel, A. (2009). Im-
proved flexibility and scalability by interpreting story
diagrams. In Boronat, A. and Heckel, R., editors, Pro-
ceedings of the 8th International Workshop on Graph
Transformation and Visual Modeling Techniques (GT-
VMT 2009), volume 18 of Electronic Communications
of the EASST, York, UK. 12 p.
Jakumeit, E., Buchwald, S., and Kroll, M. (2010). Gr-
Gen.NET — the expressive, convenient and fast graph
rewrite system. International Journal on Software
Tools for Technology Transfer, 12:263–271.
Norbisrath, U., Z
¨
undorf, A., and Jubeh, R. (2013). Story
Driven Modeling. CreateSpace Independent Publish-
ing Platform. ISBN-10: 1483949257.
OMG (2011). Meta Object Facility (MOF) 2.0
Query/View/Transformation, v1.1. OMG.
Sch
¨
urr, A., Winter, A., and Z
¨
undorf, A. (1999). The PRO-
GRES approach: Language and environment. In
Handbook of Graph Grammars and Computing by
Graph Transformation: vol. 2: Applications, Lan-
guages, and Tools, pages 487–550. World Scientific
Publishing.
Steinberg, D., Budinsky, F., Paternostro, M., and Merks,
E. (2009). EMF Eclipse Modeling Framework. The
Eclipse Series. Addison Wesley, Boston, MA, 2nd edi-
tion.
Varr
´
o, D. and Balogh, A. (2007). The model transforma-
tion language of the VIATRA2 framework. Science of
Computer Programming, 68(3):214–234.
Winetzhammer, S. (2012). ModGraph — generating ex-
ecutable EMF models. In Margaria, T., Padberg, J.,
Taentzer, G., Krause, C., and Westfechtel, B., editors,
Proceedings of the 7th International Workshop on
Graph Based Tools, volume 54 of Electronic Commu-
nications of the EASST, pages 32–44, Bremen, Ger-
many. EASST.
Winetzhammer, S. and Westfechtel, B. (2013). ModGraph
meets Xcore: Combining rule-based and procedural
behavioral modeling for EMF. In Tichy, M., Ribeiro,
L., Margaria, T., Padberg, J., and Taentzer, G., edi-
tors, Proceedings of the 12th International Workshop
on Graph Transformation and Visual Modeling Tech-
niques (GTVMT 2013), volume 58 of Electronic Com-
munications of the EASST, page 13 p., Rome, Italy.
EASST.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
424
