
Transformation BPEL Processes to RECATNet for Analysing Web
Services Compositions
Ahmed Kheldoun
1
and Malika Ioualalen
2
1
Computer Science Department, Yahia Fares University, Medea, Algeria
2
Computer Science Department, USTHB University, Algiers, Algeria
Keywords:
RECATNet, BPEL, Conditional Rewriting Logic.
Abstract:
One of the most important advantages of Web services technology is the possibility of combining existing
services to create a new composite Web process according to the given requirements. BPEL is a promising
language which describes web service composition in form of business processes. However, BPEL is an
XML-based language and lack of a sound formal semantic, which hinders the formal analysis and verification
of business processes specified in it. In this paper, we propose an approach based RECATNet to model and
verify BPEL processes. We present some transformation rules of BPEL business processes into RECATNet.
Since RECATNets semantics may be defined in terms of the conditional rewriting logic, Maude tools may be
used for model-checking the correctness of BPEL processes. A case study is given to show the efficiency of
our approach.
1 INTRODUCTION
As a single Web service can provide limited function.
It is necessary and feasible to compose functions of-
fered by different individual services into a composite
service. Among the results, BPEL (Business Process
Execution Language) (A. Alves and al., 2007) is the
most popular one that is used to specify business pro-
cesses for service composition. Nevertheless, BPEL
still remains at the descriptive level, without provid-
ing any kind of mechanisms or tools support for veri-
fying a composite service.
Therefore, modelling and analysing BPEL busi-
ness processes with a formal tool becomes critical.
This allows designers to detect erroneous properties
or verify whether a service process does have certain
desired properties (such as reachability, liveness, and
so on). This paper presents the mapping of BPEL to
RECATNets (Barkaoui and Hicheur, 2007). RECAT-
Nets model offers mechanisms for a direct and intu-
itive support of dynamic creation/suppression of pro-
cesses at design time. These dynamic mechanisms of
RECATNets are adequate to model, in a concise way,
the most complex routing construct (flow pattern).
The remainder of this paper is organized as fol-
lows. Section 2 discusses related work. Section 3
presents the basic concepts of RECTANets. Sec-
tion 4 presents transformation rules from BPEL busi-
ness processes to RECATNet. Section 5 describes a
worked example. Section 6 defines the RECATNets
semantics in term of conditional rewriting logic. Fi-
nally, section 7 concludes the paper and outlines some
ideas for future works.
2 RELATED WORKS
The modelling of BPEL processes is addressed in sev-
eral papers. In this section, we briefly overview some
approaches that are closely related to our work.
Aalst et al.(Verbeek and van der Aalst, 2005) pro-
pose a method specially towards mapping a BPEL
process model onto WF-net in order to use the tool
Woflan (Verbeek and van der Aalst, 2000) for their
analysis. Hinz et al. (S. Hinz and Stahl, 2005) trans-
late a BPEL process into a pattern based Petri net
semantics in order to use the tool LoLA for validat-
ing their semantics. CP-nets are used in (Y. Yang and
Yu, 2006) to analyse and verify effectively the net to
investigate several behavioural properties. Howover,
most of these works lack from modularity and they
can not allow compact and concise modeling when
translating complex construct of BPEL processes.
Since RECATNets are a kind of high level alge-
braic Petri nets combining the expressive power of
425
Kheldoun A. and Ioualalen M..
Transformation BPEL Processes to RECATNet for Analysing Web Services Compositions.
DOI: 10.5220/0004728004250430
In Proceedings of the 2nd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2014), pages 425-430
ISBN: 978-989-758-007-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

abstract data types and Recursive Petri nets, we claim
that using our model based RECATNet to model the
BPEL process and its different message types is more
natural. The major advatages of the proposed modal
is (1) it can model the control flow and data flow
in BPEL process; (2) it can model communication,
concurrency and synchronisation among processes.
These two requirements must be fulffiled by a formal
model in order to analyse and verify BPEL processes.
3 RECURSIVE ECATNet REVIEW
Recursive ECATNets (abbreviated RECATNets)
(Barkaoui and Hicheur, 2007) are a kind of high
level algebraic Petri nets combining the expressive
power of abstract data types and Recursive Petri
nets (Haddad and Poitrenaud, 2007). Each place in
such a net is associated to a sort (i.e. a data type of
the underlying algebraic specification associated to
this net). The marking of a place is a multiset of
algebraic terms (without variables) of the same sort
of this place. Moreover, transitions in RECATNet
are partitioned into two types (Fig.1): elementary
and abstract transitions. Each abstract transition is
associated to a starting marking represented graph-
ically in a frame. A capacity associated to a place p
specifies the number of algebraic terms which can be
contained in this place for each element of the sort
associated to p.
(a) Elementary transition (b) Abstract transition
Figure 1: Transition types in RECATNets.
As shown in Fig.1, the places p and p
0
are respec-
tively associated to the sorts s and s
0
and to the ca-
pacity c and c
0
. An arc from an input place p to a
transitiont (elementary or abstract) is labelled by two
algebraic expressions IC(p,t) (Input Condition) and
DT (p, t) (Destroyed Tokens). The expression IC(p, t)
specifies the partial condition on the marking of the
place p for the enabling of t (see Table.1).
The expression DT (p, t) specifies the multiset of
terms to be removed from the marking of place p
when t is fired. Also, each transition t may be labelled
by a Boolean expression TC(t) which specifies an
additional enabling condition on the values taken
by contextual variables of t (i.e. local variables of
the expressions IC and DT labelling all the input
arcs of t). When the condition TC(t) is omitted, the
Table 1: Different forms of Input Condition IC(p, t).
IC(p, t) Enabling Condition
a
0
The marking of the place p must be equal
to a. (e.g. IC(p, t) = φ
0
means the
marking of p must empty)
a
+
The marking of the place p must include
a (e.g. IC(p, t) = φ
+
means condition is
always satisfied)
a
−
The marking of the place p must not
include a, with a 6= φ
α1 ∧ α2 Conditions α1 and α2 are both true
α1 ∨ α2 α1 or α2 is true
default value is the term True. For an elementary
transition t, an output arc (t, p
0
) connecting this
transition t to a place p
0
is labelled by the expression
CT (t, p
0
) (Created Tokens). However, for an abstract
transition t, an output arc (t, p
0
) is labelled by the
expression ICT (t, p
0
, i) (Indexed Created Tokens).
These two algebraic expressions specify the multiset
of terms to produce in the output place p
0
when the
transition t is fired. In the graphical representation
of RECATNets, we note the capacity of a place
regarding an element of its sort only if this number
is finite. If IC(p, t) =
de f
DT (p, t) on input arc (p, t)
(e.g. IC(p,t) = a
+
and DT (p, t) = a), the expression
DT (p, t) is omitted on this arc. In what follows, we
note Spec = (S, E) an algebraic specification of an
abstract data type associated to a RECATNet, where
Σ=(S, OP) is its multi-sort signature (S is a finite set
of sort symbols and OP is a finite set operations, such
OP
T
S = φ). E is the set of equations associated
to Spec. X = (X
s
)
s∈S
is a set of disjoint variables
associated to Spec where OP
T
X = φ and X
s
is
the set of variables of sort s. We denote by T
Σ,s
(X)
the set of S-sorted S-terms with variables in the set
X.[T
Σ
(X)]
⊕
denotes the set of the multisets of the
Σ-terms T
Σ
(X) where the multiset union operator (⊕)
is associative, commutative and admits the empty
multiset φ as the identity element. For a transition t,
X(t) denotes the set of the variables of the context
of this transition and Assign(t) denotes the set of
all the possible affectations of this variables set,
i.e.Assign(t) = {sub : X(t) → T
Σ
(φ) | x
i
∈ X(t) of sort
s, sub(x
i
) ∈ T
Σ,s
(φ)}.
Definition 1. A recursive ECAT-
Net is a tuple: RECATNet =
(Spec, P, T, sort,Cap, IC, DT,CT, TC, I, ϒ, ICT )
where:
• Spec = (Σ, E) is a many sorted algebra where the
sorts domains are finite (with Σ = (S, OP) ), and
X = (X
s
)
s∈S
is a set of S-sorted variables
• P is a finite set of places.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
426
• T = T
elt
S
T
abs
is finite set of transitions (T
T
P =
φ) partitioned into abstract and elementary ones.
T
abs
and T
elt
denoted the set of abstract and ele-
mentary transitions.
• sort: P → S, is a mapping called a sort assign-
ment.
• Cap: is a P-vector on capacity places: p∈P,
Cap(p): T
Σ
(φ) → N
S
{∞},
• IC : PxT → [T
Σ
(X)]
∗
⊕
where [T
Σ
(X)]
∗
⊕
=
{α
+
}
S
{α
−
}
S
{α
0
}, such that α ∈
[T
Σ,sort(p)
(X)]
⊕
• DT : PxT → [T
Σ
(X)]
⊕
, such that DT (p,t) ∈
[T
Σ,sort(p)
(X)]
⊕
,
• CT : PxT → [T
Σ
(X)]
⊕
, such that DT(p,t) ∈
[T
Σ,sort(p)
(X)]
⊕
,
• TC : T → [T
Σ,bool
(X)],
• I is a finite set of indices, called termination in-
dices,
• ϒ is a family, indexed by I, of effective representa-
tion of semi-linear sets of final markings,
• ICT : PxT
abs
xI → [T
Σ
(X)]
⊕
, where ICT (p, t, i) ∈
[T
Σ,sort(p)
(X)]
⊕
.
Informally, a RECATNet generates during its ex-
ecution a dynamical tree of marked threads called
an extended marking, which reflects the global state
of such net. This latter denotes the fatherhood
relation between the generated threads (describing
the inter-threads calls). Each of these threads has
its own execution context. (Barkaoui and Hicheur,
2007) presents more details about RECATNet such
firing transitions and generating extended reachabil-
ity graph.
4 TRANSFORMATION OF BPEL
TO RECATNet
The aim of this section is to provide translations from
BPEL business processes to RECATNet. We present
the semantic representation of BPEL basic and struc-
tured activities by RECATNet. The basic idea behind
using RECATNets is to allow modeler to construct
a large model by using a number of small RECAT-
Nets which are related to each other in a well-defined
way. The idea behind abstract transition is to allow
user to relate a transition to a more complex RECAT-
Net called a subactivity. This subactivity gives more
detailes descritpion of the activity represented by the
abstract transition.
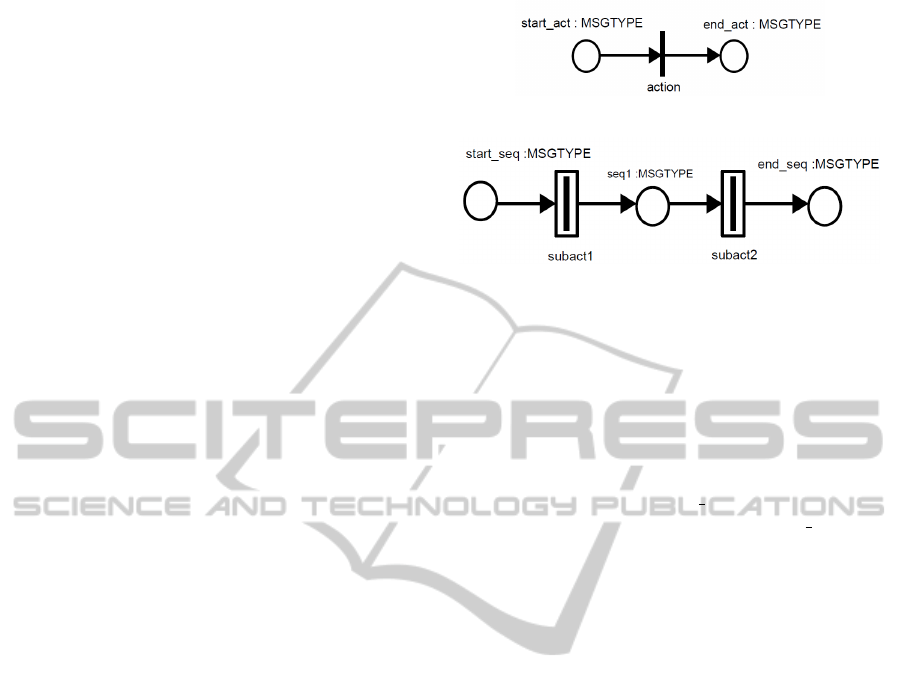
Figure 2: RECATNet construct of basic activities.
Figure 3: RECATNet construct of Sequence activity.
4.1 Basic Activities Transformation
Basic activities are those which describe atomic
steps of a process behaviour like Receive, Invoke,
Reply,...etc.
Due to the abstraction from data and message ex-
changes, all basic activities share the general model
shown in Fig.2. Place start act models when the
basic activity is ready to start. Place end act indi-
cates that the activity has finished its execution. The
transition labelled action models the action to be per-
formed.
4.2 Structured Activities
Transformation
In order to enable the presentation of complex struc-
tures in BPEL, the following structured activities are
translated: sequence, for defining an execution order;
switch, for choice routing; while, for looping; and
f low for parallel routing.
4.2.1 Sequence Structure
The sequence construct of BPEL contains one or
more activities that are performed sequentially. The
RECATNet construct of sequence structure is shown
in Fig.3.
Note that each subactivity is modelled by an ab-
stract transition. In fact, firing an abstract transition
means that the associate subactivity is invoked. This
allows our model be hierarchical and modular and is
very clear to understand.
4.2.2 Switch Structure
The switch construct of BPEL supports conditional
behaviour. Its RECATNet construct is shown in Fig.4.
Note that all the abstract transitions modelled sub-
activities are in conflict. The first abstract transition
TransformationBPELProcessestoRECATNetforAnalysingWebServicesCompositions
427

Figure 4: RECATNet construct of Switch activity.
Figure 5: RECATNet construct of While activity.
whose condition holds true is taken and provides the
activity performed for the switch. The switch activ-
ity is complete when the subactivity of the enabled
abstract transition completes.
4.2.3 While Structure
The while construct of BPEL supports repeated per-
formance of a specified iterative activity. Its RECAT-
Net construct is shown in Fig.5. The transition exit
and continue represents empty activities. The abstract
transition labelled subact models the subactivity to be
performed iteratively.
4.2.4 Flow Structure
The flow construct of BPEL allows to specify one or
more activities to be performed concurrently. A flow
completes when all of the activities in the flow have
completed. The RECATNet construct of flow struc-
ture is shown in Fig.6. Note that the activity mod-
elled by the abstract transition labelled subact3 can-
not perform before the activity subact2 completes due
to control link between them.
5 CASE STUDY
The following example shows how the structure of a
BPEL process model is mapped onto a RECATNet.
The example is taken from (A. Alves and al., 2007).
In the following example, five basic activities are
defined: getBuyerIn f o, getSellerIn f o, settleTrade,
con f irmBuyer and con f irmSeller.
Figure 6: RECATNet construct of Flow activity.
Figure 7: RECATNet construct of the example.
The activities getBuyerIn f o and getSellerIn f o
can run concurrently. The settleTrade activity is
not performed before both these activities are com-
pleted. After settleTrade completes, the two activi-
ties con f irmBuyer and con f irmSeller are performed
concurrently again.
The RECATNet model for this example is shown
in Fig.7.
Fig.8 shows a set of simplified RECATNet con-
structs model the above five activities.
Since our model is modular and hierarchical, it
simplifies for designers to add/remove activities in a
flexible way.
Figure 8: RECATNet construct of basic activities of the ex-
ample.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
428

6 ANALYSIS METHOD
In order to analyse the soundness and compositional-
ity of services in BPEL, we propose to express the
semantic of RECATNet in terms of rewriting logic
(Bruni and Meseguer, 2006), the input of model-
checker MAUDE.
6.1 RECATNet Semantics in Terms of
Rewriting Logic
Since we choose to express the RECATNet seman-
tics in terms of rewriting logic, we define each RE-
CATNet as a conditional theory, where transitions
firing and cut step execution are formally expressed
by labelled rewrites rules. Each extended mark-
ing Tr is expressed, in a recursive way, as a term
[MT h, tabs, T hreadChilds], where MT h represents
the internal marking of T h, tabs represents the name
of the abstract transition whose firing (in its thread
father) gave birth to the thread T h. Note that the
root thread is not generated by any abstract transi-
tion, so the abstract transition which gave birth to it
is represented by the constant nullTrans. The term
T hreadChilds represents a finite multiset of threads
generated by the firing of abstract transitions in the
thread T h. We denote by the constant nullT hread,
the empty thread.
Consequently, an extended marking
Tr is expressed as a general term of sort
T hread with the following recursive form:
[MT h
0
, nullTrans, [MT h
1
,tabs
1
, [MT h
11
,tabs
11
, ...]
...[MT h
1n
,tabs
1n
, ...]]...[MT h
n
,tabs
n
, [MT h
n1
,tabs
n1
, ...]...[MT h
nn
,tabs
nn
, ...]]] where MT h
0
is the mark-
ing of the root thread. In fact, the state space of
RECATNet is formalized by the following equational
theories.
fmod PLACE-MARKING is
sorts Place Multiset Place-marking.
op ems : -> Multiset .
----- The constant implementing the empty
˜marking ems
op _(+)_ : Multiset Multiset -> Multiset
˜[assoc comm id: ems].
op <_;_>: Place Multiset-> Place-marking.
endfm
fmod MARKING is
including PLACE-MARKING .
sort Marking .
subsort Place-marking < Marking .
op em : -> Marking .
----- The constant implementing the empty
marking em
op _(*)_ : Marking Marking -> Marking
[assoc comm id: em] .
endfm
fmod THREAD is
including MARKING .
sorts Thread Trans TransAbs.
subsort TransAbs < Trans.
op nullTrans : -> TransAbs.
op nullThread : -> Thread.
op [_,_,_]:Marking TransAbs Thread->Thread.
op _ _ : Thread Thread -> Thread
[assoc comm id: nullThread] .
endfm
Each firing step in a RECATNet is expressed by a
rewrite rule of the form T h => T h
0
i f C which means
that a fragment of the RECATNet state fitting pattern
T h can change to a new local state fitting pattern T h
0
if the condition C holds. We give the general form of
the rewrite rules describing the behaviour of RECAT-
Nets firing steps:
---Elementary rules
crl[telt] : <p, mp (+) DT(p, telt)> (*)
<p’, mp’> => <p, mp> (*)
<p’, mp’(+)CT(p’,telt)> if (InputCond
and TC(telt) and
Nbr(mp’(+)CT(p’,telt) < Cap(p’))) .
---Abstract rules
crl[tabs] : [M (*)<p, mp (+) DT(p, tabs)>,
T, Th] => [M (*)<p, mp> , T, Th
[<p’’, CT(p’’,tabs) >, tabs, nullThread]]
if (InputCond and TC(tabs)) .
---A cut step occuring in a Thread
crl[cut] : <Mf (*) <p’, mp’> , T,
mThf [M (*)<pfinal, mpfinal>, tabs, mTh]>
=> [Mf (*)<p’, mp’ (+) ICT(p’, tabs, i),
T, mThf>]
if ( ϒ i and Nbr(mp’(+)
ICT(p’,tabs,i) < Cap(p’)) .
For instance, if we consider the RECATNet of Fig.7,
the rewrite rule describing the elementary transition
labelled t1 is given as follows:
rl[t1] : < start-bpel; token> (*) M =>
[ M (*)<p1 ; token>(*) <p2 ;token>(*)
<p3 ; token>(*)<p4 ; token>(*)<p5 ; token>.
Another example, the rewrite rule describing the ab-
stract transition labelled getBuyerIn f o is given as fol-
lows:
rl[getBuyerInfo]: [ M(*) < p1; token >, T,
Th] => [ M, T, Th [<start-GBI; token>,
geBuyerInfo, nullThread ]].
TransformationBPELProcessestoRECATNetforAnalysingWebServicesCompositions
429

Figure 9: Execution of the example under Maude environ-
ment.
Figure 10: Checking the proper termination property using
MAUDE LTL model-checker.
6.2 Implementation using the Maude
System
In the framework of this work, we use as platform,
the version 2.6 of the Maude system under Win-
dows. One of the main commands of Maude system
is rewrite. This command rewrites a given expression
until no more rules can be applied. An execution for
the example is shown in Fig.9.
An important property will be checked called proper
termination. This property means that starting from
an initial state, every possible execution path prop-
erly terminates (evetually). This property is expressed
in LTL (Linear Temporal Logic) by the formula :
F finalState where f inalState is a proposition repre-
sents the set of final states of the modelled system.
The temporal oerator F (Futur) is denoted by <> in
MAUDE notation. In Fig.10, we check the validity of
this property by applying the LTL model-checker of
MAUDE.
7 CONCLUSIONS
In this paper, we present an approach to formalize and
analyse BPEL processes based on RECATNet. We
present the transformation rules from BPEL business
processes to RECATNet. In order to analyse the result
model, we define the RECATNets semantics in term
of conditional rewriting logic the input of the model-
checker Maude (Clavel and al., 2007).
For further research, we will provide more trans-
lation rules from BPEL to RECATNet such as scopes,
fault handlers and possibly correlations. Also, we
plan to finish our tool under construction in order to
automate the translation from BPEL to RECATNet.
REFERENCES
A. Alves, A. Arkin, S. A. and al. (April 2007). Web ser-
vices business process execution language. In TEM-
PLATE’06, 1st International Conference on Template
Production. Version 2.0.
Barkaoui, K. and Hicheur, A. (2007). Towards analysis
of flexible and collaborative workflow using recursive
ecatnets. In pp.206-217, LNCS 4928 (26-28 2007).
Springer Berlin/Heidelberg, Benatallah, B., ter Hofst-
ede, A., Paik, H. In CBP 2007.
Bruni, R. and Meseguer, J. (2006). Semantic foundations
for generalized rewrite theories. In Theor. Comput.
Sci. 360(1), pp.386-414.
Clavel, M. and al. (2007). Maude manual (ver-
sion 2.3). In SRI International and Univer-
sity of Illinois at Urbana-Champaign. Available at
http://maude.cs.uiuc.edu.
Haddad, S. and Poitrenaud, D. (December 2007). Recur-
sive petri nets. theory and application to discrete event
systems. In Acta Informatica. pp.44-78.
S. Hinz, K. S. and Stahl, C. (Sep 6-9 2005). Transforming
bpel to petri nets. In 3rd International Conference on
Business Process Management (BPM’05). pages 220-
235, Nancy, France, Springer-Verlag.
Verbeek, H. M. W. and van der Aalst, W. M. P. (2000).
Woflan 2.0: A petri-net-based workflow diagnosis
tool. In 21st International Conference of Application
and Theory of Petri Nets (ICATPN 2000). pages 475-
484.
Verbeek, H. M. W. and van der Aalst, W. M. P. (2005). An-
alyzing bpel processes using petri nets. In 2nd In-
ternational Workshop on Applications of Petri Nets
to Coordination,Workflow and Business Process Man-
agement. pages 59-78.
Y. Yang, Q. Tan, Y. X. F. L. and Yu, J. (2006). Transform
bpel workflow into hierarchical cp-nets to make tool
support for verification. In 8th Asia-Pacific Web Con-
ference. pages 275-284.
MODELSWARD2014-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
430
